7.2 Answers

1. Short answers:
   1. Since \(x\) is defined over a continuous region, \(X\) is a continuous rv.
   2. The cdf is found: \[ F_Y(y) = \int_{-\infty}^x \lambda \exp(-\lambda t)\,dt = \Big| -\exp(-\lambda t)\Big|_{0}^x = -\exp(-\lambda x) + 1 \] since \(\lambda > 0\). That is, the cdf is \(F_Y(y) = 1 - \exp(-\lambda x)\) for \(x > 0\), and \(F_Y(y) = 0\) for \(x \le 0\). See Fig. 7.1.
   3. There are two ways: \(\int_3^\infty \exp(-x)\,dx\) (using the pdf), or \(1 - F_Y(3)\) using the cdf. Either way, \(\Pr(X > 3) = \exp(-3) \approx 0.0498\).
   4. By definition, \(\displaystyle E[X] = \int_0^\infty x \lambda \exp(-\lambda x)\, dx\), which requires integration by parts; then \(E[X] = 1/\lambda\).
      Also by definition, \(\displaystyle E[X^2] = \int_0^\infty x^2 \lambda \exp(-\lambda x)\, dx\), which requires integration by parts twice; then \(E[X] = 2/\lambda^2\). So \(\text{var}[X] = E[X^2] - E[X]^2 = 1/\lambda^2\).

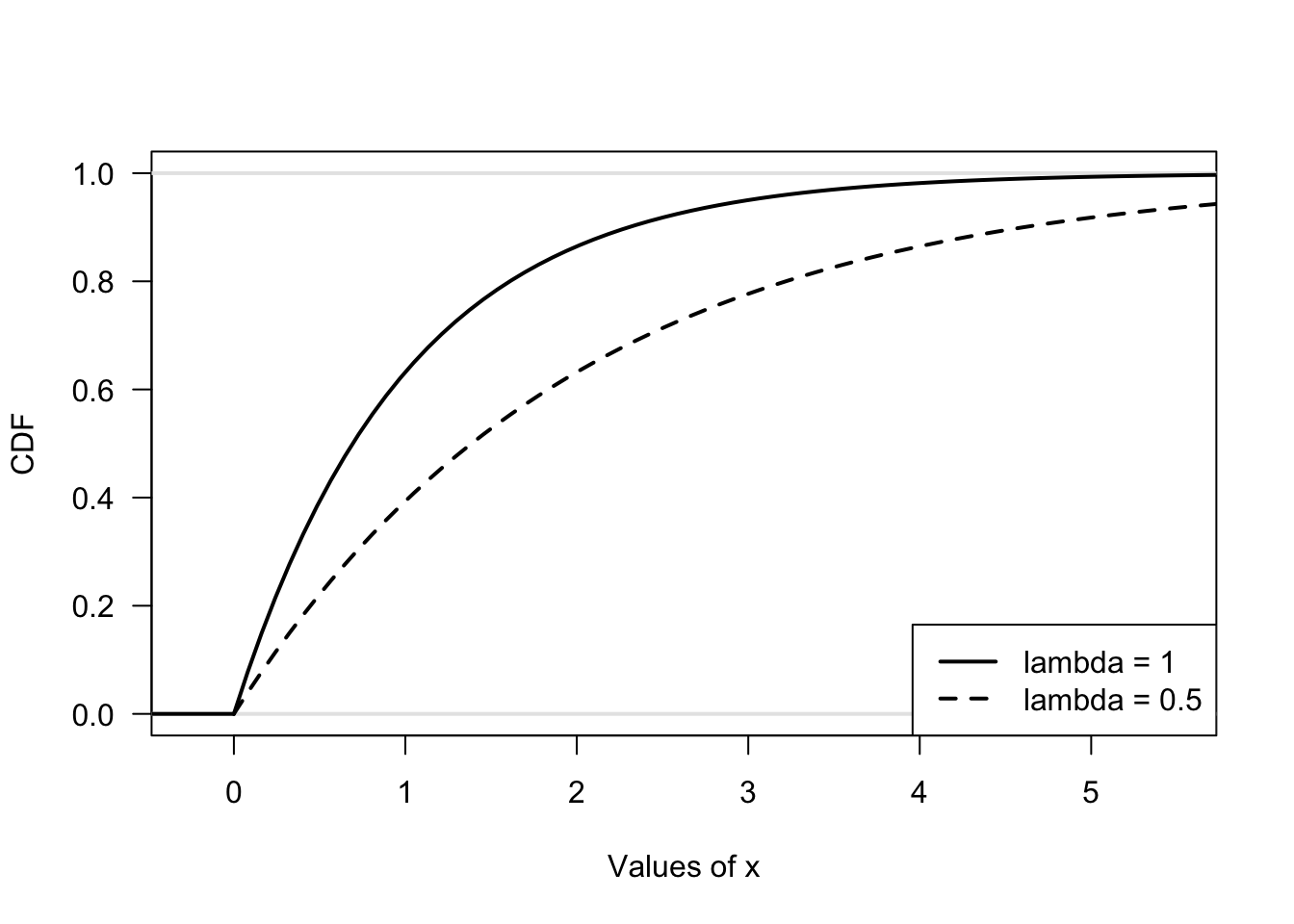
FIGURE 7.1: The CDF for Exercise 1

2. Short answers:
   1. Since \(w\) is defined over a discrete region, \(W\) is a discrete rv.
   2. To be a pmf, all probabilities must be non-negative (that is, \(f_W(w) \ge 0\) for all \(w\), which is true), and \(\sum_S f_W(w) = 1\).
      For the second condition, use a result from the sum of a geometric series, that \(\sum_0^\infty a r^k = a/(1 - r)\), where here \(a = 0.6\) and \(r = 0.4\).
   3. The cdf is: \[ F_W(w) = \left\{ \begin{array}{ll} 0 & \text{for $W < 1$}\\ 0.6 & \text{for $1 \le W < 2$} \\ 0.6 + (0.6 \times 0.4) & \text{for $2 \le W < 3$}\\ 0.6 + (0.6 \times 0.4) + (0.6 \times 0.4^2) & \text{for $3 \le W < 4$}\\ \end{array} \right. \] and a pattern can be seen to be developing. See Fig. 7.2.
   4. Here \(\Pr(W > 2) = 1 - \Pr(W = 1) - Pr(W = 2)\), so \(\Pr(W > 2) = 1 - 0.6 - (0.6\times 0.4) = 0.16\),
   5. You will need to use some results about sums of infinite series.

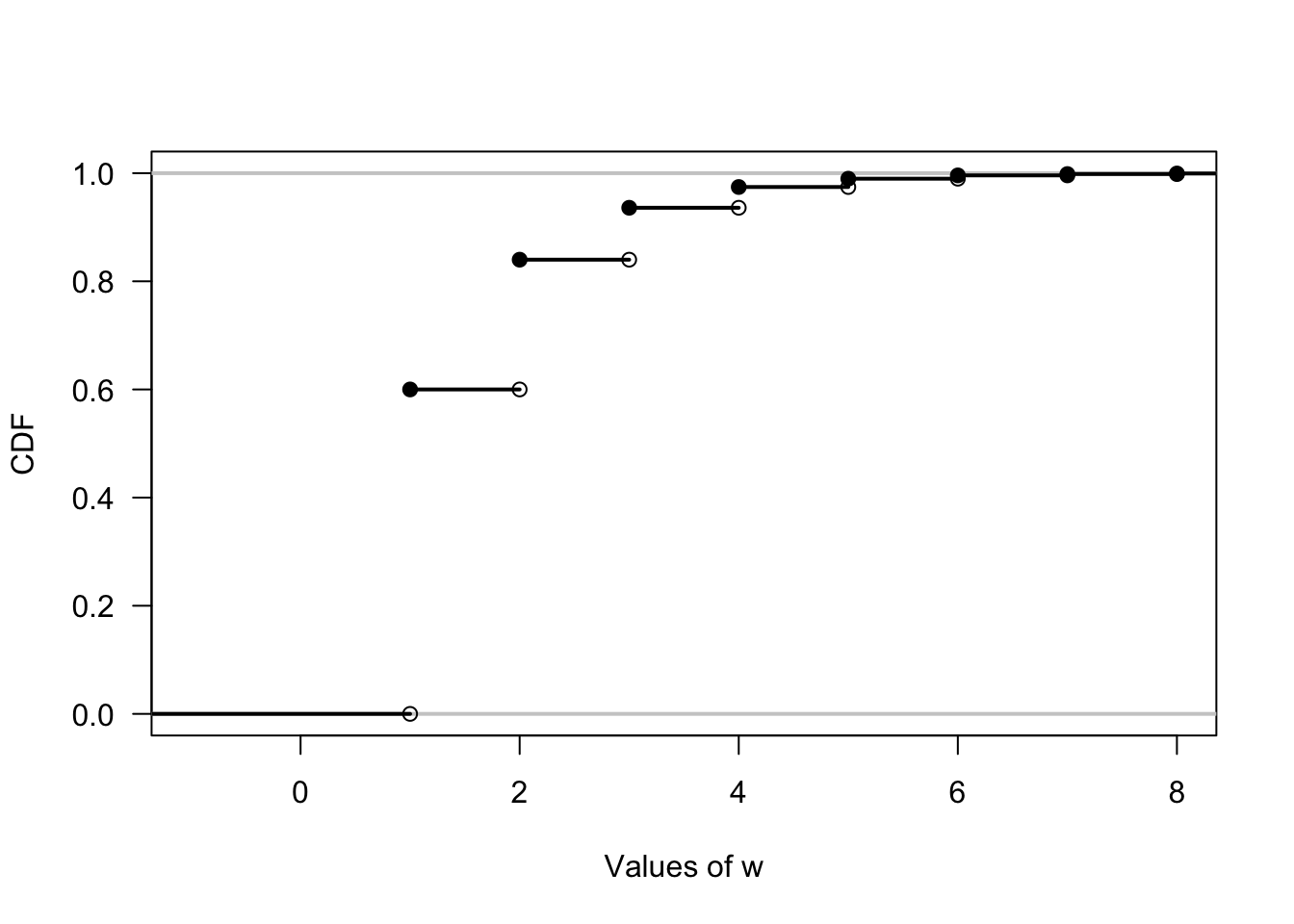
FIGURE 7.2: The CDF for Exercise 2

3. Short solutions (and see Exercise 1):
   1. We need \(\int_W f_X(x)\, dx = 1\), so \(\int_0^\infty k\exp(-x/4)\,dx = 1\). Solving, \(k = 1/4\).
   2. The cdf is \(F_X(x) = 1 - \exp(-x/4)\).
      See Fig. 7.3.
   3. \(\Pr<X \le 2) = F_X(2) = 1 - \exp(-2/4) \approx 0.393\).
   4. \(\Pr(2 < X < 4) = F_X(4) - F(X(2) \approx 0.239\).

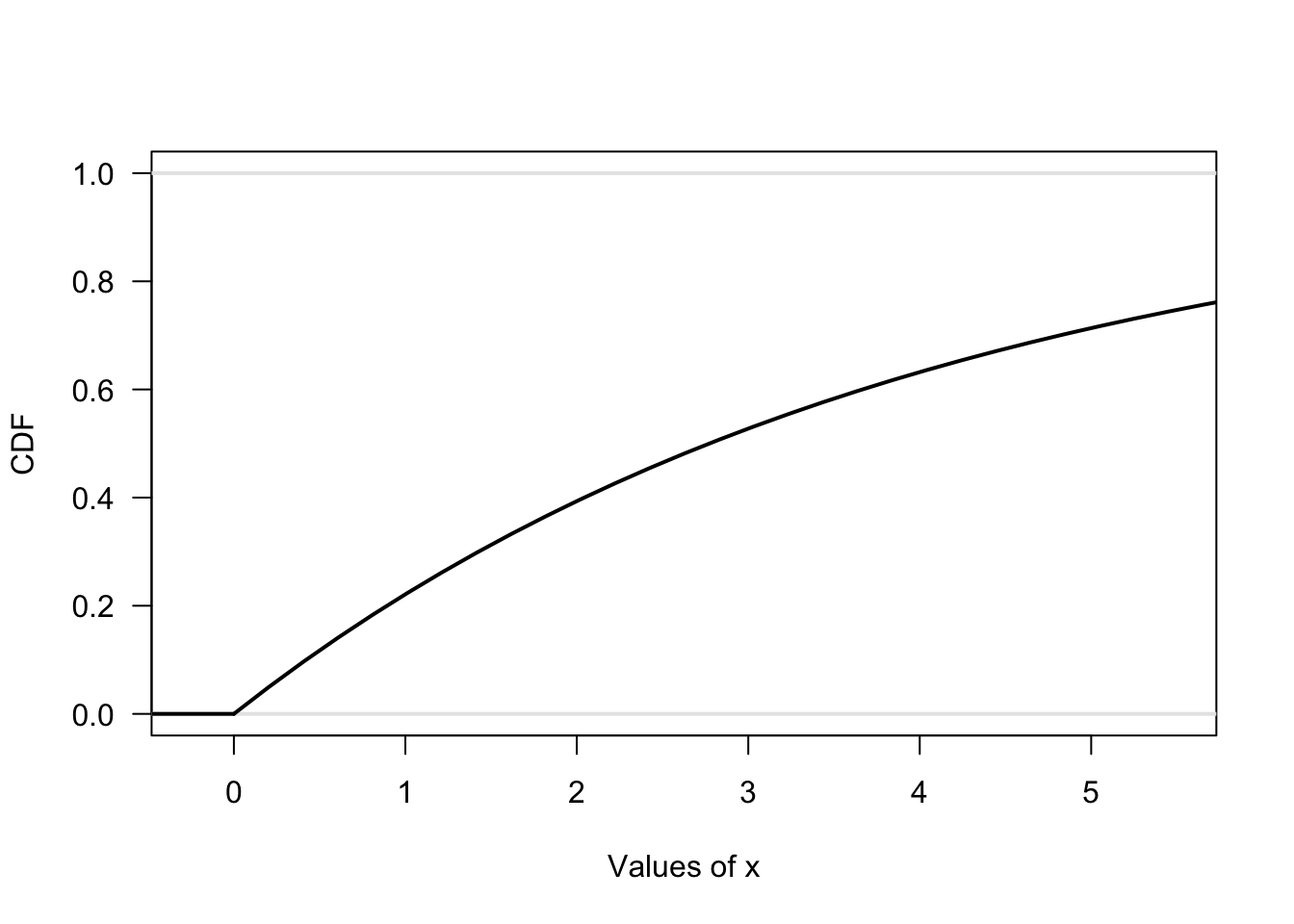
FIGURE 7.3: The CDF for Exercise 1

4. First we need to find the value of \(k\), by solving \[ 1 = k \int_0^2 \!\!\! \int_0^1 3x^2 + xy\, dx\, dy, \] showing that \(k = 1/3\).
   Then the marginal distribution for \(x\) is: \[ f_X(x) = \frac{1}{3}\int_0^2 3x^2 + xy\, dy = 2x^2 + \frac{2x}{3} \] for \(0 < x < 1\).
   Also, the marginal distribution for \(y\) is: \[ f_Y(y) = \frac{1}{3}\int_0^1 3x^2 + xy\, dx = \frac{y + 2}{6} \] for \(0 < y < 2\).

5. This question has an irregular sample space, so care is needed!

   1. See Fig. 7.4.
   2. We need to solve \[ 1 = k \int_{z=0}^{z=1}\!\!\int_{y=0}^{y = z} y + z\, dy\, dz, \] when we find that \(k = 2\).

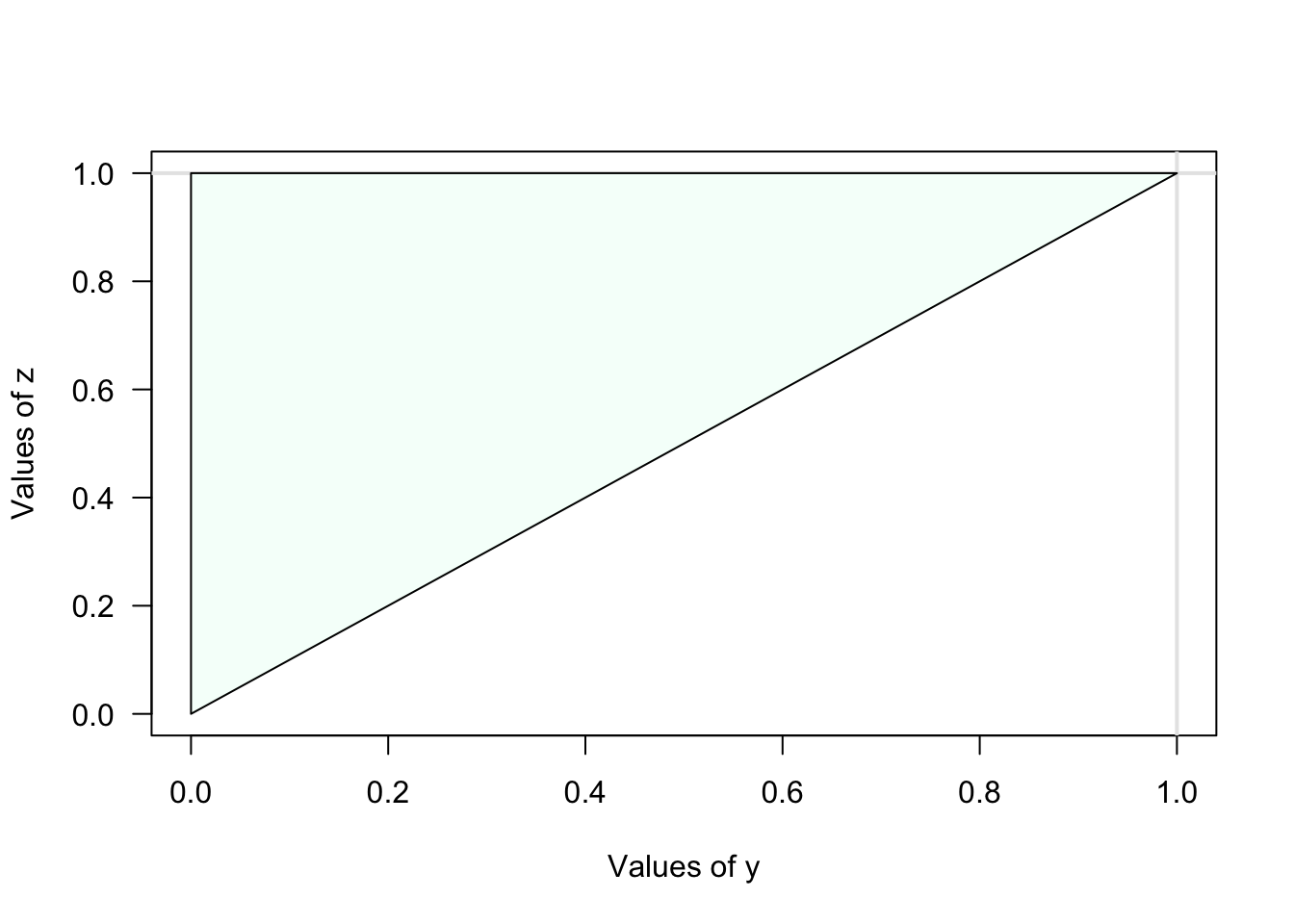
FIGURE 7.4: The sample space for Exercise 5

6. Proceed: \[\begin{align*} \text{Var}[ \bar{X} ] &= \text{Var}[ (X_1 + X_2 + \cdots + X_n)/n]\\ &= \frac{1}{n^2} \text{Var}[ X_1 + X_2 + \cdots + X_n ]\qquad \text{(since $\text{Var}[cX] = c^2\text{Var}[X]$))}\\ &= \frac{1}{n^2} \left( \text{Var}[ X_1] + \text{Var}[X_2] + \cdots + \text{Var}[X_n] \right)\\ &= \frac{1}{n^2} (n \times \sigma^2)\qquad \text{(since $\text{Var}(X) = \sigma^2$ for all $X$)}\\ &= \frac{\sigma^2}{n}. \end{align*}\]

---

Copyright © Peter K. Dunn, 2021