4.4 The Asymmetric Adjacency Matrix

Conversely, a directed graph describing a network of asymmetric or anti-symmetric ties will create an asymmetric matrix. An asymmetric graph means that the values contained in the matrix do not mirror each other. In other words, an asymmetric graph means that the cell values are not necessarily the same (the relationship is not necessarily equivalent) between two of the cases.

Figure 3.2 shows the previous example of an directed graph.The corresponding asymmetric adjacency matrix is the following:

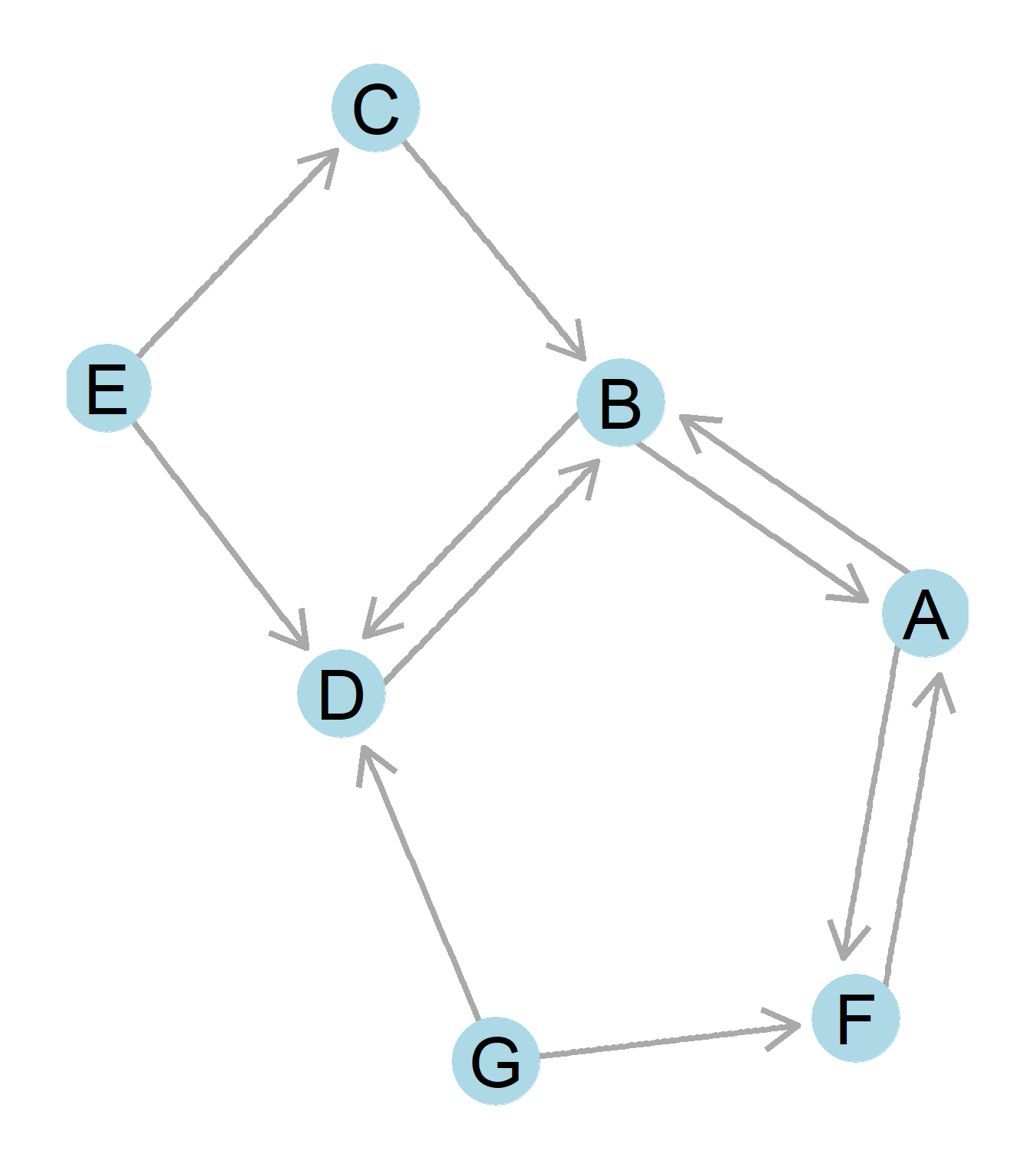Figure 3.2: A directed graph.

\[\begin{array}{ccccccccc} & A & B & C & D & E & F & G \\ A & - & 1 & 0 & 0 & 0 & 1 & 0 \\ B & 1 & - & 0 & 1 & 0 & 0 & 0 \\ C & 0 & 1 & - & 0 & 0 & 0 & 0 \\ D & 0 & 1 & 0 & - & 0 & 0 & 0 \\ E & 0 & 0 & 1 & 1 & - & 0 & 0 \\ F & 1 & 0 & 0 & 0 & 0 & - & 0 \\ G & 0 & 0 & 0 & 1 & 0 & 1 & - \\ \end{array} \]

Note that while some relationships (such as between node A and B) are reciprocated, not all connections in the network are reciprocated. Node G sends ties to D and F, but does not receive any ties back. In the resulting matrix, A to B and B to A each have a 1 listed for the value, while G to D and G to F also have a value of 1. However, the cells corresponding to F to G and D to G each have a value of 0 because the ties are unreciprocated. These unreciprocated ties make the resulting matrix asymmetric. The two halves across the diagonal are no longer mirror images, but contain different entries.

Why are the ties are not reciprocated? You might remember this was discussed in Chapter 3, but it is because of the type of data that the graph and matrix are representing. For example, the matrix and graph in Figure 3.2 could represent a intramural basketball club where they ask everyone in the club who they like to have as a teammate. Not everyone could agree that they like to have one another as teammates, and the matrix and graph in Figure 3.2 would represent that. In this case, a node like G and E look really lonely since they have nobody who wants to play with them. However, if the tie were to be about advice, such that actually G gives advice to D and F, but does not take their advice back, G (and E) now look like respected figures in the network.