Skip to main content

Geostatystyka w R

10 Estymacje wielozmienne

Odtworzenie obliczeń z tego rozdziału wymaga załączenia poniższych pakietów oraz wczytania poniższych danych:

10.1 Kokriging

10.1.1 Kokriging (ang. co-kriging)

Kokriging pozwala na wykorzystanie dodatkowej zmiennej (ang. auxiliary variable), zwanej inaczej kozmienną (ang. co-variable), która może być użyta do prognozowania wartości badanej zmiennej w nieopróbowanej lokalizacji. Zmienna dodatkowa może być pomierzona w tych samych miejscach, gdzie badana zmienna, jak też w innych niż badana zmienna. Możliwa jest też sytuacja, gdy zmienna dodatkowa jest pomierzona w dwóch powyższych przypadkach. Kokriging wymaga, aby obie zmienne były istotnie ze sobą skorelowane. Najczęściej kokriging jest stosowany w sytuacji, gdy zmienna dodatkowa jest łatwiejsza (tańsza) do pomierzenia niż zmienna główna. W efekcie, uzyskany zbiór danych zawiera informacje o badanej zmiennej oraz gęściej opróbowane informacje o zmiennej dodatkowej. Jeżeli informacje o zmiennej dodatkowej są znane dla całego obszaru wówczas bardziej odpowiednią techniką będzie kriging z zewnętrznym trendem (KED).

10.1.2 Wybór dodatkowej zmiennej

Wybór zmiennej dodatkowej może opierać się na dwóch kryteriach:

  • Teoretycznym
  • Empirycznym

10.2 Krossemiwariogramy

10.2.1 Krossemiwariogramy (ang. crossvariogram)

Metoda kokrigingu opiera się nie o semiwariogram, lecz o krossemiwariogramy. Krossemiwariogram jest to wariancja różnicy pomiędzy dwiema zmiennymi w dwóch lokalizacjach. Wyliczając krossemiwariogram otrzymujemy empiryczne semiwariogramy dla dwóch badanych zmiennych oraz krosswariogram dla kombinacji dwóch zmiennych.

W poniższym przykładzie istnieją dwie zmienne, savi ze zbioru punkty pomierzona w 242 lokalizacjach oraz ndvi ze zbioru punkty_ndvi pomierzona w 992 punktach (ryciny 10.1 i 10.1).

tm_shape(punkty) +
        tm_symbols(col = "savi")
Mapa wartości zmiennej savi.

Rycina 10.1: Mapa wartości zmiennej savi. 

tm_shape(punkty_ndvi) +
        tm_symbols(col = "ndvi")
Mapa wartości zmiennej ndvi.

Rycina 10.2: Mapa wartości zmiennej ndvi.

Tworzenie krossemiwariogramów odbywa się z użyciem funkcji gstat(). Na początku definiujemy pierwszy obiekt g. Składa się on z obiektu pustego (NULL), nazwy pierwszej zmiennej (nazwa może być dowolna), wzoru (w przykładzie savi ~ 1), oraz pierwszego zbioru punktowego. Następnie do pierwszego obiektu g dodajemy nowe informacje również poprzez funkcję gstat(). Jest to nazwa obiektu (g), nazwa drugiej zmiennej, wzór, oraz drugi zbiór punktowy.

g = gstat(NULL, 
          id = "SAVI", 
          form = savi ~ 1, 
          data = punkty)
g = gstat(g, 
          id = "NDVI", 
          form = ndvi ~ 1, 
          data = punkty_ndvi)
g
## data:
## SAVI : formula = savi`~`1 ; data dim = 242 x 5
## NDVI : formula = ndvi`~`1 ; data dim = 992 x 1

Z uzyskanego w ten sposób obiektu tworzymy krossemiwariogram (funkcja variogram()), a następnie go wizualizujemy używając funkcji plot() (rycina 10.3).

v = variogram(g)
plot(v)
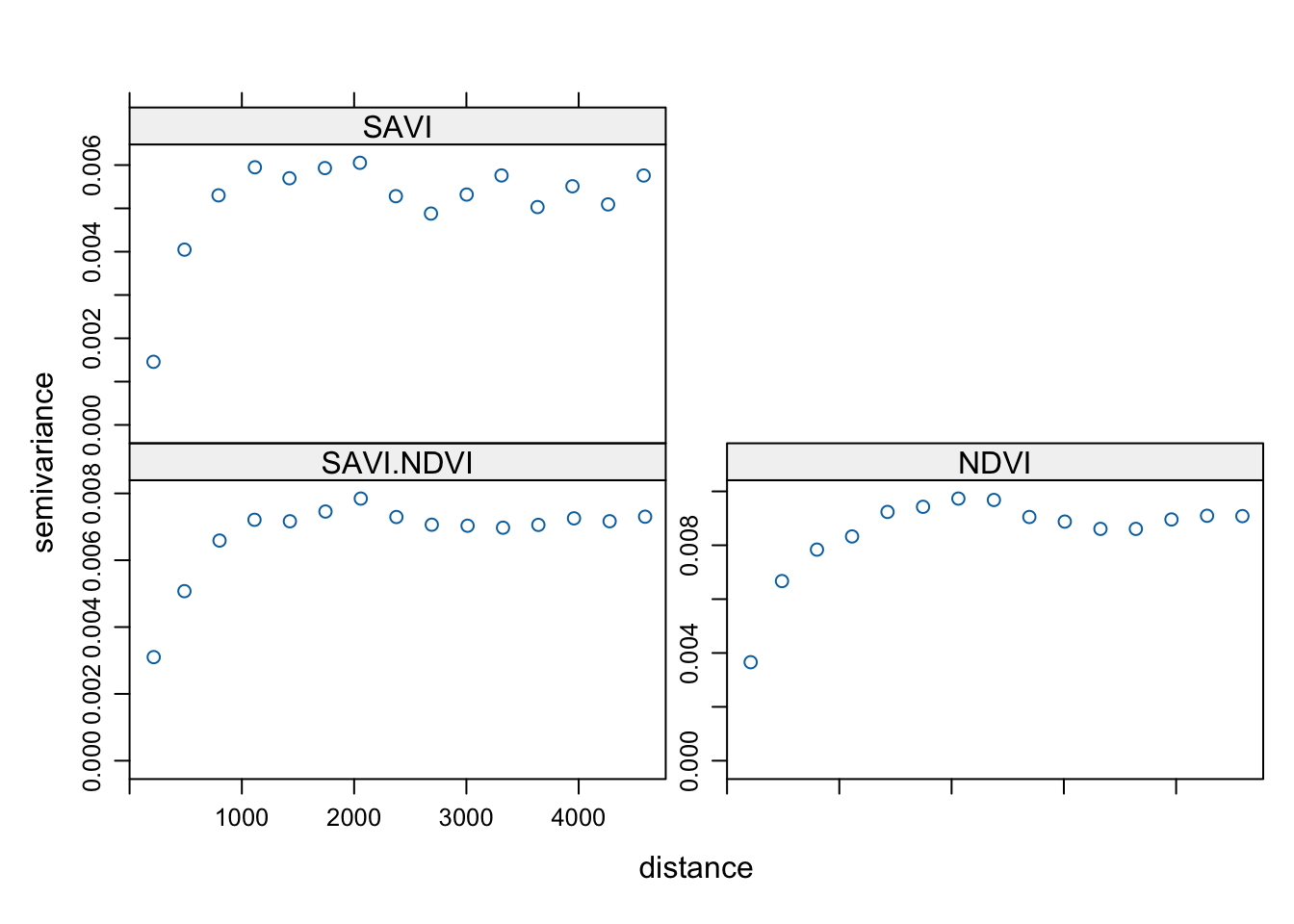
Krossemiwariogram zmiennych savi i ndvi.

Rycina 10.3: Krossemiwariogram zmiennych savi i ndvi.

10.3 Modelowanie krossemiwariogramów

Modelowanie krossemiwariogramów, podobnie jak ich tworzenie, odbywa się używając funkcji gstat(), gdzie podaje się wcześniejszy obiekt g, model, oraz argument fill.all = TRUE. Ten ostatni parametr powoduje, że model dodawany jest do wszystkich elementów krossemiwariogramu.

g_model = vgm(0.006, model = "Sph",
              range = 1200, nugget = 0.001)
g1 = gstat(g, model = g_model, fill.all = TRUE)
g1
## data:
## SAVI : formula = savi`~`1 ; data dim = 242 x 5
## NDVI : formula = ndvi`~`1 ; data dim = 992 x 1
## variograms:
##              model psill range
## SAVI[1]        Nug 0.001     0
## SAVI[2]        Sph 0.006  1200
## NDVI[1]        Nug 0.001     0
## NDVI[2]        Sph 0.006  1200
## SAVI.NDVI[1]   Nug 0.001     0
## SAVI.NDVI[2]   Sph 0.006  1200

W przypadku semiwariogramów funkcja fit.variogram() służyła dopasowaniu parametrów modelu do semiwariogramu empirycznego. Podobną rolę w krossemiwariogramach spełnia funkcja fit.lmc() - dopasowuje ona liniowy model koregionalizacji do semiwariogramów wielozmienych (rycina 10.4). Funkcja fit.lmc() oczekuje co najmniej dwóch elementów, krossemiwariogramu oraz modelów krossemiwariancji. W poniższym przykładzie dodatkowo użyto parametru correct.diagonal = 1.01, z uwagi na to że analizowane zmienne wykazywały bardzo silną korelację oraz parametru fit.method. Ten ostatni parametr określa, która z użytych metod automatycznego dopasowania semiwariogramów jest używana. Pakiet gstat ma domyślnie ustawione fit.method = 7, co daje największe znaczenie parom punktów o najmniejszym zasięgu. Ta opcja nie jest zazwyczaj optymalna w przypadku krossemiwariogramów - tutaj częściej stosuje się fit.method = 6 (wagi nie są nadawane) lub fit.method = 1 (wagi proporcjonalne do liczby par punktów w każdym przedziale).

g2 = fit.lmc(v, g1,
                correct.diagonal = 1.01,
                fit.method = 6)
g2
## data:
## SAVI : formula = savi`~`1 ; data dim = 242 x 5
## NDVI : formula = ndvi`~`1 ; data dim = 992 x 1
## variograms:
##              model        psill range
## SAVI[1]        Nug 0.0009873135     0
## SAVI[2]        Sph 0.0050465345  1200
## NDVI[1]        Nug 0.0023006100     0
## NDVI[2]        Sph 0.0070299532  1200
## SAVI.NDVI[1]   Nug 0.0014922022     0
## SAVI.NDVI[2]   Sph 0.0055018027  1200
plot(v, g2)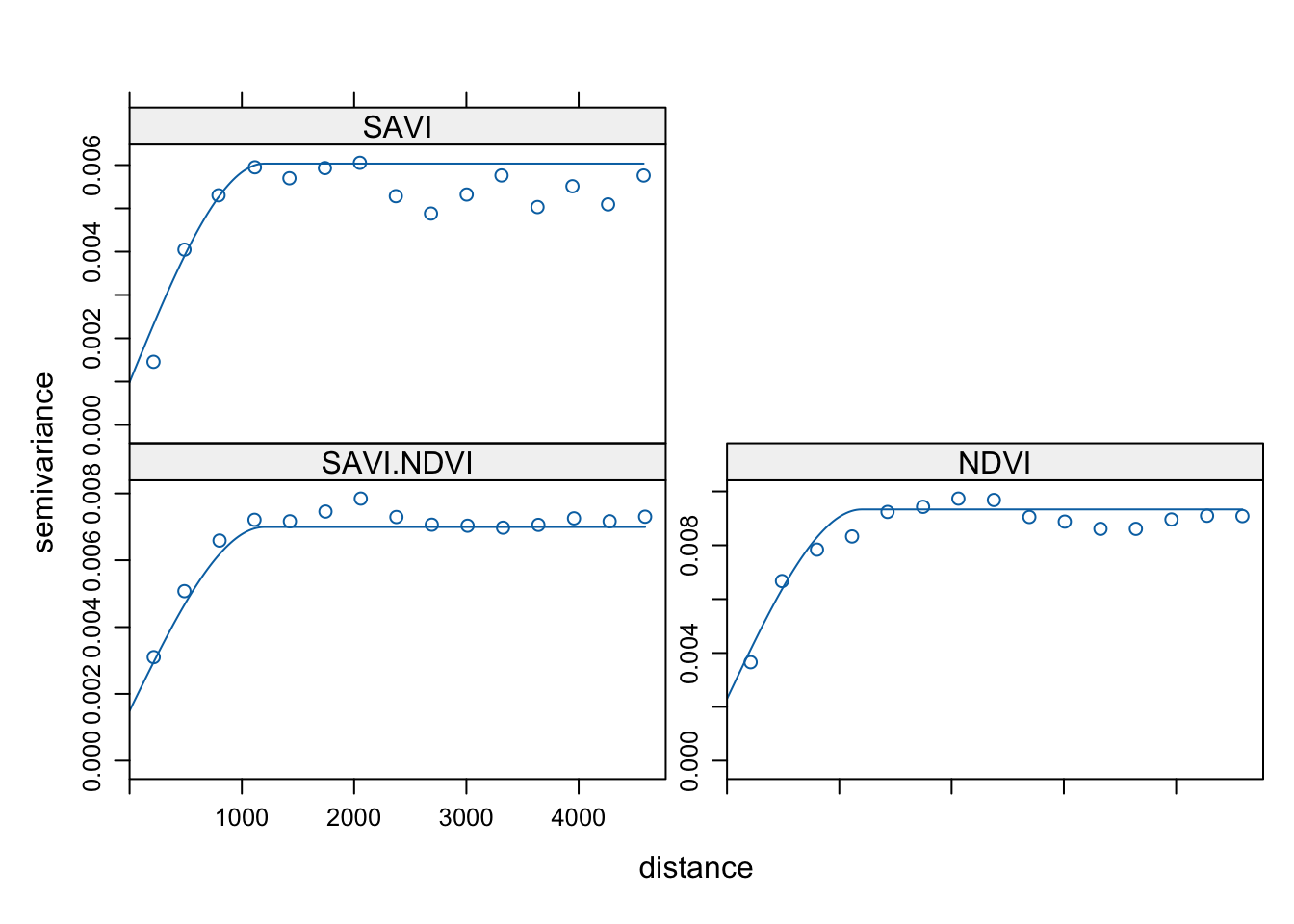
Automatycznie dopasowane modele krossemiwariogramu zmiennych savi i ndvi.

Rycina 10.4: Automatycznie dopasowane modele krossemiwariogramu zmiennych savi i ndvi.

10.4 Kokriging

Posiadając dopasowane modele oraz siatkę można uzyskać wynik używając funkcji predict() (rycina 10.5).

ck = predict(g2, newdata = siatka)
## Linear Model of Coregionalization found. Good.
## [using ordinary cokriging]

W efekcie otrzymujemy pięć zmiennych:

  1. SAVI.pred - estymacja zmiennej savi
  2. SAVI.var - wariancja zmiennej savi
  3. NDVI.pred - estymacja zmiennej ndvi
  4. NDVI.var - wariancja zmiennej ndvi
  5. cov.SAVI.NDVI - kowariancja zmiennych savi oraz ndvi 
ck
## stars object with 2 dimensions and 5 attributes
## attribute(s):
##                       Min.     1st Qu.      Median        Mean     3rd Qu.
## SAVI.pred      0.077243684 0.290908153 0.321211504 0.315700226 0.348022981
## SAVI.var       0.001525063 0.002379011 0.002638353 0.002652832 0.002905902
## NDVI.pred      0.205549518 0.468630003 0.508090071 0.501150702 0.542080400
## NDVI.var       0.003082640 0.003893078 0.004212984 0.004272496 0.004578181
## cov.SAVI.NDVI  0.001930305 0.002625231 0.002885524 0.002929714 0.003180885
##                       Max. NA's
## SAVI.pred      0.437090600 1270
## SAVI.var       0.004777928 1270
## NDVI.pred      0.658528553 1270
## NDVI.var       0.007378830 1270
## cov.SAVI.NDVI  0.005432433 1270
## dimension(s):
##   from  to offset delta               refsys x/y
## x    1 127 745542    90 ETRS89 / Poland CS92 [x]
## y    1  96 721256   -90 ETRS89 / Poland CS92 [y]
tm_shape(ck) +
        tm_raster(col = c("SAVI.pred", "SAVI.var"),
                  style = "cont", 
                  palette = list("-Spectral", "viridis")) +
        tm_layout(legend.frame = TRUE)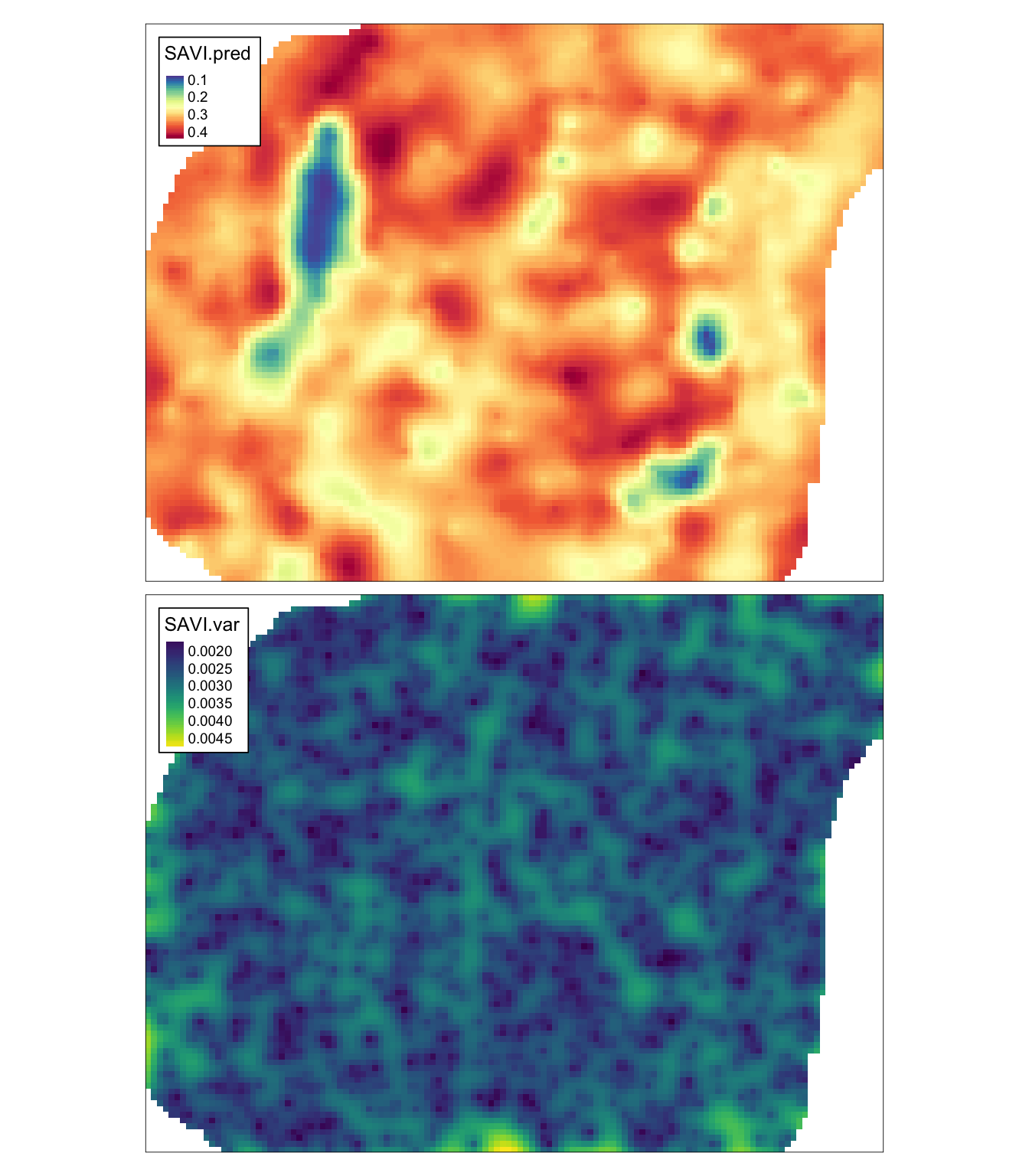
Estymacja i wariancja estymacji zmiennej savi używając metody kokrigingu (CK).

Rycina 10.5: Estymacja i wariancja estymacji zmiennej savi używając metody kokrigingu (CK).

10.5 Zadania

Zadania w tym rozdziale są oparte o dane z meuse.all z pakietu gstat.

data("meuse.all")
meuse = st_as_sf(meuse.all, coords = c("x", "y"))

Na jego podstawie wydziel dwa obiekty - meuse164 zawierający tylko zmienną cadmium (kadm) dla 164 punktów, oraz meuse60 zawierający tylko zmienną copper (miedź) dla 60 punktów.

set.seed(431)
meuse164 = meuse["cadmium"]
meuse60 = meuse[sample(nrow(meuse), 60), "copper"]
  1. Stwórz siatkę interpolacyjną o rozdzielczości 100 jednostek dla obszaru, w którym znajdują się punkty meuse.
  2. Zbuduj optymalne modele semiwariogramu zmiennej cadmium dla obiektu meuse164 oraz zmiennej copper dla obiektu meuse60. Porównaj graficznie uzyskane modele.
  3. Korzystając z obiektów meuse164 oraz meuse60 stwórz krossemiwariogram.
  4. Zbuduj ręczny model uzyskanego krossemiwariogramu. Następnie stwórz model automatyczny. Porównaj uzyskane wyniki.
  5. Stwórz estymację zmiennej copper w nowo utworzonej siatce korzystając z kokrigingu.
  6. Dodatkowe: stwórz estymację zmiennej savi z obiektu punkty używając krigingu zwykłego. Porównaj uzyskaną estymację z estymacją przedstawioną w tym rozdziale, stworzoną używając kokrigingu.