Skip to main content

Geostatystyka w R

8 Estymacje jednozmienne

Odtworzenie obliczeń z tego rozdziału wymaga załączenia poniższych pakietów oraz wczytania poniższych danych:

8.1 Kriging

8.1.1 Interpolacja geostatystyczna

Kriging (interpolacja geostatystyczna) to grupa metod estymacji zaproponowana w latach 50. przez Daniego Krige. Główna zasada mówi, że prognoza w danej lokalizacji jest kombinacją obokległych obserwacji. Waga nadawana każdej z obserwacji jest zależna od stopnia (przestrzennej) korelacji - stąd też bierze się istotna rola semiwariogramów.

8.1.2 Metod krigingu

Istnieje szereg metod krigingu, w tym:

  • Kriging prosty (ang. Simple kriging) (sekcja 8.2)
  • Kriging zwykły (ang. Ordinary kriging) (sekcja 8.3)
  • Kriging z trendem (ang. Kriging with a trend) (sekcja 8.4)
  • Kriging stratyfikowany (ang. Kriging within strata – KWS)
  • Kriging prosty ze zmiennymi średnimi lokalnymi (ang. Simple kriging with varying local means - SKlm) (sekcja 9.1)
  • Kriging z zewnętrznym trendem/Uniwersalny kriging (ang.Kriging with an external trend/Universal kriging) (sekcja 9.2)
  • Kokriging (ang. Co-kriging) (sekcja 10.1)
  • Kriging danych kodowanych (ang. Indicator kriging) (sekcja 11.1)
  • Inne

8.2 Kriging prosty

8.2.1 Kriging prosty (ang. Simple kriging)

Kriging prosty zakłada, że średnia jest znana i stała na całym obszarze. W poniższym przykładzie po stworzeniu semiwariogramu empirycznego, dopasowano model semiwariogramu składający się z funkcji sferycznej o zasięgu 4000 metrów i wartości nuggetu równej 0,5 (rycina 8.1).

vario = variogram(temp ~ 1, locations = punkty)
model = vgm(10, model = "Sph", range = 4000, nugget = 0.5)
model
##   model psill range
## 1   Nug   0.5     0
## 2   Sph  10.0  4000
plot(vario, model = model)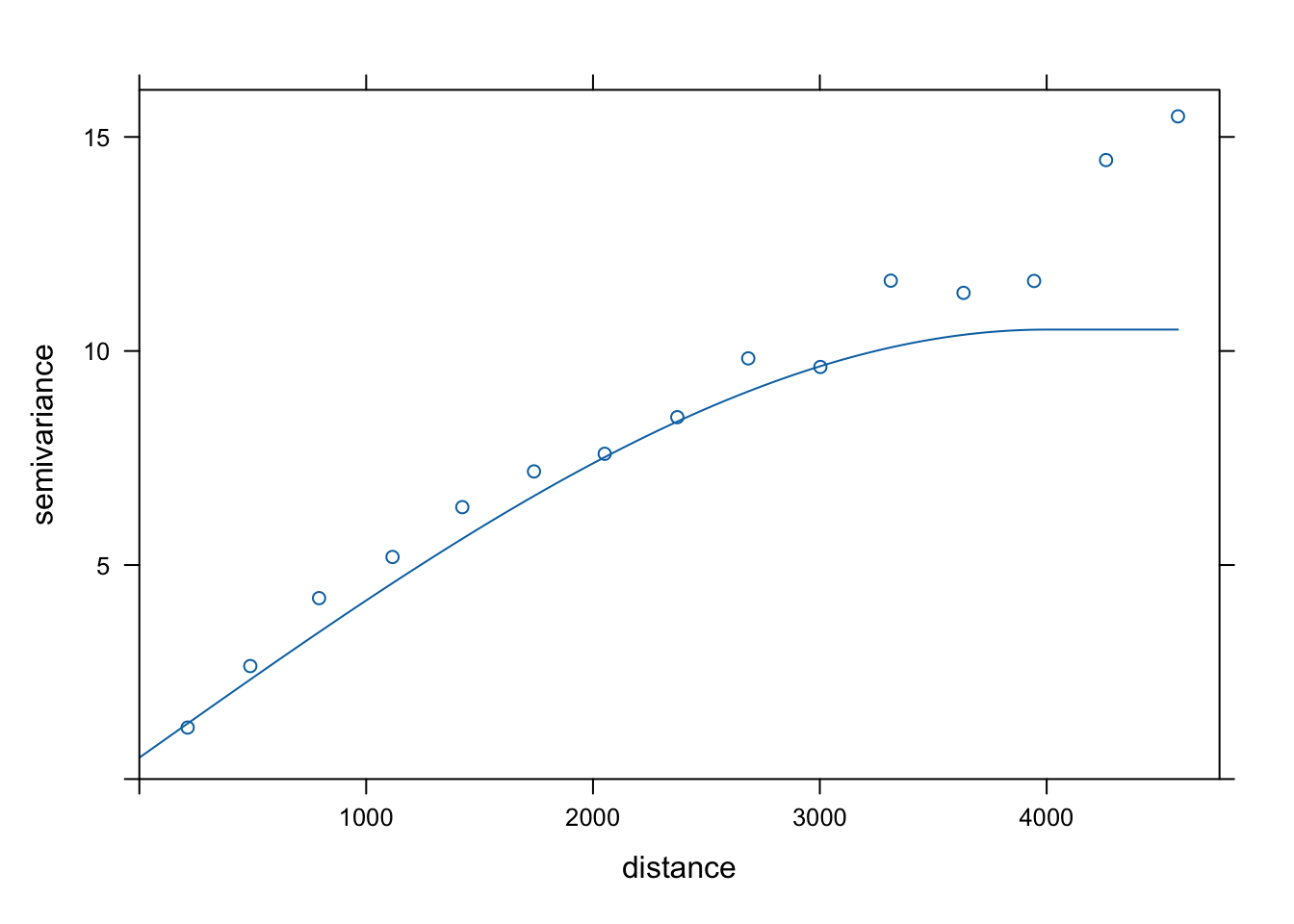
Model złożony z modelu nuggetowego i sferycznego dla zmiennej temp.

Rycina 8.1: Model złożony z modelu nuggetowego i sferycznego dla zmiennej temp. 

# fitted = fit.variogram(vario, model)

Następnie następuje estymacja wartości z użyciem metody krigingu prostego. W funkcji krige() z pakietu gstat, użycie tej metody wymaga ustalenia średniej wartości cechy za pomocą argumentu beta.

mean(punkty$temp)
## [1] 15.22251
sk = krige(temp ~ 1, 
            locations = punkty,
            newdata = siatka,
            model = model,
            beta = 15)
## [using simple kriging]

Wynik krigingu prostego, jak i każdy inny uzyskany z użyciem pakietu gstat, można podejrzeć wpisując nazwę wynikowego obiektu. Szczególnie ważne są dwie, nowe zmienne - var1.pred oraz var1.var. Pierwsza z nich oznacza wartość estymowaną dla każdego oczka siatki, druga zaś mówi o wariancji estymacji.

sk
## stars object with 2 dimensions and 2 attributes
## attribute(s):
##                Min.  1st Qu.    Median      Mean   3rd Qu.     Max. NA's
## var1.pred  8.473052 12.70587 14.961083 15.488215 17.711775 24.36355 1270
## var1.var   0.821095  1.61326  1.974793  2.041073  2.355011  6.26745 1270
## dimension(s):
##   from  to offset delta               refsys x/y
## x    1 127 745542    90 ETRS89 / Poland CS92 [x]
## y    1  96 721256   -90 ETRS89 / Poland CS92 [y]

Obie uzyskane zmienne można wyświetlić z użyciem pakietu tmap (rycina 8.2).

tm_shape(sk) +
        tm_raster(col = c("var1.pred", "var1.var"),
                  style = "cont", 
                  palette = list("-Spectral", "viridis")) +
        tm_layout(legend.frame = TRUE)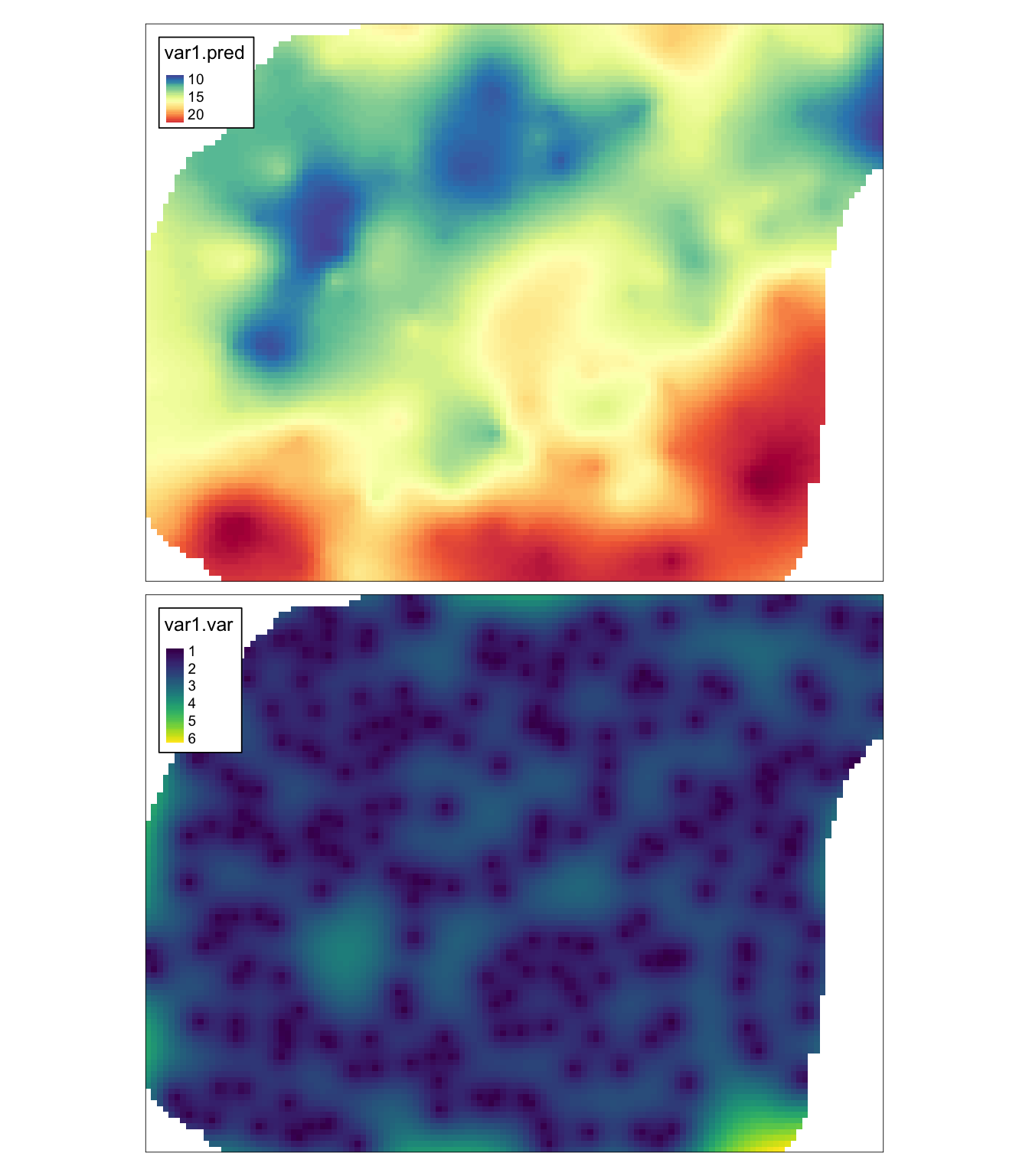
Estymacja i wariancja estymacji używając metody krigingu prostego (SK).

Rycina 8.2: Estymacja i wariancja estymacji używając metody krigingu prostego (SK).

8.2.2 Kriging prosty po transformacji danych

Zarówno kriging prosty, jak i kolejne metody krigingowe opisane w tym skrypcie, mogą używać zmiennych wejściowych poddanych transformacjom, np. logaritmizacji (sekcja 3.6). Może to mieć na celu zniwelowanie skośności rozkładu i w efekcie uzyskanie pewniejszych wyników. Tutaj konieczne jest pamiętanie o kilku koniecznych krokach: (1) wykonaniu transformacji przy budowaniu semiwariogramu, (2) wykonaniu transformacji przy tworzeniu estymacji, oraz (3) zastosowaniu transformacji odwrotnej na uzyskanych wynikach. Zobaczmy to na poniższym przykładzie.

W pierwszym etapie budujemy i modelujemy semiwariogram, jednakże zamiast używać bezpośrednio wartości zmiennej temp poddajemy ją logaritmizacji poprzez log(temp).

vario_kp2 = variogram(log(temp) ~ 1, locations = punkty)
model_kp2 = vgm(0.06, model = "Sph", range = 4000, nugget = 0.002)
model_kp2
##   model psill range
## 1   Nug 0.002     0
## 2   Sph 0.060  4000
plot(vario_kp2, model = model_kp2)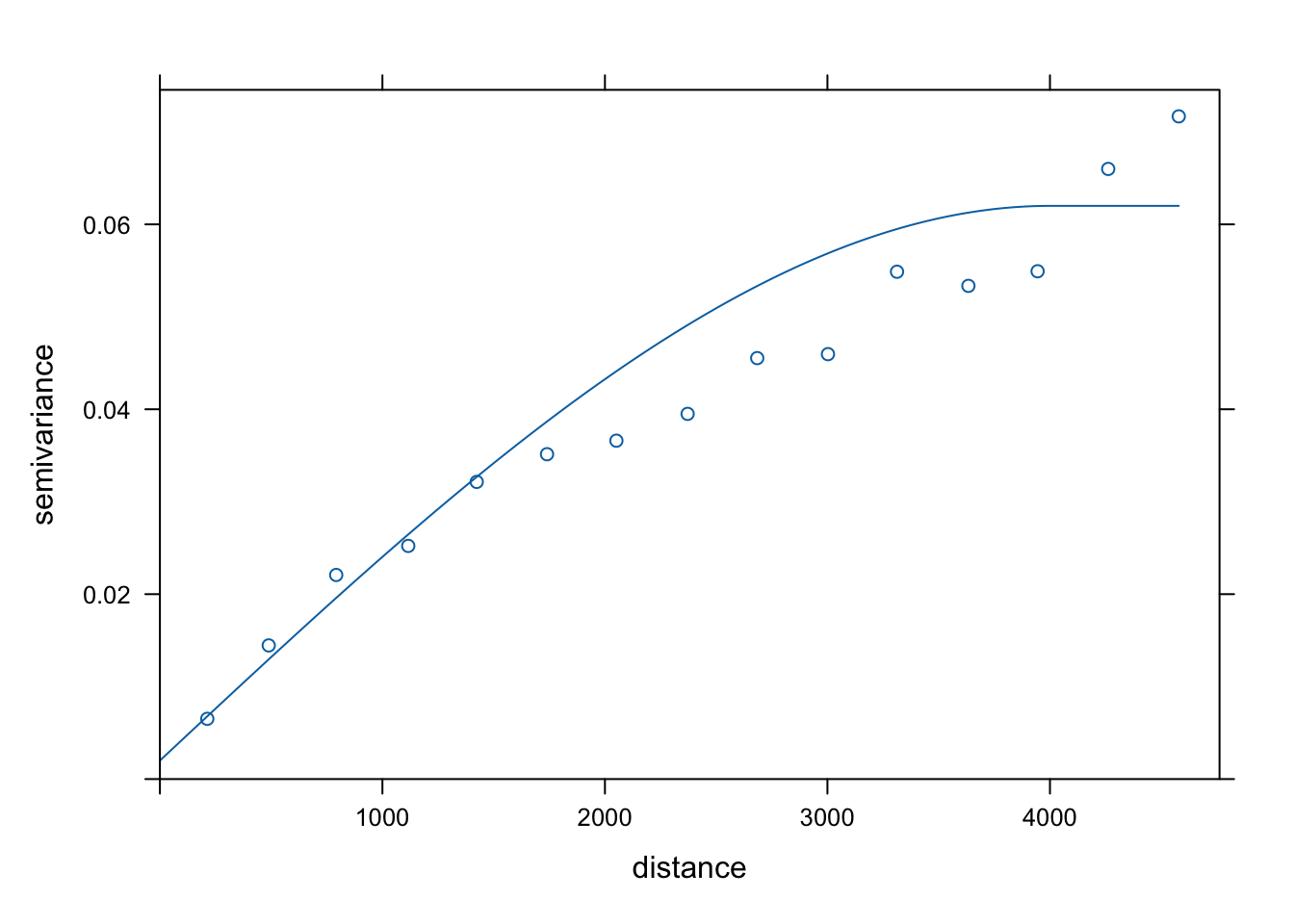
Model złożony z modelu nuggetowego i sferycznego dla zmiennej temp.

Rycina 8.3: Model złożony z modelu nuggetowego i sferycznego dla zmiennej temp. 

# fitted_kp2 = fit.variogram(vario_kp2, model_kp2)

Następnie, musimy określić logarytm średniej wartości badanej zmiennej dla całego obszaru oraz użyć logarytmu tej zmiennej do stworzenia estymacji.

mean(log(punkty$temp))
## [1] 2.689027
sk_kp2 = krige(log(temp) ~ 1, 
            locations = punkty,
            newdata = siatka,
            model = model_kp2,
            beta = 2.69)
## [using simple kriging]

Wynik krigingu prostego zawiera dwie zmienne - var1.pred oraz var1.var. Co warte podkreślenia, pierwsza z nich określa wartość estymowaną dla każdego oczka siatki w logarytmie badanej jednostki. Przykładowo, gdy nasza zmienna określała temperaturę w stopniach Celsjusza, to wynik jest przestawiony w logarytmie stopni Celsjusza.

sk_kp2
## stars object with 2 dimensions and 2 attributes
## attribute(s):
##                   Min.     1st Qu.     Median       Mean    3rd Qu.       Max.
## var1.pred  2.116458867 2.532130644 2.70146692 2.70654657 2.86844059 3.19736223
## var1.var   0.003507856 0.008334475 0.01053523 0.01092072 0.01284403 0.03625981
##            NA's
## var1.pred  1270
## var1.var   1270
## dimension(s):
##   from  to offset delta               refsys x/y
## x    1 127 745542    90 ETRS89 / Poland CS92 [x]
## y    1  96 721256   -90 ETRS89 / Poland CS92 [y]

W związku z tym, koniecznym ostatnim krokiem jest przywrócenie oryginalnej jednostki. Możemy to zrobić używając funkcji rev_trans() z pakietu geostatbook (sekcja 3.6.4), która przyjmuje naszą zlogaritmizowaną estymację, wariancję estymacji i oryginalne wartości pomiarów w punktach.

sk_kp2$temp = rev_trans(sk_kp2$var1.pred, sk_kp2$var1.var, punkty$temp)
sk_kp2
## stars object with 2 dimensions and 3 attributes
## attribute(s):
##                   Min.      1st Qu.      Median        Mean     3rd Qu.
## var1.pred  2.116458867  2.532130644  2.70146692  2.70654657  2.86844059
## var1.var   0.003507856  0.008334475  0.01053523  0.01092072  0.01284403
## temp       8.187681121 12.430871960 14.72626722 15.22250747 17.40643717
##                   Max. NA's
## var1.pred   3.19736223 1270
## var1.var    0.03625981 1270
## temp       24.10950341 1270
## dimension(s):
##   from  to offset delta               refsys x/y
## x    1 127 745542    90 ETRS89 / Poland CS92 [x]
## y    1  96 721256   -90 ETRS89 / Poland CS92 [y]

W efekcie otrzymujemy estymację w oryginalnych jednostkach - stopniach Celsjusza. Trzy uzyskane zmienne można wyświetlić z użyciem pakietu tmap (rycina 8.4).

tm_shape(sk_kp2) +
        tm_raster(col = c("var1.pred", "var1.var", "temp"),
                  style = "cont", 
                  palette = list("-Spectral", "viridis", "-Spectral")) +
        tm_layout(legend.frame = TRUE)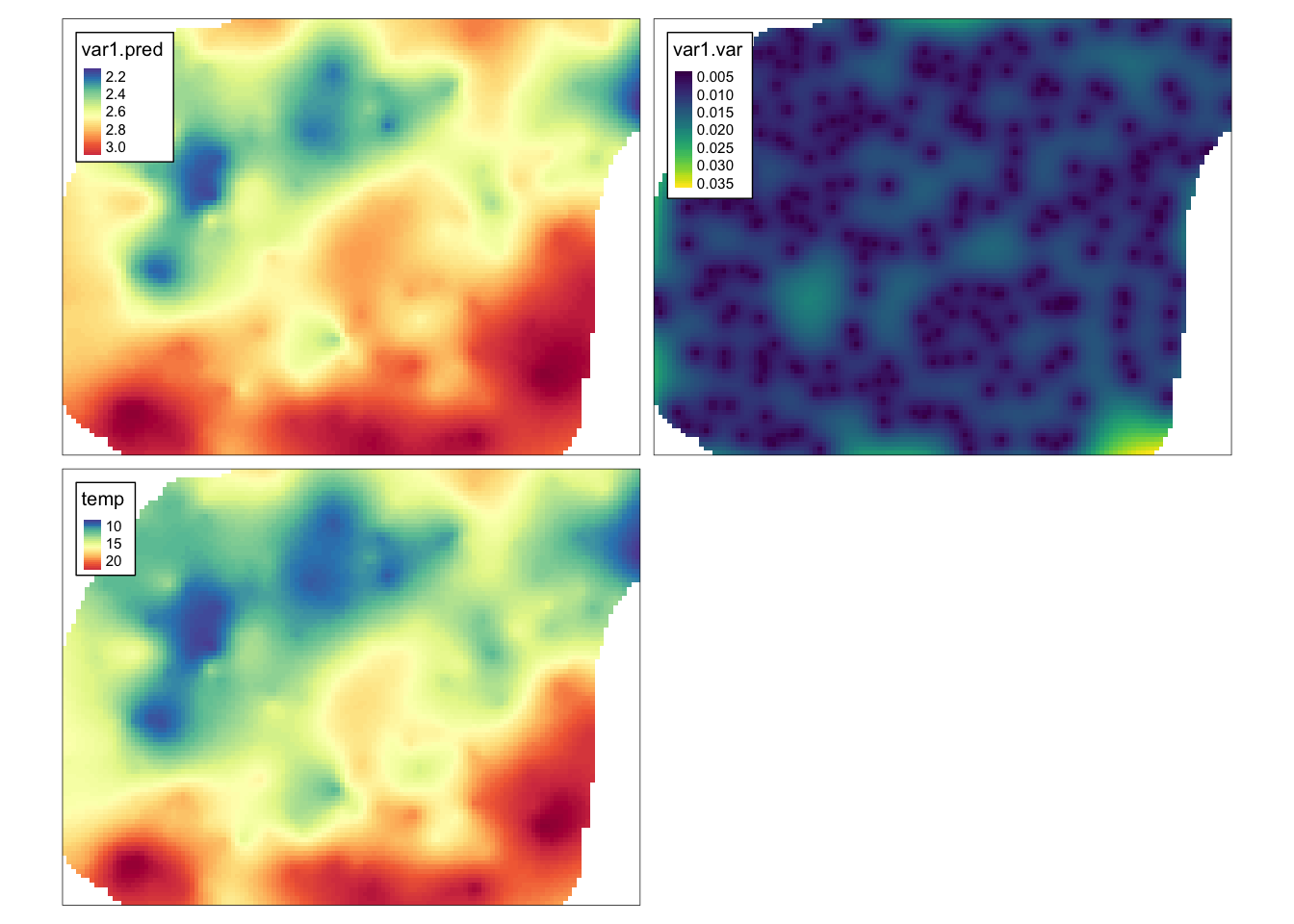
Estymacja logarytmu zmiennej temp, jej wariancja estymacji, oraz estymacja wartości tej zmiennej po przeprowadzeniu procesu transformacji odwrotnej.

Rycina 8.4: Estymacja logarytmu zmiennej temp, jej wariancja estymacji, oraz estymacja wartości tej zmiennej po przeprowadzeniu procesu transformacji odwrotnej.

8.3 Kriging zwykły

8.3.1 Kriging zwykły (ang. Ordinary kriging)

W krigingu zwykłym średnia traktowana jest jako wartość nieznana. Metoda ta uwzględnia lokalne fluktuacje średniej poprzez stosowanie ruchomego okna. Parametry ruchomego okna można określić za pomocą jednego z dwóch argumentów:

  • nmax - użyta zostanie określona liczba najbliższych obserwacji.
  • maxdist - użyte zostaną jedynie obserwacje w zadanej odległości.
# ok = krige(temp ~ 1,
#             locations = punkty,
#             newdata = siatka, 
#             model = model, 
#             nmax = 30)
ok = krige(temp ~ 1,
            locations = punkty,
            newdata = siatka, 
            model = model, 
            maxdist = 1500)
## [using ordinary kriging]

Podobnie jak w przypadku krigingu prostego, można przyjrzeć się wynikom estymacji podając nazwę wynikowego obiektu oraz wyświetlić je używając funkcji tm_shape() and tm_raster() (rycina 8.5).

ok
## stars object with 2 dimensions and 2 attributes
## attribute(s):
##                 Min.  1st Qu.    Median      Mean  3rd Qu.      Max. NA's
## var1.pred  8.4763353 12.71717 14.967146 15.531098 17.70921 24.326622 1270
## var1.var   0.8215425  1.62057  1.990971  2.082008  2.39254  9.882173 1270
## dimension(s):
##   from  to offset delta               refsys x/y
## x    1 127 745542    90 ETRS89 / Poland CS92 [x]
## y    1  96 721256   -90 ETRS89 / Poland CS92 [y]
tm_shape(ok) +
        tm_raster(col = c("var1.pred", "var1.var"),
                  style = "cont", 
                  palette = list("-Spectral", "viridis")) +
        tm_layout(legend.frame = TRUE)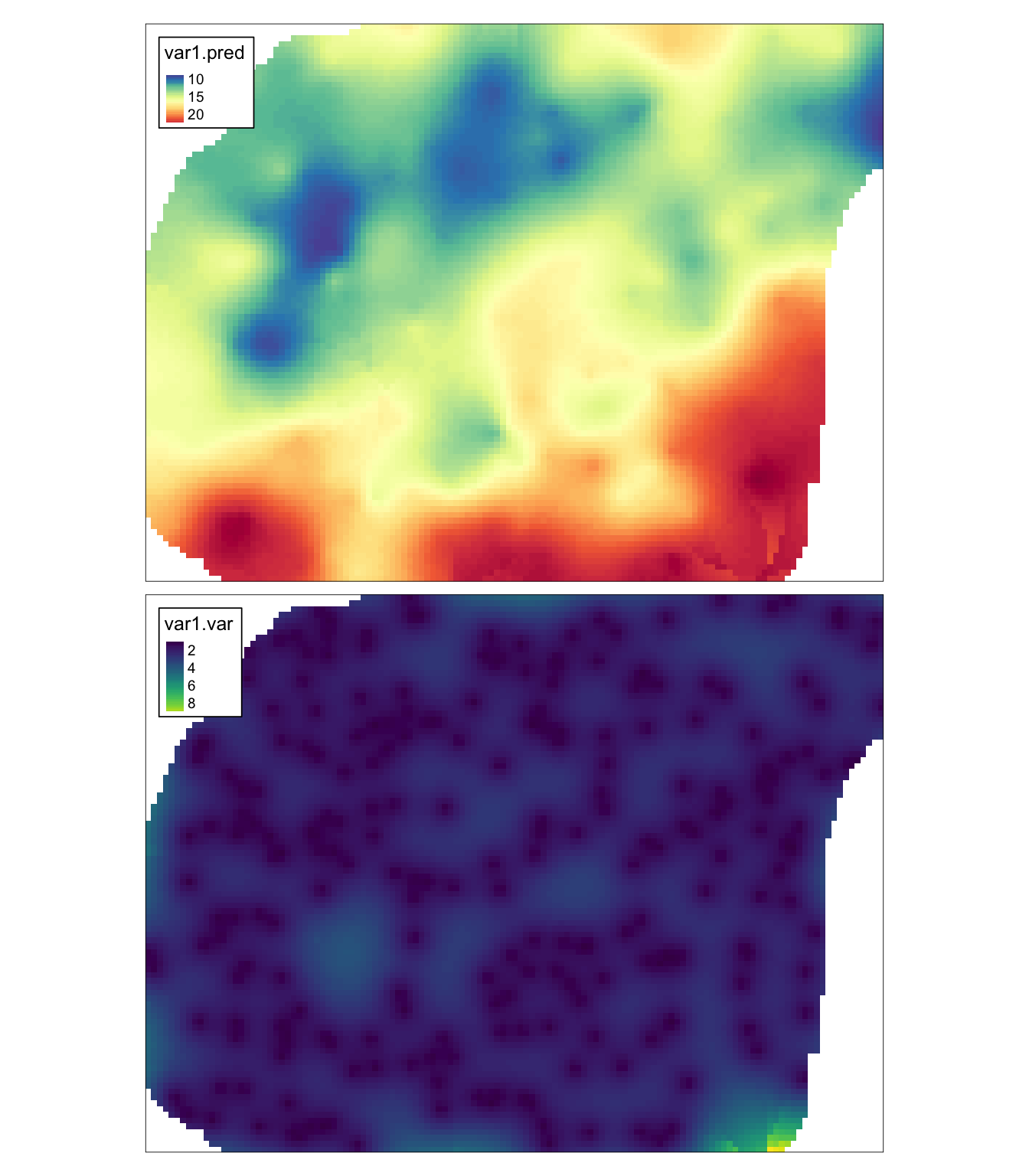
Estymacja i wariancja estymacji używając metody krigingu zwykłego (OK).

Rycina 8.5: Estymacja i wariancja estymacji używając metody krigingu zwykłego (OK).

8.4 Kriging z trendem

8.4.1 Kriging z trendem (ang. Kriging with a trend)

Kriging z trendem, określany również jako kriging z wewnętrznym trendem, do estymacji wykorzystuje (oprócz zmienności wartości wraz z odległością) położenie analizowanych punktów. W pierwszym kroku konieczne jest dodanie współrzędnych do używanego obiektu i do używanej siatki.

# dodanie współrzędnych do punktów
punkty$x = st_coordinates(punkty)[, 1]
punkty$y = st_coordinates(punkty)[, 2]
# dodanie współrzędnych do siatki
siatka$x = st_coordinates(siatka)[, 1]
siatka$y = st_coordinates(siatka)[, 2]

Współrzędne dodawane są do całej (regularnej) siatki. Możemy przyciąć je do badanego obszaru poprzez wpisanie wartości NA w miejscach poza naszym obszarem zainteresowań.

siatka$x[is.na(siatka$X2)] = NA
siatka$y[is.na(siatka$X2)] = NA

Następnie pierwszy z argumentów w funkcji variogram() musi przyjąć postać temp ~ x + y, co oznacza, że uwzględniamy liniowy trend zależny od współrzędnej x oraz y (rycina 8.6).

vario_kzt = variogram(temp ~ x + y, locations = punkty)
plot(vario_kzt)
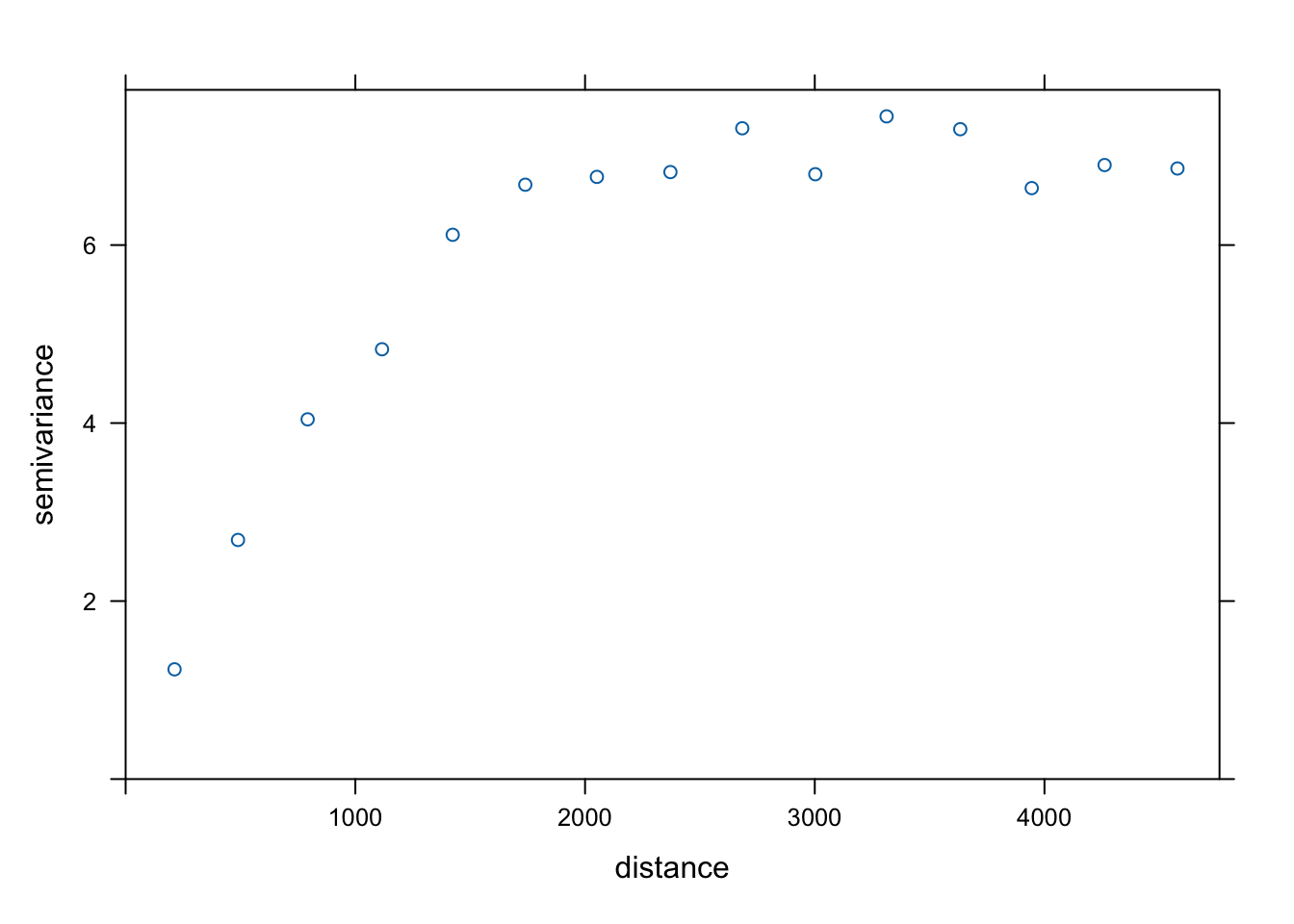
Semiwariogram zmiennej temp uwzględniający współrzędne x i y.

Rycina 8.6: Semiwariogram zmiennej temp uwzględniający współrzędne x i y.

Dalszym etapem jest dopasowanie modelu semiwariancji, a następnie wyliczenie estymowanych wartości z użyciem funkcji krige(). Należy tutaj pamiętać, aby wzór (w przykładzie temp ~ x + y) był taki sam podczas budowania semiwariogramu, jak i estymacji (rycina 8.7).

model_kzt = vgm(model = "Sph", nugget = 1)
fitted_kzt = fit.variogram(vario_kzt, model_kzt)
fitted_kzt
##   model     psill    range
## 1   Nug 0.2568762    0.000
## 2   Sph 6.7107464 2087.465
plot(vario_kzt, fitted_kzt)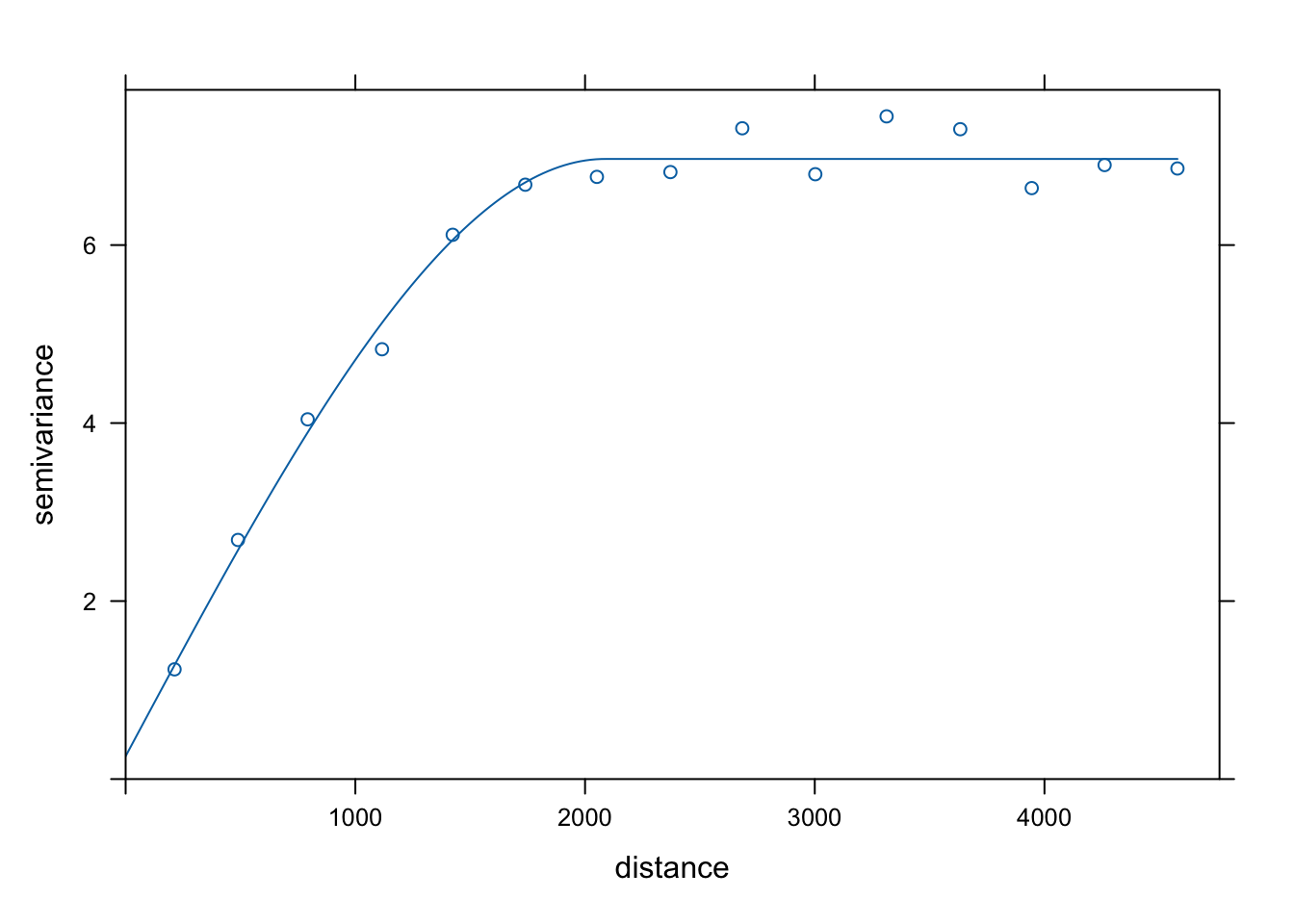
Model semiwariogramu zmiennej temp uwzględniający współrzędne x i y.

Rycina 8.7: Model semiwariogramu zmiennej temp uwzględniający współrzędne x i y. 

kzt = krige(temp ~ x + y, 
             locations = punkty, 
             newdata = siatka, 
             model = fitted_kzt)
## [using universal kriging]

Wyświetlenie wyników odbywa się używając pakietu tmap.

tm_shape(kzt) +
        tm_raster(col = c("var1.pred", "var1.var"),
                  style = "cont", 
                  palette = list("-Spectral", "viridis")) +
        tm_layout(legend.frame = TRUE)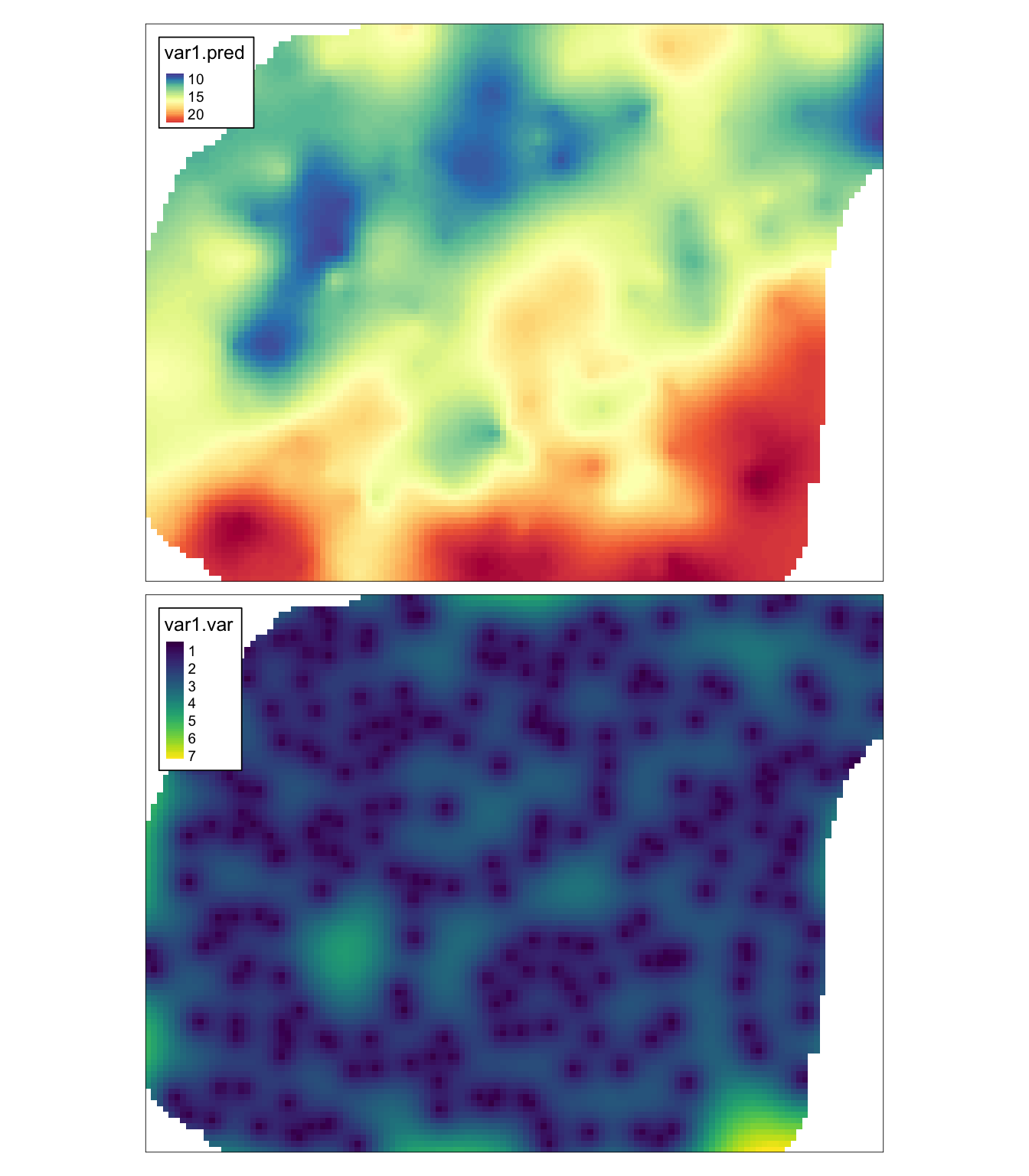
Estymacja i wariancja estymacji używając metody krigingu z trendem (KZT).

Rycina 8.8: Estymacja i wariancja estymacji używając metody krigingu z trendem (KZT).

8.5 Porównanie wyników SK, SK (trans), OK i KZT

Poniższe porównanie krigingu prostego (SK), krigingu prostego po zastosowaniu transformacji (SK trans), zwykłego (OK) i z trendem (KZT) wykazuje niewielkie różnice w uzyskanych wynikach (rycina 8.9).

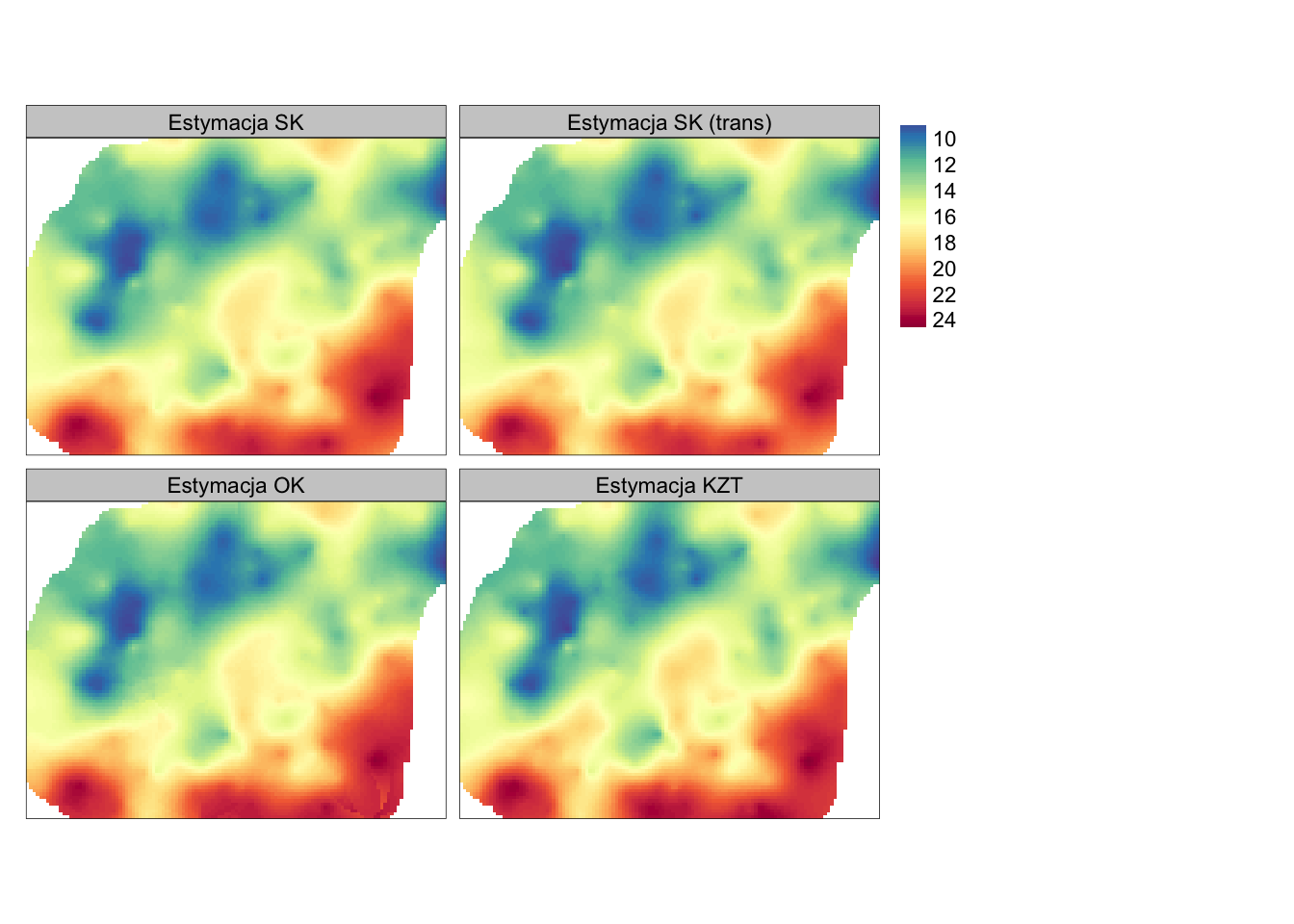
Porównanie wyników estymacji używając metody krigingu prostego (SK), krigingu zwykłego (OK) i krigingu z trendem (KZT).

Rycina 8.9: Porównanie wyników estymacji używając metody krigingu prostego (SK), krigingu zwykłego (OK) i krigingu z trendem (KZT).

W rozdziałach 10 oraz 9 pokazane będą uzyskane wyniki interpolacji temperatury powietrza korzystając z innych metod krigingu.

8.6 Zadania

Zadania w tym rozdziale są oparte o dane z obiektu punkty_pref. Możesz go wczytać używając poniższego kodu:

data(punkty_pref)

Na jego podstawie stwórz trzy obiekty - punkty_pref1 zawierający wszystkie punkty, punkty_pref2 zawierający losowe 100 punktów, oraz punkty_pref3 zawierający losowe 30 punktów.

set.seed(2018-11-25)
punkty_pref1 = punkty_pref
punkty_pref2 = punkty_pref[sample(nrow(punkty_pref), 100), ]
punkty_pref3 = punkty_pref[sample(nrow(punkty_pref), 30), ]
  1. Zbuduj optymalne modele semiwariogramu zmiennej srtm dla trzech zbiorów danych - punkty_pref1, punkty_pref2, punkty_pref3. Porównaj graficznie uzyskane modele.
  2. W oparciu o uzyskane modele stwórz estymacje zmiennej srtm dla trzech zbiorów danych - punkty_pref1, punkty_pref2, punkty_pref3 używając krigingu prostego. Porównaj graficznie zarówno mapy estymacji jak i mapy wariancji. Opisz zaobserwowane różnice.
  3. W oparciu o uzyskane modele stwórz estymacje zmiennej srtm dla zbioru danych punkty_pref3 używając krigingu zwykłego. Sprawdź jak wygląda wynik estymacji uwzględniając (i) 10 najbliższych obserwacji, (ii) 30 najbliższych obserwacji, (iii) obserwacje w odległości do 2 km.
  4. Używając krigingu z trendem, stwórz optymalne modele zmiennej srtm dla dwóch zbiorów danych - punkty_pref1 oraz punkty_pref3.
  5. Porównaj graficznie zarówno mapy estymacji jak i mapy wariancji dla krigingu prostego, zwykłego oraz z trendem dla danych punkty_pref3. Jakie można zauważyć podobieństwa a jakie różnice?
  6. Dla zmiennej temp z obiektu punkty_pref1 stwórz mapę semiwariogramu. Czy ta zmienna wykazuje anizotropię przestrzenną? Jeżeli tak to stwórz semiwariogramy kierunkowe i ich modele, a następnie estymację zmiennej temp.