C Przykład analizy geostatystycznej

Jakub Nowosad

C.1 Analiza geostatystyczna

Analiza geostatystyczna jest złożonym procesem, często wymagającym sprawdzenia jakości danych i ich korekcji oraz wypróbowania wielu możliwości modelowania. Poniższy appendiks skupia się na pokazaniu przykładu uproszczonej analizy geostatystycznej, w której głównym celem jest estymacja średniej wartości temperatury.

C.2 Przygotowanie danych

Pierwszym krokiem analizy geostatystycznej jest załadowanie pakietów, które zostaną użyte. Brakujące pakiety można także załadować także w trakcie analizy geostatystycznej.

library(sf)
library(stars)
library(gstat)
library(tmap)
library(ggplot2)

Kolejnym krokiem jest wczytanie danych oraz sprawdzenie ich jakości.

moje_punkty = read_sf("dane/moje_punkty.gpkg")
summary(moje_punkty)

##       tavg               X                Y                     geom    
##  Min.   :-0.8726   Min.   :345007   Min.   :312609   POINT        :188  
##  1st Qu.: 1.0871   1st Qu.:347681   1st Qu.:314664   epsg:2180    :  0  
##  Median : 1.6470   Median :351093   Median :316628   +proj=tmer...:  0  
##  Mean   : 1.6204   Mean   :350809   Mean   :316827                      
##  3rd Qu.: 2.1644   3rd Qu.:353591   3rd Qu.:319037                      
##  Max.   : 4.0310   Max.   :357010   Max.   :321540

Obiekt moje_punkty zawiera tylko jedną zmienną tavg, która ma być użyta do stworzenia estymacji. Warto zwizualizować rozkład wartości tej zmiennej w postaci histogramu oraz mapy (rycina C.1 i C.2).

ggplot(moje_punkty, aes(tavg)) + geom_histogram()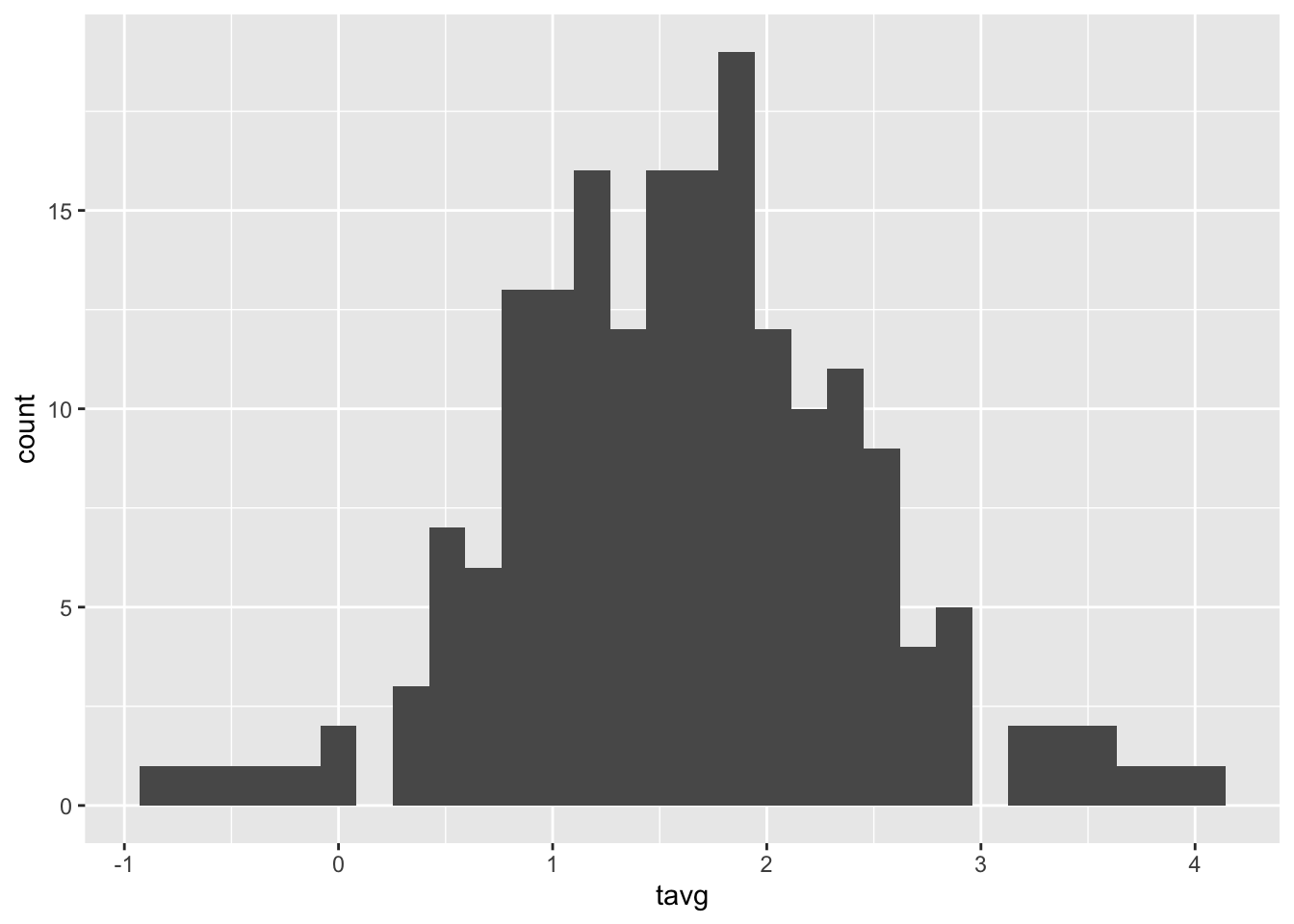

Rycina C.1: Rozkład wartości zmiennej tavg.

tm_shape(moje_punkty) + 
        tm_symbols(col = "tavg")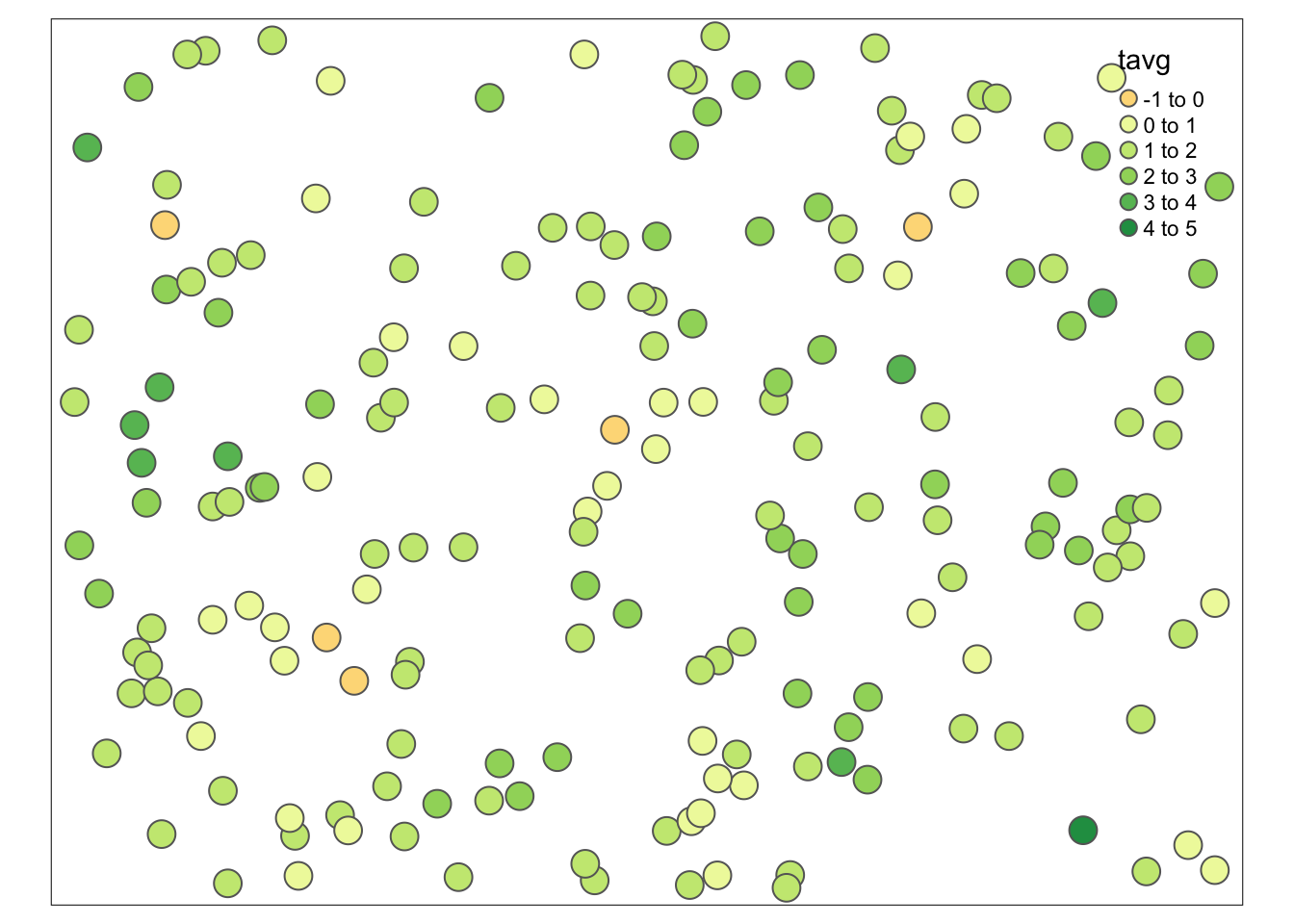

Rycina C.2: Rozkład przestrzenny wartości zmiennej tavg.

Pozwala to na zauważenie, że w badanej zmiennej występują co najmniej dwie wartości odstające.

moje_punkty[moje_punkty$tavg == max(moje_punkty$tavg), ]

## Simple feature collection with 1 feature and 3 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 355581.8 ymin: 313212.1 xmax: 355581.8 ymax: 313212.1
## Projected CRS: ETRF2000-PL / CS92
## # A tibble: 1 × 4
##    tavg       X       Y                geom
##   <dbl>   <dbl>   <dbl>         <POINT [m]>
## 1  4.03 355582. 313212. (355581.8 313212.1)

moje_punkty[moje_punkty$tavg == min(moje_punkty$tavg), ]

## Simple feature collection with 1 feature and 3 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 353849 ymin: 319540.7 xmax: 353849 ymax: 319540.7
## Projected CRS: ETRF2000-PL / CS92
## # A tibble: 1 × 4
##     tavg       X       Y              geom
##    <dbl>   <dbl>   <dbl>       <POINT [m]>
## 1 -0.873 353849. 319541. (353849 319540.7)

Jedna z nich ma wartość ok. -3,5 °C i jest znacznie niższa od pozostałych, druga natomiast jest znacznie wyższa od pozostałych i ma wartość ok. 9,2 °C. Należy w tym momencie zastanowić się czy te wartości odstające są prawidłowymi wartościami, czy też są one błędne. W tej sytuacji, nie posiadając zewnętrznej informacji, bezpieczniej jest usunąć te dwa pomiary. Można to zrobić wyszukując id punktów za pomocą pakietu tmap.

Teraz id punktów można użyć do ich wybrania i zastąpienia potencjalnie błędnych wartości wartościami NA.

# usunięcie wartości według id
moje_punkty[60, "tavg"] = NA
moje_punkty[72, "tavg"] = NA

Te punkty nadal istnieją jednak w obiekcie moje_punkty. Można je usunąć korzystając z funkcji is.na oraz indeksowania:

moje_punkty = moje_punkty[!is.na(moje_punkty$tavg), ]

Po tej zmianie powinno się po raz kolejny obejrzeć dokładnie dane w celu stwierdzenia, czy problem został naprawiony i czy nie występują dodatkowe sytuacje problemowe (rycina C.3 i C.4).

ggplot(moje_punkty, aes(tavg)) + geom_histogram()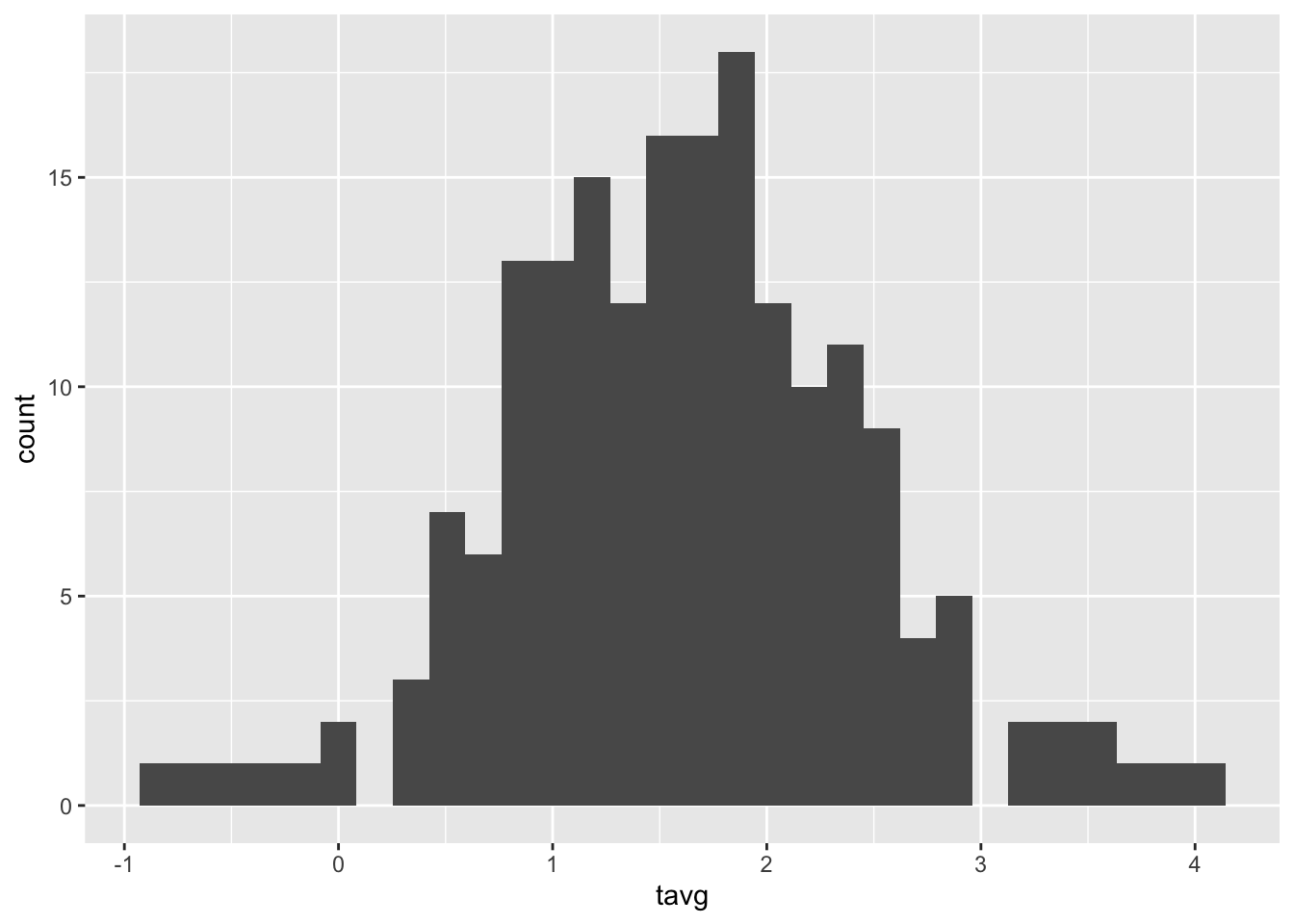

Rycina C.3: Rozkład wartości zmiennej tavg po usunięciu wartości odstających.

tm_shape(moje_punkty) + 
        tm_symbols(col = "tavg")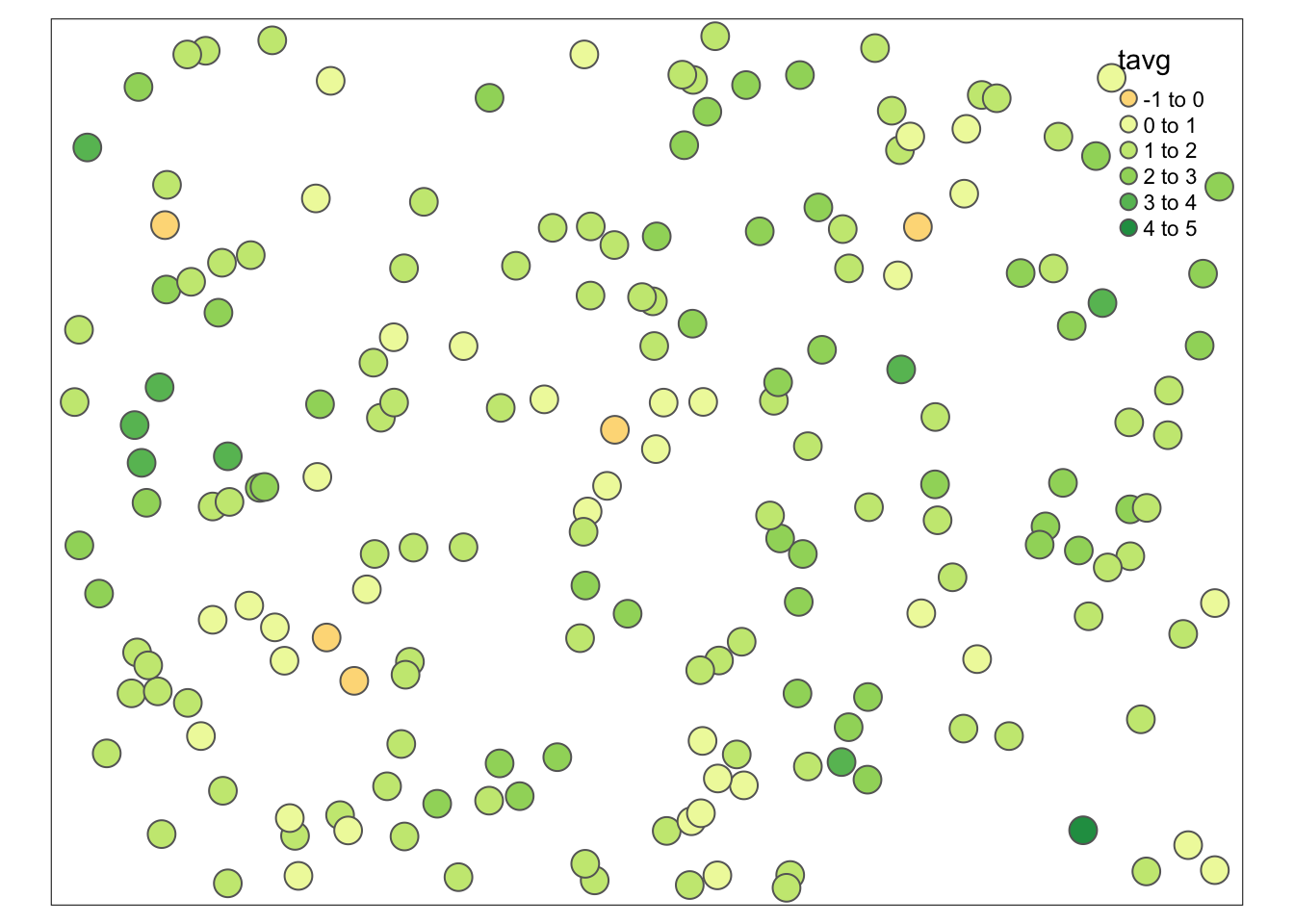

Rycina C.4: Rozkład przestrzenny wartości zmiennej tavg po usunięciu wartości odstających.

Można dodatkowo stworzyć chmurę semiwariogramu w celu wyszukania potencjalnych wartości lokalnie odstających (rycina C.5).

moja_chmura = variogram(tavg ~ 1, moje_punkty, cloud = TRUE)
plot(moja_chmura)

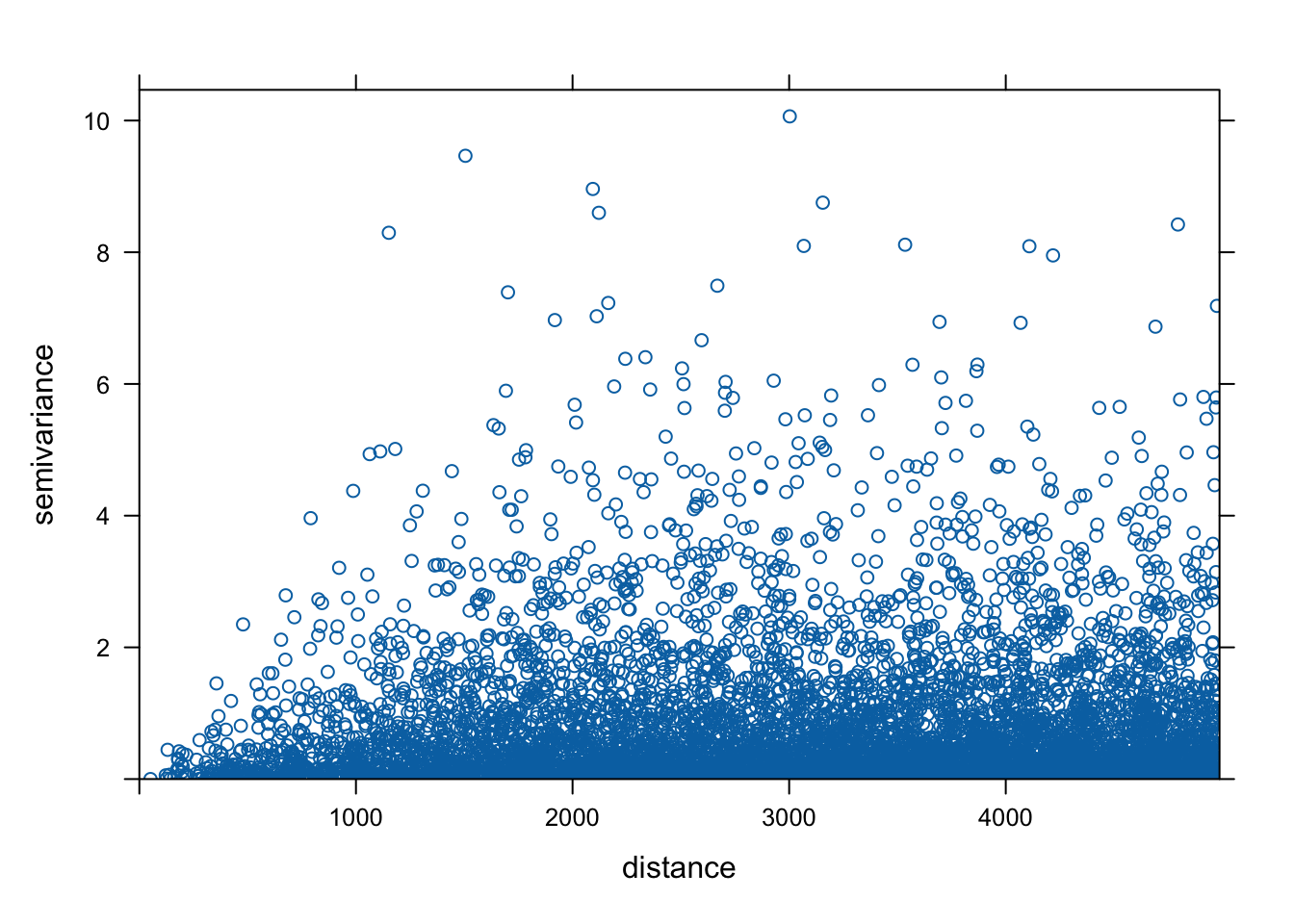
Rycina C.5: Chmura semiwariogramu zmiennej tavg.

C.3 Tworzenie modeli semiwariogramów

Posiadając już poprawne dane można sprawdzić czy badane zjawisko wykazuje anizotropię przestrzenną poprzez stworzenie mapy semiwariogramu (rycina C.6).

moja_mapa = variogram(tavg ~ 1, 
                      locations = moje_punkty,
                      cutoff = 4500,
                      width = 850, 
                      map = TRUE)
plot(moja_mapa, threshold = 30, 
     col.regions = hcl.colors(40, palette = "ag_GrnYl", rev = TRUE))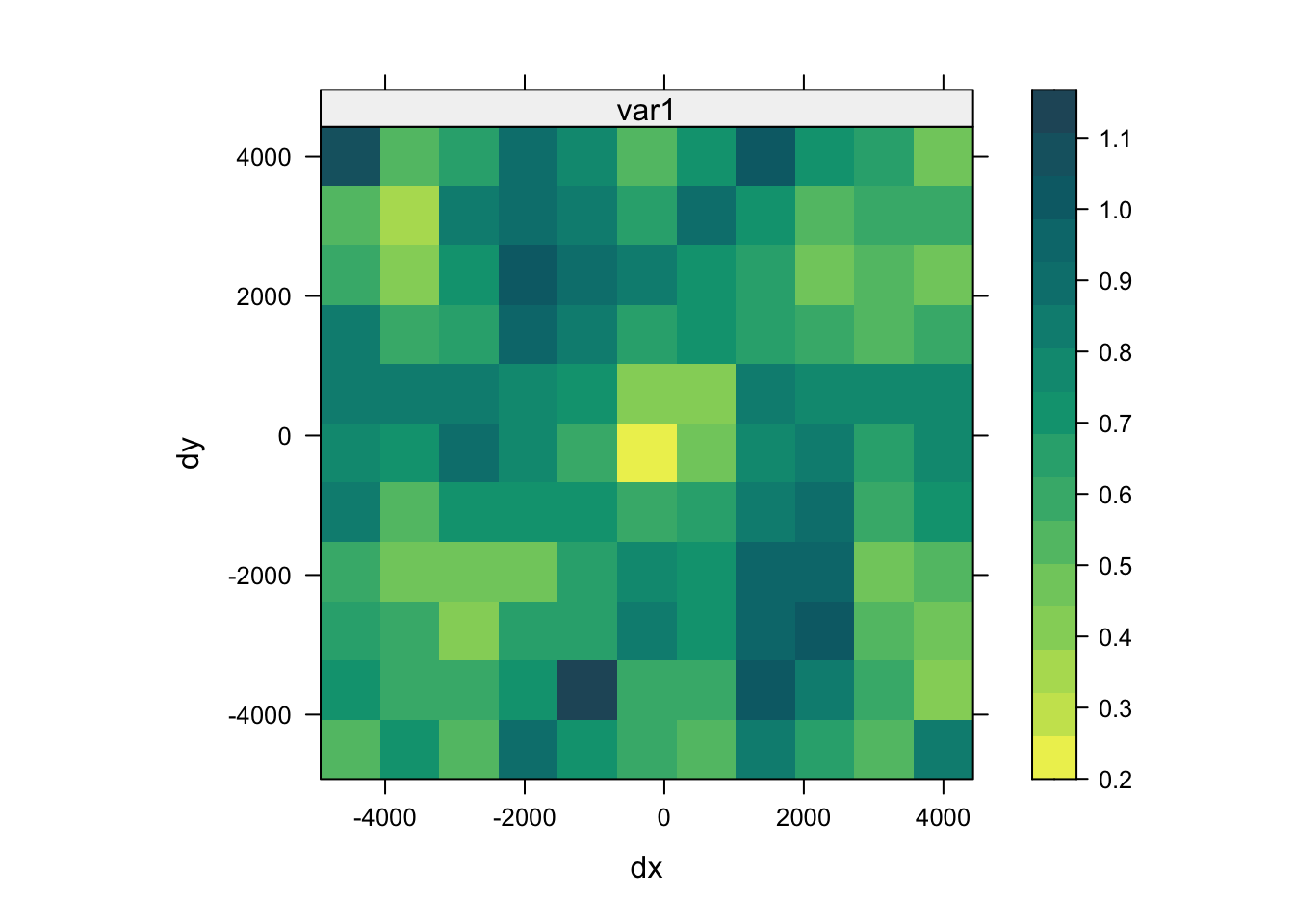

Rycina C.6: Mapa semiwariogramu zmiennej tavg.

Uzyskana mapa nie pozwala na jednoznaczne stwierdzenie kierunkowej zmienności podobieństwa badanej cechy, w związku z tym można skupić się na modelowaniu izotropowym. Kolejnym etapem jest stworzenie semiwariogramu oraz jego modelowanie. Optymalnie tworzy się więcej niż jeden model semiwariogramu, co pozwala na porównanie uzyskanych wyników i wybór lepszego modelu. Do tego przykładu zostały stworzone dwa modele semiwariogramu. Pierwszy z nich używa tylko zmiennej tavg oraz modelu ręcznego o wybranych parametrach (ryciny C.7, C.8, C.9, C.10).

moj_semiwar = variogram(tavg ~ 1, 
                        locations = moje_punkty)
plot(moj_semiwar)

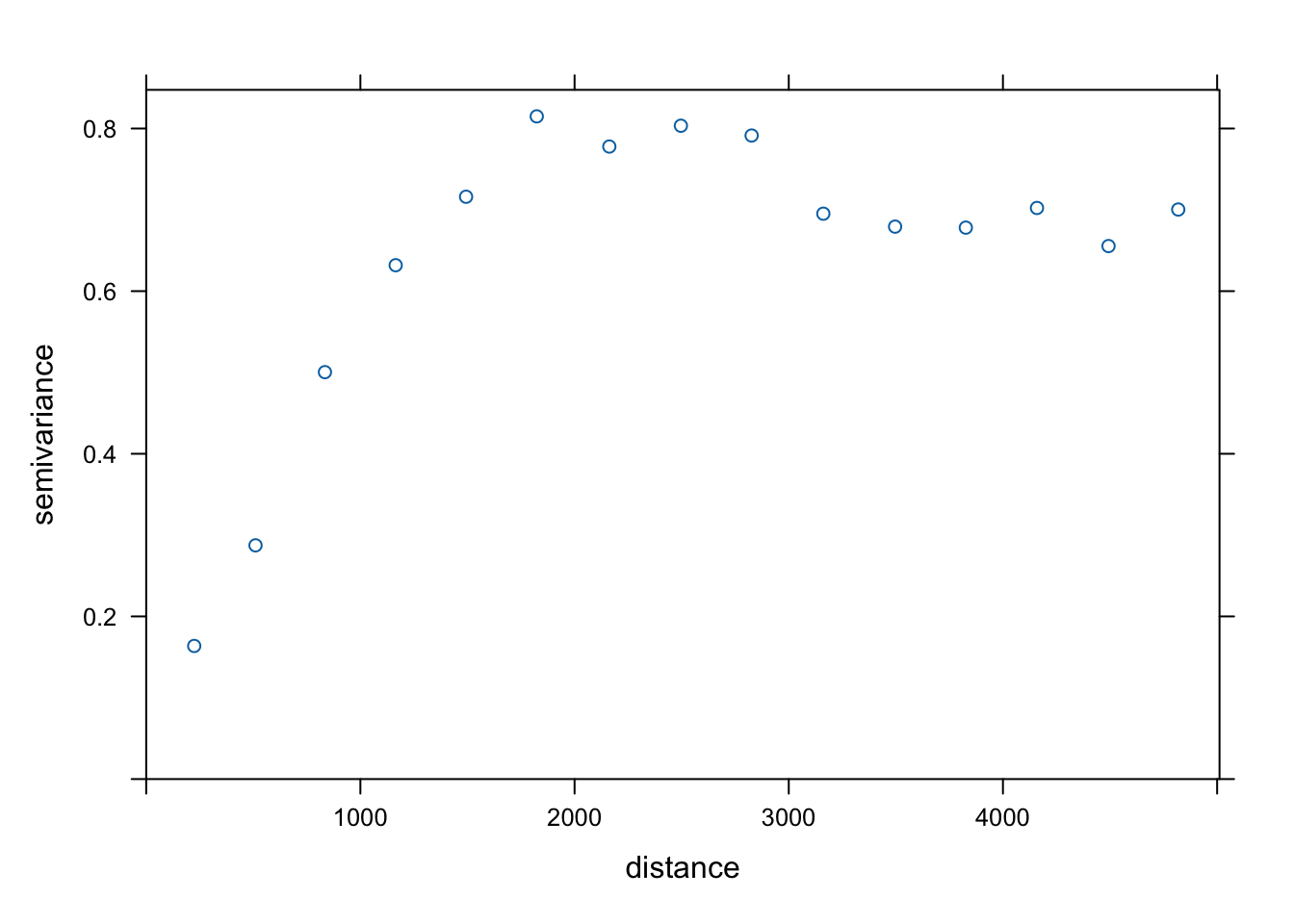
Rycina C.7: Semiwariogram zmiennej tavg.

moj_model = vgm(psill = 0.65,
        model = "Sph",
        range = 2000,
        nugget = 0.15)
plot(moj_semiwar, moj_model)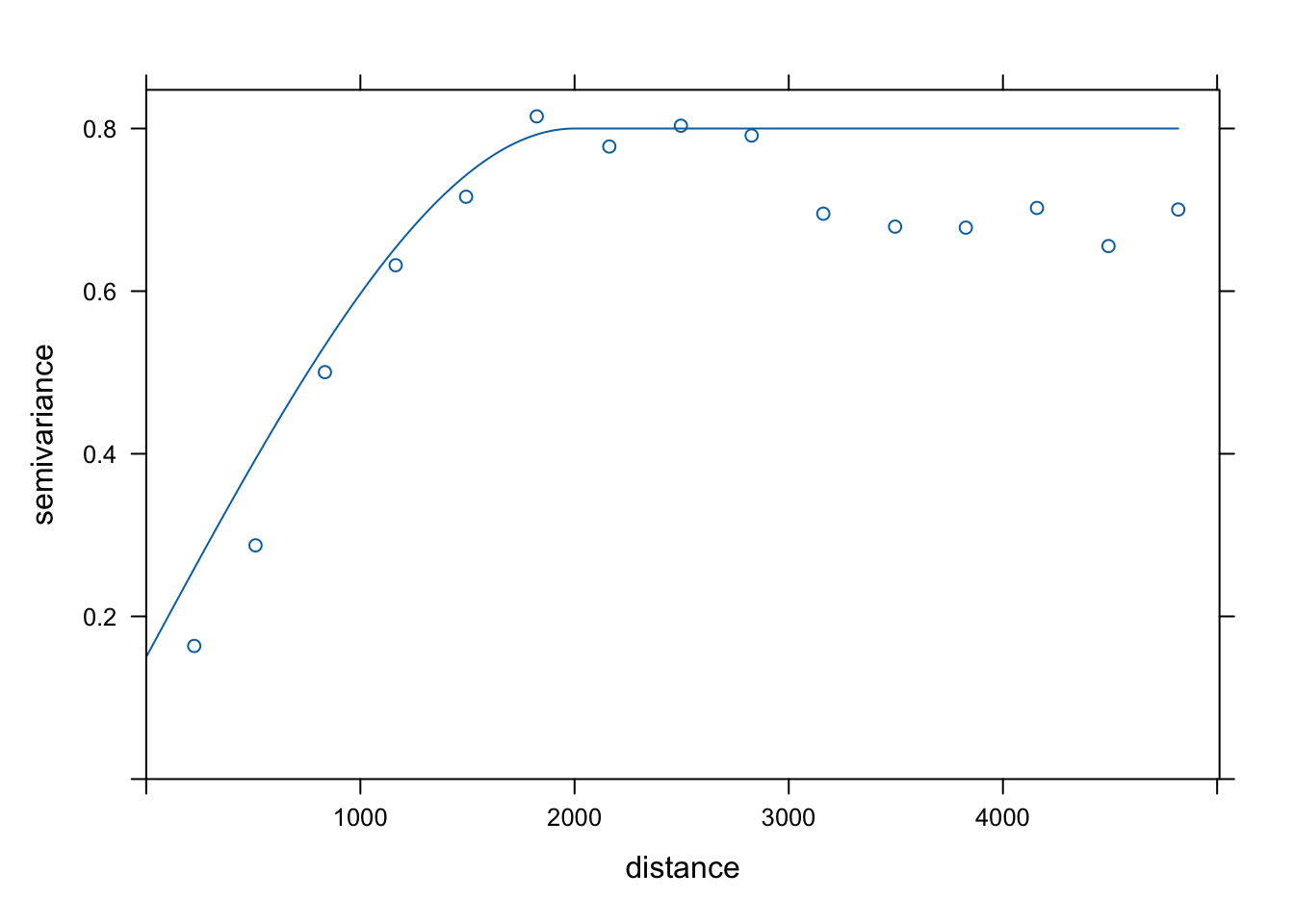

Rycina C.8: Model semiwariogramu zmiennej tavg.

Drugi model, oprócz zmiennej tavg, używa też wartości współrzędnych oraz modelu o parametrach zmodyfikowanych przez funkcję fit.variogram().

moje_punkty$X = st_coordinates(moje_punkty)[, 1]
moje_punkty$Y = st_coordinates(moje_punkty)[, 2]
moj_semiwar2 = variogram(tavg ~ X + Y,
                         locations = moje_punkty)
plot(moj_semiwar2)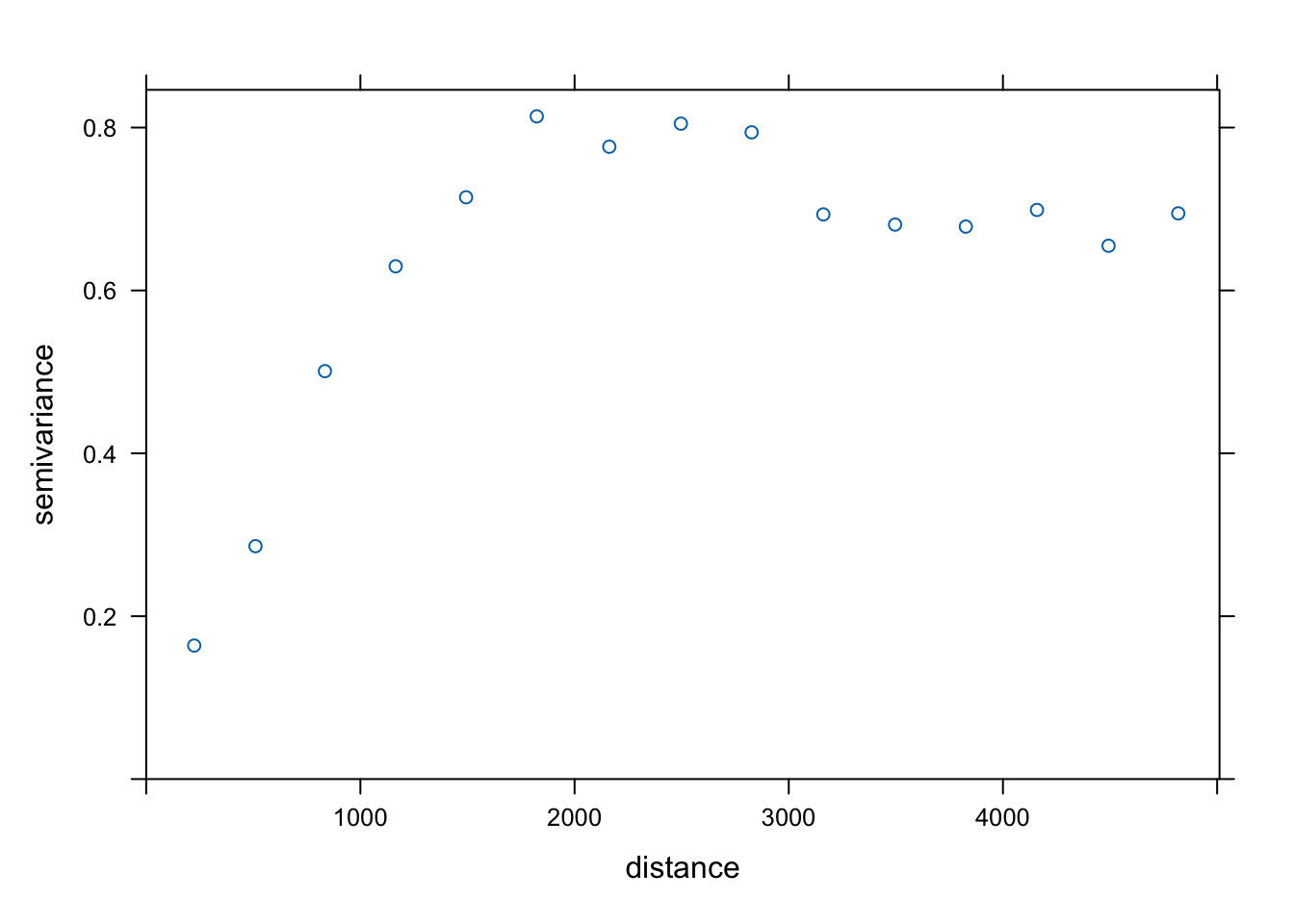

Rycina C.9: Semiwariogram zmiennej tavg uwzględniający współrzędne x i y.

moj_model2 = vgm(model = "Sph", nugget = 0.1)
moj_model2 = fit.variogram(moj_semiwar2, moj_model2)
moj_model2

##   model      psill    range
## 1   Nug 0.01750625    0.000
## 2   Sph 0.73618909 1852.585

plot(moj_semiwar2, moj_model2)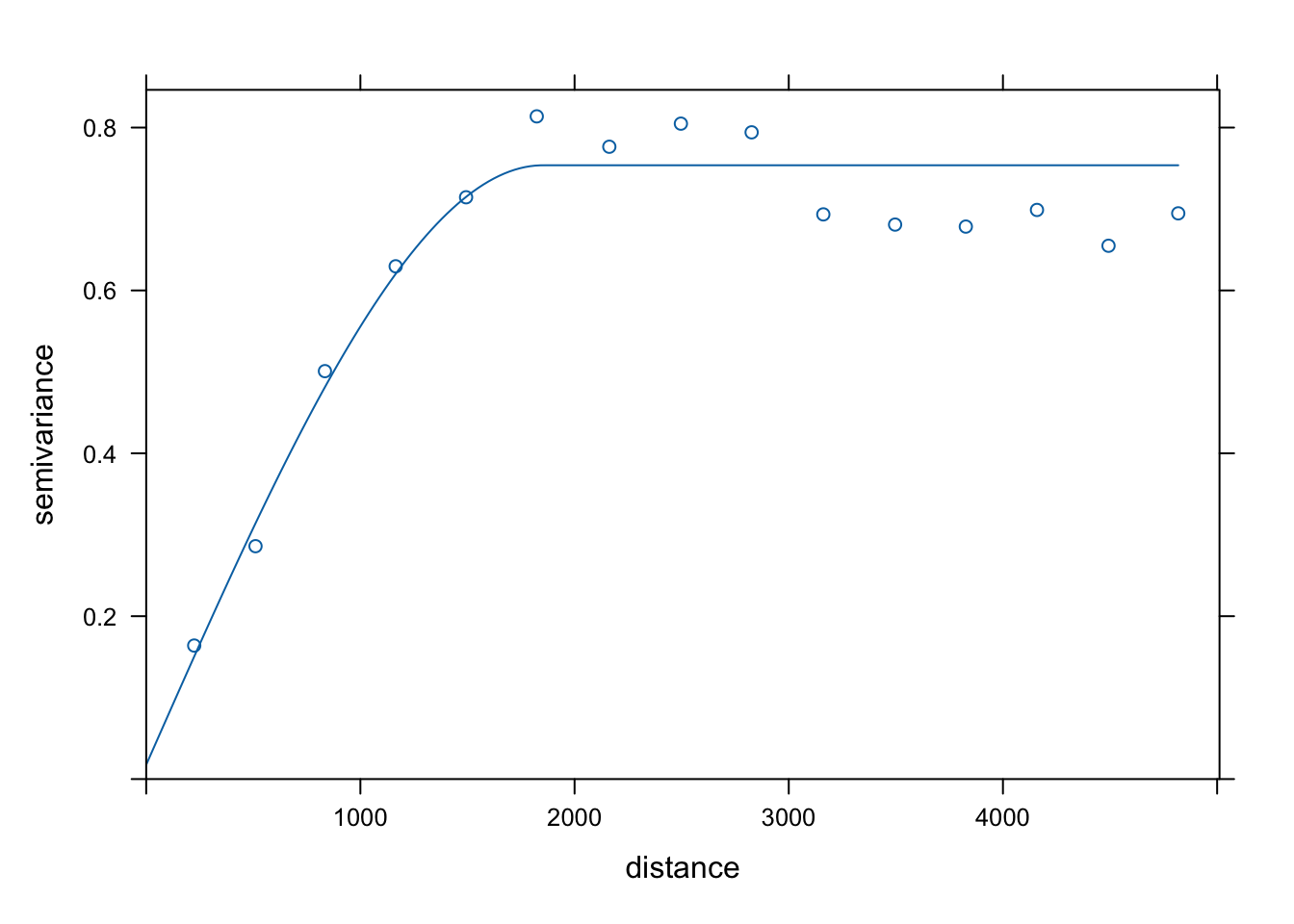

Rycina C.10: Model semiwariogramu zmiennej tavg uwzględniający współrzędne x i y.

C.4 Ocena jakości modeli

Aby porównać oba modele należy przyjąć metodę walidacji oraz współczynnik jakości estymacji. W tym przykładzie użyto kroswalidacji metodą LOO (funkcja krige.cv) oraz pierwiastek błędu średniokwadratowego (RMSE) jako miarę jakości.

ocena1 = krige.cv(tavg ~ 1,
                  locations = moje_punkty,
                  model = moj_model,
                  beta = 30)
RMSE1 = sqrt(mean((ocena1$residual) ^ 2))

ocena2 = krige.cv(tavg ~ X + Y,
                  locations = moje_punkty,
                  model = moj_model2)
RMSE2 = sqrt(mean((ocena2$residual) ^ 2))

Porównanie dwóch wartości RMSE pozwala zdecydowanie stwierdzić, że drugi model charakteryzuje się lepszą jakością estymacji.

RMSE1

## [1] 6.233389

RMSE2

## [1] 0.586952

C.5 Stworzenie siatki

Przedostatnim krokiem jest utworzenie siatki do estymacji. Do niej zostaną wpisane wartości uzyskane z modelu semiwariogramu.

punkty_bbox = st_bbox(moje_punkty)
moja_siatka = st_as_stars(punkty_bbox, 
                          dx = 100,
                          dy = 100)
moja_siatka$X = st_coordinates(moja_siatka)[, 1]
moja_siatka$Y = st_coordinates(moja_siatka)[, 2]

C.6 Stworzenie estymacji

Następnie nowo utworzona siatka może posłużyć do stworzenia estymacji (rycina C.11).

moja_estymacja = krige(tavg ~ X + Y,
                       locations = moje_punkty,
                       newdata = moja_siatka,
                       model = moj_model2)

## [using universal kriging]

tm_shape(moja_estymacja) +
        tm_raster(col = "var1.pred", style = "cont", palette = "-Spectral")
tm_shape(moja_estymacja) +
        tm_raster(col = "var1.var", style = "cont", palette = "viridis")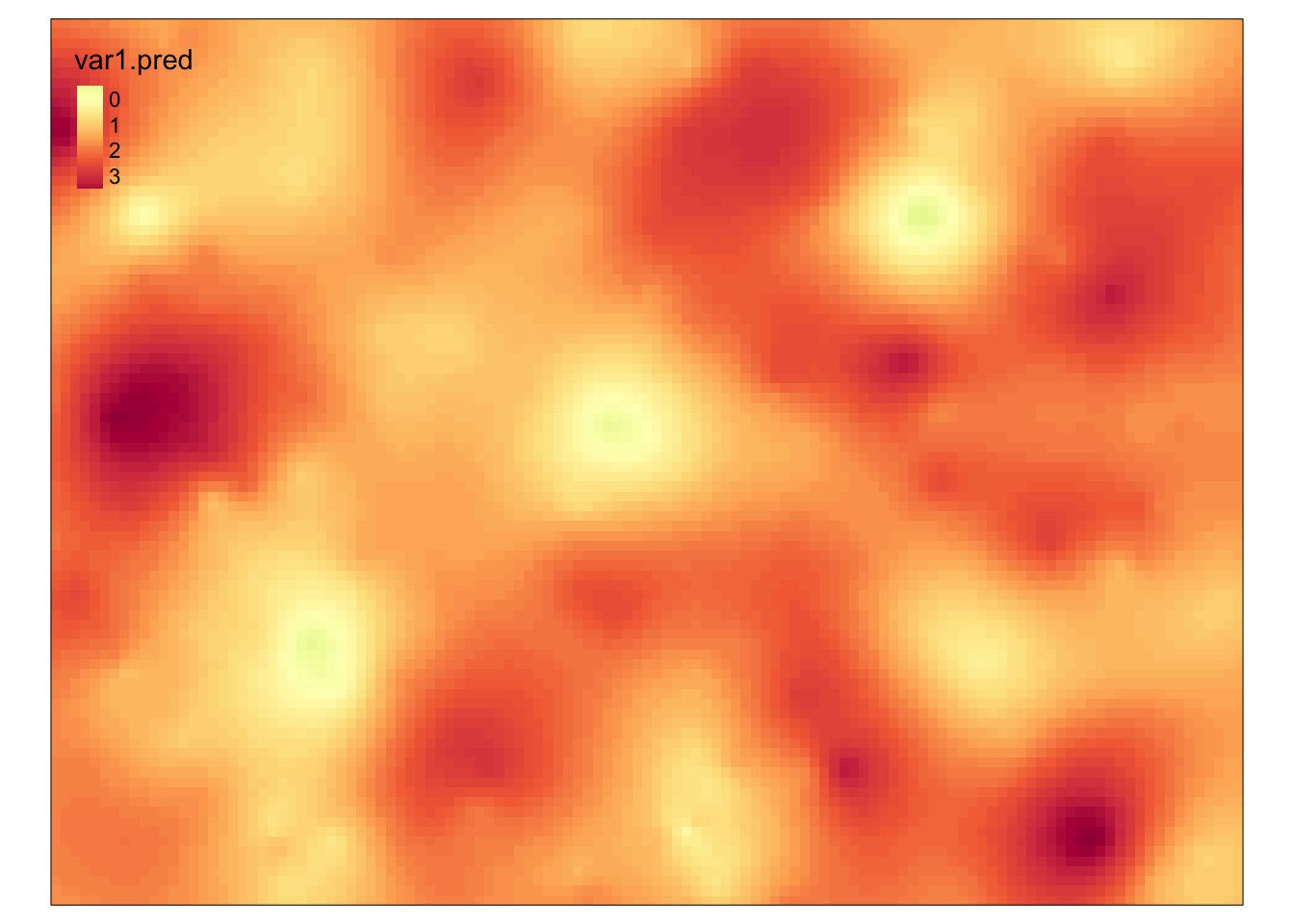

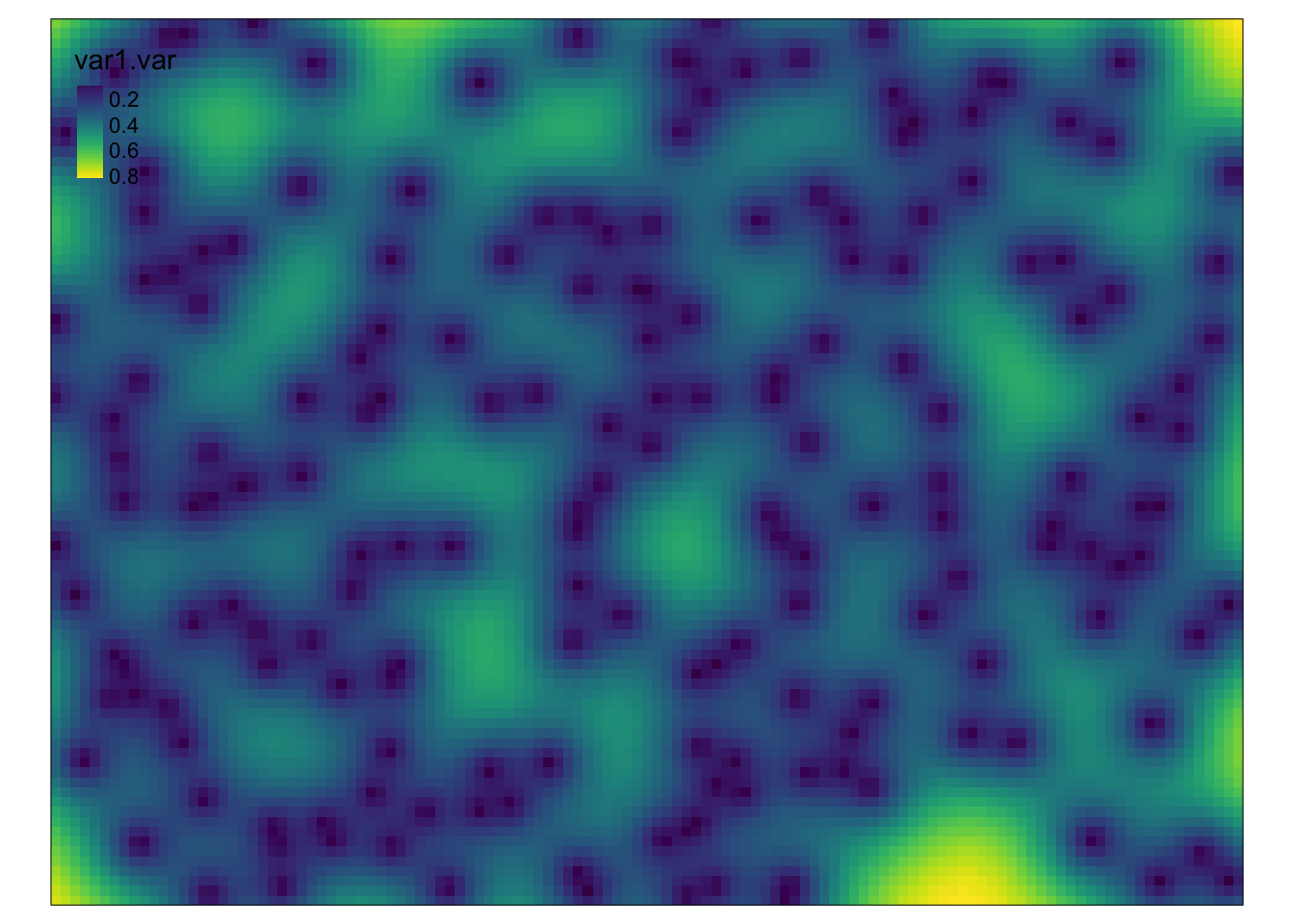
Rycina C.11: Estymacja i wariancja estymacji drugiego modelu zmiennej tavg.

Wynikiem uproszczonej analizy geostatystycznej jest mapa estymowanych wartości temperatury dla całego badanego obszaru oraz mapa przedstawiająca wariancję estymacji temperatury.

B Dane

Bibliografia