Chapter 7 Poisson regression

When the response is a count (a positive integer,e.g.: number of cases of a disease, number of infected plants, firms going bankrupt etc …), we can use a count regression model to explain this response in terms of the given predictors. Sometimes, the total count is bounded, in which case a binomial response regression should probably be used. In other cases, the counts might be sufficiently large that a normal approximation is justified so that a normal linear model may be used.

When exploratory variables are categorical (i.e. you have a contingency table with counts in the cells), the models are usually called log-linear models. If they are numerical/continuous, convention is to call them Poisson regression.

Poisson regression may also be appropriate for rate data, where the rate is a count of events occurring to a particular unit of observation, divided by some measure of that unit’s exposure. For example, the number of deaths may be affected by the underlying population at risk, in demography death rates are modelled as the count of deaths divided by person-years. We include the exposure (exp) in the denominator and form a rate such as: \[rate=Y/exp\Rightarrow Y=rate \times exp.\]

Linear regression methods (constant variance, normal errors) are not appropriate for count data for 4 main reasons:

The linear model might lead to the prediction of negative counts
The variance of the response variable is likely to increase with the mean
The errors will not be normally distributed
Zeros are difficult to handle in transformations

7.1 Poisson distribution

The Poisson distribution is widely used for the description of count data that refer to cases where we know how many times something happened, but we have no way of knowing how many times it did not happen (recall that with the binomial distribution we know how many times something did not happen as well as how often it did happen)

A discrete random variable \(\mathbf{Y}\) is distributed as Poisson with parameter \(\mu>0\), if, for \(k=0,1,2,\ldots\) the probability mass function of \(\mathbf{Y}\) is given by: \[Pr(Y=k)=\frac{e^{-\mu}\mu^k}{k!}.\] Also, \(E[\mathbf{Y}]=Var[\mathbf{Y}]=\mu\).

7.2 Parameters estimation and inference

As in de case of logistic regression, we will not model directly the mean of the response variable, but a transformation. In the case of Poisson regression the usual link function if the log, therefore: \[log(\mu)=\beta_0+\beta_1X_1+\ldots +\beta_k X_k=\mathbf{X}\boldsymbol{\beta}\] In order to estimate the parameters, we will use maximun likelihood. The likelihood would be: \[\mathcal{L}(y_1,\ldots , y_n)=\prod_{i=1}^n\frac{e^{-\mu}\mu^{y_i}}{y_i!}.\] and the log-likelihood; \[log\,\mathcal{L}(y_1,\ldots , y_n)=\sum_{i=1}^n -\mu+y_ilog(\mu)-log(y_i!)=\sum_{i=1}^n exp(X_i^\prime\boldsymbol{\beta})+y_ilog(X_i^\prime\boldsymbol{\beta})-log(y_i!) \] Taking derivatives with respect to \(\boldsymbol{\beta}\), we get: \[\frac{\partial log\,\mathcal{L}}{\partial \beta}=\sum_{i=1}^n (y_i-exp(X_i^\prime\boldsymbol{\beta}))X_i \] Again, it is not possible to solve that equation and we use a Newton-Rapson approximation.

Since the \(log(\mu)\) is a linear function of the predictors, \(\mu\) is a multiplicative function of the predictors: \[\mu=e^\beta_o\times e^{\beta_1X_1}\times \ldots \times e^{\beta_kX_k}=e^{\mathbf{X}\boldsymbol{\beta}}\] This means that \(e^{\beta_j}\) represents a multiplier effect of the j\(^{th}\) predictor on the mean, such that a 1 unit increase on \(x_j\) has a multiplicative effect of \(e^{\beta_j}\) on \(\mu\).

Suppose of a single predictor \(x\), and 2 values of \(x\) (i.e. \(x1\) and \(x2\)), with a difference of 1 unit, i.e. x1 = 10 and x2 = 11, where \(\mu_1 = E(Y|x = 10)\) and \(\mu2 = E(Y |x = 11)\)

If \(\beta=0\), them \(e^\beta=1\) and \(\mu_2=\mu_1\). That is \(\mu\) does not depend on \(x\)
If \(\beta>0\), \(e^\beta>1\), and \(\mu_2\) is \(e^\beta\) times larger than \(\mu_1\)
If \(\beta<0\), \(e^\beta<1\), and \(\mu_2\) is \(e^\beta\) times smaller than \(\mu_1\)

As in the case of logistic regression we will use the deviance to compare models: \[D=-2\log\left [ \frac{\text{likelihood of the fitted model}}{\text{likelihood of the saturated model}}\right]\] For large samples \(D\sim \chi^2_{n-{k+1}}\).

Testing wether a variable is significant or not will be done using the likelihood ratio test (expressed in terms of difference between deviances) in a similar way as in the logistic regression.

In the case of Poisson data, goodness of fit is carried out using the Pearson’s chi-squared statistic: \[\chi^2=\frac{\sum_{i=1}^n (y_i-\hat \mu_i)^2}{\hat \mu_i}\] we compare this value with the value of a \(\chi^2_{k+1}\).

residual plots are carried out using the standarized (Pearson) residuals: \[r_i=\frac{y_i-\hat \mu_i}{\sqrt{\hat \mu_i}}\quad r_i\approx N(0,1)\]

7.3 Case study: Species richness

A long-term agricultural experiment had 90 grassland plots, each 25m x 25m, differing in biomass, soil pH and species richness (the count of species in the whole plot). It is well known that species richness declines with increasing biomass, but the question addressed here is whether the slope of that relationship differs with soil pH. The plots were classified according to a 3-level factor as high, medium or low pH with 30 plots in each level. The response variable is the count of species.

Table 7.1: First 10 rows of the `Species` dataset.
pH	Biomass	Species
2	0.4692972	30
2	1.7308704	39
2	2.0897785	44
2	3.9257871	35
2	4.3667927	25
2	5.4819747	29
2	6.6846859	23
2	7.5116506	18
2	8.1322025	19
2	9.5721286	12

First we will fit a linear regression model to the data:

#define pH as factor
species$pH=factor(species$pH)
#plot the result of fitting a linear model
library(ggplot2)
ggplot(species, aes(x = Biomass, y = Species, colour = pH)) + 
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

## `geom_smooth()` using formula = 'y ~ x'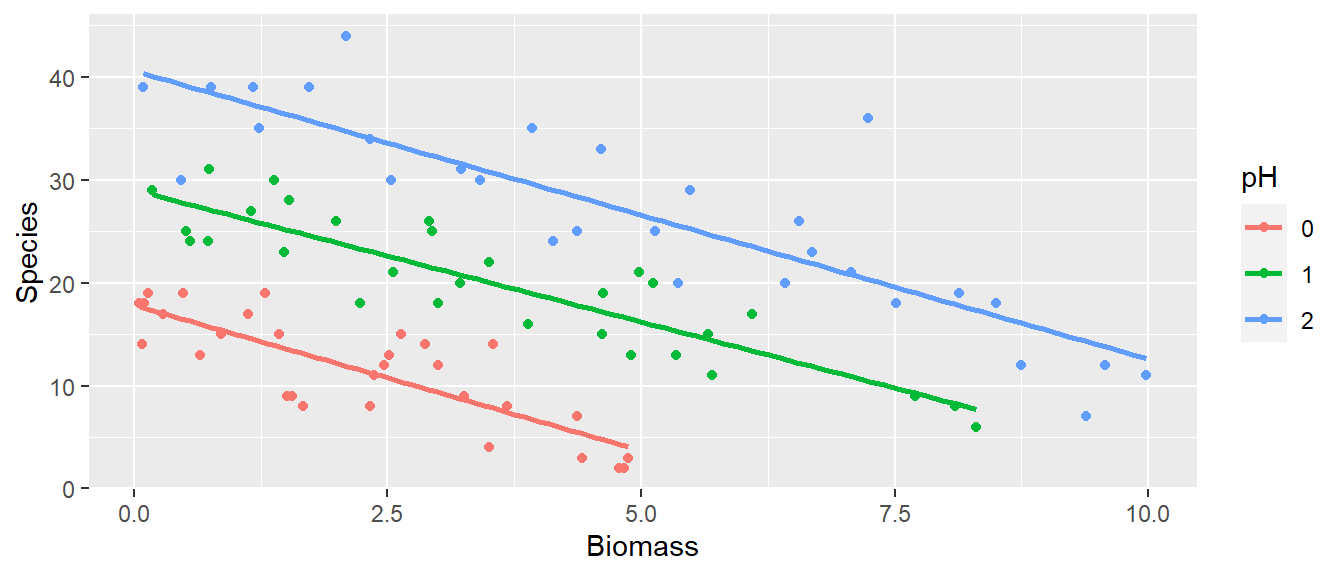

This model will predict a negative value of species when the biomass is 7.5 in soils with low pH.

It is clear that Species declines with Biomass, and that soil pH has a big effect on Species. Let start by fitting each preditor separately and testing if they are significant:

#Fit and test Biomass
m0=glm(Species~Biomass,family=poisson,data=species)
summary(m0)

## 
## Call:
## glm(formula = Species ~ Biomass, family = poisson, data = species)
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  3.184094   0.039159   81.31  < 2e-16 ***
## Biomass     -0.064441   0.009838   -6.55 5.74e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 452.35  on 89  degrees of freedom
## Residual deviance: 407.67  on 88  degrees of freedom
## AIC: 830.86
## 
## Number of Fisher Scoring iterations: 4

anova(m0,test="Chisq")

## Analysis of Deviance Table
## 
## Model: poisson, link: log
## 
## Response: Species
## 
## Terms added sequentially (first to last)
## 
## 
##         Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
## NULL                       89     452.35              
## Biomass  1   44.673        88     407.67 2.328e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#Fit and test Ph
m1=glm(Species~pH,family=poisson,data=species)
summary(m1)

## 
## Call:
## glm(formula = Species ~ pH, family = poisson, data = species)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  2.44813    0.05368   45.60  < 2e-16 ***
## pH1          0.54760    0.06744    8.12 4.68e-16 ***
## pH2          0.84027    0.06423   13.08  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 452.35  on 89  degrees of freedom
## Residual deviance: 265.12  on 87  degrees of freedom
## AIC: 690.31
## 
## Number of Fisher Scoring iterations: 4

Now, we will test if the effect of biomass on species richness depends on soil pH, and the strength of the relationship varies with soil pH

m2 <- glm(Species~Biomass+pH,family=poisson,data=species)
m3 <- glm(Species~Biomass*pH,family=poisson,data=species)
anova(m2,m3,test="Chisq")

## Analysis of Deviance Table
## 
## Model 1: Species ~ Biomass + pH
## Model 2: Species ~ Biomass * pH
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1        86     99.242                          
## 2        84     83.201  2    16.04 0.0003288 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

So, although when using a linear model the slopes look very similar, using Poisson regression the interaction between pH and species is significant.

yv2<-predict(m2,type="response") 
yvs2<-split(yv2,species$pH)
yv3<-predict(m3,type="response") 
yvs3<-split(yv3,species$pH)
bvs<-split(species$Biomass,species$pH) 
svs<-split(species$Species,species$pH)
plot(species$Biomass,species$Species, type="n",xlab="Biomass",ylab="Species")
points(bvs[[1]],svs[[1]],col=2, pch=16)
points(bvs[[2]],svs[[2]],col=3, pch=16)
points(bvs[[3]],svs[[3]],col=4, pch=16)
for(i in 1:3){
  o=order(bvs[[i]])
  lines((bvs[[i]])[o],(yvs2[[i]])[o],lty=2,col=i+1)
  lines((bvs[[i]])[o],(yvs3[[i]])[o],col=i+1)
}
legend(7,45, legend=c("without interaction", 
  "with interaction"),lty=c(2,1),bty="n",cex=0.8)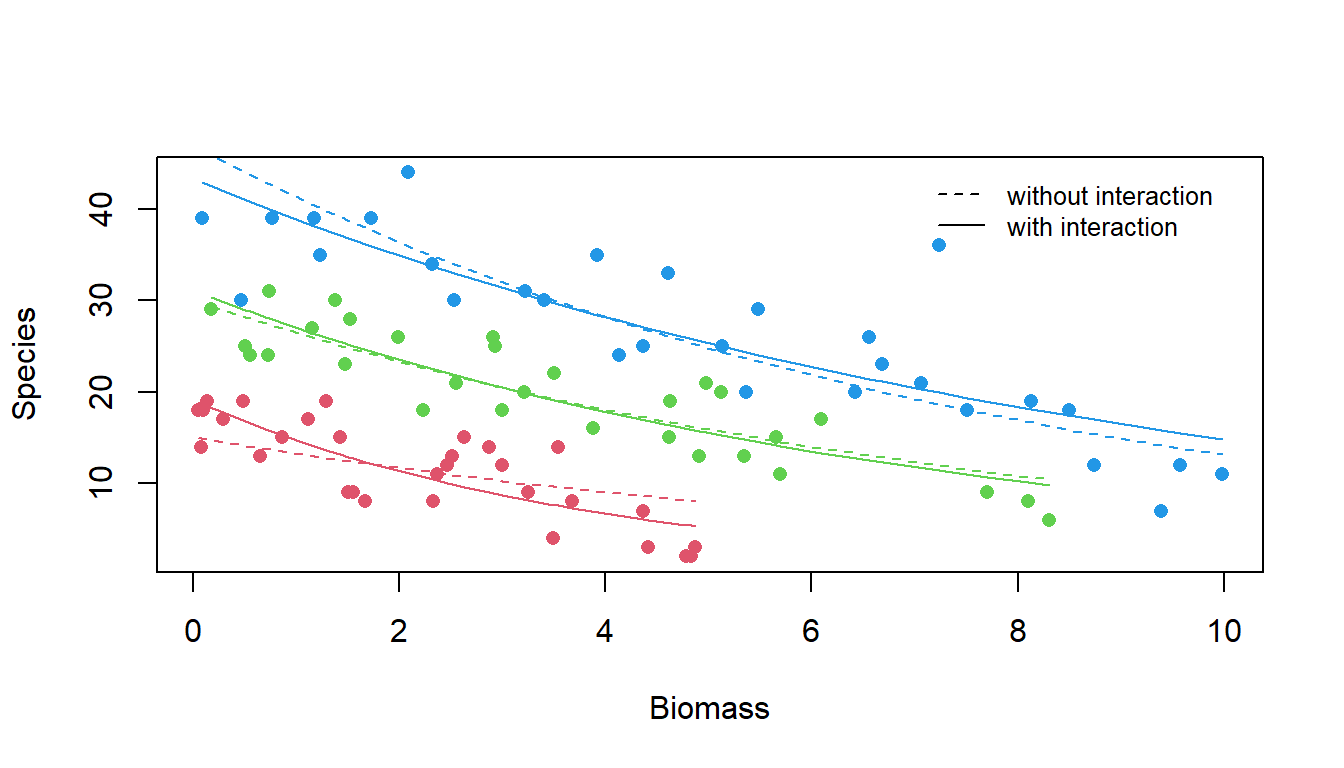

Now, we use the residuals plots to check the model assumptions (remember we use the Pearson’s residuals)

#Fit and test Biomass
par(mfrow=c(1,2))
#Plot residuals versus fitted values
plot(predict(m3),residuals(m3,type="pearson"))
#Qauntile plot
qqnorm(residuals(m3,type="pearson"))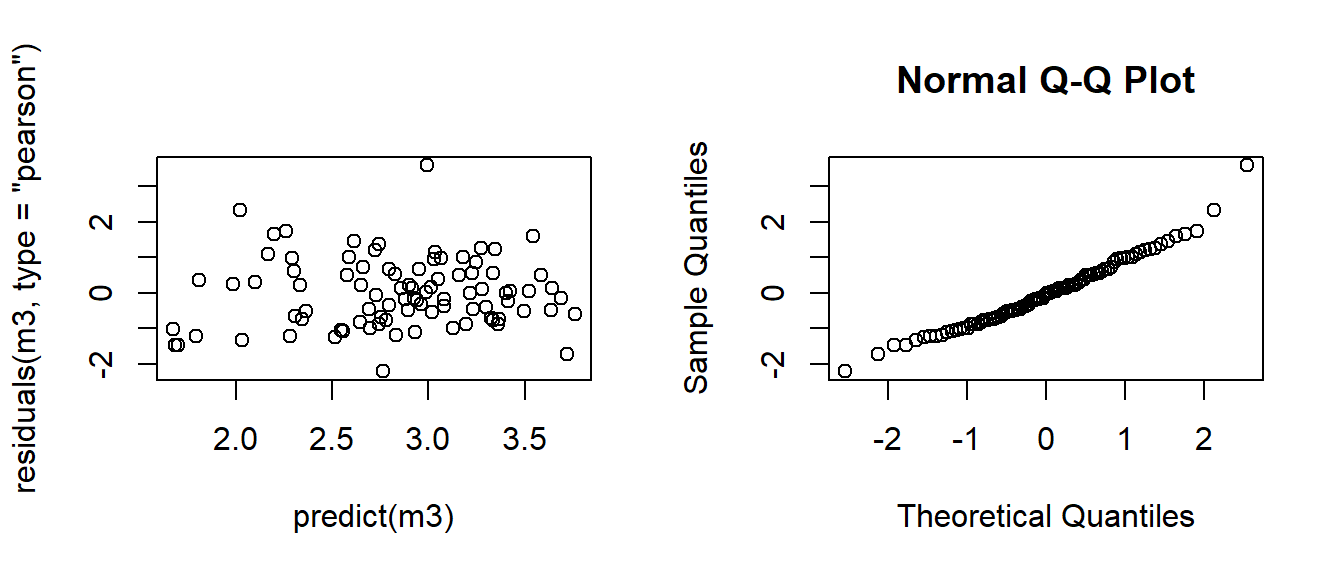

The residual plots look reasonably well (maybe one or two possible outliers). Now we need to check the goodness of fit of the model using Pearson’s chi-squared statistic:

#Pearson's chi-squared statistic
pchisq(m3$deviance,m3$df.residual,lower.tail=FALSE)

## [1] 0.5041192

We conclude that the model fits reasonably well because the goodness-of-fit chi-squared test is not statistically significant. If the test had been statistically significant, it would indicate that the data do not fit the model well. In that situation, we may try to determine if there are omitted predictor variables, if our linearity assumption holds and/or if there is an issue of over-dispersion.

7.4 Poisson regression for incidence rates

The number of events observed may depend on a size variable that determines the number of opportunities for the events to occur. For example, if we record the number of burglaries reported in different cities, the observed number will depend on the number of households in these cities. In other cases, the size variable may be time. For example, the number of violent incidents exhibited over a 6 month period by patients who had been treated in the ER of a psychiatric hospital. The number of violent acts depends on the opportunity to commit them; that is, the number of days out of the 6 month period in which a patient is in the community.

If \(Y\) = count (e.g., number violent acts) and \(t\) = index of the time or space or population (e.g., days in the community). The sample rate of occurrence is \(Y /t\). The expected value of the rate is \[E[Y/t]=E[Y]/t=\mu/t.\] The Poisson regression model for the expected rate of the occurrence of event is: \[log(\mu/t) =\beta_0+\beta_1x\] This can be rearranged as: \[ log(\mu)-log(t)= \beta_0+\beta_1x \Rightarrow log(\mu)=\beta_0+\beta_1x+log(t) \] The term \(log(t)\) is referred to as an offset. It is an adjustment term and a group of observations may have the same offset, or each individual may have a different value of t. It is known and does not need to be estimated from the data, but it will change the value of the estimated counts: \[\hat \mu=t\times e^{\hat \beta_0}e^{\hat \beta_1x}\] That is, the mean count is proportional to \(t\). Note that the interpretation of parameter estimates, will stay the same as for the model of counts; you just need to multiply the expected counts by \(t\).

In Poisson regression we also have relative risk (RR) interpretations, i.e. the estimated effect of an explanatory variable is multiplicative on the rate, and thus leads to a risk ratio or relative risk. Let \(\lambda_0=\mu_0/t\) be the incidence rate when \(x=x_0\) and \(\lambda_1\) when \(x= x_0 + 1\), then \[ log\left ( \frac{\lambda_1}{\lambda_0} \right )= log(\lambda_1)-log(\lambda_0)=\beta\Rightarrow RR=\frac{\lambda_1}{\lambda_0} =e^\beta\]

7.5 Case study: Campus Crime

Students like to feel safe and secure when attending a College or University. In response to legislation, the US Department of Education seeks to provide data and reassurances to students and parents alike. The dataset correspond to the number of property or violent crimes reported in 81 Colleges or Universities in the US in an academic year.

The dataset contains the following variables:

Type = college (C) or university (U)
Region = region of the country (C = Central, MW = Midwest, NE = Northeast, SE = Southeast, SW = Southwest, and W = West)
Violent = the number of violent crimes for that institution for the given year
Property = the number of property crimes for that institution for the given year
Enrollment = enrollment at the school

crime <- read.table(file = "./Datasets/Campus_Crime.txt", header = TRUE)
crime$Region=factor(crime$Region)
crime$Type=factor(crime$Type)
knitr::kable(
  head(crime, 10),
  booktabs = TRUE,
  longtable = TRUE,
  caption = 'First 10 rows of the `Campus Crime` dataset.')

Table 7.2: First 10 rows of the `Campus Crime` dataset.
Region	Type	Enrollment	Property	Violent
SE	U	5590	266	30
SE	C	540	10	0
W	U	35747	1233	23
W	C	28176	210	1
SW	U	10568	116	1
SW	U	3127	29	0
W	U	20675	284	7
W	C	12548	43	0
C	U	30063	660	19
C	C	4429	94	4

The main question to be answer is: Are there regional differences in violent crime on campus controlling for differences in the type of school?

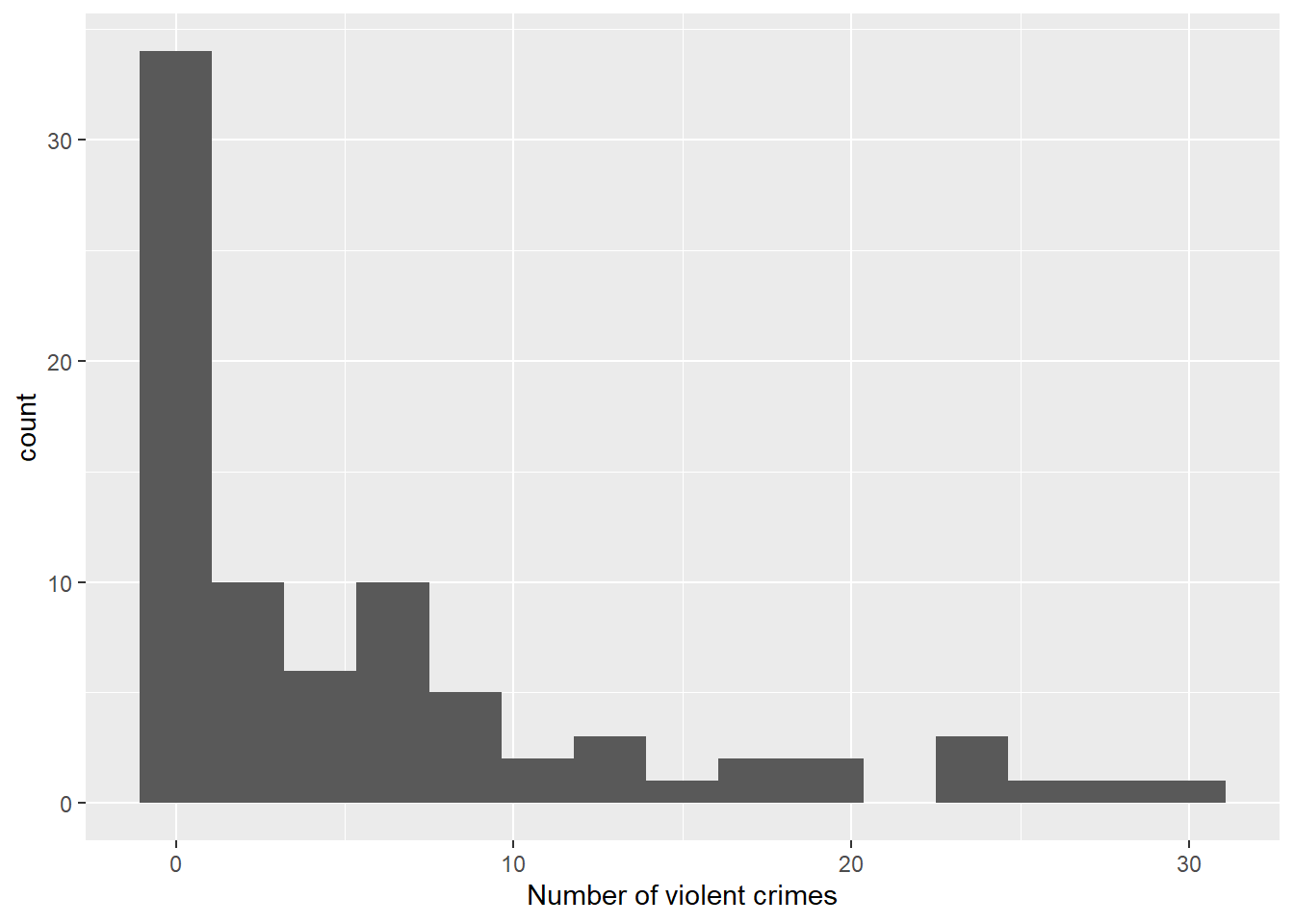
Figure 7.1: Histogram of number of violent crimes by institution

Many schools reported no violent crimes or very few crimes. A few schools have a large number of crimes making for a distribution that appears to be far from normal. A Poisson regression may be helpful here.

Let’s take a look at the covariates of interest for these schools, type of institution and region. In our data, the majority of institutions are universities, 65% of the 81 schools, only 35% are colleges. Interest centers on whether the different regions tend to have different crime rates

It is important to note that the counts are not directly comparable because they come from different size schools. We cannot compare the 30 violent crimes from the first school in the dataset to no violent crimes for the second school when their enrollments are vastly different; 5,590 for school 1 versus 540 for school 2. This is why we need to model the rates instead of the counts. The roll of \(t\) above is played by the underlying population at risk (Enrollment). For the remainder of the case study, we examine the violent crime counts in terms of the rate per 1,000 enrolled, that is the (number of violent crimes)/(number enrolled) *1,000.

#boxplot per type and region
ggplot(crime, aes(x = Region, y = 1000*Violent/Enrollment, fill = Type)) +
  geom_boxplot() +
  ylab("Violent crimes per 1000 students")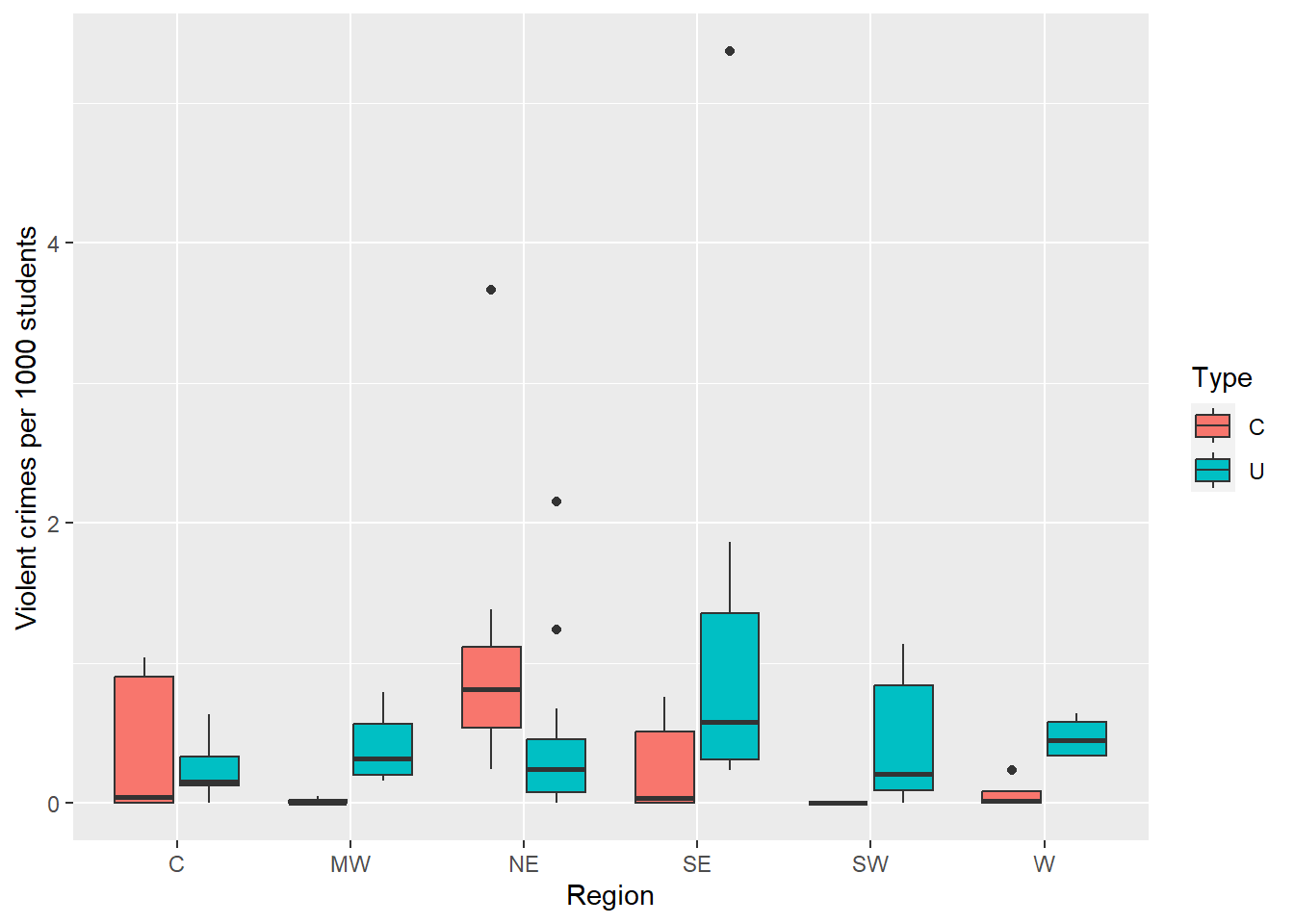

Figure 7.2: .

Although working with the observed rates is useful during the exploratory data analysis, it is not the rates that go into the model; the counts are the responses when modeling. So we must take into account the Enrollment in another way, and we use it as an offset.

We are interested primarily in differences in violent crime between institutional types controlling for difference in regions, so we fit a model with both Region and Type:

## Modeling
modeltr = glm(Violent~Type+Region,family=poisson,offset=log(Enrollment),
              data=crime)
summary(modeltr)


Call:
glm(formula = Violent ~ Type + Region, family = poisson, data = crime, 
    offset = log(Enrollment))

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -8.50936    0.17120 -49.704  < 2e-16 ***
TypeU        0.34011    0.13234   2.570  0.01017 *  
RegionMW     0.09942    0.17752   0.560  0.57547    
RegionNE     0.78109    0.15305   5.103 3.33e-07 ***
RegionSE     0.87668    0.15314   5.725 1.04e-08 ***
RegionSW     0.50251    0.18508   2.715  0.00663 ** 
RegionW      0.27324    0.18741   1.458  0.14484    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 491.00  on 80  degrees of freedom
Residual deviance: 426.01  on 74  degrees of freedom
AIC: 657.89

Number of Fisher Scoring iterations: 6

The Region coefficients each compare the mean rate for that region to the Central region. According to the p-values, the Northeast, the Southeast and the Southwest differ significantly from the Central region. The estimated coefficient of 0.78103 translates to the violent crime rate per 1,000 in the Northeast being nearly \(2.2\approx e^{0.78}\) times that of the Central

What would be the meaning of the coefficient for Type?

Comparisons to regions other than the Central region can be accomplished by changing the reference region. If many comparisons are made, it would be best to use a multiple comparisons method such as Bonferroni’s, or Tukey’s Honestly Significant Differences. We can do it using the function glht() in the package multcomp

library(multcomp)
summary(glht(modeltr, mcp(Region="Tukey")))


     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: glm(formula = Violent ~ Type + Region, family = poisson, data = crime, 
    offset = log(Enrollment))

Linear Hypotheses:
             Estimate Std. Error z value Pr(>|z|)    
MW - C == 0   0.09942    0.17752   0.560   0.9933    
NE - C == 0   0.78109    0.15305   5.103   <0.001 ***
SE - C == 0   0.87668    0.15314   5.725   <0.001 ***
SW - C == 0   0.50251    0.18508   2.715   0.0704 .  
W - C == 0    0.27324    0.18741   1.458   0.6857    
NE - MW == 0  0.68168    0.15544   4.385   <0.001 ***
SE - MW == 0  0.77727    0.15554   4.997   <0.001 ***
SW - MW == 0  0.40310    0.18709   2.155   0.2545    
W - MW == 0   0.17383    0.18931   0.918   0.9405    
SE - NE == 0  0.09559    0.12684   0.754   0.9743    
SW - NE == 0 -0.27858    0.16410  -1.698   0.5271    
W - NE == 0  -0.50785    0.16581  -3.063   0.0262 *  
SW - SE == 0 -0.37417    0.16414  -2.280   0.1980    
W - SE == 0  -0.60344    0.16655  -3.623   0.0038 ** 
W - SW == 0  -0.22927    0.19667  -1.166   0.8499    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

The boxplot in the previous figure suggest the effect of the type of institution may vary depending upon the region, so we consider a model with an interaction between region and type:

#Model with interaction
modeli = glm(Violent~Type+Region+Type:Region,family=poisson, offset=log(Enrollment),
             data=crime)
summary(modeli)


Call:
glm(formula = Violent ~ Type + Region + Type:Region, family = poisson, 
    data = crime, offset = log(Enrollment))

Coefficients:
               Estimate Std. Error z value Pr(>|z|)    
(Intercept)     -8.3819     0.3536 -23.707  < 2e-16 ***
TypeU            0.1959     0.3775   0.519  0.60377    
RegionMW        -1.9765     1.0607  -1.863  0.06239 .  
RegionNE         1.5529     0.3819   4.066 4.77e-05 ***
RegionSE         0.2508     0.4859   0.516  0.60577    
RegionSW       -15.4630   736.9341  -0.021  0.98326    
RegionW         -1.8337     0.7906  -2.319  0.02037 *  
TypeU:RegionMW   2.1965     1.0765   2.040  0.04132 *  
TypeU:RegionNE  -1.0698     0.4200  -2.547  0.01086 *  
TypeU:RegionSE   0.6944     0.5122   1.356  0.17516    
TypeU:RegionSW  16.0837   736.9341   0.022  0.98259    
TypeU:RegionW    2.4106     0.8140   2.962  0.00306 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 491.0  on 80  degrees of freedom
Residual deviance: 344.7  on 69  degrees of freedom
AIC: 586.57

Number of Fisher Scoring iterations: 13

These results provide convincing evidence of an interaction between the effect of region and the type of institution. A drop-in-deviance test like the one we carried out in the previous chapter confirms the significance of the contribution of the interaction to this model:

#Chisq test
anova(modeltr,modeli,test="Chisq")

Analysis of Deviance Table

Model 1: Violent ~ Type + Region
Model 2: Violent ~ Type + Region + Type:Region
  Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
1        74     426.01                          
2        69     344.70  5   81.312 4.459e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

For example, our model estimates that violent crime rates are 13.55 (\(e^{0.1959+2.4106}\)) times higher in universities in the West compared to colleges, while in the Northeast we estimate that violent crime rates are 2.4 (\(1/e^{0.1959-1.0698}\)) times higher in colleges.

Exercise 20

How many times is the rate of Southeastern Universities higher (or smaller) that Northeaster Universities?

We also need to check the goodness of fit of the model. For large samples \(D\sim \chi^2_{n-{k+1}}\). :

#Pearson's chi-squared statistic
pchisq(modeli$deviance,modeli$df.residual,lower.tail=FALSE)

[1] 2.881954e-38

This suggests that the interaction model does not fit well. One possibility is that there are other important covariates that should be in the model. Another posibility is overdispersion (the variance is larger than the mean) as a possible explanation of the significant lack-of-fit.

Exercise 21

Find the best model for the property crime rates and interpret the parameters

7.6 Overdispersion

In Poisson regression, it is assumed that \(Var(Y)=\mu\). Sometimes the data do not hold this assumption, this yields to wrong estimation of the standard errors of the parameters estimates. We will say that there is Overdispersion if \(Var(y)>\mu\).

A simple option to account for this phenomena is to include a dispersion parameter \(\phi\), such that \(Var(Y) = \phi\mu\), then when \(\phi= 1\) we are in the Poisson case. We can estimate a dispersion parameter, by dividing the model deviance by its corresponding degrees of freedom: \[\hat \phi=\frac{Deviance}{n-(k+1)}\] We inflate the standard errors by multiplying the variance by \(\phi\) so that the standard errors are larger than the likelihood approach would imply; i.e., \[SE_Q(\hat \beta)=\sqrt{\hat \phi}SE(\hat \beta)\] If we choose to use a dispersion parameter with our model, we refer to the approach as quasilikelihood. In R we can use it specifying family=quasipoisson:

#Quasipoisson Model
modeliq = glm(Violent~Type+Region+Type:Region,family=quasipoisson, 
              offset=log(Enrollment),data=crime)
summary(modeliq)


Call:
glm(formula = Violent ~ Type + Region + Type:Region, family = quasipoisson, 
    data = crime, offset = log(Enrollment))

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)      -8.3819     0.9171  -9.139 1.67e-13 ***
TypeU             0.1959     0.9794   0.200    0.842    
RegionMW         -1.9765     2.7514  -0.718    0.475    
RegionNE          1.5529     0.9906   1.568    0.122    
RegionSE          0.2508     1.2605   0.199    0.843    
RegionSW        -15.4630  1911.6645  -0.008    0.994    
RegionW          -1.8337     2.0508  -0.894    0.374    
TypeU:RegionMW    2.1965     2.7926   0.787    0.434    
TypeU:RegionNE   -1.0698     1.0894  -0.982    0.330    
TypeU:RegionSE    0.6944     1.3287   0.523    0.603    
TypeU:RegionSW   16.0837  1911.6645   0.008    0.993    
TypeU:RegionW     2.4106     2.1115   1.142    0.258    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasipoisson family taken to be 6.72924)

    Null deviance: 491.0  on 80  degrees of freedom
Residual deviance: 344.7  on 69  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 13

In the absence of overdispersion, we expect the dispersion parameter estimate to be 1. The estimated dispersion parameter here is much larger than 1 (6.729) indicating overdispersion (extra variance) that should be accounted for. The larger estimated standard errors in the quasipoisson model reflect the adjustment. For example, the standard error for the West region term from a likelihood based approach is 0.7906, whereas the quasilikelihood standard error is \(2.0508=\sqrt{6.729}\times 0.7906\). This term is no longer significant under the quasipoisson model. In fact, after adjusting for overdispersion (extra variation), none of the model coefficients in the quasipoisson model are significant at the .05 level!.

In this case, two models fitted using the quasipoisson distribution should be compared using a \(F\) test instead of a \(\chi^2\).

7.6.1 Negative Binomial models

Another approach to dealing with overdispersion is to model the response using a negative binomial instead of Poisson. It also include an extra parameter to deal with the overdispersion, but it has the advantage that it assumes an explicit likelihood model. In the negative binomial: \[E(Y)=\mu\quad Var(Y)=\mu+\mu^2\kappa\] If \(\kappa=0\) we have the Poisson case

#Negative Binomial Model
#Now the offset is passed as weights
modelinb = glm.nb(Violent~Type+Region+Type:Region, 
            weights=offset(log(Enrollment)),link=log,data=crime)
summary(modelinb)


Call:
glm.nb(formula = Violent ~ Type + Region + Type:Region, data = crime, 
    weights = offset(log(Enrollment)), link = log, init.theta = 1.166849073)

Coefficients:
                 Estimate Std. Error z value Pr(>|z|)    
(Intercept)       0.47367    0.18762   2.525 0.011582 *  
TypeU             1.12894    0.21065   5.359 8.36e-08 ***
RegionMW         -1.44611    0.41057  -3.522 0.000428 ***
RegionNE          1.33657    0.22411   5.964 2.46e-09 ***
RegionSE          0.06019    0.25570   0.235 0.813894    
RegionSW        -20.77626 3760.12009  -0.006 0.995591    
RegionW          -1.16739    0.33468  -3.488 0.000486 ***
TypeU:RegionMW    2.03409    0.43782   4.646 3.38e-06 ***
TypeU:RegionNE   -1.10559    0.26046  -4.245 2.19e-05 ***
TypeU:RegionSE    0.88541    0.29235   3.029 0.002457 ** 
TypeU:RegionSW   21.12796 3760.12009   0.006 0.995517    
TypeU:RegionW     2.10174    0.37991   5.532 3.16e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Negative Binomial(1.1668) family taken to be 1)

    Null deviance: 1219.15  on 80  degrees of freedom
Residual deviance:  787.86  on 69  degrees of freedom
AIC: 3966.8

Number of Fisher Scoring iterations: 1

              Theta:  1.1668 
          Std. Err.:  0.0787 

 2 x log-likelihood:  -3940.7560

These results differ from the quasipoisson model. Several effects are now statistically significant at the .05 level. Compared to the quasipoisson model, negative binomial coefficient estimates are generally in the same direction and similar in size, but negative binomial standard errors are smaller. The different conclusions obtained when fitting quasipoisson and negative binomial implies that we should look for additional covariates and/or more data.

Exercise 22

The dataset ships2 (available in datasets for Chapter 6) concern a type of damage caused by waves to the forward section of cargo-carrying vessels. The variables are:

incidents: the number of damage incidents (you need to remo)
service: aggregate moth of service
period: period of operation (to be defined as a factor), : 1960-74, 75-79
year: year of construction (to be defined as a factor): 1960-64, 65-69, 70-74, 75-79
type: A to E Develop a model for the rate of incidents per aggregate months of service. Check and correct for overdispersion (if necessary). Given the final model, answer the following questions:

Which type of ship has the lowest and the highest risk of incidents?
By how much does the incident rate increases after 1974?
In which year where built the safest ships?

7.6.2 Zero inflated (ZIP) count models

Sometimes we see count response data where the number of zeroes appearing is significantly greater than the Poisson or negative binomial models would predict. For example, in the insurance portfolios for many policies there are no claims observed in the insurance history for a given period of time. This means that the data contains lots of zeros and, as a consequence, the Poisson regression may not give satisfactory results.

Suppose we ask people how many times they have been to the theater in the last month. Some will say zero because they do not like theater, but some zero responses will be from theater goers who have not managed to go in the last month. Circumstances such as these require a mixture model. So we will assume that the response, \(Y_i\), takes value \(0\) with probability \(\phi\), or it takes values from a Poisson distribution \(Y_i\sim P(\mu_i)\) with probability \(1-\phi\). That is \[ \begin{aligned} Pr(Y=0)&= \phi +(1-\phi) p(0)=\phi +(1-\phi)e^{-\mu} \\ Pr(Y=j)&= (1-\phi)p(j)= (1-\phi)\frac{e^{-\mu}\mu^j}{j!}\quad j>0\\ \end{aligned} \] The parameter \(\phi\) represents the proportion who will always respond zero.

Exercise 23

Show why \(Pr(Y=0)=\phi +(1-\phi)e^{-\mu}\)

Thus in the ZIP model we have two parameters: \(\mu\) and \(\phi\). Both parameters, as in case of Poisson regression, are linked with predictor variables with the following link functions: \[ \begin{aligned} log(\mu)=&= \beta_0+\beta_1X_1+\ldots +\beta_k X_k\\ log \left ( \frac{\phi}{1-\phi}\right )&= \alpha_0+\alpha_1Z_1+\ldots +\alpha_k Z_k\\ \end{aligned} \] The covariates that affect the Poisson mean may or may not be the same as the covariates that affect the proportion of true zeros.

Likelihood methods are at the core of this methodology, but fitting is an iterative process.

7.6.3 Case study: PhD publications

The dataset for this case study is an example of over dispersed and zero-inflated counts. The response is a count of publications produced by a PhD Biochemistry student; and the dataset consists of a sample of 915 biochemistry graduate students with the following variables:

art: the count of articles produced during the last three years of PhD
fem: the factor indicating the gender of a student, with levels Men and Women
mar: the factor indicating the marital status of a student, with levels Single and Married
kid5: the number of children aged five or younger
phd: the prestige of the PhD department
ment: the count of articles produced by a PhD mentor during the last three years

The data are available in the pscl package

Table 7.3: First 10 rows of the `bioChemists` dataset.
fem	mar	kid5	phd	ment
Men	Married	0	2.52	7
Women	Single	0	2.05	6
Women	Single	0	3.75	6
Men	Married	1	1.18	3
Women	Single	0	3.75	26
Women	Married	2	3.59	2
Women	Single	0	3.19	3
Men	Married	2	2.96	4
Men	Single	0	4.62	6
Women	Married	0	1.25	0

We find that over 30% of the students did not produced any articles during the last three years of PhD. The Mean Count of articles produced is 1.693.

#Histogram of counts
hist(bioChemists$art,breaks=0:max(bioChemists$art))

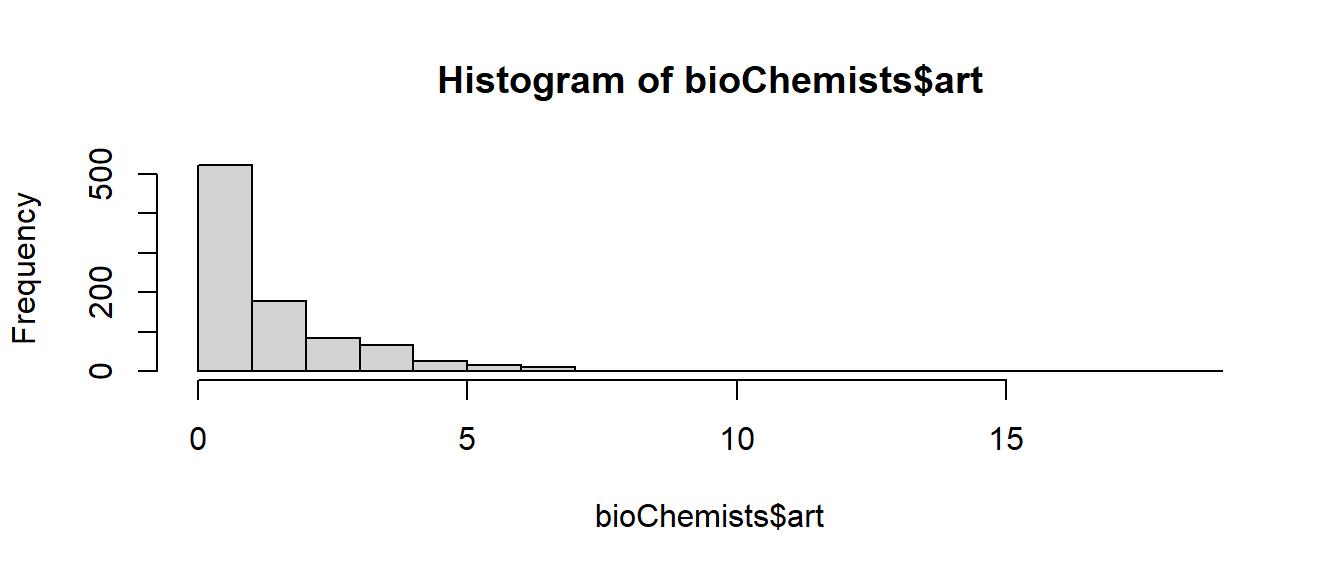The histogram for the count of articles further indicates that this dataset has an abundance of zeros. To account for the extra zeros in the number of publications by PhD biochemists (about 30% in the sample didn’t publish any article), we can imagine that there were two groups of PhD candidates. For one group, the publications would not be important, while for the other group, a large number of publications would be important. The members of the first group would publish no articles, whereas the members of the second group would publish 0, 1, 2, \(\ldots\), articles that may be assumed to have a Poisson or a Negative Binomial distribution. Therefore, this dataset is a classic example of zero-inflated and over dispersed count data.

We start by fitting a Poisson model with all predictors

# Poisson Model with Predictors
pois.m1=glm(art~.,family=poisson, data=bioChemists)
summary(pois.m1)


Call:
glm(formula = art ~ ., family = poisson, data = bioChemists)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.304617   0.102981   2.958   0.0031 ** 
femWomen    -0.224594   0.054613  -4.112 3.92e-05 ***
marMarried   0.155243   0.061374   2.529   0.0114 *  
kid5        -0.184883   0.040127  -4.607 4.08e-06 ***
phd          0.012823   0.026397   0.486   0.6271    
ment         0.025543   0.002006  12.733  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 1817.4  on 914  degrees of freedom
Residual deviance: 1634.4  on 909  degrees of freedom
AIC: 3314.1

Number of Fisher Scoring iterations: 5

We carry out a goodness of fit test:

# Goodness of fit test
gof.ts = pois.m1$deviance
gof.pvalue = 1 - pchisq(gof.ts, pois.m1$df.residual)
gof.pvalue

[1] 0

Almost all covariates are statistically significant, but a goodness-of-fit test reveals that there remains significant lack-of-fit. This lack-of-fit may be explained by the presence candidates that have no interest in publishing articles.

When fitting a ZIP model we need to specify the predictors used to predict the proportion of zeros and the predictors used to predict the positive counts. The function in R used to fit a ZIP model is zeroinfl in the package pscl.

the predictors used for the positive counts appear in the formula in the usual way, the predictors for the proportion of zeros appear after the formula:

zeroinfl(response~predictors1 | predictors2)

We will start by using all predictors in both parts of the model, in that case we only need to specify them once:

# ZIP Model with Predictors
library(pscl)
pois.m2=zeroinfl(art~., data=bioChemists)
summary(pois.m2)


Call:
zeroinfl(formula = art ~ ., data = bioChemists)

Pearson residuals:
    Min      1Q  Median      3Q     Max 
-2.3253 -0.8652 -0.2826  0.5404  7.2976 

Count model coefficients (poisson with log link):
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.640839   0.121307   5.283 1.27e-07 ***
femWomen    -0.209144   0.063405  -3.299 0.000972 ***
marMarried   0.103750   0.071111   1.459 0.144567    
kid5        -0.143320   0.047429  -3.022 0.002513 ** 
phd         -0.006166   0.031008  -0.199 0.842376    
ment         0.018098   0.002294   7.888 3.07e-15 ***

Zero-inflation model coefficients (binomial with logit link):
             Estimate Std. Error z value Pr(>|z|)   
(Intercept) -0.577060   0.509386  -1.133  0.25728   
femWomen     0.109752   0.280082   0.392  0.69517   
marMarried  -0.354018   0.317611  -1.115  0.26501   
kid5         0.217095   0.196483   1.105  0.26920   
phd          0.001275   0.145263   0.009  0.99300   
ment        -0.134114   0.045243  -2.964  0.00303 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Number of iterations in BFGS optimization: 19 
Log-likelihood: -1605 on 12 Df

We can use the standard likelihood testing theory to compare nested models. For example, suppose we consider a simplified version of the ZIP model where we now have different predictors for the two components of the model

# ZIP Model with selected Predictors
pois.m3=zeroinfl(art~fem+kid5+ment |ment, data=bioChemists)
summary(pois.m3)


Call:
zeroinfl(formula = art ~ fem + kid5 + ment | ment, data = bioChemists)

Pearson residuals:
    Min      1Q  Median      3Q     Max 
-2.2802 -0.8807 -0.2718  0.5131  7.4788 

Count model coefficients (poisson with log link):
             Estimate Std. Error z value Pr(>|z|)    
(Intercept)  0.694517   0.053025  13.098  < 2e-16 ***
femWomen    -0.233857   0.058400  -4.004 6.22e-05 ***
kid5        -0.126516   0.039668  -3.189  0.00143 ** 
ment         0.018004   0.002224   8.096 5.67e-16 ***

Zero-inflation model coefficients (binomial with logit link):
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -0.68488    0.20529  -3.336 0.000849 ***
ment        -0.12680    0.03981  -3.185 0.001448 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 

Number of iterations in BFGS optimization: 22 
Log-likelihood: -1608 on 6 Df

Twice the difference in the log-likelihood will be approximately \(\chi^2\) with degrees of freedom equal to the difference in the number of parameters.

# likelihood ratio test
lrt <- 2*(pois.m2$loglik-pois.m3$loglik)
df=pois.m3$df.residual-pois.m2$df.residual
1-pchisq(lrt,df)

[1] 0.4041153

Given the large p-value of 0.4, we conclude that our simplification of the model is justifiable.

In order to interpret the parameters we have to take into account that in the case of the proportion of students who will never publish a paper we are using the logit link and in the case of the mean counts we are using a Poisson. In both cases we need to calculate the exponential of the coefficients, but the interpretation is different.

# parameter interpretation
exp(coef(pois.m3))

count_(Intercept)    count_femWomen        count_kid5        count_ment  zero_(Intercept) 
        2.0027411         0.7914748         0.8811604         1.0181669         0.5041522 
        zero_ment 
        0.8809081

We see that among students who are inclined to write articles, women produce at a rate 0.79 times that for men and each child under five reduces production by about 12% while each additional article produced by the mentor increases production by about 1.8%. We see that each extra article from the mentor reduces the odds of a nonproductive student by a factor of 0.88.

We can use the model to make predictions. Consider a single male with no children whose mentor produced six articles:

# prediction of new observations
newman <- data.frame(fem="Men",kid5=0,ment=6)
predict(pois.m3, newdata=newman, type="prob")

          0         1       2         3          4          5          6           7
1 0.2775879 0.1939403 0.21636 0.1609142 0.08975799 0.04005363 0.01489462 0.004747556
            8            9           10           11           12           13           14
1 0.001324094 0.0003282578 7.324092e-05 1.485593e-05 2.762214e-06 4.740812e-07 7.555503e-08
            15           16          17          18           19
1 1.123857e-08 1.567219e-09 2.05693e-10 2.54968e-11 2.994131e-12

We see that most likely outcome for this student is that no articles will be produced with a probability of 0.278. We can query the probability of no production from the zero part of the model:

# prediction from the zero part of the model
predict(pois.m3, newdata=newman, type="zero")

       1 
0.190666

So the additional probability to make this up to 0.278 comes from the Poisson count part of the model. This difference might be attributed to the student who had the potential to write an article but just didn’t do it.

Exercise 24

The aim of this task is to examine the relationship between the number of physician office visits for a person (ofp) and a set of explanatory variables for individuals on Medicare. Their data are contained in the file dt.csv.

The explanatory variables are number of hospital stays (hosp), number of chronic conditions (numchron), gender (gender; male = 1, female = 0), number of years of education (school), private insurance (privins; yes = 1, no = 0), health_excellent and health_poor, these two are self-perceived health status indicators that take on a value of yes = 1 or no = 0, and they cannot both be 1 (both equal to 0 indicates “average” health). Using these data, complete the following:

1. Estimate the Poisson regression model to predict the number of physician office visits and interpret the coefficients
1. Compare the number of zero-visit counts in the data to the number predicted by the model and comment. Can you think of a possible explanation for why there are so many zeroes in the data?
1. Estimate the zero-inflated Poisson regression model to predict the number of physician office visits. Use all of the explanatory variables for the \(log(\mu)\) part of the model and no explanatory variables in the \(\phi\) part of the model. Interpret the model fit results
1. Complete part (c) again, but now use all of the explanatory variables to estimate \(\phi\). Interpret the model fit results and compare this model to the previous ZIP model using a LRT
1. Examine how well each model estimates the number of 0 counts

Exercise 25

The data.frame fasttrakg contains data from the Canadian National Cardiovascular Disease registry during 1996-1998 with the following variables: - die: number died from MI (myocardial infarction) - cases: number of cases with same covariate pattern - anterior: 1=anterior site MI; 0=inferior site MI hcabg: 1=history of CABG (coronary artery bypass graft); 0=no history of CABG - killip: Killip level of cardiac event severity (1-4)

The following model is fitted:

modelo1=glm(die ~ anterior + hcabg + killip,family=poisson,
offset=log(cases),data=heart)
summary(modelo1)
Coefficients:
Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -4.0698     0.1459 -27.893  < 2e-16 
anterior1     0.6749     0.1596   4.229 2.34e-05 
hcabg1        0.6614     0.9267   2.024 0.0829   
killip2       0.9020     0.1724   5.234 1.66e-07 
killip3       1.1133     0.2513   4.430 9.44e-06 
killip4       2.5126     0.2743   9.160  < 2e-16 

Null deviance: 116.232  on 14  degrees of freedom
Residual deviance:  10.932  on  9  degrees of freedom
AIC: 73.992

Write down the equation of the fitted model
What is the expected number of deaths ina group of 150 people with anterior MI have hcabg and the level of the MI was the lowest possible?.
Can you conclude that the area where the MI happens does not depend on the mortality rate? Why?
Give an interpretation for the estimated parameter of killip4.

Now we consider the following model:

modelo2=glm(die ~ anterior* hcabg +killip,family=poisson,
offset=log(cases),data=heart)
summary(modelo2)
Coefficients:
Estimate Std. Error z value Pr(>|z|)    
(Intercept)       -4.0608     0.1480 -27.443  < 2e-16 
anterior1          0.6618     0.7642   4.029    0.058 
hcabg1             0.5360     0.5170   1.037    0.030    
killip2            0.9007     0.1724   5.224 1.75e-07 
killip3            1.1105     0.2515   4.416 1.01e-05 
killip4            2.5162     0.2745   9.165  < 2e-16 
anterior1:hcabg1   0.2169     0.6670   0.325    0.172  

Null deviance: 116.232  on 14  degrees of freedom
Residual deviance:  10.825  on  8  degrees of freedom
AIC: 75.885

Calculate how many more times is the mortality rate larger/smaller in people who suffered posterior MI and had hcabg compared people who suffered anterior MI without hcabg (assume that all people have the same severity of MI).
Which model is best?, Why?. Indicate the test statistic used and its distribution
Does the model chosen in f) fit the date well? Indicate which test you are using, the null and alternative hypothesis and the value of the test statistic and its distribution.

For the last two question you might need some of the following results:
```
  qchisq(0.95, df = 1:15)
  [1]  3.841459  5.991465  7.814728  9.487729 11.070498 12.591587 14.067140
  [8] 15.507313 16.918978 18.307038 19.675138 21.026070 22.362032 23.684791 
  [15] 24.995790
```

Akaike, H. 1973. “Information Theory and an Extention of the Maximum Likelihood Principle.” Edited by B.N. Petrof and Csaki. Akademia Kiado, Budapest.

Galton, F. R. S. 1886. “Regression Togards Mediocrity in Hereditary Stature.” Antropological Miscellanea 15: 246–63.

Hoerl, A. E., and R. Kennard. 1970. “Ridge Regression: Biased Estimation for Nonorthogonal Problems.” Technometrics 12: 55–67.

Hosmer, D. W., and S. Lemeshow. 1980. “A Goodness-of-Fit Test for the Multiple Logistic Regression Model.” Communication in Statistics 10: 1043–69.