4.3 Introducing data visualisation in R

Data visualisation is such an important topic there are many books and blogs devoted to this topic. One general, i.e., not specific to R, book that is ongoing is (Dougherty and Ilyankou 2020). Entertaining examples of poor visualisations abound but include this blog on junk charts and a simple journalistic piece by Carson MacPherson-Krutsky on “Three Questions To Ask Yourself Next Time You See a Graph, Chart or Map”.

In R there are multiple ways to do the same thing, especially with visualisation. Base R comes has a good deal of built-in functionality for charts and graphs. Then on top of this there are many R packages that extend this functionality of which {ggplot2} authored by Hadley Wickham is by far the most popular.

4.3.1 Visualisation using ggplot2

Until now we have used the plot facilities within Base R however there is an extremely powerful graphics package {ggplot2} which is very widely used. It offers a number of advantages:

ggplot provides a great deal of flexibility
it enables us to add complexity and detail incrementally
it is based on Leland Wilkinson’s landmark book The Grammar of Graphics (hence “gg”) so rigorous and complete
the default colours and other aesthetics are nice (usually!)
you can easily produce production quality graphics
you can save plots (or the beginnings of a plot) as objects
as the programmer you have complete control
multivariate exploration is simplified through faceting and use of colouring
multiple themes are provided for aesthetics which helps produce a consistent style of output for longer or more complex reports

The downside is that ggplot can be a little more complex but I believe it is well worth persevering with.

To start with you need to install the {ggplot2} package which is actually part of {tidyverse} as install.package("tidyverse"). Do this once. Then every new R session load the package from your R library into memory, so if you just want ggplot2 then library(ggplot2) will do.

The package is very well-documented on the tidyverse website and for the impatient there is a cheatsheet(pdf).

As a simple example, lets say we want to visualise the distribution of the arrest rate for murder in the US using the built-in data set USArrests. As an alternative to the boxplot we can use a kernel density estimator. For a technical explanation see (Schucany 2004) and a rather nice visualisation from (Conlen 2020). I’ve chosen to superimpose this on a histogram which can be helpful when the sample is small so we can see the relationship between the actual observations and the smoothed kernel density. In order to make the y-axis meaningful it’s necessary to show the histogram as a probability rather than a count so that the density plot can be properly superimposed.

In Base R this can be achieved in the following code.

# Density plot and histogram of murder arrests using Base R
hist(USArrests$Murder, 
     probability = T,      # use probability rather than count for y-axis
     main = "Histogram and density plot of murder arrests by US state",
     xlab = "Arrests per 100,000 population")
lines(density(USArrests$Murder), col="blue", lwd=2)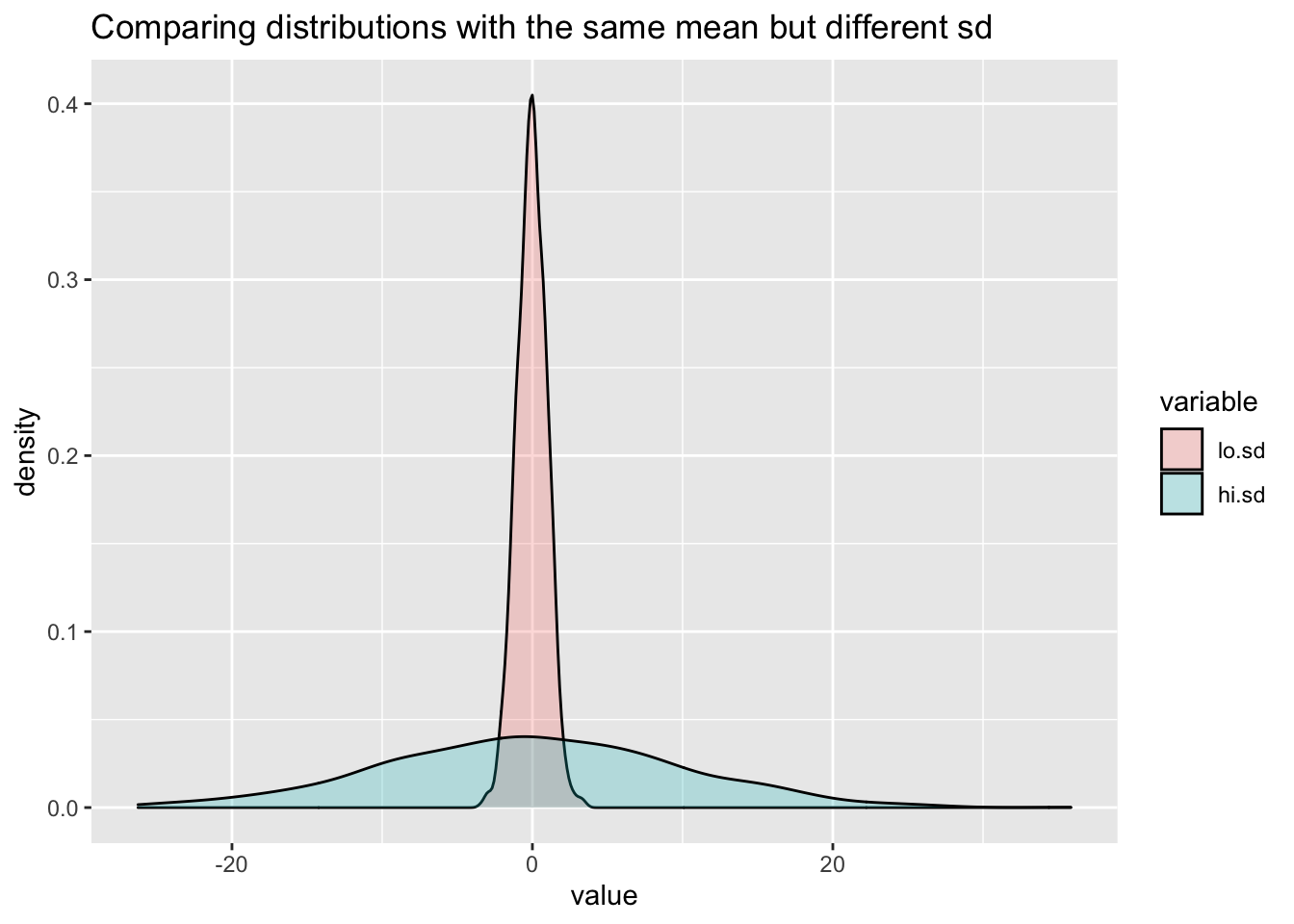

Alternatively we can use {ggplot2}. Notice how we store the output in a new R object that we have created my.plot. This can be manipulated like any other data object. Notice also the structure where the + operator is used to compose the different ggplot2 functions, e.g., geom_density() and ggtitle() into a single plot.

# Using ggplot  
my.plot <- ggplot(USArrests, aes(x=Murder)) + 
# Histogram with scaled density instead of count on y-axis  
           geom_histogram(aes(y=..density..),  
                          binwidth=1, 
                          colour="black", 
                          fill="grey") +
# Overlay with transparent blue density plot  
           geom_density(alpha=.2, fill="blue") +   
           ggtitle("Histogram and density plot of murder arrests by US state") +
           labs(x="Arrests per 100,000 population")
# Output my.plot
my.plot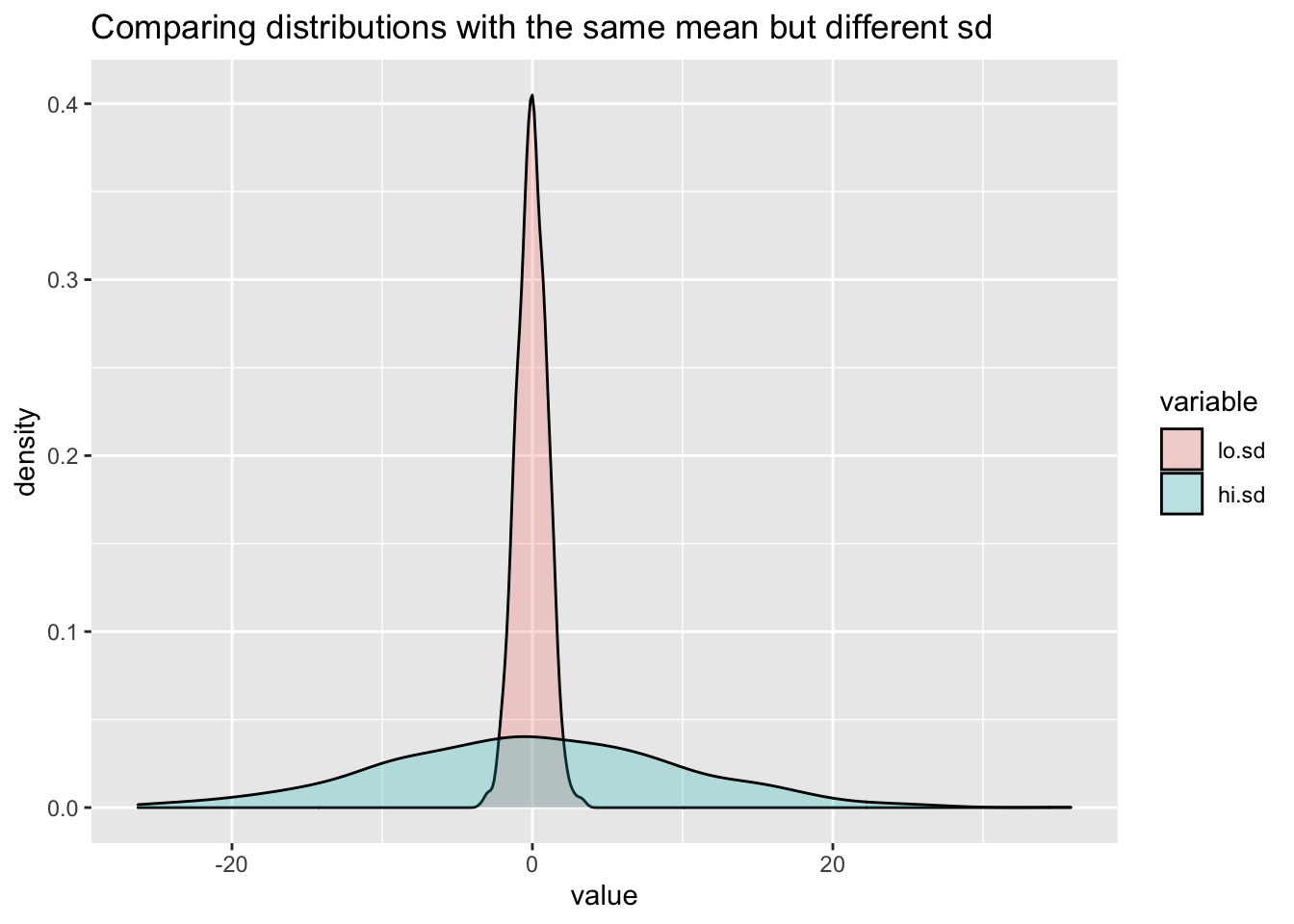

4.3.2 Visualising model fit

Although potentially at a later stage another benefit of visualising your data lies in checking a model and its fit to the data.

Andrew Gelman’s blog (2020) highlighted the following example. A recently published paper (Islam et al. 2020) in the BMJ used regression discontinuity modelling to estimate the effect of social distancing.

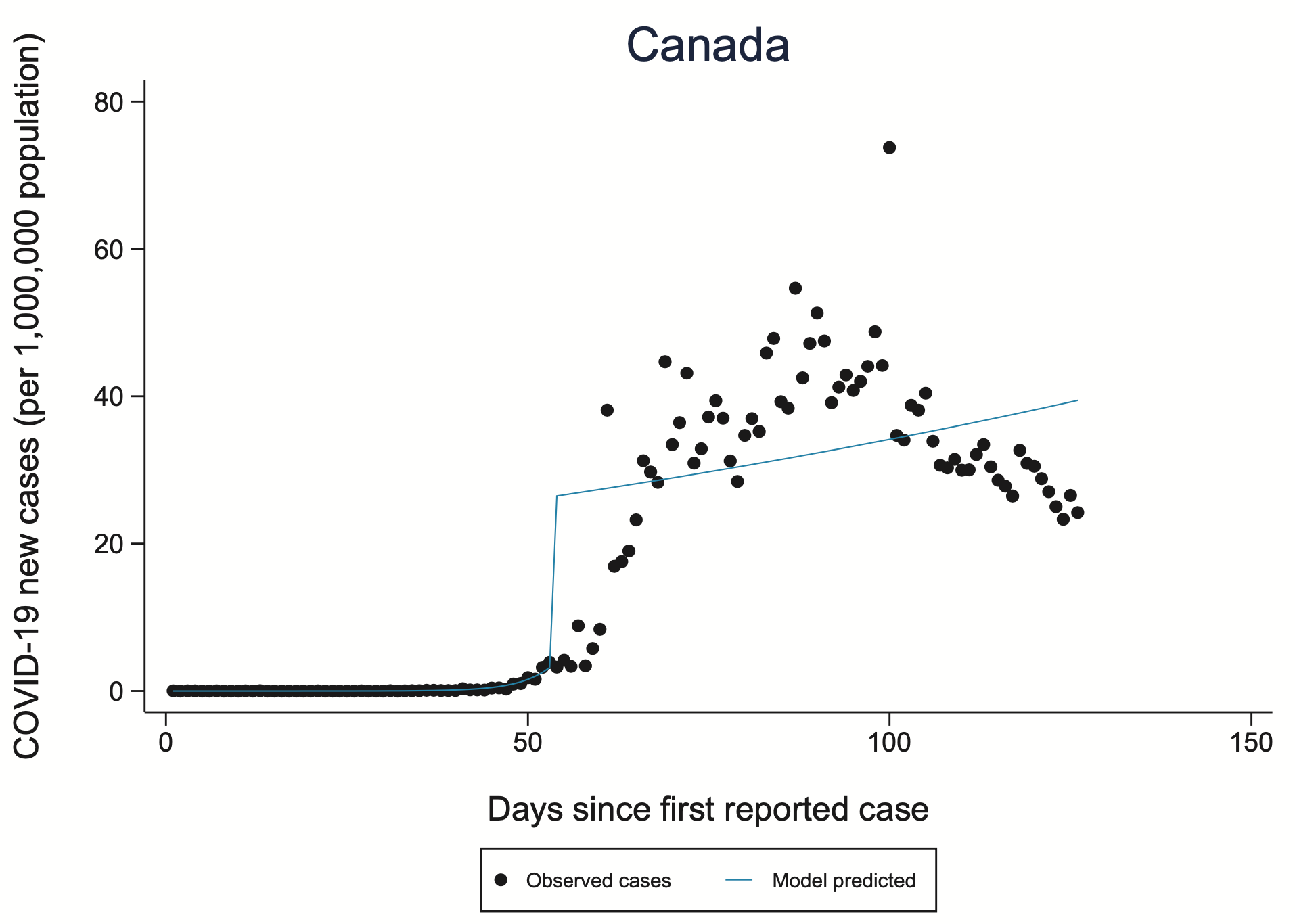
However, even a quick glance at the model fit, as denoted by the blue line suggests quite poor fit. It is not obvious that the Covid-19 infection rate is anything like linear and the discontinuity in the model leading to two lines and relationships appears highly arbitrary even if it equates to the introduction of new public health measures such as social distancing. By visualising the model and its fit such problems and underlying questions become immediately apparent.

Lessons from this discontinuity modelling example include:

The chart of Canada is buried deep in the appendix of the article, and the fit is better for many other countries
The authors are expert epidemiologists
We should not be intimidated by the Schneidelgrüber Hyper-transverse spline method²⁹ or more seriously by technically dense methods and techniques
Often a good starting point is to look; it can help us spot problems

References

Conlen, Matthew. 2020. “Kernel Density Estimation.” https://mathisonian.github.io/kde/.

Dougherty, Jack, and Ilya Ilyankou. 2020. Hands-on Data Visualization: Interactive Storytelling from Spreadsheets to Code. https://handsondataviz.org/.

Gelman, Andrew. 2020. “Please Socially Distance Me from This Regression Model!” https://statmodeling.stat.columbia.edu/2020/07/18/please-socially-distance-me-from-this-regression-model/; Statistical Modeling, Causal Inference; Social Science Blog.

Islam, Nazrul, Stephen J Sharp, Gerardo Chowell, Sharmin Shabnam, Ichiro Kawachi, Ben Lacey, Joseph M Massaro, Ralph B D’Agostino, and Martin White. 2020. “Physical Distancing Interventions and Incidence of Coronavirus Disease 2019: Natural Experiment in 149 Countries.” BMJ 370.

Schucany, William R. 2004. “Kernel Smoothers: An Overview of Curve Estimators for the First Graduate Course in Nonparametric Statistics.” Statistical Science, 663–75.

For a start there is no such method (well to the best of my knowledge)!↩︎