Anhang A — Programmieren in R

In diesem Anhang lernen Sie elementare Programmiertechniken in R kennen. Einige dieser Techniken kommen nicht nur in R, sondern in praktisch allen Programmiersprachen vor, nämlich die bedingte Ausführung von Befehlen (if) und Schleifen (for, while und repeat). Im folgenden Abschnitt wird jedoch zunächst vorgestellt, wie man in R mit Vektoren arbeitet. Vektoren sind R-spezifisch, kommen aber auch in einigen anderen Programmiersprachen vor, die in den Wirtschaftswissenschaften verwendet werden (z.B. Matlab oder Python).

A.1 Vektoren

Die grundlegendsten Objekte in R sind Vektoren. Ein Vektor ist eine Zusammenfassung von Zahlen oder Zeichenketten. Die Länge eines Vektors x wird durch die Funktion length ermittelt.

A.1.1 Erzeugen von Vektoren

Es gibt viele Möglichkeiten, Vektoren in R zu erzeugen. Für diesen Kurs sollten Sie die folgenden drei Funktionen kennen:

Funktion `c` (concatenate)

Mit der Funktion c fasst man Zahlen (oder Zeichenketten) zu einem Vektor zusammen. Mit dem Zuweisungsoperator <- kann der Vektor in eine Variable geschrieben werden.

x <- c(8, 0, -5, 3, 1)

Anschließend sind die Zahlen 8, 0, \(-5\), 3 und 1 Elemente des Vektors x. Der Vektor kann mit der print-Funktion ausgegeben werden.

print(x)

[1]  8  0 -5  3  1

Es ist auch möglich, abkürzend einfach nur x zu schreiben.

[1]  8  0 -5  3  1

Man kann auch einen Vektor aus anderen Vektoren zusammensetzen.

a <- c(1, 3, 5)
b <- c(2, 4, 6)
x <- c(a, b)
x

[1] 1 3 5 2 4 6

Funktion `seq` (sequence)

Mit der Funktion seq erzeugt man einen Vektor von äquidistanten Werten (man spricht oft auch von Gitterpunkten). Die Funktion erwartet drei der folgenden vier Argumente:

from (erster Wert)
to (letzter Wert)
length (Anzahl der Werte)
by Schrittlänge

Mit dem Befehl

x <- seq(from=1, to=2, length=11)

erhält man einen Vektor mit 11 gleich weit voneinander entfernten Elementen, dessen erstes Element 1 und dessen letztes Element 2 ist:

 [1] 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0

Das nächste Beispiel zeigt die Verwendung der Option by:

y <- seq(from=0, to=100, by=5)
y

 [1]   0   5  10  15  20  25  30  35  40  45  50  55  60  65  70  75  80  85  90
[20]  95 100

Für ganzzahlige Elemente mit einer Schrittlänge von 1 gibt es die Kurzschreibweise a:b. Dadurch erhält man einen Vektor aller ganzen Zahlen von a bis b inklusive. Zum Beispiel

1:20

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

In der Hilfefunktion zu seq erfährt man, dass die ersten beiden Argument from und to sind. Es ist also erlaubt, diese beiden Angaben ohne die Argumentnamen einzugeben. Es ist also gleichgültig, ob man

x <- seq(from=0, to=20, length=100)

oder

x <- seq(0, 20, length=100)

eingibt. Das dritte Argument sollte in jedem Fall benannt werden, damit beim Lesen klar ist, ob length oder by gemeint ist.

Funktion `rep` (repeat)

Die Funktion rep hat zwei Argumente. Das erste Argument ist eine Zahl oder ein Vektor. Das zweite Argument gibt an, wie oft das erste Argument wiederholt werden soll. Mit

x <- rep(0, 7)

erzeugt man einen Vektor, der sieben Nullen enthält.

[1] 0 0 0 0 0 0 0

Mit

y <- rep(9, 4)

erhält man einen Vektor aus vier Neunen.

Wenn das erste Objekt keine Zahl, sondern ein Vektor aus Zahlen ist, kann man wählen, ob das zweite Argument times oder each heißen soll. Wählt man times=n, dann wird der komplette Vektor \(n\) Mal vervielfältigt. Wählt man each=n, dann wird jedes Element \(n\) Mal wiederholt. Die beiden Beispiele zeigen die Funktionsweise.

x <- rep(0:4, times=3)
x

 [1] 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4

Hingegen ergibt

y <- rep(0:4, each=3)
y

 [1] 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4

In diesem Kurs dient die Funktion rep vor allem dazu, einen Vektor zu initialisieren, den man anschließend in einer Schleife Element für Element befüllt (siehe Kapitel A.3).

A.1.2 Numerische Indizierung

Auf die Elemente eines Vektors kann man durch die Angabe von Indizes in eckigen Klammern hinter dem Vektornamen zugreifen. Man kann die Elemente eines Vektors lesen oder schreiben. Bei der numerischen Indizierung gibt man in den eckigen Klammern an, welche Elemente ausgelesen (oder beschrieben) werden sollen.

Besonders einfach ist die Indizierung mit einer einzelnen Zahl.

x <- c(6, 1, 2, -3, 0, 0, 4)
x[3]

[1] 2

Zum Indizieren kann auch ein Vektor von ganzen Zahlen benutzt werden. Dann werden so viele Elemente ausgelesen, wie der Indexvektor lang ist.

a <- c(1,1,3,7)
x[a]

[1] 6 6 2 4

Um beispielsweise die ersten drei Elemente auszulesen, kann man so vorgehen:

x[1:3]

[1] 6 1 2

Mit negativen Indizes kann man einzelne (oder mehrere) Elemente ausschließen.

x[-6]

[1]  6  1  2 -3  0  4

A.1.3 Logische Indizierung

Neben der Indizierung durch ganze Zahlen ist es in R auch möglich, einen Vektor von logischen Ausdrücken (FALSE/TRUE) als Index zu verwenden. Der logische Indizierungsvektor muss die gleiche Länge haben wie der zu indizierende Vektor.

Mit der logischen Indizierung kann man gezielt Elemente aus einem Vektor herausgreifen. Das ist besonders einfach an einem Beispiel zu verstehen. Wir betrachten einen Vektor

x <- c(1, 9, 8, -1, 10, 5, 6, -3, 4)

Aus diesem Vektor möchten wir gerne nur die negativen Elemente herauslesen. Dazu bilden wir einen logischen Vektor

b <- (x < 0)

Dieser Vektor hat den Datentyp logical, d.h. er enthält ausschließlich die Werte TRUE oder FALSE (oder gegebenenfalls noch NA, was wir hier aber ignorieren). Der Vektor b sieht so aus:

print(b)

[1] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE

Das vierte und das vorletzte Element sind negativ. Den Vektor b geben wir jetzt in eckigen Klammern als Indexvektor an. Das Resultat wird als Vektor y gespeichert.

y <- x[b]
y

[1] -1 -3

Oft wird der Umweg über einen logischen Vektor mit eigener Bezeichnung übersprungen. Man gibt dann die logische Bedingung direkt in den Indizierungsklammern ein, z.B.

y <- x[x < 0]
y

[1] -1 -3

Es gibt noch eine zweite wichtige Anwendung der logischen Indizierung: Sie kann benutzt werden, um zu zählen, wie groß die Anzahl (oder der Anteil) der Elemente eines Vektors ist, die eine bestimmte Bedingung erfüllen. Da die logischen Ausdrücke TRUE und FALSE den Zahlen 1 und 0 entsprechen, erhält man durch Summieren aller Elemente eines logischen Vektors mit der Funktion sum die Anzahl der TRUE-Werte. Und durch Bilden des Mittelwerts mit der Funktion mean ergibt sich der Anteil der TRUE-Werte.

Das folgende Beispiel illustriert das. Wir betrachten wieder den Vektor

x <- c(1, 9, 8, -1, 10, 5, 6, -3, 4)

und wollen zählen, wie viele Element von x negativ sind. Das erreicht man durch

sum(x < 0)

[1] 2

Der Anteil der negativen Elemente ergibt sich durch

mean(x < 0)

[1] 0.2222222

A.2 Bedingte Ausführung

In Computerprogrammen kommt es oft vor, dass manche Befehle nur unter bestimmten Bedingungen ausgeführt werden sollen. Dafür gibt es in R die Befehle if und else. Der Befehl if hat folgende Syntax:

if(BEDINGUNG){
  ...
  Code
  ...
}

Der Code in den geschweiften Klammern wird nur dann ausgeführt, wenn die Bedingung TRUE ist. Falls die Bedingung FALSE ist, wird der Code übersprungen und das Programm läuft am Ende der eingeklammerten Blocks weiter.

Es ist auch möglich, einen alternativen Code-Block ausführen zu lassen, wenn die Bedingung FALSE ist. Dazu dient der Befehl else, der immer nur in Verbindung mit if vorkommen kann. Die Syntax ist:

if(BEDINGUNG){
  ...
  Code
  ...
} else {
  ...
  Alternativer Code
  ...
}

Es ist empfehlenswert, den Befehl else in die gleiche Zeile zu setzen, in der die schließende geschweifte Klammer des if-Befehls steht, und anschließend sofort die öffnende Klammer für den else-Block zu setzen.

A.3 Schleifen

Schleifen werden beim Programmieren eingesetzt, wenn dieselbe Folge von Befehlen wieder und wieder durchgeführt werden soll. In R sind Schleifen im Vergleich zu einer vektoriellen Programmierung oft recht langsam. Falls es in Ihrem Programm auf eine hohe Geschwindigkeit ankommt, sollten Sie darum Schleifen nur einsetzen, wenn eine vektorielle Programmierung nicht möglich oder zu umständlich ist. Eine typische Anwendung, in der Schleifen sinnvoll eingesetzt werden können, sind Monte-Carlo-Simulationen (s. Kapitel 7.2 und Kapitel 7.4).

A.3.1 `for`-Schleifen

In einer for-Schleife durchläuft ein Index alle Elemente eines Vektors. Die Syntax ist wie folgt,

for(i in vektor){
  ...
}

Dabei ist i der Laufindex, hier kann natürlich ein beliebiger anderer Name gewählt werden. Mit vektor wird angegeben, welche Werte i in jedem Durchlauf nacheinander annehmen soll. In der Mehrzahl aller Fälle sind das die ganzen Zahlen von 1 bis zu einer Obergrenze n. In diesem Fall schreibt man

for(i in 1:n){
  ...
}

Die Schleife wird nun so oft ausgeführt, wie vektor lang ist. In dem Fall 1:n sind es also \(n\) Durchläufe. Innerhalb der Schleife, d.h. in dem Bereich zwischen den geschweiften Klammern, kann beliebiger und beliebig langer Code stehen. Der Code darf insbesondere den Index i enthalten. Für eine bessere Lesbarkeit des Codes sollten alle Zeilen innerhalb der Schleife eingerückt werden.

Das folgende Beispiel illustriert eine for-Schleife für einen einzelnen Befehl innerhalb der Schleife.

n <- 8
for(i in 1:n){
  print(i^2)
}

[1] 1
[1] 4
[1] 9
[1] 16
[1] 25
[1] 36
[1] 49
[1] 64

In vielen Anwendungen benutzt man den Laufindex, um nacheinander auf die Elemente eines Vektors zuzugreifen. Der folgende Code berechnet die Summe der quadrierten Elemente des Vektors x.

x <- c(6, 1, 2, -3, 0, 0, 4)
S <- 0
for(i in 1:length(x)){
  S <- S + x[i]^2
}
print(S)

[1] 66

In ähnlicher Weise kann man den Laufindex benutzen, um die Elemente eines (schon vorhandenen) Vektors mit irgendwelchen Werten zu füllen.

n <- 10
x <- rep(0,n)
for(i in 1:n){
  x[i] <- i*(i+1)
}
print(x)

 [1]   2   6  12  20  30  42  56  72  90 110

A.3.2 `while`-Schleifen

Eine while-Schleife hat eine ähnliche Syntax wie eine for-Schleife, es gibt jedoch keinen Laufindex.

while(BEDINGUNG){
  ...
}

Die while-Schleife wird solange wiederholt, bis die BEDINGUNG verletzt ist. Sollte die Bedingung schon beim Start der Schleife verletzt sein, wird der Code in der Schleife gar nicht ausgeführt.

Oft wird eine while-Schleife in gleicher Weise wie eine for-Schleife verwendet. Anstelle des Laufindexes gibt es dann eine Variable, die in jedem Durchlauf um 1 erhöht wird. Beispielsweise wird die Summe der quadrierten Vektorelemente mit einer while-Schleife so bestimmt:

x <- c(6, 1, 2, -3, 0, 0, 4)
j <- 1
S <- 0
while(j <= length(x)){
  S <- S + x[j]^2
  j <- j+1
}
print(S)

[1] 66

A.3.3 `repeat`-Schleifen

Im Gegensatz zu for-Schleifen und while-Schleifen haben repeat-Schleifen im Prinzip kein Ende, sondern durchlaufen den Code innerhalb der Schleife immer wieder.

repeat{
  ...
}

Es gibt jedoch die Möglichkeit, die Schleife mit dem Befehl break zu beenden. Typischerweise wird eine Bedingung festgelegt, unter der break aktiviert wird.

repeat{
  ...
  if(BEDINGUNG){
    break
  }
  ...
}

Die Schleife läuft so lange, bis die Bedingung erfüllt ist. Der Unterschied zu einer while-Schleife besteht im wesentlichen darin, dass die Bedingung auch in der Mitte der Schleife stehen kann, wohingegen sie bei while-Schleifen immer am Anfang steht.

Mit einer repeat-Schleife kann man beispielsweise einen Zufallsvektor ziehen und auf eine bestimmte Bedingung hin überprüfen. Wenn die Bedingung erfüllt ist, wird die Schleife beendet. Will man einen Zufallsvektor der Länge 100 aus einer Standardnormalverteilung ziehen, bei dem das größte Element mindestens 4 ist, dann kann man das durch folgenden R-Code erreichen:

repeat{
  x <- rnorm(n=100)
  if(max(x) >= 4){
    break
  }
}
print(max(x))

[1] 4.163262

Die Wahrscheinlichkeit, dass von 100 Ziehungen aus \(N(0,1)\) mindestens eine Ziehung einen Wert größer als 4 liefert, beträgt nur rund 0.3 Prozent. Vermutlich ist die repeat-Schleife also oft durchlaufen worden, bis die Bedingung erfüllt wurde.

Es kann beim Programmieren von Schleifen passieren, dass die Rechenzeit viel länger dauert als gedacht. Bei einer repeat-Schleife kann versehentlich eine Abbruchbedingung gefordert sein, die niemals oder fast niemals erfüllt ist, so dass die repeat-Schleife nicht endet. In solchen Fällen kann man die Ausführung des R-Codes abbrechen. Der Abbruch erfolgt entweder mit der Escape-Taste oder mit einem Mausklick auf das kleine rote Stoppzeichen in der rechten oberen Ecke des Konsolen-Fensters (das ist gewöhnlich das linke untere Fenster).

A.4 Funktionsaufrufe

Funktionsargumente haben in R immer einen Namen. Es gibt zwei Arten, Argumente in R an Funktionen zu übergeben.

Erstens, die Argumente werden in der Reihenfolge eingegeben, die in der Definition der Funktion vorgegeben ist. Welche Reihenfolge das ist, kann man mit der Hilfefunktion herausfinden.

Das Beispiel zeigt den Aufruf der Verteilungsfunktion einer Normalverteilung mit Erwartungswert 10 und Standardabweichung 3 an der Stelle 8. Für den korrekten Funktionsaufruf muss man wissen, dass die Funktion pnorm zuerst die Stelle erwartet, an der die Verteilungsfunktion berechnet werden soll, anschließend folgt der Erwartungswert und danach die Standardabweichung.

pnorm(8, 10, 3)

[1] 0.2524925

Zweitens, die Argumente werden mit ihrem Namen übergeben. In dieser Variante spielt es keine Rolle, in welcher Reihenfolge die Funktionsargument angegeben sind. Die Namen der Argumente findet man ebenfalls über die Hilfefunktion heraus.

Den Funktionsaufruf aus dem obigen Beispiel könnte man etwa so eingeben:

pnorm(q=8, mean=10, sd=3)

[1] 0.2524925

oder auch

pnorm(sd=3, q=8, mean=10)

[1] 0.2524925

Es ist auch möglich, die beiden Arten zu mischen und das erste Argument (oder die führenden Argumente) in der Standardreihenfolge anzugeben und einige weitere Argumente mit Namen zu versehen. Zum Beispiel

pnorm(8, mean=10, sd=3)

[1] 0.2524925

Gelegentlich haben die Argumente eine Default-Einstellung. Wenn das Argument nicht ausdrücklich angegeben wird, nimmt es den vorgegebenen Standardwert an. Ob und wenn ja, welche Defaults die Funktionsargumente haben, findet man in der Hilfefunktion.

Zum Beispiel hat die Verteilungsfunktion der Normalverteilung als Default für den Erwartungswert mean=0 und als Default für die Standardabweichung sd=1. Man kann also Verteilungsfunktion der Standardnormalverteilung an der Stelle 2 einfach durch

pnorm(2)

[1] 0.9772499

berechnen.

A.5 Grafiken

In R gibt es mehrere Wege Grafiken zu erzeugen. In diesem Kurs werden Grafiken nur eingesetzt, um einfache Sachverhalte zu illustrieren. Komplizierte Datenstrukturen und ihre Darstellung spielen in diesem Kurs keine Rolle. Daher wird im Gegensatz zu “Data Science 1” nicht ggplot als Grafikmethode verwendet, sondern nur die Grafikbefehle aus der Basisversion von R. Die wichtigsten Funktionen werden im folgenden kurz vorgestellt.

A.5.1 `plot`

Mit der Funktion plot wird eine neue Grafik erstellt. In diese Grafik können später weitere Elemente eingefügt werden, z.B. weitere Linien oder Punkte. Die ersten beiden Argumente von plot sind zwei Vektoren x und y gleicher Länge n. Die Vektoren enthalten die x- und y-Koordinaten der Punkte, die geplottet werden sollen.

Nach den beiden Vektoren können mehrere Optionen gesetzt werden. Die wichtigsten Optionen sind:

type: Mit dieser Option lässt sich angeben, wie die Punkte gezeichnet werden sollen. Die wichtigsten Fälle sind: "p" (als Punkte, das ist der Default), "l" (als Linien), "n" (es wird nichts gezeichnet, sondern nur ein leeres Koordinatensystem vorbereitet).
main="Titel": Angabe einer Überschrift
xlab="Label": Label für die x-Achse
ylab="Label": Label für die y-Achse
xlim=c([Wert], [Wert]): Angabe eines Intervalls für die x-Achse
ylim=c([Wert], [Wert]): Angabe eines Intervalls für die y-Achse

Ferner gibt es eine Reihe von Optionen, mit denen die Linieneigenschaften verändert werden können. Die wichtigsten Linien-Optionen sind:

col: Festlegen der Farbe der Linie; die meisten Farben können verbal angegeben werden, z.B. col="red" oder col="orange".
lwd=[Wert]: line width, mit dieser Option wird die Dicke der Linie festgelegt
lty: line type, diese Option legt den Linientyp fest, mögliche Werte sind lty="solid" (default, durchgezogene Linie), lty="dotted" (gepunktet), lty="dashed" (gestrichelt).

Mit der plot-Funktion kann man sehr einfach den Verlauf einer Funktion zeichnen. Als Beispiel zeigt der folgende Plot den Verlauf der Funktion \[ f(x)=\exp(-x^2) \] in dem Intervall \([-4,4]\). Zuerst wird ein Gitter von x-Werten erzeugt, anschließend wird die Funktion an den Gitterpunkten berechnet.

x <- seq(from=-4, to=4, length=200)
f <- exp(-x^2)
plot(x, f, type="l", main="Beispiel", xlab="x", ylab="f(x)")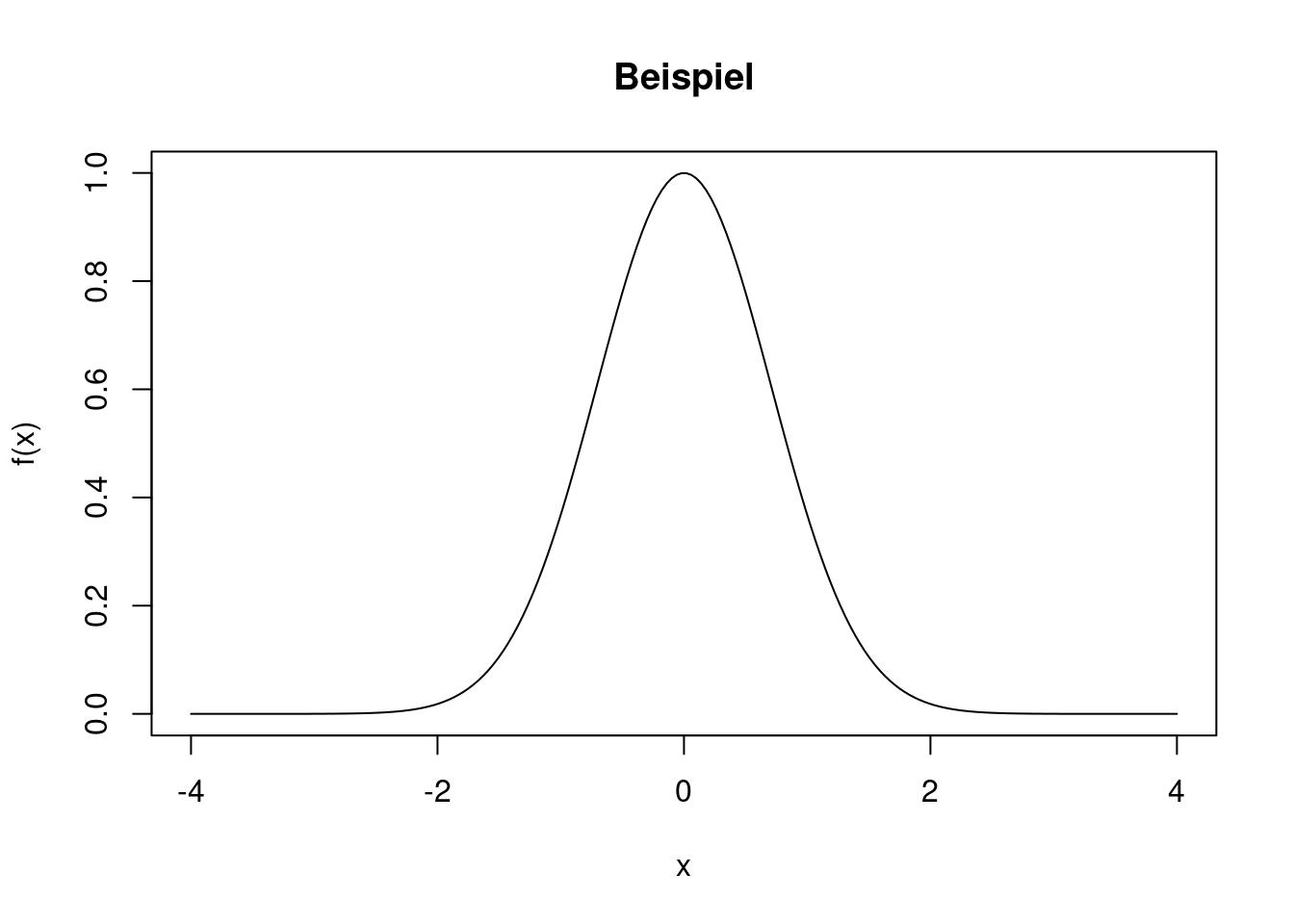

In einen bereits existieren Plot kann man mit der Funktion lines eine weitere Linie einfügen. Die Funktion hat die zwei Argumente x und y für die x- und y-Koordinaten der Punkte, die miteinander verbunden werden sollen. Außerdem darf man Linienoptionen angeben (z.B. col, lty, lwd).

Beispiel: In die vorherige Grafik soll die Funktion \(g(x)=\exp(-|x|)\) als rote Linie eingefügt werden.

x <- seq(from=-4, to=4, length=200)
f <- exp(-x^2)
g <- exp(-abs(x))

plot(x, f, type="l", main="Beispiel", xlab="x", ylab="f(x)")
lines(x,g, col="red")

Die Funktion points fügt Punkte in eine existierende Grafik ein. Die Syntax ist im wesentlichen analog zu lines.

Um eine Gerade in einen Plot hinein zu zeichnen, ist die Funktion abline gut geeignet. Man kann horizontale oder vertikale Geraden mit den Angaben h=[Wert] oder v=[Wert] zeichnen. Eine beliebige lineare Funktion wird mit den beiden Angaben a=[Wert] für den Achsenabschnitt und b=[Wert] für die Steigung erzeugt.

Beispiel: In den vorherigen Plot soll zusätzlich eine vertikale Gerade an der Stelle \(x=0\) gezeichnet werden. Außerdem sollen eine graue gepunktete horizontale Linie in Höhe \(y=0.5\) und die Winkelhalbierende, d.h. eine Gerade mit Achsenabschnitt 0 und Steigung 1, als gestrichelte Linie ergänzt werden.

x <- seq(from=-4, to=4, length=200)
f <- exp(-x^2)
g <- exp(-abs(x))

plot(x, f, type="l", main="Beispiel", xlab="x", ylab="f(x)")
lines(x,g, col="red")
abline(v=0)
abline(h=0.5, col="grey", lty="dotted")
abline(a=0, b=1, lty="dashed")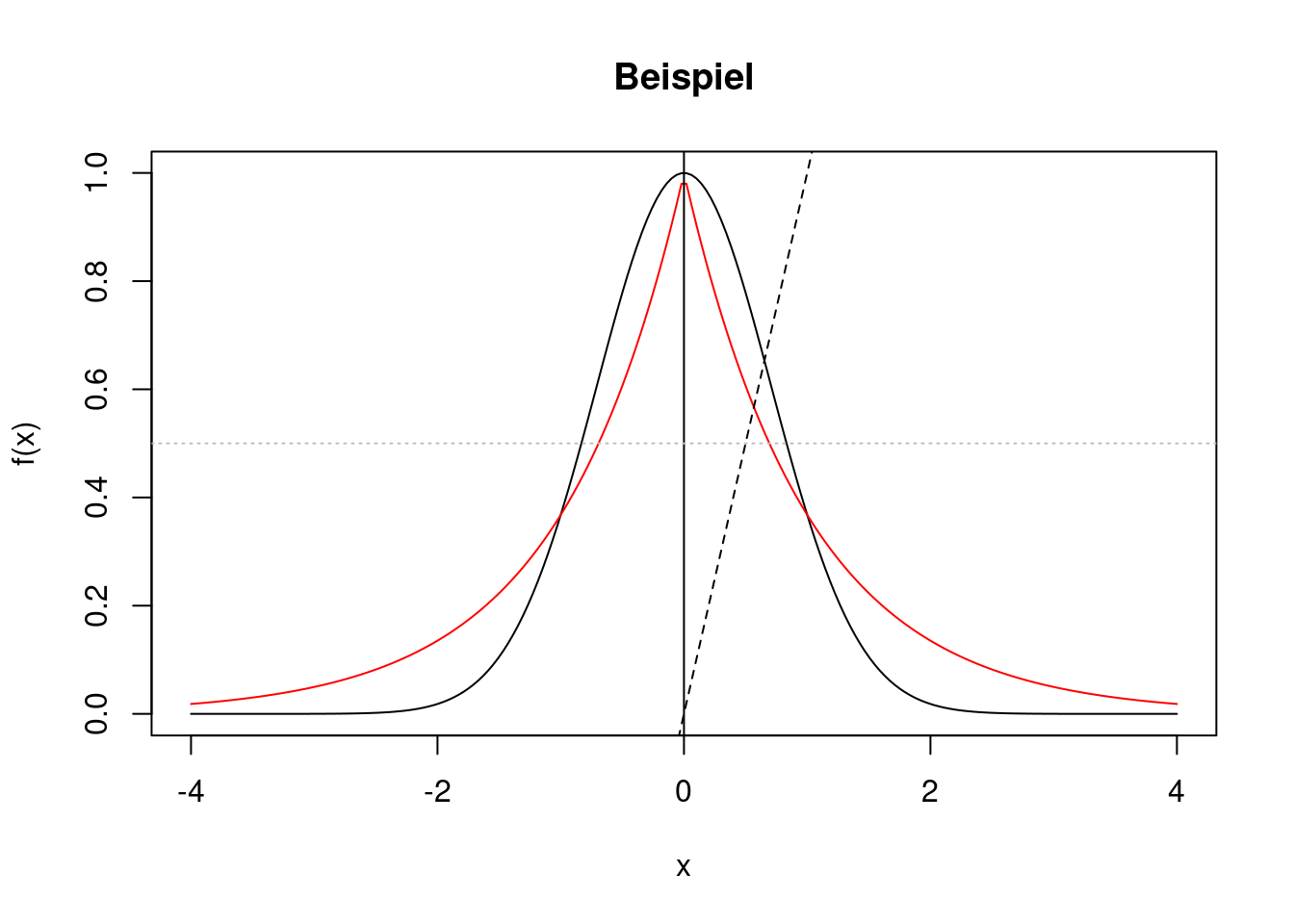

A.5.2 `hist`

Der Basis-R-Befehl zum Erzeugen eines Histogramms ist die Funktion hist. Als erstes Argument x erwartet diese Funktion einen Vektor mit den Daten. Das zweite Argument ist breaks. Hier kann man entweder die Anzahl der Klassen als Zahl oder die Klassengrenzen als Vektor angeben. Wenn die Anzahl der Klassen vorgegeben wird, werden sie zwischen dem kleinsten und dem größten Wert im Vektor x mit gleichen Klassenbreiten erzeugt. Damit das Histogramm alle Eigenschaften einer Dichte hat, sollte man die Option probability=TRUE setzen.

Das folgende Bild zeigt das Histogramm für eine einfache Stichprobe vom Umfang 1000 aus einer Standardnormalverteilung:

x <- rnorm(n=1000, mean=0, sd=1)
hist(x, breaks=40, probability=TRUE)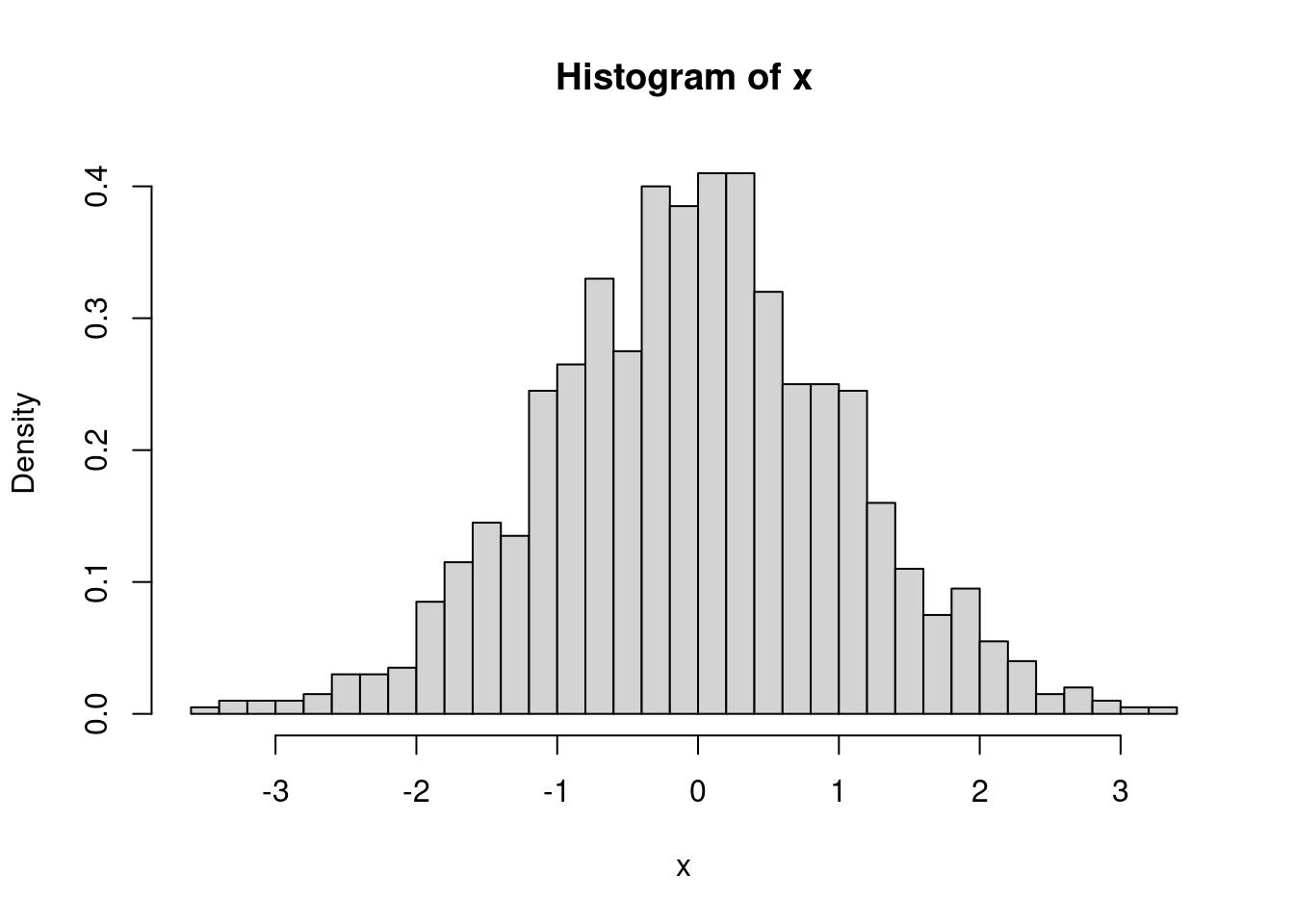

Wie bei einer plot-Grafik lassen sich die Achsenbeschriftungen mit den Optionen xlab und ylab, und die Überschrift mit der Option main verändern.

In eine Histogramm-Grafik kann man mit den Funktionen lines, points und abline Linien, Punkte und Geraden einfügen. Das erfolgt auf die gleiche Weise wie bei den plot-Grafiken.

A.1 Vektoren

A.1.1 Erzeugen von Vektoren

Funktion c (concatenate)

Funktion seq (sequence)

Funktion rep (repeat)