7  Grenzwertsätze

In diesem Kapitel gehen wir davon aus, dass eine Zufallsvariable immer wieder neu gezogen wird. Als Ausgangspunkt der Überlegungen dient eine Folge von unabhängigen, identisch verteilten (engl. independent and identically distributed, i.i.d.) Zufallsvariablen \[ X_1,X_2,X_3,\ldots \] Man kann sich diese Folge als unabhängige Wiederholungen einer Zufallsvariable \(X\) vorstellen, z.B. als immer wieder neu geworfene Würfel. Im folgenden bezeichnen wir den Erwartungswert der einzelnen Folgenelemente mit \(E(X)=\mu\) und die Varianz mit \(Var(X)=\sigma^2\).

7.1 Gesetz der großen Zahl

Aus den Elementen der Folge von Zufallsvariablen berechnen wir für jedes \(n\) das arithmetische Mittel (den Durchschnitt) \[ \bar X_n=\frac{1}{n}\sum_{i=1}^n X_i. \] Der Subindex \(n\) soll verdeutlichen, dass der Durchschnitt aus den ersten \(n\) Elementen der Folge berechnet wird. Für unterschiedliche \(n\) erhält man also Durchschnitte von unterschiedlich vielen Folgenelementen.

Achtung: Es handelt sich bei \(\bar X_n\) um den Durchschnitt von \(n\) Zufallsvariablen, also von Zahlen, deren Wert man noch nicht kennt. Darum kennt man natürlich auch den Wert des Durchschnitts noch nicht. Mit anderen Worten: Der Durchschnitt \(\bar X_n\) ist ebenfalls eine Zufallsvariable.

Da der Durchschnitt \(\bar X_n\) eine Zufallsvariable ist, kann man seinen Erwartungswert und seine Varianz ausrechnen. Sie sind mit den Rechenregeln aus Kapitel 6.3 leicht zu finden. Es gilt

\[\begin{align*} E(\bar X_n) &= E\left(\frac{1}{n}\sum_{i=1}^n X_i\right) \\ &= \frac{1}{n}\sum_{i=1}^n E(X_i) \\ &= \frac{1}{n}\sum_{i=1}^n \mu \\ &= \mu \end{align*}\]

und

\[\begin{align*} Var(\bar X_n) &= Var\left(\frac{1}{n}\sum_{i=1}^n X_i\right) \\ &= \frac{1}{n^2}\sum_{i=1}^n Var(X_i) \\ &= \frac{1}{n^2}\sum_{i=1}^n \sigma^2 \\ &= \frac{\sigma^2}{n}. \end{align*}\]

Mit anderen Worten: Wenn man den Durchschnitt aus immer mehr Folgenelementen bildet, dann ist der Erwartungswert des Durchschnitts immer \(\mu\), aber seine Varianz wird mit steigendem \(n\) immer kleiner. Der Durchschnitt \(\bar X_n\) streut also mit steigendem \(n\) immer weniger um den Erwartungswert \(E(X)=\mu\) der Zufallsvariable \(X\).

Diese Einsicht lässt sich mathematisch präzise formulieren.

Gesetz der großen Zahl

Das Gesetz der großen Zahl besagt, dass (unter einigen Bedingungen) für jedes noch so kleine \(\epsilon >0\) gilt \[ \lim_{n\to\infty} P(|\bar X_n-\mu|\ge \epsilon)=0. \]

Als alternative Notation findet man oft \[ \text{plim}_{n\to\infty}\bar X_n=\mu, \] wobei man “plim” als “Wahrscheinlichkeits-Limes” (engl. probability limit) spricht.

Für die Gültigkeit des Gesetzes der großen Zahl müssen einige Voraussetzungen erfüllt sein. Die Folgenelemente müssen identisch und unabhängig verteilt sein. Außerdem muss der Erwartungswert der Zufallsvariable \(X\) existieren. Es gibt neben diesem Gesetz der großen Zahl, das auch als “schwaches Gesetz der großen Zahl” bezeichnet wird, noch weitere Varianten, die andere Voraussetzungen fordern, die aber im Kern ebenfalls aussagen: Der Durchschnitt konvergiert in einem gewissen Sinn gegen den Erwartungswert.

Das Gesetz der großen Zahl gilt nicht nur für den Erwartungswert, sondern auch für andere wichtige Kenngrößen der Zufallsvariablen. So konvergiert die Varianz der Folgenelemente gegen die Varianz der Zufallsvariable; die empirische Verteilungsfunktion der Folgenelemente konvergiert gegen die Verteilungsfunktion der Zufallsvariable; die Quantile der Folgenelemente konvergieren gegen die Quantile der Zufallsvariable; und das Histogramm der Folgenelmente konvergiert gegen die Dichte der Zufallsvariable.

7.2 Monte-Carlo (I)

Das Gesetz der großen Zahl hat eine weitreichende Konsequenz, denn daraus folgt: Um die Verteilung einer Zufallsvariable zu kennen, muss man nicht unbedingt die Verteilungsfunktion, Dichte oder Wahrscheinlichkeitsfunktion kennen, sondern es reicht aus, wenn man einen Algorithmus zur Verfügung hat, der viele unabhängige Ziehungen aus der Zufallsvariable liefert. Solche Algorithmen gibt es - und viele davon sind in R implementiert. Die Ziehungen, die vom Computer generiert werden, nennt man Zufallszahlen (engl. random numbers). Verfahren, die auf solchen Algorithmen beruhen, werden Monte-Carlo-Simulationen genannt, weil das Casino von Monte Carlo früher als Inbegriff von Zufälligkeit galt.

Die R-Funktionen zum Erzeugen von Zufallszahlen haben alle die Form

rVERTEILUNG(n, PARAMETER)

Dabei gibt n an, wie viele Folgenelemente gezogen werden sollen. Für die Standardverteilungen, die in Kapitel 4 behandelt wurden, lauten die Funktionsnamen:

• rbinom(n, size, prob)
• rpois(n, lambda)
• rnorm(n, mean, sd)
• rexp(n, rate)
• runif(n, min, max)
• rt(n, df)

Für die Paretoverteilung gibt es keinen vorgefertigten Algorithmus. Das Paket distributionsrd stellt jedoch die Funktion

• rpareto(n, k, xmin)

bereit, mit der Zufallszahlen aus einer Paretoverteilung gezogen werden können.

Die Vorgehensweise einer Monte-Carlo-Simulation versteht man am einfachsten anhand eines Beispiels: Einige Kennzahlen einer Normalverteilung mit Erwartungswert \(\mu=10\) und Standardabweichung \(\sigma=3\) sollen durch eine Monte-Carlo-Simulation bestimmt werden.

Achtung: Die R-Funktionen zur Normalverteilung erwarten als Parameter für die Streuung nicht die Varianz, sondern die Standardabweichung. Zuerst werden \(n=100000\) Zufallszahlen gezogen (Sie können die Zahl der Ziehungen durchaus noch höher setzen) und in einen Vektor x geschrieben.

n <- 100000
x <- rnorm(n, mean=10, sd=3)

Der Erwartungswert wird approximiert durch den Durchschnitt der 100000 Zufallszahlen. In diesem Beispiel ergibt sich aus den Ziehungen

mean(x)

[1] 9.99398

Dieser Wert liegt sehr nahe an dem theoretischen Erwartungswert \(E(X)=\mu=10\). Zieht man erneut 100000 Zufallszahlen, erhält man natürlich einen etwas anderen Wert.

Die Varianz der Zufallszahlen ist

var(x)

[1] 8.967859

Der Wert weicht nur wenig von der theoretischen Varianz \(Var(X)=\sigma^2=9\) ab.

Als 0.75-Quantil erhält man

quantile(x, 0.75)

     75% 
12.01152 

Zum Vergleich: Das theoretische 0.75-Quantil der \(N(10,3^2)\) ist

qnorm(0.75, mean=10, sd=3)

[1] 12.02347

Auch hier ist die Approximation durch die Monte-Carlo-Simulation also sehr präzise.

Der folgende Plot zeigt das Histogramm der Zufallszahlen zusammen mit der theoretischen Dichtefunktion der Normalverteilung, die als rote Linie ergänzt ist.

hist(x, breaks=100, probability=TRUE,
     main="Histogramm der N(0,1)-Zufallszahlen")

g <- seq(from=0, to=20, length=200)
lines(g, dnorm(g, mean=10, sd=3), col="red")

Eine Beschreibung des Befehls hist findet man im Kapitel A.5. Dort wird auch erklärt, wie man die Funktion lines einsetzt.

Im folgenden Plot sieht man die empirische Verteilungsfunktion der Ziehungen \(X_1,\ldots,X_n\). Die R-Funktion dafür lautet ecdf. Es handelt sich zwar um eine Treppenfunktion, aber die Stufen sind so klein (nämlich jeweils \(1/n=0.00001\)), dass sie nicht zu erkennen sind. Mit Hilfe der Funktion lines wird die theoretische Verteilungsfunktion der Normalverteilung als rote Linie ergänzt.

plot(ecdf(x),
     main="Verteilungsfunktion")

g <- seq(from=-5, to=25, length=200)
lines(g, pnorm(g, mean=10, sd=3), col="red")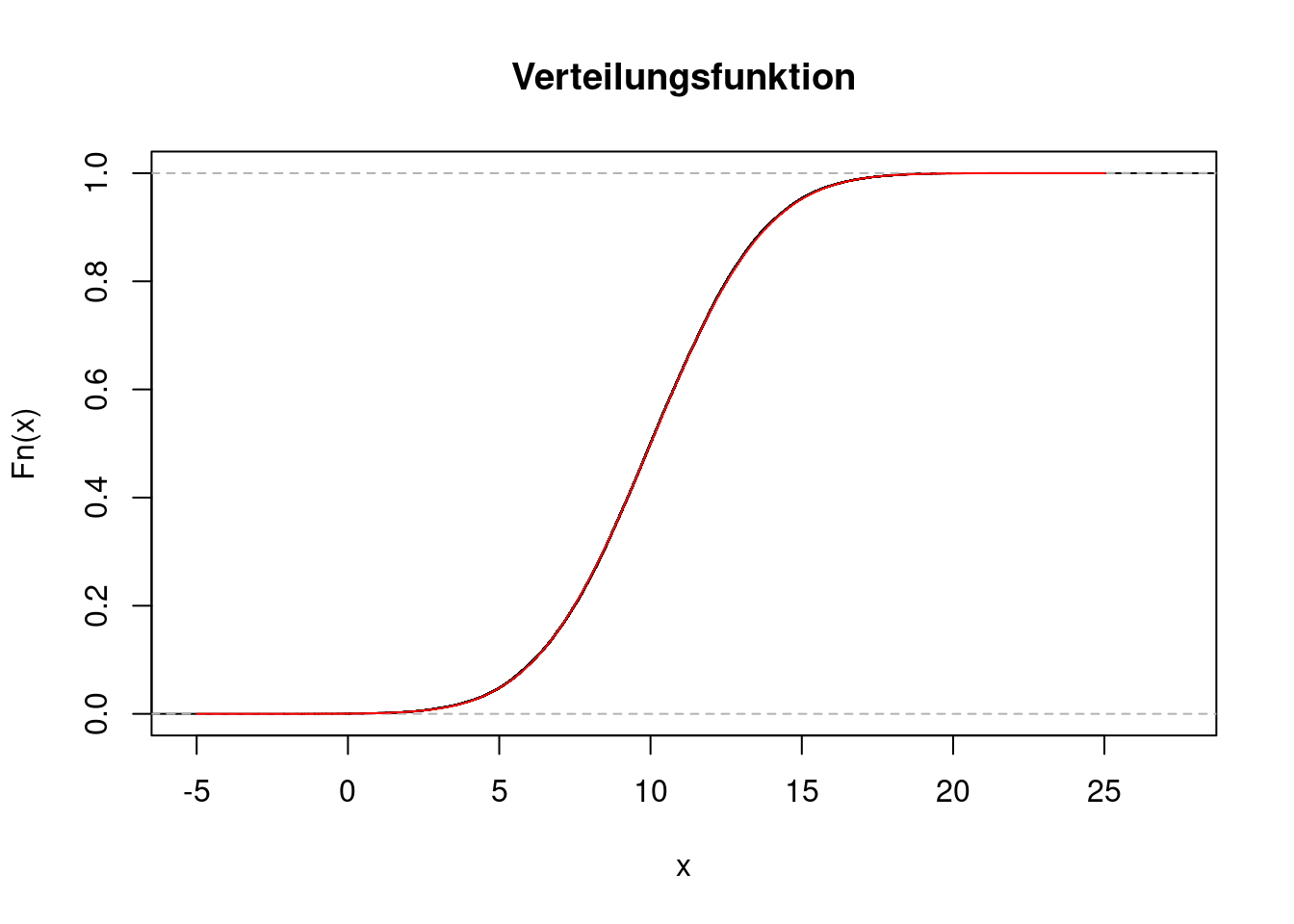

Die beiden Linien stimmen praktisch perfekt überein. Man kann also die theoretische Verteilungsfunktion beliebig genau bestimmen, indem man eine große Zahl von Zufallszahlen generiert und ihre empirische Verteilungsfunktion bestimmt.

Offensichtlich ist es nicht sinnvoll, eine Monte-Carlo-Simulation durchzuführen, um Erwartungswert, Varianz, Quantile und Histogramm einer Verteilung zu finden, für die man diese Größen auch einfach theoretisch herleiten oder irgendwo nachschlagen kann. Monte-Carlo-Simulationen sind jedoch immer dann extrem hilfreich,

• wenn es zwar schwierig oder aufwendig ist, die theoretischen Größen zu bestimmen,
• wenn man aber sehr leicht und schnell Zufallszahlen erzeugen kann aus der Verteilung, die einen interessiert.

Das passiert beispielsweise, wenn wir uns für eine Zufallsvariable interessieren, die zwar nicht unmittelbar einer Standardverteilung folgt, die sich aber aus einer anderen Zufallsvariable ergibt, welche wiederum einer Standardverteilung folgt. Das nächste Beispiel zeigt das.

Die Zufallsvariable \(X\) folge einer Normalverteilung mit Erwartungswert \(\mu=8\) und Standardabweichung \(\sigma=0.5\). Die Zufallsvariable \(Y=e^X\) soll den Bruttomonatslohn von Angestellten einer bestimmten Branche modellieren. Wir interessieren uns nicht für den Brutto-, sondern den Nettolohn. Letzterer ergibt sich, indem man die Abgaben und Steuern vom Bruttolohn subtrahiert. Die Höhe der Abgaben und Steuern werde durch folgende Funktion beschrieben: \[ S(y)=\left\{ \begin{array}{ll} 0 & \text{ falls }y\le 2000\\ 0.35(y-2000) & \text{ falls }y> 2000\\ \end{array} \right. \] wobei \(y\) der Bruttolohn ist. Es handelt sich also um eine “flat tax” von 35 Prozent mit einem Freibetrag von 2000. Steuern in Höhe von 35 Prozent fallen nur an auf den Betrag des Bruttoeinkommens, der über 2000 Euro liegt. Der Nettolohn wird modelliert durch die Zufallsvariable \[ Z=Y-S(Y). \] Wie hoch ist der Erwartungswert des Nettolohns? Das lässt sich recht einfach durch eine Monte-Carlo-Simulation ermitteln. Die Anzahl der Zufallszahlen sei \(n=100000\).

n <- 100000
x <- rnorm(n, mean=8, sd=0.5)
y <- exp(x)
s <- ifelse(y <= 2000, 0, 0.35*(y-2000))
z <- y-s
mean(z)

[1] 2865.98

Zur Erläuterung: Die Funktion ifelse erwartet als Argumente drei Vektoren gleicher Länge. Der erste Vektor ist ein Vektor logischer Ausdrücke (TRUE/FALSE). Für jedes Element mit dem Wert TRUE gibt die Funktion als Output den entsprechenden Wert des zweiten Vektors (der if-Vektor), für jedes Element mit dem Wert FALSE ist der Output der entsprechende Wert des dritten Vektors (der else-Vektor). In diesem Beispiel gibt die Funktion also als Steuerlast eine 0 aus, wenn die Bedingung y <= 2000 wahr ist. Wenn die Bedingung falsch ist, wird die Steuerlast nach der Flat-Rate-Formel berechnet.

Die Dichte des Nettolohns kann durch das Histogramm approximiert werden. Diese Form der Dichte entspricht keiner bekannten Standardverteilung.

hist(z, probability=TRUE, breaks=100, xlim=c(0, 10000),
     main="Histogramm des Nettolohns")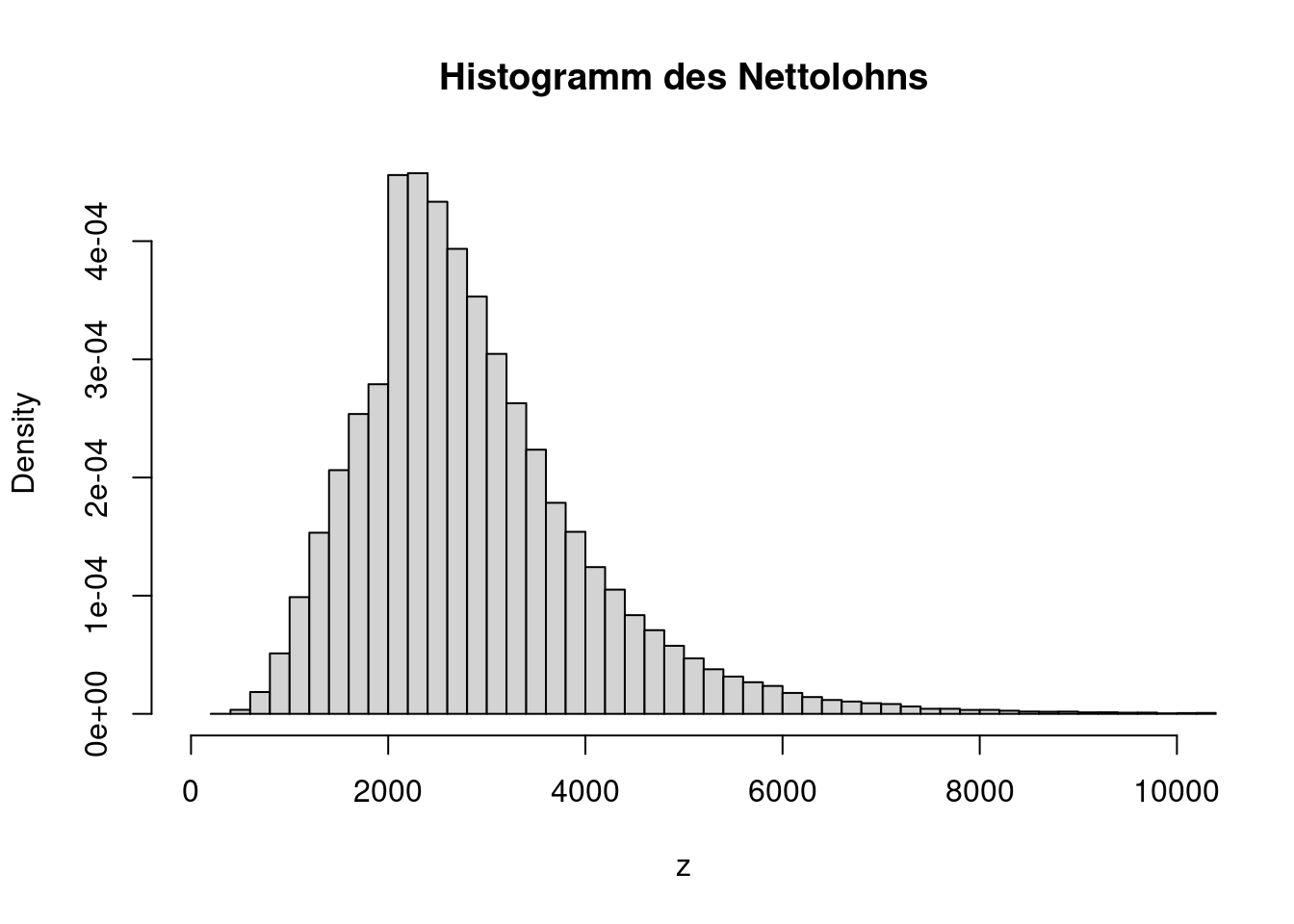

Das Beispiel zeigt, wie man aus einer Zufallsvariable x eine andere Zufallsvariable z berechnet. Die Berechnungen wie z.B. y <- exp(x) werden in R automatisch für alle Elemente des Vektors x durchgeführt und in die entsprechenden Elemente des Vektors y geschrieben. Intern wird in R eine Schleife durchlaufen, die für jedes einzelne Element des Vektors die Berechnung ausführt. Diese Schleife lässt sich auch explizit schreiben, z.B. als for-Schleife. Das hat den Vorteil, dass das Programm den Ablauf der Simulation genauer abbildet. Außerdem kann man in einer for-Schleife auch komplexe Berechnungen durchführen, für die es in R keine Funktionen gibt, die mit Vektoren arbeiten. Ein gewisser Nachteil einer for-Schleife ist jedoch die längere Rechenzeit.

Der folgende R-Code wiederholt das letzte Beispiel und zeigt, wie man eine for-Schleife einsetzt.

n <- 100000
z <- rep(n, 0)

for(i in 1:n){

  x <- rnorm(1, mean=8, sd=0.5)
  y <- exp(x)
  if(y <= 2000){
    s <- 0
  } else {
    s <- 0.35*(y-2000)
  }
  z[i] <- y-s

}
mean(z)

[1] 2862.214

Vor dem Start der Schleife wird der Vektor z initialisiert, also so vorbereitet, dass er die Ergebnisse der einzelnen Schleifendurchläufe aufnehmen kann. Es ist gleichgültig, welche Werte anfangs in z stehen, da sie ohnehin überschrieben werden. In diesem Beispiel ist z zu Beginn ein Vektor aus Nullen.

7.3 Zentraler Grenzwertsatz

Der zentrale Grenzwertsatz (engl. central limit theorem) ist aus zwei Gründen relevant. Zum einen liefert er eine mathematische Begründung dafür, warum in der Realität so viele Verteilungen zu finden sind, die gut durch eine Normalverteilung modelliert werden können. Zum zweiten ist er der Ausgangspunkt für die Herleitung von Konfidenzintervallen (Kapitel 10) und Hypothesentests (Kapitel 11 und Kapitel 12).

Für den zentralen Grenzwertsatz betrachtet man nicht die Folge von Zufallsvariablen \[ \bar X_n=\frac{1}{n}\sum_{i=1}^n X_i \] (d.h. die Durchschnitte), sondern die Folge der standardisierten Durchschnitte. Dazu subtrahiert man den Erwartungswert und dividiert durch die Standardabweichung. Zur Erinnerung: Der Erwartungswert und die Standardabweichung von \(\bar X_n\) sind

\[\begin{align*} E(\bar X_n) &= \mu \\ \sqrt{Var(\bar X_n)}&=\sqrt{\frac{\sigma^2}{n}}=\frac{\sigma}{\sqrt{n}}. \end{align*}\]

Die Folge der standardisierten Durchschnitte bezeichnen wir mit \[ U_n=\frac{\bar X_n-\mu}{\sqrt{\sigma^2/n}}. \] Die Wurzel von \(n\) wird oft aus dem Nenner heraus vor den Bruch gezogen, \[ U_n=\sqrt{n}\frac{\bar X_n-\mu}{\sigma}. \]

Zentraler Grenzwertsatz

Der zentrale Grenzwertsatz besagt, dass (unter einigen Bedingungen) für alle \(u\in\mathbb{R}\) gilt \[ \lim_{n\to\infty} P(U_n\le u)=\Phi(u), \] wobei \(\Phi\) die Verteilungsfunktion der Standardnormalverteilung \(N(0,1)\) ist.

Etwas weniger präzise - aber dafür leichter verständlich - sagt der zentrale Grenzwertsatz: Der standardisierte Durchschnitt von vielen Zufallsvariablen folgt im Limes einer Standardnormalverteilung. Natürlich ist \(n\) niemals wirklich unendlich groß, aber selbst wenn \(n\) nur “ausreichend groß” ist, gilt \[ U_n\stackrel{appr}{\sim}N(0,1). \] Der standardisierte Durchschnitt von “vielen” Zufallsvariablen folgt näherungsweise einer Standardnormalverteilung. Diese Aussage ist deswegen bemerkenswert, weil es gleichgültig ist, wie die zugrundeliegenden \(X_i\) verteilt sind! Sie müssen nicht einmal stetig verteilt sein. Es gibt jedoch ein paar Bedingungen, die für die Gültigkeit des zentralen Grenzwertsatzes erfüllt sein müssen. So müssen die Folgenelemente \(X_1,\ldots,X_n\) unabhängig und identisch verteilt sein und ihre Varianz muss existieren.

Wenn der standardisierte Durchschnitt approximativ standardnormalverteilt ist, dann ist der Durchschnitt selber approximativ normalverteilt. Für ausreichend große \(n\) gilt also \[ \bar X_n \stackrel{appr}{\sim}N\left(\mu,\frac{\sigma^2}{n}\right). \] Und wenn beide Seiten mit \(n\) multipliziert werden, dann gilt für die Summe \[ \sum_{i=1}^n X_i \stackrel{appr}{\sim}N\left(n\mu,n\sigma^2\right), \] wobei zu beachten ist, dass bei der Multiplikation mit \(n\) sich die Varianz um den Faktor \(n^2\) erhöht.

Die intuitive Bedeutung des zentralen Grenzwertsatzes lautet also: Wenn man viele unabhängige Zufallsvariablen addiert oder ihren Durchschnitt berechnet, dann ist die Summe bzw. der Durchschnitt ebenfalls eine Zufallsvariable, und zwar mit einer Normalverteilung. Das Besondere daran ist, dass die Verteilung der Summanden nicht normal sein muss. Die Normalverteilung ergibt sich quasi “aus dem Nichts”!

Auf den Beweis des zentralen Grenzwertsatzes gehen wir in diesem Kurs nicht ein, er wird in dem Bachelor-Wahlpflichtmodul Advanced Statistics vorgestellt. Der zentrale Grenzwertsatz kann erheblich verallgemeinert werden. Er gilt z.B. auch dann noch, wenn die Zufallsvariablen nicht unabhängig sind, sondern eine (nicht zu starke) Abhängigkeit aufweisen. Die Summanden müssen auch nicht unbedingt identisch verteilt sein. Die Verallgemeinerungen des zentralen Grenzwertsatzes sind aber fortgeschrittene Materie, sie werden beispielsweise in dem Master-Modul Time Series Analysis behandelt.

7.4 Monte-Carlo (II)

Wie lässt sich der zentrale Grenzwertsatz durch eine Monte-Carlo-Simulation illustrieren? Um das zu verstehen, muss man sich zunächst klar machen, dass die Folge \(U_1,U_2,\ldots\) nicht gegen einen bestimmten Wert, sondern gegen eine Verteilung konvergiert.

Um die Verteilung von \(U_n\) zu simulieren, müssen wir für gegebenes \(n\) viele Ziehungen aus \(U_n\) generieren, die wir beispielsweise \[ U_{n,1},U_{n,2},\ldots,U_{n,R} \] nennen können, wobei \(R\) die vorgegebene (große) Zahl von Ziehungen ist, z.B. \(R=10000\). Für jede dieser Ziehungen müssen die Zufallsvariablen \(X_1,\ldots,X_n\) neu gezogen werden. Das lässt sich am elegantesten durch eine Schleife programmieren. Genauere Erklärungen zum Programmieren mit Schleifen finden Sie in Kapitel A.3.

Bevor man die Schleife durchlaufen lässt, initialisiert man einen Vektor, der die Ergebnisse der Schleifendurchläufe aufnimmt. Welche Werte in diesem Vektor stehen, ist gleichgültig, da sie in der Schleife anschließend überschrieben werden. Es geht also nur darum, Platz für die Ergebnisse vorzubereiten. Hier wird der Vektor mit Nullen gefüllt.

R <- 10000
u <- rep(0, R)

Innerhalb der Schleife werden nun in jedem Durchlauf die Zufallszahlen \(X_1,\ldots,X_n\) neu gezogen. Konkret nehmen wir an dieser Stelle an, dass die Folge \(n=50\) Elemente umfasst und dass sie unabhängig exponentialverteilt mit Parameter \(\lambda=2\) sind, \[ X\sim Exp(2). \] Erwartungswert und Standardabweichung sind (vgl. Kapitel 4.3.2)

\[\begin{align*} E(X) &= \mu=\frac{1}{2}\\ \sqrt{Var(X)}& =\sigma=\sqrt{\frac{1}{4}}=\frac{1}{2}. \end{align*}\]

Der R-Code sieht folgendermaßen aus:

mu <- 1/2
sigma <- 1/2
n <- 50

for(r in 1:R){

    x <- rexp(n, rate=2)
    xquer <- mean(x)
    u[r] <- sqrt(n)*(xquer - mu)/sigma

}

Zur Erklärung: Der Laufindex der Schleife r durchläuft alle Werte von 1 bis R. Bei jedem Durchlauf wird zuerst die Folge x vom Umfang n aus der Exponentialverteilung gezogen. Anschließend wird der Durchschnitt der Elemente der Folge gebildet und unter dem Namen xquer abgespeichert. In der letzten Zeile der Schleife wird der Durchschnitt standardisiert und an die r-te Stelle des Vektors u geschrieben.

Das Histogramm der \(R=10000\) Zufallszahlen \(U_{n,1},\ldots,U_{n,R}\) kann trotz des noch kleinen Umfang \(n=50\) schon recht gut durch eine Standardnormalverteilung approximiert werden.

hist(u, probability=TRUE, breaks=50,
     main="Verteilung von U_50")

g <- seq(from=-4, to=4, length=200)
lines(g, dnorm(g), col="red")

Reduziert man die Länge der Folge auf nur \(n=5\) Elemente, greift der zentrale Grenzwertsatz nicht gut und die Approximation ist ungenau, wie das folgende Bild zeigt:

n <- 5

for(r in 1:R){

    x <- rexp(n, rate=2)
    xquer <- mean(x)
    u[r] <- sqrt(n)*(xquer - 1/2)/sqrt(1/4)

}
hist(u, prob=TRUE, breaks=50,
     main="Verteilung von U_5")

g <- seq(from=-3, to=5, length=200)
lines(g, dnorm(g), col="red")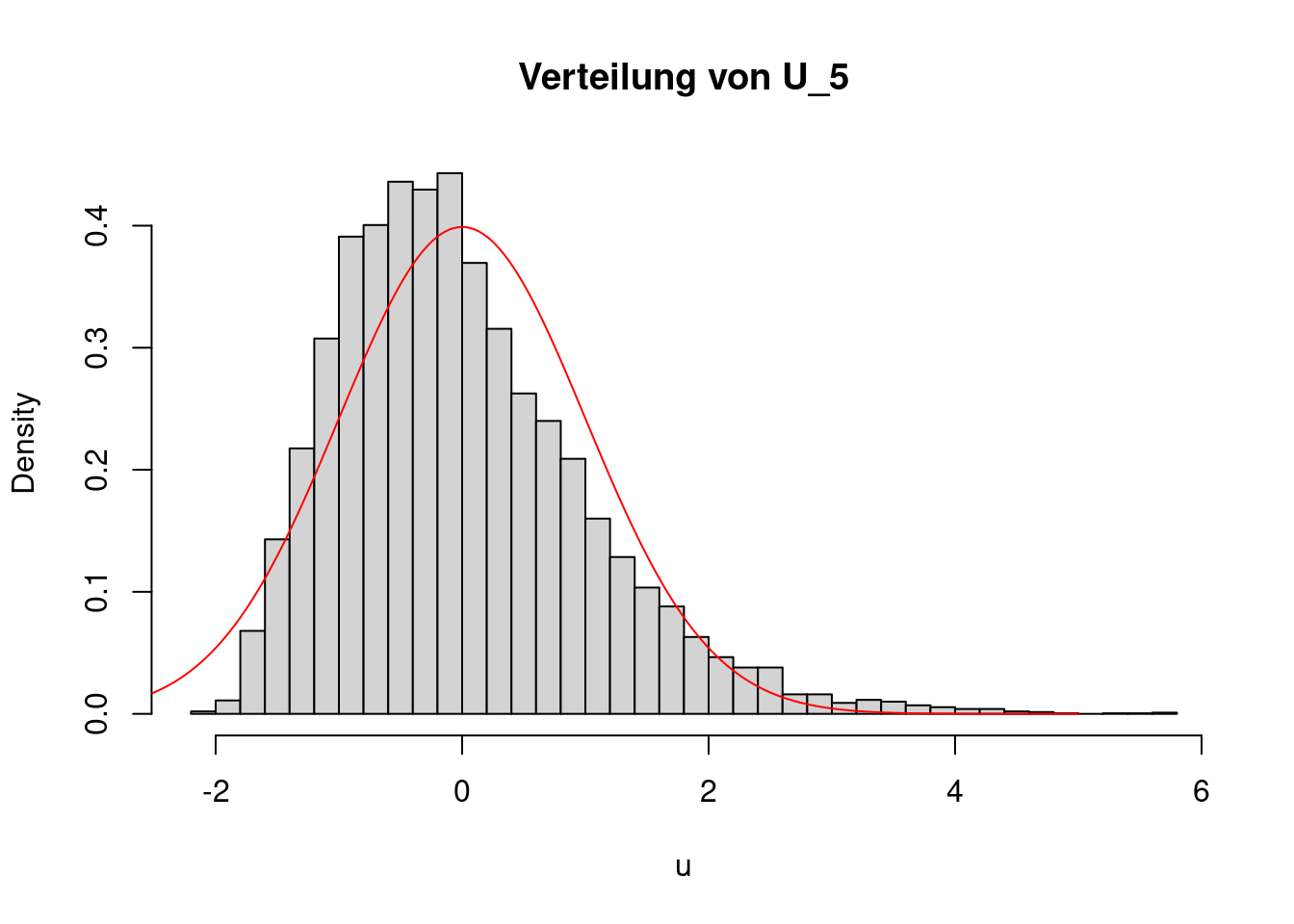

Wie viele Elemente die Folge \(X_1,\ldots,X_n\) haben muss, damit der zentrale Grenzwertsatz greift, hängt von ihrer Verteilung ab. Es kann sein, dass schon für \(n=10\) die Approximation sehr gut ist, es kann jedoch auch sein, dass selbst ein Umfang von \(n=1000\) oder sogar \(n=10000\) noch zu klein ist. Erfahrungsgemäß ist in vielen Fällen ein Umfang von \(n=50\) schon ausreichend groß, um eine einigermaßen gute Annäherung an die Standardnormalverteilung zu erreichen. Das ist jedoch nur eine Faustregel, sie kann im konkreten Einzelfall vollkommen falsch sein.