dbinom(k, size=n, prob=p)4 Standardverteilungen
Für viele Anwendungsfälle gibt es Standardverteilungen, die bestimmte Zufallsvorgänge sehr gut beschreiben können. Eine übersichtliche Liste wichtiger Standardverteilungen finden Sie auf der deutschsprachigen Wikipedia-Seite (-> Link). Die entsprechende englischsprachige Seite (-> Link) listet noch mehr Verteilungen auf, stellt ihre Eigenschaften aber nicht so übersichtlich dar. In diesem Kurs lernen Sie exemplarisch einige ausgewählte diskrete und stetige Standardverteilungen kennen. Der Transfer auf beliebige weitere Standardverteilungen fällt dann leicht.
4.1 Standardverteilungen in R
Die meisten Standardverteilungen sind in R implementiert oder lassen sich leicht durch R-Pakete ergänzen. Zu jeder Standardverteilung gibt es R-Funktionen, mit denen man ihre Verteilungs- und Quantilfunktion sowie die Dichte- bzw. Wahrscheinlichkeitsfunktion auswerten kann. Außerdem stellt R Funktionen bereit, mit denen sich Realisationen von Zufallsvariablen generieren lassen, die einer Standardverteilung folgen.
Die Syntax der R-Funktionen ist sehr einfach und für alle Standardverteilungen nahezu gleich:
dVERTEILUNG(x, PARAMETER): Dichte- oder WahrscheinlichkeitsfunktionpVERTEILUNG(q, PARAMETER): VerteilungsfunktionqVERTEILUNG(p, PARAMETER): Quantilfunktion
Dabei ist VERTEILUNG eine Abkürzung für den Namen der Standardverteilung und PARAMETER ist der Parameter der Verteilung (bzw. die Parameter, wenn es mehrere sind). Mit x, q und p werden die Stellen bezeichnet, an denen die Dichte- oder Wahrscheinlichkeitsfunktion, die Verteilungsfunktion und die Quantilfunktion ausgewertet werden sollen. Im Kapitel A.4 wird genauer erklärt, auf welche Weisen man Funktionsargumente eingeben kann.
Um Realisationen der Zufallsvariable zu ziehen, nutzt man die R-Funktionen
rVERTEILUNG(n, PARAMETER)
Das erste Argument (n) gibt an, wie viele (unabhängige) Ziehungen aus der Zufallsvariable simuliert werden sollen. Die Ziehungen werden als Zufallszahlen bezeichnet. Die Funktion liefert als Output einen Vektor der Länge n.
Es gibt noch eine weitere R-Funktion zum Ziehen von Zufallszahlen, nämlich die Funktion
sample
Sie dient dazu, aus einem Vektor zufällig Elemente auszuwählen. Eine ausführliche Beschreibung folgt in Kapitel 4.4. In Kapitel 7.2 und Kapitel 7.4 wird erklärt, wie man in R mit Hilfe von Zufallszahlen sogenannte Monte-Carlo-Simulationen durchführt.
4.2 Diskrete Verteilungen
4.2.1 Bernoulli-Verteilung
Ein Zufallsexperiment heißt Bernoulli-Experiment, wenn es nur darauf ankommt, ob etwas eintritt (“Erfolg”, \(A\)) oder nicht eintritt (“Misserfolg”, \(\bar A\)). Die Wahrscheinlichkeit eines Erfolgs bezeichnen wir mit dem Parameter \(\pi\) (der hier nichts mit der Kreiszahl 3.14159… zu tun hat), \[ P(A)=\pi. \] Die Indikatorvariable \(1_A\) ist eine Zufallsvariable mit \[ 1_A=\left\{ \begin{array}{ll} 1 & \text{ wenn }A\text{ eintritt}\\ 0 & \text{ wenn }\bar A\text{ eintritt}\\ \end{array} \right. \] Die Zufallsvariable \(1_A\) heißt Bernoulli-verteilt (engl. Bernoulli distributed) mit Parameter \(\pi\). Die Wahrscheinlichkeitsfunktion lautet \[ f(x)=\left\{ \begin{array}{ll} 1-\pi & \text{ wenn }x=0\\ \pi & \text{ wenn }x=1\\ 0 & \text{ sonst.} \end{array} \right. \] Der Erwartungswert lässt sich nun leicht ausrechnen. Es gilt \[ E(1_A)=0\cdot (1-\pi)+1\cdot \pi=\pi. \] Und die Varianz beträgt
\[\begin{align*} Var(1_A)&=(0-\pi)^2\cdot (1-\pi)+(1-\pi)^2\cdot \pi\\ &=\pi^2(1-\pi)+(1-\pi)^2\pi\\ &=\pi^2-\pi^3+(1-2\pi+\pi^2)\pi\\ &=\pi^2-\pi^3+\pi-2\pi^2+\pi^3\\ &=\pi-\pi^2\\ &=\pi (1-\pi). \end{align*}\]
4.2.2 Binomialverteilung
Eine Zufallsvariable \(X\) folgt einer Binomialverteilung (engl. binomial distribution) mit den Parametern \(n\) und \(\pi\), wenn der Träger \[ T_X=\{0,1,2,\ldots,n\} \] ist und die Wahrscheinlichkeitsfunktion für \(k=0,1,2,\ldots,n\) \[ P(X=k)={n \choose k} \pi^k (1-\pi)^{n-k} \] lautet. Der Ausdruck \({n \choose k}\) heißt Binomialkoeffizient, er ist eine Kurzschreibweise für \[ {n \choose k} =\frac{n!}{k!(n-k)!}, \] wobei \(n!\) die Fakultät von \(n\) ist, d.h. \[ n!=1\cdot 2\cdot\ldots\cdot n. \] Die Binomialverteilung ergibt sich, wenn ein Bernoulli-Experiment \(n\)-mal unabhängig wiederholt wird. Mit \(A_1, A_2,\ldots, A_n\) bezeichnen wir die Ereignisse, ob bei der \(i\)-ten Wiederholung ein Erfolg oder Misserfolg aufgetreten ist. Dazu werden die \(n\) Zufallsvariablen \[ 1_{A_i}=\left\{ \begin{array}{ll} 1 & \text{ wenn }A_i\text{ eintritt}\\ 0 & \text{ wenn }\bar A_i\text{ eintritt} \end{array} \right. \] definiert. Dann ist die Summe \[ X=\sum_{i=1}^n 1_{A_i} \] eine binomialverteilte Zufallsvariable. Sie gibt an, wie viele Erfolge bei den \(n\) Wiederholungen aufgetreten sind. Die Verteilung von \(X\) hängt davon ab, welche Werte \(n\) und \(\pi\) annehmen. Für \(n=1\) ergibt sich als Spezialfall die Bernoulli-Verteilung mit Parameter \(\pi\).
Die übliche Kurzschreibweise für eine binomialverteilte Zufallsvariable mit den Parametern \(n\) und \(\pi\) lautet \[ X\sim B(n,\pi). \] Der Erwartungswert und die Varianz betragen
\[\begin{align*} E(X) &= n\pi\\ Var(X) &= n\pi (1-\pi). \end{align*}\]
Auf die Herleitungen verzichten wir an dieser Stelle. Sie sind sehr einfach mit den Methoden durchführbar, die in Kapitel 6 behandelt werden.
In R ist die Abkürzung für die Binomialverteilung binom. Die R-Funktion zur Berechnung der Wahrscheinlichkeitsfunktion \(P(X=k)\) einer binomialverteilten Zufallsvariable \(X\) mit den Parametern \(n\) und \(p\) ist
Die Verteilungsfunktion \(F(x)=P(X\le x)\) wird in R berechnet durch
pbinom(x, size=n, prob=p)Und die Quantilfunktion kann in R ausgewertet werden mit der R-Funktion
qbinom(q, size=n, prob=p)Diese Funktion berechnet das \(q\)-Quantil.
Alle drei Funktionen können auch an mehreren Stellen gleichzeitig ausgewertet werden, indem man für k, x oder q einen Vektor einsetzt.
Beispiel: Urnenmodell
Die prototypische Anwendung der Binomialverteilung hat keinen ökonomischen Bezug, ist aber trotzdem für das Verständnis hilfreich. Es geht um das Ziehen von Kugeln aus einer Urne mit Zurücklegen. Als Beispiel betrachten wir eine Urne mit 10 Kugeln, von denen 3 rot und 7 weiß sind. Aus dieser Urne werden nun (mit Zurücklegen) fünf Kugeln gezogen.
Die Zufallsvariable \(X\) sei die Anzahl der gezogenen roten Kugeln. Offenbar kann \(X\) Werte zwischen 0 und 5 annehmen. Die Wahrscheinlichkeit, bei einem Zug eine rote Kugel zu ziehen, beträgt jedesmal 3/10=0.3. Also gilt \[ X\sim B(5,0.3). \] Die Wahrscheinlichkeit, dass genau 2 rote Kugeln gezogen werden, beträgt \(P(X=2)\),
dbinom(2, size=5, prob=0.3)[1] 0.3087Die Wahrscheinlichkeit, dass höchstens 1 rote Kugel gezogen wird, ist \(P(X\le 1)\),
pbinom(1, size=5, prob=0.3)[1] 0.52822Der Median ist
qbinom(0.5, size=5, prob=0.3)[1] 1Wenn man den Vektor 0:5 als Argument in die Funktion dbinom einsetzt, erhält man die komplette Wahrscheinlichkeitsfunktion,
dbinom(0:5, size=5, prob=0.3)[1] 0.16807 0.36015 0.30870 0.13230 0.02835 0.00243Die Summe dieser Wahrscheinlichkeiten ist 1.
Warum wird eine gezogene Kugel vor der nächsten Ziehung wieder in die Urne zurückgelegt? Eine Binomialverteilung liegt nur vor, wenn die einzelnen Ziehungen identisch und unabhängig Bernoulli-verteilt sind. Würde man eine gezogene Kugel nicht wieder zurücklegen, dann würden sich die Anteile bei jedem Zug verändern. Wenn aus der Urne in diesem Beispiel beim ersten Zug eine rote Kugel gezogen würde, dann wäre der Anteil roter Kugeln beim zweiten Zug nicht mehr 3/10, sondern 2/9. Und wenn beim ersten Zug eine weiße Kugel gezogen würde, hätte man anschließend einen Anteil roter Kugeln von 3/9. Die Verteilungen wären also nicht mehr identisch. Natürlich kann man sich trotzdem überlegen, wie die Verteilung aussieht, wenn die Kugeln nicht zurückgelegt werden. Das Ergebnis ist dann aber keine Binomialverteilung mehr.
Beispiel: Überbuchung eines Flugzeugs
Die Plätze in einem Flugzeug werden gewöhnlich überbucht. Es werden mehr Passagiere gebucht als Plätze vorhanden sind. Das hat einen einfachen Grund: Erfahrungsgemäß kommen nicht alle Passagiere, die einen Platz gebucht haben. Es gibt einen gewissen Anteil an “no-shows”. Die Überbuchung hilft, dass nicht regelmäßig Plätze ungenutzt bleiben.
Für einen Flug von Münster nach München ist eine Maschine mit 90 Plätzen vorgesehen. Angenommen, die Wahrscheinlichkeit eines “no-shows” beträgt für jeden Passagier 0.08. Die Wahrscheinlichkeit, dass ein gebuchter Passagier tatsächlich erscheint, ist also 0.92. Ferner nehmen wir an, dass das Erscheinen jedes Passagiers stochastisch unabhängig ist vom Erscheinen der übrigen Passagiere. Die Anzahl der tatsächlich erscheinenden Passagiere \(X\) ist dann binomialverteilt, \[ X\sim B(N,0.92), \] wobei \(N\) die Zahl der gebuchten Passagiere ist. Wie hoch ist die Wahrscheinlichkeit, dass die Maschine überbucht ist, wenn die Fluggesellschaft \(N=94\) Passagiere bucht? Zu einer Überbuchung kommt es, wenn \(X>90\) ist. Die Wahrscheinlichkeit beträgt \[ P(X>90)=1-P(X\le 90). \] In R erhält man
1-pbinom(90, size=94, prob=0.92)[1] 0.05142848Wie groß ist die Wahrscheinlichkeit, dass genau zwei Personen zu viel erscheinen (und dann von der Fluggesellschaft entschädigt werden müssen)? Die Wahrscheinlichkeit für \(X=92\) ist
dbinom(92, size=94, prob=0.92)[1] 0.01303894.2.3 Poisson-Verteilung
Eine Zufallsvariable \(X\) heißt Poisson-verteilt (engl. Poisson distributed) mit dem Parameter \(\lambda\), wenn sie die Wahrscheinlichkeitsfunktion \[ P(X=x)=e^{-\lambda}\frac{\lambda^x}{x!} \] für \(x=0,1,2,\ldots\) hat. Die übliche Kurzschreibweise ist \(X\sim Po(\lambda)\).
Der Träger der Poisson-Verteilung besteht aus allen natürlichen Zahlen (und der Null). Erwartungswert und Varianz sind beide
\[\begin{align*} E(X) &= \lambda\\ Var(X) &= \lambda. \end{align*}\]
In R ist die Abkürzung für die Poisson-Verteilung pois. Die R-Funktion zur Berechnung der Wahrscheinlichkeitsfunktion \(P(X=x)\) einer Poisson-verteilten Zufallsvariable \(X\) mit dem Parameter \(\lambda\) ist
dpois(x, lambda)Die Verteilungsfunktion \(F(x)=P(X\le x)\) wird in R berechnet durch
ppois(x, lambda)Und die Quantilfunktion ist
qpois(p, lambda)Es gibt zwei Anwendungsbereiche, in denen die Poisson-Verteilung besonders gut zur Modellierung geeignet ist. Zum einen ist es die Approximation einer Binomialverteilung, wenn die Zahl der Ziehungen groß und die Wahrscheinlichkeit eines Erfolgs klein ist. Zum anderen kann die Poisson-Verteilung gut zur Modellierung von “Schalterproblemen” eingesetzt werden.
Die Approximation einer Binomialverteilung durch eine Poisson-Verteilung ist sehr präzise möglich, wenn \(n\) groß und gleichzeitig \(\pi\) klein ist. Die Poisson-Verteilung ergibt sich als Grenzwert, wenn \(n\to\infty\) und \(\pi\) so gegen 0 konvergiert, dass \(n\pi\) gegen eine Konstante konvergiert. In diesem Fall gilt \[ P(X=x)={n\choose x}\pi^x (1-\pi)^{n-x}\approx e^{-\lambda}\frac{\lambda^x}{x!} \] mit \(\lambda=n\pi\), d.h. der Parameter \(\lambda\) der Poisson-Verteilung wird bei der Approximation auf den Erwartungswert der Binomialverteilung gesetzt. Die folgende Tabelle zeigt die Wahrscheinlichkeiten \(P(X=k)\) für \(k=0,1,\ldots,5\) bei einigen Binomialverteilungen und ihre Approximation durch eine Poisson-Verteilung.
| k | B(10, 0.1) | B(100, 0.01) | B(1000, 0.001) | Po(1) |
|---|---|---|---|---|
| 0 | 0.34868 | 0.36603 | 0.36770 | 0.36788 |
| 1 | 0.38742 | 0.36973 | 0.36806 | 0.36788 |
| 2 | 0.19371 | 0.18486 | 0.18403 | 0.18394 |
| 3 | 0.05740 | 0.06100 | 0.06128 | 0.06131 |
| 4 | 0.01116 | 0.01494 | 0.01529 | 0.01533 |
| 5 | 0.00149 | 0.00290 | 0.00305 | 0.00307 |
Man erkennt, dass selbst bei \(n=10\) und \(\pi=0.1\) die Approximation schon einigermaßen gut ist. Für \(n=1000\) und \(\pi=0.001\) sind die Unterschiede zwischen Binomial- und Poisson-Verteilung vernachlässigbar.
Beispiel: Postwurfsendungen
Ein Unternehmen verschickt einen Werbebrief an 10000 Personen. Wie viele Kunden tatsächlich auf den Brief reagieren, ist vor der Werbeaktion nicht bekannt. Die Zufallsvariable \(X\) sei die Anzahl der Personen, die auf den Brief reagieren. Die Reaktionen der Personen seien unabhängig voneinander. Die Reaktionswahrscheinlichkeit sei für jede Person 0.0003, d.h. bei 10000 Briefen ist der Erwartungswert der Anzahl der Reaktionen 3. Natürlich ist die tatsächliche Reaktionswahrscheinlichkeit in der Praxis nicht bekannt. Wie man damit umgeht, dass der Parameter (oder die Parameter) einer Verteilung unbekannt sind und aus Daten geschätzt werden müssen, wird ausführlich in dem Bachelor-Wahlpflicht-Modul Advanced Statistics behandelt.
Die Anzahl der Reaktionen ist binomialverteilt mit \[ X\sim N(10000, 0.0003). \] Diese Binomialverteilung kann gut approximiert werden durch \[ X\sim Po(3). \] Die Wahrscheinlichkeit, dass genau 2 Personen auf die Werbeaktion reagieren, beträgt \(P(X=2)\),
dpois(2, lambda=3)[1] 0.2240418Die Wahrscheinlichkeit, dass mindestens 5 Personen reagieren, ist \[ P(X\ge 5)=1-P(X<5)=1-P(X\le 4). \] In R ergibt sich
1 - ppois(4, lambda=3)[1] 0.1847368Ein weiterer wichtiger Anwendungsbereich der Poisson-Verteilung sind “Schalterprobleme”. Dabei wird die Zahl von Kunden als Zufallsvariable modelliert, die innerhalb einer bestimmten Zeitspanne am Schalter eintreffen. Eine besondere Eigenschaft der Poisson-Verteilung ist es, dass dann auch die Zahl der eintreffenden Kunden für eine längere oder kürzere Zeitspanne poisson-verteilt ist. Der Parameter der Verteilung verändert sich proportional zur Länge der Zeitspanne.
Beispiel: Kunden treffen ein
Sei \(X\sim Po(\lambda)\) die Zahl der Passagiere, die innerhalb einer Viertelstunde am Terminal ankommen. Wir nehmen an, dass die erwartete Zahl \(\lambda=9\) beträgt. Sei nun \(Y\) die Anzahl der Ankommenden innerhalb von fünf Minuten, dann gilt \(Y\sim Po(3)\). Allgemein bleibt bei einer Verlängerung oder Verkürzung des Intervalls die Poisson-Verteilung erhalten und der Parameter \(\lambda\) wächst oder schrumpft proportional zu der Veränderung der Intervalllänge.
Die Wahrscheinlichkeit, dass in der Zeit von 10:00 bis 10:15 genau sechs Passagiere ankommen, beträgt
dpois(6, lambda=9)[1] 0.09109032Die Wahrscheinlichkeit, dass zwischen 14:30 und 14:35 mehr als 7 Passagiere eintreffen, ist \(P(Y>7)=1-P(Y\le 7)\),
1 - ppois(7, lambda=3)[1] 0.01190454.3 Stetige Verteilungen
4.3.1 Normalverteilung
Die mit großem Abstand wichtigste Verteilung überhaupt ist die Normalverteilung (engl. normal distribution), manchmal auch Gauß-Verteilung (engl. Gaussian distribution) genannt. Sie ist aus zwei Gründen so wichtig. Zum einen lassen sich viele empirische Phänomene sehr gut durch eine Normalverteilung modellieren, z.B. biometrische Größen (Körpergröße und -gewicht), ökonomische Größen (Jahresrenditen von Aktien oder Anleihen), Messfehler und Produktionsabweichungen. Zum anderen spielt die Normalverteilung eine extrem wichtige Rolle in der Schätz- und Testtheorie, die später in diesem Kurs in Kapitel 10 und Kapitel 11 behandelt werden.
Everybody believes in the normal distribution: the experimenters because they think it is a mathematical theorem and the mathematicians because they think it is an experimental fact. (Quelle nicht rekonstruierbar.)
Bevor die allgemeine Normalverteilung eingeführt wird, definieren wir zuerst die Standardnormalverteilung. Eine Zufallsvariable \(U\) heißt standardnormalverteilt, wenn sie für \(u\in\mathbb{R}\) die Dichte \[ \phi(u)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}u^2\right) \] hat. Die Kurzschreibweise lautet \(U\sim N(0,1)\). Das Symbol \(\phi\) (“klein phi”) ist die gängige Notation für die Dichte der Standardnormalverteilung.
Das “Herz” der Standardnormalverteilung ist die Funktion \(e^{-u^2}\). Alle anderen Bestandteile der Dichte dienen letztlich nur der Normierung. Ein Plot der Dichte zeigt, dass sie eine Glockenkurve beschreibt, die symmetrisch um die Null herum verläuft.
R-Code zeigen
x <- seq(from=-4, to=4, length=200)
plot(x, dnorm(x),
type="l",
main="Dichte der Standardnormalverteilung",
xlab="x",
ylab=expression(phi(x)),
yaxs="i",
ylim=c(0,0.45))
abline(v=0)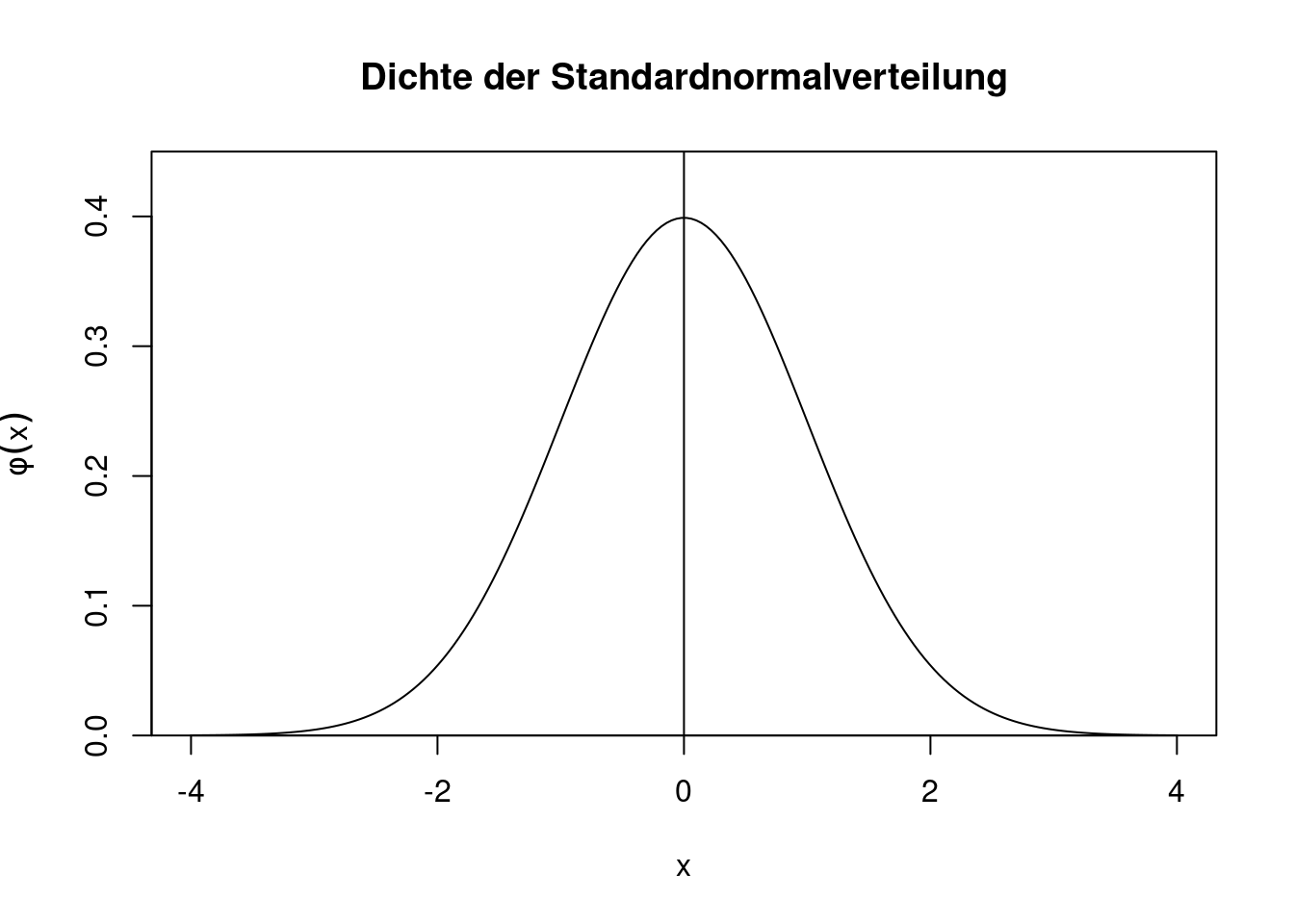
Die zugehörige Verteilungsfunktion wird mit \(\Phi(u)=P(U\le u)\) (“groß phi”) bezeichnet, \[ \Phi(u)=\int_{-\infty}^u \phi(t)dt. \] Die Funktion \(\Phi(u)\) ist auf ganz \(\mathbb{R}\) streng monoton wachsend, jedoch sind Werte betragsmäßig größer als 4 extrem unwahrscheinlich, wie man an der folgenden Abbildung erkennt.
R-Code zeigen
x <- seq(from=-4, to=4, length=200)
plot(x, pnorm(x),
type="l",
main="Verteilungsfunktion der Standardnormalverteilung",
xlab="x",
ylab=expression(Phi(x)),
yaxs="i",
ylim=c(0,1.1))
abline(v=0)
abline(h=1,
lty="dotted")
Wegen der Symmetrie der Standardnormalverteilung um die Null herum gilt \[ \Phi(u)=1-\Phi(-u). \] Die Inverse der Verteilungsfunktion ist die Quantilfunktion \(\Phi^{-1}(p)\),
R-Code zeigen
x <- seq(from=0.001, to=0.999, length=200)
plot(x, qnorm(x),
type="l",
main="Quantilfunktion der Standardnormalverteilung",
xlab="x",
ylab=expression(Phi^-1 (x)),
xaxs="i")
abline(h=0)
Auch hier gibt es eine Symmetriebeziehung, nämlich
\[\begin{align*} \Phi^{-1}(p) &= -\Phi^{-1}(1-p)\\ \text{bzw.}\qquad u_p &= -u_{1-p}. \end{align*}\]
Der Erwartungswert der Standardnormalverteilung ist \(E(U)=0\), die Varianz ist \(Var(U)=1\). Die Zufallsvariable \(U\) ist also standardisiert.
Leider gibt es keine geschlossene Formel für das Integral der Dichtefunktion. Die Verteilungsfunktion \(\Phi(u)\) kann daher nicht einfach formelmäßig notiert werden. Dennoch lassen sich Dichte-, Verteilungs- und Quantilfunktion in R sehr einfach berechnen. Die Abkürzung in R für die Normalverteilung ist norm. Genauere Hinweise zu Funktionsaufrufen finden Sie in Kapitel A.4.
Die Standardnormalverteilung ist ein Spezialfall der Normalverteilung. Die allgemeine Normalverteilung hat zwei Parameter, die meistes mit \(\mu\) und \(\sigma^2\) (oder \(\sigma\)) bezeichnet werden. Die Dichtefunktion der Normalverteilung ist \[ f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right). \] Die Kurzschreibweise für eine normalverteilte Zufallsvariable mit den Parametern \(\mu\in\mathbb{R}\) und \(\sigma^2>0\) lautet: \(X\sim N(\mu,\sigma^2)\).
Der Parameter \(\mu\) bewirkt eine Verschiebung der Dichte. Für positive Werte von \(\mu\) liegt die Dichte weiter rechts, für negative Werte weiter links. Wenn \(\mu=0\) ist, weist die Dichte eine Symmetrie um die 0 herum auf. Die Abbildung zeigt drei Dichten von \(N(\mu,1)\) für \(\mu=-1,1,5\).
R-Code zeigen
x <- seq(from=-4, to=9, length=500)
plot(x,dnorm(x, mean=-1, sd=1),
type="l",
col="red",
yaxs="i",
ylim=c(0, 0.45),
ylab="Dichten",
main=expression(paste("Einfluss von ",mu)))
lines(x,dnorm(x, mean=1, sd=1), col="green")
lines(x,dnorm(x, mean=5, sd=1), col="blue")
legend("topright",
fill=c("red", "green", "blue"),
legend=c(expression(mu==-1),
expression(mu==1),
expression(mu==5)))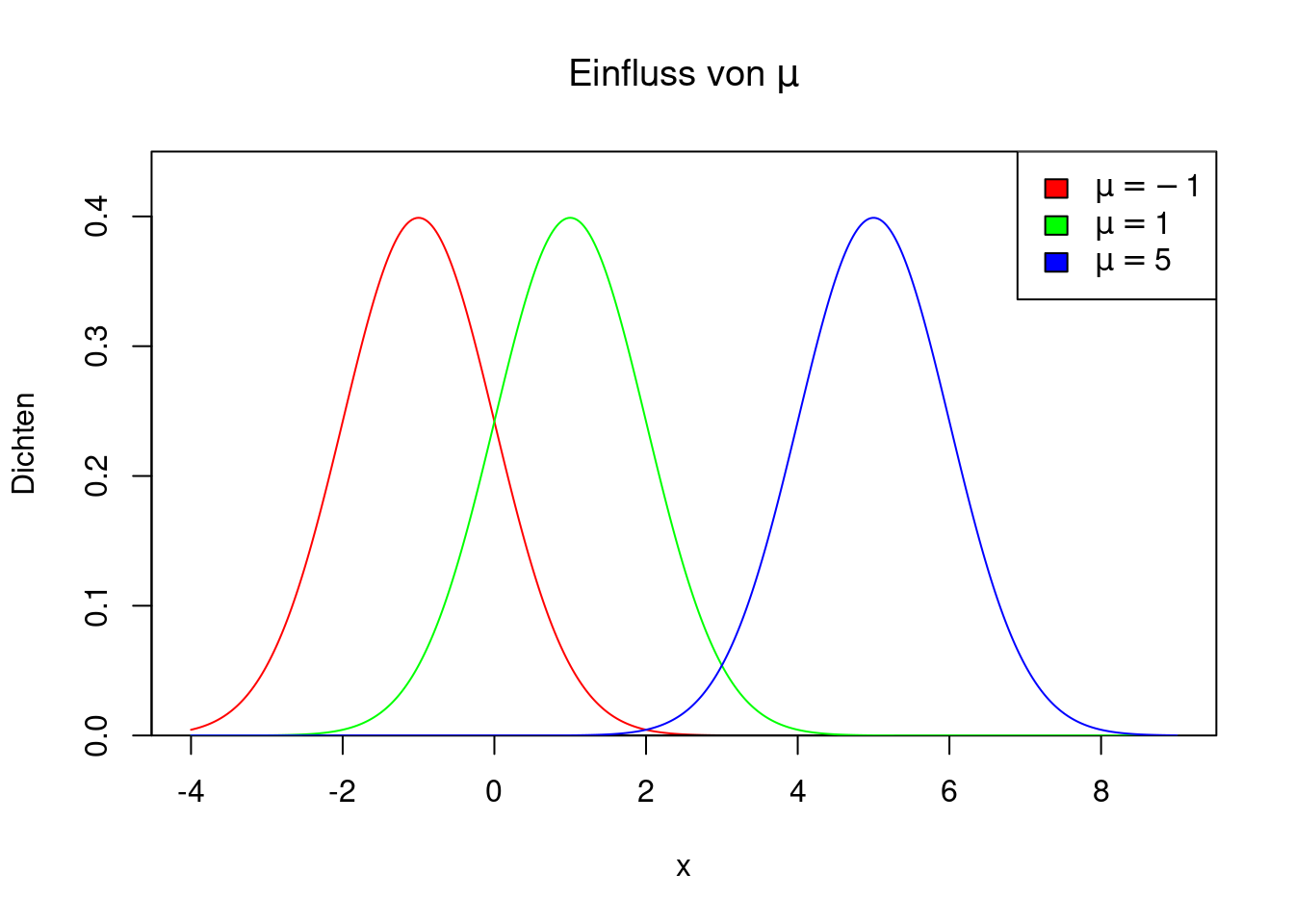
Der Parameter \(\sigma^2\) hat einen Einfluss auf die Form der Dichte. Wenn \(\sigma^2\) klein ist (also nahe 0), dann ist die Dichte schmal und hoch und nah um den Wert \(\mu\) herum konzentriert. Je größer \(\sigma^2\) ist, desto breiter und flacher ist die Dichte. Die Abbildung zeigt drei Dichten von \(N(0,\sigma^2)\) für \(\sigma^2=0.3,1,3\).
R-Code zeigen
x <- seq(from=-7, to=7, length=500)
plot(x, dnorm(x, mean=0, sd=sqrt(0.3)),
type="l",
col="red",
yaxs="i",
ylim=c(0, 0.8),
ylab="Dichten",
main=expression(paste("Einfluss von ",sigma^2)))
lines(x,dnorm(x, mean=0, sd=1), col="green")
lines(x,dnorm(x, mean=0, sd=sqrt(3)), col="blue")
legend("topright",
fill=c("red","green","blue"),
legend=c(expression(sigma^2==0.3),
expression(sigma^2==1),
expression(sigma^2==3)))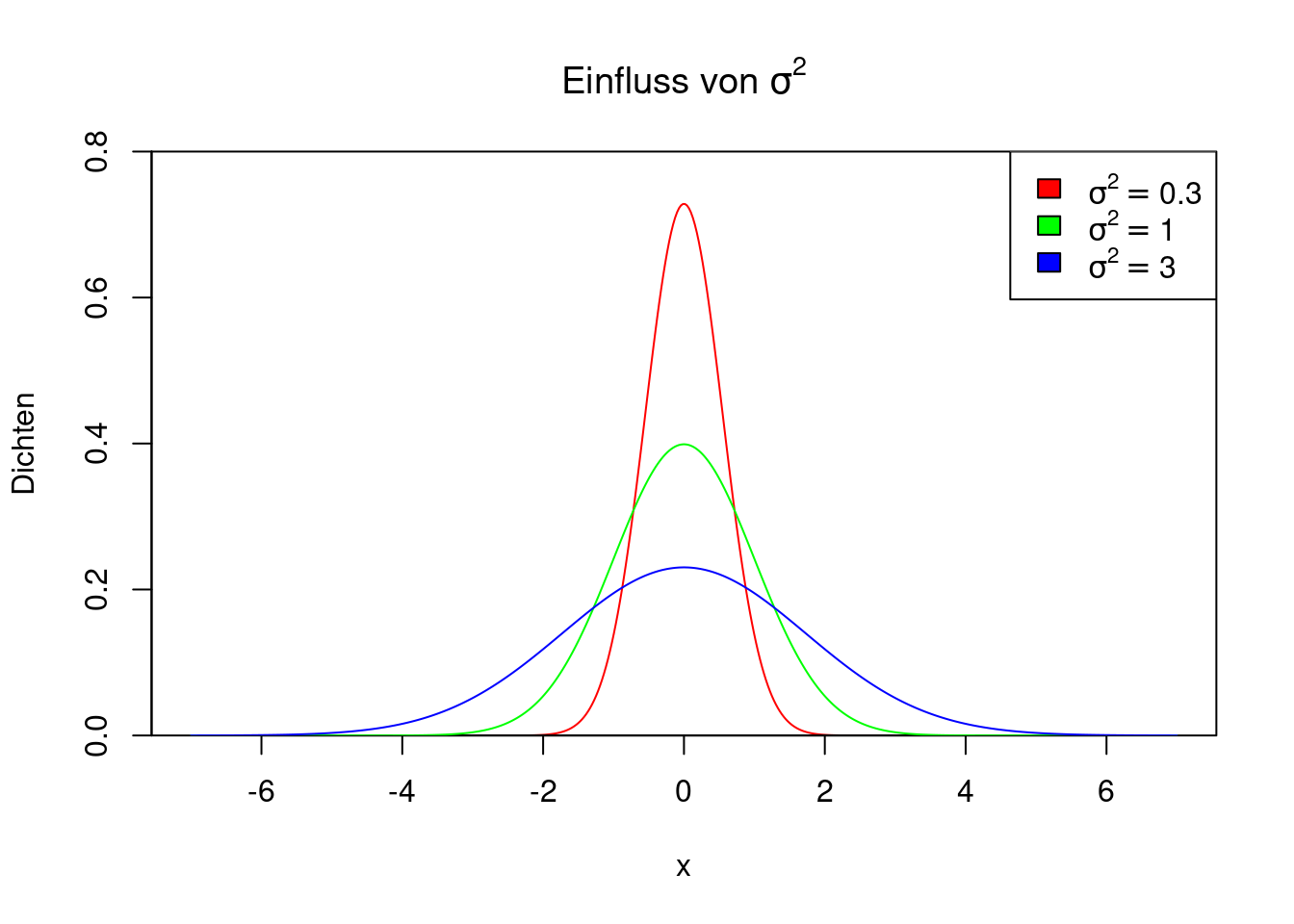
Zwischen der Dichte der \(N(\mu,\sigma^2)\) und der Dichte der Standardnormalverteilung besteht eine enge Beziehung. Es gilt \[ f(x)=\phi\left(\frac{x-\mu}{\sigma}\right). \] Die Verteilungsfunktion der allgemeinen Normalverteilung \(N(\mu,\sigma^2)\) wird indirekt durch die Verteilungsfunktion der Standardnormalverteilung \(N(0,1)\) ausgedrückt. Sie ist \[ F(x)=\Phi\left(\frac{x-\mu}{\sigma}\right). \] Das bedeutet, dass eine standardisierte Normalverteilung einer Standardnormalverteilung folgt (die Begriffe sind also gut gewählt). Wegen dieses Zusammenhangs ist es möglich, die Verteilungsfunktion einer beliebigen Normalverteilung selbst dann auszuwerten, wenn man nur die Verteilungsfunktion der Standardnormalverteilung kennt. In älteren Lehrbüchern zur Statistik findet man deshalb im Anhang Tabellen mit den Funktionswerten der Verteilungsfunktion der Standardnormalverteilung. Mit ihrer Hilfe konnte man früher die Verteilungsfunktion jeder Normalverteilung bestimmen. Heutzutage ist das nicht mehr nötig, da die Verteilungsfunktion der allgemeinen Normalverteilung in praktisch jedem Computerprogramm implementiert ist.
Auch die Quantilfunktion der \(N(\mu,\sigma^2)\) wird durch die Quantilfunktion der \(N(0,1)\) ausgedrückt, und zwar gilt \[ F^{-1}(p) = \mu+\sigma \cdot\Phi^{-1}(p). \] Erwartungswert und Varianz der \(N(\mu,\sigma^2)\) sind
\[\begin{align*} E(X) &= \mu\\ Var(X) &= \sigma^2. \end{align*}\]
In R verwendet man für die allgemeine Normalverteilung die gleichen Funktionen wie für die Standardnormalverteilung. Nur die beiden Parameter \(\mu\) (mean) und \(\sigma\) (sd) werden als zusätzliche Argumente angefügt.
Achtung: Anstelle der Varianz \(\sigma^2\) erwarten die R-Funktionen zur Normalverteilung als Argument die Standardabweichung \(\sigma\)! Es ist ein häufiger und leider leicht zu übersehender Fehler, als Parameter die Varianz anzugeben.
Die R-Funktionen für die Dichte-, Verteilungs- und Quantilfunktion der Normalverteilung sind also
dnorm(x, mean=mu, sd=sigma)pnorm(x, mean=mu, sd=sigma)qnorm(p, mean=mu, sd=sigma)
Beispiel: Produktionsfehler
Die Normalverteilung ist ein gutes Modell für die Verteilung von Fehlern (z.B. Messfehler oder Produktionsabweichungen). Mit der Zufallsvariable \(X\) bezeichnen wir das Gewicht (in g) einer zufällig ausgewählten 200g-Tafel Schokolade. Da bei der Produktion der Tafeln immer kleine Abweichungen von der nominalen Menge auftreten, sind die 200g-Tafeln nicht immer 200g schwer. Wir gehen davon aus, dass das tatsächliche Gewicht einer Normalverteilung folgt mit den Parametern \(\mu=201\) (Erwartungswert) und \(\sigma=2\) (Standardabweichung). Die 200g-Tafeln sind also im Erwartungswert ein klein schwerer als nötig. Trotzdem kann es passieren, dass eine zufällig ausgewählte Tafel tatsächlich weniger als 200g wiegt.
Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Tafel Schokolade weniger als 200g wiegt, beträgt \(P(X\le 200)\),
pnorm(200, mean=201, sd=2)[1] 0.3085375Es ist also gar nicht unwahrscheinlich, dass man eine zu leichte Tafel zieht.
Wenn \(X\sim N(201, 2^2)\) ist, welches Gewicht wird dann mit einer Wahrscheinlichkeit von nur 5 Prozent unterschritten? Gesucht ist nun das 0.05-Quantil von \(X\). Es ist
qnorm(0.05, mean=201, sd=2)[1] 197.7103Die Wahrscheinlichkeit, eine Tafel zu ziehen, die leichter als 197.7g ist, beträgt nur 5 Prozent.
4.3.2 Exponentialverteilung
Die Exponentialverteilung ist oft gut geeignet zur Modellierung von Wartezeiten oder Dauern. Eine Zufallsvariable \(X\) heißt exponentialverteilt (engl. exponentially distributed) mit Parameter \(\lambda>0\), wenn ihre Dichte \[ f(x)=\left\{ \begin{array}{ll} \lambda e^{-\lambda x} & \text{ wenn }x\ge 0\\ 0 & \text{ wenn }x<0. \end{array} \right. \] ist. Die Kurzschreibweise für eine exponentialverteilte Zufallsvariable ist \(X\sim Exp(\lambda)\).
Der Plot zeigt den Verlauf der Dichtefunktion von \(Exp(1)\).
R-Code zeigen
x <- seq(from=0.0001, to=5, length=200)
plot(x, dexp(x),
type="l",
main="Dichte der Exponentialverteilung",
xlab="x",
ylab="Dichte",
yaxs="i",
ylim=c(0, 1.1),
xlim=c(-0.5, 5))
lines(c(0,0), c(0,1), lty="dotted")
Die Verteilungsfunktion erhält man durch Integration der Dichte. Außerdem muss die Verteilungsfunktion an der Stelle 0 den Wert 0 annehmen. Für die Verteilungsfunktion ergibt sich \[ F(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x<0\\ 1-e^{-\lambda x}& \text{ wenn }x\ge 0. \end{array} \right. \] Durch Invertieren der Verteilungsfunktion erhält man die Quantilfunktion. Dazu löst man die Gleichung \(F(x)=p\) nach \(x\) auf.
\[\begin{align*} &&F(x)&=p\\ \Leftrightarrow &&1-e^{-\lambda x}&=p \\ \Leftrightarrow &&1-p&=e^{-\lambda x} \\ \Leftrightarrow &&\ln(1-p)&=-\lambda x \\ \Leftrightarrow &&x &=-\frac{1}{\lambda}\ln(1-p). \end{align*}\]
Die Quantilfunktion lautet also \[ F^{-1}(p)=-\frac{1}{\lambda}\ln(1-p). \] Der Erwartungswert und die Varianz sind
\[\begin{align*} E(X) &= \frac{1}{\lambda}\\ Var(X) &= \frac{1}{\lambda^2}. \end{align*}\]
In R ist die Abkürzung für die Exponentialverteilung exp. Die Funktionen für die Dichte, Verteilungs- und Quantilfunktion sind:
dexp(x, rate=lambda)pexp(x, rate=lambda)qexp(p, rate=lambda)
Beispiel: Transaktionsdauern
Mit der Zufallsvariable \(X\) sei die Dauer in Sekunden bis zur nächsten Transaktion einer bestimmten Aktie an der Xetra-Börse bezeichnet. Die Dauer wird modelliert durch eine Exponentialverteilung mit Parameter \(\lambda=0.04\). Wie groß ist die Wahrscheinlichkeit, dass man bis zur nächsten Transaktion mehr als 1 Minute warten muss?
Die gesuchte Wahrscheinlichkeit \(P(X>60)=1-P(X\le 60)\) beträgt
1 - pexp(60, rate=0.04)[1] 0.09071795Die Wahrscheinlichkeit, dass 60 Sekunden lang keine Transaktion ausgeführt wird, beträgt also weniger als 10 Prozent.
Der Median der Transaktionsdauer ist
qexp(0.5, rate=0.04)[1] 17.32868Die Hälfte der Transaktionsdauern ist also geringer als 17.3 Sekunden (und die andere Hälfte größer).
4.3.3 Paretoverteilung
Die Paretoverteilung (engl. Pareto distribution) kann in vielen Anwendungen extreme Ereignisse gut beschreiben. Beispielsweise folgt die Vermögensverteilung bei den Superreichen einer Paretoverteilung. Auch extreme Aktienrenditen oder extreme Schadensereignisse können gut durch eine Paretoverteilung beschrieben werden.
Die Paretoverteilung hat zwei Parameter, und zwar \(x_{min}>0\) und \(k>0\). Die Dichte lautet \[ f(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x<x_{min}\\ \frac{k}{x_{min}}\left(\frac{x_{min}}{x}\right)^{k+1}& \text{ wenn }x\ge x_{min}. \end{array} \right. \] Für \(x_{min}=1\) und \(k=2\) ergibt sich folgendes Bild:
R-Code zeigen
k <- 2
xmin <- 1
x <- seq(from=1, to=5, length=200)
plot(x, (k/xmin)*(xmin/x)^(k+1),
type="l",
main="Dichte der Paretoverteilung",
xlab="x",
ylab="Dichte",
yaxs="i",
ylim=c(0, 2.2),
xlim=c(0, 5))
lines(c(xmin, xmin),
c(0, 2),
lty="dotted")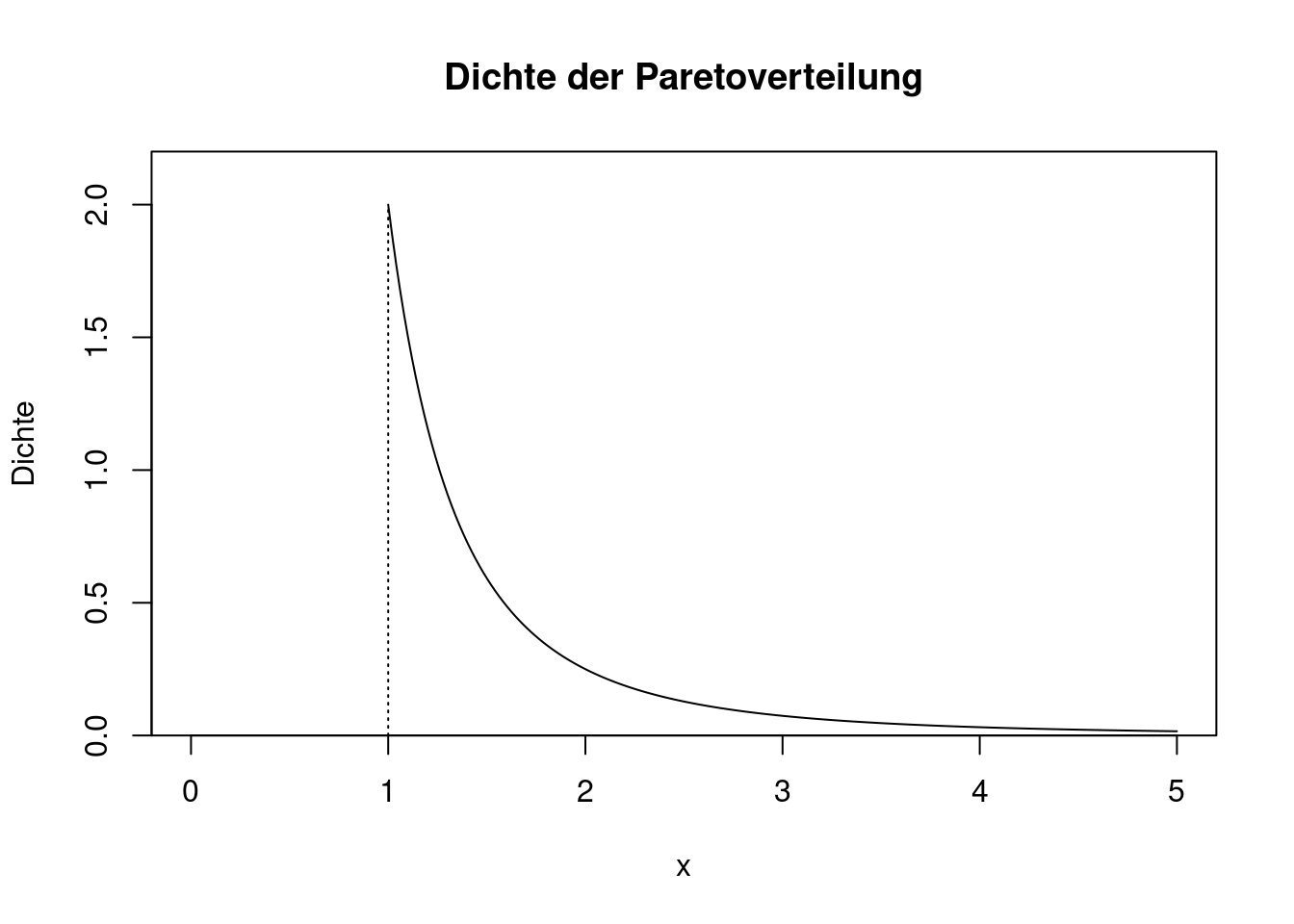
Der Verlauf der Dichte ist auf den ersten Blick ähnlich wie bei der Exponentialverteilung. Jedoch fällt die Dichte der Paretoverteilung deutlich langsamer gegen 0 als die Dichte der Exponentialverteilung. Bei der Paretoverteilung können daher extrem große Ausreißer auftreten. Ein weiterer Unterschied zur Exponentialverteilung besteht darin, dass die Paretoverteilung als Untergrenze den Parameter \(x_{min}>0\) hat, die Exponentialverteilung startet hingegen immer bei 0.
Durch Integration der Dichte erhält man die Verteilungsfunktion. \[ F(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x<x_{min}\\ 1-\left(\frac{x_{min}}{x}\right)^k & \text{ wenn }x\ge x_{min}. \end{array} \right. \]
Invertieren der Verteilungsfunktion führt auf die Quantilfunktion. \[ F^{-1}(p)=x_{min}(1-p)^{-1/k}. \] Erwartungswert und Varianz der Paretoverteilung sind
\[\begin{align*} E(X) &= \frac{k x_{min}}{k-1}\\ Var(X) &= \frac{k x_{min}^2}{(k-2)(k-1)^2}. \end{align*}\]
Der Erwartungswert ist nur definiert, wenn der \(k>1\) ist, die Varianz ist sogar nur dann definiert, wenn \(k>2\) ist. Wie kann es passieren, dass die Varianz oder der Erwartungswert nicht existieren? Der Grund dafür liegt im Flankenverhalten von Zufallsvariablen mit einem unendlichen Träger (z.B. \(\mathbb{R}\)). Das Integral für den Erwartungswert, \[ \int_{-\infty}^\infty xf_X(x)dx, \] ist streng genommen ein Grenzwert, bei dem man die Integralgrenzen gegen (minus) unendlich gehen lässt. Für \(x\to\infty\) wächst \(x\), während die Dichte \(f_X(x)\) schrumpft. Wenn nun \(x\) schneller wächst als \(f_X(x)\) schrumpft, dann wird der Ausdruck unter dem Integral immer größer und die gesamte Fläche divergiert gegen unendlich. Für die Varianz gilt das analog. Kurz gesagt: Es kann passieren, dass eine Zufallsvariable mit unendlichem Träger keine Varianz oder keinen Erwartungswert besitzt. Zum Glück kommt das in den Wirtschaftswissenschaften nicht sehr oft vor, so dass wir dieses Problem in diesem Kurs weitgehend ignorieren können.
In R gibt es die Funktionen für die Dichte, Verteilungsfunktion und Quantilfunktion der Paretoverteilung nur in Zusatzpaketen. Installieren und aktivieren Sie das Paket distributionsrd. Nun stehen die Funktionen
dpareto(x, k, xmin)ppareto(x, k, xmin)qpareto(p, k, xmin)
zur Verfügung.
Beispiel: Reichtum
Die Zufallsvariable \(X\) soll die Verteilung sehr hoher Einkommen modellieren. Konkret soll \(X\) das Nettojahreseinkommen eines zufällig ausgewählten Haushalts in Deutschland sein. Der Haushalt wird jedoch nicht aus allen Haushalten ausgewählt, sondern aus den Haushalten mit einem Mindesteinkommen von \(x_{min}=250000\) Euro. Die Paretoverteilung approximiert die sehr hohen Einkommen sehr gut, als Flankenparameter setzen wir \(k=1.5\).
Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Haushalt ein Einkommen von mehr als 1 Million Euro hat?
Die gesuchte Wahrscheinlichkeit \(P(X>1000000)=1-P(X\le 1000000)\) beträgt
library(distributionsrd)
1 - ppareto(1000000, k=1.5, xmin=250000)[1] 0.125Wie hoch ist der Median des Einkommens in der Gruppe der Haushalte mit einem Einkommen von mindestens 250000 Euro? Der Median beträgt
qpareto(0.5, k=1.5, xmin=250000)[1] 396850.3Von den Haushalten, die mehr als 250000 Euro Einkommen haben, hat also die Hälfte sogar mehr als knapp 400000 Euro.
4.3.4 Rechteckverteilung
Mit einer Rechteckverteilung (manchmal auch Gleichverteilung genannt) kann beispielsweise die Wartezeit an einer Ampel (oder im ÖPNV) modelliert werden. Die Ampel springt in regelmäßigen Abständen auf Grün (bzw. die U-Bahn kommt alle 10 Minuten). Wenn man ohne genaue Planung zur Ampel oder zum Bahnsteig geht, ist die Wartedauer rein zufällig und folgt einer Rechteckverteilung. Die Rechteckverteilung spielt auch eine wichtige Rolle in sogenannten Monte-Carlo-Simulationen (siehe Kapitel 7.2), weil sie Ausgangspunkt aller im Computer generierten Zufallszahlen ist.
Eine Zufallsvariable \(X\) heißt rechteckverteilt (engl. uniformly distributed) mit den Parametern \(a\) und \(b\) (wobei \(a<b\) ist), wenn ihre Dichte \[ f(x)=\left\{ \begin{array}{ll} \frac{1}{b-a} & \text{ wenn }a\le x\le b\\ 0 & \text{ sonst} \end{array} \right. \] ist. Die Kurzschreibweise für eine rechteckverteilte Zufallsvariable ist \(X\sim U(a,b)\).
Der Plot zeigt den Verlauf der Dichtefunktion von \(U(1,2)\).
R-Code zeigen
plot(c(0.5, 2.5),c(0, 1.1),
type="n",
main="Dichte der Rechteckverteilung",
xlab="x",
ylab="Dichte",
yaxs="i")
lines(c(1,2), c(1,1))
lines(c(1,1), c(0,1), lty="dotted")
lines(c(2,2), c(0,1), lty="dotted")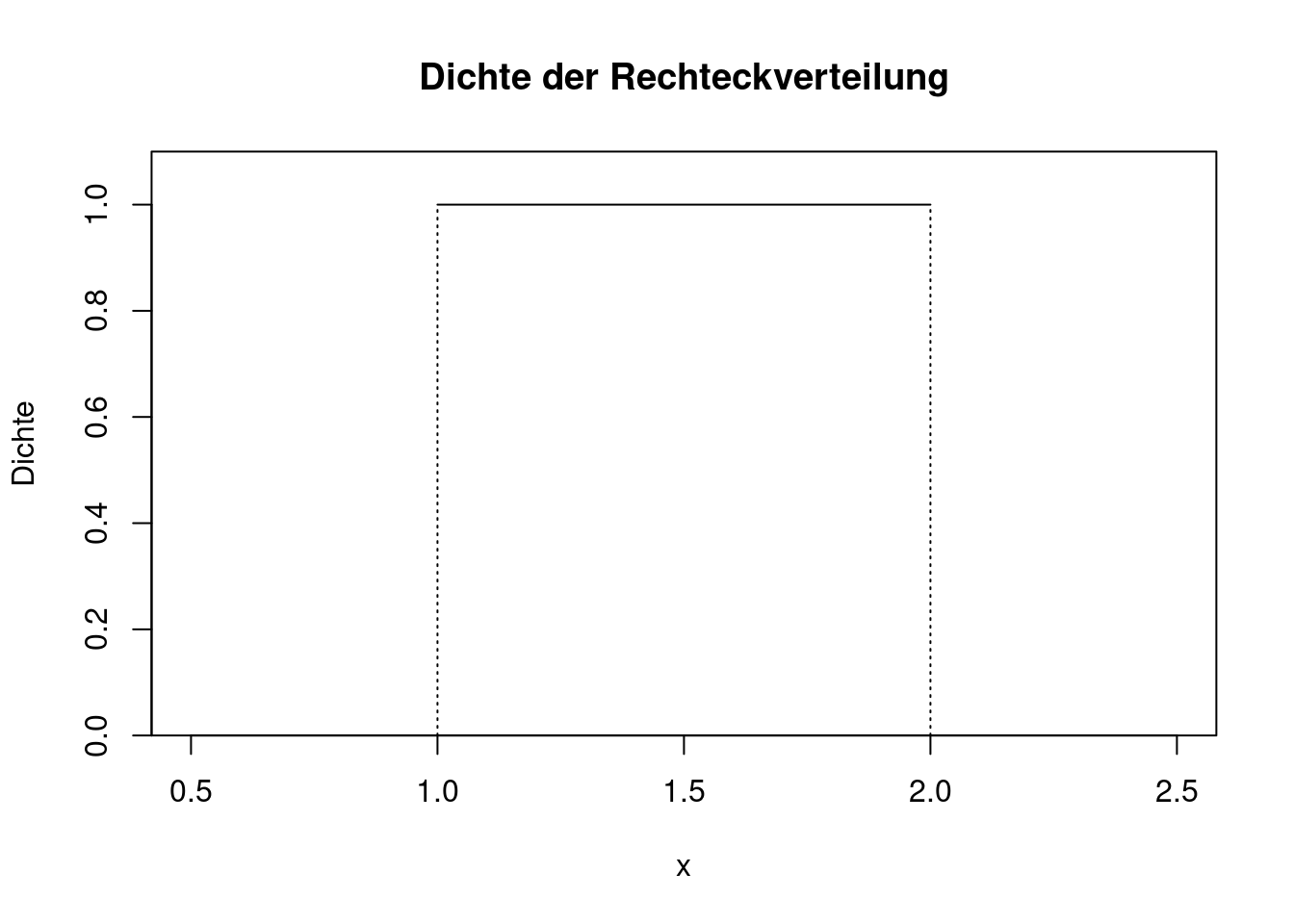
Die Verteilungsfunktion erhält man durch Integration der Dichte. Außerdem muss die Verteilungsfunktion an der Stelle \(a\) den Wert 0 annehmen. Für die Verteilungsfunktion ergibt sich \[ F(x)=\left\{ \begin{array}{ll} 0 & \text{ wenn }x<a\\ \frac{x-a}{b-a}& \text{ wenn }a\le x\le b\\ 1 & \text{ wenn }x>b.\\ \end{array} \right. \] Die Verteilungsfunktion von \(U(1,2)\) sieht wie folgt aus.
R-Code zeigen
plot(c(0.5, 2.5), c(0, 1.1),
type="n",
main="Verteilungsfunktion der Rechteckverteilung",
xlab="x",
ylab="F(x)",
yaxs="i")
lines(c(0.5, 1, 2, 2.5),c(0, 0, 1, 1))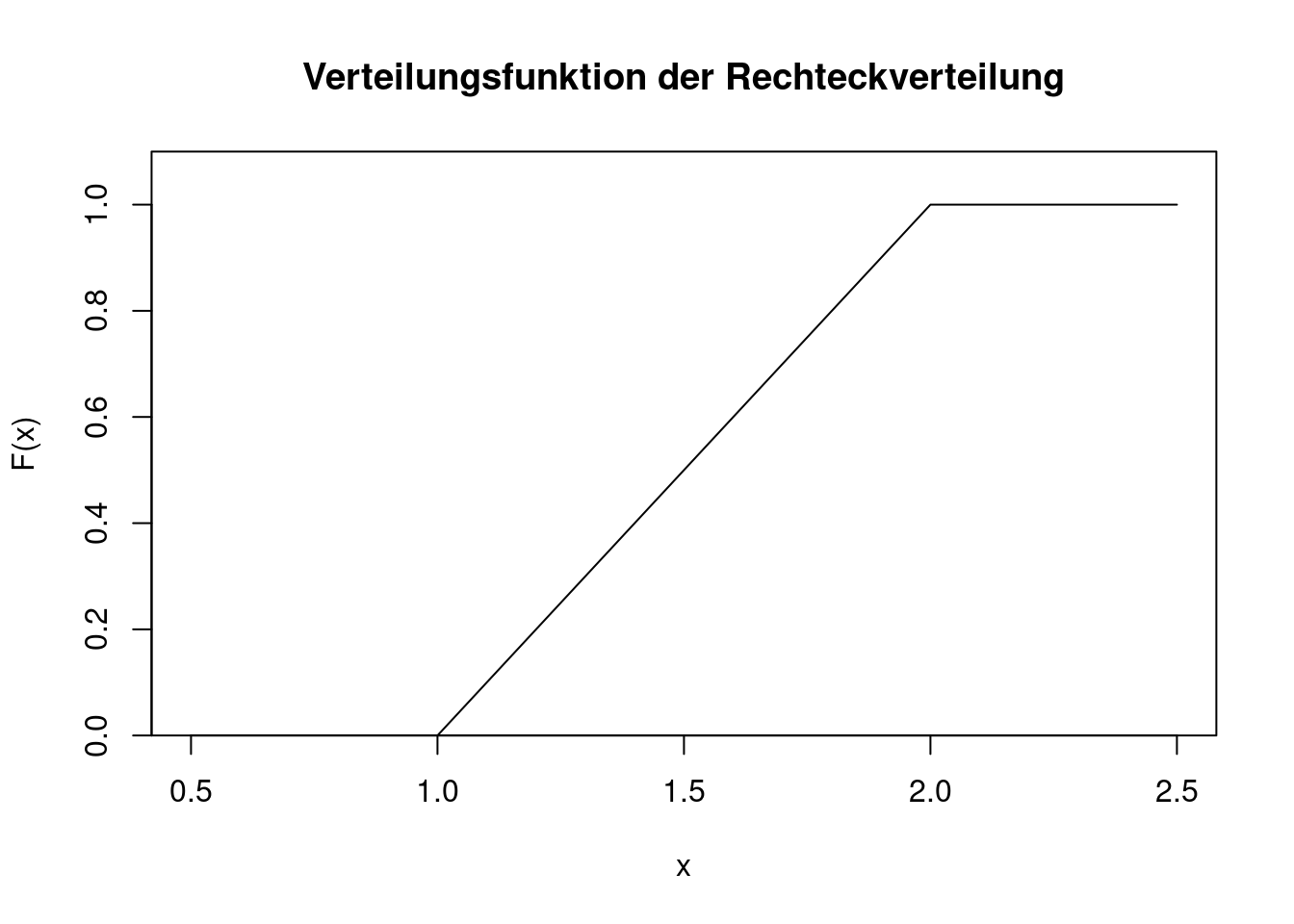
Durch Invertieren der Verteilungsfunktion erhält man die Quantilfunktion. Dazu löst man die Gleichung \(F(x)=p\) nach \(x\) auf.
\[\begin{align*} &&F(x)&=p\\ \Leftrightarrow &&\frac{x-a}{b-a}&=p \\ \Leftrightarrow &&x &=a+(b-a)p. \end{align*}\]
Eine Fallunterscheidung ist hier nicht nötig, weil \(0<p<1\) ist. Die Quantilfunktion lautet \[ F^{-1}(p)=a+(b-a)p. \] Als Erwartungswert und Varianz errechnet man
\[\begin{align*} E(X) &= \frac{a+b}{2}\\[1ex] Var(X) &= \frac{(b-a)^2}{12}. \end{align*}\]
In R ist die Abkürzung für die Rechteckverteilung unif. Die Funktionen für die Dichte, Verteilungs- und Quantilfunktion sind:
dunif(x, min, max)punif(x, min, max)qunif(p, min, max)
Beispiel: Wartezeiten
Die Rechteckverteilung spielt in der statistischen Theorie eine wichtige Rolle. Sie kann jedoch auch eingesetzt werden, um bestimmte Arten von Wartezeiten zu modellieren. Angenommen, die U-Bahn fährt an einer Station regelmäßig und pünktlich alle 10 Minuten. Wenn jemand rein zufällig, ohne auf die Uhr zu sehen, zu dieser Station geht, dann ist die Wartezeit rechteckverteilt auf dem Intervall \([0,10]\) (Minuten).
Die Wahrscheinlichkeit, dass man weniger als 5 Minuten warten muss, beträgt also
punif(5, min=0, max=10)[1] 0.5Die Wahrscheinlichkeit, mehr als 8 Minuten zu warten, ist
1-punif(8, min=0, max=10)[1] 0.24.3.5 t-Verteilung
Die t-Verteilung (engl. t distribution) ist ein gutes Modell für die Verteilung der Tagesrendite von Aktien oder anderen stark volatilen Vermögenswerten (z.B. Kryptowährungen). Eine Zufallsvariable \(X\) heißt t-verteilt mit dem Parameter \(\nu>0\), wenn sie für \(x\in\mathbb{R}\) die Dichte \[ f(x)=C_\nu \cdot \left(1+\frac{x^2}{\nu}\right)^{-\frac{\nu+1}{2}} \] hat. Die Konstante \(C_\nu\) dient nur der Normierung. Ihre genaue Form ist komplex, aber an dieser Stelle nicht relevant. Die Kurzschreibweise für eine t-verteilte Zufallsvariable ist \(X\sim t_\nu\). Der Parameter \(\nu\) heißt auch “Zahl der Freiheitsgrade” (engl. degrees of freedom).
Der Plot zeigt den Verlauf der Dichtefunktion einer t-Verteilung mit \(\nu=2\) Freiheitsgraden (schwarze Linie) und \(\nu=10\) Freiheitsgraden (rote Linie). Zum Vergleich ist auch die Dichte der Standardnormalverteilung eingefügt (gepunktete blaue Linie).
R-Code zeigen
x <- seq(from=-5, to=5, length=300)
plot(x, dt(x,df=2),
type="l",
main="Dichte der t-Verteilung",
xlab="x",
ylab="Dichte",
yaxs="i",
ylim=c(0, 0.43))
lines(x, dt(x, df=10), col="red")
lines(x, dnorm(x), col="blue", lty="dotted")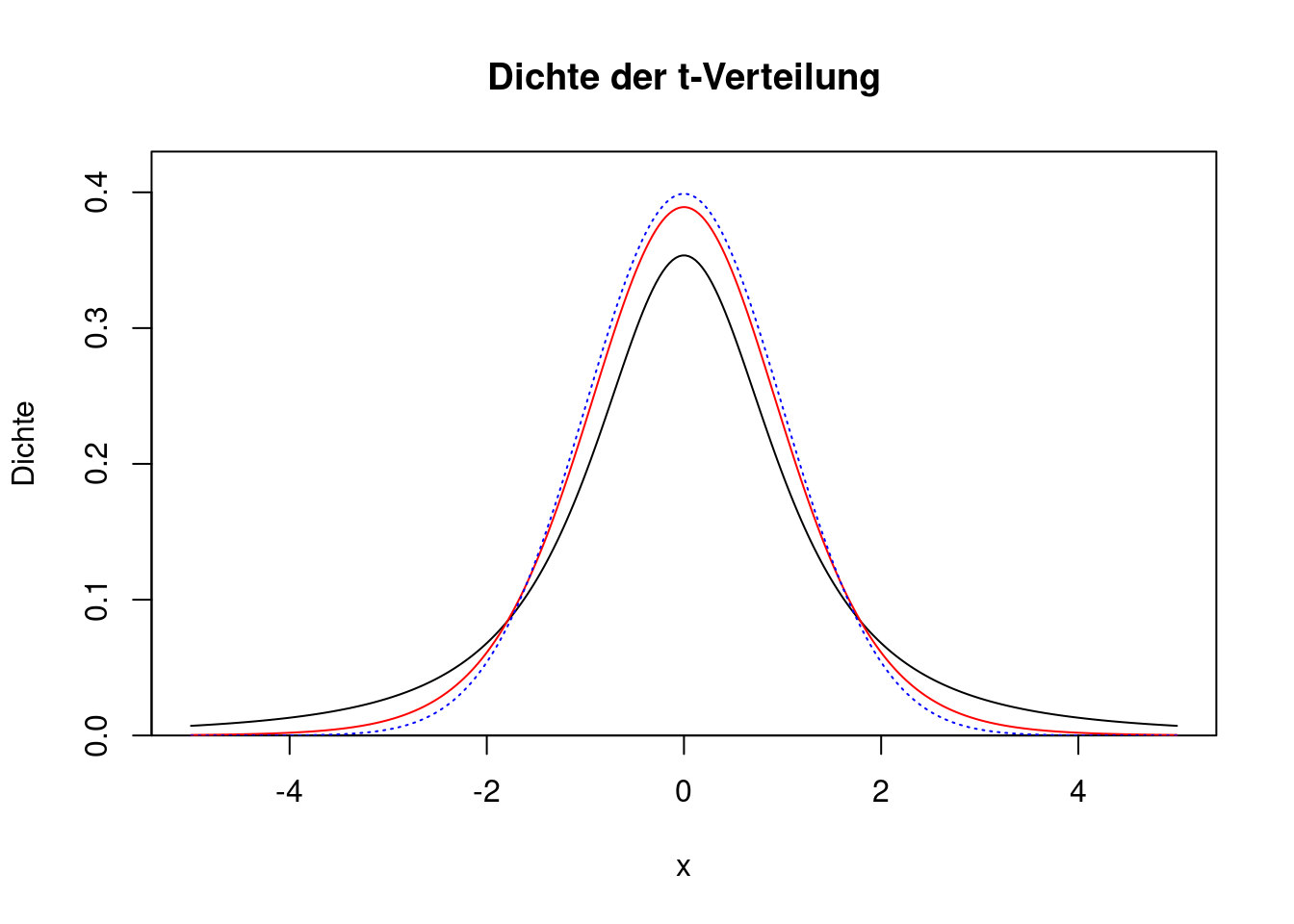
Je größer die Zahl der Freiheitsgrade, desto ähnlicher ist die t-Verteilung der Standardnormalverteilung. Bei sinkenden Freiheitsgraden werden die Flanken der Verteilung immer stärker, d.h. es gibt immer mehr extreme Werte (Ausreißer).
Die Verteilungsfunktion lässt sich (wie schon bei der Normalverteilung) nicht durch elementare Integrationsregeln herleiten. Sie ist jedoch numerisch lösbar und in den meisten Computerprogrammen implementiert.
Erwartungswert und Varianz der t-Verteilung sind (für \(\nu>2\))
\[\begin{align*} E(X) &= 0\\ Var(X) &= \frac{\nu}{\nu-2}. \end{align*}\]
In R ist die Abkürzung für die t-Verteilung t. Die Funktionen für die Dichte, Verteilungs- und Quantilfunktion sind:
dt(x, df=nu)pt(x, df=nu)qt(p, df=nu)
Die Parameter-Abkürzung df steht für “degrees of freedom”, also die Zahl der Freiheitsgrade.
Übrigens: Die t-Verteilung wurde 1908 von William Gosset hergeleitet, der als Brauer und Statistiker für die Qualitätssicherung in der Guinessbrauerei zuständig war. Damit konkurrierende Brauereien nichts über die Verfahren der Qualitätssicherung erfahren, durfte er seine Forschungsergebnisse nicht unter seinem eigenen Namen veröffentlichen. Er hat sie unter dem Pseudonym “Student” publiziert. Daher nennt man die t-Verteilung oft auch die Studentsche Verteilung (engl. Student’s t-distribution). Sie spielt auch in der statistischen Inferenz eine wichtige Rolle (vor allem in Kapitel 10 und Kapitel 11).
Beispiel: Rendite von Crypto-Währungen
Die Zufallsvariable \(X\): “Tagesrendite einer Kryptowährung” soll durch eine t-Verteilung mit 3 Freiheitsgraden modelliert werden. (In einer vollwertigen Anwendung würde man die t-Verteilung noch umskalieren und etwas verschieben, das ignorieren wir hier jedoch zur Vereinfachung. Daher Vorsicht: Dieses Beispiel ist nicht ernsthaft empirisch fundiert.) Die Tagesrendite folgt also \(X\sim t_3\). Im Finance-Bereich wird das Risiko gewöhnlich durch die Standardabweichung per annum ausgedrückt (also auf ein Jahr hochgerechnet), die im Finance-Bereich meist als “Volatilität” bezeichnet wird. Die Volatilität per annum ergibt sich aus der Standardabweichung der Tagesrendite, indem der Wert mit \(\sqrt{n}\) multipliziert wird, wobei \(n\) die Anzahl der Handelstage pro Jahr ist. Da Kryptowährungen jeden Tag gehandelt werden, ergibt sich die Volatilität als \[
\sqrt{365}\cdot \frac{\nu}{\nu-2}=3\cdot\sqrt{365}=57.3.
\] Wie hoch ist die Wahrscheinlichkeit, dass der Krypto-Kurs an einem Tag um mehr als 10 Prozent fällt? In R erhält man
pt(-10, df=3)[1] 0.0010642Die Wahrscheinlichkeit eines so starken Kursrückgangs ist also mit nur ca. 0.1 Prozent ziemlich klein.
Wie hoch ist die Wahrscheinlichkeit, dass der Kurs betragsmäßig sich an einem Tag um nicht mehr als 2 Prozent verändert? Gesucht ist \[ P(|X|\le 2)=P(X\le 2)-P(X\le -2). \] In R erhält man
pt(2, df=3) - pt(-2, df=3)[1] 0.860674Die Wahrscheinlichkeit beträgt also 86 Prozent.
4.4 Empirische Verteilungen
In den Wirtschaftswissenschaften (und allgemein in den Sozialwissenschaften) interessiert man sich sehr oft für empirische Verteilungen: Wie sind bestimmte Größen in der Population verteilt? Wie sieht die Einkommensverteilung oder die Vermögensverteilung aus? Wie ist die Altersstruktur der Bevölkerung? Welche Parteienpräferenzen gibt es in der wahlberechtigten Population? Wie hoch ist der Anteil der Kunden, die ihren Versicherungsvertrag stornieren wollen? Nur in den seltensten Fällen kann man diese Fragen exakt beantworten, indem man alle Populationsmitglieder untersucht oder befragt, denn die Untersuchung (oder Befragung) ist oft aufwendig und kostspielig. Das gilt natürlich vor allem dann, wenn die Population sehr groß ist.
Die gesamte Verteilung lässt sich jedoch durch eine Zufallsvariable repräsentieren, wenn man ein kleines Gedankenexperiment macht. Dazu stellt man sich vor, dass aus der gesamten Population ein Element (z.B. eine Person, ein Haushalt, eine Firma,…) zufällig ausgewählt wird, und zwar so, dass jedes Element die gleiche Ziehungswahrscheinlichkeit hat.
Wie sieht die Verteilungsfunktion dieser Zufallsvariable aus? Um diese Frage zu beantworten, brauchen wir ein wenig Notation. Seien \(x_1^*,x_2^*,\ldots,x_N^*\) die tatsächlichen Werte für alle \(N\) Elemente der Population. Es handelt sich dabei nicht um Zufallsvariablen, sondern um reelle Zahlen, beispielsweise die Einkommen aller Personen in der Population. Mit \(X\) bezeichnen wir die Zufallsvariable, die den Wert eines zufällig gezogenen Elements annimmt, wobei alle Element die gleiche Ziehungswahrscheinlichkeit von \(1/N\) haben sollen.
Die Verteilungsfunktion von \(X\) ist gemäß der Definition \[ F_X(x)=P(X\le x). \] Wie groß ist die Wahrscheinlichkeit, dass \(X\) den Wert \(x\) nicht überschreitet? Da alle Element die gleiche Ziehungswahrscheinlichkeit haben, liegt hier ein Laplace-Experiment vor. Es gilt \[ P(X\le x)=\frac{\text{Anzahl der Elemente}\le x}{N}. \] Das erscheint zunächst nicht sehr spektakulär. Es bedeutet aber, dass die Zufallsvariable \(X\), die durch die Verteilungsfunktion \(F_X\) beschrieben wird, die komplette Verteilung der Population repräsentiert. Wir sprechen von einer empirischen Verteilung. Es handelt sich bei \(X\) um eine spezielle Art von diskreter Verteilung. Die Wahrscheinlichkeitsfunktion lautet \[ f_X(x)=\left\{ \begin{array}{ll} 1/N & \text{ für }x\in\{x_1^*,\ldots,x_N^*\}\\ 0 &\text{ sonst.} \end{array} \right. \] Da \(X\) eine (diskrete) Zufallsvariable ist, können wir ihren Erwartungswert und ihre Varianz berechnen. Für den Erwartungswert gilt
\[\begin{align*} E(X)&=\sum_{i=1}^N x_i^* P(X=x_i^*)\\ &= \frac{1}{N}\sum_{i=1}^N x_i^*. \end{align*}\]
Mit anderen Worten: Der Erwartungswert einer empirischen Verteilung entspricht gerade dem Populationsmittel \(\bar x\) aus dem Kurs “Data Science 1”.
Die Varianz von \(X\) ist
\[\begin{align*} Var(X)&=\sum_{i=1}^N (x_i^*-\bar x)^2 P(X=x_i^*)\\ &= \frac{1}{N}\sum_{i=1}^N (x_i^*-\bar x)^2. \end{align*}\]
Es handelt sich also um die Populationsvarianz \(s^2\) aus dem Kurs “Data Science 1”.
In R dient die Funktion sample dazu, zufällig Elemente aus einem Vektor zu ziehen. Wenn x_star der Vektor mit den Populationswerten \(x_1^*,\ldots,x_N^*\) ist, dann erhält man mit
x <- sample(x_star, size=n, replace=TRUE)eine einfache Stichprobe \(X_1,\ldots,X_n\) vom Umfang \(n\) aus der empirischen Verteilung.