Kapitel 1 Vektoren

1.1 Definition

Es gibt verschiedene Sichtweisen oder Interpretationen von Vektoren. Sie lassen sich etwas plakativ unter den Labels Physik-Sicht, Daten-Sicht und Mathematik-Sicht zusammenfassen. Auch wenn man aus den Wirtschaftswissenschaften kommt, sollte man alle drei Sichtweisen kennen, denn manchmal ist die eine Sichtweise hilfreicher oder intuitiver, manchmal ist es eine andere.

1.1.1 Physik-Sicht

Ein Vektor ist ein Pfeil mit einer gegebenen Länge, der in eine gegebene Richtung zeigt. Wenn zwei Pfeile die gleiche Länge haben und auch in die gleiche Richtung zeigen, dann repräsentieren sie den gleichen Vektor, sie gehören sozusagen zur gleichen Pfeilklasse. Die Physik-Sicht wird üblicherweise nur im zwei- oder dreidimensionalen Raum eingenommen. Die Physik-Sicht ist - wenig überraschend - besonders gut für manche Vorgänge in der Natur geeignet, bei denen sowohl die Richtung als auch die Stärke eine Rolle spielt, z.B. Wind oder elektrische Felder.

Beispiel:

Die folgende Abbildung zeigt zwei Vektoren (in unterschiedlichen Farben). Beide Vektoren sind als Pfeile an mehreren Stellen zu sehen.

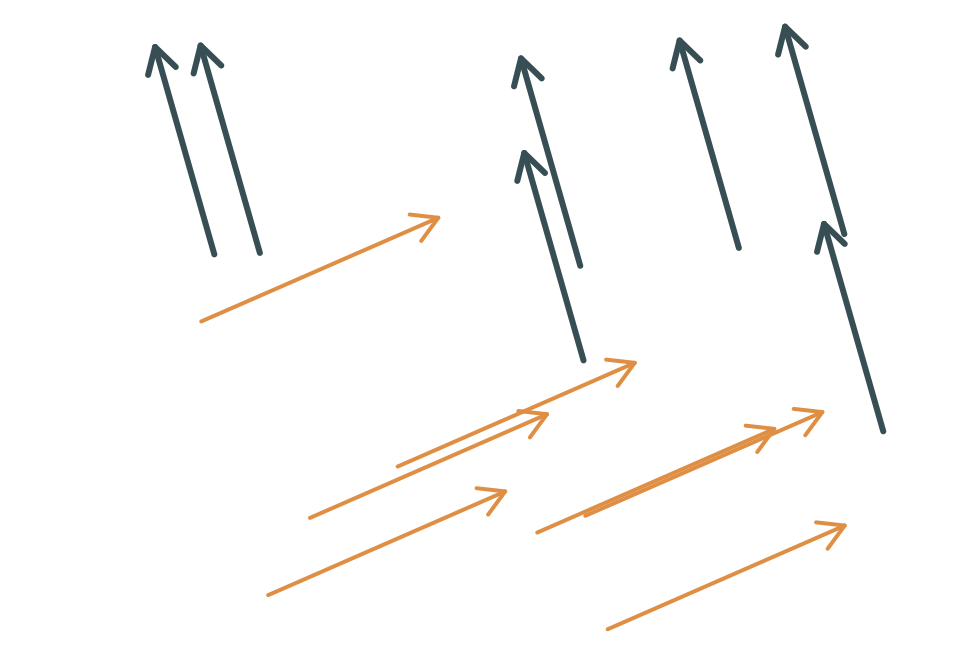
1.1.2 Daten-Sicht

In der Daten-Sicht ist ein Vektor schlicht und einfach eine Liste von Zahlen. Die Reihenfolge der Zahlen spielt dabei eine Rolle, es handelt sich also um eine geordnete Liste von Zahlen. Eine Liste mit zwei Elementen ist dann ein Vektor der Dimension 2, eine Liste mit drei Elementen ein Vektor der Dimension 3. Einen Vektor der Dimension 2 kann man sich auch als einen Punkt im zweidimensionalen Raum vorstellen, und entsprechend einen Vektor der Dimension 3 als einen Punkt im dreidimensionalen Raum (darauf gehen wir später noch näher ein). In dieser Sichtweise sind aber auch höhere Dimensionen kein Problem. Eine Liste mit \(n\) Elementen ist schlicht und einfach ein Vektor der Dimension \(n\), auch wenn \(n\) sehr groß ist.

In der Daten-Sicht ist ein Vektor eine kompakte und bequeme Kurzschreibweise für komplexe Informationen.

Beispiel 1:

Wir fassen zwei Variablen in einer Liste zusammen: das Alter einer Person (in Jahren) und das Einkommen dieser Person (in Euro/Monat). Zwei mögliche Vektoren wären \[ \mathbf{v}=\left[\begin{array}{r} 20\\1500\end{array}\right] \] und \[ \mathbf{w}=\left[\begin{array}{r} 42\\6400\end{array}\right] \] Die erste Person (\(\mathbf{v}\)) ist also 20 Jahre alt und hat ein Monatseinkommen von 1500 Euro, die zweite Person (\(\mathbf{w}\)) hat das Alter 42 und das Monatseinkommen 6400 Euro. Vektoren erlauben es also, mehrere Informationen durch einen einzigen Buchstaben zu repräsentieren. Ein Hinweis zur Notation: Die Elemente eines Vektors schreiben wir im Allgemeinen untereinander (man spricht darum auch von einem “Spaltenvektor”). Vektoren werden im Allgemeinen (und auch in diesem Kurs) mit fett gedruckten Kleinbuchstaben notiert.

Beispiel 2:

Von einer Person wird der jährliche Lohn im Alter von 20, 21, …, 67 Jahren erhoben. Die Angaben werden in einem Vektor zusammengefasst, z.B. \[ \mathbf{v}=\left[\begin{array}{r} 7000\\1200\\\vdots\\84000\end{array}\right] \] Dies ist ein Vektor mit 48 Elementen, das heißt ein Vektor der Dimension 48.

Beispiel 3:

In einem Warenkorb seien \(n\) Güter enthalten, z.B. ein Laib Brot, ein Pfund Nudeln etc. Wir fassen die Preise dieser Güter in einem Vektor zusammen. Der folgende Vektor enthält die Preise im Jahr 2020, \[ \mathbf{p}_{2020}=\left[\begin{array}{r} 3.80\\1.25\\\vdots\end{array}\right] \] Im Jahr 2023 wurden die Preise erneut erhoben. Der Preisvektor ist \[ \mathbf{p}_{2023}=\left[\begin{array}{r} 4.10\\0.95\\\vdots\end{array}\right] \] Man erkennt, dass in diesem Beispiel Brot teurer, aber Nudeln billiger geworden sind.

1.1.3 Mathematik-Sicht

In der mathematischen Sichtweise ist ein Vektor ein Element eines Vektorraums. Was ein Vektorraum in der mathematischen Sichtweise ist, behandeln wir in diesem Kurs jedoch nicht.

1.2 Koordinatensystem

In diesem Kurs werden wir immer wieder den zweidimensionalen Raum betrachten, an einigen Stellen auch den dreidimensionalen Raum. Für das Verständnis der Methoden der linearen Algebra sind diese Fälle am besten geeignet, weil eine anschauliche geometrische Interpretation möglich ist. Das bedeutet jedoch, dass wir die Daten-Sicht, in der Vektoren vor allem als kompakte Notation für komplexe Informationen in höherdimensionalen Räumen dienen, für eine Weile verlassen, obwohl gerade diese Sichtweise in der Ökonomik und in der Ökonometrie später eine wichtige Rolle spielt.

Häufig ist die Vorstellung eines Vektors als Pfeil hilfreich, der nicht frei im Raum positioniert ist, sondern im Ursprung des Koordinatensystems startet. Das erste Element des Vektors gibt die x-Koordinate (Abszisse) an, das zweite Element die y-Koordinate (Ordinate). Die folgende Abbildung zeigt beispielhaft fünf Vektoren, nämlich \[ \left[\begin{array}{c} 3\\5 \end{array}\right],\quad \left[\begin{array}{c} -6\\1 \end{array}\right],\quad \left[\begin{array}{c} -1\\-7 \end{array}\right],\quad \left[\begin{array}{c} 8\\-8 \end{array}\right],\quad \left[\begin{array}{c} 5\\0 \end{array}\right] \]

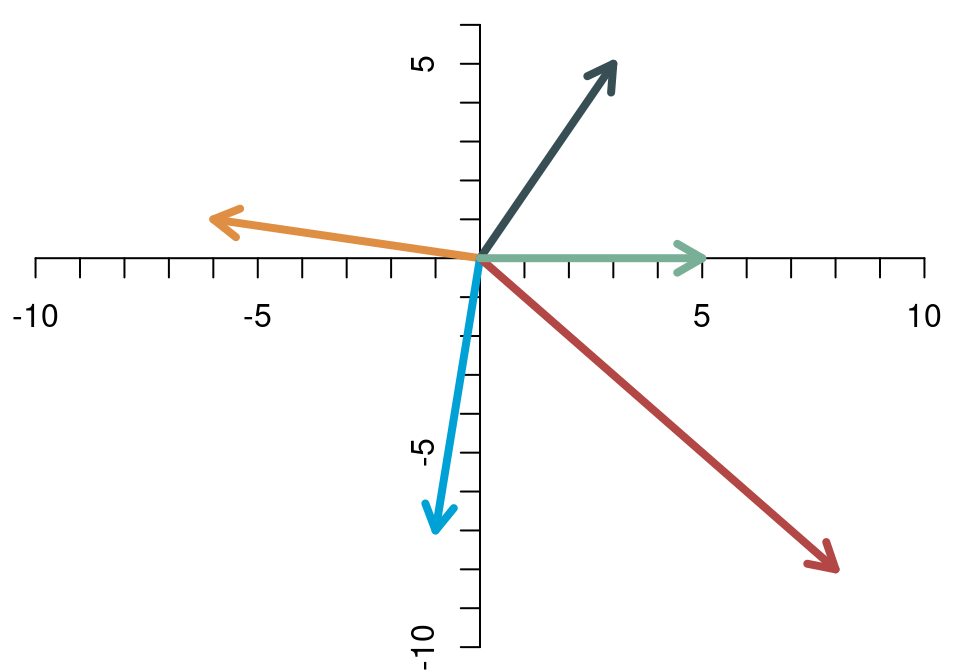
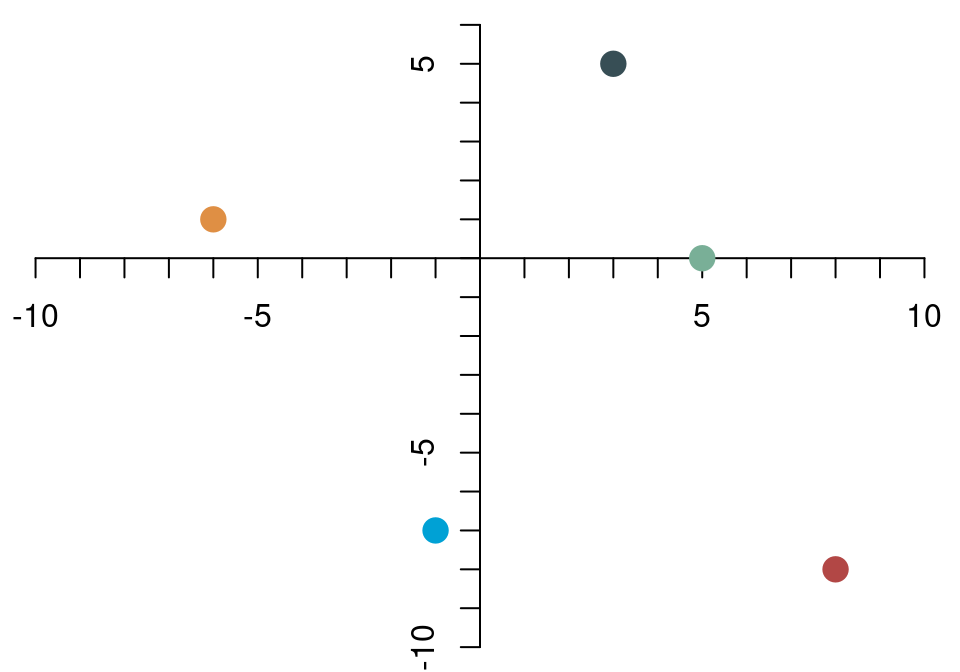
Jeder Vektor kann auch einfach als Repräsentation eines Punkts im zweidimensionalen Raum interpretiert werden. Jeder Punkt im zweidimensionalen Raum kann durch einen Vektor der Dimension 2 dargestellt werden. Es ist hilfreich, wenn man in Gedanken zwischen diesen verschiedenen Blickwinkeln auf Vektoren hin- und herschalten kann.

Um einen Punkt im dreidimensionalen Raum durch einen Vektor darzustellen, braucht man einen Vektor der Dimension 3. Die folgende Abbildung zeigt fünf Vektoren im dreidimensionalen Raum. Sie können das Bild mit Hilfe Ihrer Maus drehen und vergrößern oder verkleinern, indem Sie die linke Maustaste gedrückt halten. \[ \left[\begin{array}{c} 3\\7\\2 \end{array}\right],\quad \left[\begin{array}{c} -6\\1\\0 \end{array}\right],\quad \left[\begin{array}{c} -1\\-7\\3 \end{array}\right],\quad \left[\begin{array}{c} 9\\-9\\-4 \end{array}\right],\quad \left[\begin{array}{c} 5\\0\\0 \end{array}\right] \]

1.3 Länge und Norm

Unter der Länge eines Vektors versteht man die (geometrische) Länge des Pfeils, den der Vektor darstellt. Zeichnet man den Vektor \[ \mathbf{x}=\left[\begin{array}{c} 4\\3 \end{array}\right] \] in ein Koordinatensystem, ergibt sich

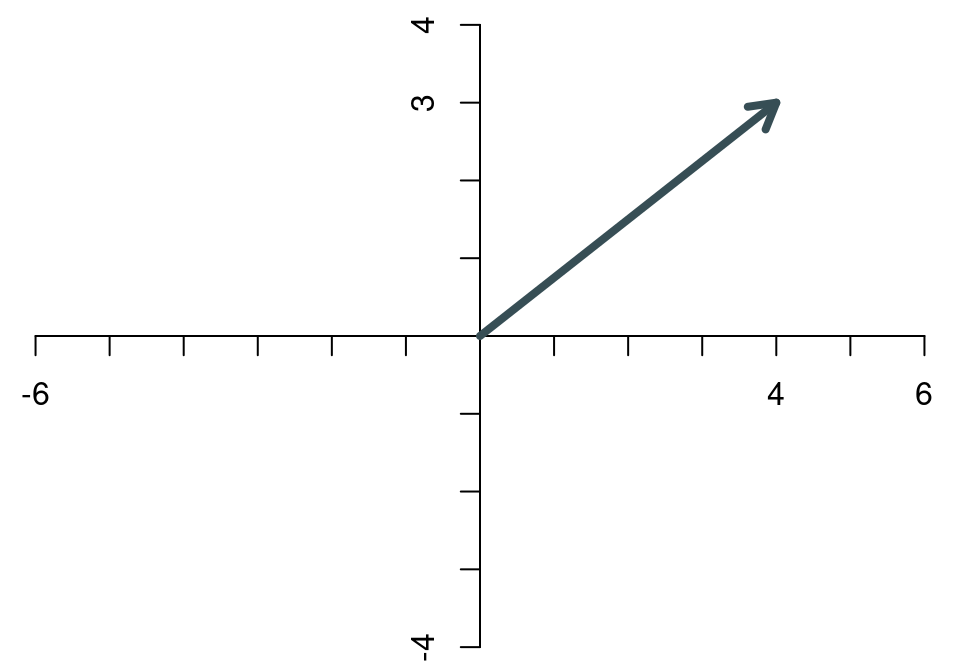
Mit Hilfe der folgenden beiden Hilfslinien

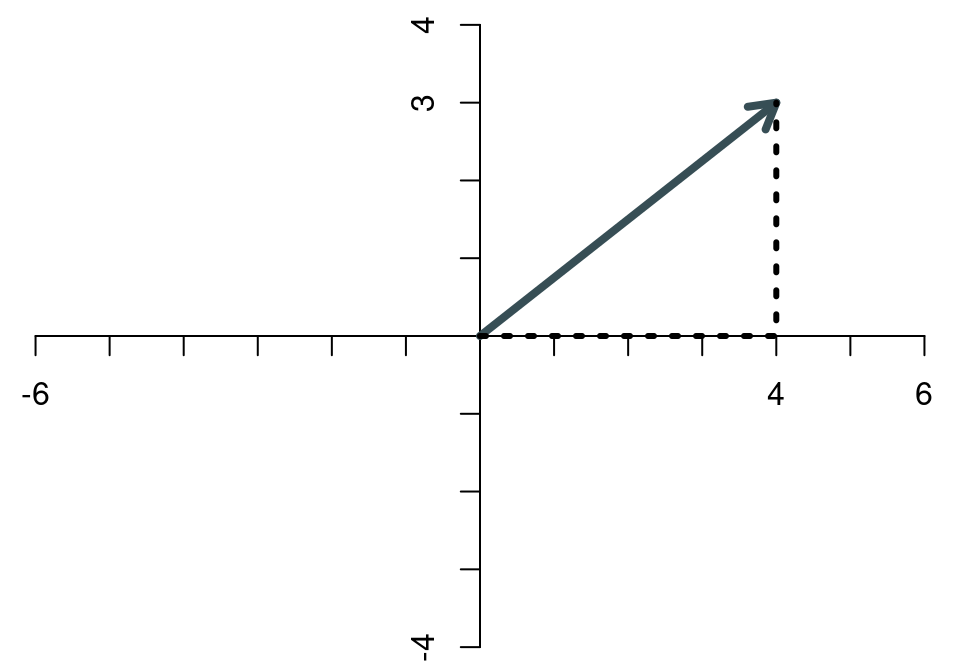
wird deutlich, dass die Länge des Vektors nach dem Satz des Pythagoras \[ ||\mathbf{x}|| = \sqrt{4^2+3^2} = 5 \] beträgt. Die (geometrische) Länge eines Vektors nennen wir im folgenden die Norm des Vektors. Die gängige Notation für die Norm eines Vektors sind die beiden doppelten vertikalen Striche.

1.4 Vektoren in R

Wenn man in R ein Objekt neu definiert, handelt es sich meist um einen Vektor. Zur Eingabe eines Vektors dient die Funktion c() (für concatenate). Die beiden Vektoren \[ \mathbf{x}=\left[\begin{array}{c} 3\\7 \end{array}\right],\quad \mathbf{y}=\left[\begin{array}{c} -6\\1 \end{array}\right] \] gibt man in R folgendermaßen ein:

x <- c(3, 7)
y <- c(-6, 1)

Will man einen Vektor x anzeigen lassen, kann man entweder die Funktion print(x) eingeben oder einfach nur x.

x
#> [1] 3 7

Die Elemente des Vektors werden von R einfach nebeneinander geschrieben. In der eckigen Klammer steht die Nummer des ersten Elements in der Zeile. Das ist zum Lesen nützlich, wenn man sehr lange Vektoren ausgibt, bei denen sich der Output über mehrere Zeilen erstreckt. Diese Schreibweise weicht jedoch von der üblichen Notation von Vektoren als Spaltenvektoren ab.

Für spezielle Vektoren gibt es eigene Funktionen. So erzeugt zum Beispiel die Funktion rep (für repeat) einen Vektor, in dem ein Element mehrmals vorkommt (oder mehrere Elemente mehrmals vorkommen). Einen zehndimensionalen Vektor, in dem nur Nullen stehen, also \[ \mathbf{n}=\left[\begin{array}{c} 0\\\vdots\\0 \end{array}\right] \] erhält man durch folgenden Befehl

n <- rep(0, 10)
print(n)
#>  [1] 0 0 0 0 0 0 0 0 0 0

Die Hilfefunktion zu der Funktion rep zeigt Ihnen, wie mehrere Elemente wiederholt werden können.

Sehr nützlich ist ferner die Funktion seq (für sequence). Sie erzeugt einen Vektor mit äquidistanten Einträgen. Als Argument erwartet die Funktion drei der folgenden vier Eingaben: from (erster Wert), to (letzter Wert), by (Schrittweite) und length (Anzahl der Vektorelemente). Mit dem Befehl

g <- seq(1, 2, length=11)

erhält man einen Vektor mit 11 gleich weit voneinander entfernten Elemente, dessen erstes Element 1 und dessen letztes Element 2 ist.

print(g)
#>  [1] 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0

Für ganzzahlige Element mit einer Schrittweite von 1 gibt es die Kurzschreibweise a:b. Dadurch erhält man einen Vektor, der die ganzen Zahlen von a bis b enthält. Zum Beispiel

0:20
#>  [1]  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17
#> [19] 18 19 20

Um ein einzelnes Element aus einem Vektor herauszulesen, kann man den Index des Elements in eckigen Klammern angeben. Als Beispiel betrachten wir den Vektor

x <- c(4, 1, 7, 3, 9, -3, 0, 4, -1, 0)

Das fünfte Element ist

x[5]
#> [1] 9

In der eckigen Klammer kann auch ein Vektor von Indizes stehen, dann werden alle Elemente des Vektors herausgelesen, die an den entsprechenden Stellen stehen. So ist zum Beispiel

x[c(1,3,5)]
#> [1] 4 7 9

oder

x[6:10]
#> [1] -3  0  4 -1  0

Manchmal möchte man ein einzelnes Element aus einem Vektor ausschließen. Das erfolgt in R durch einen negativen Index, z.B.

x[-7]
#> [1]  4  1  7  3  9 -3  4 -1  0

Neben der Indizierung durch ganze Zahlen ist es auch möglich, einen Vektor von logischen Ausdrücken (FALSE/TRUE) als Index zu verwenden. Der logische Vektor muss die gleiche Länge haben wie der zu indizierende Vektor.

Als Beispiel für eine logische Indizierung wählen wir aus dem Vektor x alle Elemente aus, die kleiner als 4 sind. In einem ersten Schritt schreiben wir die logischen Werte in den Vektor sel (für selection).

sel <- (x < 4)
print(sel)
#>  [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE  TRUE FALSE  TRUE
#> [10]  TRUE

Mit dem logischen Vektor sel werden nun die Elemente aus x herausgelesen.

x[sel]
#> [1]  1  3 -3  0 -1  0

1.5 Addition

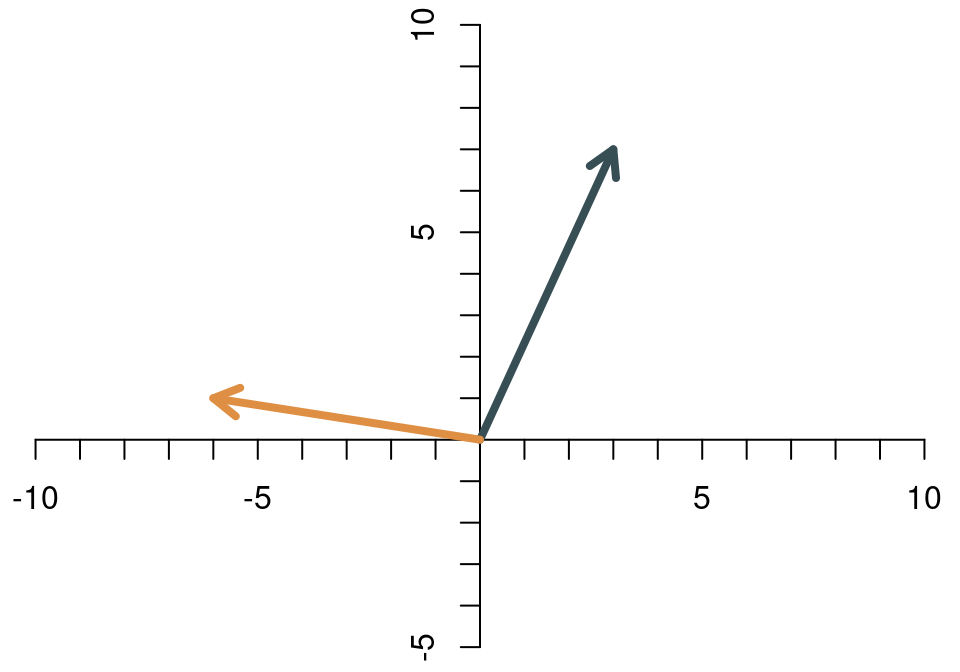
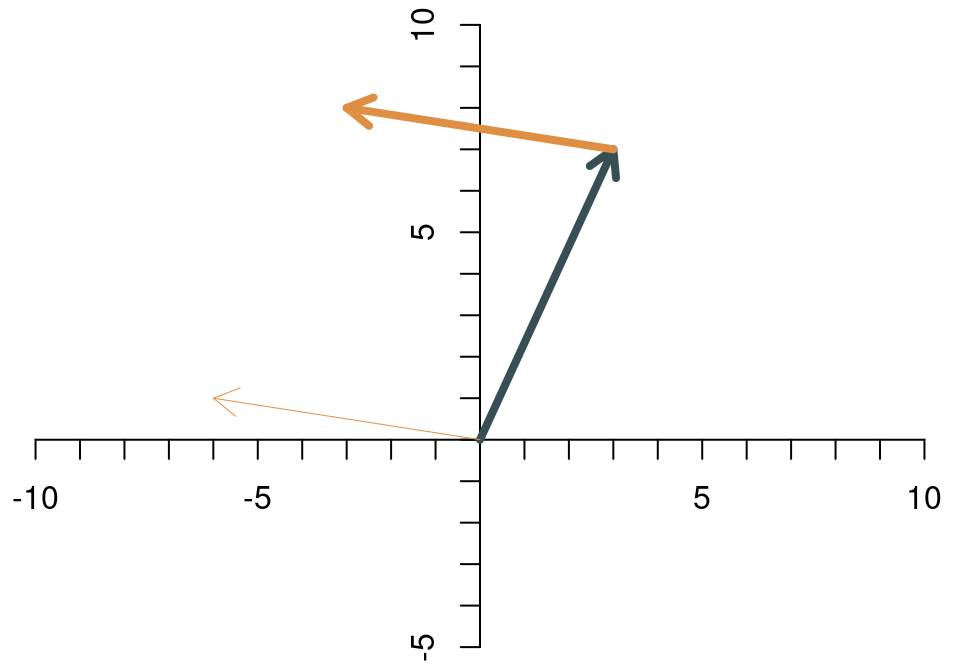
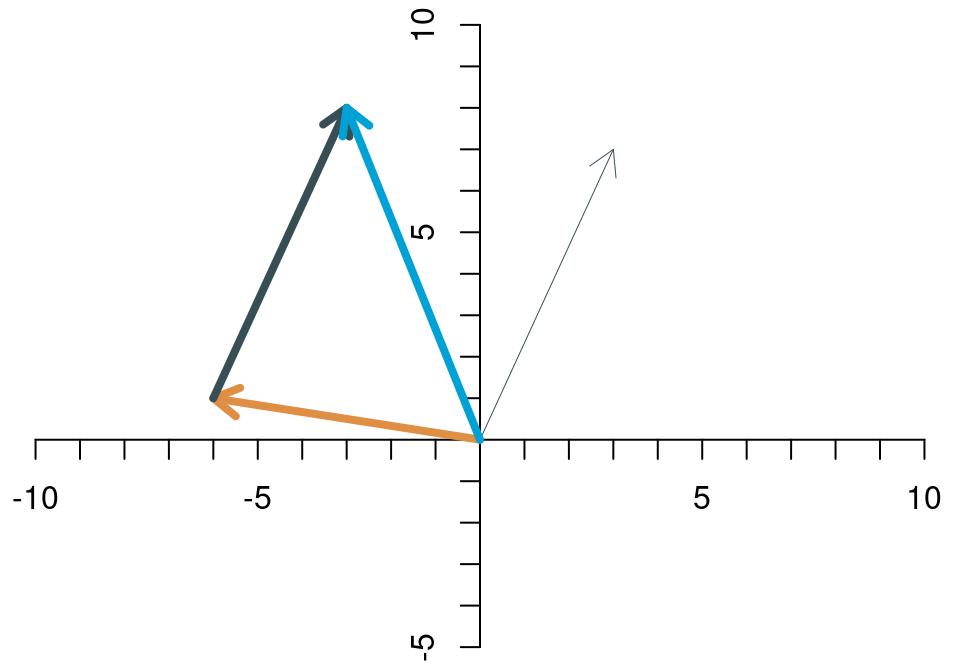
Zwei Vektoren werden addiert, indem man die Elemente des einen Vektors und die entsprechenden Elemente des anderen Vektors addiert. Die Summe der beiden Vektoren \[ \begin{align*} \mathbf{x} &= \left[\begin{array}{c} x_1\\x_2 \end{array}\right]\\ \mathbf{y} &= \left[\begin{array}{c} y_1\\y_2 \end{array}\right], \end{align*} \] ist \[ \mathbf{x}+\mathbf{y}= \left[\begin{array}{c} x_1\\x_2 \end{array}\right]+ \left[\begin{array}{c} y_1\\y_2 \end{array}\right]= \left[\begin{array}{c} x_1+y_1\\x_2+y_2 \end{array}\right]. \] Das sieht dann für die beiden Beispiel-Vektoren \[ \mathbf{x}=\left[\begin{array}{c} 3\\7 \end{array}\right],\quad \mathbf{y}=\left[\begin{array}{c} -6\\1 \end{array}\right] \] so aus: \[ \mathbf{x}+\mathbf{y}=\left[\begin{array}{c} 3\\7 \end{array}\right]+ \left[\begin{array}{c} -6\\1 \end{array}\right]= \left[\begin{array}{c} -3\\8 \end{array}\right]. \] Die Addition zweier Vektoren hat eine klare und intuitive geometrische Bedeutung. Wenn man die Vektoren als Pfeile interpretiert, dann erhält man die Summe der beiden Vektoren, indem man den einen Pfeil so verschiebt, dass er an der Spitze des anderen Pfeils startet. Die Summe der beiden Vektoren ist dann der Pfeil vom Ursprung zur Spitze des verschobenen Pfeils. Für die Vektoren \(\mathbf{x}\) und \(\mathbf{y}\) sieht das Schritt für Schritt wie folgt aus.

1. Die beiden Vektoren sind zwei Pfeile.

2. Den gelblichen Pfeil verschiebenen wir so, dass er an der Spitze des dunklen Pfeils startet.

3. Die Summe ist der Pfeil vom Ursprung bis zur Spitze des verschobenen Pfeils.

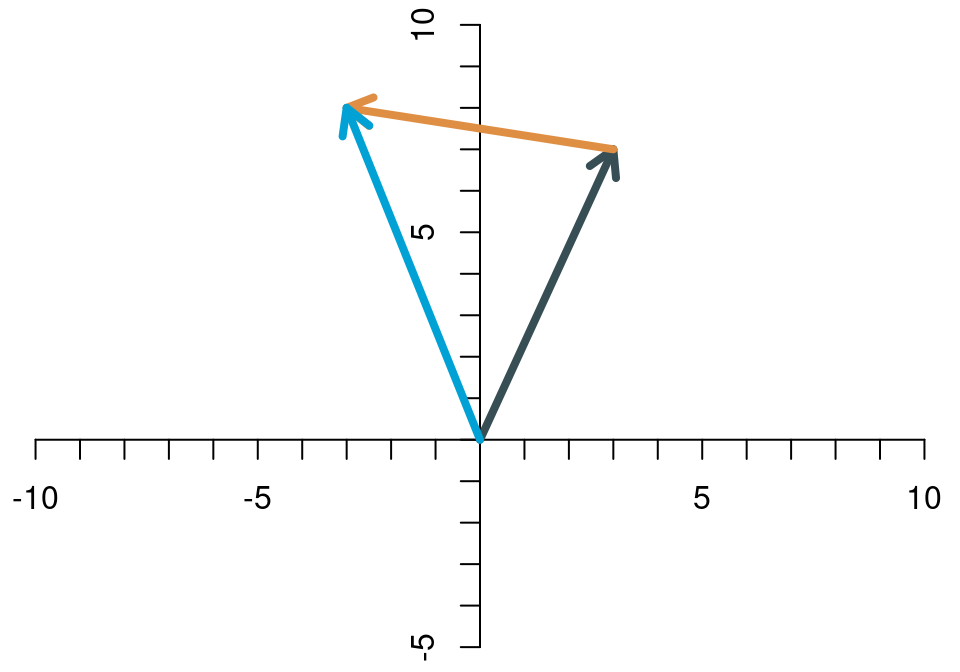
Die Addition ist kommutativ, d.h. es kommt das gleiche Ergebnis heraus, wenn man die Reihenfolge umdreht. Geometrisch bedeutet das, dass man auch den anderen Pfeil verschieben kann. Als Summe ergibt sich derselbe Pfeil wie vorher.

Will man mehr als zwei Vektoren addieren, werden sie einfach alle hintereinander gehängt. Als Beispiel betrachten wir wieder die fünf Vektoren aus Abschnitt 1.2, nämlich \[ \left[\begin{array}{c} 3\\5 \end{array}\right],\quad \left[\begin{array}{c} -6\\1 \end{array}\right],\quad \left[\begin{array}{c} -1\\-7 \end{array}\right],\quad \left[\begin{array}{c} 8\\-8 \end{array}\right],\quad \left[\begin{array}{c} 5\\0 \end{array}\right] \]

Die Abbildung der Summe sieht so aus, der dicke schwarze Pfeil stellt das Ergebnis der Addition dar.

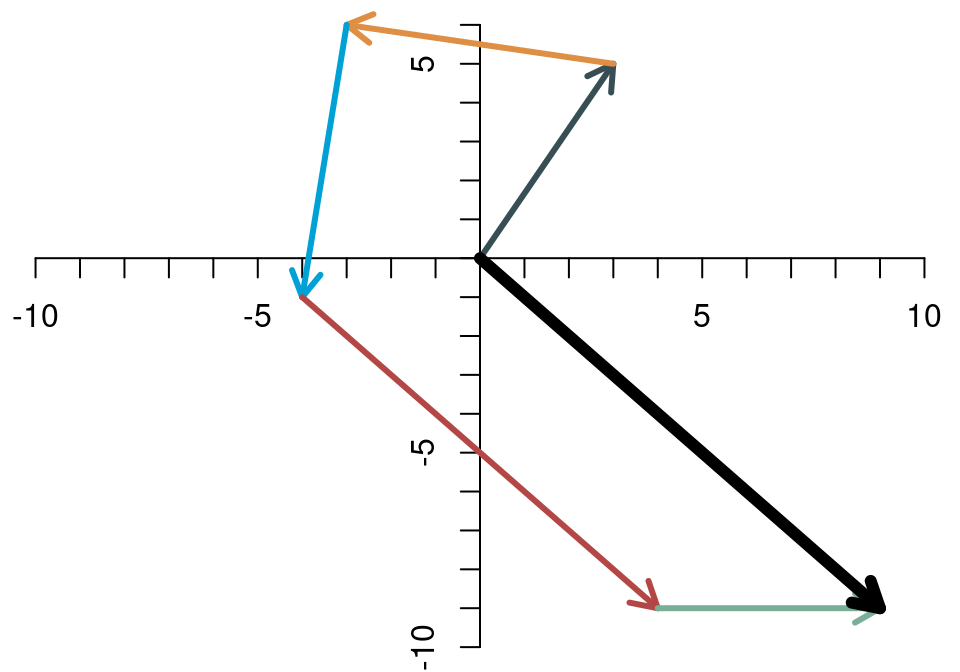
Die Addition der einzelnen Elemente liefert natürlich das gleiche Ergebnis. \[ \begin{align*} \left[\begin{array}{c} 3\\5 \end{array}\right]+ \left[\begin{array}{c} -6\\1 \end{array}\right]+ \left[\begin{array}{c} -1\\-7 \end{array}\right]+ \left[\begin{array}{c} 8\\-8 \end{array}\right]+ \left[\begin{array}{c} 5\\0 \end{array}\right]&= \left[\begin{array}{c} 3-6-1+8+5\\5+1-7-8+0 \end{array}\right]\\ &= \left[\begin{array}{c} 9\\-9 \end{array}\right]. \end{align*} \] Wegen der Kommutativität spielt es auch hier keine Rolle, in welcher Reihenfolge man die Vektoren aneinanderhängt. Als Summe kommt immer der schwarze Pfeil heraus.

In höherdimensionalen Räumen geht man analog vor. Im dreidimensionalen Raum ist die Summe zweier Vektoren \[ \left[\begin{array}{c} x_1\\x_2\\x_3 \end{array}\right]+ \left[\begin{array}{c} y_1\\y_2\\y_3 \end{array}\right]= \left[\begin{array}{c} x_1+y_1\\x_2+y_2\\x_3+y_3 \end{array}\right]. \] Die geometrische Interpretation der Summe ist im dreidimensionalen Raum analog zum zweidimensionalen Raum. Erhöht man die Dimension noch weiter, dann ist eine anschauliche Interpretation nicht mehr möglich. Die Summe ist aber weiterhin definiert. Allgemein ist im \(n\)-dimensionalen Raum die Summe zweier Vektoren \[ \left[\begin{array}{c} x_1\\\vdots\\x_n \end{array}\right]+ \left[\begin{array}{c} y_1\\\vdots\\y_n \end{array}\right]= \left[\begin{array}{c} x_1+y_1\\\vdots\\x_n+y_n \end{array}\right]. \] Es ist nicht möglich, Vektoren unterschiedlicher Dimension zu addieren.

Die Addition von Vektoren in R wird einfach mit einem normalen Pluszeichen dargestellt. Will man die beiden Vektoren \[ \mathbf{x}=\left[\begin{array}{c} 3\\7 \end{array}\right],\quad \mathbf{y}=\left[\begin{array}{c} -6\\1 \end{array}\right] \] in R addieren und das Ergebnis als \(\mathbf{z}\) abspeichern, so lautet der Code

x <- c(3, 7)
y <- c(-6, 1)
z <- x + y

Gibt man den Vektor \(\mathbf{z}\) aus, erhält man den Output

z
#> [1] -3  8

R formaliert den Output nicht der üblichen Vektordarstellung als Spalte, sondern schreibt die Elemente einfach nebeneinander.

Ob die Vektoren zweidimensional oder höherdimensional sind, spielt keine Rolle. Es ist also problemlos möglich, Vektoren mit sehr vielen Elementen zu addieren, sofern die Vektoren alle die gleiche Dimension haben. Der Versuch, zwei Vektoren unterschiedlicher Dimension zu addieren, führt zu einer Warnmeldung:

x <- c(3, 7)
y <- c(-6, 1, 4)
z <- x + y

#> Warning in x + y: Länge des längeren Objektes
#>       ist kein Vielfaches der Länge des kürzeren Objektes

Tatsächlich addiert R auch Vektoren unterschiedlicher Dimension, indem der Vektor mit der niedrigeren Dimension recycelt wird. In diesem Beispiel wird also der zweidimensionale Vektor x auf die Dimension 3 erhöht, indem an sein Ende das Element von Anfang angehängt wird, so dass sich (3,7,3) ergibt. Man sollte bei der Benutzung von R jedoch auf alle Fälle vermeiden, Vektoren unterschiedlicher Dimension zu addieren. Die einzige Ausnahme stellt die Addition eines Skalars dar:

x + 1
#> [1] 4 8

oder auch

6 + y
#> [1] 0 7

Diese Schreibweise ist so intuitiv naheliegend, dass R keine Warnmeldung ausgibt, sondern jedes Element des Vektors um die additive Konstante erhöht (oder bei einer Subtraktion verringert).

1.6 Skalarmultiplikation

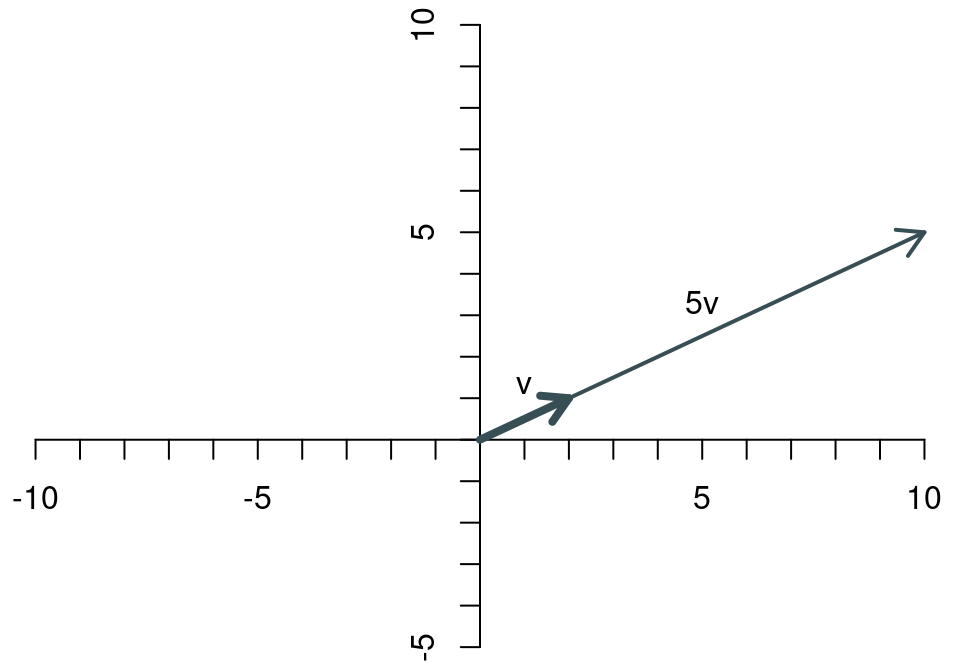
Bei der Skalarmultiplikation wird ein Vektor mit einem Skalar (d.h. mit einer reellen Zahl) multipliziert. Als Ergebnis erhält man einen Vektor, bei dem jedes Element mit dem Skalar multipliziert wird. Für einen Skalar \(\lambda\in\mathbb{R}\) gilt \[ \lambda \left[\begin{array}{c} x_1 \\ x_2 \end{array}\right]= \left[\begin{array}{c} \lambda x_1\\ \lambda x_2 \end{array}\right]. \] Durch die Multiplikation ändert sich die Länge des Vektors. Multipliziert man ihn beispielsweise mit 5, dann wird er fünfmal so lang wie ursprünglich.

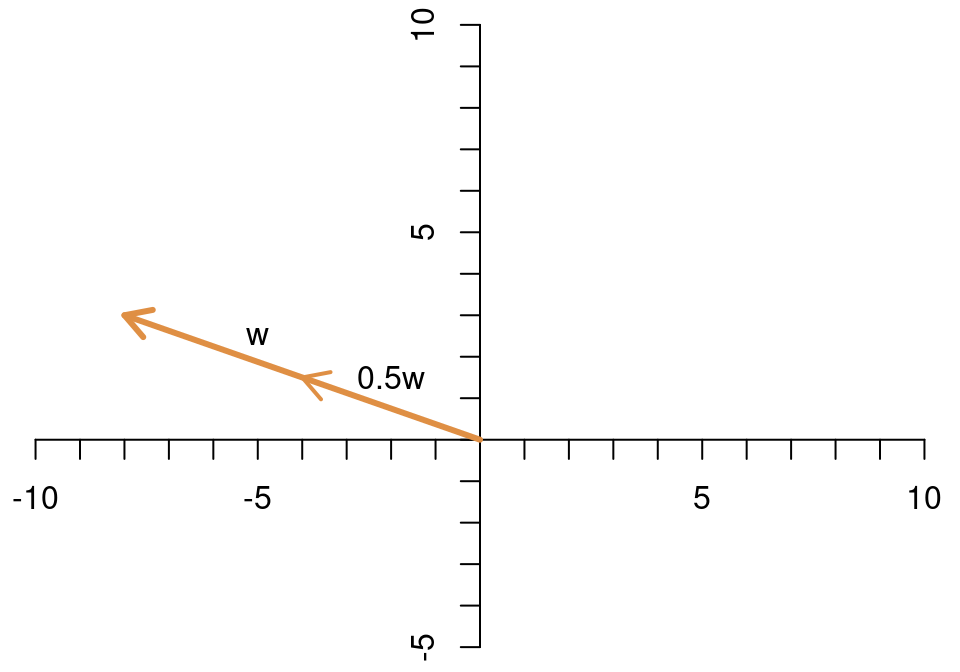
Multipliziert man ihn mit \(\frac{1}{2}\), dann schrumpft er auf die Hälfte seiner ursprünglichen Länge.

Und wenn man den Vektor mit einer negativen Zahl multipliziert, zeigt er anschließend genau in die entgegengesetzte Richtung und wird (je nach Betrag) gestreckt oder gestaucht.

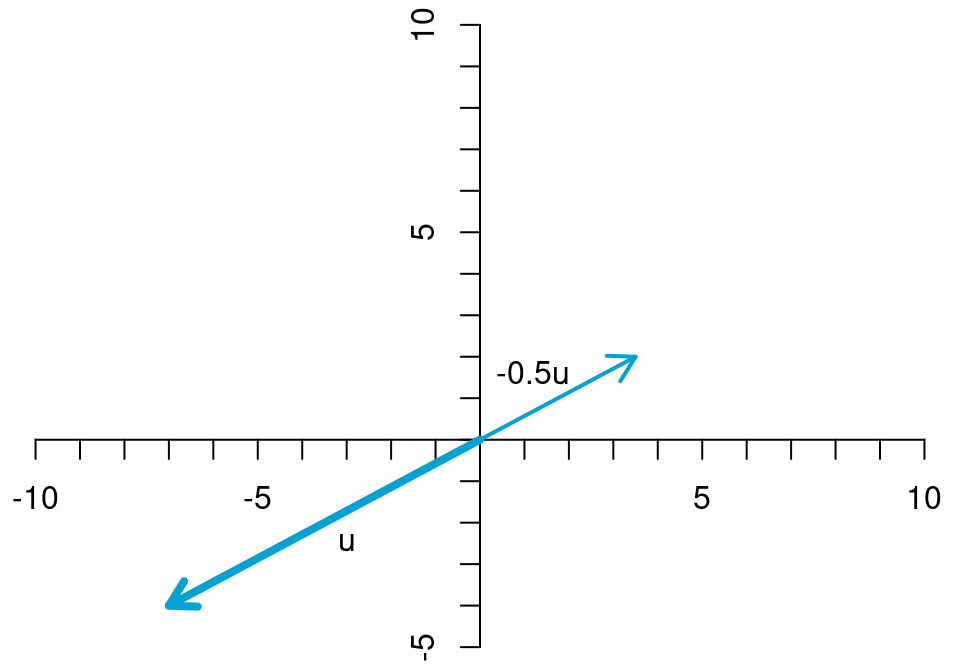
Die Skalarmultiplikation eines Vektor mit 0 ist auch erlaubt. In diesem Fall ergibt sich ein Vektor aus Nullen. Dieser Vektor hat weder eine Länge, noch eine Richtung.

Im \(n\)-dimensionalen Fall gilt allgemein \[ \lambda \left[\begin{array}{c} x_1 \\ \vdots\\x_n \end{array}\right]= \left[\begin{array}{c} \lambda x_1\\ \vdots\\\lambda x_n \end{array}\right], \] d.h. alle Elemente des Vektors werden mit dem Skalar multipliziert.

Die Skalarmultiplikation in R wird mit dem Sternchen (Asterisk, *) dargestellt. Will man den Vektor \[ \mathbf{v}=\left[\begin{array}{c} 3\\7 \end{array}\right] \] in R mit dem Skalar \(-5\) multiplizieren und das Ergebnis als \(\mathbf{u}\) abspeichern, so lautet der Code

v <- c(3, 7)
u <- -5*v

Gibt man den Vektor \(\mathbf{u}\) aus, erhält man den Output

u
#> [1] -15 -35

Ob der Vektor zweidimensional oder höherdimensional ist, spielt keine Rolle. Jedes Element des Vektors wird mit dem Skalar multipliziert.

1.7 Linearkombinationen

1.7.1 Definition

Eine Summe skalierter Vektoren heißt Linearkombination. Wenn \(\mathbf{x}_1,\ldots,\mathbf{x}_n\) Vektoren sind und \(\lambda_1,\ldots,\lambda_n\) Skalare, dann lautet die Linearkombination \[ \lambda_1\mathbf{x}_1+\ldots+\lambda_n\mathbf{x}_n. \] Das gilt für beliebige Dimensionen. Es spielt keine Rolle, ob die Vektoren zwei oder mehr Elemente haben. Sie müssen jedoch alle die gleiche Dimension haben, weil die Addition sonst nicht definiert ist.

Als Beispiel betrachten wir die Linearkombination der beiden Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}3\\2\end{array}\right],\quad \mathbf{x}_2=\left[\begin{array}{c}-4\\1\end{array}\right] \] mit den Skalaren \(\lambda_1=2\) und \(\lambda_2=3\). Es ergibt sich \[ 2\cdot\left[\begin{array}{c}3\\2\end{array}\right]+ 3\cdot\left[\begin{array}{c}-4\\1\end{array}\right]= \left[\begin{array}{c}-6\\7\end{array}\right]. \] Für die beiden Skalare \(\lambda_1=-0.5\) und \(\lambda_2=-1.5\) ergibt sich \[ -0.5\cdot\left[\begin{array}{c}3\\2\end{array}\right]- 1.5\cdot\left[\begin{array}{c}-4\\1\end{array}\right]= \left[\begin{array}{c}4.5\\-2.5\end{array}\right]. \] Grafisch kann man die beiden Linearkombinationen so darstellen:

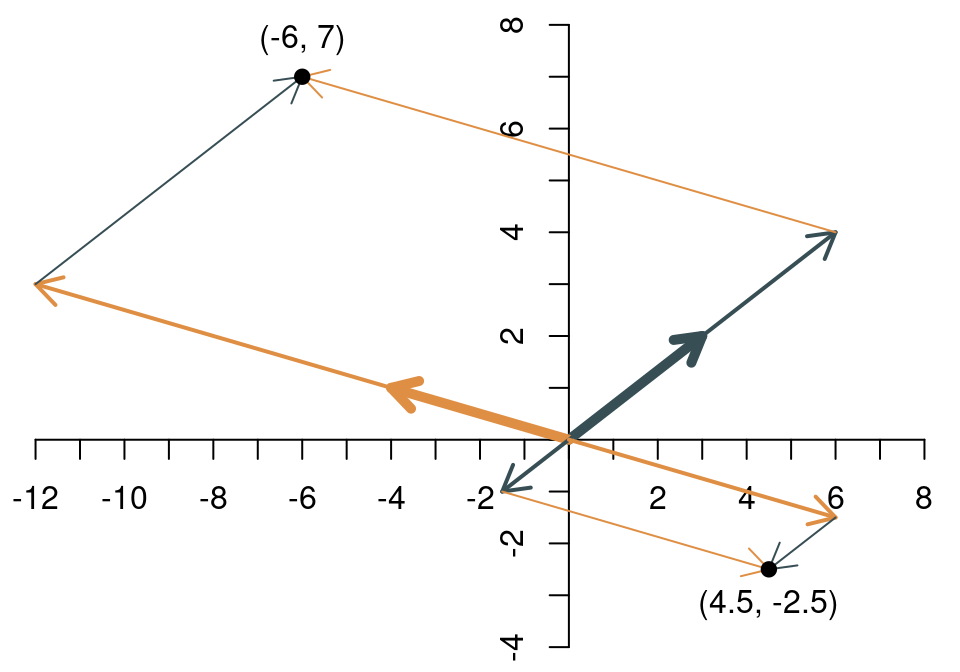
Welche Punkte im \(\mathbb{R}^2\) kann man durch geeignete Wahl der beiden Skalare erreichen? Die Antwort darauf erkennt man an der Abbildung: Alle. Denn durch geeignete Wahl der Skalare lässt sich jeder Punkt entlang der beiden Linien (deswegen heißt es auch Linearkombination) erreichen, die durch die beiden Vektoren festgelegt sind.

1.7.2 Basisvektoren

Wir haben bereits gesehen, dass man Vektoren als Repräsentationen von Punkten auffassen kann. Ein Vektor der Dimension 2 kann einen Punkt im zweidimensionalen darstellen, ein Vektor der Dimension 3 einen Punkt im dreidimensionalen Raum und noch längere Vektoren stehen für Punkte in höherdimensionalen Räumen. Diese Sichtweise verfeinern wir nun ein wenig.

Dazu stellen wir uns jede Koordinate des Vektors als einen Skalar vor. Wir wissen aus dem letzten Abschnitt, dass Skalare Vektoren strecken oder stauchen (oder, wenn sie negativ sind, auch die Richtung umklappen). Wir interpretieren nun die Elemente eines Vektors als Skalare, die Vektoren strecken oder stauchen: \[ \left[\begin{array}{c} x_1\\ x_2 \end{array}\right]= x_1 \left[\begin{array}{c}1\\0\end{array}\right]+ x_2 \left[\begin{array}{c}0\\1\end{array}\right]. \] Die beiden Vektoren auf der rechten Seite bezeichnen wir mit \(\mathbf{e}_1\) und \(\mathbf{e}_2\) (sie werden oft auch \(\mathbf{i}\) und \(\mathbf{j}\) genannt, was jedoch den Nachteil hat, dass es sich schlecht auf höhere Dimensionen erweitern lässt), \[ \mathbf{e}_1 = \left[\begin{array}{c}1 \\ 0\end{array}\right], \quad \mathbf{e}_2 = \left[\begin{array}{c}0 \\ 1\end{array}\right]. \] Die Vektoren \(\mathbf{e}_1\) und \(\mathbf{e}_2\) heißen natürliche Basisvektoren oder Standard-Basisvektoren von \(\mathbb{R}^2\).

Ein Vektor \(\mathbf{x}\) mit den beiden Elementen \(x_1\) und \(x_2\) gibt also letztlich an, wie man die beiden Basisvektoren skalieren muss, damit ihre Summe den Punkt mit den Koordinaten \((x_1,x_2)\) ergibt. Zwischen den Elementen eines Vektors und den Koordinaten des Punktes, den der Vektor repräsentiert, besteht also ein sehr einfacher Zusammenhang. Der Zusammenhang ist so einfach, dass man die beiden oft einfach gleichsetzt, wie wir ja bereits gesehen haben.

Als Beispiel stellen wir den Vektor \[ \mathbf{x}=\left[\begin{array}{c} 4\\2.5 \end{array}\right] \] graphisch als Summe der skalierten Basisvektoren dar.

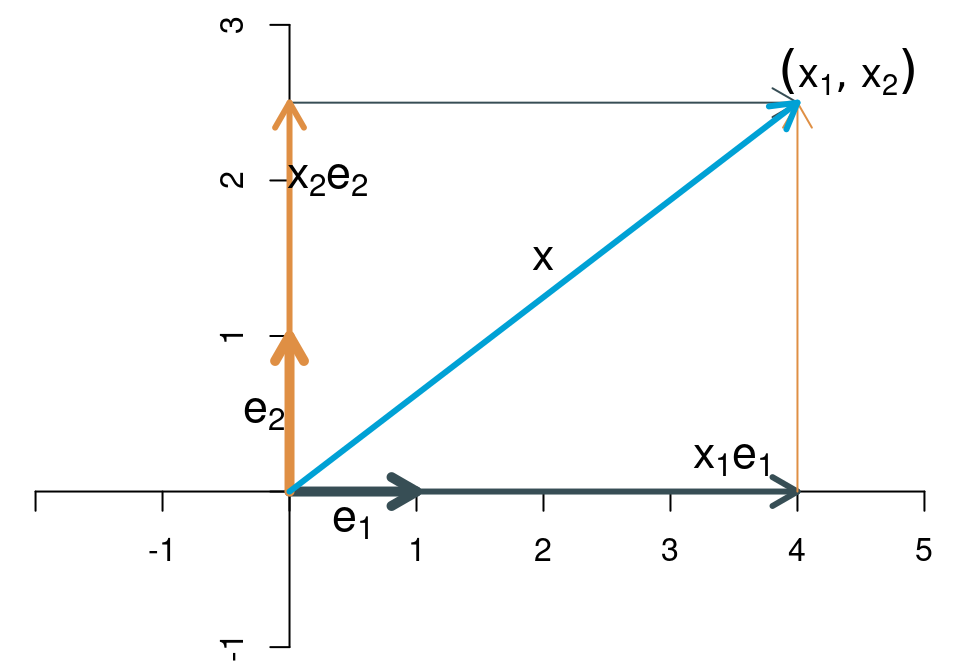
Offensichtlich kann man jeden Punkt in \(\mathbb{R}^2\) als Summe der beiden geeignet skalierten Basisvektoren \(\mathbf{e}_1\) und \(\mathbf{e}_2\) darstellen.

Natürliche Basisvektoren gibt es auch in höheren Dimensionen. Die natürlichen Basisvektoren im dreidimensionalen Raum sind \[ \mathbf{e}_1=\left[\begin{array}{c}1\\0\\0\end{array}\right],\quad \mathbf{e}_2=\left[\begin{array}{c}0\\1\\0\end{array}\right],\quad \mathbf{e}_3=\left[\begin{array}{c}0\\0\\1\end{array}\right]. \] Allgemein gilt im \(n\)-dimensionalen Raum, dass \(\mathbf{e}_1,\ldots,\mathbf{e}_n\) die natürlichen Basisvektoren sind. Dabei hat jeder Basisvektor \(\mathbf{e}_k\) (für \(k=1,\ldots,n\)) die Dimension \(n\), alle Elemente sind 0, nur das Element an der \(k\)-ten Stelle ist 1.

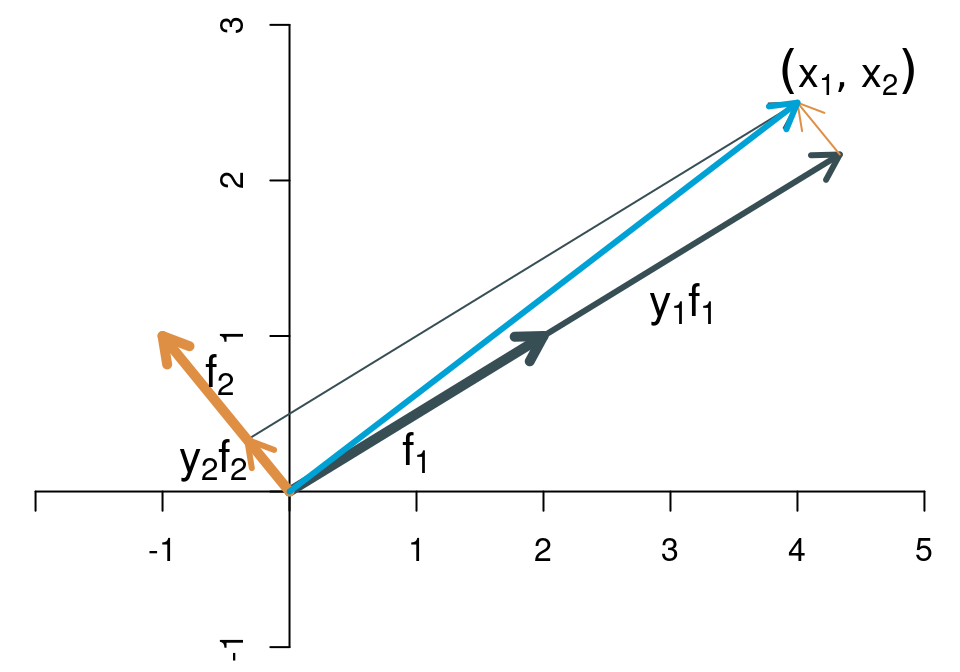
Der Ausdruck “natürliche Basisvektoren” legt nahe, dass es auch andere Basisvektoren gibt. Tatsächlich können wir im zweidimensionalen Raum die beiden natürlichen Basisvektoren \(\mathbf{e}_1\) und \(\mathbf{e}_2\) durch zwei andere Vektoren ersetzen. Als Beispiel nehmen wir die beiden Vektoren \[ \mathbf{f}_1=\left[\begin{array}{c}2\\1\end{array}\right],\qquad \mathbf{f}_2=\left[\begin{array}{c}-1\\1\end{array}\right]. \] Auch für diese beiden Vektoren kann mit geeigneter Skalierung jeder Punkt in \(\mathbb{R}^2\) erreicht werden. Wie würde das für den Punkt \[ \mathbf{x}=\left[\begin{array}{c} 4\\2.5 \end{array}\right] \] aus dem Beispiel von oben aussehen? Wir suchen zwei Skalare (nennen wir sie \(y_1\) und \(y_2\)), für die gilt \[ \left[\begin{array}{c} 4\\ 2.5 \end{array}\right]= y_1 \left[\begin{array}{c}2\\1\end{array}\right]+ y_2 \left[\begin{array}{c}-1\\1\end{array}\right]. \] Als Lösung dieses Gleichungssystems erhält man \(y_1=\frac{13}{6}\) und \(y_2=\frac{1}{3}\). Wenn wir von der natürlichen Basis übergehen zu der Basis \(\mathbf{f}_1\) und \(\mathbf{f}_2\), dann wird aus dem Punkt \((4, 2.5)\) der Punkt \((13/6, 1/3)\). Die Basis verändert also das Koordinatensystem. Grafisch lässt sich das für den Punkt (4, 2.5) wie folgt darstellen:

Kann man zwei beliebige Vektoren als Basisvektoren des \(\mathbb{R}^2\) verwenden? Die Antwort auf diese Frage lautet: Nein. Wenn die beiden Vektoren in genau die gleiche Richtung zeigen (oder in die genau entgegengesetzte Richtung), dann lassen sich nicht alle Punkte des \(\mathbb{R}^2\) erreichen. Auch wenn einer der Vektoren nur aus Nullen besteht, kann er offensichtlich nicht als Basisvektor dienen. Es stellt sich also die Frage, welche Bedingung erfüllt sein muss, damit Vektoren Basisvektoren sein können. Auf diese Frage gehen wir im nächsten Abschnitt ein.

1.7.3 Lineare Unabhängigkeit

Sei \(S=\{\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k\}\) eine endliche Menge von Vektoren. Die Vektoren in \(S\) heißen linear unabhängig, wenn sich keiner der Vektoren als Linearkombination der übrigen Vektoren ausdrücken lässt.

Es gibt eine alternative, äquivalente Definition der linearen Unabhängigkeit: Die Vektoren in \(S\) sind linear unabhängig, sofern sich der Nullvektor \(\mathbf{0}\) nur dann als Linearkombination ausdrücken lässt, wenn alle Skalare gleich Null sind. Mit anderen Worten, die Vektoren in \(S\) sind genau dann linear unabhängig, wenn die Gleichung \[ \lambda_1\mathbf{x}_1+\ldots+\lambda_k\mathbf{x}_k=\mathbf{0} \] nur für \(\lambda_1=\ldots=\lambda_k=0\) erfüllt ist. Wenn die Vektoren nicht linear unabhängig sind, heißen sie linear abhängig.

Als Beispiel betrachten wir die beiden Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}-2\\1\end{array}\right],\qquad \mathbf{x}_2=\left[\begin{array}{c}6\\-3\end{array}\right]. \] Diese beiden Vektoren sind linear abhängig, denn \[ (-3)\cdot\left[\begin{array}{c}-2\\1\end{array}\right]= \left[\begin{array}{c}6\\-3\end{array}\right] \] bzw. \[ 3\mathbf{x}_1 + 1\mathbf{x}_2=0, \] d.h. der Nullvektor kann durch eine Linearkombination erreicht werden, bei der nicht alle Skalare 0 sind.

Die beiden Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}-2\\1\end{array}\right],\qquad \mathbf{x}_2=\left[\begin{array}{c}5\\-3\end{array}\right]. \] sind dagegen linear unabhängig, denn \(\mathbf{x}_2\) kann nicht als Vielfaches von \(\mathbf{x}_1\) ausgedrückt werden.

Zwei Vektoren sind - grafisch betrachtet - linear abhängig, wenn sie in die genau gleiche (oder genau entgegengesetzte) Richtung zeigen. Diese beiden Vektoren sind also linear abhängig:

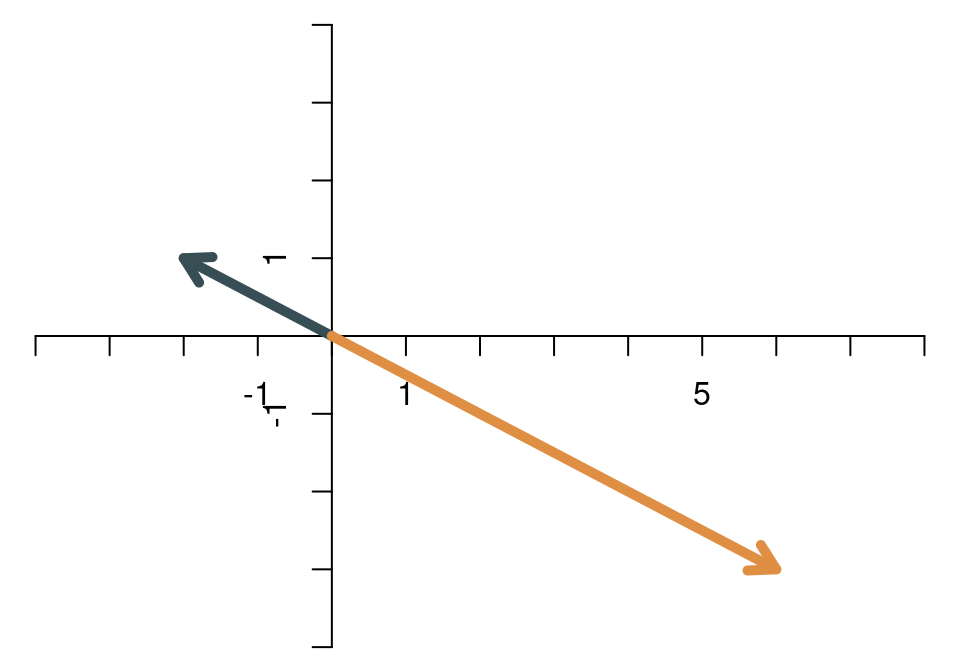
Auch diese beiden Vektoren sind linear abhängig:

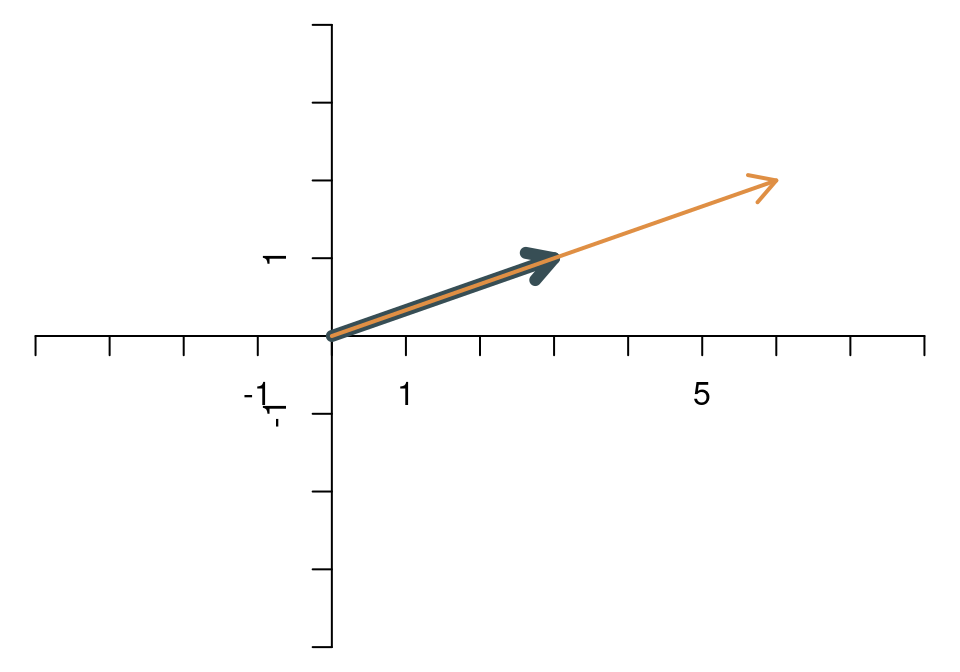
Dagegen sind diese beiden Vektoren linear unabhängig:

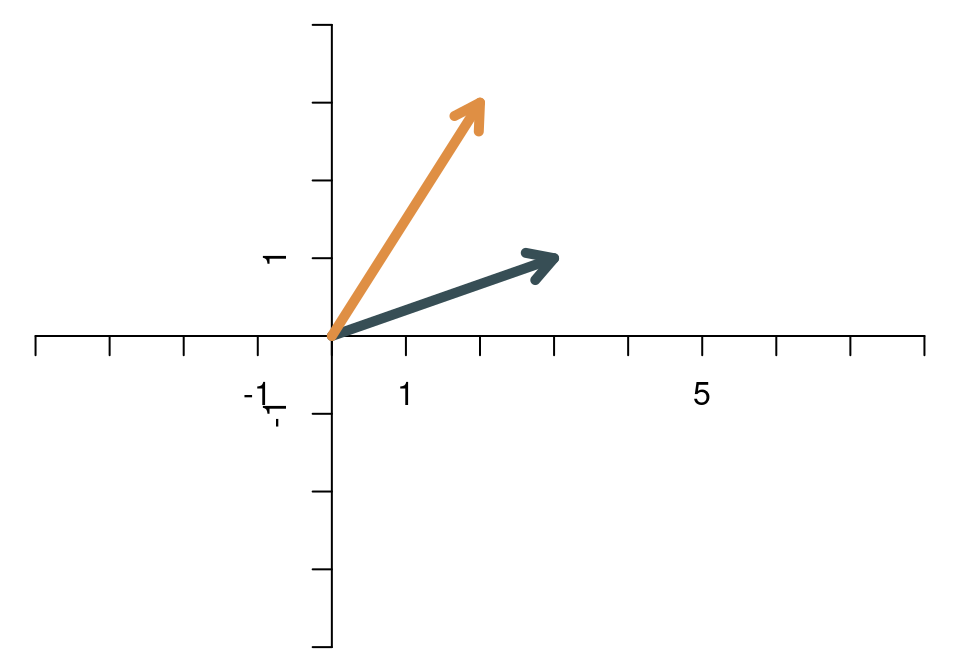
Wenn wir den Vektor, der nur aus Nullen besteht, einmal ignorieren, dann lässt sich folgendes sagen: Im zweidimensionalen Raum sind zwei Vektoren linear abhängig, wenn sie in die gleiche Richtung zeigen (oder genau entgegengesetzt). Sonst sind sie linear unabhängig. Wenn man zu zwei linear unabhängigen Vektoren der Dimension 2 einen dritten zweidimensionalen Vektor hinzunimmt, dann kann er in jedem Fall als Linearkombination der beiden anderen Vektoren ausgedrückt werden. Daher können im zweidimensionalen Raum nie mehr als zwei Vektoren linear unabhängig sein.

Wie sieht es mit dem Nullvektor aus? Er ist laut Definition sogar für sich alleine betrachtet linear abhängig, denn offensichtlich gilt für jeden beliebigen Skalar \(\lambda\neq 0\), dass \[ \lambda\mathbf{x}=\lambda\left[\begin{array}{c}0\\0\end{array}\right] =\left[\begin{array}{c}0\\0\end{array}\right]. \] Folglich ist eine Menge \(S\), die den Nullvektor enthält, immer linear abhängig.

Wir können nun auf die Frage des letzten Abschnitts zurück kommen, welche Vektoren als Basisvektoren geeignet sind. Die Antwort auf diese Frage lautet für den zweidimensionalen Fall: Man braucht zwei linear unabhängige Vektoren. Im dreidimensionalen Fall braucht man drei linear unabhängige Vektoren, und im \(n\)-dimensionalen Fall braucht man \(n\) linear unabhängige Vektoren.

Wie lässt sich die lineare Unabhängigkeit einer Menge von Vektoren überprüfen? Im zweidimensionalen Fall ist das sehr einfach, weil nur untersucht werden muss, ob die zwei Vektoren in die gleiche Richtung zeigen (also der eine Vektor ein Vielfaches des anderen ist). Im höherdimensionalen Fall wird es jedoch schwieriger. In Abschnitt 3.8 wird gezeigt, wie man mit Hilfe von R numerisch überprüfen kann, ob eine Menge von Vektoren linear unabhängig ist. An dieser Stelle gehen wir kurz darauf ein, wie man lineare Unabhängigkeit “per Hand” feststellen kann. Es handelt sich um das Gauß-Jordan-Verfahren. Leichte Variationen dieses Verfahrens helfen einem unter anderem dabei, die Inverse einer Matrix zu finden (Abschnitt 3.10) oder ein lineares Gleichungssystem zu lösen (Kap. 4).

Das Verfahren wird an einem Beispiel im dreidimensionalen Raum vorgestellt. Wir untersuchen, ob die drei Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}4\\2\\0\end{array}\right],\quad \mathbf{x}_2=\left[\begin{array}{c}5\\3\\2\end{array}\right],\quad \mathbf{x}_3=\left[\begin{array}{c}7\\4\\2\end{array}\right]. \] linear unabhängig sind. Zunächst werden die Vektoren nebeneinander geschrieben. Die Zeilen bezeichnen wir mit römischen Zahlen \[ \begin{array}{cccl} 4 & 5 & 7 & \quad(I)\\ 2 & 3 & 4 & \quad(II)\\ 0 & 2 & 2 & \quad(III) \end{array} \] Wir formen dieses Schema nun Schritt für Schritt so um, dass unterhalb (und überhalb) der Diagonale Nullen stehen. Die folgenden sogenannten “elementare Zeilenumformungen” sind dabei erlaubt:

• zwei Zeilen miteinander vertauschen;
• alle Elemente einer Zeile mit einer Konstanten ungleich 0 multiplizieren;
• eine Zeile wird durch die Summe (oder Differenz) von dieser Zeile mit dem Vielfachen einer anderen Zeile ersetzt.

Wir starten mit dem Feld unter der 4. Um dort eine Null zu erhalten, subtrahieren wir \(2\times (II)\) von \((I)\). Es ergibt sich \[ \begin{array}{cccl} 4 & 5 & 7 & \quad(I)\\ 0 & -1 & -1 & \quad(II)\\ 0 & 2 & 2 & \quad(III) \end{array} \] Um das mittlere Element der letzten Zeile auf Null zu setzen, addieren wir \(2\times (II)\) zu \((III)\) und erhalten: \[ \begin{array}{cccl} 4 & 5 & 7 & \quad(I)\\ 0 & -1 & -1 & \quad(II)\\ 0 & 0 & 0 & \quad(III) \end{array} \] Alle Elemente unterhalb der Diagonalen sind nun schon einmal Null. Dass die letzte Zeile nur Nullen enthält, zeigt die lineare Abhängigkeit der drei Vektoren. Es ist also nicht nötig weiter umzuformen um zusätzlich oberhalb der Diagonalen Nullen zu erzeugen. Tatsächlich gilt \(\mathbf{x}_3=0.5\mathbf{x}_1+\mathbf{x}_2\), so dass \[ \frac{1}{2}\times\mathbf{x}_1+\mathbf{x}_2-\mathbf{x}_3=\mathbf{0}. \] Das ist offensichtlich nicht die einzige Lösung. Die drei Skalare können mit einer beliebigen Konstante multipliziert werden (z.B. \(5,\) \(10\) und \(-10\)).

1.7.4 Lineare Hülle

Als lineare Hülle (oder Erzeugnis oder auch Aufspann, engl. span) einer Menge von Vektoren \(S\) bezeichnet man die Menge aller Vektoren, die man durch Linearkombinationen der Vektoren aus \(S\) erreichen kann. Man sagt auch, dass die Vektoren aus \(S\) einen Raum aufspannen.

Beispiele:

Die beiden Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}-2\\1\end{array}\right],\qquad \mathbf{x}_2=\left[\begin{array}{c}5\\-3\end{array}\right]. \] spannen den Raum \(\mathbb{R}^2\) auf, weil sich alle Punkte von \(\mathbb{R}^2\) durch eine geeignete Linearkombination von \(\mathbf{x}_1\) und \(\mathbf{x}_2\) ausdrücken lassen.

Die beiden Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}-2\\1\end{array}\right],\qquad \mathbf{x}_2=\left[\begin{array}{c}6\\-3\end{array}\right]. \] spannen dagegen nur die Gerade \[ \lambda \left[\begin{array}{c}-2\\1\end{array}\right],\quad \lambda\in\mathbb{R} \] auf, die durch den Ursprung verläuft und eine Steigung von \(-0.5\) hat.

Interessanter als der zweidimensionale Fall ist der dreidimensionale Fall, denn hier gibt es mehr Möglichkeiten: Drei linear unabhängige Vektoren spannen den gesamten \(\mathbb{R}^3\) auf. Wenn einer der drei Vektoren sich als Linearkombination der beiden anderen Vektoren ergibt (die ihrerseits linear unabhängig voneinander sind), dann wird eine Ebene im dreidimensionalen Raum aufgespannt. Als Beispiel betrachten wir die drei Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}4\\2\\0\end{array}\right],\quad \mathbf{x}_2=\left[\begin{array}{c}5\\3\\2\end{array}\right],\quad \mathbf{x}_3=\left[\begin{array}{c}7\\4\\2\end{array}\right]. \] Der Vektor \(\mathbf{x}_3\) ergibt sich als \(0.5\mathbf{x}_1+\mathbf{x}_2\), die drei Vektoren sind also linear abhängig, obwohl sie alle in unterschiedliche Richtungen zeigen. Alle Paare von zwei Vektoren sind jedoch linear unabhängig voneinander.

Die drei Vektoren liegen alle in einer Ebene, wie die folgende Abbildung illustriert (um das Bild vollständig zu erfassen, sollte man es mit der Maus bei gedrückter linker Maustaste bewegen).

Wenn die drei Vektoren alle in die gleiche (oder genau entgegengesetzte) Richtung zeigen, spannen sie nur eine Gerade auf. Das wird in der nachfolgenden Abbildung für die Vektoren \[ \mathbf{x}_1=\left[\begin{array}{c}1\\2\\3\end{array}\right],\quad \mathbf{x}_2=\left[\begin{array}{c}3\\6\\9\end{array}\right],\quad \mathbf{x}_3=\left[\begin{array}{c}-1\\-2\\-3\end{array}\right]. \] gezeigt. Auch hier sollten Sie das Bild mit der Maus bewegen, um sich in die Situation hineinzufühlen.

1.8 Inneres Produkt

Unter dem inneren Produkt (auch: Skalarprodukt, engl. inner product, oft auch dot product) zweier Vektoren \[ \mathbf{x}=\left[\begin{array}{c}x_1\\ \vdots\\x_n\end{array}\right],\qquad \mathbf{y}=\left[\begin{array}{c}y_1\\ \vdots\\ y_n\end{array}\right] \] gleicher Dimension \(n\) versteht man den Skalar \[ \mathbf{x}\cdot\mathbf{y}=x_1y_1+x_2y_2+\ldots+x_ny_n. \] Ein kurzer Hinweis zur Terminologie: In diesem Kurs sprechen wir meist vom inneren Produkt, denn der Begriff Skalarprodukt bewegt sich gefährlich nahe an dem Begriff der Skalarmultiplikation (Abschnitt 1.6), so dass es zu einer Verwechslung kommen könnte. Im Englischen ist die gängigste Bezeichnung “dot product”. Und ein Hinweis zur Notation: Eine alternative Schreibweise für das innere Produkt sind eckige Klammern um das Vektorenpaar, z.B. \(<\mathbf{x},\mathbf{y}>\). Diese Notation wird in den Naturwissenschaften gern verwendet, ist in den Wirtschaftswissenschaften aber eher selten.

Aus der Definition des inneren Produkts ergeben sich sofort einige Rechenregeln, \[ \begin{align*} \mathbf{a}\cdot\mathbf{b} &= \mathbf{b}\cdot\mathbf{a}\\ \mathbf{a}\cdot (\mathbf{b}+\mathbf{c}) &= \mathbf{a}\cdot\mathbf{b}+\mathbf{a}\cdot\mathbf{c}\\ \mathbf{a}\cdot \mathbf{a} &\ge 0\\ (\mathbf{a}+\mathbf{b})\cdot (\mathbf{a}+\mathbf{b}) &= \mathbf{a}\cdot \mathbf{a}+2(\mathbf{a}\cdot\mathbf{b})+\mathbf{b}\cdot\mathbf{b}\\ (\lambda\mathbf{a})\cdot\mathbf{b}&=\mathbf{a}\cdot(\lambda\mathbf{b})=\lambda(\mathbf{a}\cdot\mathbf{b}), \end{align*} \] wobei \(\lambda\in\mathbb{R}\) ist.

Beispiel:

In einem Warenkorb seien 5 Produkte. Die Preise (in geeigneten Einheiten) können in einem fünfdimensionalen Vektor zusammengefasst werden, \[ \mathbf{p}=\left[\begin{array}{r} 4.10\\0.95\\10.00\\7.25\\1.98 \end{array}\right]. \] Die zugehörigen Mengen (in geeigneten Einheiten) des Warenkorbs können ebenfalls in einem Vektor zusammengefasst werden, \[ \mathbf{q}=\left[\begin{array}{r} 2\\5\\0.5\\3\\2.5 \end{array}\right]. \] Der Wert des gesamten Warenkorbs ist \[ \begin{align*} \mathbf{p\cdot q}&=4.10\times 2+0.95\times 5+10\times 0.5+7.25\times 3+1.98\times 2.5\\ &=44.65. \end{align*} \] Vorsicht in R: Mit dem einfachen Stern (Asterisk) * berechnet man in R nicht das innere Produkt, sondern den Vektor der elementweisen Produkte zweier Vektoren. Das innere Produkt zweier Vektoren wird in R mit dem Multiplikationszeichen %*% berechnet.

p <- c(4.1, 0.95, 10, 7.25, 1.98)
q <- c(2, 5, 0.5, 3, 2.5)
p %*% q
#>       [,1]
#> [1,] 44.65

Dagegen erhält man bei einer Multiplikation mit dem Sternchen den Vektor

p*q
#> [1]  8.20  4.75  5.00 21.75  4.95

Die Summe aller dieser Vektorelemente ergibt dann wieder das innere Produkt:

sum(p*q)
#> [1] 44.65

Noch ein Beispiel:

Angenommen, ein Portfolio enthält \(n\) Wertpapiere. Den wertmäßigen Anteil des Wertpapiers \(i\) am Gesamtportfolio nennen wir \(w_i\) und fassen die Anteile in einem Vektor \[ \mathbf{w}=\left[\begin{array}{c} w_1\\\vdots\\w_n\end{array}\right] \] zusammen. Die Summe aller Anteile muss 1 ergeben, d.h. \[ \mathbf{w}\cdot\mathbf{\iota}=w_1\times 1+\ldots+w_n\times 1=1, \] wobei \(\mathbf{\iota}\) ein Vektor der Dimension \(n\) aus Einsen ist. Übrigens ist es nicht unbedingt erforderlich, dass alle Anteile positiv sind. Wenn ein Wertpapier als Short-Position gehalten wird, ist der Anteil negativ.

Die Renditen aller Wertpapiere werden in einen Vektor \[ \mathbf{r}=\left[\begin{array}{c} r_1\\\vdots\\r_n\end{array}\right] \] geschrieben. Dann beträgt die Gesamtrendite des Portfolios \(\mathbf{r}\cdot\mathbf{w}\).

Das innere Produkt hat auch eine geometrische Interpretation. Sie wird in dem folgenden Beispiel illustriert. Die beiden Vektoren \[ \mathbf{x}=\left[ \begin{array}{c} 5\\ -2 \end{array} \right],\qquad \mathbf{y}= \left[ \begin{array}{c} 4\\ 3 \end{array} \right] \] haben das innere Produkt \(5\times 4-2\times 3=14\). Das innere Produkt ergibt sich grafisch, indem man die Norm des Vektors \(\mathbf{y}\) mit der Norm der Projektion von \(\mathbf{x}\) auf \(\mathbf{y}\) multipliziert. Wir sehen uns das Schritt für Schritt an. Zuerst zeichnen wir die beiden Vektoren.

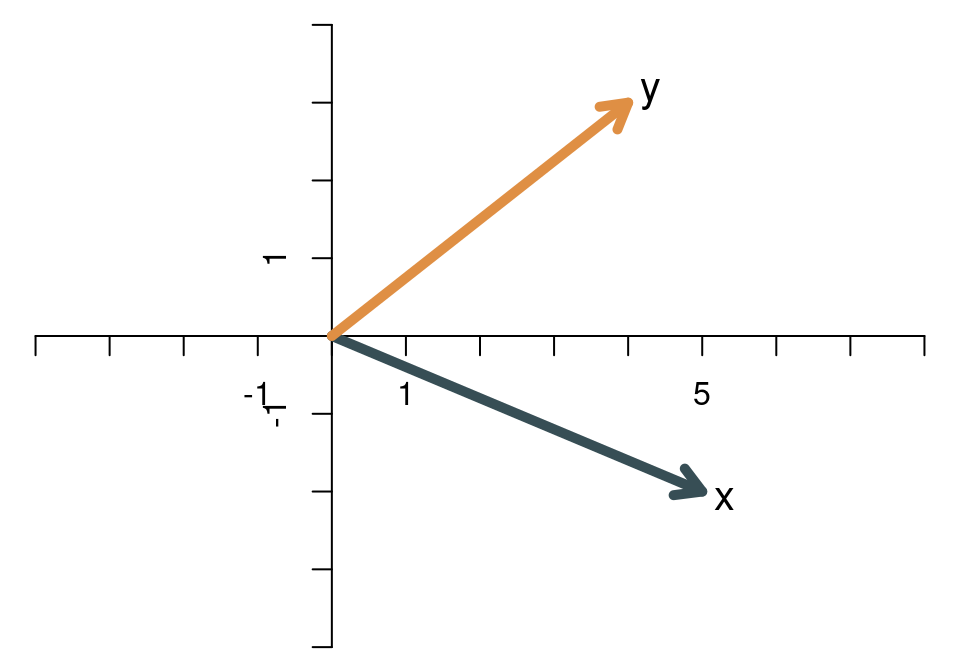
Anschließend wird \(\mathbf{x}\) auf die Gerade projiziert, die durch \(\mathbf{y}\) aufgespannt wird. Die gepunktete Linie trifft in einem rechten Winkel auf \(\mathbf{y}\). 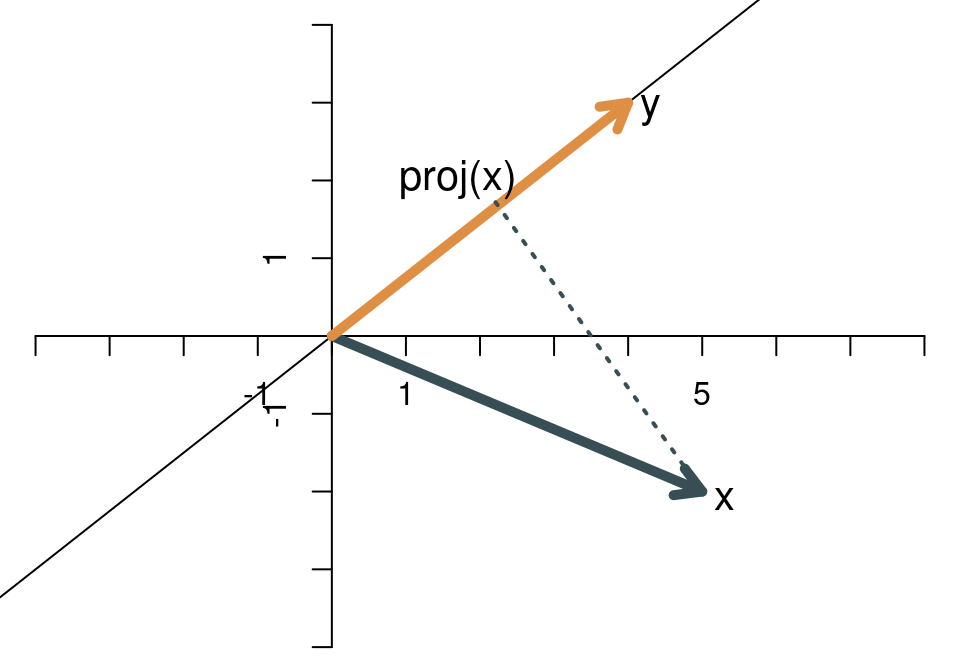Es gibt eine einfache Formel zur analytischen Berechnung der Projektion von \(\mathbf{x}\) auf \(\mathbf{y}\), und zwar \[ proj(\mathbf{x})=\frac{\mathbf{x}\cdot\mathbf{y}}{\mathbf{y}\cdot\mathbf{y}}~\mathbf{y}. \] Setzt man die Werte an, so erhält man \[ proj(\mathbf{x})=\frac{14}{25}~\left[ \begin{array}{c} 4\\3 \end{array} \right]= \left[ \begin{array}{c} 56/25\\42/25 \end{array} \right]. \]

Die Norm (also die geometrische Länge) von \(\mathbf{y}\) beträgt \(||y||=\sqrt{4^2+3^2}=5\). Die Norm der Projektion ist der Abstand vom Ursprung bis zu der Stelle \(proj(x)\), an der die gepunktete Linie auf \(\mathbf{y}\) trifft. Dieser Abstand ist \[ ||proj(\mathbf{x})||=\sqrt{(56/25)^2+(42/25)^2}=2.8. \] Auch auf diesem Weg erhält man den Wert des inneren Produkts, nämlich \(5\times 2.8=14\) ist.

Das innere Produkt ist symmetrisch. Man könnte es also auch grafisch bestimmen, indem man \(\mathbf{y}\) auf \(\mathbf{x}\) projiziert und dann die Norm der Projektion mit \(||\mathbf{x}||\) multipliziert.

Es gibt noch eine weitere Sichtweise auf das innere Produkt. Zwischen dem inneren Produkt zweier Vektoren und dem Winkel zwischen den Vektoren gibt es eine enge Beziehung (was nicht überrascht, wenn man sich die Projektionen ansieht). Es gilt \[ \cos(\theta)=\frac{\mathbf{x}\cdot\mathbf{y}}{||\mathbf{x}||~||\mathbf{y}||}. \] Das innere Produkt der normierten Vektoren (also der Vektoren, die auf die Länge 1 gestaucht oder gestreckt wurden) entspricht dem Kosinus des Winkels zwischen den Vektoren. Daraus folgt, dass ein positives inneres Produkt anzeigt, dass die Vektoren gleichgerichtet sind, und ein negatives inneres Produkt, dass sie gegengerichtet sind. Wenn das innere Produkt den Wert 0 annimmt, sind die Vektoren orthogonal (d.h. rechtwinklig zueinander).

Beispiel:

Die beiden Vektoren \[ \left[\begin{array}{c}1\\2\\3\end{array}\right],\quad \left[\begin{array}{c}3\\0\\-1\end{array}\right] \] haben das innere Produkt 0, d.h. sie sind rechtwinklig zueinander.

Durch diesen Zusammenhang kann man die Idee eines Winkels zwischen zwei Vektoren auch für Dimensionen größer als 3 definieren. Auch wenn man sich nicht anschaulich vorstellen kann, was es bedeutet, dass zwei Vektoren der Dimension 100 orthogonal sind, so weiß man doch, wie man es überprüft, nämlich durch das innere Produkt. Ist es 0, dann stehen Vektoren rechtwinklig zueinander.