Kapitel 7 Differentialrechnung
Die Matrix- und Vektornotation erlaubt eine sehr kompakte und elegante Darstellung von Optimierungsproblemen von Funktionen mit mehreren Argumenten. Als Ausgangspunkt betrachten wir eine Funktion mit \(n\) Argumenten \(x_1,\ldots,x_n\). Die Argumente fassen wir zu einem Vektor zusammen, \[ f(x_1,\ldots,x_n)=f(\mathbf{x}). \] Es handelt sich also um eine Funktion aus dem \(\mathbb{R}^n\) nach \(\mathbb{R}\). Es ist auch möglich, dass die Funktion aus dem \(\mathbb{R}^n\) in den \(\mathbb{R}^m\) (mit \(m>1\)) abbildet, aber diesen Fall betrachten wir in diesem Kurs nicht weiter.
7.1 Gradient
Die Funktion \(f(\mathbf{x})\) hat \(n\) Argumente. Es gibt folglich \(n\) partielle erste Ableitungen von \(f\). Diese Ableitungen werden in einem Vektor zusammengefasst. Er heißt Gradient von \(f\) und wird meistens mit einem auf der Spitze stehenden Dreieck (auch “Nabla” genannt) notiert, \[ \nabla f(\mathbf{x})=\left[ \frac{\partial f(\mathbf{x})}{\partial x_1},\ldots,\frac{\partial f(\mathbf{x})}{\partial x_n} \right]'. \] Der Gradient ist sozusagen die multivariate erste Ableitung. Er gibt an, in welche Richtung die Funktion am steilsten ansteigt. Will man das Minimum erreichen, bietet es sich also an, genau in die entgegengesetzte Richtung zu gehen.
In der ökonometrischen Literatur wird der Gradient manchmal auch als \(Df(\mathbf{x})\) oder \(\partial f/\partial\mathbf{x}\) geschrieben.
Beispiel:
Als Beispiel untersuchen wir eine Funktion mit zwei Argumenten, da sie sich im Gegensatz zu Funktionen mit mehr als zwei Argumenten noch gut visualisieren lässt. Die Funktion lautet \[ f(\mathbf{x}) = x_1^2-x_2^2 \] mit \(\mathbf{x}=(x_1,x_2)'\). Ein Plot der Funktion sieht so aus:
Der Gradient der Funktion ist der Spaltenvektor der beiden partiellen Ableitungen, \[ \begin{align*} \nabla f(\mathbf{x})&=\left[\begin{array}{cc} \frac{\partial f}{\partial x_1}& \frac{\partial f}{\partial x_2} \end{array} \right]'\\ &= \left[\begin{array}{c} 2x_1\\ -2x_2\end{array}\right]. \end{align*} \] Noch ein Beispiel:
Auch in diesem Beispiel hat die Funktion nur zwei Argumente. Sie lautet \[ f(\mathbf{x}) = 2-x_1^2-x_2^2 \] mit \(\mathbf{x}=(x_1,x_2)'\). Ein Plot der Funktion sieht so aus:
Der Gradient der Funktion ist der Zeilenvektor der beiden partiellen Ableitungen, \[ \begin{align*} \nabla f(\mathbf{x})&=\left[\begin{array}{cc} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2}\end{array} \right]'\\[1ex] &= \left[\begin{array}{c} -2x_1\\ -2x_2\end{array}\right]. \end{align*} \]
7.2 Lineare Approximation
In den Wirtschaftswissenschaften sind viele Zusammenhänge nicht linear. Beispielsweise ist es fast immer sinnvoll, von abnehmenden Grenzerträgen auszugehen. Eine lineare Produktionsfunktion ist daher nur in sehr wenigen Fällen plausibel. Obwohl Nichtlinearitäten weitverbreitet sind, ist es nützlich, mit linearen Gleichungssystemen zu arbeiten. Der Grund dafür ist einfach: Ein nichtlineares Gleichungssystem kann linearisiert werden. Das lineare Gleichungssystem ist dann eine lokale Approximation, die um so besser ist, je weniger man sich von dem Punkt entfernt, um den herum man approximiert.
Zur Auffrischung sehen wir uns kurz an, wie eine Funktion mit nur einem Argument linear approximiert wird, und zwar anhand eines Beispiels.
Beispiel:
Die Funktion
\[
f(x)=e^{-x^2/4}
\]
sieht folgendermaßen aus:
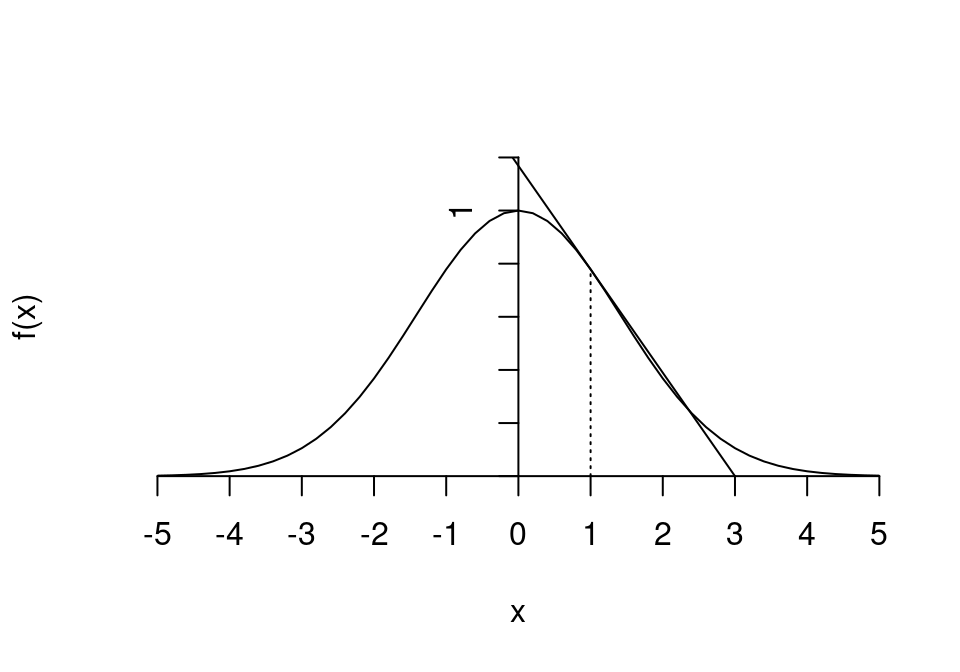
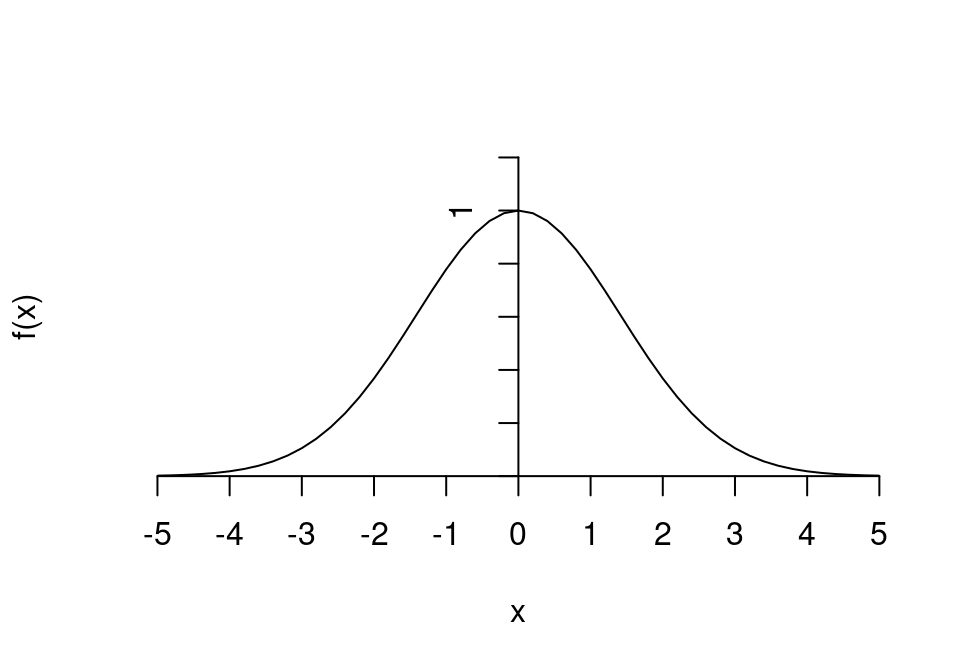Der Verlauf der Funktion soll an der Stelle \(x=1\) linear approximiert werden.
Allgemein lautet die Formel für eine Taylor-Approximation erster Ordnung
um eine Stelle \(x_0\) herum
\[
f(x)\approx f(x_0)+f'(x_0)(x-x_0).
\]
Die Beispielfunktion hat die Ableitung
\[
f'(x)=-\frac{1}{2}x\cdot e^{-x^2/4}.
\]
Die Taylorapproximation an der Stelle \(x_0=1\) ist folglich
\[
\begin{align*}
f(x)&\approx f(1)+f'(1)(x-1)\\
&=e^{-1/4}-\frac{1}{2}e^{-1/4}(x-1)\\
&=e^{-1/4}(1.5-0.5x).
\end{align*}
\]
Fügt man diese lineare Funktion in den Plot ein, so ergibt sich
Wie lässt sich das auf multivariate Funktionen übertragen? Unter
Verwendung der Matrixnotation ist die Analogie deutlich, es gilt nämlich
\[
f(\mathbf{x})\approx f(\mathbf{x_0})+\nabla f(\mathbf{x_0})'(\mathbf{x}-\mathbf{x_0})
\]
Beispiel:
Wir suchen eine lineare Approximation für die Funktion \[ f(\mathbf{x}) = 2-x_1^2-x_2^2 \] an der (willkürlich ausgewählten) Stelle \(\mathbf{x_0}=(0.5,1)'\). Der Funktionswert und der Gradient an der Approximationsstelle sind \[ \begin{align*} f(\mathbf{x_0})&=2-0.5^2-1^2=0.75\\ \nabla f(\mathbf{x_0})'&=[\begin{array}{cc}-2\cdot 0.5 & -2\cdot1\end{array}]=[\begin{array}{cc}-1 & -2\end{array}], \end{align*} \] so dass die Taylorapproximation erster Ordnung um \((-0.5,1)\) herum so aussieht: \[ \begin{align*} f(\mathbf{x}) &= 0.75 + [-1\quad -2] \left[\begin{array}{c} x_1-0.5\\ x_2-1 \end{array} \right]\\[2ex] &=0.75-(x_1-0.5)-2(x_2-1)\\[1ex] &=3.25-x_1-2x_2. \end{align*} \] Zeichnet man diese Ebene in den Funktionsplot mit hinein, so ergibt sich:
Selbstverständlich wäre die lineare Approximation eine andere, wenn die Ebene an einer anderen Stelle angepasst würde.
7.3 Hesse-Matrix
Der Gradient entspricht der ersten Ableitung einer univariaten Funktion. Leitet man die erste Ableitung erneut ab, so erhält man die zweite Ableitung. Damit stellt sich die Frage: Was ist das multivariate Gegenstück zur zweiten Ableitung?
Die Ableitung des Gradienten (bzw. genauer gesagt, aller Komponenten des Gradienten) nach \(\mathbf{x}\) führt auf die Hesse-Matrix \[ Hf(\mathbf{x})=\left[ \begin{array}{cccc} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_1\partial x_2} & \ldots & \frac{\partial^2 f(\mathbf{x})}{\partial x_1\partial x_n}\\ \frac{\partial^2 f(\mathbf{x})}{\partial x_2\partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} & \ldots & \frac{\partial^2 f(\mathbf{x})}{\partial x_2\partial x_n}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial^2 f(\mathbf{x})}{\partial x_n\partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_n\partial x_2} & \ldots & \frac{\partial^2 f(\mathbf{x})}{\partial x_n^2} \end{array} \right]. \] Es handelt sich bei der Hesse-Matrix also um die Matrix der zweiten Ableitungen. Da es gleichgültig ist, ob zuerst nach \(x_i\) und anschließend nach \(x_j\) oder anders herum abgeleitet wird, ist die Hesse-Matrix symmetrisch.
Beispiel:
Die Hesse-Matrix der Funktion \(f(\mathbf{x}) = x_1^2-x_2^2\) ist \[ \begin{align*} Hf(\mathbf{x})&=\left[ \begin{array}{cc} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_1\partial x_2}\\ \frac{\partial^2 f(\mathbf{x})}{\partial x_2\partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} \end{array} \right]\\[1.5ex] &=\left[ \begin{array}{cc} 2 & 0\\ 0 & -2 \end{array} \right]. \end{align*} \]
7.4 Optimierung
Der Vektor \(\mathbf{x}\) soll nun so gewählt werden, dass \(f(\mathbf{x})\) minimal wird. Da die Maximierung von \(f(\mathbf{x})\) der Minimierung von \(-f(\mathbf{x})\) entspricht, braucht man das Maximierungsproblem nicht separat zu betrachten. Es ist quasi nur ein Spiegelbild der Minimierung.
Da in diesem Kurs der Schwerpunkt nicht auf der Optimierung von Funktionen liegt, betrachten wir nur den Spezialfall von überall differenzierbaren Funktionen, deren Minimum (oder Minima) nicht am Rand des Definitionsbereichs liegen. Auch Nebenbedingungen, die in der Ökonomik natürlich eine wichtige Rolle spielen, blenden wir aus.
Die Bedingung erster Ordnung für ein Minimum lautet \[ \nabla f(\mathbf{x})=\mathbf{0}. \] Alle partiellen Ableitungen müssen also im Minimum Null sein. Wäre es anders, könnte man den Funktionswert noch weiter verringern, indem man ein Argument, dessen partielle Ableitung nicht Null ist, ein wenig erhöht oder reduziert (je nach Vorzeichen der Ableitung).
Beispiel:
Die Funktion \(f(x_1,x_2)=-4x_1 x_2+x_1^4+x_2^4\) sieht so aus (der Plot ist am oberen Ende abgeschnitten, eigentlich würde die Funktion noch deutlich weiter nach oben verlaufen):
An welchen Stellen erfüllt diese Funktion die Bedingung erster Ordnung? Dazu berechnen wir zuerst den Gradienten, \[ \nabla f(x_1,x_2)=[\begin{array}{cc}-4x_2+4x_1^3 & -4x_1+4x_2^3\end{array}]. \] Damit beide partiellen Ableitungen Null sind, müssen die folgenden beiden Gleichungen erfüllt sein, \[ \begin{align*} x_1^3&=x_2\\ x_2^3&=x_1 \end{align*} \] Die drei Lösungen lassen sich direkt erkennen. Sie lauten \[ \begin{align*} x_1=x_2=0,\qquad x_1=x_2=1,\qquad x_1=x_2=-1. \end{align*} \] Offensichtlich weist die Funktion jedoch nicht an allen drei Stellen lokale Minima auf. Wie lässt sich formal prüfen, ob eine Stelle, an der der Gradient \(\mathbf{0}\) ist, ein Minimum ist? Die Antwort ist analog zum univariaten Fall. Dort überprüft man die zweite Ableitung an der Stelle, an der die erste Ableitung 0 ist. Wenn die zweite Ableitung negativ ist, handelt es sich um ein Maximum, wenn sie positiv ist, liegt ein Minimum vor.
Für multivariate Funktionen lautet die Bedingung zweiter Ordnung für ein Minimum: Die Hesse-Matrix muss positiv definit sein an der Stelle, an der der Gradient \(\mathbf{0}\) ist. Ist die Hesse-Matrix dort negativ definit, handelt es sich um ein Maximum.
Beispiel:
Die Hesse-Matrix der Funktion \(f(x_1,x_2)=-4x_1 x_2+x_1^4+x_2^4\) ist \[ \begin{align*} Hf(\mathbf{x})&=\left[ \begin{array}{cc} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_1\partial x_2}\\ \frac{\partial^2 f(\mathbf{x})}{\partial x_2\partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} \end{array} \right]\\[1.5ex] &=\left[ \begin{array}{cc} 12x_1^2 & -4\\ -4 & 12x_2^2 \end{array} \right]. \end{align*} \] An den beiden Stellen \(x_1=x_2=1\) und \(x_1=x_2=-1\) gilt \[ Hf\left(\left[\begin{array}{c}1\\1\end{array}\right]\right)= Hf\left(\left[\begin{array}{c}-1\\-1\end{array}\right]\right)=\left[ \begin{array}{cc} 12 & -4\\ -4 & 12 \end{array} \right]. \] Die Eigenwerte dieser Matrix sind \(\lambda_1=16\) und \(\lambda_2=8\). Beide Eigenwerte sind positiv, d.h. die Hesse-Matrix ist positiv definit. Folglich handelt es sich bei den beiden Stellen um lokale Minima, was ein Blick auf den Plot der Funktion ja auch bestätigt.
An der Stelle \(x_1=x_2=0\) ist die Hesse-Matrix \[ Hf\left(\left[\begin{array}{c}0\\0\end{array}\right]\right)=\left[ \begin{array}{cc} 0 & -4\\ -4 & 0 \end{array} \right]. \] Sie hat die beiden Eigenwerte \(\lambda_1=4\) und \(\lambda_2=-4\). Diese Matrix ist also weder positiv, noch negativ definit. In diesem Fall zeigt ein Blick auf den Plot der Funktion, dass an dieser Stelle ein Sattelpunkt ist.
7.5 Ableitungen in Matrixnotation
Die Matrixnotation ist oft eine große Hilfe, wenn es darum geht, mit vielen Ableitungen zu arbeiten. Eine umfangreiche Darstellung der Ableitungsregeln für Funktionen von Vektoren oder Matrizen geben Magnus und Neudecker, 1999 (die Quelle ist im Anhang A zu finden). An dieser Stelle soll ein Überblick über einige wichtige Spezialfälle ausreichen.
Zuerst untersuchen wir die Funktion \[ f(\mathbf{x})=\mathbf{a'x}, \] wobei \(\mathbf{a}\) ein Vektor von \(n\) reellen Zahlen ist. Wie lässt sich der Gradient \(\nabla f\) in Matrixnotation ausdrücken?
Ausgeschrieben gilt \[ f(x_1,\ldots,x_n)=a_1 x_1+a_2 x_2+\ldots+a_n x_n. \] Die partielle Ableitung nach \(x_1\) ist offenbar \(a_1\), nach \(x_2\) ist es \(a_2\) usw. Fasst man alle partiellen Ableitungen zu einem Spaltenvektor zusammen, so ergibt sich der Gradient \[ \nabla \mathbf{a'x}=\mathbf{a}. \]
Als nächstes sehen wir uns eine quadratische Funktion an, nämlich die quadratische Form \[ f(\mathbf{x})=\mathbf{x'Ax}, \] wobei \(\mathbf{A}\) eine (nicht unbedingt symmetrische) \((n\times n)\)-Matrix reeller Zahlen ist. Die partiellen Ableitungen lassen sich besser ermitteln, wenn man die quadratische Form ausschreibt. Es gilt \[ f(x_1,\ldots,x_n)=\sum_{i=1}^n \sum_{j=1}^n a_{ij}x_ix_j. \] Für die partielle Ableitung nach \(x_1\) benötigt man nur die Summanden, in denen \(x_1\) vorkommt, alle anderen fallen weg. Übrig bleiben die Summanden mit \(i=1\) und/oder \(j=1\), d.h. \[ \sum_{j=1}^n a_{1j}x_1 x_j + \sum_{i=1}^n a_{i1}x_ix_1=x_1\sum_{j=1}^n a_{1j}x_j+x_1\sum_{j=1}^n a_{j1}x_j. \] Dass der Laufindex der hinteren Summe von \(i\) auf \(j\) geändert wurde, ändert nichts an dem Ausdruck, vereinfacht aber im folgenden die Schreibweise. Die partielle Ableitung nach \(x_1\) ist also \[ \sum_{j=1}^n a_{1j}x_j+\sum_{j=1}^n a_{j1}x_j. \] Entsprechend ist die partielle Ableitung nach einem beliebigen \(x_i\) \[ \sum_{j=1}^n a_{ij}x_j+\sum_{j=1}^n a_{ji}x_j. \] In Matrixnotation ergibt sich der Gradient \[ \nabla\mathbf{x'Ax}=\mathbf{Ax+A'x}=\mathbf{(A+A')x}. \] Wenn die Matrix \(\mathbf{A}\) symmetrisch ist, kommt die Analogie zu der univariaten Ableitung von \(f(x)=ax^2\), also \(f'(x)=2ax\), deutlich zum Ausdruck, denn dann gilt \[ \nabla\mathbf{x'Ax}=\mathbf{2Ax}. \]