Kapitel 5 Eigenwerte

In Kapitel 2 wurde gezeigt, dass durch eine lineare Transformation alle Punkte im \(\mathbb{R}^2\) auf andere Punkte im \(\mathbb{R}^2\) bewegt (transformiert) werden können (für höhere Dimensionen gilt das auch, aber wir betrachten hier nur den einfacheren zweidimensionalen Fall). Die Linearität der Transformation führt dazu, dass Geraden auch nach der Transformation wieder Geraden sind und dass Parallelen weiterhin parallel zueinander liegen. Schließlich bleibt der Nullpunkt unverändert.

5.1 Grundidee

Für manche Anwendungen ist die Frage interessant, ob es bei einer gegebenen Transformation auch Geraden gibt, die durch diese Transformation nicht in ihrer Lage verändert werden. Für eine vollständige Untersuchung dieser Frage braucht man als mathematisches Werkzeug komplexe Zahlen (die eine reelle und eine imaginäre Komponente haben). Wir beschränken uns im Folgenden zur Vereinfachung jedoch auf Fälle, in denen man ausschließlich mit reellen Zahlen arbeiten kann.

Wenn eine Gerade durch die lineare Transformation nicht verändert wird, dann bedeutet das, dass die Vektoren, die auf dieser Gerade liegen, ihre Richtung nicht ändern, sondern höchstens ihre Länge (Norm). Die folgenden beiden Abbildungen zeigen das für die lineare Transformation, die durch die Matrix \[ \mathbf{A}=\left[ \begin{array}{cc} 4 & -3\\ -1 & 1 \end{array} \right] \] beschrieben wird. In der ersten Abbildung sieht man vier Vektoren vor der Transformation.

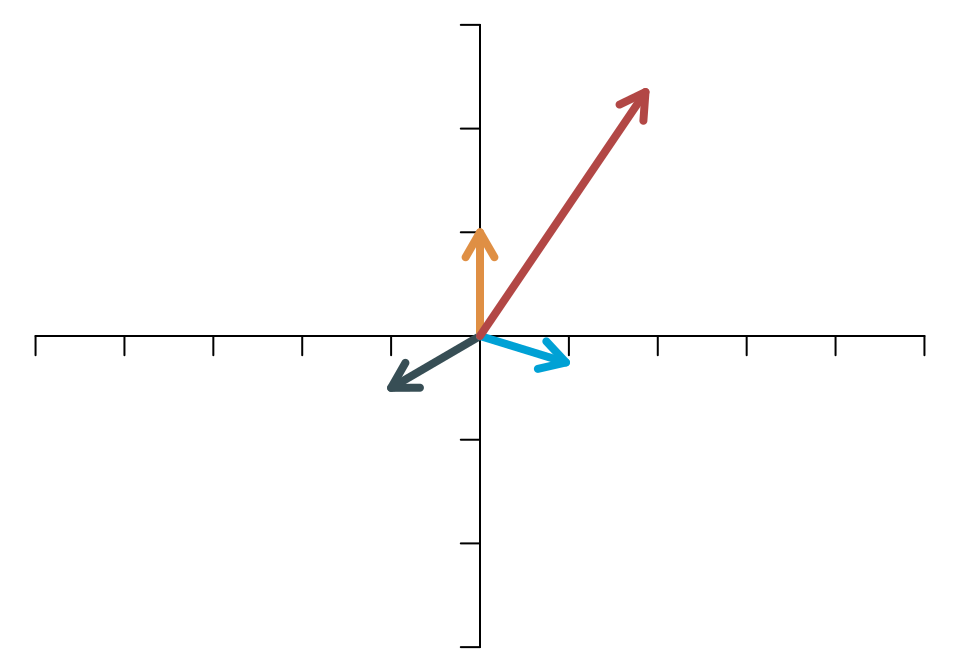
In der zweiten Abbildung sieht man die transformierten vier Vektoren sowie (in den gleichen Farben) in dünnen Linien noch die Lage der Vektoren vor der Transformation.

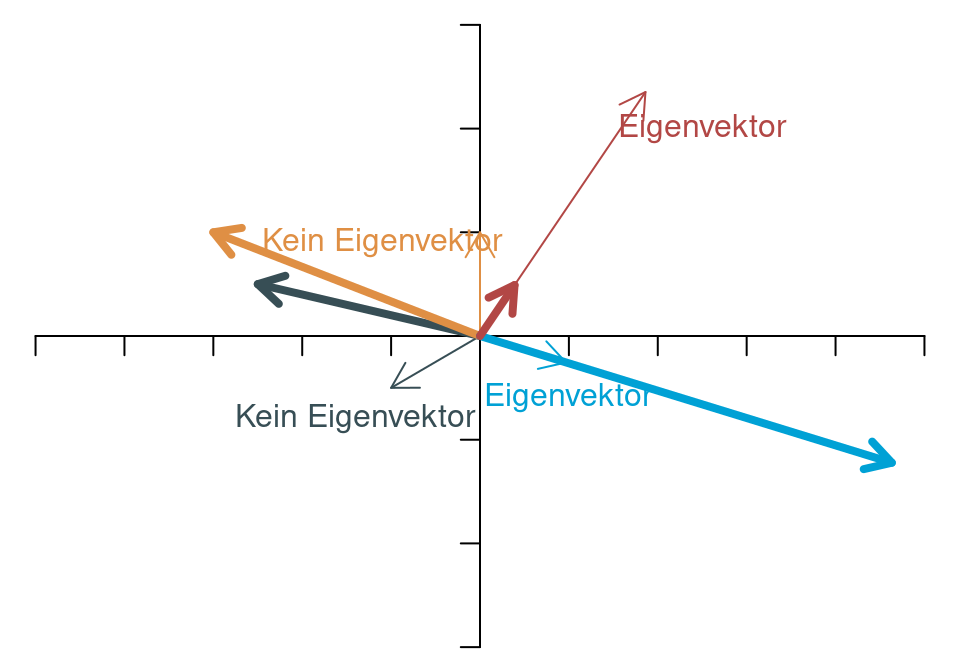
Man erkennt, dass zwei Vektoren ihre Richtung verändert haben (nämlich der gelbliche Vektor, der nach oben gezeigt hat, und der dunkle Vektor, der nach links unten gezeigt hat). Die beiden anderen Vektoren haben ihre Richtung durch die Transformation nicht geändert. Nur ihre Länge (Norm) ist anders als vor der Transformation.

Vektoren, die ihre Richtung bei einer linearen Transformation nicht verändern, nennt man Eigenvektoren (engl. eigen vectors). Die Skalare, die angeben, wie sich die Länge der Eigenvektoren verändert, heißen Eigenwerte (engl. eigen values). In der obigen Abbildung sieht man, dass einer der beiden Eigenwerte größer als 1 ist (nämlich für den blauen Vektor, der nach rechts unten zeigt), und dass der andere Eigenwert kleiner ist als 1 (denn der rötliche Eigenvektor verkürzt sich).

5.2 Definition

Formal definieren wir Eigenvektoren und Eigenwerte einer \((n\times n)\)-Matrix \(\mathbf{A}\) wie folgt. Wenn für \(\lambda\in\mathbb{R}\) und \(\mathbf{x}\neq\mathbf{0}\) \[ \mathbf{Ax}=\lambda\mathbf{x} \] gilt, dann heißt \(\mathbf{x}\) Eigenvektor von \(\mathbf{A}\) zum Eigenwert \(\lambda\).

An der Gleichung erkennt man leicht, dass die Eigenvektoren nicht eindeutig sind, denn wenn \(\mathbf{x}\) ein Eigenvektor ist, dann ist auch ein Vielfaches von \(\mathbf{x}\) wieder ein Eigenvektor.

5.3 Berechnung

Wie findet man die Eigenwerte und -vektoren? Formt man die Definitionsgleichung um, so erhält man \[ \mathbf{Ax}-\lambda\mathbf{Ix}=\mathbf{0}, \] wobei \(\mathbf{I}\) die \((n\times n)\)-Einheitsmatrix ist. Nun kann \(\mathbf{x}\) ausgeklammert werden, \[ (\mathbf{A}-\lambda\mathbf{I})\mathbf{x}=\mathbf{0}. \] Aus Kapitel 4 wissen wir, dass diese Gleichung nur dann eine (nicht eindeutige) Lösung \(\mathbf{x}\neq\mathbf{0}\) hat, wenn die Matrix \((\mathbf{A}-\lambda\mathbf{I})\) singulär ist. Das bedeutet, dass die Determinante 0 sein muss. Mit anderen Worten: Damit \(\lambda\) ein Eigenwert ist, muss es so gewählt werden, dass \[ \det(\mathbf{A}-\lambda\mathbf{I})=0 \] ist. Man nennt diese Gleichung (in \(\lambda\)) die charakteristische Gleichung oder das charakteristische Polynom der Matrix.

Beispiel:

Wenn die Matrix numerisch komplett spezifiziert ist, berechnet man die Eigenwerte und -vektoren gewöhnlich nicht “per Hand”, sondern mit dem Computer. In höheren Dimensionen wäre eine Berechnung per Hand zeitraubend, im zweidimensionalen Fall ist es noch machbar und illustriert das prinzipielle Vorgehen. Darum sehen wir uns die Berechnung der Eigenwerte an der Beispielmatrix \[ \mathbf{A}=\left[ \begin{array}{cc} 4 & -3\\ -1 & 1 \end{array} \right] \] genauer an. Die Determinante von \[ \mathbf{A}-\lambda\mathbf{I}=\left[ \begin{array}{cc} 4-\lambda & -3\\ -1 & 1-\lambda \end{array} \right] \] beträgt \((4-\lambda)(1-\lambda)-(-3)\cdot(-1)\). Es handelt sich also um einen quadratischen Ausdruck in \(\lambda\). Nullsetzen und Umformen ergibt \[ \begin{align*} (4-\lambda)(1-\lambda)-3 &= 0\\ 4-5\lambda+\lambda^2-3 &= 0\\ \lambda^2 -5\lambda+1 &= 0\\ \lambda &= \frac{5}{2}\pm\sqrt{\frac{25}{4}-1}\\ \lambda_1 &\approx 4.7913\\ \lambda_2 &\approx 0.2087. \end{align*} \] In R lautet die Funktion zum Berechnen der Eigenwerte eigen. Sie gibt als Output nicht nur den Vektor der Eigenwerte aus, sondern auch eine Matrix, in der die zugehörigen Eigenvektoren zusammengefasst sind. Wir speichern den Output hier unter dem Namen E.

A <- matrix(c(4,-1,-3,1), 2, 2)
E <- eigen(A)

Diese beiden Bestandteile des Outputs werden in einer Liste zusammengefasst. Das erste Listenelement ist der Vektor der Eigenwerte ($values), das zweite Element ist die Matrix der Eigenvektoren ($vectors) Die Eigenwerte sind

E$values
#> [1] 4.791288 0.208712

Und die Eigenvektoren sind (spaltenweise angeordnet)

E$vectors
#>          [,1]    [,2]
#> [1,]  0.96693 0.62052
#> [2,] -0.25504 0.78419

Da die Eigenvektoren nicht eindeutig, sondern nur bis auf die Skalierung gegeben sind, werden sie hier auf die Norm 1 skaliert. Jedes beliebige Vielfache eines Eigenvektors ist ebenfalls ein Eigenvektor.

Eigenwerte hängen eng mit der Determinante zusammen. Das Produkt aller Eigenwerte ist genauso groß wie die Determinante, \[ \prod_{i=1}^n \lambda_i =\det(\mathbf{A}). \] Daraus folgt unmittelbar, dass eine Matrix singulär ist, wenn sie (mindestens) einen Eigenwert 0 hat.

Die Summe der Eigenwerte entspricht der Spur (also der Summe der Diagonalelemente der Matrix).

Nicht für jede Matrix sind die Eigenwerte reell. Es kann durchaus vorkommen, dass einige oder alle Eigenwerte (und auch die Eigenvektoren) komplexe Zahlen sind. Wir ignorieren das in diesem Kurs. Seien Sie aber nicht verwundert, wenn Ihnen von R ein Output geliefert wird, der ungefähr so aussieht:

B <- matrix(c(1,2,-2,1), 2, 2)
eigen(B)
#> eigen() decomposition
#> $values
#> [1] 1+2i 1-2i
#> 
#> $vectors
#>                    [,1]               [,2]
#> [1,] 0.000000+0.707107i 0.000000-0.707107i
#> [2,] 0.707107+0.000000i 0.707107+0.000000i

5.4 Symmetrische Matrizen

Für symmetrische Matrizen (mit reellen Elementen) sind die Eigenwerte immer reell. Das ist ein Spezialfall, der in der Ökonometrie recht häufig vorkommt. Das ist auch der Grund, warum es in einem Grundlagenkurs gerechtfertigt ist, komplexe Eigenwerte zu ignorieren.

Ferner gilt für symmetrische Matrizen, dass der Rang einer Matrix der Anzahl der Eigenwerte entspricht, die nicht 0 sind.