Kapitel 3 Matrizen

3.1 Definition

Unter einer Matrix (pl. Matrizen, engl. matrix, pl. matrices) versteht man allgemein eine Anordnung von Zahlen in einer rechteckigen Form. Die Matrix \[ \mathbf{A}= \left[ \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots &\vdots &\ddots &\vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array} \right] \] hat \(m\) Zeilen (engl. rows) und \(n\) Spalten (engl. columns). Man sagt auch, dass es sich um eine Matrix der Dimension \(m\times n\) (“m Kreuz n”) handelt, oder einfacher: \(\mathbf{A}\) ist eine \((m\times n)\)-Matrix. Die Matrix enthält \(m\cdot n\) Elemente, jedes Element wird durch zwei Subindizes bezeichnet. Der erste Subindex steht dabei immer für die Zeile, der zweite für die Spalte (“zuerst die Zeile, später die Spalte”). Wenn es zu Verwechselungen kommen kann, trennt man Zeilen- und Spaltenindex durch ein Komma. Es ist gängige Praxis, Matrizen mit fett gedruckten Großbuchstaben und ihre Elemente mit den entsprechenden normal gedruckten Kleinbuchstaben zu bezeichnen. Matrizen, bei denen die Zahl der Zeilen und die Zahl der Spalten gleich ist, nennt man quadratisch.

In R wird eine Matrix durch die Funktion matrix generiert. Die Funktion hat meist drei Argumente. Das erste Argument data enthält die Werte, die in der Matrix stehen, das zweite Argument nrow ist die Zahl der Zeilen, das dritte Argument ncol die Zahl der Spalten (die Namen der Argumente werden zur Vereinfachung oft weggelassen).

A <- matrix(data=c(1, 2, 3, 4), 
            nrow=2, 
            ncol=2)

Die Matrix wird standardmäßig spaltenweise aufgefüllt. In diesem Beispiel erhält man also die Matrix

A
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

Diese Anordnung ist manchmal unpraktisch. Um die Daten zeilenweise aufzufüllen, gibt es in der Funktion matrix die Option byrow. Setzt man diese Option auf TRUE, dann werden die Daten zeilenweise in die Matrix eingefügt.

A <- matrix(data=c(1, 2, 3, 4), 
            nrow=2, 
            ncol=2,
            byrow=TRUE)
A
#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    3    4

Wenn die Länge des Datenvektors data kleiner ist als die Zahl der Matrixelemente, wird der Vektor recycelt. Zum Beispiel gilt

matrix(data=c(1, 2), nrow=2, ncol=2)
#>      [,1] [,2]
#> [1,]    1    1
#> [2,]    2    2

und

matrix(data=c(1, 2), nrow=2, ncol=2, byrow=TRUE)
#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    1    2

Wenn das Produkt aus Zeilen- und Spaltenzahl kein ganzzahliges Vielfaches der Anzahl der Elemente in data ist, gibt R eine Warnung aus.

matrix(data=c(1, 2, 3), ncol=2, nrow=2)

#> Warnung: Datenlänge [3] ist kein Teiler oder Vielfaches der Anzahl der Zeilen [2]
#> [1,]    1    3
#> [2,]    2    1

Wenn nur ein einziger Wert angegeben ist, wird er in alle Zellen eingesetzt (und R verzichtet auf eine Warnung). Zum Beispiel:

matrix(5, ncol=3, nrow=3)
#>      [,1] [,2] [,3]
#> [1,]    5    5    5
#> [2,]    5    5    5
#> [3,]    5    5    5

Die Dimensionen einer Matrix liefert die Funktion dim. Der Return der Funktion dim ist ein Vektor der Länge 2, das erste Elemente ist die Zeilenzahl, das zweite Element ist die Spaltenzahl. Als Beispiel betrachten wir die Matrix

A <- matrix(1:6, 2, 3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    3    5
#> [2,]    2    4    6

Die Dimensionen von A sind

dim(A)
#> [1] 2 3

Wenn wir uns nur für die Zeilenzahl interessieren, können wir sie so finden:

dim(A)[1]
#> [1] 2

Matrizen können mit logischen Operatoren miteinander verglichen werden. Die Operatoren werden elementweise auf die Matrizen angewendet, die Dimensionen der Matrizen müssen daher gleich sein. Der wichtigste logische Operator ist ==, mit ihm wird Gleichheit überprüft (beachten Sie das doppelte Gleichheitszeichen, das einfache Gleichheitszeichen ist in R auch erlaubt, es ist jedoch ein Synonym für den Zuweisungsoperator <-).

Beispiel:

Wir betrachten die beiden \((3\times 3)\)-Matrizen

A <- matrix(1:9, 3, 3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    4    7
#> [2,]    2    5    8
#> [3,]    3    6    9

und

B <- matrix(c(1, 2, 4, 4, 5, 6, 8, 8, 9),3,3)
B
#>      [,1] [,2] [,3]
#> [1,]    1    4    8
#> [2,]    2    5    8
#> [3,]    4    6    9

Der Gleichheitsoperator ergibt eine \((3\times 3)\)-Matrix von logischen Werten,

A == B
#>       [,1] [,2]  [,3]
#> [1,]  TRUE TRUE FALSE
#> [2,]  TRUE TRUE  TRUE
#> [3,] FALSE TRUE  TRUE

In diesem Fall sieht man sofort, dass die Matrizen nicht gleich sind, da es FALSE-Einträge gibt. Bei sehr großen Matrizen mit vielen Tausend Elementen ist es aber nicht sinnvoll, alle Einträge einzeln zu untersuchen. Hier bietet sich die Funktion all an.

all(A==B)
#> [1] FALSE

Man erkennt unmittelbar, dass nicht alle Elemente der beiden Matrizen gleich sind.

Matrizen werden in R ähnlich wie Vektoren durch eckige Klammern indiziert. Der einfachste Fall ist das Herauslesen eines einzelnen Elements aus einer Matrix.

A[3,2]
#> [1] 6

Eine komplette Zeile wird ausgelesen, indem der Spaltenindex weggelassen wird. Die zweite Zeile von A ist also

A[2,]
#> [1] 2 5 8

Für die Spaltenauszahl lässt man den Zeilenindex weg.

A[,3]
#> [1] 7 8 9

Beim Auslesen einer Zeile oder Spalte erhält man einen Vektor, keine Matrix. Das ist in manchen Fällen unpraktisch. Darum kann man den Datentyp “matrix” erzwingen, indem man als Option drop=FALSE in die eckigen Klammern schreibt.

A[,3,drop=FALSE]
#>      [,1]
#> [1,]    7
#> [2,]    8
#> [3,]    9

oder (achten Sie auf das doppelte Komma)

A[2,,drop=FALSE]
#>      [,1] [,2] [,3]
#> [1,]    2    5    8

Dann erhält man beim Auslesen einer Spalte einen Spaltenvektor und beim Auslesen eines Zeilenvektors einen Zeilenvektor.

Die logische Indizierung von Matrizen ist ebenfalls analog zu den Vektoren möglich, wird aber relativ selten benötigt.

3.2 Transponierte Matrix

Wenn man die Zeilen und Spalten miteinander vertauscht, ergibt sich die transponierte Matrix bzw. die Transponierte (engl. transpose). Es gibt zwei gängige Arten der Notation für die Transponierte. Zum einen durch einen angehängten Hochstrich (\(\mathbf{A}'\)), zum anderen durch ein hochgestelltes T (\(\mathbf{A}^\top\) oder \(\mathbf{A}^T\)). Es gibt mehrere Möglichkeiten, diese Ausdrücke auszusprechen. Gängig sind: “A Strich” oder “A transponiert” (engl. “A prime” oder “A transpose”). In diesem Kurs verwenden wir die Notation \(\mathbf{A}'\).

Die Transponierte sieht so aus: \[ \mathbf{A}'= \left[ \begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{m1}\\ a_{12} & a_{22} & \ldots & a_{m2}\\ \vdots &\vdots &\ddots &\vdots \\ a_{1n} & a_{2n} & \ldots & a_{mn} \end{array} \right]. \] Es handelt sich also um eine \((n\times m)\)-Matrix.

In R erhält man die Transponierte einer Matrix mit Hilfe der Funktion t. Da der Buchstabe t in R eine Funktion ist, sollte man möglichst vermeiden, andere Objekte oder Variablen mit t zu benennen. Als Beispiel sehen wir uns die folgende \((2\times 3)\)-Matrix an:

A <- matrix(1:6, 2, 3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    3    5
#> [2,]    2    4    6

Die Transponierte von A ist

t(A)
#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    3    4
#> [3,]    5    6

Die Dimensionen von t(A) sind:

dim(t(A))
#> [1] 3 2

Transponiert man eine transponierte Matrix noch einmal, so erhält man wieder die Ausgangsmatrix, \[ (\mathbf{A}')'=\mathbf{A}. \] Für die Beispielmatrix bestätigt R die Gleichheit:

all(A == t(t(A)))
#> [1] TRUE

Wenn eine Matrix gleich ihrer Transponierten ist, d.h. wenn \[ \mathbf{A}=\mathbf{A}', \] dann nennt man sie symmetrisch. Offensichtlich müssen symmetrische Matrizen quadratisch sein. Die Elemente oberhalb der Diagonale sind identisch zu den Elementen unterhalb der Diagonale.

Beispiel:

Die Matrix

A <- matrix(c(1,7,8,7,2,-3,8,-3,3),3,3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    7    8
#> [2,]    7    2   -3
#> [3,]    8   -3    3

ist symmetrisch, denn

t(A) == A
#>      [,1] [,2] [,3]
#> [1,] TRUE TRUE TRUE
#> [2,] TRUE TRUE TRUE
#> [3,] TRUE TRUE TRUE

bzw.

all(t(A) == A)
#> [1] TRUE

3.3 Vektoren als Spezialfälle

Vektoren können als Matrizen mit nur einer Zeile oder nur einer Spalte geschrieben werden. Als Konvention hat sich weltweit durchgesetzt, dass Vektoren als Matrix mit einer Spalte aufgefasst werden, sofern nichts anderes angegeben ist. Man spricht auch von einem Spaltenvektor. Der zweite Subindex ist in diesem Fall überflüssig und wird daher meist einfach weggelassen. Der Vektor \[ \mathbf{x}= \left[ \begin{array}{cccc} x_{1}\\ x_{2}\\ \vdots\\ x_{m} \end{array} \right] \] der Länge \(m\) kann also formal als eine \((m\times 1)\)-Matrix aufgefasst werden. Folglich ist die Transponierte \[ \mathbf{x}'= \left[x_{1}\quad x_{2}\quad \ldots\quad x_{m}\right] \] ein Zeilenvektor. Spaltenvektoren werden in ökonometrischen Texten sehr oft als \((x_1,\ldots,x_n)'\) notiert, also als transponierter Zeilenvektor. In diesem Kurs nutzen wir diese Notation ebenfalls oft.

Wie wir in Kapitel 1 gesehen haben, sind Vektoren in R keine Matrizen, sie haben keine Dimensionen (dim), sondern nur eine Länge (length). Es ist jedoch auch in R möglich, Vektoren als Matrizen mit nur einer Spalte (oder Zeile) zu schreiben.

Beispiel:

a <- c(3,7,2)
x <- matrix(a, ncol=1)
x
#>      [,1]
#> [1,]    3
#> [2,]    7
#> [3,]    2

Die Dimensionen von x sind

dim(x)
#> [1] 3 1

3.4 Addition von Matrizen

Zwei Matrizen \(\mathbf{A}\) und \(\mathbf{B}\), die beide die gleiche Dimension \((n\times m)\) haben, können addiert werden. Die Summe der beiden Matrizen ist ebenfalls eine Matrix der Dimension \((n\times m)\). Ihre Elemente ergeben sich als die Summe der entsprechenden Elemente von \(\mathbf{A}\) und \(\mathbf{B}\), \[ \begin{align*} \mathbf{A}+\mathbf{B}&= \left[ \begin{array}{ccc} a_{11} & \ldots & a_{1n}\\ \vdots &\ddots &\vdots \\ a_{m1} & \ldots & a_{mn} \end{array} \right]+ \left[ \begin{array}{ccc} b_{11} & \ldots & b_{1n}\\ \vdots &\ddots &\vdots \\ b_{m1} & \ldots & b_{mn} \end{array} \right] \\[2ex] &= \left[ \begin{array}{ccc} a_{11}+b_{11} & \ldots & a_{1n}+b_{1n}\\ \vdots &\ddots &\vdots \\ a_{m1}+b_{m1} & \ldots & a_{mn}+b_{mn} \end{array} \right]. \end{align*} \] Zwei Matrizen A und B können in R addiert werden, indem man A+B eingibt. Dabei wird vorausgesetzt, dass die Dimensionen von A und B gleich sind.

Addiert man zu der Matrix

A <- matrix(1:4, 2, 2)
A
#>      [,1] [,2]
#> [1,]    1    3
#> [2,]    2    4

die Matrix

B <- matrix(c(5, 7, 3, -2), 2, 2)
B
#>      [,1] [,2]
#> [1,]    5    3
#> [2,]    7   -2

so erhält man

A+B
#>      [,1] [,2]
#> [1,]    6    6
#> [2,]    9    2

Der Versuch, zwei Matrizen mit unterschiedlichen Dimensionen zu addieren, führt zu einer Fehlermeldung:

A <- matrix(1:4, 2, 2)
B <- matrix(1:6, 3, 2)
A+B

# Fehler in A + B : nicht passende Arrays

Es gibt in R jedoch Matrix-Additionen, die in der Mathematik so nicht vorgesehen sind. Beispielsweise kann man einen Skalar zu einer Matrix addieren (oder subtrahieren). In diesem Fall wird jedes Element der Matrix mit der Skalar addiert (bzw. subtrahiert).

A <- matrix(1:4, 2, 2)
A+3
#>      [,1] [,2]
#> [1,]    4    6
#> [2,]    5    7

A-5
#>      [,1] [,2]
#> [1,]   -4   -2
#> [2,]   -3   -1

Es ist auch erlaubt (jedoch nicht empfehlenswert!), einen Vektor und eine Matrix zu addieren. Dabei werden die Vektorelemente nacheinander mit den Matrixelementen summiert, wobei die Matrixelemente spaltenweise durchlaufen werden.

A <- matrix(1:4, 2, 2)
A + c(1,5)
#>      [,1] [,2]
#> [1,]    2    4
#> [2,]    7    9

Da diese Art von Operationen jedoch in der Mathematik nicht vorgesehen sind, sollte man sie beim Programmieren in R möglichst vermeiden. Es wäre eine häufige Fehlerquelle.

Für die Transponierte der Summe gilt \[ (\mathbf{A}+\mathbf{B})'=\mathbf{A}'+\mathbf{B}'. \] Die Matrixaddition ist kommutativ, d.h. \[ \mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}, \] und assoziativ, d.h. \[ (\mathbf{A}+\mathbf{B})+\mathbf{C}=\mathbf{A}+(\mathbf{B}+\mathbf{C}). \] In Kombination mit der Skalarmultiplikation (s. Abschnitt 1.6) gilt für alle \(\lambda,\mu\in\mathbb{R}\) \[ \lambda (\mathbf{A}+\mathbf{B})=\lambda\mathbf{A}+\lambda\mathbf{B} \] und \[ (\lambda+\mu)\mathbf{A} = \lambda\mathbf{A}+\mu\mathbf{A}. \]

3.5 Matrixmultiplikation

Für die Matrixmultiplikation muss die Spaltenzahl der ersten (vorderen) Matrix der Zeilenzahl der zweiten (hinteren) Matrix entsprechen. Wir betrachten die Matrix \(\mathbf{A}\) der Dimension \((m\times k)\) und die Matrix \(\mathbf{B}\) der Dimension \((k\times n)\). Das Produkt \(\mathbf{AB}\) ist die \((m\times n)\)-Matrix \[ \mathbf{AB}=\left[\begin{array}{cccc} \sum_{i=1}^k a_{1i}b_{i1} & \sum_{i=1}^k a_{1i}b_{i2} & \ldots & \sum_{i=1}^k a_{1i}b_{in}\\ \sum_{i=1}^k a_{2i}b_{i1} & \sum_{i=1}^k a_{2i}b_{i2} & \ldots & \sum_{i=1}^k a_{2i}b_{in}\\ \vdots & \vdots & \ddots & \vdots \\ \sum_{i=1}^k a_{mi}b_{i1} & \sum_{i=1}^k a_{mi}b_{i2} & \ldots & \sum_{i=1}^k a_{mi}b_{in} \end{array}\right]. \] Die Berechnung des Matrixprodukt kann man sich in Form des folgenden Schemas merken, in dem man die hintere Matrix nach oben schiebt: \[ \begin{array}{lc} & \left[\begin{array}{ccc} b_{11} \qquad & \ldots & \qquad b_{1n}\\ \vdots \qquad & & \qquad \vdots \\ b_{k1} \qquad & \ldots & \qquad b_{kn} \end{array}\right]\\ & \begin{array}{ccc} \downarrow~\qquad & \ldots & \qquad ~\downarrow\\ \end{array}\\ \left[\begin{array}{ccc} a_{11} & \ldots & a_{1k}\\ \vdots & & \vdots\\ a_{m1} & \ldots & a_{mk}\\ \end{array}\right] \begin{array}{l} \longrightarrow\\\vdots\\\longrightarrow \end{array}& \left[\begin{array}{ccc} \sum_{i=1}^k a_{1i}b_{i1} & \ldots & \sum_{i=1}^k a_{1i}b_{in}\\ \vdots & & \vdots\\ \sum_{i=1}^k a_{mi}b_{i1} & \ldots & \sum_{i=1}^k a_{mi}b_{in}\\ \end{array}\right] \end{array} \] Um in der Produktmatrix das Element in Zeile \(i\) und Spalte \(j\) zu berechnen, braucht man also die \(i\)-te Zeile von \(\mathbf{A}\) und die \(j\)-te Spalte von \(\mathbf{B}\). Ihr inneres Produkt ist der gesuchte Wert.

Wenn Matrizen miteinander multipliziert werden, müssen die Dimensionen an den “Schnittstellen” zueinander passen. Zur Kontrolle ist es oftmals hilfreich, die Dimensionen unter die Matrizen zu schreiben. \[ \underset{m\times k}{\mathbf{A}}~~\underset{k\times n}{\mathbf{B}} =\underset{m\times n\rule{0mm}{7pt}}{\mathbf{C}}. \]

Die Matrixmultiplikation in R erfolgt mit dem Operator %*%, nicht mit dem normalen Multiplikationszeichen *.

Die folgenden Beispiele zeigen, wie Matrizen unterschiedlicher Dimensionen miteinander multipliziert werden.

Als erstes wird eine \((3\times 2)\)-Matrix mit einer \((2\times 4)\)-Matrix multipliziert. Man erhält eine \((3\times 4)\)-Matrix: \[ \left[ \begin{array}{cc} 1 & 3 \\ 2 & 1 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{cccc} 2 & 1 & -2 & -1\\ -2 & 1 & 3 & -5 \end{array} \right] = \left[ \begin{array}{cccc} -4 & 4 & 7 & -16\\ 2 & 3 & -1 & -7\\ -2 & 9 & 7 & -29 \end{array} \right]. \] In R erhält man dieses Ergebnis wie folgt (wir nennen die erste Matrix A und die zweite B).

A <- matrix(c(1, 2, 4, 3, 1, 5), 3, 2)
B <- matrix(c(2, -2, 1, 1, -2, 3, -1, -5), 2, 4)
A %*% B
#>      [,1] [,2] [,3] [,4]
#> [1,]   -4    4    7  -16
#> [2,]    2    3   -1   -7
#> [3,]   -2    9    7  -29

Wenn an eine \((3\times 3)\)-Matrix ein Spaltenvektor der Länge 3 (also eine Matrix der Dimension \((3\times 1)\)) multipliziert wird, erhält man wieder einen Spaltenvektor der Länge 3 (nämlich die lineare Transformation): \[ \left[ \begin{array}{ccc} 2 & 0 & -1\\ 1 & -0.5 & 2\\ 1 & 1 & -2 \end{array} \right] \left[ \begin{array}{c} 2 \\ -2 \\ 1 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 5 \\ -2 \end{array} \right]. \] In diesem Fall darf man in R auch einen Vektor, der nicht als Spaltenmatrix definiert wurde, an die Matrix heranmultiplizieren. Im folgenden Code nennen wir die Matrix A und den Vektor x.

A <- matrix(c(2, 1, 1, 0, -0.5, 1, -1, 2, -2), 3, 3)
x <- c(2, -2, 1)
A %*% x
#>      [,1]
#> [1,]    3
#> [2,]    5
#> [3,]   -2

Multipliziert man einen Zeilenvektor an eine Matrix, so ergibt sich wieder ein Zeilenvektor: \[ \left[ \begin{array}{cc} 2 & -3 \end{array} \right] \left[ \begin{array}{ccc} 2 & 1 & 3\\ -2 & 0 & 0.5 \end{array} \right] = \left[ \begin{array}{ccc} 10 & 2 & 4.5 \end{array} \right]. \]

Auch hier ist es in R möglich, einen Vektor an die Matrix heranzumultiplizieren. In dem Code heißt der Vektor y und die Matrix B.

y <- c(2, -3)
B <- matrix(c(2, -2, 1, 0, 3, 0.5), 2, 3)
y %*% B
#>      [,1] [,2] [,3]
#> [1,]   10    2  4.5

Bei der Multiplikation von Zeilen- und Spaltenvektoren sind zwei Situationen relevant. Multipliziert man einen Zeilenvektor \(\mathbf{x}\) der Dimension \((1\times n)\) mit einem Spaltenvektor \(\mathbf{y}\) der Dimension \((n\times 1)\), so erhält man einen Skalar (bzw. eine Matrix der Dimension \((1\times 1)\)).

Als Beispiel sehen wir uns das Produkt aus \[ \mathbf{x}=[1\quad 2\quad 3] \] und \[ \mathbf{y}=\left[ \begin{array}{c} 5\\ -1\\ 2 \end{array} \right] \] an. Wir erhalten

x <- matrix(c(1, 2, 3), 1, 3)
y <- matrix(c(5, -1, 2), 3, 1)
x %*% y
#>      [,1]
#> [1,]    9

Multipliziert man hingegen einen \((n\times 1)\)-Spaltenvektor mit einem \((1\times n)\)-Zeilenvektor, so ergibt sich eine \((n\times n)\)-Matrix. Zum Beispiel gilt

y %*% x
#>      [,1] [,2] [,3]
#> [1,]    5   10   15
#> [2,]   -1   -2   -3
#> [3,]    2    4    6

Was passiert, wenn man bei einer Matrixmultiplikation versehentlich anstelle von %*% das übliche Multiplikationszeichen * verwendet? Sofern die Matrizen unterschiedliche Dimensionen haben, wird es eine Fehlermeldung (oder in wenigen Fällen zumindest eine Warnung) geben. Wenn die beiden Matrizen jedoch die gleichen Dimensionen haben, berechnet R die elementweisen Produkte. Mit anderen Worten: A * B ist im Allgemeinen ungleich A %*% B!

Die Verwechslung dieser beiden Operatoren %*% und * ist ein häufiger Fehler.

Die Matrixmultiplikation ist im Gegensatz zu der normalen Multiplikation reeller Zahlen nicht kommutativ. Selbst wenn die Dimensionen eine Multiplikation in beide Richtungen erlauben, so gilt im Allgemeinen \[ \mathbf{AB}\neq \mathbf{BA}. \] Das wird an folgendem Gegenbeispiel deutlich. Wir betrachten die beiden Matrizen \[ \mathbf{A}= \left[ \begin{array}{cc} 1 & 3\\ 2 & 4\\ \end{array} \right],\qquad \mathbf{B}= \left[ \begin{array}{cc} -1 & 1\\ 1 & 2\\ \end{array} \right]. \] Dann gilt

A <- matrix(c(1, 2, 3, 4), 2, 2)
B <- matrix(c(-1, 1, 1, 2), 2, 2)
A %*% B
#>      [,1] [,2]
#> [1,]    2    7
#> [2,]    2   10

aber

B %*% A
#>      [,1] [,2]
#> [1,]    1    1
#> [2,]    5   11

Die Matrixmultiplikation ist assoziativ, d.h. \[ (\mathbf{AB})\mathbf{C}=\mathbf{A}(\mathbf{BC}), \] sofern die Dimensionen der Matrizen zueinander passen.

Ferner gilt das Distributivgesetz (wenn die Dimensionen alle passend sind), \[ (\mathbf{A}+\mathbf{B})\mathbf{C}=\mathbf{AC}+\mathbf{BC} \] bzw. \[ \mathbf{A}(\mathbf{B}+\mathbf{C})=\mathbf{AB}+\mathbf{AC}. \]

Als Beispiel nehmen wir die beiden \((2\times 2)\)-Matrizen \(\mathbf{A}\) und \(\mathbf{B}\) und multiplizieren ihre Summe an die \((2\times 3)\)-Matrix \[ \mathbf{C}= \left[ \begin{array}{ccc} -3 & 0.5 & 5 \\ 1 & 1 &0 \end{array} \right]. \] In R erhält man für den Ausdruck \((\mathbf{A}+\mathbf{B})\mathbf{C}\)

C <- matrix(c(-3, 1, 0.5, 1, 5, 0), 2, 3)
(A+B) %*% C
#>      [,1] [,2] [,3]
#> [1,]    4  4.0    0
#> [2,]   -3  7.5   15

und für \(\mathbf{AC}+\mathbf{BC}\) ergibt sich

A %*% C + B %*% C
#>      [,1] [,2] [,3]
#> [1,]    4  4.0    0
#> [2,]   -3  7.5   15

Für die Transponierte des Produkts gilt \[ (\mathbf{AB})'=\mathbf{B}'\mathbf{A}', \] d.h. die Reihenfolge dreht sich um. Es ist instruktiv, hier die Dimensionen unter die Matrizen zu schreiben: \[ (\underset{m\times k}{\mathbf{A}}~ \underset{k\times n}{\mathbf{B}})'= \underset{n\times k}{\mathbf{B}'}~ \underset{k\times m}{\mathbf{A}'}. \] Gleichungen mit Matrizen und Vektoren können so ähnlich wie “normale” Gleichungen umgeformt werden, z.B. indem man auf beiden Seiten der Gleichung einen Term addiert oder mit einer Matrix multipliziert. Natürlich müssen die Dimensionen immer passend sein. Bei der Multiplikation mit einer Matrix muss darauf geachtet werden, dass die Matrixmultiplikation nicht kommutativ ist. Es macht also einen Unterschied, ob die Matrix von links oder von rechts an die beiden Seiten der Gleichung heranmultipliziert wird. Man spricht daher auch von Links- oder Rechtsmultiplizieren (engl. left or right multiplication).

3.6 Matrix als lineare Transformation

Eine Matrix kann als kompakte Schreibweise für eine lineare Transformation aufgefasst werden. Die Spalten der Matrix geben an, wohin die natürlichen Basisvektoren transformiert werden. Und \(\mathbf{Ax}\) ist die lineare Transformation des Vektors \(\mathbf{x}\).

Wenn zwei lineare Transformationen nacheinander ausgeführt werden, entspricht das dem Matrixprodukt. Wenn ein Vektor \(\mathbf{x}\) zuerst durch eine Matrix \(\mathbf{A}\) transformiert wird und anschließend noch eine lineare Transformation \(\mathbf{B}\) durchgeführt wird, dann erhält man \[ \mathbf{y}=\mathbf{BAx}. \] Das gleiche Resultat erhält man durch eine einzelne lineare Transformation mit der Matrix \(\mathbf{C}=\mathbf{BA}\). Die Matrixmultiplikation fasst also zwei Schritte zu einem zusammen. Damit wird auch klar, warum das Matrixprodukt nicht kommutativ ist.

3.7 Einheitsmatrix

Eine besondere Matrix ist die Einheitsmatrix (engl. identity matrix). Sie transformiert einen Vektor auf sich selber. Sie hat auf der Diagonalen Einsen und überall sonst Nullen. Die Einheitsmatrix der Dimension \((n\times n)\) wird als \(\mathbf{I}_n\) oder (wenn die Dimension klar ist) einfach als \(\mathbf{I}\) notiert. Einheitsmatrizen sind quadratisch und sehen so aus: \[ \mathbf{I}_n=\left[ \begin{array}{cccc} 1 & 0 & \ldots & 0\\ 0 & 1 & \ldots & 0\\ \vdots & \vdots & \ddots &\vdots\\ 0 & 0 & \ldots & 1 \end{array} \right]. \] Für jede beliebige Matrix \(\mathbf{A}\) (also auch für Spalten- oder Zeilenvektoren) gilt \[ \mathbf{AI}=\mathbf{IA}=\mathbf{A}, \] sofern die Dimensionen passen.

In R generiert man eine Einheitsmatrix der Dimension \((n\times n)\) mit der Funktion diag (leider ist dieser Name nicht sehr intuitiv):

diag(3)
#>      [,1] [,2] [,3]
#> [1,]    1    0    0
#> [2,]    0    1    0
#> [3,]    0    0    1

3.8 Rang einer Matrix

Unter dem Rang einer Matrix versteht man die Anzahl der linear unabhängigen Spalten (oder Zeilen) einer Matrix. Der Rang kann niemals größer sein als das Minimum von Spaltenzahl und Zeilenzahl der Matrix. Für eine Matrix \(\mathbf{A}\) mit Dimensionen \((m\times n)\) gilt also immer, dass \(rg(\mathbf{A})\le \min(m,n)\). Da die Zahl der linear unabhängigen Zeilen immer gleich der Zahl der linear unabhängigen Spalten ist, braucht man nicht zu sagen, ob man den “Zeilenrang” oder den “Spaltenrang” angibt - die beiden sind gleich: \[ rg(A)=rg(A'). \] Wenn \(rg(\mathbf{A})=\min(m,n)\) ist, sagt man auch, dass die Matrix vollen Rang hat. Eine quadratische Matrix der Dimension \((n\times n)\) mit vollem Rang nennt man auch regulär. Wenn sie keinen vollen Rang hat, heißt sie singulär.

Für den Rang gibt es eine Reihe von Rechenregeln. So gilt \[ rg(\mathbf{A})=rg(\mathbf{A}')=rg(\mathbf{A}'\mathbf{A})=rg(\mathbf{A}\mathbf{A}'). \] Der Rang eines Matrixprodukt kann nicht größer sein als die Ränge der beiden Faktormatrizen, d.h. \[ rg(\mathbf{AB})\le \min(rg(\mathbf{A}),rg(\mathbf{B})). \] Multipliziert man eine Matrix \(\mathbf{A}\) mit einer quadratischen Matrix \(\mathbf{B}\) vollen Rangs, so hat das Produkt den Rang von \(\mathbf{A}\), \[ rg(\mathbf{AB})=rg(\mathbf{A}). \] Auch für die Summe zweier Matrizen lässt sich eine Aussage über den Rang treffen. Es gilt \[ rg(\mathbf{A}+\mathbf{B})\le rg(\mathbf{A})+rg(\mathbf{B}). \]

Leider gibt es in R standardmäßig keine Funktion, die den Rang einer Matrix berechnet. Das Paket pracma stellt jedoch die Funktion Rank zur Verfügung, mit der man den Rang leicht ausrechnen kann. Beispielsweise hat die Matrix

library(pracma)
A <- matrix(1:9, 3, 3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    4    7
#> [2,]    2    5    8
#> [3,]    3    6    9

den Rang

Rank(A)
#> [1] 2

Diese Matrix hat also keinen vollen Rang, sie ist singulär. Jede der drei Spalten lässt sich als Linearkombination der beiden anderen Spalten ausdrücken. Mit Hilfe der Funktion nullspace, die ebenfalls von dem Paket pracma bereit gestellt wird, kann man die Skalare finden, für die gilt \[ \lambda_1\mathbf{x}_1+\ldots+\lambda_n\mathbf{x}_n=\mathbf{0}. \] Für die Beispielmatrix ergibt sich

lambda <- nullspace(A)
lambda
#>            [,1]
#> [1,]  0.4082483
#> [2,] -0.8164966
#> [3,]  0.4082483

Wir überprüfen, ob die Linearkombination der drei Spalten von A mit diesen drei Skalaren tatsächlich den Nullvektor ergibt.

lambda[1]*A[,1] + lambda[2]*A[,2] + lambda[3]*A[,3]
#> [1] -4.440892e-16 -4.440892e-16  8.881784e-16

Zur Notation: Mit e-16 ist die wissenschaftliche Schreibweise \(\times 10^{-16}\) gemeint. Der Nullvektor wird zwar nicht exakt getroffen, aber die Abweichung ist erst in der 16. Nachkommastelle zu sehen. Diese kleinen Abweichungen werden durch Rundungsfehler verursacht. Wenn das Ergebnis auf viele Stellen (z.B. 12) nach dem Komma gerundet wird, ergibt sich tatsächlich der Nullvektor,

round(lambda[1]*A[,1] + lambda[2]*A[,2] + lambda[3]*A[,3], 12)
#> [1] 0 0 0

Die exakte Lösung ist \(\lambda_1=\lambda_3=20/49\) und \(\lambda_2=-40/49\).

Die drei Skalare, die in dem Vektor lambda zusammengefasst sind, stellen nicht die einzige Lösung dar. Multipliziert man sie mit einer beliebigen Konstante (außer Null), so erhält man drei andere Skalare, die ebenfalls auf den Nullvektor führen.

Der Rang einer Matrix lässt sich auch mit dem Gauß-Jordan-Verfahren bestimmen, das wir ja bereits in Kapitel 1.7.3 kennen gelernt haben. Wie sieht das an der Beispielmatrix \(\mathbf{A}\) aus? \[ \begin{array}{cccl} 1 & 4 & 7 & \quad(I)\\ 2 & 5 & 8 & \quad(II)\\ 3 & 6 & 9 & \quad(III) \end{array} \] Zuerst subtrahieren wir \(2(I)\) von \((II)\) und im gleichen Schritt \(3(I)\) von \((III)\). \[ \begin{array}{cccl} 1 & 4 & 7 & \quad(I)\\ 0 & -3 & -6 & \quad(II)\\ 0 & -6 & -12 & \quad(III) \end{array} \] In nächsten Schritt subtrahieren wir \(2(II)\) von \((III)\). \[ \begin{array}{cccl} 1 & 4 & 7 & \quad(I)\\ 0 & -3 & -6 & \quad(II)\\ 0 & 0 & 0 & \quad(III) \end{array} \] Da die letzte Zeile nur aus Nullen besteht, hat die Matrix keinen vollen Rang. Dass der Rang der Matrix 2 (und nicht nur 1) beträgt, erkennt man daran, dass die ersten beiden Zeilen linear unabhängig voneinander sind. Wenn als Ergebnis der Gauß-Jordan-Methode an Ende zwei Zeilen ausschließlich Nullen enthalten, dann hat die Matrix den Rang 1.

3.9 Determinante

Die Determinante einer \((2\times 2)\)-Matrix gibt an, auf das Wie-viel-Fache eine Fläche sich durch eine lineare Transformation verändert. Wenn die Determinante 2 beträgt, dann verdoppelt sich eine Fläche durch die lineare Transformation. Ist die Determinante 0.5, dann halbiert sich die Fläche.

Als Beispiel betrachten wir die lineare Transformation \[ \mathbf{A}=\left[ \begin{array}{cc} 2 & -1\\ 1 & 1 \end{array} \right] \] Die folgende Abbildung zeigt, wie sich das Einheitsquadrat (das durch die beiden natürlichen Basisvektoren gebildet wird) vergrößert.

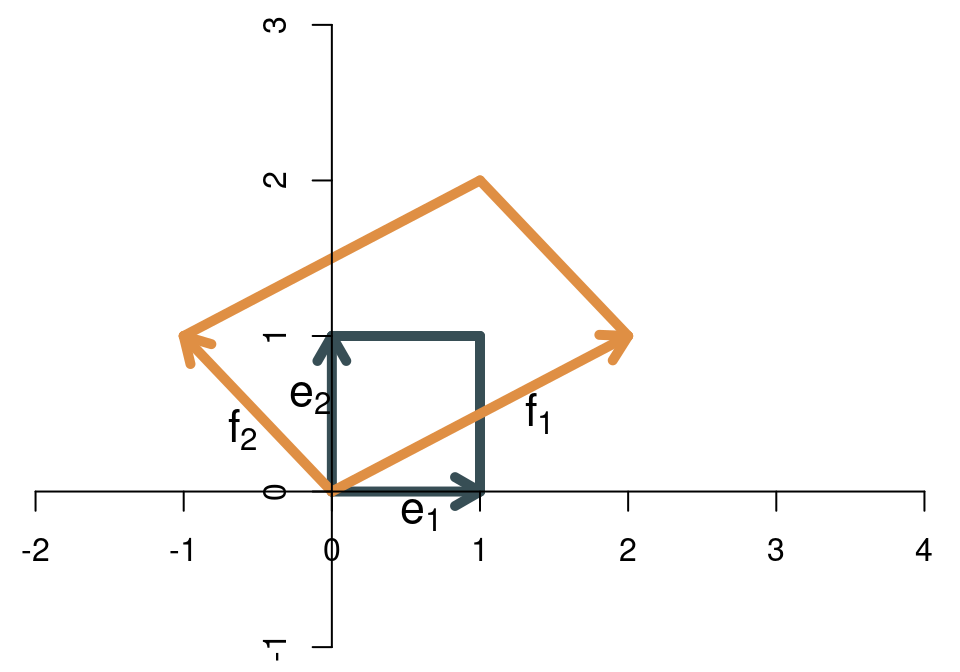
Die Fläche des Einheitsquadrats ist 1, die Fläche der Transformation (also des Parallelogramms) beträgt 3. Die Determinante der Matrix ist also \[ \det(\mathbf{A})=3. \] Ein Hinweis zur Notation: In der ökonometrischen Literatur wird die Determinante sehr häufig auch als \(|\mathbf{A}|\) geschrieben.

Die Determinante einer \((2\times 2)\)-Matrix kann allgemein wie folgt berechnet werden: \[ \det(\mathbf{A})=a_{11}a_{22}-a_{12}a_{22}. \] Für die Beispielmatrix erhält man \[ \det\left( \left[ \begin{array}{cc} 2 & -1\\ 1 & 1 \end{array} \right] \right)=2\cdot 1-(-1)\cdot 1=3. \] Wenn die Basisvektoren ihre relative Ausrichtung ändern - wenn also der erste Basisvektor nach der Transformation nicht mehr rechts, sondern links vom zweiten Basisvektor liegt, dann “klappt die Abbildung um” und die Determinante ist negativ. Als Beispiel sehen wir uns die folgende lineare Transformation an: \[ \mathbf{B}=\left[ \begin{array}{cc} -2 & -1\\ -1 & 1 \end{array} \right] \] Die beiden Basisvektoren vor und nach der Transformation zeigt die Abbildung:

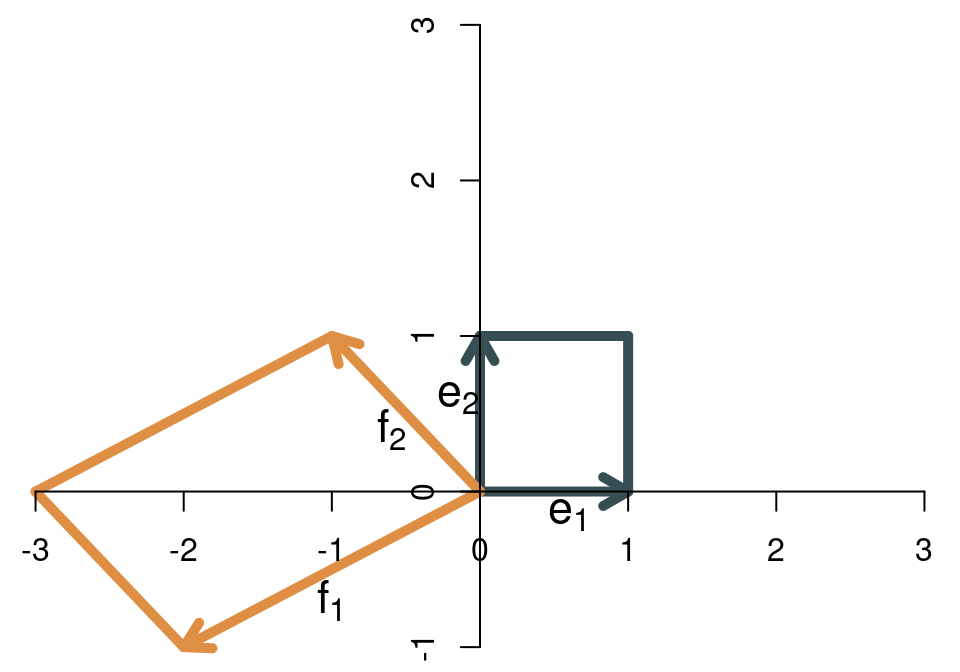
Die Determinante ist betragsmäßig genauso groß wie in dem vorherigen Beispiel. Da die Abbildung aber “umgeklappt” ist, ist jetzt negativ, nämlich \(\det(\mathbf{B})=-3\). Das ergibt sich auch durch die Formel \[ \det\left( \left[ \begin{array}{cc} -2 & -1\\ -1 & 1 \end{array} \right] \right)=-2\cdot 1-(-1)\cdot (-1)=-3. \] Kann es auch passieren, dass die Determinante den Wert Null annimmt? Ja, und zwar dann, wenn die Fläche der Abbildung auf Null schrumpft, weil die beiden Basisvektoren nach der Transformation linear abhängig sind. Sie zeigen dann in die gleiche (oder genau entgegengesetzte) Richtung, so dass die Abbildung kein Parallelogramm ergibt, sondern nur eine Gerade. Die Fläche einer Gerade ist 0, so dass die Determinante in diesem Fall 0 ist. Mit anderen Worten: An der Determinante kann man erkennen, ob die Matrix vollen Rang hat. Der Rang ist nicht voll, wenn die Determinante Null ist. Da der Rang einer Matrix mit der linearen Unabhängigkeit der Spaltenvektoren zusammenhängt, kann die Determinante auch zur Feststellung der linearen Unabhängigkeit von Vektoren dienen: Wenn die Determinante ungleich Null ist, dann sind die Vektoren linear unabhängig.

Im dreidimensionalen Raum hat die Determinante eine ähnliche geometrische Interpretation. Sie gibt für eine \((3\times 3)\)-Matrix an, auf das Wie-viel-Fache sich das Volumen eines Einheitswürfels durch die lineare Transformation vergrößert (oder verkleinert). Wenn die transformierten Basisvektoren alle in einer Ebene liegen (also einer durch eine Linearkombination der beiden anderen darstellbar ist), dann ist das Volumen Null. In diesem Fall nimmt auch die Determinante den Wert 0 an. Das gleiche gilt, wenn die transformierten Basisvektoren alle auf einer Geraden liegen. Die Determinante gibt also auch für \((3\times 3)\)-Matrizen an, ob sie vollen Rang haben oder nicht. Wenn die Determinante 0 ist, hat die Matrix keinen vollen Rang. Ob der Rang 2 oder 1 (oder 0) ist, kann man an der Determinante jedoch nicht erkennen.

Die analytische Formel für die Berechnung der Determinante ist bei (\(3\times 3)\)-Matrizen schon recht komplex, nämlich \[ \begin{align*} \det(\mathbf{A})&=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}\\ &\quad-a_{31}a_{22}a_{13}-a_{32}a_{23}a_{11}-a_{33}a_{21}a_{12}. \end{align*} \] Determinanten sind auch für noch höherdimensionale Räume definiert. Für eine quadratische \((n\times n)\)-Matrix (\(n>1\)) ist die Determinante rekursiv definiert. \[ \det(\mathbf{A})=\sum_{j=1}^n (-1)^{j+1}a_{1j}\det(\mathbf{A_{1j}}), \] wobei \(\mathbf{A}_{1j}\) die Matrix ist, die sich aus \(\mathbf{A}\) ergibt, wenn man die erste Zeile und die \(j\)-te Spalte herausstreicht. Ab Dimension \((4\times 4)\) ist es sehr aufwendig, Determinanten “per Hand” zu berechnen, nur für den zweidimensionalen (und teilweise den dreidimensionalen) Fall sind die Formeln noch einigermaßen übersichtlich.

Determinanten berechnet man natürlich normalerweise nicht “per Hand”. In R gibt es die Funktion det für die Berechnung von Determinanten. Für die \((2\times 2)\)-Matrix \[ \mathbf{A}=\left[ \begin{array}{cc} 1 & 3\\ 2 & 4 \end{array} \right] \] ergibt sich zum Beispiel

A <- matrix(1:4, 2, 2)
det(A)
#> [1] -2

Die Determinante der \((3\times 3)\)-Matrix \[ \mathbf{A}=\left[ \begin{array}{ccc} 1 & 4 & 7\\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{array} \right] \] ist

A <- matrix(1:9, 3, 3)
det(A)
#> [1] 0

Die drei Vektoren \((1,2,3)\), \((4,5,6)\) und \((7,8,9)\) sind folglich linear abhängig (wie wir ja weiter oben bereits gesehen haben) .

Allgemein gilt für \((n\times n)\)-Matrizen \[ \det(\mathbf{A})\neq 0 \qquad\Longleftrightarrow\qquad rg(\mathbf{A})=n. \] Reguläre Matrizen haben vollen Rang und eine Determinante ungleich 0, singuläre Matrizen haben keinen vollen Rang und eine Determinante von 0.

Es gibt noch weitere Rechenregeln für Determinanten, die manchmal hilfreich sind. Die Determinante der Transponierten entspricht der Determinante der Ausgangsmatrix, \[ \det(\mathbf{A}')=\det(\mathbf{A}). \]

Für die Determinante des Produkts zweier Matrizen gilt \[ \det(\mathbf{AB})=\det(\mathbf{A})\cdot\det(\mathbf{B}). \] Mit der geometrischen Interpretation ist dieser Zusammenhang klar: Wenn wir eine Fläche zuerst mit \(\mathbf{B}\) transformieren und anschließend mit \(\mathbf{A}\), so vervielfacht sich die Fläche im ersten Schritt um \(\det(\mathbf{B})\) und die so vergrößerte (oder verkleinerte) Fläche vervielfacht sich im zweiten Schritt um \(\det(\mathbf{A})\).

Ferner gilt für eine \((n\times n)\)-Matrix \[ \det(\lambda\mathbf{A})=\lambda^n\det(\mathbf{A}). \] Auch dieser Zusammenhang erschließt sich intuitiv mit der geometrischen Sichtweise. Wenn jede Spalte in \(\mathbf{A}\) mit \(\lambda\) multipliziert wird, bedeutet das, dass alle Basisvektoren um das \(\lambda\)-fache weiter gestreckt (oder gestaucht werden) als ohne die Skalarmultiplikation. Im zweidimensionalen Fall werden also beide Vektoren um das \(\lambda\)-fache verlängert (oder verkürzt), so dass die Fläche sich um \(\lambda^2\) verändert. Für jede weitere Dimension muss der Faktor mit einem weiteren \(\lambda\) multipliziert werden.

3.10 Inverse Matrix

Matrizen können als Repräsentation von linearen Transformationen aufgefasst werden. Wie in Kapitel 2 für den zweidimensionalen Fall gezeigt wurde, gibt eine Matrix \[ \mathbf{A}=\left[ \begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array} \right] \] an, dass der erste natürliche Basisvektor nach \((a_{11},a_{21})'\) transformiert wird, der zweite nach \((a_{12},a_{22})'\). Entsprechend wird jeder andere Punkt \((x_1,x_2)'\) nach \[ \mathbf{y}=\mathbf{Ax}= \left[ \begin{array}{c} a_{11}x_1+a_{12}x_2\\ a_{21}x_1+a_{22}x_2 \end{array} \right] \] bewegt. Kann man die lineare Transformation wieder rückgängig machen? Gibt es eine andere lineare Transformation, die dazu führt, dass der transformierte Punkt \(\mathbf{y}\) wieder an seinen Ursprungsort \(\mathbf{x}\) zurückkehrt? Die Antwort auf diese Frage lautet: Ja, aber nicht immer.

Eine Rücktransformation ist unter der Bedingung möglich, dass die Basisvektoren durch die lineare Transformation nicht linear abhängig werden. Mit anderen Worten, wenn die lineare Transformation dazu führt, dass die Basisvektoren linear abhängig sind, dann kann die Transformation nicht mehr rückgängig gemacht werden. Die Matrix \(\mathbf{A}\) muss also vollen Rang haben bzw. es muss sich um eine reguläre Matrix handeln.

Die Matrix, die die lineare Transformation \(\mathbf{A}\) rückgängig macht, nennt man inverse Matrix oder kurz Inverse (engl. inverse - mit der Betonung auf der zweiten Silbe) von \(\mathbf{A}\) und schreibt \(\mathbf{A}^{-1}\). Wenn also \[ \mathbf{y}=\mathbf{Ax}, \] dann gilt \[ \mathbf{x}=\mathbf{A}^{-1}\mathbf{y}. \] Da \(\mathbf{A}^{-1}\) den Effekt von \(\mathbf{A}\) aufhebt, gilt \[ \mathbf{A}^{-1}\mathbf{A}=\mathbf{I}, \] es ergibt sich also die Einheitsmatrix. Das gleiche gilt auch in die andere Richtung, d.h. \[ \mathbf{A}\mathbf{A}^{-1}=\mathbf{I}. \]

Beispiel:

Die Inverse der Matrix \[ \mathbf{A}=\left[ \begin{array}{cc} 2 & -1\\ 1 & 1 \end{array} \right] \] ist \[ \mathbf{A}^{-1}=\left[ \begin{array}{cc} \frac{1}{3} & \frac{1}{3}\\ -\frac{1}{3} & \frac{2}{3} \end{array} \right]. \] Wie man leicht nachprüfen kann, ergibt sowohl \(\mathbf{AA}^{-1}\) als auch \(\mathbf{A}^{-1}\mathbf{A}\) die Einheitsmatrix.

Die Inverse der Transponierten ist \[ (\mathbf{A}')^{-1}=(\mathbf{A}^{-1})'. \]

Beim Invertieren einer Matrixmultiplikation muss man aufpassen, weil das Matrixprodukt nicht kommutativ ist. Es gilt \[ (\mathbf{A}\mathbf{B})^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1}. \] Dass die Reihenfolge sich ändert, wird in der geometrischen Sichtweise klar: Die Transformation \(\mathbf{AB}\) bedeutet, dass zuerst \(\mathbf{B}\) angewendet wird und anschließend \(\mathbf{A}.\) Um die beiden Transformationen wieder rückgängig zu machen, muss nun zuerst \(\mathbf{A}\) durch \(\mathbf{A}^{-1}\) zurücktransformiert werden. Und anschließend wird der Effekt von \(\mathbf{B}\) durch \(\mathbf{B}^{-1}\) aufgehoben.

Die Determinante der Inversen ist \[ \det(\mathbf{A}^{-1})=\det(\mathbf{A})^{-1}=\frac{1}{\det(\mathbf{A})}. \] Dieser Zusammenhang ist leicht geoemtrisch interpretierbar. Die Determinante der Inversen gibt an, auf das Wie-viel-Fache sich eine Fläche durch die Transformation \(\mathbf{A}^{-1}\) verändert. Da \(\mathbf{A}^{-1}\) die Transformation \(\mathbf{A}\) gerade zurückgängig macht, muss die Fläche wieder auf ihre ursprüngliche Größe zurückgesetzt werden. Wenn sie also bei der Transformation mit \(\mathbf{A}\) auf das \(\det(\mathbf{A})\)-Fache angewachsen ist, dann muss sie bei der inversen Transformation um den Faktor \(1/\det(\mathbf{A})\) wachsen.

Die Inverse hat nicht nur die geometrische Interpretation, dass sie eine lineare Transformation rückgängig macht. Das wichtigste Einsatzfeld der Inversen besteht in den Wirtschaftswissenschaften und speziell in der Ökonometrie darin, bei der Lösung linearer Gleichungssysteme zu helfen. Darauf gehen wir in Kapitel 4 näher ein.

Wie findet man konkret die Inverse einer gegebenen Matrix? Man kann die Inverse entweder per Hand oder mit R (bzw. anderen Computerprogrammen) finden. Der Weg per Hand ist natürlich mühsamer, aber dennoch sollte man ihn kennen, weil in einigen Situationen R als Werkzeug nicht zur Verfügung steht, z.B. weil einige (oder alle) Matrixelemente nicht mit ihren konkreten numerischen Werten gegeben sind, sondern nur als Symbole. Wir sehen uns zuerst an, wie man die Inverse in R berechnet.

Leider hat die R-Funktion für die Berechnung der Inversen einen nicht gerade intuitiven Namen. Sie lautet solve.

Beispiel:

Die Inverse von

A <- matrix(c(2,1,-1,1), 2, 2)
A
#>      [,1] [,2]
#> [1,]    2   -1
#> [2,]    1    1

ist die Matrix

invA <- solve(A)
invA
#>            [,1]      [,2]
#> [1,]  0.3333333 0.3333333
#> [2,] -0.3333333 0.6666667

Zur Kontrolle berechnen wir die beiden Matrixprodukte

A %*% invA
#>              [,1] [,2]
#> [1,] 1.000000e+00    0
#> [2,] 5.551115e-17    1

und

invA %*% A
#>      [,1]          [,2]
#> [1,]    1 -5.551115e-17
#> [2,]    0  1.000000e+00

Als Ergebnis erhält man in beiden Fällen die Einheitsmatrix. Die kleinen Abweichungen sind wieder darauf zurückzuführen, dass reelle Zahlen in R (oder anderen Computerprogrammen) nicht immer exakt repräsentiert werden können. Es kommt dann zu Rundungsfehlern, die jedoch meist nicht ins Gewicht fallen. Die Möglichkeit von Rundungsfehlern sollte man bei der Arbeit mit numerischen Verfahren immer im Hinterkopf behalten. Eine naive Kontrolle, ob invA wirklich die Inverse von A ist, führt nämlich zum falschen Ergebnis:

all(A %*% invA == diag(2))
#> [1] FALSE

Runden auf 12 Stellen hilft.

all(round(A %*% invA, 12) == diag(2))
#> [1] TRUE

Achtung: Die Schreibweise A^(-1) ist in R möglich, es gibt keine Fehlermeldung. Das Ergebnis von A^(-1) ist aber nicht die inverse Matrix von A. Stattdessen werden von allen Elementen der Matrix die Kehrwerte berechnet. In R ergibt also

A^(-1) %*% A
#>      [,1] [,2]
#> [1,]    0 -1.5
#> [2,]    3  0.0

nicht die Einheitsmatrix! Das ist ein gefährlicher Fehler, weil er nicht zu einer Fehlermeldung führt.

Für die Berechnung per Hand ist eine Variante des Gauß-Jordan-Verfahrens gut geeignet (vgl. Abschnitt 1.7.3). An einem Beispiel lässt sich das am besten veranschaulichen. Wir suchen die Inverse der \((3\times 3)\)-Matrix \[ \mathbf{A}=\left[ \begin{array}{ccc} 2 & -1 & 3\\ 4 & 3 & 0\\ 1 & -2 &3 \end{array} \right]. \] Zunächst ergänzt man die Matrixelemente auf der rechten Seite um die Einheitsmatrix (abgetrennt mit einem senkrechten Strich). Die Zeilen numerieren wir mit römischen Ziffern. \[ \begin{array}{ccc|cccl} 2 & -1 & 3&1&0&0&\quad (I)\\ 4 & 3 & 0&0&1&0&\quad (II)\\ 1 & -2 &3&0&0&1&\quad (III) \end{array} \] Nun werden die drei Zeilen mit den üblichen erlaubten Umformungen Schritt für Schritt so verändert, dass auf der linken Seite die Einheitsmatrix entsteht. Die Elemente rechts vom Strich werden dabei mit verändert. Zuerst wird das Element unten links auf 0 gesetzt, dazu rechnen wir \((II)-4(III)\) und erhalten: \[ \begin{array}{ccc|cccl} 2 & -1 & 3&1&0&0&\quad (I)\\ 4 & 3 & 0 & 0 & 1 & 0 &\quad (II)\\ 0 & 11 &-12 & 0 & 1 & -4&\quad (III) \end{array} \] Als nächstes eleminieren wir die 4 in der ersten Spalte, indem wir \((II)\) durch \(2(I)-(II)\) ersetzen: \[ \begin{array}{ccc|cccl} 2 & -1 & 3 & 1 & 0 & 0 &\quad (I)\\ 0 & -5 & 6 & 2 & -1 & 0 &\quad (II)\\ 0 & 11 &-12 & 0 & 1 & -4&\quad (III) \end{array} \] Nun ersetzt man die 11 in der unteren Zeile, anschließend die 3 in der ersten Zeile usw., bis die Seite links vom senkrechten Strich eine Diagonalmatrix ist. Dann wird die Diagonalmatrix durch geeignete Multiplikationen der drei Zeilen zur Einheitsmatrix umgeformt. Wenn links vom Strich die Einheitsmatrix steht, dann hat man rechts vom Strich die Inverse. Wir lassen die einzelnen weiteren Schritte hier aus Platzgründen aus. Am Ende erhält man \[ \begin{array}{ccc|cccl} 1 & 0 & 0 & -3 & 1 & 3 &\quad (I)\\ 0 & 1 & 0 & 4 & -1 & -4 &\quad (II)\\ 0 & 0 & 1 & \frac{11}{3} & -1 & -\frac{10}{3}&\quad (III) \end{array} \] Die Inverse von \[ \mathbf{A}=\left[ \begin{array}{ccc} 2 & -1 & 3\\ 4 & 3 & 0\\ 1 & -2 &3 \end{array} \right] \] ist also \[ \mathbf{A}^{-1}=\left[ \begin{array}{ccc} -3 & 1 & 3\\ 4 & -1 & -4 \\ \frac{11}{3} & -1 & -\frac{10}{3} \end{array} \right]. \] Was geschieht, wenn die Matrix \(\mathbf{A}\) singulär ist und es keine Inverse gibt? Das Gauß-Jordan-Verfahren kann bei singulären Matrizen eingesetzt werden, man muss also nicht wissen, ob die Matrix, deren Inverse man sucht, überhaupt invertierbar ist. Bei den Umformungen einer singulären Matrix tritt an irgendeiner Stelle die Situation auf, dass alle Elemente einer Zeile gleich Null sind. Damit lässt sich die Matrix links vom Strich nicht in die Einheitsmatrix überführen.

Beispiel:

Wir versuchen, die singuläre Matrix \[ \left[ \begin{array}{ccc} 2 & -1 & 3\\ 4 & 3 & 0\\ 6 & 2 & 3 \end{array} \right] \] mit dem Gauß-Jordan-Verfahren zu invertieren. \[ \begin{array}{ccc|cccl} 2 & -1 & 3 & 1 & 0 & 0 &\quad (I)\\ 4 & 3 & 0 & 0 & 1 & 0 &\quad (II)\\ 6 & 2 & 3 & 0 & 0 & 1 &\quad(III) \end{array} \] Der erste Schritt soll auf eine 0 in der unteren linken Ecke führen. Dazu rechnen wir (z.B.) 3(I)-(III) und erhalten \[ \begin{array}{ccc|cccl} 2 & -1 & 3 & 1 & 0 & 0 &\quad (I)\\ 4 & 3 & 0 & 0 & 1 & 0 &\quad (II)\\ 0 & -5 & 6 & 3 & 0 & -1 &\quad(III) \end{array} \] Der nächste Schritt ersetzt die 4 in der zweiten Zeile durch eine 0, dazu rechnen wir 2(I)-(II): \[ \begin{array}{ccc|cccl} 2 & -1 & 3 & 1 & 0 & 0 &\quad (I)\\ 0 & -5 & 6 & 2 & -1 & 0 &\quad (II)\\ 0 & -5 & 6 & 3 & 0 & -1 &\quad(III) \end{array} \] Subtrahiert man nun die dritte von der zweiten Zeile und schreibt die Differenz in die letzte Zeile, dann bestehen alle Elemente der letzten Zeile (links vom Strich) aus Nullen. Das zeigt, dass die Matrix singulär ist. Man kann also das Verfahren abbrechen, denn es gibt keine Inverse.

3.11 Spezielle Matrizen

3.11.1 Einsen-Matrix

Eine \((m\times n)\)-Matrix, die nur aus Einsen besteht, schreibt man meist als \(\mathbf{1}_{mn}\) oder \(\mathbf{J}_{mn}.\) Die Indizes entfallen, wenn die Dimensionen klar sind. Nützlich sind vor allem Zeilen- oder Spaltenvektoren aus Einsen. Mit ihnen kann man leicht die Zeilen- oder Spaltensummen von Matrizen ermitteln.

Beispiel: Sei
\[ \mathbf{A}=\left[ \begin{array}{ccc} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{array} \right]. \] Mit \(\mathbf{\iota}_3=\mathbf{J}_{3,1}\) bezeichnen man häufig den Spaltenvektor aus drei Einsen. Der Zeilenvektor aus drei Einsen ist dann \(\mathbf{\iota}_3'\), also der transponierte Spaltenvektor.

A <- matrix(1:9, 3, 3)
iota <- matrix(1, 3, 1)

Dann ist

t(iota) %*% A
#>      [,1] [,2] [,3]
#> [1,]    6   15   24

der Zeilenvektor der Spaltensummen und

A %*% iota
#>      [,1]
#> [1,]   12
#> [2,]   15
#> [3,]   18

der Spaltenvektor der Zeilensummen.

Manchmal begegnet man in ökonometrischen Texten dem Ausdruck \(\mathbf{\iota}_n'\mathbf{\iota}_n\). Dieser Ausdruck entspricht schlicht und einfach dem Skalar \(n\), denn \[ \left[ \begin{array}{cccc} 1 & 1 & \ldots & 1 \end{array} \right] \left[ \begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array} \right]= 1\cdot 1+1\cdot 1+\ldots+1\cdot 1=n. \]

In R ist es sehr einfach, Einsenmatrizen zu erzeugen, z.B.

J <- matrix(1, nrow=2, ncol=4)
J
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    1    1    1
#> [2,]    1    1    1    1

3.11.2 Nullen-Matrix

Eine \((m\times n)\)-Matrix aus Nullen schreibt man meist als \(\mathbf{0}_{mn}\). Wenn die Dimension sich klar aus dem Kontext ergibt, kann der Subindex entfallen. Addiert man eine Nullenmatrix zu einer beliebigen Matrix \(\mathbf{A}\) passender Dimensionen, so erhält man wieder \(\mathbf{A}\). In R werden Nullenmatrizen auf die gleiche Weise wie Einsenmatrizen generiert.

3.11.3 Permutationsmatrizen

Ordnet man die Spalten (oder Zeilen) einer Einheitsmatrix in einer anderen Reihenfolge an, dann erhält man eine Permutationsmatrix. Permutationsmatrizen heißen so, weil sie die Elemente eines Vektors permutieren (d.h. in eine andere Reihenfolge bringen). Das folgende Beispiel zeigt das für eine \((4\times 4)\)-Matrix. \[ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{array} \right] \left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ x_4 \end{array} \right]= \left[ \begin{array}{c} x_3\\ x_4\\ x_1\\ x_2 \end{array} \right]. \]

3.11.4 Diagonalmatrizen

Eine Matrix, bei der alle Nichtdiagonalelemente Null sind, nennt man Diagonalmatrix. Beispielsweise sind Einheitsmatrizen Diagonalmatrizen. Die Funktion diag, die wir schon zum Erzeugen von Einheitsmatrizen kennen gelernt haben, dient auch zum Erzeugen von allgemeinen Diagonalmatrizen. Wenn das Argument ein Vektor der Länge \(n\) ist, dann erhält man eine \((n\times n)\)-Diagonalmatrix mit den Vektorelementen auf der Diagonale.

Beispiel:

v <- c(1,3,5,7,9)
diag(v)
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    0    0    0    0
#> [2,]    0    3    0    0    0
#> [3,]    0    0    5    0    0
#> [4,]    0    0    0    7    0
#> [5,]    0    0    0    0    9

3.11.5 Dreiecksmatrizen

In einer oberen Dreiecksmatrix sind alle Elemente unterhalb der Diagonale Null. In einer unteren Dreiecksmatrix sind die Elemente über der Diagonalen Null. Bei Dreiecksmatrizen ist die Determinante das Produkt aller Diagonalelemente. Wenn \(\mathbf{A}\) eine (\(n\times n\))-Dreiecksmatrix ist, dann gilt also \[ \det(\mathbf{A})=\prod_{i=1}^n a_{ii}. \] Da Diagonalmatrizen ein Spezialfall von Dreiecksmatrizen sind, gilt das natürlich auch für Diagonalmatrizen.

Beispiel:

A <- diag(c(1,3,5,7))
det(A)
#> [1] 105

3.11.6 Orthogonale Matrizen

Eine \((n\times n)\)-Matrix \(\mathbf{A}\) heißt orthogonal, wenn \[ \mathbf{A}'\mathbf{A}=\mathbf{A}\mathbf{A}'=\mathbf{I}. \] Bei einer orthogonalen Matrix ist also die Transponierte die Inverse.

Wählt man zwei beliebige unterschiedliche Spalten (oder Zeilen) einer orthogonalen Matrizen, dann ist deren inneres Produkt 0, d.h. sie sind rechtwinklig (orthogonal) zueinander. Das innere Produkt einer Spalte mit sich selber ist 1. Die Spalten haben also die Norm 1. Die \((2\times 2)\)-Rotationsmatrizen, die wir in Abschnitt 2.1 kennen gelernt haben, sind ein Beispiel für orthogonale Matrizen. Lineare Transformationen mit einer orthogonalen Matrix verändern folglich weder die Winkel noch führen sie zu einer Streckung oder Stauchung.

Bei der numerischen Überprüfung auf Orthogonalität müssen mögliche Rundungsfehler berücksichtigt werden.

Beispiel:

Die 35-Grad-Rotationsmatrix

M <- matrix(c(cos((35/180)*pi),sin((35/180)*pi),-sin((35/180)*pi),cos((35/180)*pi)),2,2)

ist orthogonal. Wenn man jedoch mit der all-Funktion nachprüft, ob \(\mathbf{M}'\mathbf{M}=\mathbf{I}\) ist, dann erhält man das falsche Ergebnis:

all(t(M) %*% M == diag(2))
#> [1] FALSE

Das liegt an Rundungsfehlern. Das Tükische ist, dass R dennoch die Einheitsmatrix ausgibt, wenn man die zugehörige Transponierte von links an die 35-Grad-Rotationsmatrix multipliziert.

t(M) %*% M
#>               [,1]          [,2]
#> [1,]  1.000000e+00 -4.032299e-19
#> [2,] -4.032299e-19  1.000000e+00

Das liegt daran, dass R standardmäßig nur 6 Nachkommastellen ausgibt. Erst wenn man die Anzahl der auszugebenden Nachkommastellen auf (z.B) 16 Stellen erhöht, sieht man die Rundungsfehler.

options(digits=16)
t(M) %*% M
#>                        [,1]                   [,2]
#> [1,]  9.999999999999999e-01 -4.032298572641752e-19
#> [2,] -4.032298572641752e-19  9.999999999999999e-01

Die Rundungsfehler sind zwar extrem klein, aber die Ergebnismatrix ist offenbar nicht exakt gleich der Einheitsmatrix. Durch Runden auf (z.B.) 12 Stellen nach dem Komma ergibt sich aber das richtige Ergebnis,

all(round(t(M) %*% M, 12) == diag(2))
#> [1] TRUE

3.11.7 Idempotente Matrizen

Wenn für eine quadratische \((n\times n)\)-Matrix \(\mathbf{A}\) gilt \[ \mathbf{A}=\mathbf{AA}, \] dann heißt \(\mathbf{A}\) idempotent. Da die Determinante eines Matrixprodukt dem Produkt der beiden Determinanten entsprechen muss, können die Determinanten von idempotenten Matrizen nur 0 oder 1 sein.

3.12 Spur

Als Spur (engl. trace) einer quadratischen Matrix bezeichnet man die Summe ihrer Diagonalelemente, \[ tr(\mathbf{A})=\sum_{i=1}^n a_{ii}. \] Für die Spur gelten folgende Zusammenhänge. \[ \begin{align*} tr(\mathbf{A}+\mathbf{B})&=tr(\mathbf{A})+tr(\mathbf{B})\\ tr(\lambda \mathbf{A})&=\lambda tr(\mathbf{A})\\ tr(\mathbf{A}')&=tr(\mathbf{A}). \end{align*} \] Eine sehr nützliche Regel gilt für das Matrixprodukt. Sei \(\mathbf{A}\) eine \((n\times k)\)-Matrix und \(\mathbf{B}\) eine \((k\times n)\)-Matrix, dann gilt \[ tr(\mathbf{AB})=tr(\mathbf{BA}). \] Die Matrizen \(\mathbf{AB}\) und \(\mathbf{BA}\) sind beide quadratisch, aber sie haben unterschiedliche Dimensionen. Die Matrix \(\mathbf{AB}\) ist eine \((n\times n)\)-Matrix, dagegen ist \(\mathbf{BA}\) eine \((k\times k)\)-Matrix. Diese beiden Matrizen haben die gleiche Spur.

In R gibt es standardmäßig keine Funktion zur Berechnung der Spur. Das Paket pracma bietet jedoch die Funktion Trace, die die Summe aller Diagonalelemente für quadratische Matrizen ausgibt:

library(pracma)
A <- matrix(1:9,3,3)
A
#>      [,1] [,2] [,3]
#> [1,]    1    4    7
#> [2,]    2    5    8
#> [3,]    3    6    9

Die Spur der Matrix beträgt

Trace(A)
#> [1] 15

3.13 Partitionierte Matrizen

In der Ökonometrie gibt es Situationen, in denen Matrizen in einzelne Blöcke unterteilt werden. Man spricht dann von partitionierten Matrizen. Das sieht z.B. so aus: \[ \mathbf{A}=\left[ \begin{array}{cc} \mathbf{A}_{11} & \mathbf{A}_{12}\\ \mathbf{A}_{21} & \mathbf{A}_{22} \end{array} \right] \] Die Blöcke müssen geeignete Dimensionen haben. Zum Beispiel könnte \(\mathbf{A}_{11}\) eine \((m_1\times n_1)\)-Matrix sein, \(\mathbf{A}_{12}\) eine \((m_1\times n_2)\)-Matrix, \(\mathbf{A}_{21}\) eine \((m_2\times n_1)\)-Matrix und \(\mathbf{A}_{22}\) eine \((m_2\times n_2)\)-Matrix. Dann ist \(\mathbf{A}\) von den Dimensionen \(((m_1+m_2)\times (n_1+n_2))\).

Partitionierte Matrizen bieten eine elegante Möglichkeit, komplexe Daten strukturiert zu bearbeiten.

Für viele Matrixoperationen können die Blöcke so ähnlich behandelt werden wie normale Matrixelemente. Beispielsweise gilt für die Transponierte \[ \mathbf{A}'=\left[ \begin{array}{cc} \mathbf{A}_{11}' & \mathbf{A}_{21}'\\ \mathbf{A}_{12}' & \mathbf{A}_{22}' \end{array} \right]. \] Und für die Summe von geeignet partitionierten Matrizen gilt \[ \mathbf{A}+\mathbf{B}=\left[ \begin{array}{cc} \mathbf{A}_{11}+\mathbf{B}_{11} & \mathbf{A}_{12}+\mathbf{B}_{12}\\ \mathbf{A}_{21}+\mathbf{B}_{21} & \mathbf{A}_{22}+\mathbf{B}_{22} \end{array} \right]. \] Wenn die Dimensionen der Blöcke alle zueinander passen, gilt für die Matrizenmultiplikation \[ \mathbf{AB}=\left[ \begin{array}{cc} \mathbf{A}_{11}\mathbf{B}_{11}+\mathbf{A}_{12}\mathbf{B}_{21} & \mathbf{A}_{11}\mathbf{B}_{12}+\mathbf{A}_{12}\mathbf{B}_{22}\\ \mathbf{A}_{21}\mathbf{B}_{11}+\mathbf{A}_{22}\mathbf{B}_{21} & \mathbf{A}_{21}\mathbf{B}_{12}+\mathbf{A}_{22}\mathbf{B}_{22} \end{array} \right]. \] Wenn in einer partitionierten Matrix \(\mathbf{A}\) alle Blöcke außer den Diagonalblöcken Nullmatrizen sind, und wenn die Diagonalblöcke außerdem invertierbar sind, dann gilt \[ \mathbf{A}^{-1}=\left[ \begin{array}{cc} \mathbf{A}_{11}^{-1} & \mathbf{0}\\ \mathbf{0} & \mathbf{A}_{22}^{-1} \end{array} \right]. \]

3.14 Tensoren

In der Machine-Learning-Literatur spielen Vektoren und Matrizen eine extrem wichtige Rolle. Im Bereich des Machine-Learnings wird jedoch meistens eine bequeme Verallgemeinerung von Matrizen, Vektoren und Skalaren benutzt, nämlich Tensoren. Ein Tensor der Dimension 0 (auch 0-Tensor oder 0D-Tensor) ist ein Skalar. Ein 1-Tensor oder 1D-Tensor ist ein Vektor. Ein 2-Tensor oder 2D-Tensor ist eine Matrix. Man kann Tensoren nun für noch höhere Dimensionen definieren. Bei einem 3D-Tensor sind die Daten nicht nur in Form eines Rechtecks angeordnet (wie bei einer Matrix), sondern man hat noch eine weitere Dimension. Die Daten liegen quasi in Würfelform vor, die das folgende Bild skizziert, in dem die Daten eines 3D-Tensors der Dimensionen \((5\times 4\times 3)\) gezeigt werden (Sie können das Bild mit der Maus bewegen):

Hier liegen quasi drei Matrizen geschichtet hintereinander. Die ersten beiden Indizes geben die Position innerhalb der Matrizen an, der dritte Index gibt an, um welche Schicht es sich handelt.

Tensoren können analog auch für noch höhere Dimensionen definiert werden, sind dann aber nicht mehr anschaulich darstellbar. Für Tensoren lässt sich die Matrixmultiplikation verallgemeinern, aber darauf gehen wir in diesem Kurs nicht ein.

Noch ein Hinweis zum Begriff “Dimension”: Eine Matrix ist ein 2D-Tensor, weil sie aus Zeilen und Spalten besteht. Sind die Daten in Würfelform angeordnet, handelt es sich um einen 3D-Tensor mit Zeilen, Spalten und Schichten. Der Begriff “Dimension” bezeichnet also die Struktur eines Tensors. In diesem Kurs verwenden wir den Begriff “Dimension” jedoch, um die Länge eines Vektors oder die Zeilen- und Spaltenzahl einer Matrix zu bezeichnen.