Chapter 12 Module XI
12.1 Tests for contingency tables.
El siguiente paso es realizar ahora la prueba de hipótesis conjunta para todas las proporciones;
\(H_o: p_i=p_2=p_3 = 1/3\)
\(H_a: p_i \neq 1/3\)
(Recuerda que siempre se deben plantear bien y en el formato adecuado las pruebas de hipótesis pues ya estás en un campo de matemáticas y la formalidad es vital para dar a entender el problema a resolver)
Es decir, es la probabilidad de que las 3 proporciones sean un tercio. A esto se le conoce como una prueba de hipótesis conjunta pues está evaluando las 3 condiciones al mismo tiempo.
(observed<-tally (~ganador, data=elecciones))## ganador
## MORENA PAN PRI
## 323 324 353p<-c(1/3,1/3,1/3)
chisq.test(observed,p=p)##
## Chi-squared test for given probabilities
##
## data: observed
## X-squared = 2, df = 2, p-value = 0.4Al ser una prueba conjunta, en general los valores p no son tan puqueños como en una prueba de hipótesis sola.
De ser cierta la hipótesis podemos calcular la expectativa de frecuecnia simplemente al multiplicar \(n \cdot p\).
(total_n<-sum(observed))## [1] 1000(expectativa<-total_n*p)## [1] 333 333 333Solo para asegurarnos, manualmente realizamos la prueba de hipótesis conjunta:
(chisq<-sum((observed - expectativa)^2/(expectativa)))## [1] 1.741 - pchisq(chisq, df=2)## [1] 0.419Y aprovechamos las funciones de mosaic para entender un poco que está pasando detrás.
plotDist("chisq", df=2, groups = x > 1.9, type="h")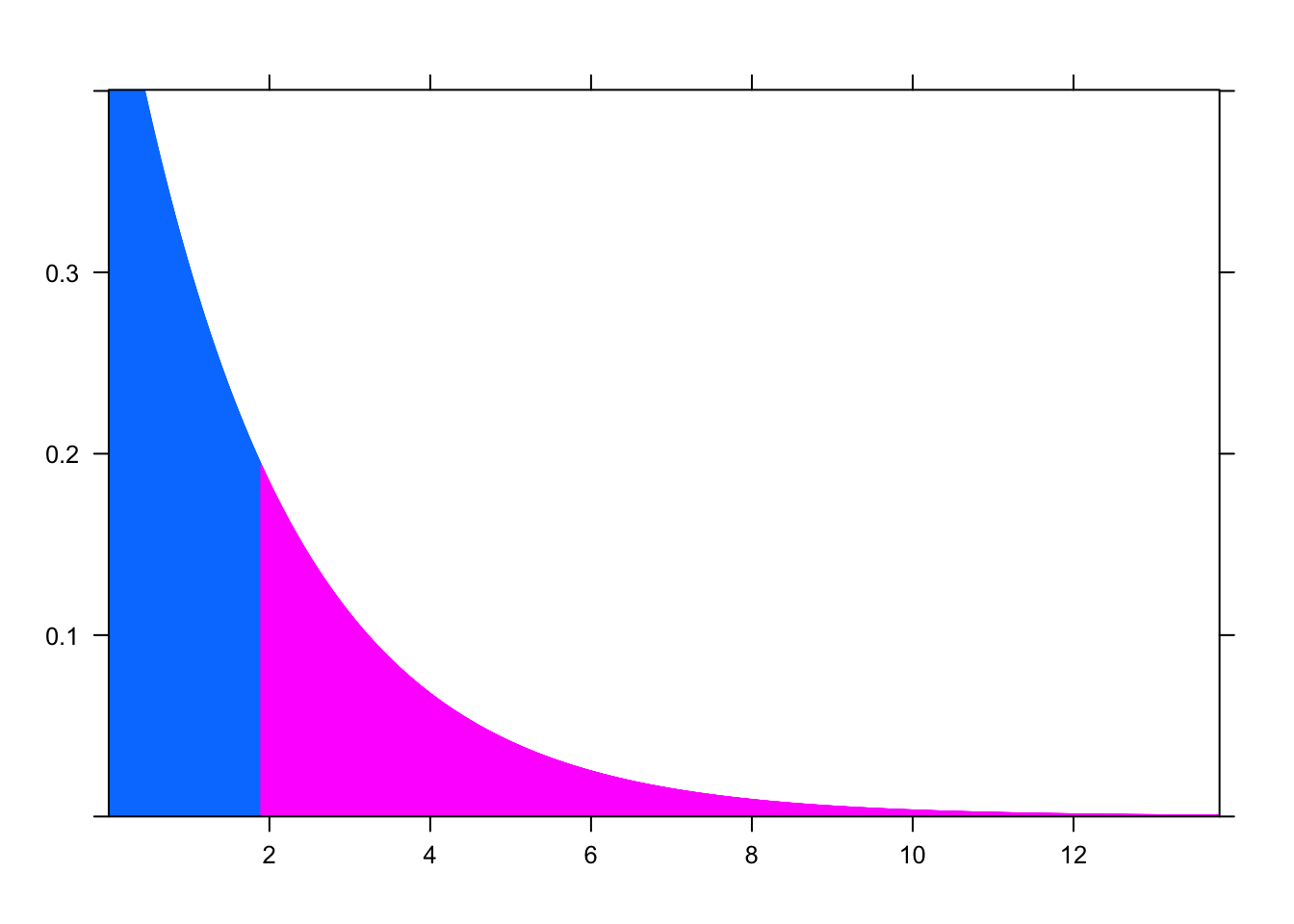
Aquí paradójicamente podemos ver que la probabilidad de que las 3 proporciones sean iguales es poca, a pesar de que sabemos por construcción de los datos que si es verdad.
(chisq<-sum((observed - expectativa)^2/(expectativa)))## [1] 1.741 - pchisq(chisq, df=2)## [1] 0.419xchisq.test(observed, p=p)##
## Chi-squared test for given probabilities
##
## data: x
## X-squared = 2, df = 2, p-value = 0.4
##
## 323 324 353
## (333.33) (333.33) (333.33)
## [0.32] [0.26] [1.16]
## <-0.57> <-0.51> < 1.08>
##
## key:
## observed
## (expected)
## [contribution to X-squared]
## <Pearson residual>12.2 two or more variables
Para este apartado simularemos una base de datos con base en una distribución normal.
#simulamos datos de estatura de hombres y mujeres (normal con diferente media y desviacion)
men <- rnorm(500,165,15)
women <- rnorm(500,155,10)
norm<-c(men,women)
#simulamos la prevalencia de personas albinas
albino <- rpois(1000,1/100)
sex<-c("H","M")
r_sex<-rep(sex,each=500)
#creamos el dataframe
estaturas<-data.frame(r_sex,norm,albino)
colnames(estaturas)<-c("sexo","estatura","albino")Y ahora realizamos algunas pruebas con los comandos de mosaic.
El comando median tautológicamente nos da la mediana. (Ojo que es diferente al promedio)
median(estatura ~ sexo|albino , data=estaturas)## H.0 M.0 H.1 M.1 0 1
## 165 154 164 138 159 159bwplot nos imprime una gráfica de caja. Imaginate que es un histograma visto desde arriba, nos muestra la distribución de cada variable. En este caso la distribución del sexo condicional a la estatura. La caja comienza con el percentil 25 y termina con el 75. El punto nos muestra la mediana (es decir el centro de la distribución). Los brazos en teoría nos representan el mínimo y el máximo, sin embargo en este caso de bwplot nos muestra una simplimificación del mínimo y máximo sin outliers. Haz click aquí para ver que es lo que representan realmente los brazos en bwplot.
bwplot(estatura ~ sexo, data=estaturas)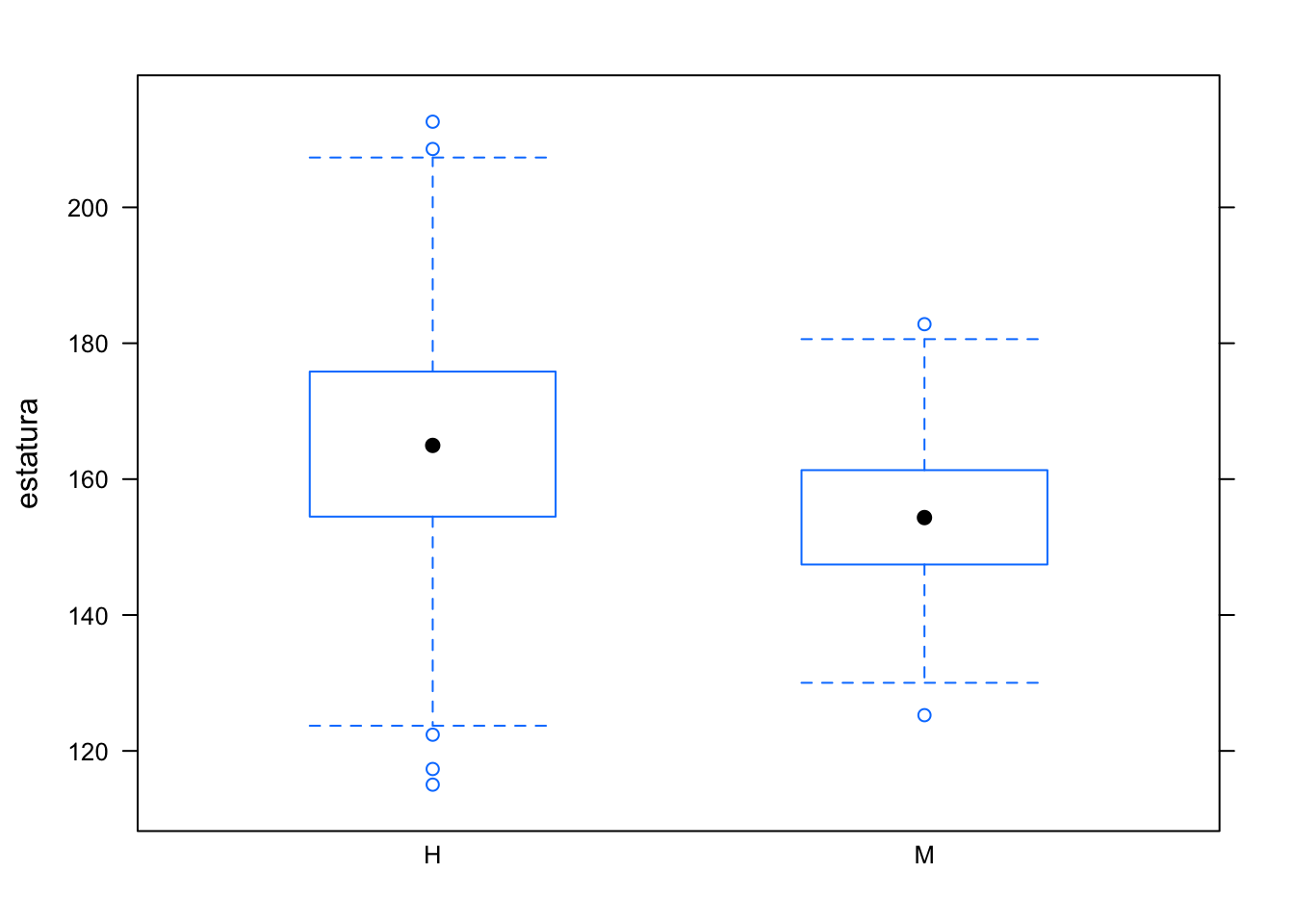
Si usamos el comando summary pero con dos variables usando el signo + obtenemos estadísticas descriptivas de cada variable. Por el contrario si usamos * ahora obtenemos las estadísticas descriptivas de la interacción (las variables por si solas más la combinación)
summary(aov(estatura ~ sexo +albino, data=estaturas))## Df Sum Sq Mean Sq F value Pr(>F)
## sexo 1 26466 26466 162.27 <0.0000000000000002 ***
## albino 1 412 412 2.53 0.11
## Residuals 997 162608 163
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summary(aov(estatura ~ sexo*albino , data=estaturas))## Df Sum Sq Mean Sq F value Pr(>F)
## sexo 1 26466 26466 162.82 <0.0000000000000002 ***
## albino 1 412 412 2.53 0.112
## sexo:albino 1 703 703 4.33 0.038 *
## Residuals 996 161905 163
## ---
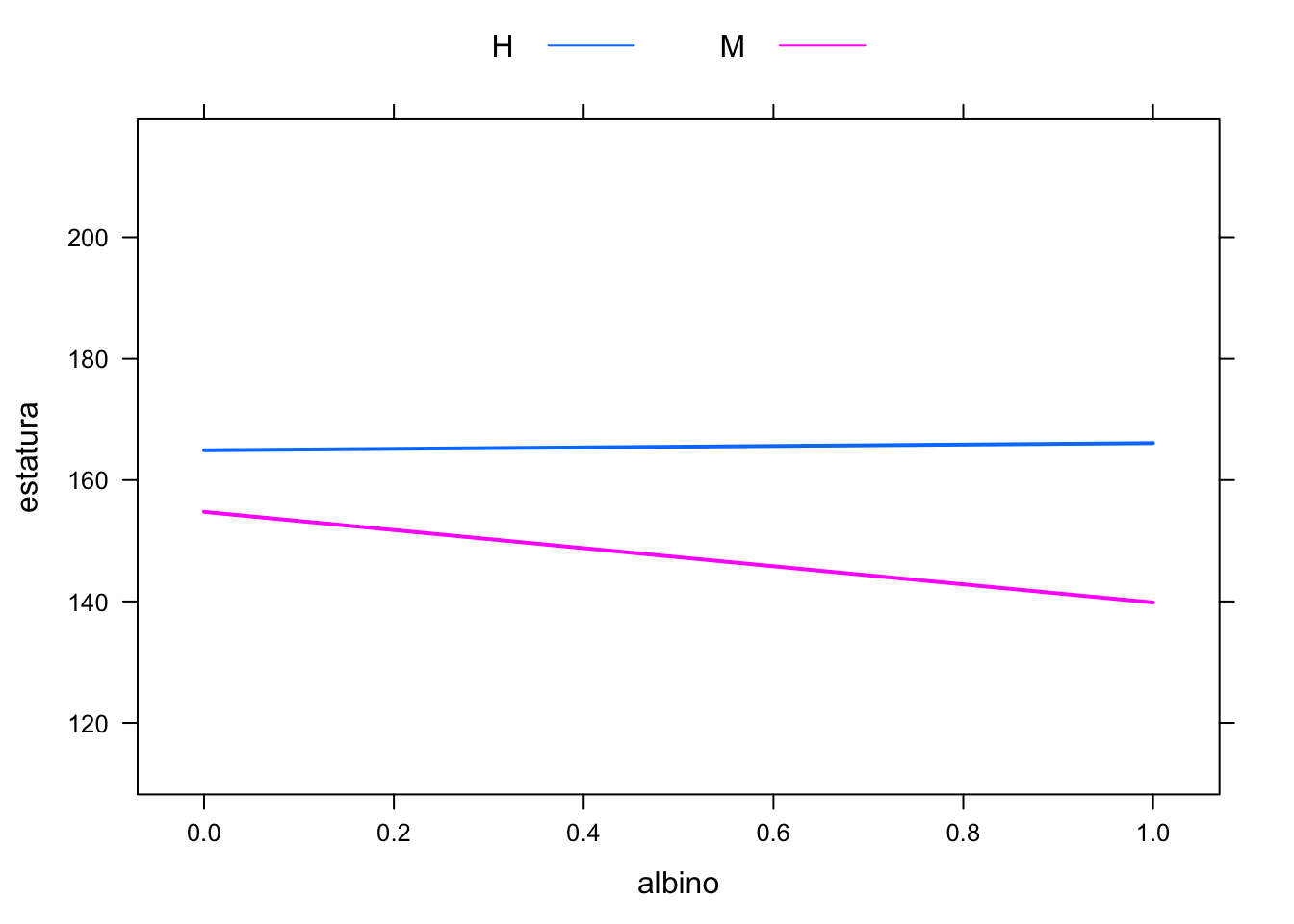
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Finalmente podemos obtener una gráfica xy. Lo que hacen está grafica es que representan el modelo lineal de cada combinación de variables. En este caso, la relación entre estatura y la probabilidad de ser albino. Evidentemente sabemos que la relación es espuria (pues desde el diseño de la base indicamos que el ser albino es completamente aleatorio) pero aún así es interesande ver los estadísticos y gráficas de resultado.
xyplot(estatura ~ albino, groups=sexo, lwd=2,
auto.key=list(columns=2, lines=TRUE, points=FALSE),
type='a', data=estaturas)