Chapter 3 Module III

3.0.1 Datos numéricos

El manejar datos numéricos en R es muy sencillo e intuitivo pues podemos conocer inmediatamente su distribución, media, mediana, rango intercuantílico y basicamente cualquier estadístico que necesitemos.

# Antes realizamos algunas preparaciones frecuentes: por ejemplo indicar que no queremos notiación científica e indicar que no queremos 
options(scipen = 999, digits = 3)

# Ahora si, cargamos una base de datos ya precargada de R
# La base mtcars brinda información sobre el desempeño de diferentes modelos de coches.

datos<-as.data.frame(mtcars)
head(datos)

##                    mpg cyl disp  hp drat   wt qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.62 16.5  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.46 20.2  1  0    3    1

3.0.2 Estadísticos con R base

mean(datos$mpg)

## [1] 20.1

sd(datos$mpg)

## [1] 6.03

var(datos$mpg)

## [1] 36.3

median(datos$mpg)

## [1] 19.2

quantile(datos$mpg)

##   0%  25%  50%  75% 100% 
## 10.4 15.4 19.2 22.8 33.9

hist(datos$mpg)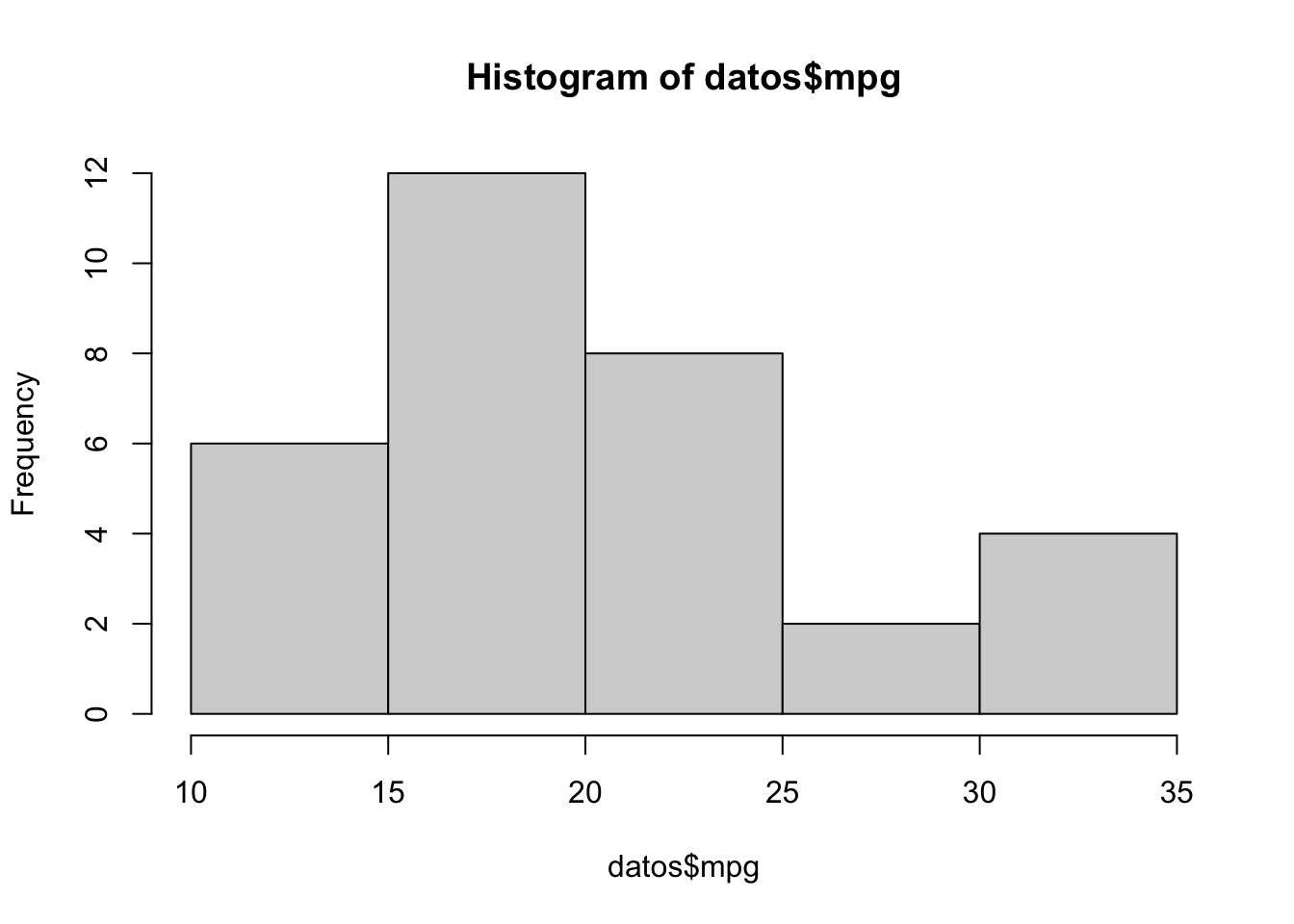

summary(datos$mpg)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    10.4    15.4    19.2    20.1    22.8    33.9

3.0.3 Estadísticos con rl paquete Mosaic

library(mosaic)
mean(~hp, data=datos)

## [1] 147

sd(~hp, data=datos)

## [1] 68.6

var(~hp, data=datos)

## [1] 4701

median(~hp, data=datos)

## [1] 123

quantile(~hp, data=datos)

##    0%   25%   50%   75%  100% 
##  52.0  96.5 123.0 180.0 335.0

histogram(~hp, data=datos)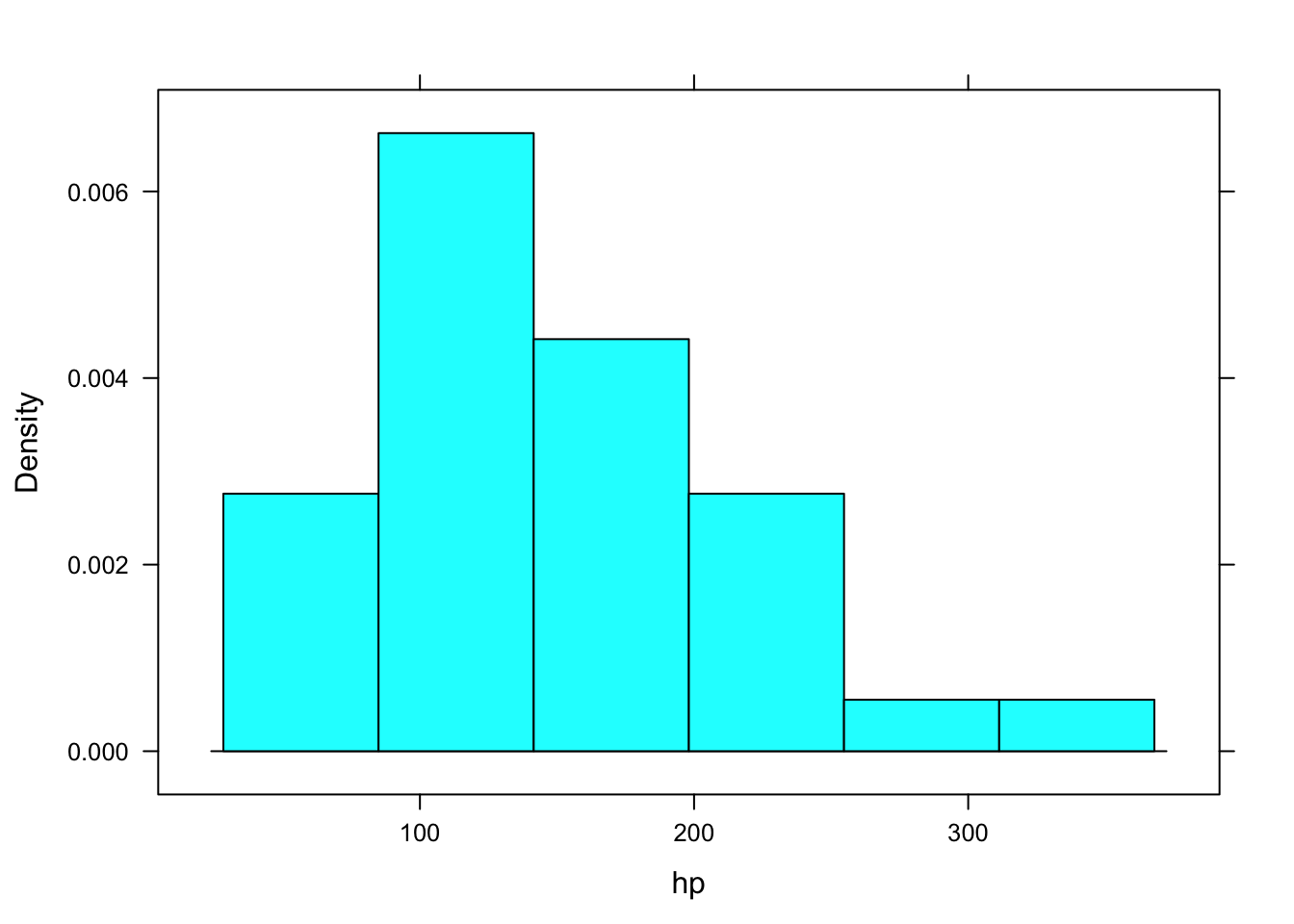

favstats(~hp, data=datos)

##  min   Q1 median  Q3 max mean   sd  n missing
##   52 96.5    123 180 335  147 68.6 32       0

with(datos, mean(mpg))

## [1] 20.1

with(datos,sd(mpg))

## [1] 6.03

with(datos,var(mpg))

## [1] 36.3

with(datos,median(mpg))

## [1] 19.2

with(datos,quantile(mpg))

##   0%  25%  50%  75% 100% 
## 10.4 15.4 19.2 22.8 33.9

with(datos,hist( mpg))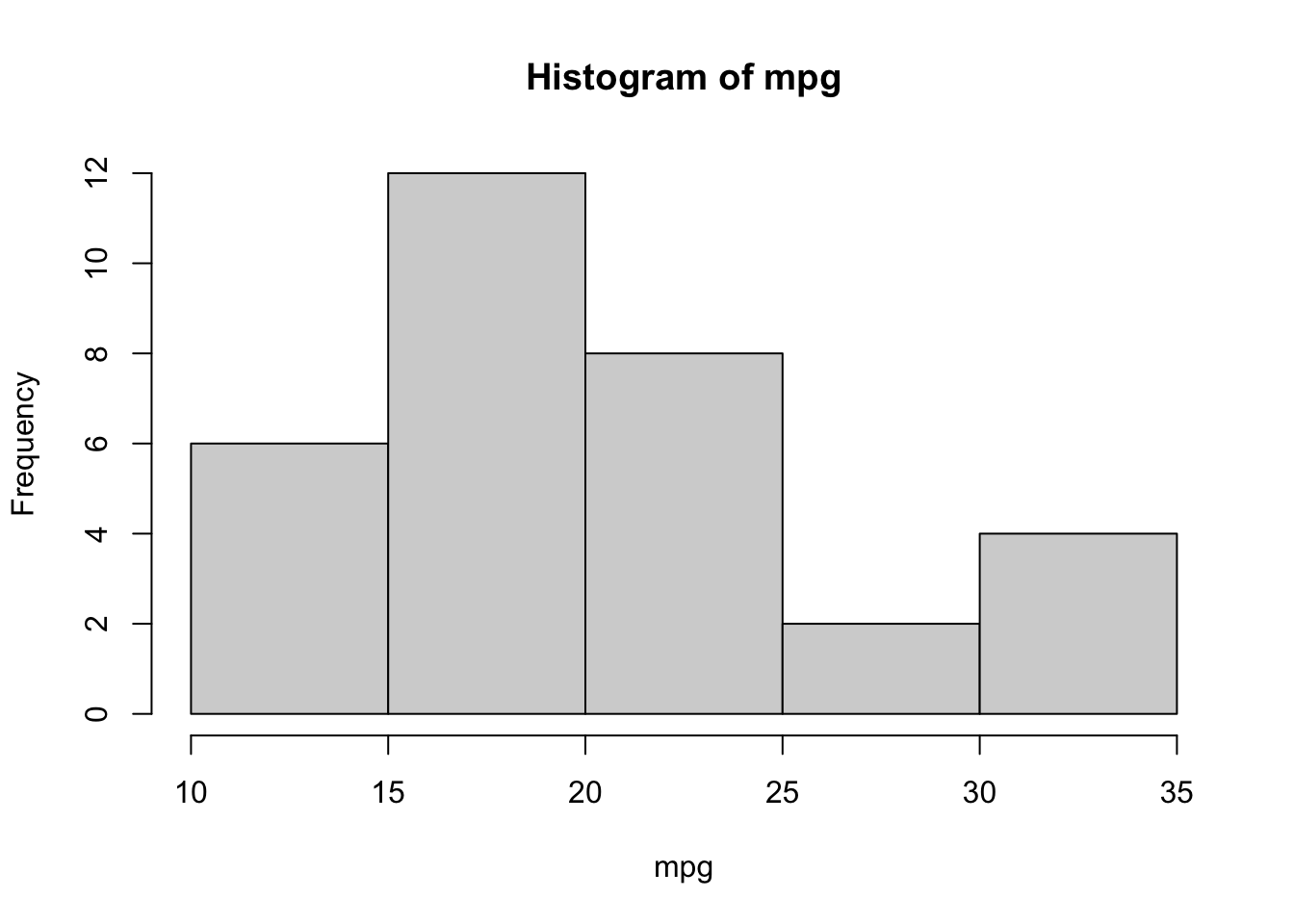

3.0.4 Análisis gráfico

Recordemos que una variable númerica se puede comprender visualmente con un histograma. Consulta este link para una guía de tipos de variables y su gráfico predilecto.

Con R base

hist(datos$mpg, breaks = 10, main = "Histograma de MPG", xlab="Miles per Gallon")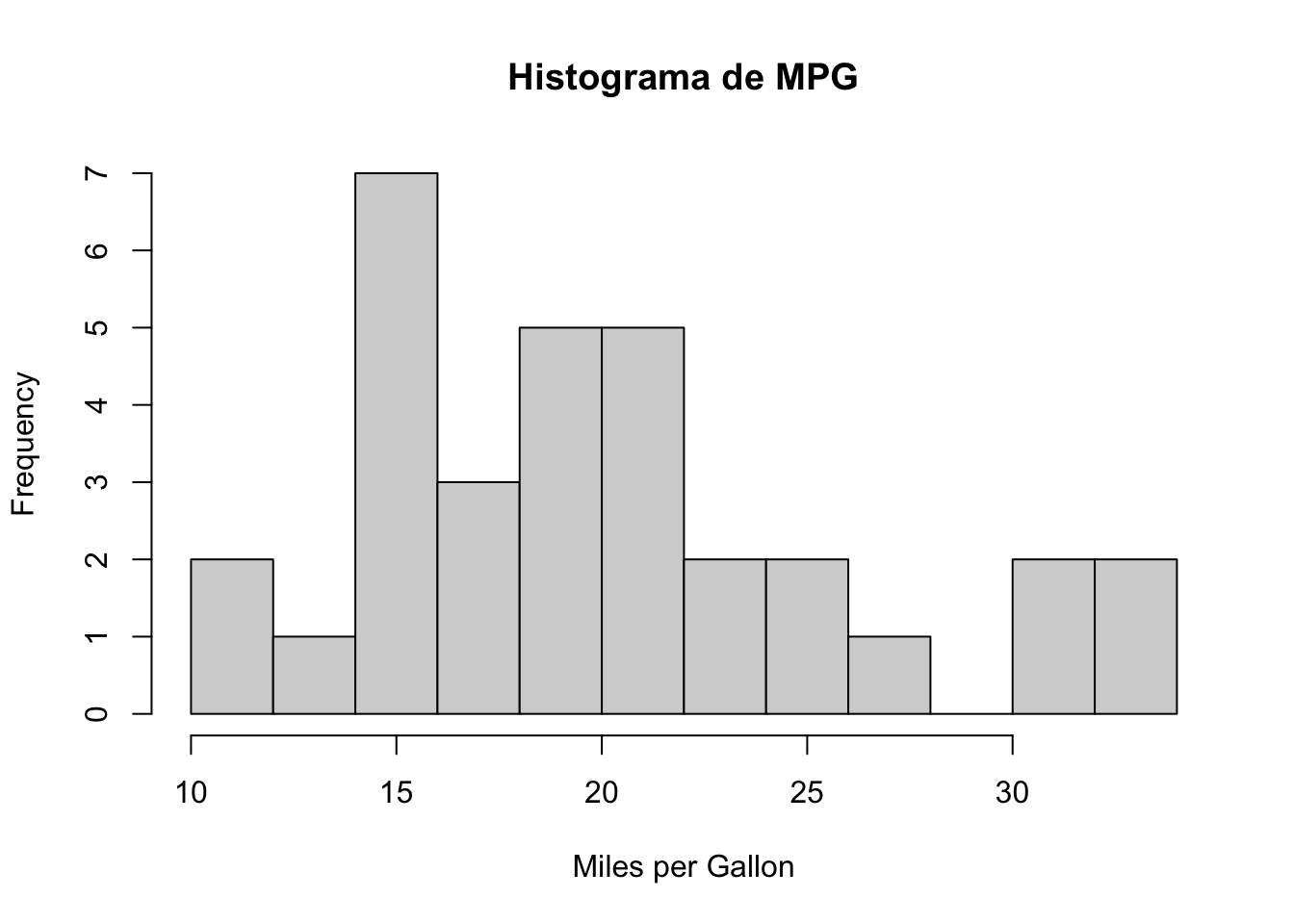

Con Mosaic

histogram(~ mpg, width=5, center=2.5, data=datos)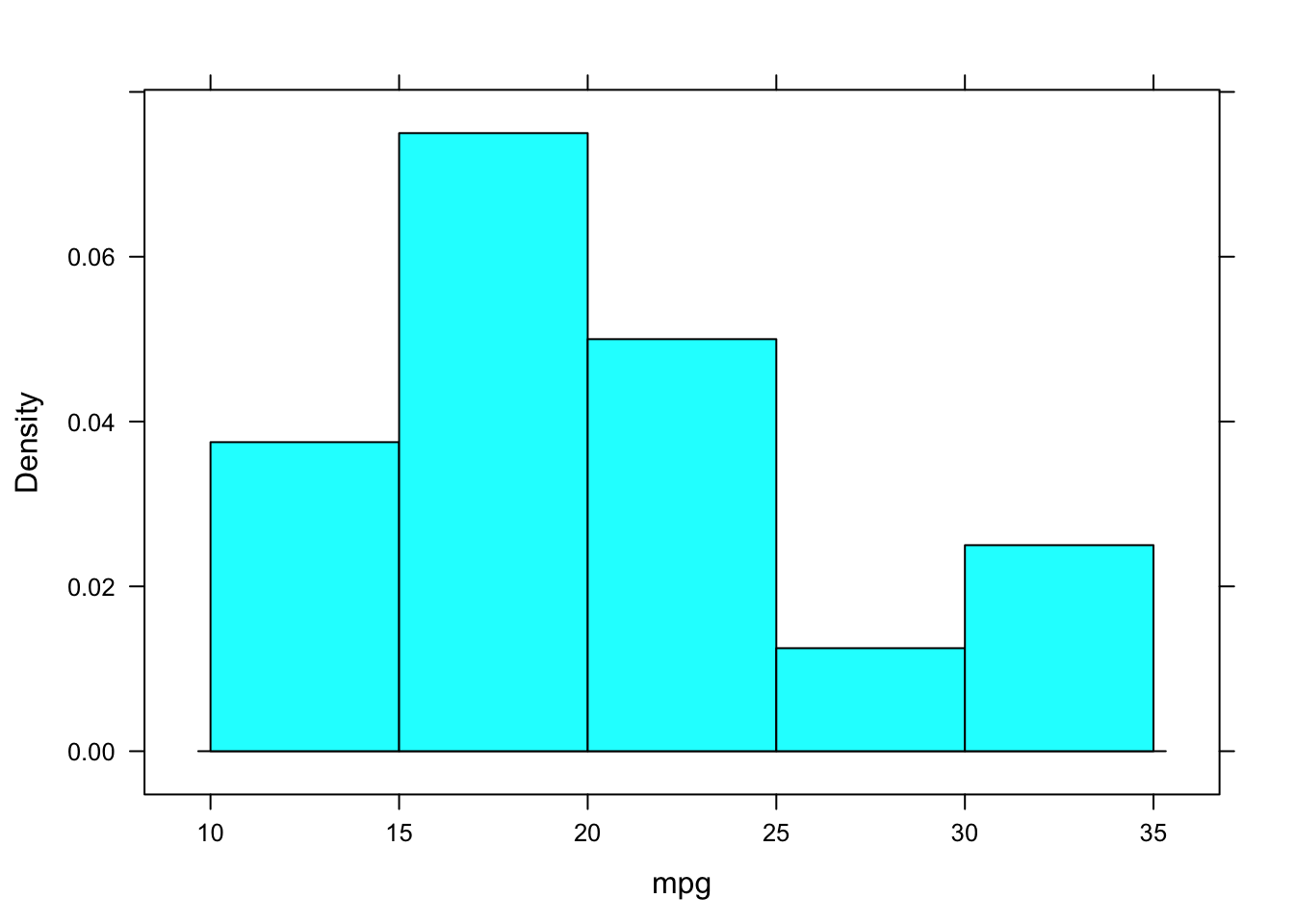

3.0.5 Otros

# dotplot
dotPlot(~ mpg, data=datos)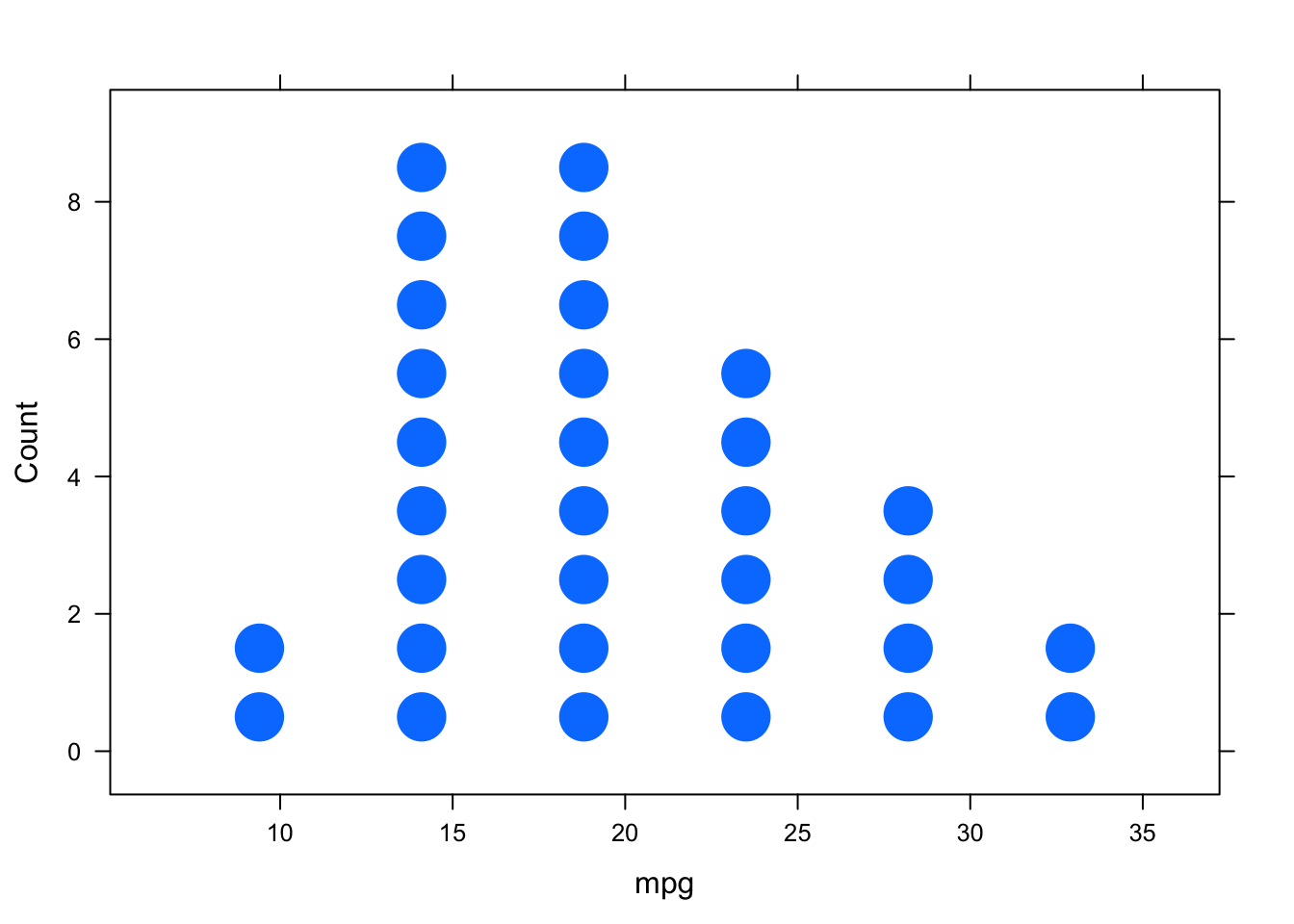

# densidades

densityplot(~ mpg, data=datos)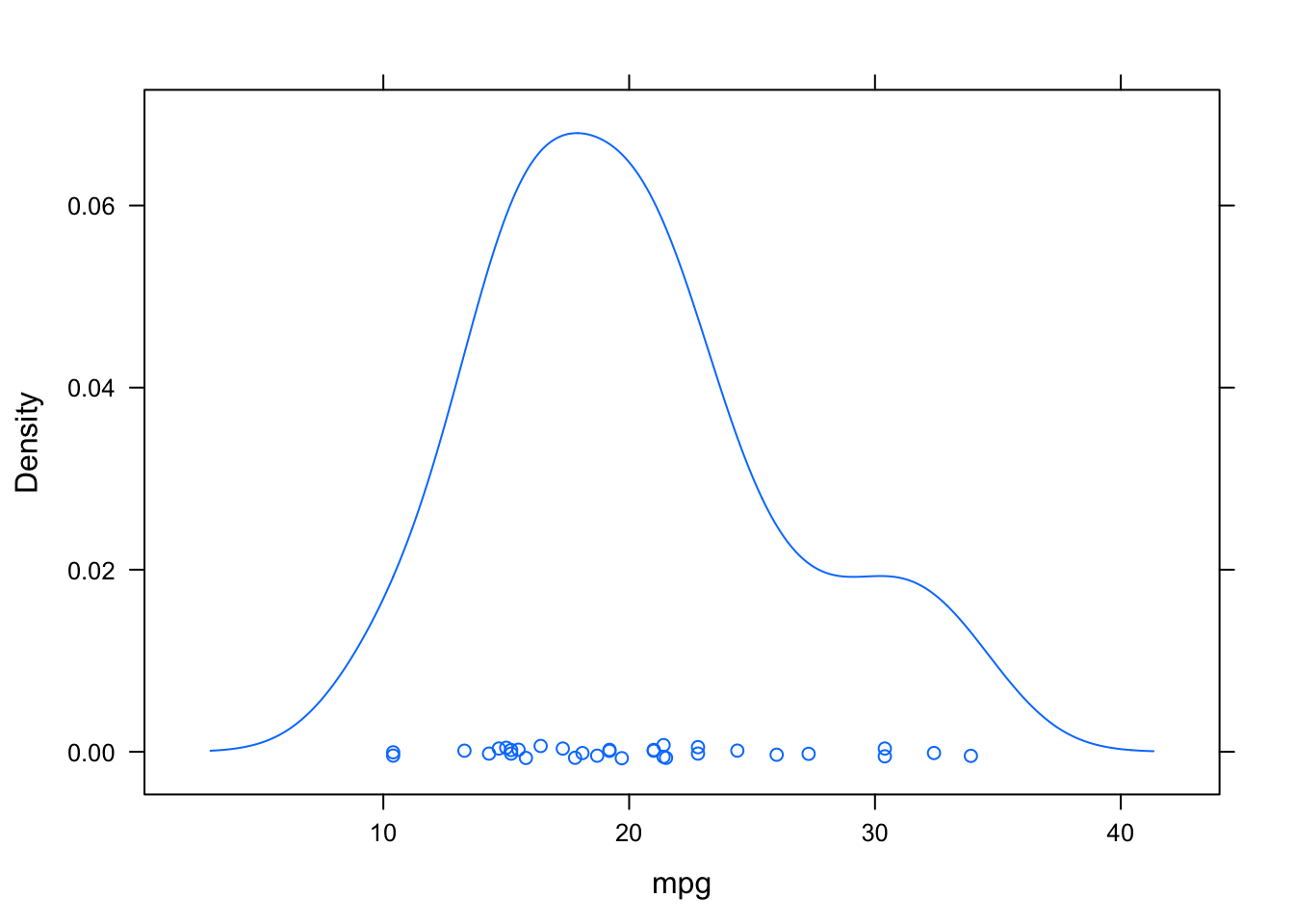

# histograma con distribución en el backgroudn
histogram(~ cesd, fit="normal", data=filter(HELPrct, sex=='female'))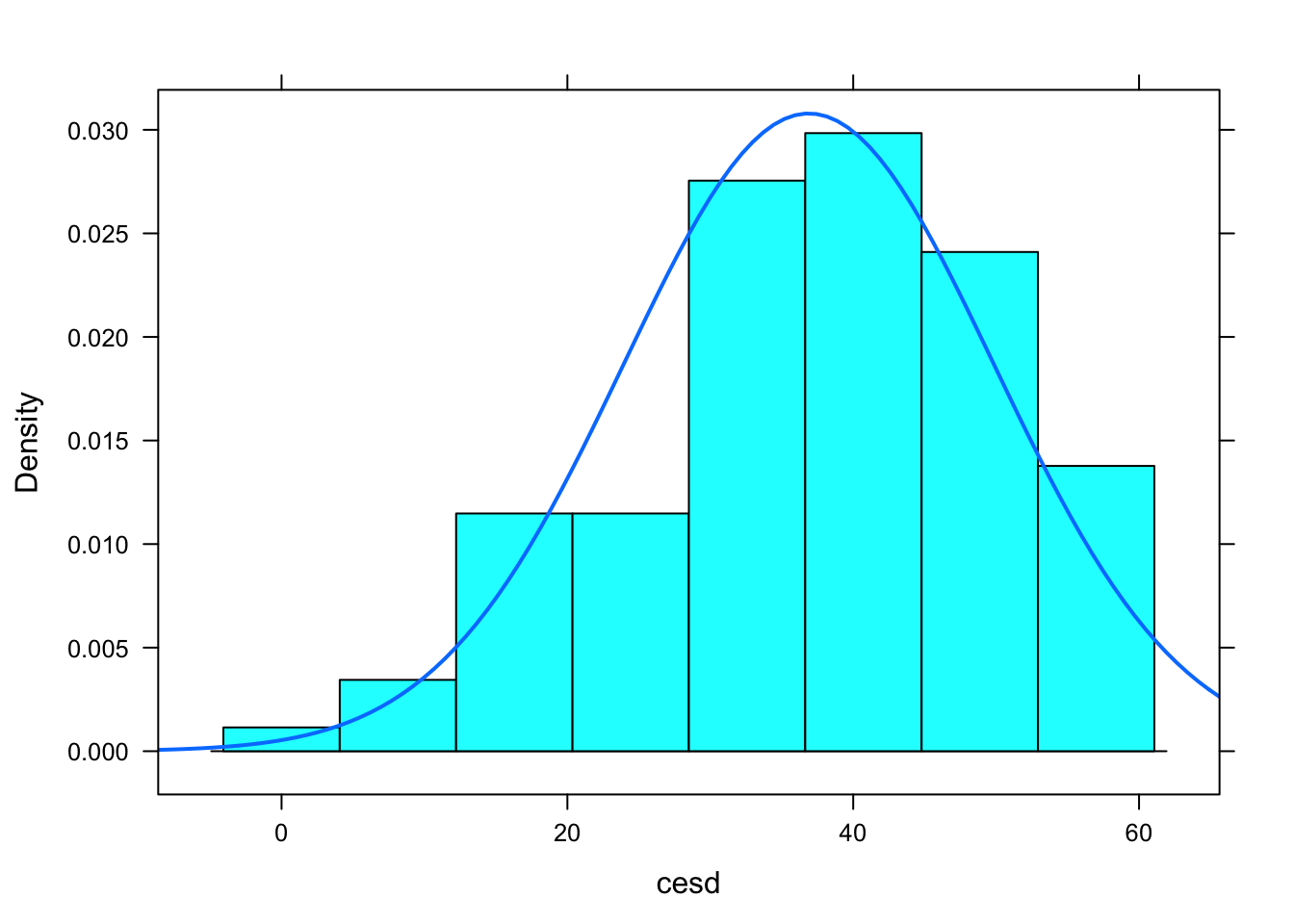

#histograma dividendo por una variable categórica
histogram(~ cesd | sex, data=HELPrct)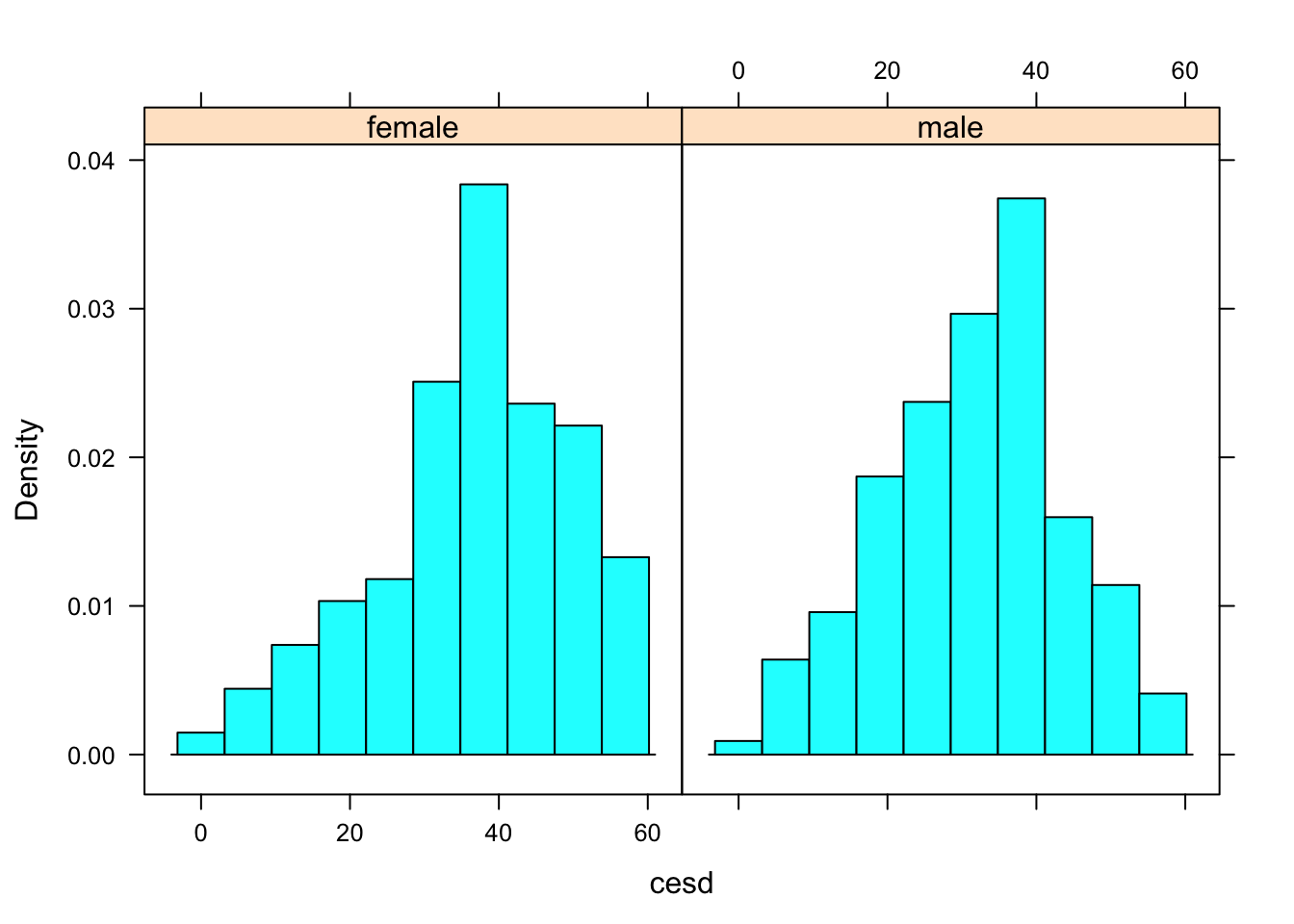

3.1 Densidad

densityplot(~ cesd, data=HELPrct) #densidad de la variable cesd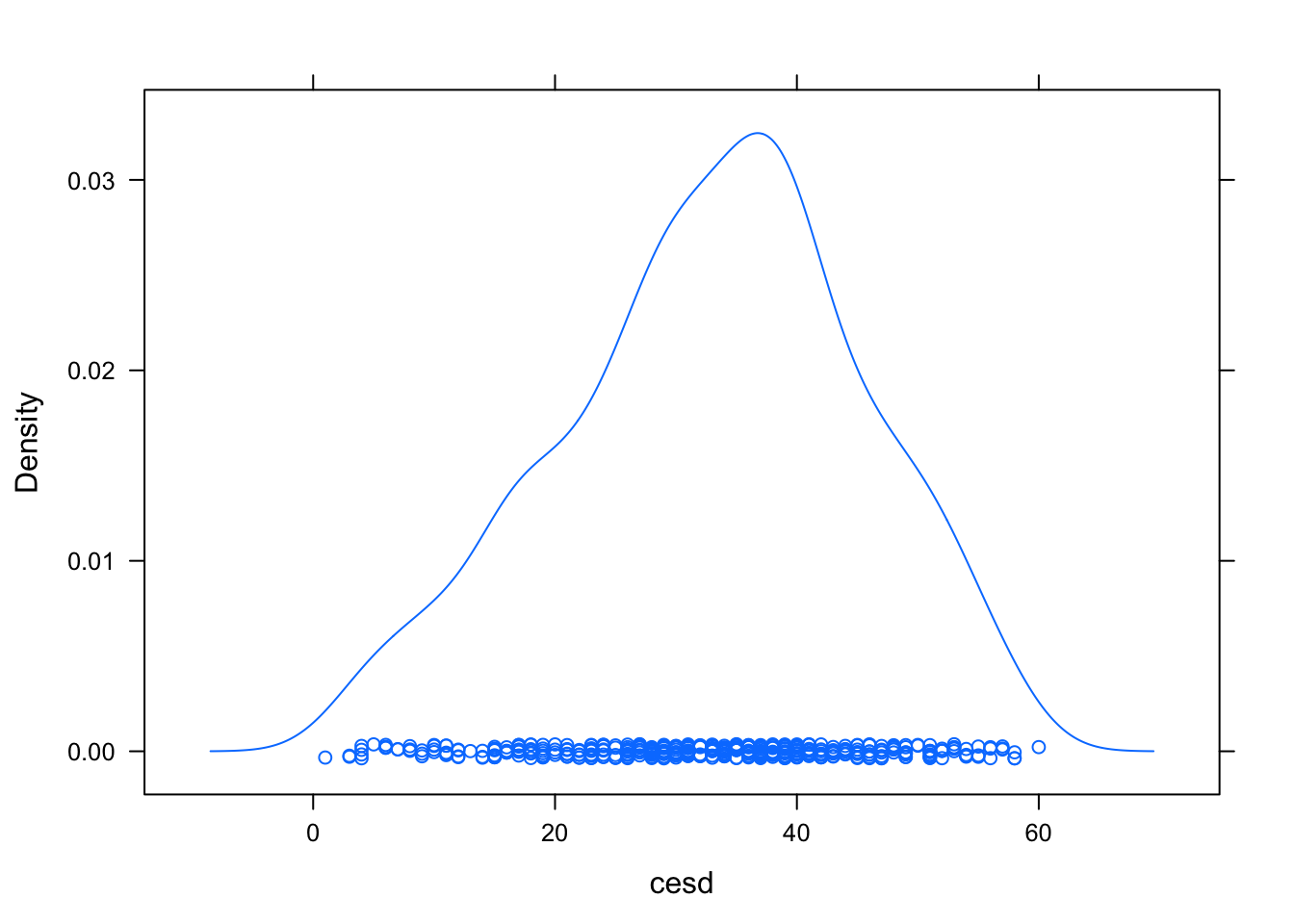

densityplot(~ cesd, data=HELPrct)

ladd(panel.abline(v=60, lty=2, lwd=2, col="grey")) #Ahora agregamos una linea vertical gris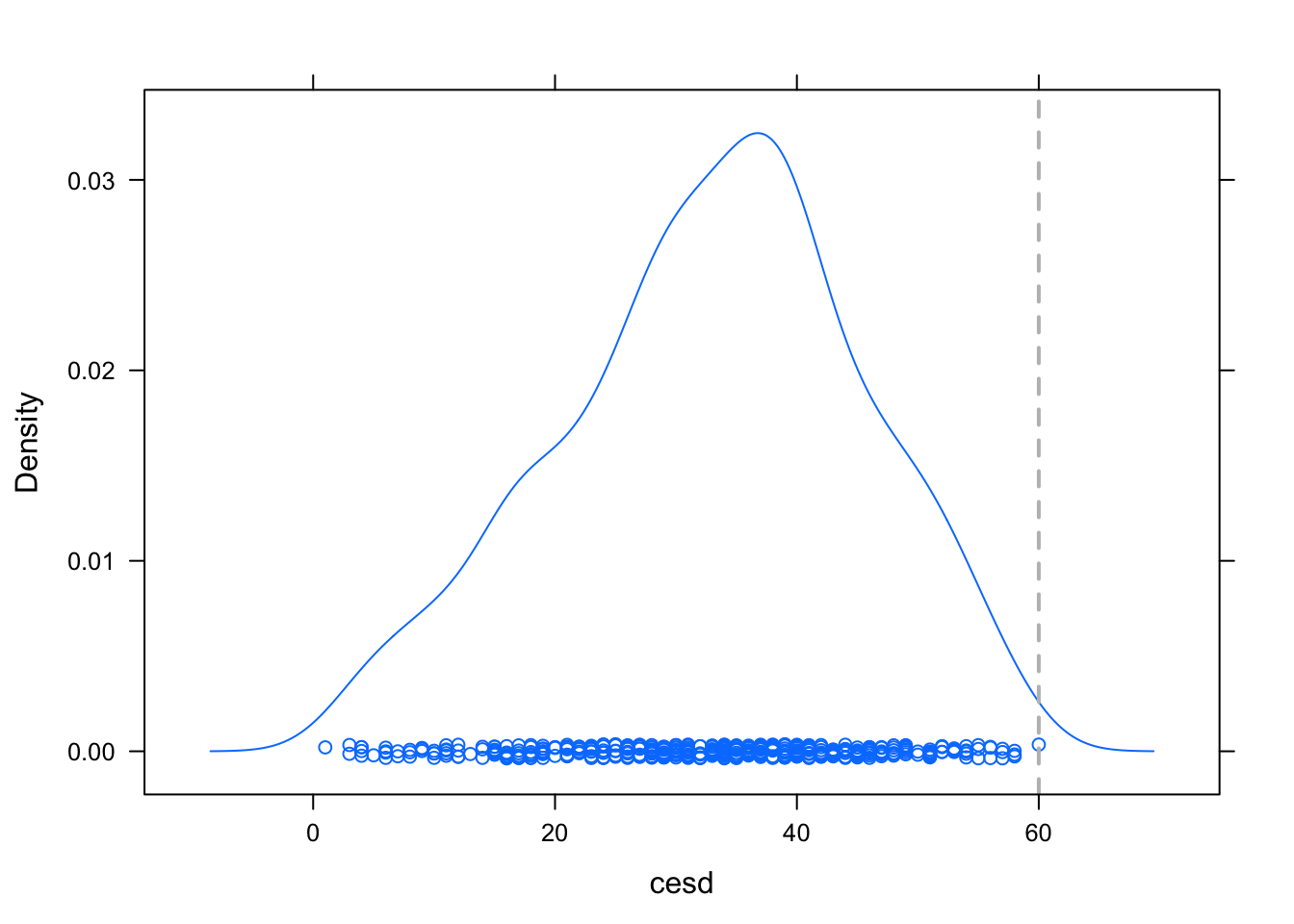

densityplot(~ cesd, data=HELPrct)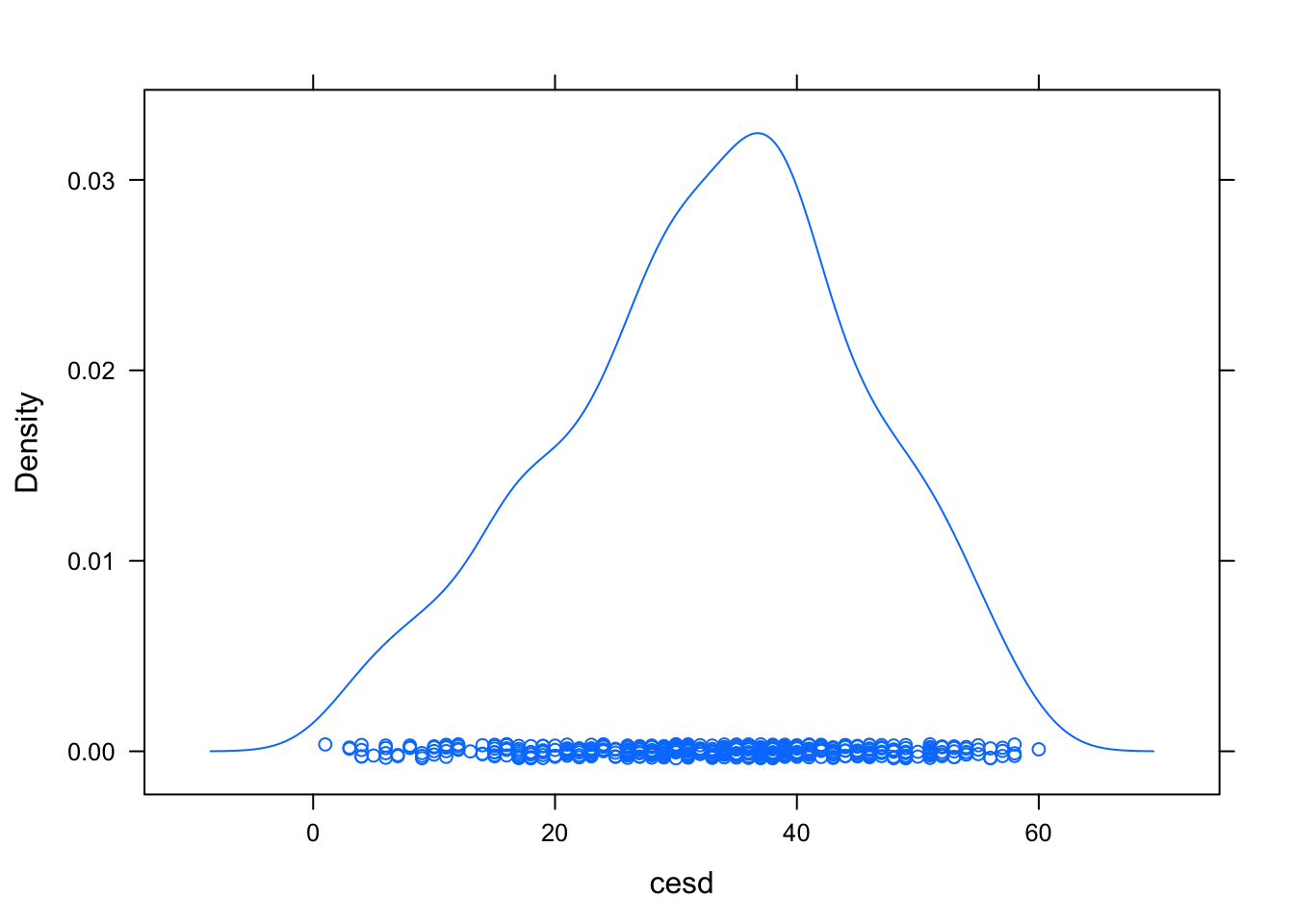

ladd(panel.mathdensity(args=list(mean=mean(cesd),
sd=sd(cesd)), col="red"), data=HELPrct)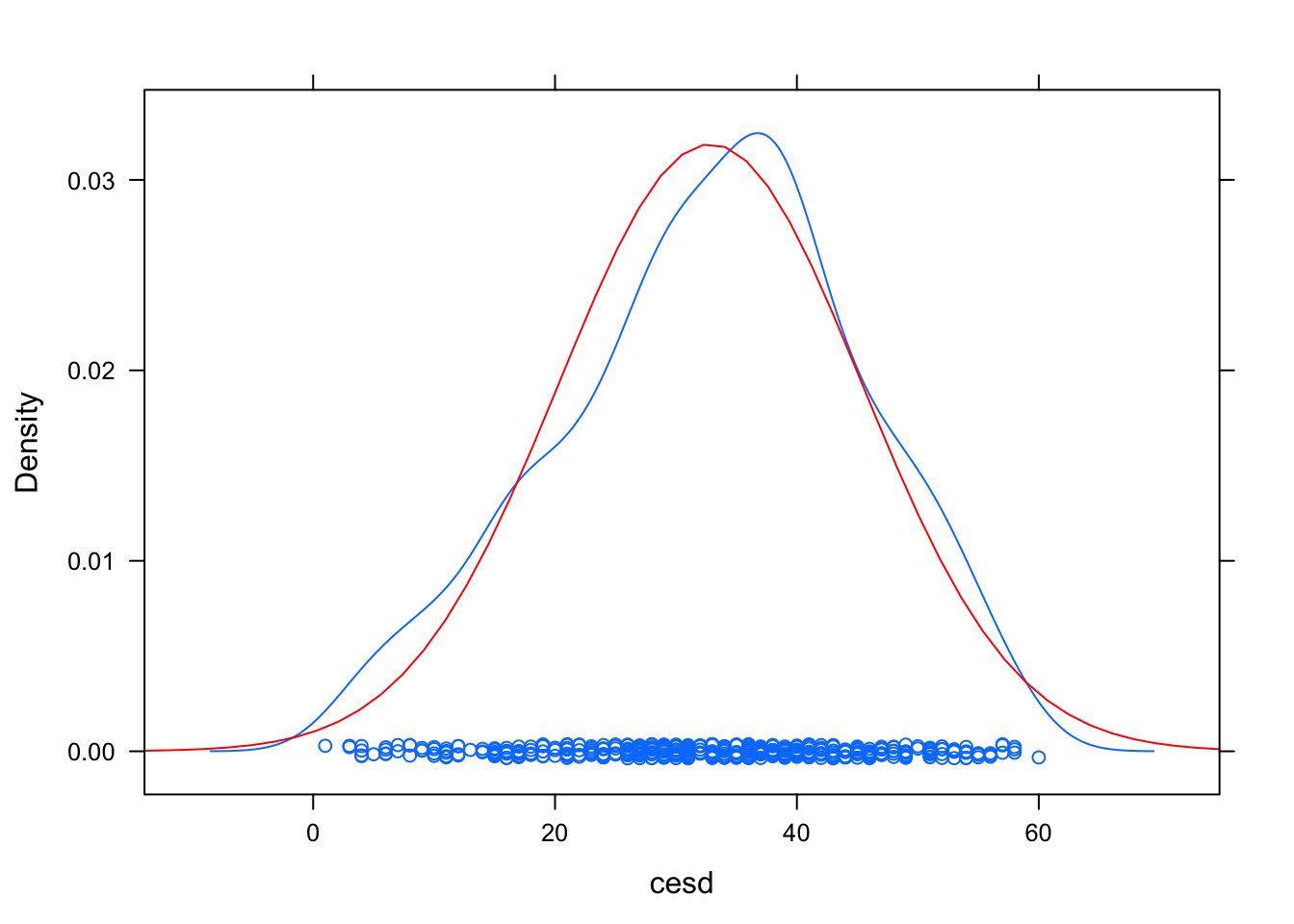

ladd(panel.abline(v=60, lty=2, lwd=2, col="grey"))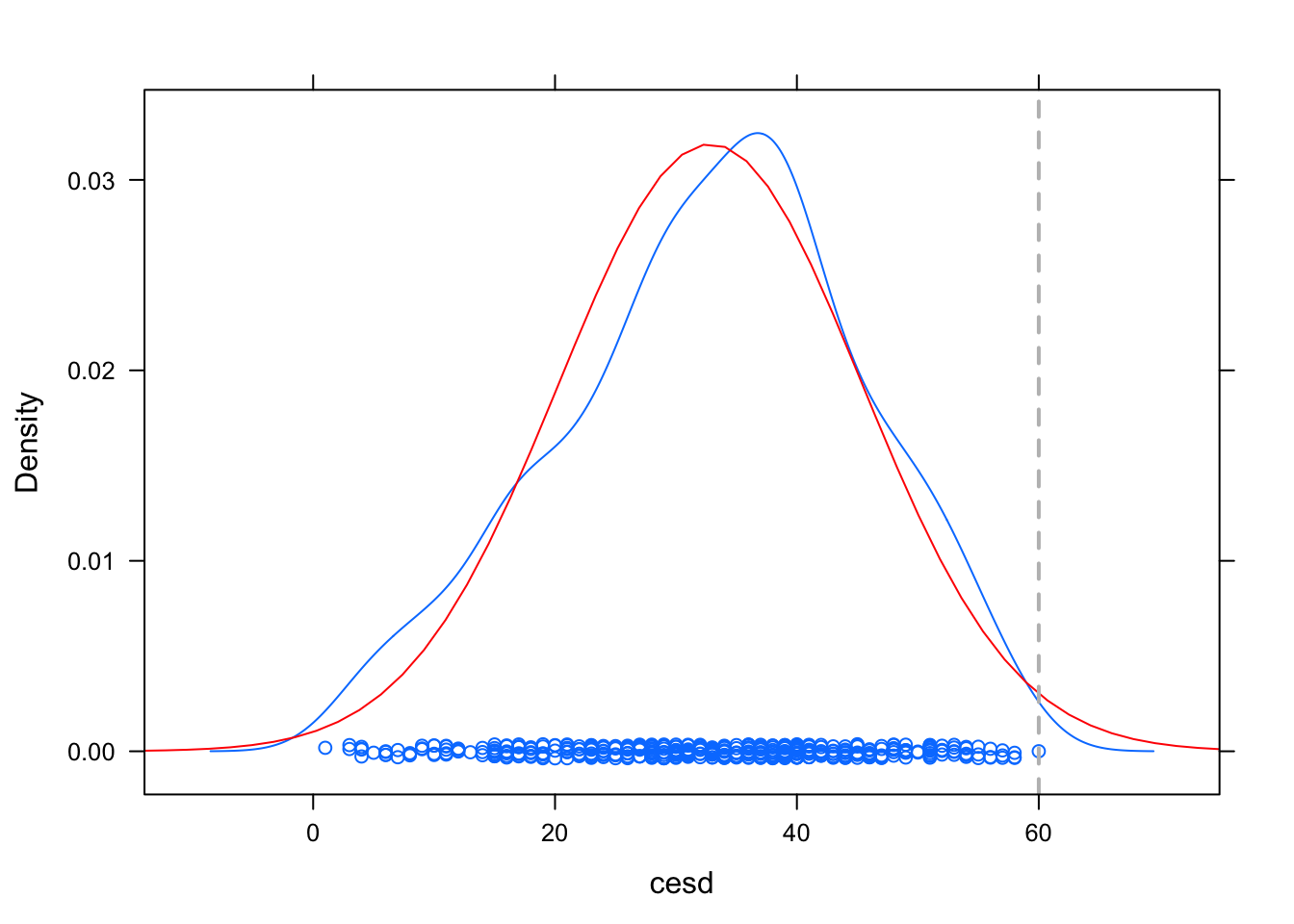

# ahora agregamos una densidad normal con fines comparativos

3.2 La distribución normal y sus pruebas de hipótesis

Las familias de comandos para cada distribución son las siguientes. Estos existen para cualquier tipo de distribución pero la más importante y por la que comenzaremos es la normal.

dnorm: densidad \(f(x)\) pnorm: densidad acumulada \(F(x)\) qnorm: densidad en cuantiles \(f(x)^{-1}\) rnorm: muestra aleatoria proveniente de una normal.

Asimismo, existen las funciones equivalentes para distintos tipos de distribuciones

dnorm(0)

## [1] 0.399

pnorm(0)

## [1] 0.5

qnorm(.5) #notese como pnorm y qnorm son inversos

## [1] 0

rnorm(5) 

## [1]  0.426  0.255 -0.108 -0.238 -0.723

Si observamos los parámetros de los comandos notamos que nos permite darle la media y desviación estandar (respectivamente) para distribuciones normales no estandarizadas.

dnorm(10,10,5)

## [1] 0.0798

pnorm(10,10,5)

## [1] 0.5

qnorm(.5,10,5) 

## [1] 10

rnorm(5,10,5) 

## [1]  2.73  9.47 10.92  4.79 13.86

En el libro te proponen un comando simplificador que se llama xporm, pero recuerda que tu puedes recrear exactamente el mismo output con los comandos anteriores y ggplot.

xpnorm(1.96, mean=0, sd=1)

## 

## If X ~ N(0, 1), then

##  P(X <= 1.96) = P(Z <= 1.96) = 0.975

##  P(X >  1.96) = P(Z >  1.96) = 0.025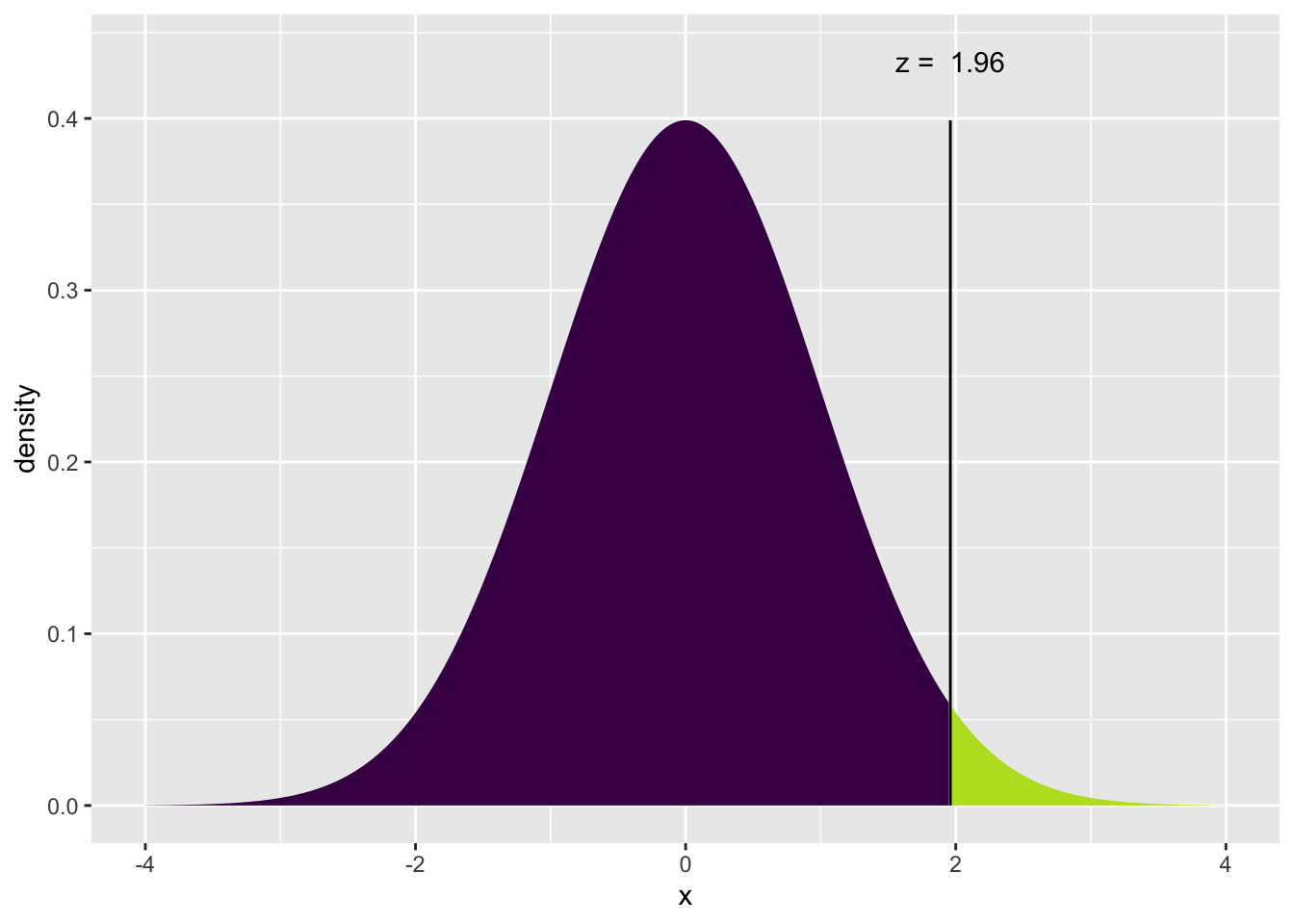

## 

## [1] 0.975

Si X ~ N(0,1), entonces P(X <= 1.96) = P(Z <= 1.96) = 0.975 P(X > 1.96) = P(Z > 1.96) = 0.025

xpnorm(10, mean=10, sd=5)

## 

## If X ~ N(10, 5), then

##  P(X <= 10) = P(Z <= 0) = 0.5

##  P(X >  10) = P(Z >  0) = 0.5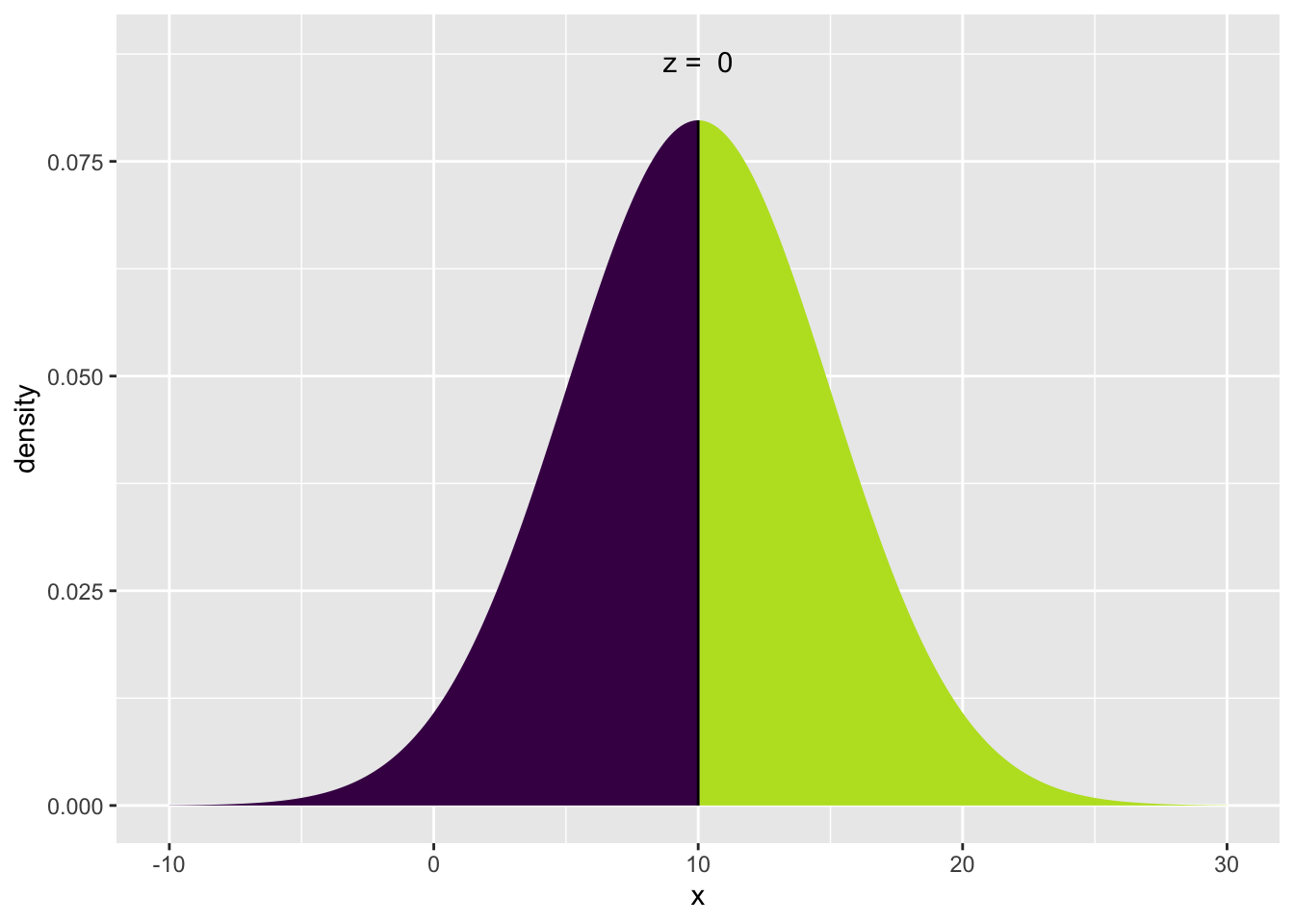

## 

## [1] 0.5

Si X ~ N(10,5), entonces P(X <= 10) = P(Z <= 0) = .5 P(X > 10) = P(Z > 0) = .5

3.3 Inferencia estadística

Sobre la media, prueba de hipotesis más sencilla con un 95% de confianza.

\(H_n: \mu=0\)

\(H_a: \mu \neq0\)

t.test (~mpg, datos)

## 
##  One Sample t-test
## 
## data:  mpg
## t = 19, df = 31, p-value <0.0000000000000002
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  17.9 22.3
## sample estimates:
## mean of x 
##      20.1

#recordemos que a menor p value podemos rechazar con mayor confianza H0

# si solo queremos el intervalo
confint(t.test (~mpg, datos))

##   mean of x lower upper level
## 1      20.1  17.9  22.3  0.95