Chapter 9 Module VII

9.1 Remuestreo

Tradicionalmente realizamos intervalos de confianza con base en supuestos y en inferencia estadística. Este es un enfoque tradicionalista. Por ejemplo de los datos anteriores:

stargazer(model, type="text")

## 
## ===============================================
##                         Dependent variable:    
##                     ---------------------------
##                                 hp             
## -----------------------------------------------
## mpg                          -8.830***         
##                               (1.310)          
##                                                
## Constant                    324.000***         
##                              (27.400)          
##                                                
## -----------------------------------------------
## Observations                    32             
## R2                             0.602           
## Adjusted R2                    0.589           
## Residual Std. Error      43.900 (df = 30)      
## F Statistic           45.500*** (df = 1; 30)   
## ===============================================
## Note:               *p<0.1; **p<0.05; ***p<0.01

el intervalo de confianza se calcula asumiendo que el parámetro $\beta_{mpg}$ muestral de interés se distribuye normal con media en el $\beta_{mpg}$ real. Por lo tanto para calcular el intervalo de confianza al 95% basta con despejar $\beta_{mpg}\pm z_{.025}\cdot\sigma$ para obtener los limites.

-8.830-1.310*1.96

## [1] -11.4

-8.830+1.310*1.96

## [1] -6.26

#aproximadamente.. porque perdemos decimales
confint(model)

##             2.5 % 97.5 %
## (Intercept) 268.1 380.11
## mpg         -11.5  -6.16

Graficamente estamos acotando el valor del parámetro a estimar dentro de ahí.

xpnorm(c(-11.4,-6.26) , mean=-8.830, sd=1.310)

## 

## If X ~ N(-8.83, 1.31), then

##  P(X <= -11.40) = P(Z <= -1.962) = 0.02489   P(X <=  -6.26) = P(Z <=  1.962) = 0.97511

##  P(X >  -11.40) = P(Z >  -1.962) = 0.97511   P(X >   -6.26) = P(Z >   1.962) = 0.02489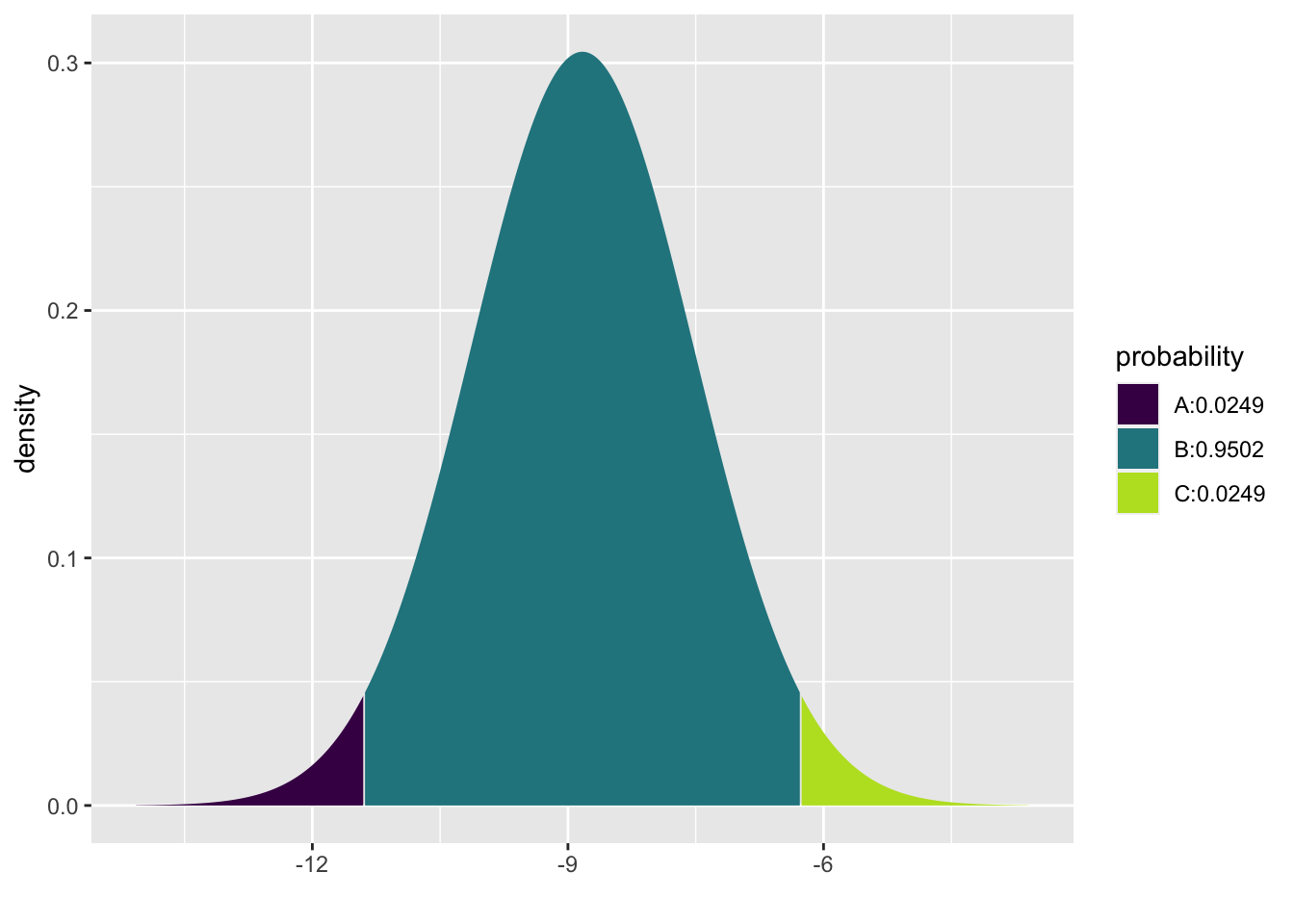

## 

## [1] 0.0249 0.9751

Pero no es el mejor método porque parte de supuestos fuertes, veamos que pasa cuando queremos estimar la media:

mean(datos$mpg)

## [1] 20.1

sd(datos$mpg)

## [1] 6.03

el intervalo de confianza se calcula asumiendo que el parámetro $\beta_{mpg}$ muestral de interés se distribuye normal con media en el $\beta_{mpg}$ real. Por lo tanto para calcular el intervalo de confianza al 95% basta con despejar $\hat{x}\pm \frac{z_{.025}\cdot\sigma}{\sqrt{n}}$ para obtener los limites.

20.1-6.03*1.96/sqrt(32) #inferior

## [1] 18

20.1+6.03*1.96/sqrt(32) #superios

## [1] 22.2

Graficamente estamos acotando el valor del parámetro a estimar dentro de ahí.

xpnorm(c(18,22.2) , mean=20.1, sd=6.03)

## 

## If X ~ N(20.1, 6.03), then

##  P(X <= 18.0) = P(Z <= -0.3483) = 0.3638 P(X <= 22.2) = P(Z <=  0.3483) = 0.6362

##  P(X >  18.0) = P(Z >  -0.3483) = 0.6362 P(X >  22.2) = P(Z >   0.3483) = 0.3638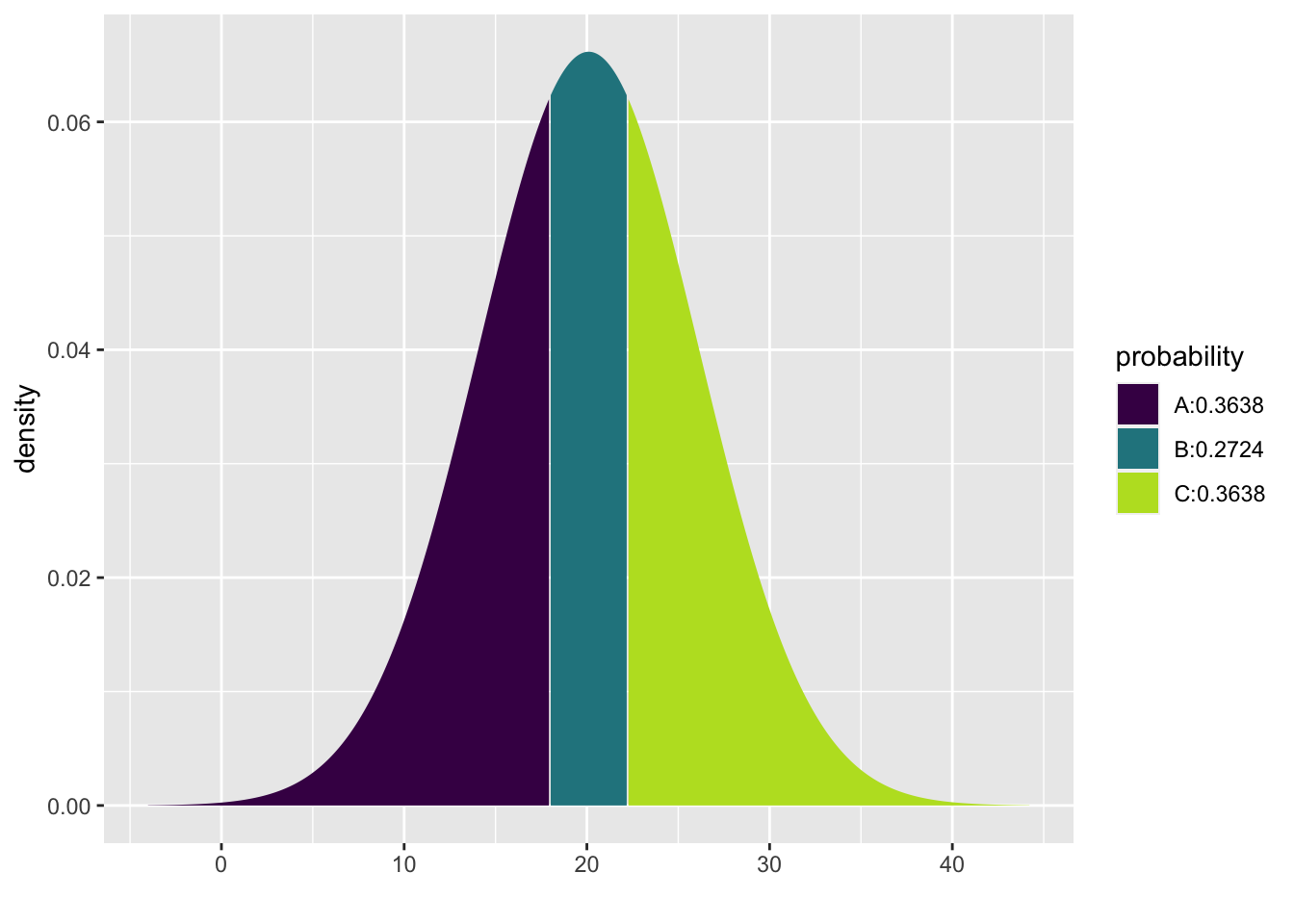

## 

## [1] 0.364 0.636

Pero existen métodos más orgánicos que aprovechan el poder computacional para no tener que hacer supuestos, como el que veremos a contnuación.

Bootstrap

El bootstrap es un método de estadística que se basa en el remuestreo de la misma variable. En este caso, vamos a remuestrear con reemplazo una variable y sobre la variable calcularemos los intervalos de confiana al elegir los cuantiles .025 y .975, de esta manera obtenemos un intervalo de confianza más orgánico y sin asumir supuestos de la distribución de la variable.

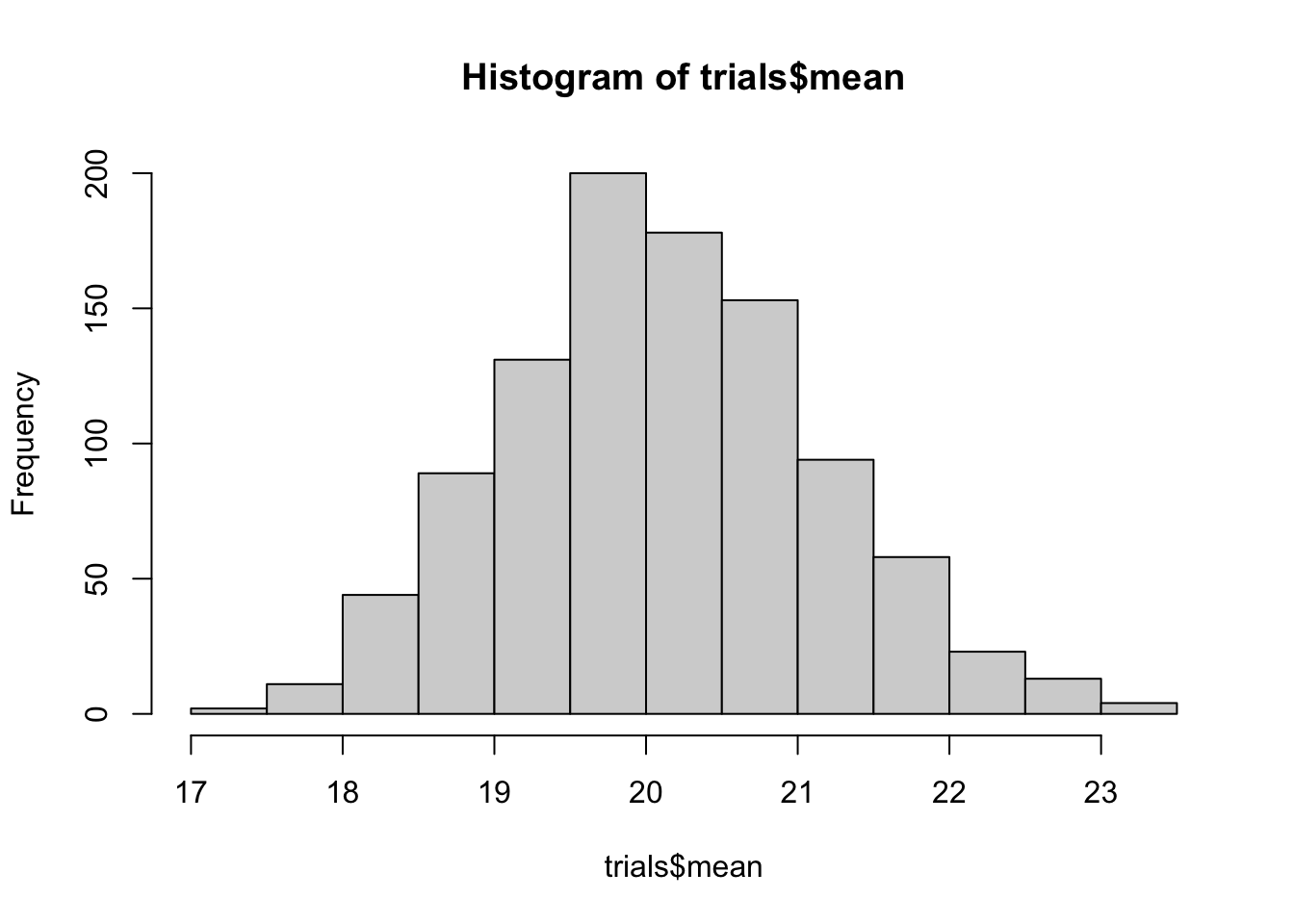
mean(datos$mpg)

## [1] 20.1

trials <- do(1000) * mean(resample(datos$mpg))

qdata(trials$mean, c(.025, .975))#05% de confianza

##  2.5% 97.5% 
##  18.2  22.2

hist(trials$mean)