Chapter 2 Module II

2.1 Variables categóricas

La función tally se puede usar para explorar variables categóricas. Para explorar su potencial primero simularemos una base de datos.

# creamos una base de datos de ganadores de presidentes municipales en un estado de 20 municipios
partidos<-c("PRI","PAN","MORENA")
mun_indigena<-c("SI","NO") #si es de mayoría indígena

ganador<-sample(partidos, 20, replace = T) # le indicamos que elija aleatoriamente un ganador del vector partidos para cada distrito
mayoria_indigena<-sample(mun_indigena, 20, replace = T) # de igual manera le indicamos que nos diga aleatoriamente si el municipio es de mayoría indígena


distrito<-seq(1:20) # indicamos un numero para cada distrito

#creamos base de datos
elecciones<-data.frame(ganador,distrito,mayoria_indigena)

Ahora usaremos el comando tally del paquete mosaic. Recordemos que cada comando tiene parametros opcionales y obligatorios (y ademas su propia sintaxis dentro de dichos parametros). Para saber con certeza estos detalles siempre es bueno googlear la documentación de cada paquete. Por el momendo, tally necesita al menos que le indiquemos una variable a analizar y la base de datos donde se encuentra.

library(mosaic)

# en este caso se pone la variable despues de ~ y los datos como respuesta al parámetro data.

tally(~ ganador, data=elecciones)

## ganador
## MORENA    PAN    PRI 
##     10      7      3

# en este caso, hay un parámetro booleano, es decir que necesita una respuesta TRUE o FALSE.
# este parámetro agrega la cantidad de observaciones

tally(~ ganador, data=elecciones,margins=TRUE)

## ganador
## MORENA    PAN    PRI  Total 
##     10      7      3     20

# en estos dos casos vemos que el parámetro format acepta caracteres, esto quiere decir que hay una lista predeterminada de palabras que acepta. Es aquí donde valdría la pena googlear que más parámetros acepta.

tally(~ ganador, data=elecciones, format="percent")

## ganador
## MORENA    PAN    PRI 
##     50     35     15

tally(~ ganador, data=elecciones, format="proportion")

## ganador
## MORENA    PAN    PRI 
##   0.50   0.35   0.15

2.2 Tablas de contingencia

Las tablas de contingencia son muy importantes en estadística porque nos permiten ver relaciones entre las distintas variables de manera muy intuitiva. En ellas se muestra la coocurrencia entre las variables.

# basta con agregar otra variable con un + o un |

tally(~ ganador + mayoria_indigena , data=elecciones)

##         mayoria_indigena
## ganador  NO SI
##   MORENA  5  5
##   PAN     1  6
##   PRI     2  1

tally(~ ganador | mayoria_indigena, data=elecciones,margins=TRUE)

##         mayoria_indigena
## ganador  NO SI
##   MORENA  5  5
##   PAN     1  6
##   PRI     2  1
##   Total   8 12

tally(~ ganador + mayoria_indigena, data=elecciones, format="percent")

##         mayoria_indigena
## ganador  NO SI
##   MORENA 25 25
##   PAN     5 30
##   PRI    10  5

tally(~ ganador + mayoria_indigena, data=elecciones, format="proportion")

##         mayoria_indigena
## ganador    NO   SI
##   MORENA 0.25 0.25
##   PAN    0.05 0.30
##   PRI    0.10 0.05

Además podemos calcular el momio. Recordemos que el momio es la frecuencia de una alternavia sobre la frecuencia de la otra. Es decir, el momio de A sobre B es \(\frac{P(A)}{P(B)}\).

Ahora, en el código esto no se ve tan inmediato. Hay que usar el comando oddsRatio y de parametro le indicamos toda el comando tally que hemos estado usando pero ahora en lugar de poner que queremos una tabla de contingencia de ganador + mayoria_indigena indicamos que solo queremos el output de la tabla de contingencia con ganador fijado en “MORENA.”

# Ade
oddsRatio(tally(~ (ganador=="MORENA") + mayoria_indigena, data=elecciones))

## [1] 0.4285714

Ahora de tarea intente hacer lo mismo para los demás partidos.

Finalmente usaremos otro paquete sugerido en el SG: g models. El comando crosstable nos arroja los momios y las tablas de contingencia de manera directa.

require(gmodels) #require es un install.packages y un library al mismo tiempo

## Loading required package: gmodels

# analicemos la sintaxis: indicamos como primer parámetro la base de datos, después la instrucción de que para cada combinación de ganador y mayoría indigena nos arroje información

with(elecciones, CrossTable(ganador, mayoria_indigena,
   prop.r=FALSE, prop.chisq=FALSE, prop.t=FALSE))

## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Col Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  20 
## 
##  
##              | mayoria_indigena 
##      ganador |        NO |        SI | Row Total | 
## -------------|-----------|-----------|-----------|
##       MORENA |         5 |         5 |        10 | 
##              |     0.625 |     0.417 |           | 
## -------------|-----------|-----------|-----------|
##          PAN |         1 |         6 |         7 | 
##              |     0.125 |     0.500 |           | 
## -------------|-----------|-----------|-----------|
##          PRI |         2 |         1 |         3 | 
##              |     0.250 |     0.083 |           | 
## -------------|-----------|-----------|-----------|
## Column Total |         8 |        12 |        20 | 
##              |     0.400 |     0.600 |           | 
## -------------|-----------|-----------|-----------|
## 
## 

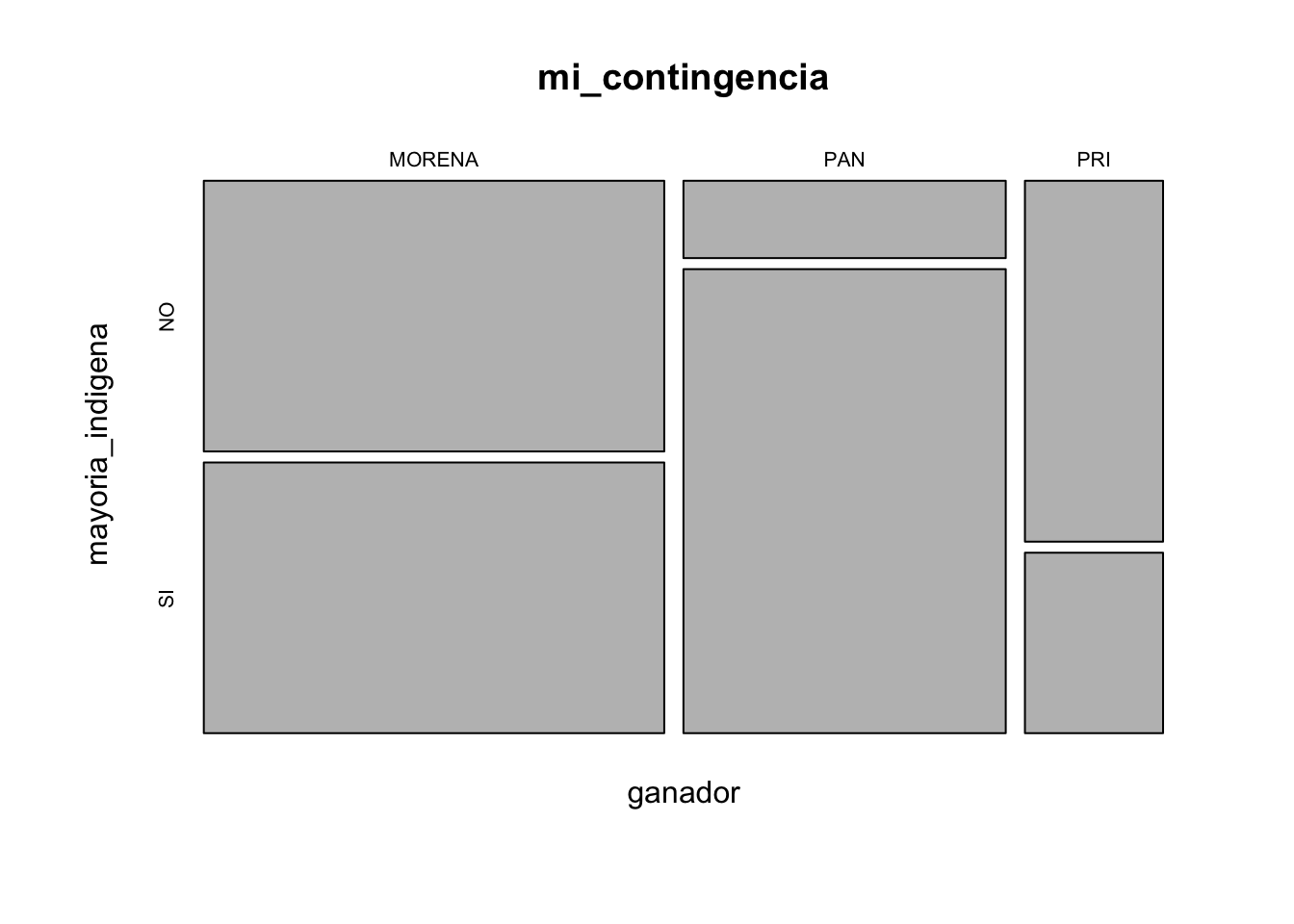
Finalmente aprovechamos el paquete mosaic para hacer una reprecentación gráfica. Primero guardamos en una variable los datos que nos arroja tally. Después aplicamos el comando mosaicplot con el parametro de nuestra variable recién creada.

mi_contingencia <- tally(~ ganador + mayoria_indigena, data=elecciones) 
mosaicplot(mi_contingencia)