Modul 5: Beslutningstræer - EKSEMPEL
library(caret)
library(DescTools)
library(dplyr)
library(ggplot2)
library(gridExtra)
##
## Vedhæfter pakke: 'gridExtra'
## Det følgende objekt er maskeret fra 'package:dplyr':
##
## combine
library(magrittr)
library(openxlsx)
library(pdp)
library(ranger)
library(rsample)
library(rpart)
library(rpart.plot)
library(vip)
##
## Vedhæfter pakke: 'vip'
## Det følgende objekt er maskeret fra 'package:utils':
##
## viKlargøring af datasæt
# tilføjelse af variabel "Kommune"
bolig$Kommune <- ifelse(bolig$Postnummer < 3000, "Gentofte", "Tønder")
# skalering af Salgspris så den angives i 1.000 kr.
# (for at lette læsningen af beslutningstræerne nedenfor)
bolig$Salgspris <- bolig$Salgspris/1000# opdeling i test- og træningsdatasæt
set.seed(4321)
split <- initial_split(bolig, 2/3)
train <- training(split)
test <- testing(split)Beslutningstræer
Valg af splitværdi
Hvordan vælges splitværdien i hver enkelt knude?
Eksempel med estimation af et beslutningstræ med 1 lag og UDEN “pruning”
# model
dt0 <- rpart(formula = Salgspris ~ Boligareal, data=train, method="anova",
control = c(maxdepth = 1, cp=0))
rpart.plot(dt0)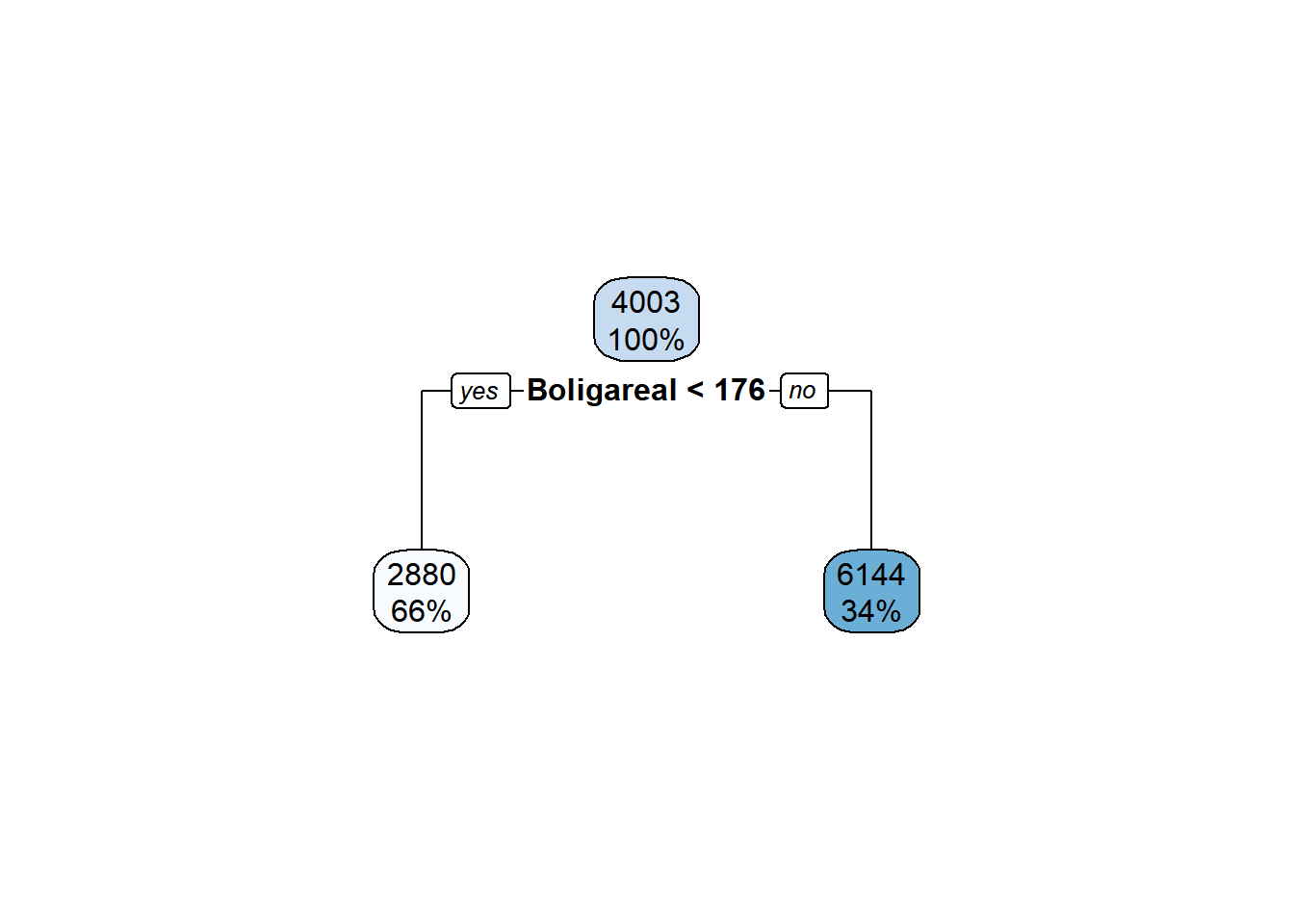
# prædiktion baseret på træningssæt
dt0.train.predict <- predict(dt0, train)
DescTools::RMSE(dt0.train.predict, train$Salgspris)
## [1] 2886.19Kontrolberegning af splitværdi i dt0 output:
# beregning af SSE for forskellige split-værdier
test.split_value <- seq(100.5, 300.5, by=1)
SSE <- c()
for(i in 1:length(test.split_value)){
test.knot2 <- train$Salgspris[train$Boligareal < test.split_value[i]]
test.knot3 <- train$Salgspris[train$Boligareal >= test.split_value[i]]
SSE[i] <- sum((test.knot2-mean(test.knot2))^2) + sum((test.knot3-mean(test.knot3))^2)
}
# figur af SSE for forskellige split-værdier
plot(test.split_value, SSE, type="l") 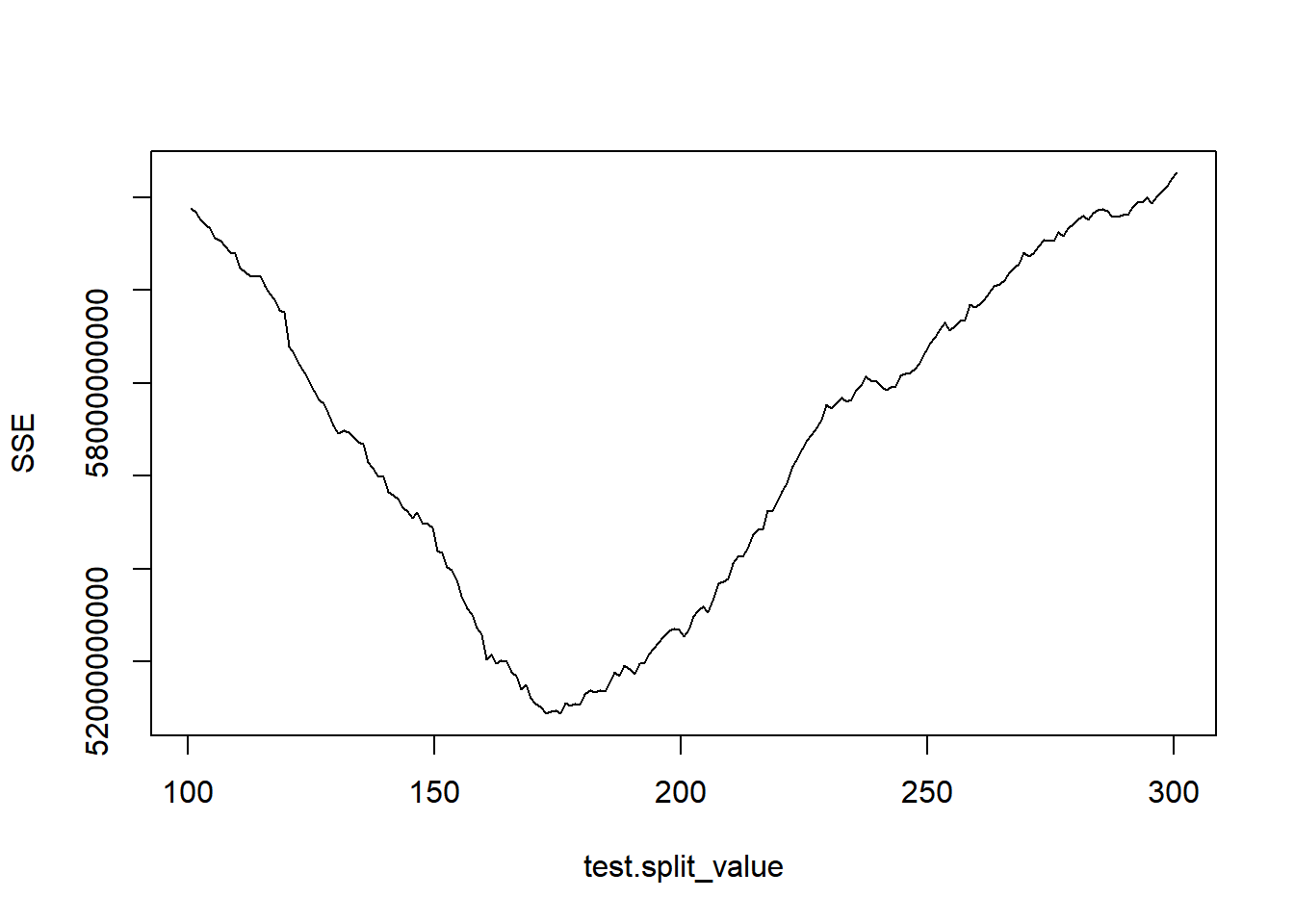
# split-værdi med mindst SSE
split_value <- test.split_value[which.min(SSE)]Kontrolberegning af RMSE i dt0
# beslutningstræets split i knude 2 og 3
knot2 <- train$Salgspris[train$Boligareal < split_value]
knot3 <- train$Salgspris[train$Boligareal >= split_value]
sqrt(( sum((knot2-mean(knot2))^2) + sum((knot3-mean(knot3))^2) ) / nrow(train))
## [1] 2886.19Output
Hvordan fremkommer beslutningstræets output?
Eksempel med estimation af et beslutningstræ med 3 lag og UDEN “pruning.”
# model
dt1 <- rpart(formula = Salgspris ~ Boligareal+Kommune, data=train, method="anova",
control = c(maxdepth = 3, cp=0))
rpart.plot(dt1)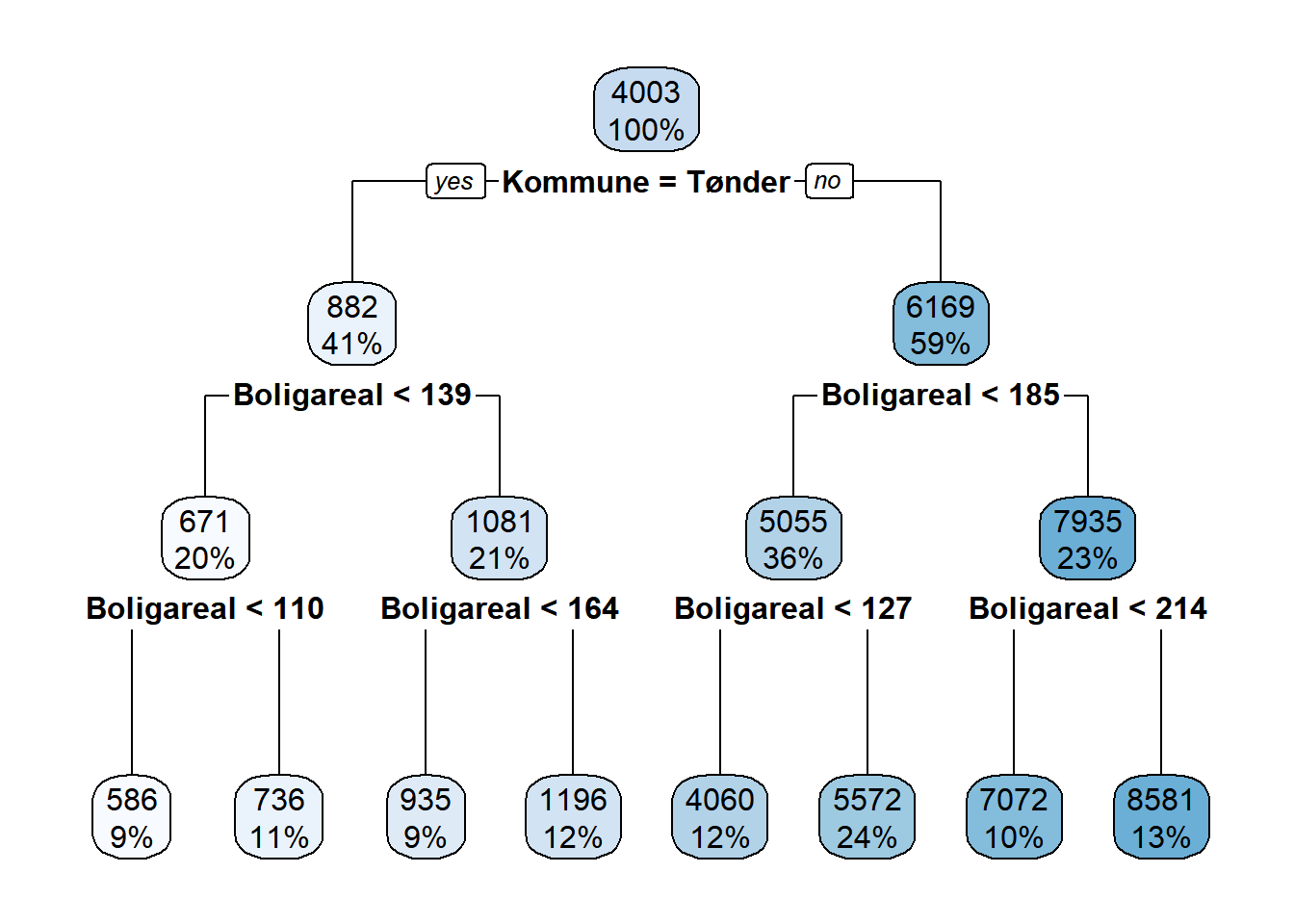
# sammenlign fit for trænings- og testdatasæt
dt1.train.predict <- predict(dt1, train)
dt1.test.predict <- predict(dt1, test)
DescTools::RMSE(dt1.train.predict, train$Salgspris)
## [1] 1573.105
DescTools::RMSE(dt1.test.predict, test$Salgspris)
## [1] 1570.103Kontrolberegninger i dt1 output:
dt1
## n= 6108
##
## node), split, n, deviance, yval
## * denotes terminal node
##
## 1) root 6108 65562630000 4002.6320
## 2) Kommune=Tønder 2503 1430496000 881.7720
## 4) Boligareal< 138.5 1214 320298900 670.5956
## 8) Boligareal< 109.5 529 60316450 585.9036 *
## 9) Boligareal>=109.5 685 253257800 736.0001 *
## 5) Boligareal>=138.5 1289 1005070000 1080.6610
## 10) Boligareal< 163.5 568 280850600 934.8211 *
## 11) Boligareal>=163.5 721 702620600 1195.5530 *
## 3) Kommune=Gentofte 3605 22827070000 6169.4880
## 6) Boligareal< 184.5 2210 6821505000 5055.0310
## 12) Boligareal< 126.5 756 1087817000 4059.8330 *
## 13) Boligareal>=126.5 1454 4595618000 5572.4790 *
## 7) Boligareal>=184.5 1395 8912244000 7935.0430
## 14) Boligareal< 213.5 597 3208348000 7071.9120 *
## 15) Boligareal>=213.5 798 4926398000 8580.7690 *
# knude 1
knot1 <- train$Salgspris
length(knot1)
## [1] 6108
sum((knot1 - mean(knot1))^2)
## [1] 65562631332
mean(knot1)
## [1] 4002.632
# knude 3
knot3 <- train$Salgspris[(train$Kommune=="Gentofte")]
sum((knot3 - mean(knot3))^2)
## [1] 22827070550
mean(knot3)
## [1] 6169.488
# knude 6
knot6 <- train$Salgspris[(train$Kommune=="Gentofte")&(train$Boligareal<198.5)]
sum((knot6 - mean(knot6))^2)
## [1] 9382568721
mean(knot6)
## [1] 5291.134
# knude 13
knot13 <- train$Salgspris[(train$Kommune=="Gentofte")&(train$Boligareal<198.5)&(train$Boligareal>=160.5)]
sum((knot13 - mean(knot13))^2)
## [1] 3948730255
mean(knot13)
## [1] 6386.468
unique(dt1.train.predict[(train$Kommune=="Gentofte")&(train$Boligareal<198.5)&(train$Boligareal>=160.5)])
## [1] 5572.479 7071.912Beslutningstræets dybde
Hvilken betydning har træets dybde?
Eksempel med estimation af maksimalt beslutningstræ (dvs. UDEN “pruning”).
# model
dt2 <- rpart(formula = Salgspris ~ Boligareal+Kommune, data=train, method="anova",
control = c(cp=0, xval=10))
rpart.plot(dt2) ## sammenlign med rpart.plot(dt1)
## Warning: labs do not fit even at cex 0.15, there may be some overplotting
plotcp(dt2)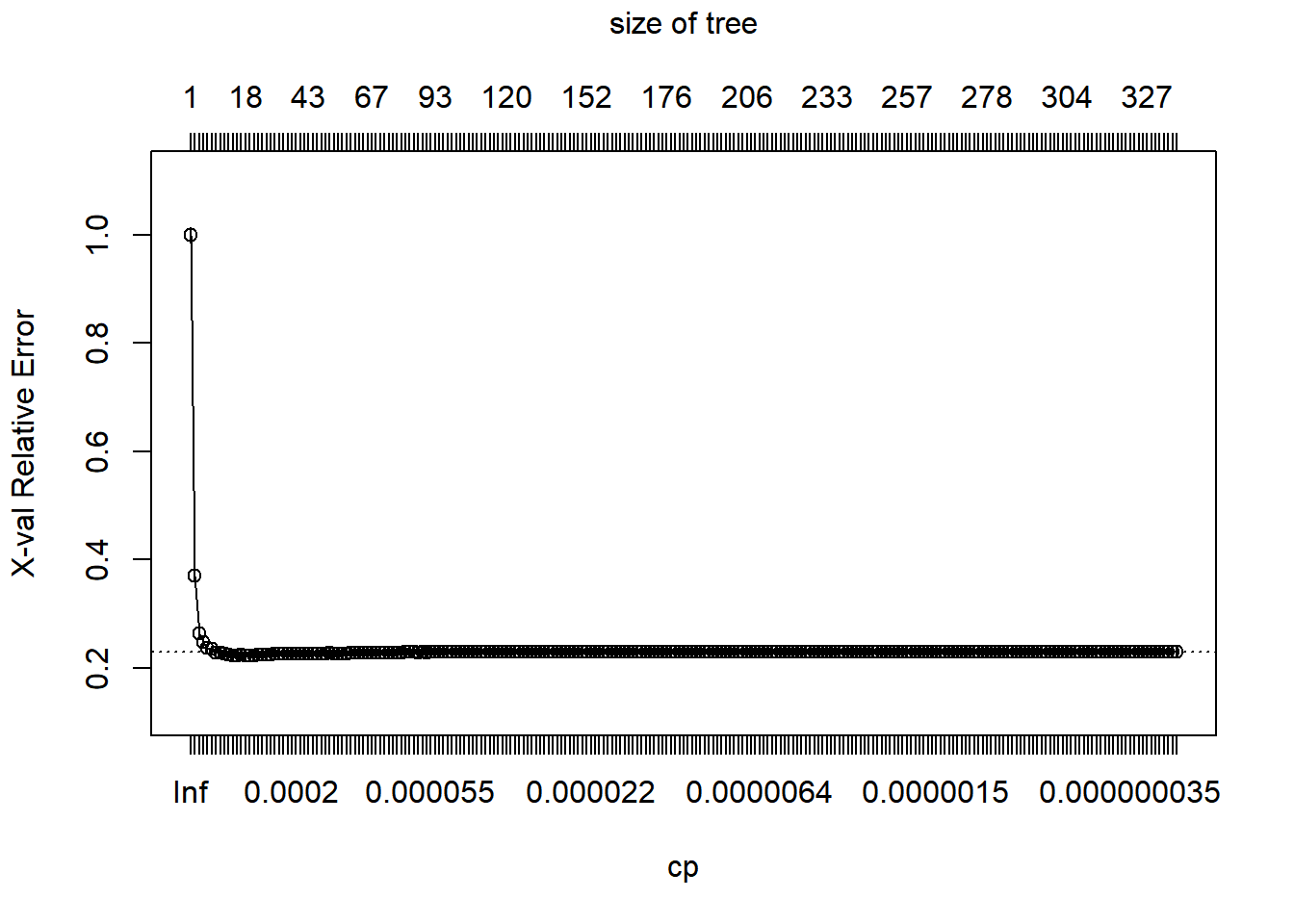
# sammenlign fit for trænings- og testdatasæt
dt2.train.predict <- predict(dt2, train)
dt2.test.predict <- predict(dt2, test)
DescTools::RMSE(dt2.train.predict, train$Salgspris)
## [1] 1467.361
DescTools::RMSE(dt2.test.predict, test$Salgspris)
## [1] 1558.686Pruning
Hvilken betydning har “pruning?”
Eksempel med estimation af beslutningstræ med 3 lag og MED “pruning.”
# model
dt3 <- rpart(formula = Salgspris ~ Boligareal+Kommune, data=train, method="anova",
control = c(maxdepth=3, xval=10))
rpart.plot(dt3) ## sammenlign med rpart.plot(dt1)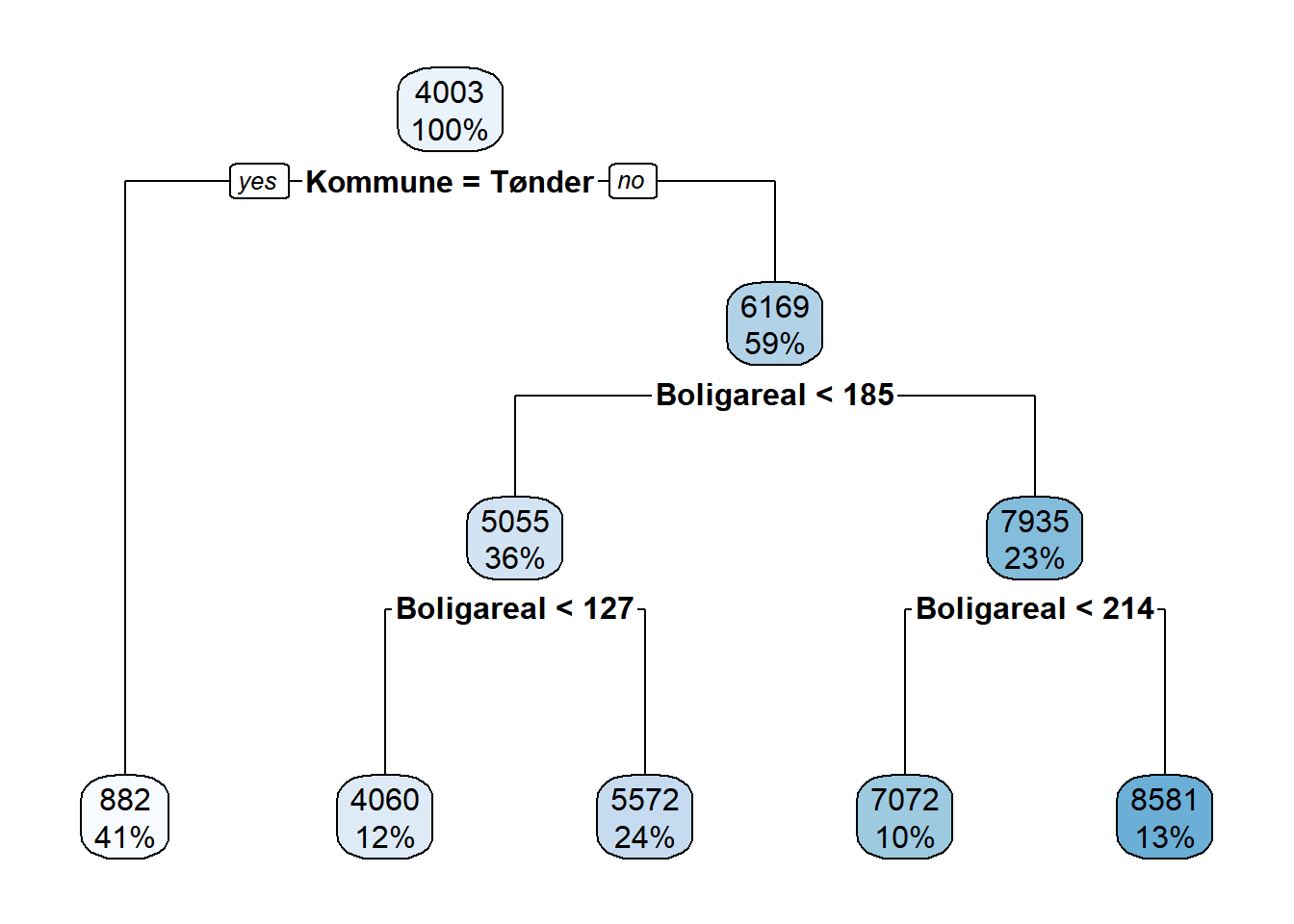
plotcp(dt3)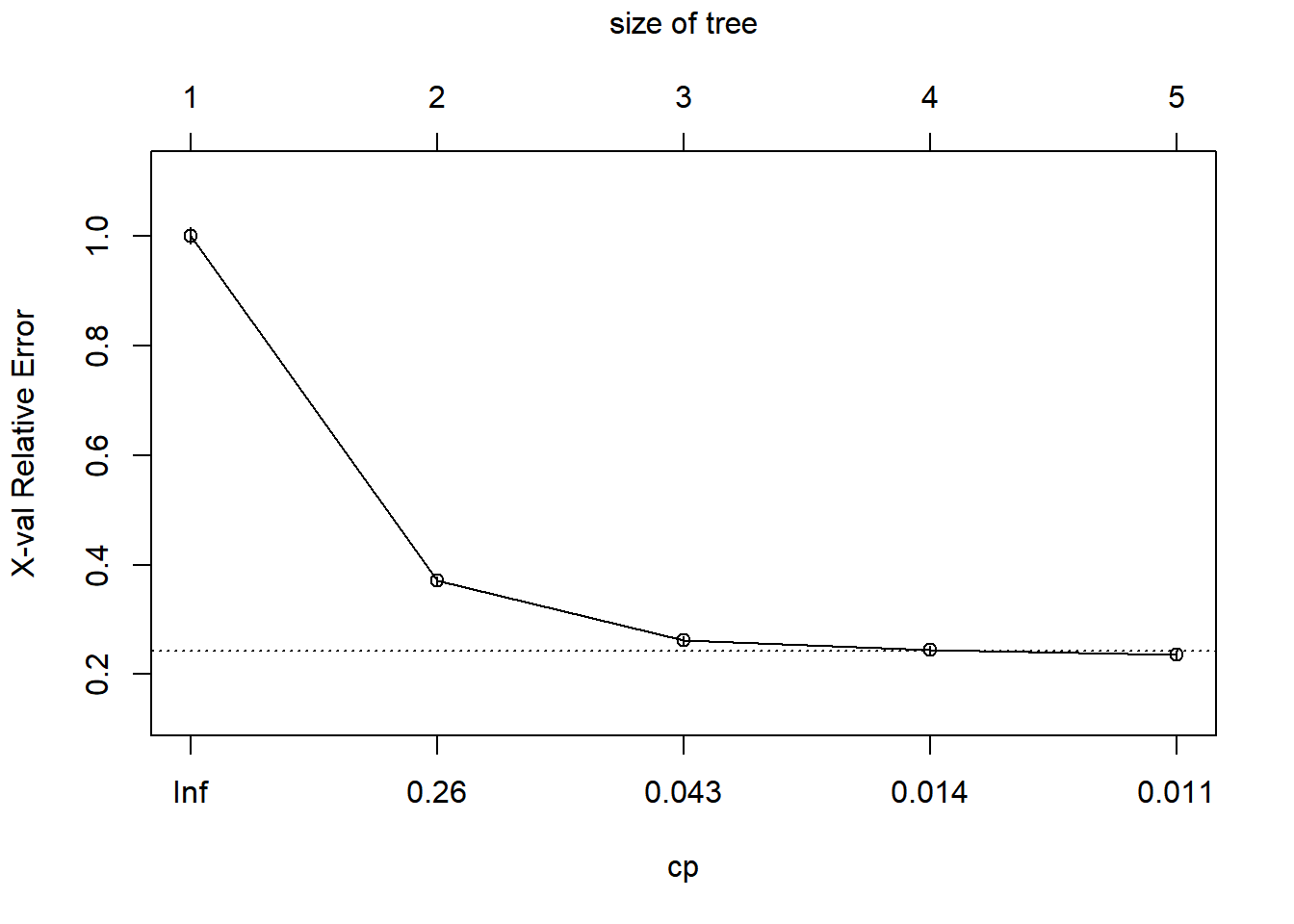
# sammenlign fit for trænings- og testdatasæt
dt3.train.predict <- predict(dt3, train)
dt3.test.predict <- predict(dt3, test)
DescTools::RMSE(dt3.train.predict, train$Salgspris)
## [1] 1580.034
DescTools::RMSE(dt3.test.predict, test$Salgspris)
## [1] 1576.344Betydning af forklarende variable
Hvor meget betyder hver forklarende variabel?
# model
dt4 <- rpart(formula = Salgspris ~ Boligareal+Opførselsår+Antal.værelser+Grundareal+Tidligere.solgt+Kommune,
data = train, method="anova", control = c(cp=0, xval=10))
# variable importance plot
vip(dt4)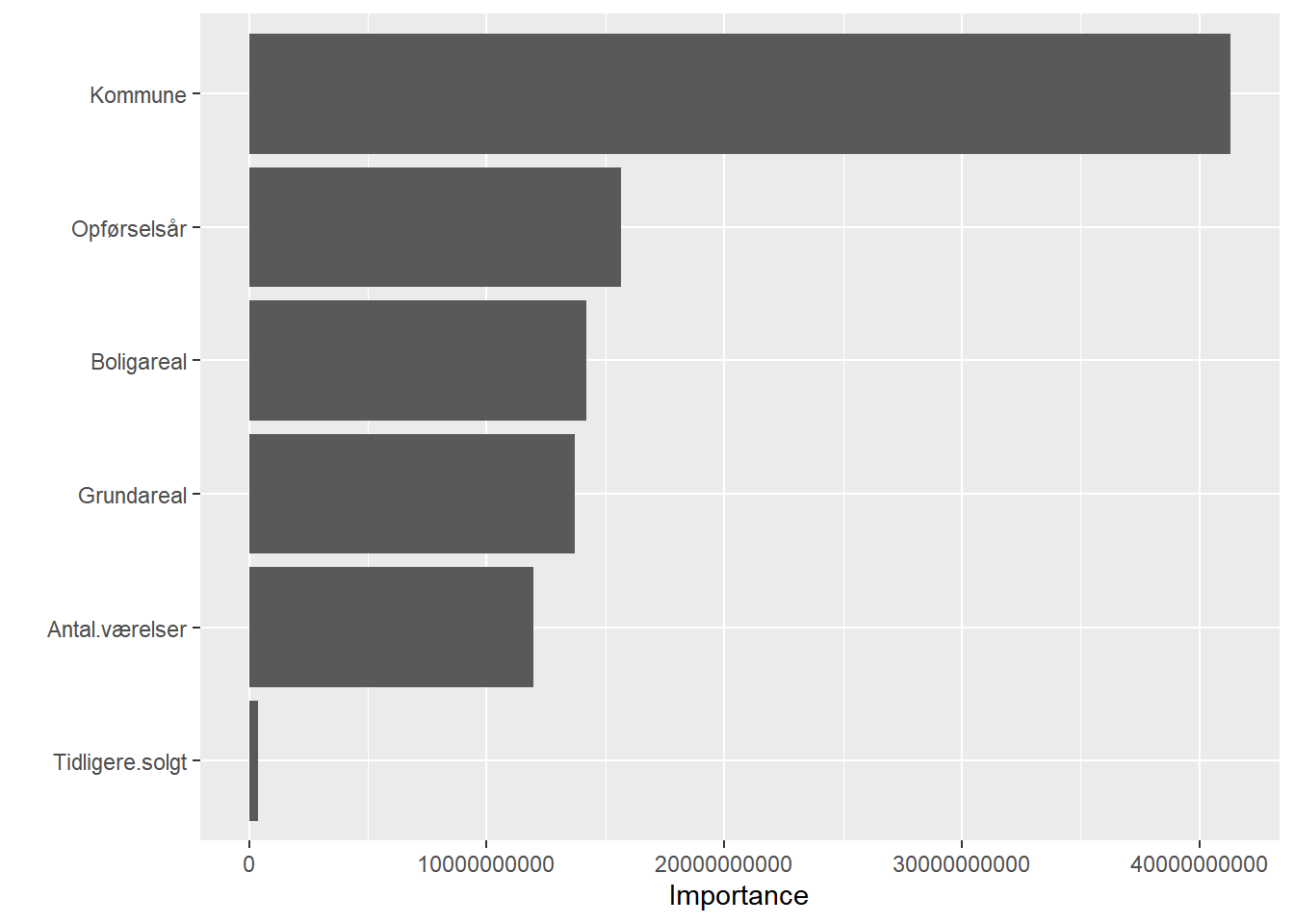
# partial dependence plots ("pdp") for kontinuerte forklarende variable: 1 variabel
pdp.Boligareal <- partial(dt4, pred.var = "Boligareal")
pdp.Boligareal
## Boligareal yhat
## 1 38.00 2095.392
## 2 57.76 2095.392
## 3 77.52 2446.473
## 4 97.28 2715.734
## 5 117.04 2932.118
## 6 136.80 3456.118
## 7 156.56 3597.617
## 8 176.32 3988.372
## 9 196.08 4453.851
## 10 215.84 5247.973
## 11 235.60 4929.438
## 12 255.36 4962.621
## 13 275.12 5035.658
## 14 294.88 5866.319
## 15 314.64 5056.218
## 16 334.40 5261.173
## 17 354.16 5272.109
## 18 373.92 5272.109
## 19 393.68 5272.109
## 20 413.44 5272.109
## 21 433.20 5272.109
## 22 452.96 5272.109
## 23 472.72 5272.109
## 24 492.48 5272.109
## 25 512.24 5272.109
## 26 532.00 5272.109
## 27 551.76 5272.109
## 28 571.52 5272.109
## 29 591.28 5272.109
## 30 611.04 5272.109
## 31 630.80 5272.109
## 32 650.56 5272.109
## 33 670.32 5272.109
## 34 690.08 5272.109
## 35 709.84 5272.109
## 36 729.60 5272.109
## 37 749.36 5272.109
## 38 769.12 5272.109
## 39 788.88 5272.109
## 40 808.64 5272.109
## 41 828.40 5272.109
## 42 848.16 5272.109
## 43 867.92 5272.109
## 44 887.68 5272.109
## 45 907.44 5272.109
## 46 927.20 5272.109
## 47 946.96 5272.109
## 48 966.72 5272.109
## 49 986.48 5272.109
## 50 1006.24 5272.109
## 51 1026.00 5272.109
autoplot(pdp.Boligareal)
## Warning: Use of `object[[1L]]` is discouraged. Use `.data[[1L]]` instead.
## Warning: Use of `object[["yhat"]]` is discouraged. Use `.data[["yhat"]]` instead.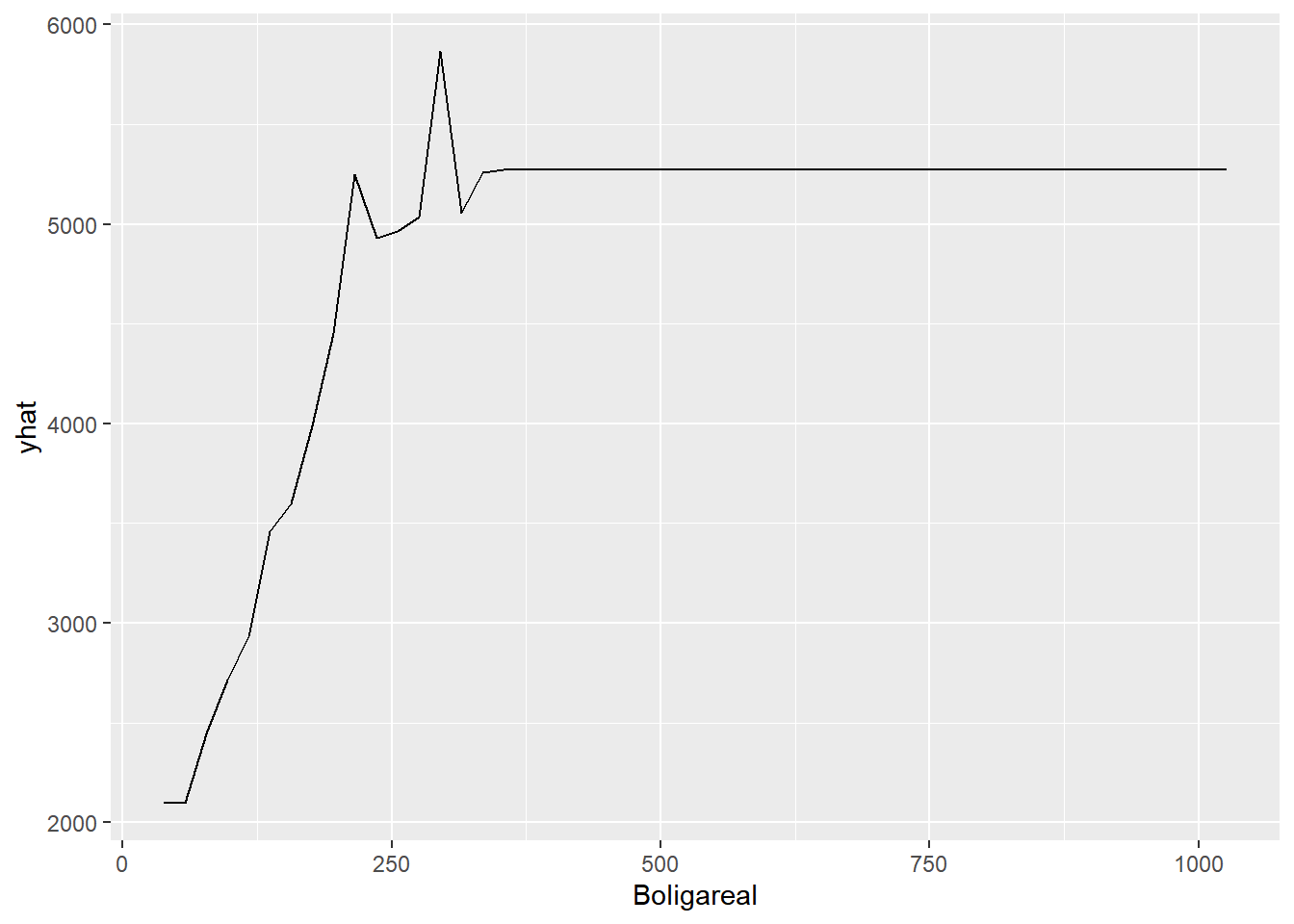
plot(train$Boligareal, train$Salgspris)
pdp.Opførselsår <- partial(dt4, pred.var = "Opførselsår")
autoplot(pdp.Opførselsår)
## Warning: Use of `object[[1L]]` is discouraged. Use `.data[[1L]]` instead.
## Warning: Use of `object[["yhat"]]` is discouraged. Use `.data[["yhat"]]` instead.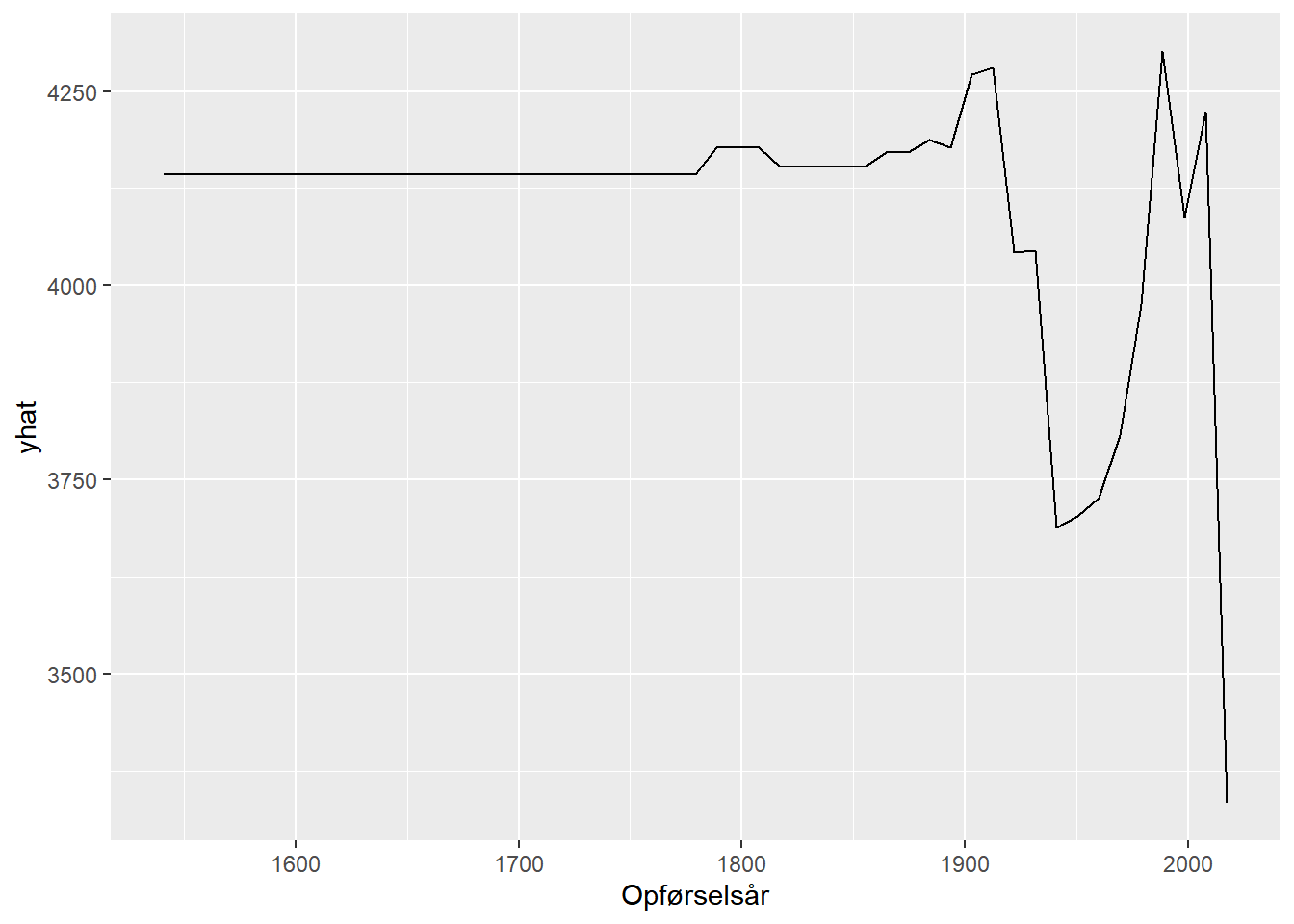
plot(train$Opførselsår, train$Salgspris)
pdp.Antal.værelser <- partial(dt4, pred.var = "Antal.værelser")
autoplot(pdp.Antal.værelser)
## Warning: Use of `object[[1L]]` is discouraged. Use `.data[[1L]]` instead.
## Warning: Use of `object[["yhat"]]` is discouraged. Use `.data[["yhat"]]` instead.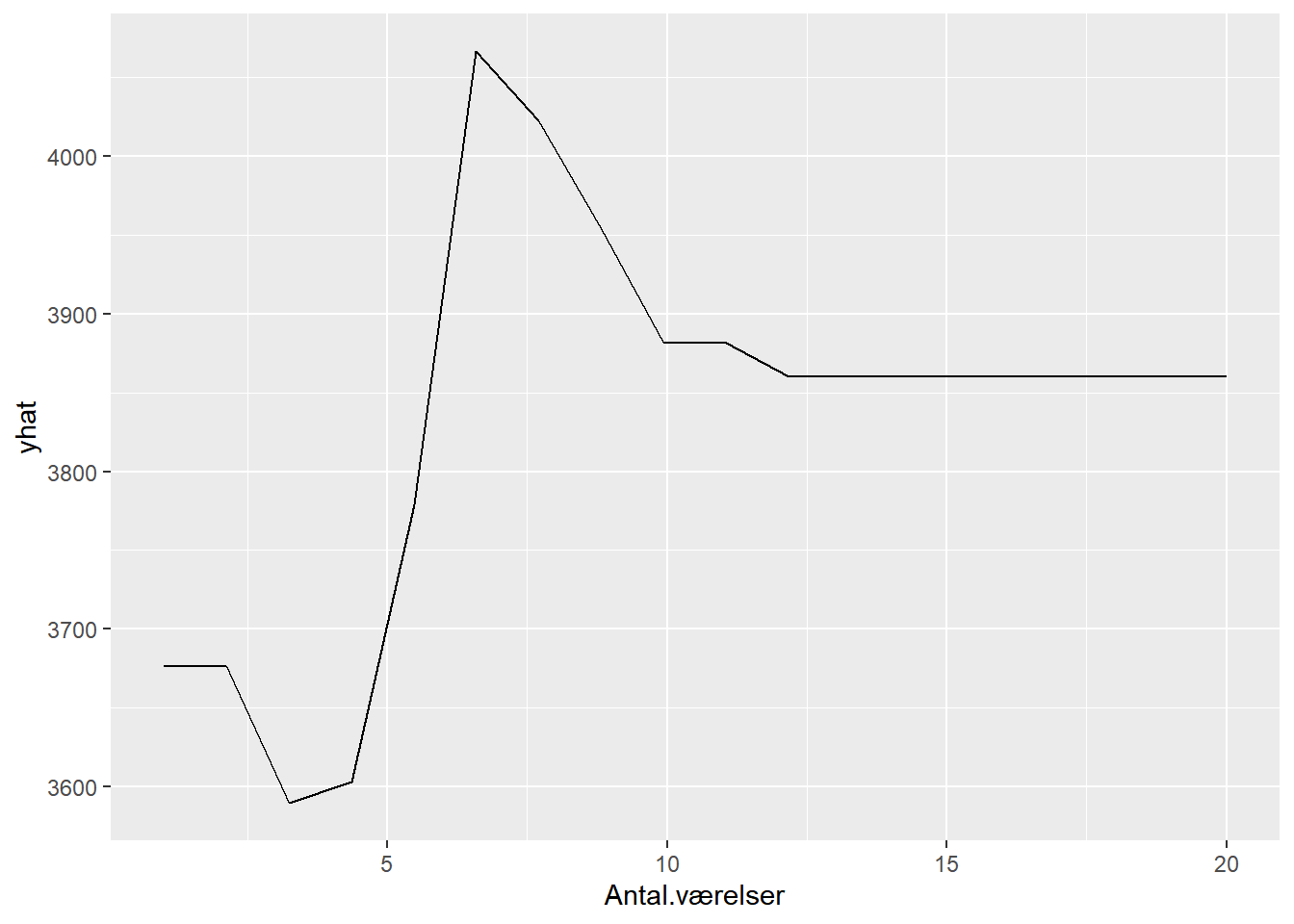
plot(train$Antal.værelser, train$Salgspris)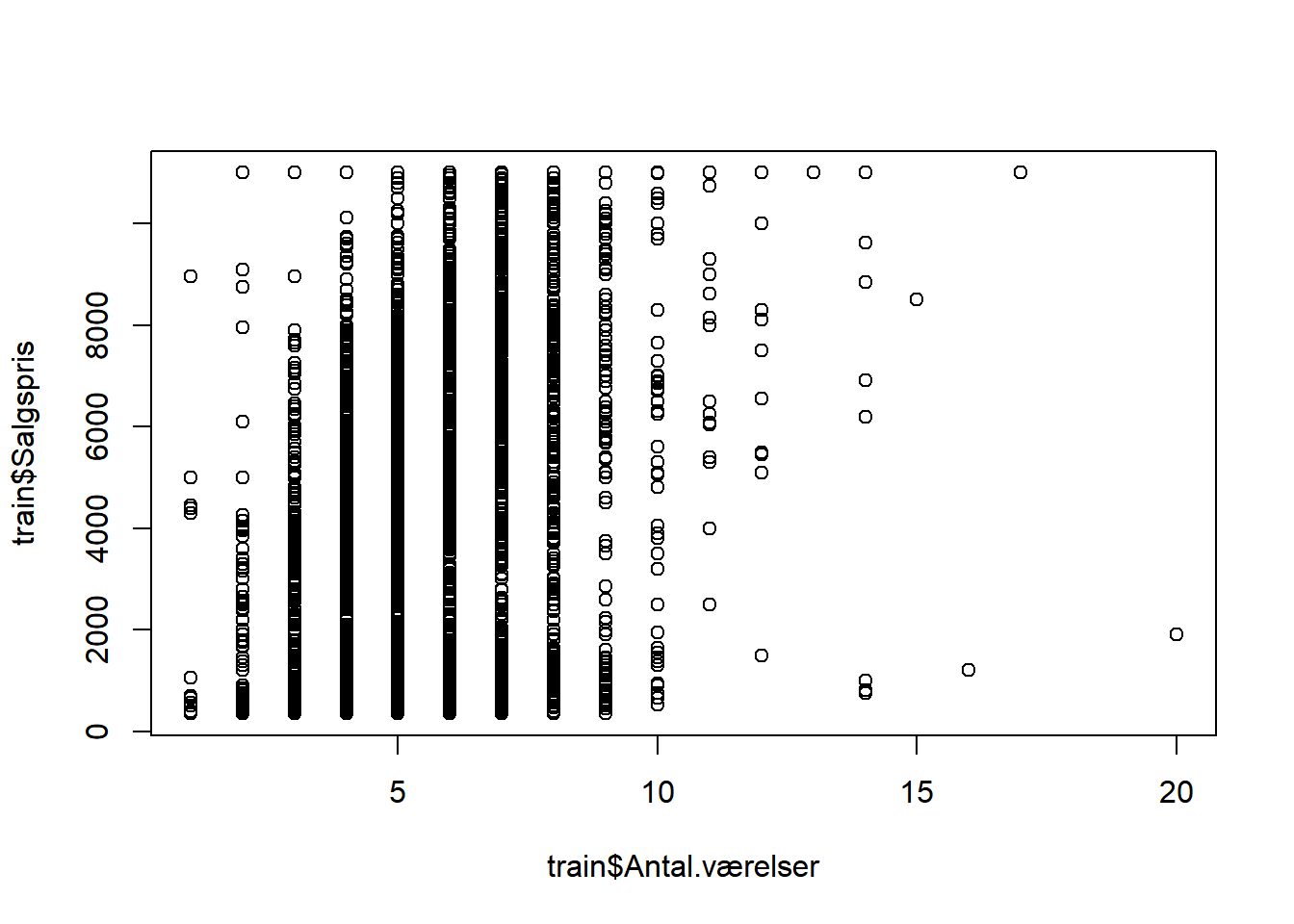
pdp.Grundareal <- partial(dt4, pred.var = "Grundareal")
autoplot(pdp.Grundareal)
## Warning: Use of `object[[1L]]` is discouraged. Use `.data[[1L]]` instead.
## Warning: Use of `object[["yhat"]]` is discouraged. Use `.data[["yhat"]]` instead.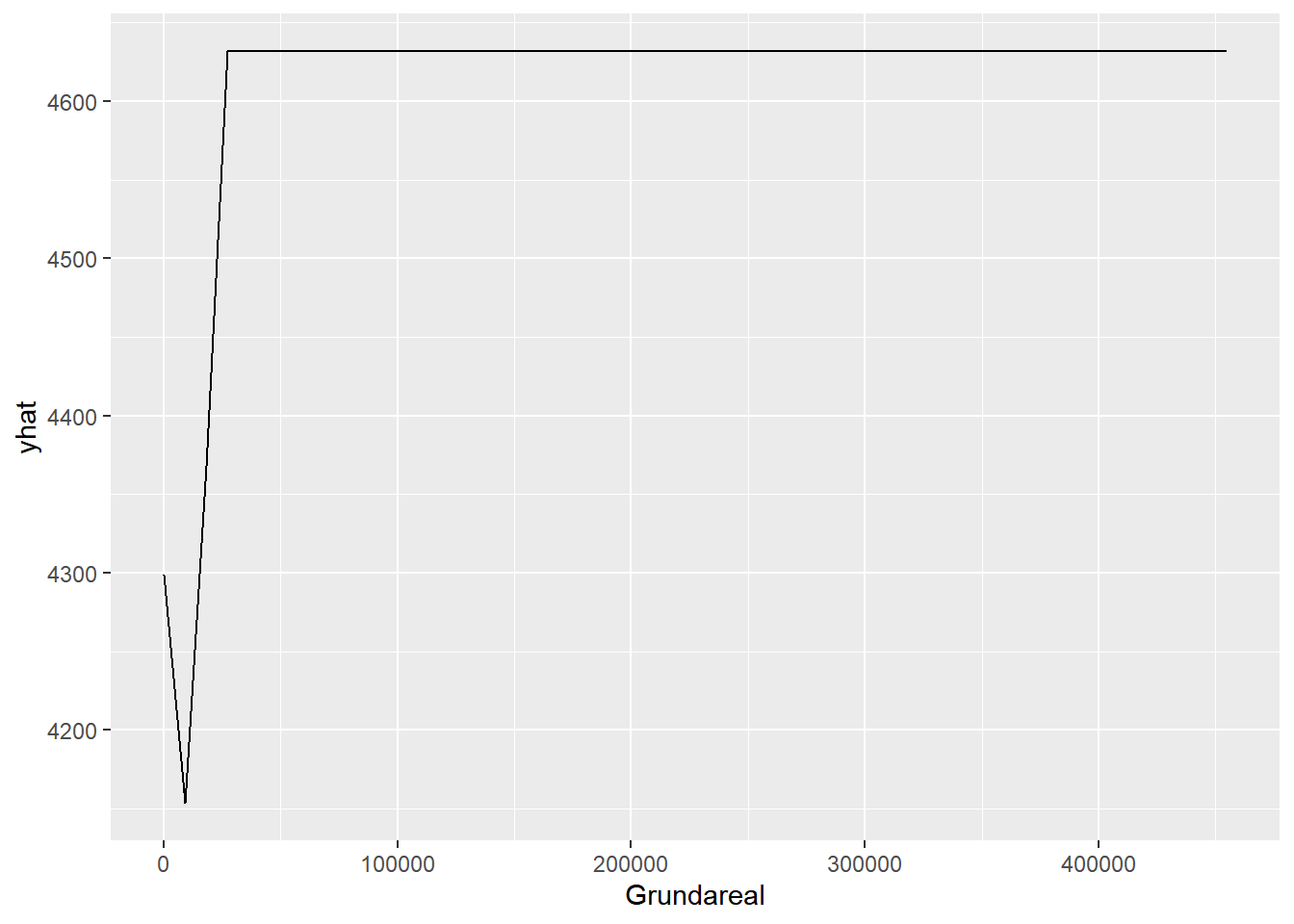
plot(train$Grundareal, train$Salgspris)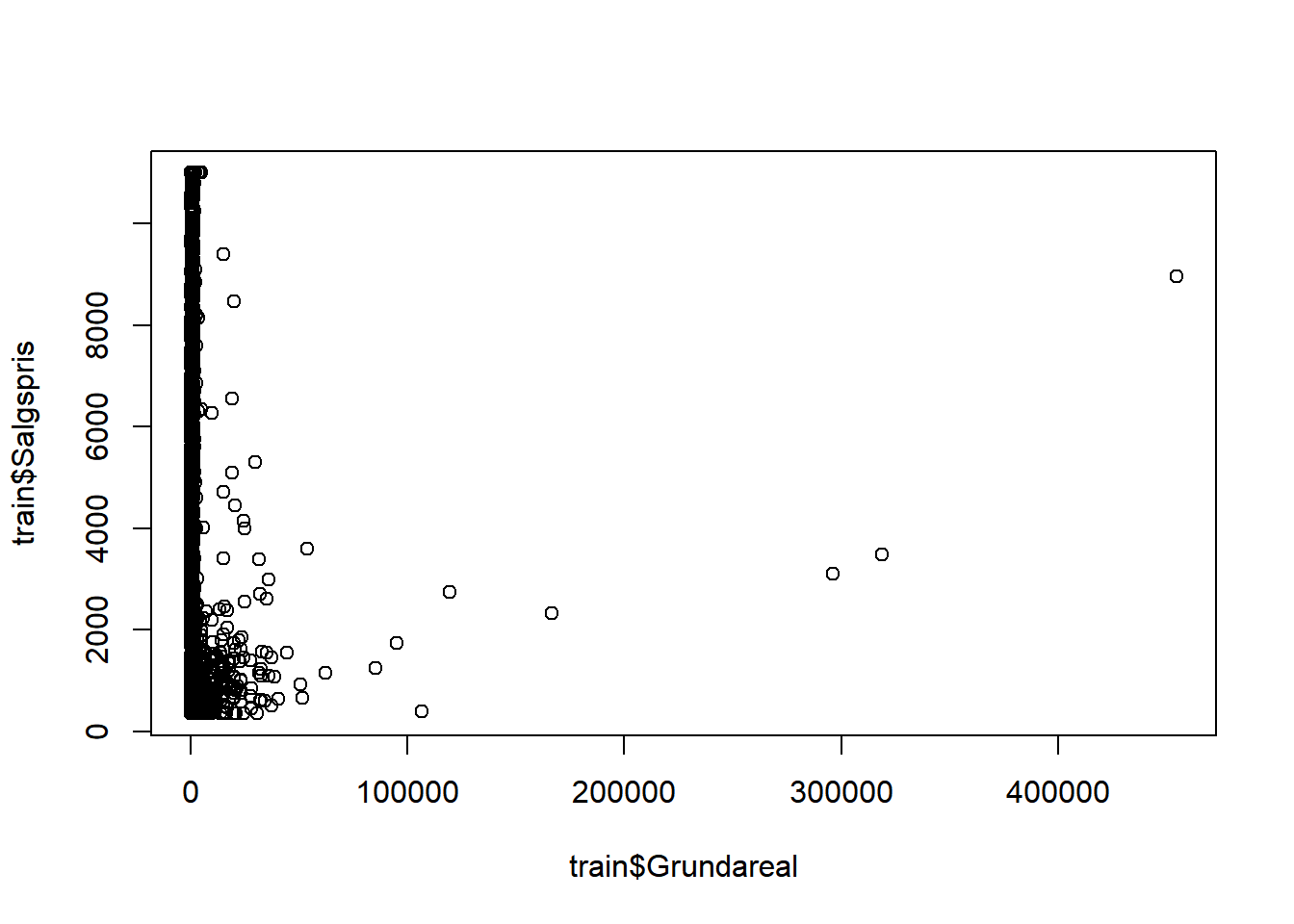
# partial dependence plots ("pdp") for kontinuerte forklarende variable: 2 variable
pdp.Boligareal.Opførselsår <- partial(dt4, pred.var = c("Boligareal", "Opførselsår"))
plotPartial(pdp.Boligareal.Opførselsår, levelplot=FALSE, drape=TRUE)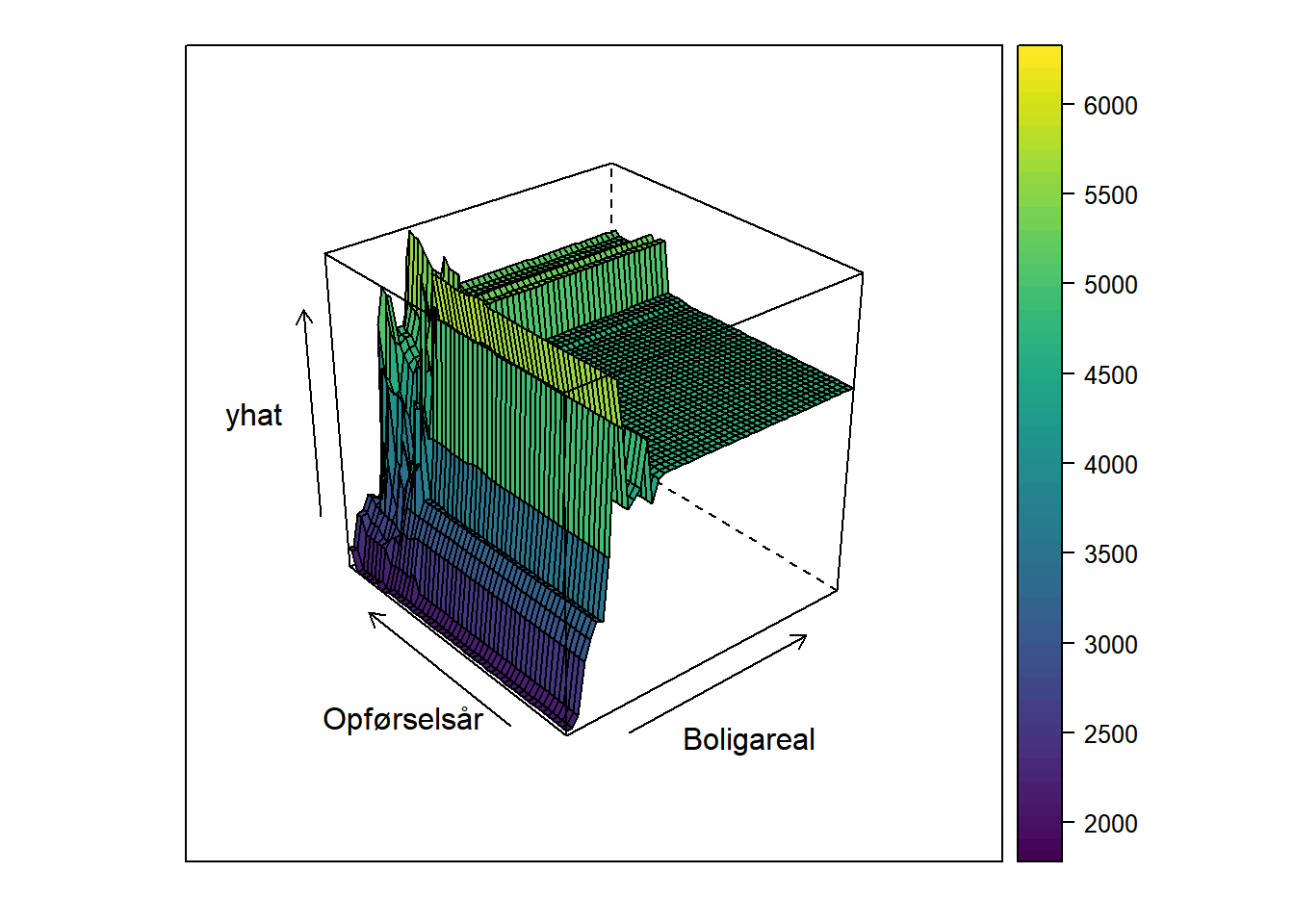
Bagging
# model
dt5 <- train(
Salgspris ~ Boligareal+Opførselsår+Antal.værelser+Grundareal+Tidligere.solgt+Kommune,
data = train,
method = "treebag",
trControl = trainControl(method="cv", number=10),
nbagg = 50,
control = rpart.control(minsplit=2, cp=0)
)
vip(dt5) ## sammenlign med vip(dt4)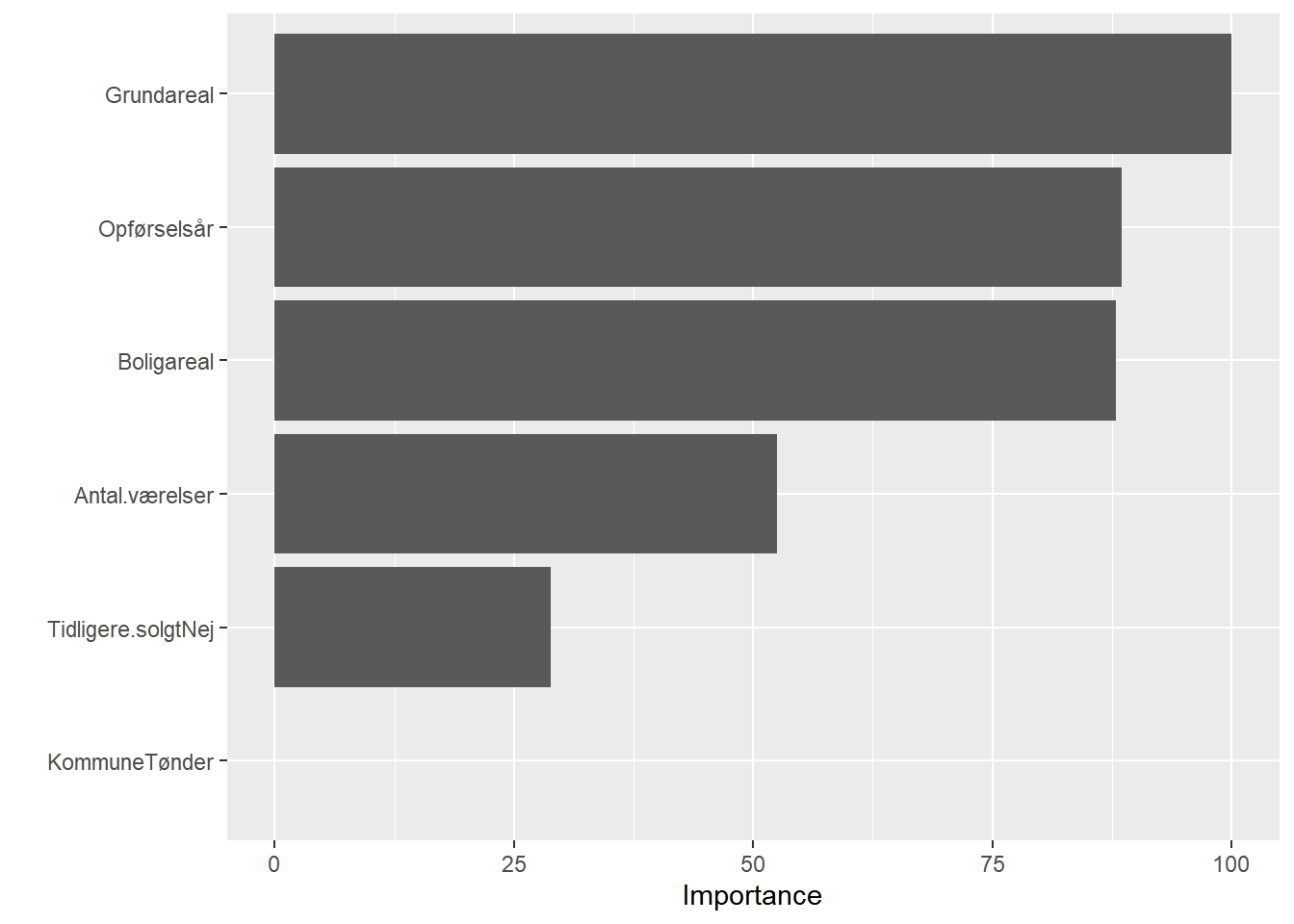
Random forests
Estimation
# model
dt6 <- train(
Salgspris ~ Boligareal+Opførselsår+Antal.værelser+Grundareal+Tidligere.solgt+Kommune,
data = train,
method = "ranger"
)Hypertuning
# vælg hvilke hyperparameterværdier, der skal undersøges
hyper_grid <- expand.grid(
mtry = c(1:5),
splitrule = c("variance","extratrees","maxstat"),
min.node.size = c(5, 10)
)# estimation af random forest model for hver kombination af hyperparametre
dt_tune <- train(
Salgspris ~ Boligareal+Opførselsår+Antal.værelser+Grundareal+Tidligere.solgt+Kommune,
data = train,
method = "ranger",
tuneGrid = hyper_grid
)# sammenligning af de estimerede modeller
results <- arrange(dt_tune$results, RMSE)
results
## mtry splitrule min.node.size RMSE Rsquared MAE RMSESD RsquaredSD MAESD
## 1 2 variance 10 1455.110 0.8038821 963.5533 33.48078 0.009276595 20.18752
## 2 2 variance 5 1458.715 0.8028612 962.4676 33.88389 0.009252204 21.58820
## 3 3 extratrees 10 1465.646 0.8009742 968.9371 34.96640 0.009651970 21.21562
## 4 3 variance 10 1467.982 0.8004989 962.4889 35.22994 0.009382435 22.59192
## 5 4 extratrees 10 1469.354 0.7999862 968.6904 36.08406 0.009910627 22.17343
## 6 3 maxstat 5 1471.402 0.7996145 980.3506 34.05371 0.009847222 20.12009
## 7 3 extratrees 5 1471.957 0.7992925 967.2131 34.52667 0.009334161 21.87398
## 8 5 extratrees 10 1472.431 0.7991919 969.7641 36.17279 0.009918929 22.30883
## 9 3 maxstat 10 1473.020 0.7992658 983.3653 35.12748 0.010241090 20.37377
## 10 4 variance 10 1475.801 0.7985254 966.0639 35.14168 0.009319587 23.03018
## 11 4 maxstat 10 1477.690 0.7977188 978.8162 36.55335 0.010318933 21.87229
## 12 4 maxstat 5 1479.209 0.7972980 977.9780 36.30596 0.010168541 22.57949
## 13 3 variance 5 1479.335 0.7976210 965.5289 34.37255 0.009059103 23.11744
## 14 4 extratrees 5 1483.452 0.7963470 971.5727 35.71164 0.009639408 23.02863
## 15 5 variance 10 1483.741 0.7964888 970.6303 35.37106 0.009321622 23.46073
## 16 2 maxstat 5 1484.736 0.7979994 1011.4640 32.71729 0.010148586 19.10762
## 17 5 extratrees 5 1487.343 0.7953623 973.9502 35.28342 0.009439750 22.68994
## 18 2 maxstat 10 1488.472 0.7971701 1014.9189 32.80092 0.010302429 19.11739
## 19 4 variance 5 1488.709 0.7952634 970.2621 35.42926 0.009303104 23.87076
## 20 2 extratrees 5 1489.168 0.7955557 1001.8671 31.49658 0.009018808 19.54391
## 21 5 maxstat 10 1491.949 0.7938191 983.4338 39.19683 0.010908063 23.98772
## 22 5 maxstat 5 1493.961 0.7933278 982.7309 38.09420 0.010581035 23.55947
## 23 2 extratrees 10 1496.582 0.7936034 1008.0833 31.22641 0.009146593 18.81949
## 24 5 variance 5 1497.279 0.7930669 975.1887 35.82601 0.009435892 24.68483
## 25 1 variance 5 1635.621 0.7841928 1219.6067 26.27294 0.009905537 18.05028
## 26 1 variance 10 1639.854 0.7835121 1223.7972 28.84381 0.010138700 20.35316
## 27 1 maxstat 10 1712.228 0.7735645 1301.9841 28.14747 0.010358127 27.39370
## 28 1 maxstat 5 1714.385 0.7739082 1306.6919 27.88852 0.010464434 26.21179
## 29 1 extratrees 5 1829.719 0.7436443 1387.6357 24.42494 0.009635193 16.76873
## 30 1 extratrees 10 1834.225 0.7440079 1393.8018 28.55343 0.008275010 22.55080