Modul 2: Regression - EKSEMPEL
Andet modul omhandler udvidelser af lineær regressionsanalyse. I slutningen af modul 1 så vi, hvorledes man kan bruge lineær regressionsanalyse til at opstille en model, der forklarer én variabel (responsvariablen) ud fra en række andre variable (forklarende variable).
Her i andet modul skal vi se på, hvorledes vi med hjælp af en række grundlæggende Machine Learning-teknikker kan gøre den lineære regressionsanalyse mere robust (dvs. skabe mere robust/pålidelige resultater) samt hvorledes den lineære regressionsanalyse kan udvides til andre typer af data.
Lineær regressionsanalyse (fortsat)
Test- og træningsdata
# vælg randomiseringsseed
set.seed(1000)# lav test- og træningsdatasæt (træning: 2/3 af data, test: 1/3 af data)
index <- sample(1:nrow(bolig0), 2/3*nrow(bolig0))
bolig1.train <- bolig0[index,]
bolig1.test <- bolig0[-index,]# estimation af model (på træningsdatasæt)
bolig1.mlr <- lm(Salgspris ~ ., data = bolig1.train)# vis estimation af regressionsmodel
summary(bolig1.mlr)
##
## Call:
## lm(formula = Salgspris ~ ., data = bolig1.train)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12595356 -2115100 -98908 2088100 8688281
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.822e+06 1.662e+06 3.503 0.000463 ***
## Opførselsår -3.625e+03 8.486e+02 -4.272 1.97e-05 ***
## Antal.værelser 5.452e+05 2.720e+04 20.042 < 2e-16 ***
## Grundareal -6.618e-01 1.573e+00 -0.421 0.674015
## Boligareal 1.355e+04 7.404e+02 18.297 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2795000 on 6103 degrees of freedom
## Multiple R-squared: 0.2716, Adjusted R-squared: 0.2711
## F-statistic: 568.9 on 4 and 6103 DF, p-value: < 2.2e-16# beregn fittede værdier (for træningsdatasæt)
bolig1.train.fit <- fitted(bolig1.mlr)
# beregn predikterede værdier (for testdatasæt)
bolig1.test.predict <- predict(bolig1.mlr, bolig1.test)# beregn mean squared error (mse)
DescTools::MSE(bolig1.train.fit, bolig1.train$Salgspris)
## [1] 7.807028e+12
DescTools::MSE(bolig1.test.predict, bolig1.test$Salgspris)
## [1] 7.819862e+12# beregn root mean squared error (rmse)
DescTools::RMSE(bolig1.train.fit, bolig1.train$Salgspris)
## [1] 2794106
DescTools::RMSE(bolig1.test.predict, bolig1.test$Salgspris)
## [1] 2796402# beregn mean absolute error (mae)
DescTools::MAE(bolig1.train.fit, bolig1.train$Salgspris)
## [1] 2357011
DescTools::MAE(bolig1.test.predict, bolig1.test$Salgspris)
## [1] 2342003Krydsvalidering
# indlæs funktionsbibliotek til brug for krydsvalidering
library(caret)
## Indlæser krævet pakke: lattice
##
## Vedhæfter pakke: 'caret'
## De følgende objekter er maskerede fra 'package:DescTools':
##
## MAE, RMSE# vælg randomiseringsseed
set.seed(100)# lav test- og træningsdatasæt (træning: 2/3 af data, test: 1/3 af data)
index <- sample(1:nrow(bolig0), 2/3*nrow(bolig0))
bolig2.train <- bolig0[index,]
bolig2.test <- bolig0[-index,]# angiv at der skal laves 10-turs krydsvalidering ("cv" = "cross validation")
xval.control <- trainControl(method = "cv", number = 10)# lav 10-turs krydsvalidering ("lm" = "linear (regression) model")
bolig2.xval <- train(Salgspris ~., data = bolig2.train, method = "lm", trControl = xval.control)
bolig2.xval
## Linear Regression
##
## 6108 samples
## 4 predictor
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 5498, 5497, 5497, 5497, 5497, 5497, ...
## Resampling results:
##
## RMSE Rsquared MAE
## 2780708 0.2779418 2331666
##
## Tuning parameter 'intercept' was held constant at a value of TRUE# beregn predikterede værdier (for testdatasæt)
bolig2.test.predict <- predict(bolig2.xval, bolig2.test)# beregn mean squared error (mse)
DescTools::MSE(bolig2.test.predict, bolig2.test$Salgspris)
## [1] 8.464192e+12# beregn root mean squared error (rmse)
DescTools::RMSE(bolig2.test.predict, bolig2.test$Salgspris)
## [1] 2909328# beregn mean absolute error (mae)
DescTools::MAE(bolig2.test.predict, bolig2.test$Salgspris)
## [1] 2360591Logistisk regressionsanalyse
# indlæs funktionsbibliotek til analyse af logistisk regression
library(ROCR)# indlæs data
kunde <- read.xlsx("Kundetilfredshed.xlsx", colNames = TRUE)
kunde$TilfredsNum <- ifelse(kunde$Tilfreds=="Ja",1,0)Estimation
# estimation af model
kunde.glm <- glm(TilfredsNum ~ Kontakt + Hjælpsom + Viderestillet + Køn + Alder, data = kunde, family=binomial(link='logit'))
summary(kunde.glm)
##
## Call:
## glm(formula = TilfredsNum ~ Kontakt + Hjælpsom + Viderestillet +
## Køn + Alder, family = binomial(link = "logit"), data = kunde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.8957 0.1730 0.2144 0.2457 1.6973
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.390187 1.096683 2.179 0.0293 *
## KontaktTelefon 0.166632 0.669872 0.249 0.8036
## KontaktTelefon & email -0.562052 1.013473 -0.555 0.5792
## HjælpsomNej -4.425916 0.686753 -6.445 1.16e-10 ***
## ViderestilletNej 0.952619 0.633568 1.504 0.1327
## KønMand 0.535522 0.576289 0.929 0.3528
## Alder 0.004416 0.017618 0.251 0.8021
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 157.35 on 385 degrees of freedom
## Residual deviance: 107.67 on 379 degrees of freedom
## AIC: 121.67
##
## Number of Fisher Scoring iterations: 6
anova(kunde.glm, test="Chisq")
## Analysis of Deviance Table
##
## Model: binomial, link: logit
##
## Response: TilfredsNum
##
## Terms added sequentially (first to last)
##
##
## Df Deviance Resid. Df Resid. Dev Pr(>Chi)
## NULL 385 157.35
## Kontakt 2 0.630 383 156.72 0.7298
## Hjælpsom 1 46.075 382 110.64 1.138e-11 ***
## Viderestillet 1 1.997 381 108.65 0.1576
## Køn 1 0.911 380 107.74 0.3398
## Alder 1 0.063 379 107.67 0.8015
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# beregn estimerede sandsynligheder for kundetilfredshed
kunde.fit <- predict(kunde.glm, kunde, type='response')
hist(kunde.fit)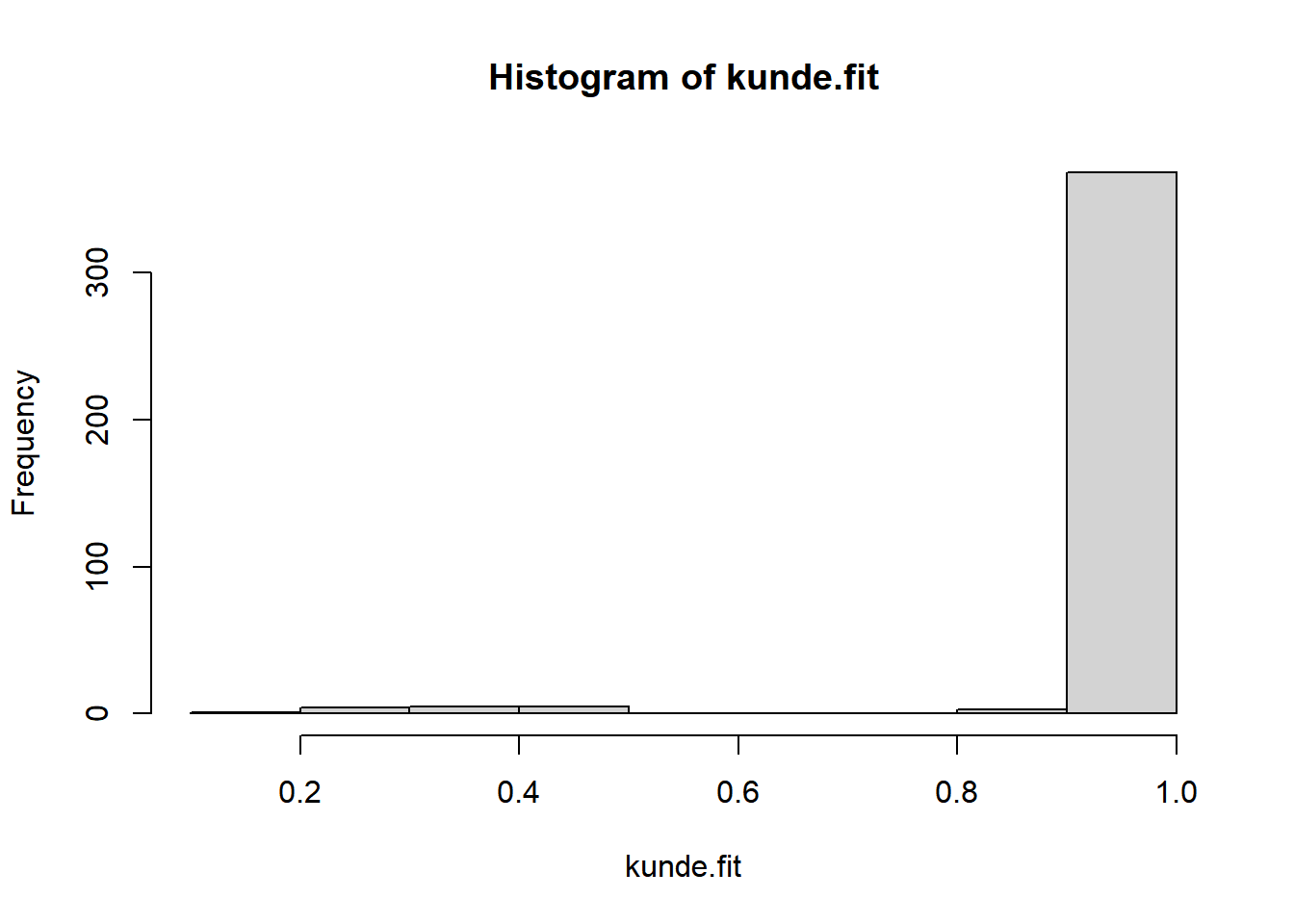
# optegn estimerede sandsynligheder opdelt på tilfredse hhv. ikke-tilfredse
kunde.faktisk_vs_fit <- data.frame(kunde$Tilfreds, kunde.fit)
hist(kunde.fit[kunde$Tilfreds=="Ja"])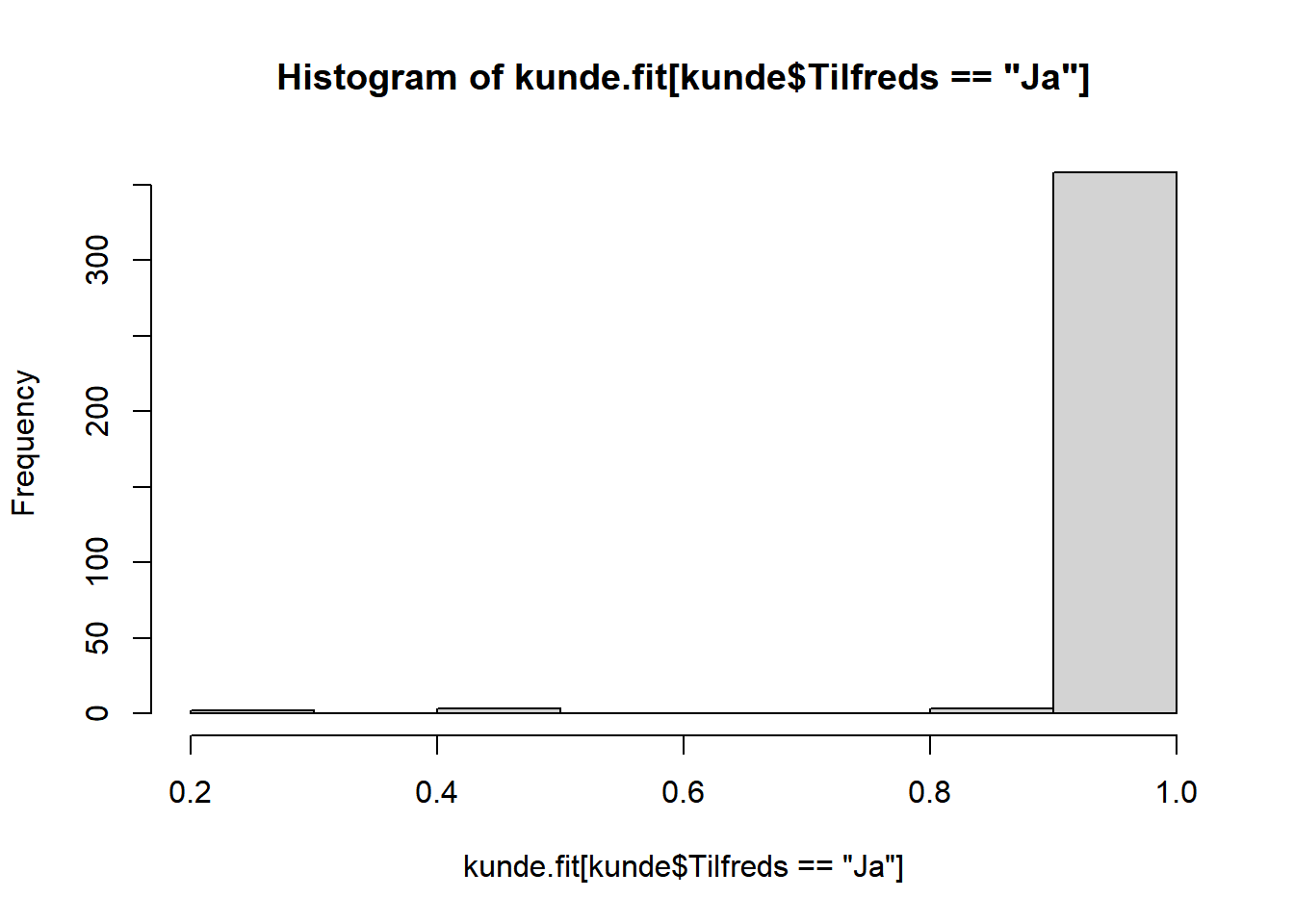
hist(kunde.fit[kunde$Tilfreds=="Nej"])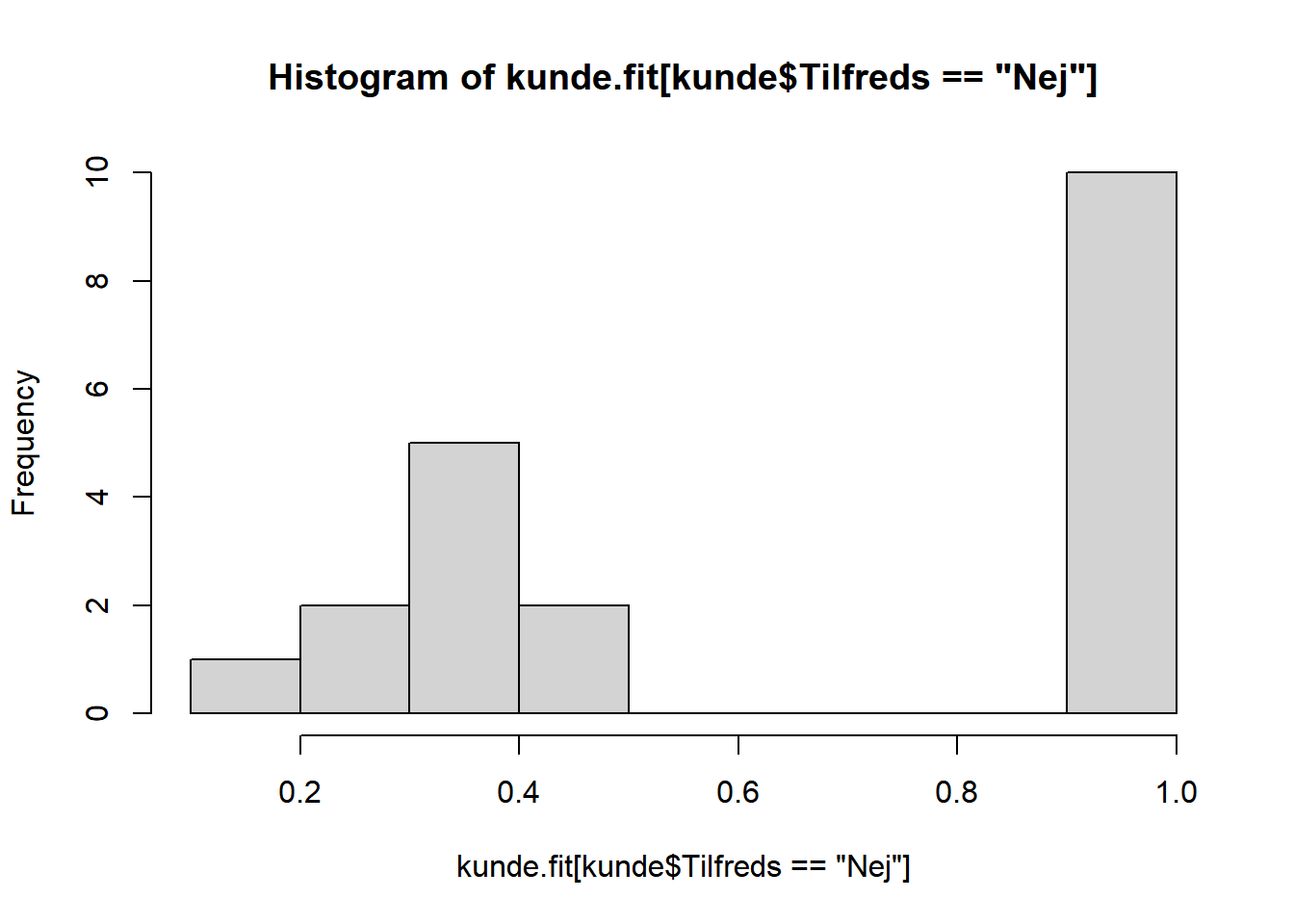
Evaluering af model fit
# konstruér "confusion matrix"
kunde.JaNej <- ifelse(kunde.fit > 0.5, "Ja", "Nej")
kunde.JaNej <- factor(kunde.JaNej, level=c("Ja","Nej"))
kunde.ConfMatrix <- table(kunde$Tilfreds, kunde.JaNej, dnn=c("Faktisk","Forudsagt"))
confusionMatrix(kunde.ConfMatrix)
## Confusion Matrix and Statistics
##
## Forudsagt
## Faktisk Ja Nej
## Ja 361 5
## Nej 10 10
##
## Accuracy : 0.9611
## 95% CI : (0.9367, 0.9781)
## No Information Rate : 0.9611
## P-Value [Acc > NIR] : 0.5681
##
## Kappa : 0.5515
##
## Mcnemar's Test P-Value : 0.3017
##
## Sensitivity : 0.9730
## Specificity : 0.6667
## Pos Pred Value : 0.9863
## Neg Pred Value : 0.5000
## Prevalence : 0.9611
## Detection Rate : 0.9352
## Detection Prevalence : 0.9482
## Balanced Accuracy : 0.8199
##
## 'Positive' Class : Ja
## # tegn ROC-kurve
kunde.ROCdata <- ROCR::prediction(1-kunde.fit, kunde$Tilfreds)
kunde.ROCkurve <- performance(kunde.ROCdata, measure="tpr", x.measure="fpr")
plot(kunde.ROCkurve)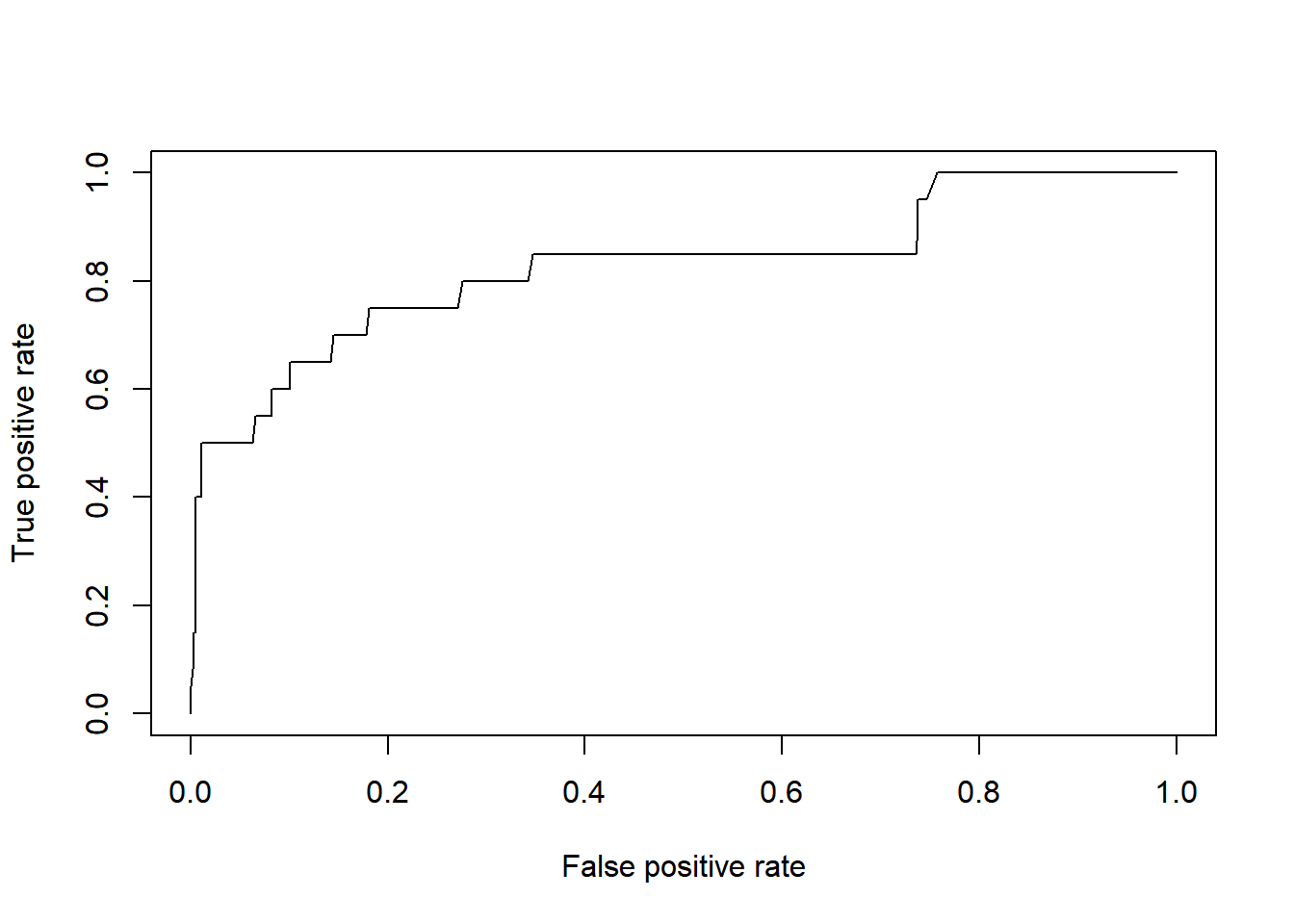
# Beregn AUC
Cstat(kunde.glm)
## [1] 0.8267077