Kapitel 3 Simulering
I dette afsnit vil der redegøres for lidt baggrundsviden omkring simulering, og hvordan tilsyneladende tilfældige tal kan genereres ved hjælp af algoritmer. Derefter vil der ses på, hvordan programmeringssproget R kan udnyttes, til at udføre disse simuleringer hurtigt og simpelt.
En definition på simulering er;
A situation or event that seems real but is not real, used especially in order to help people deal with such situations or events. - (Dictonary 2020).
Ud fra definitionen, er formålet altså ved simuleringer at efterligne virkeligheden, så de analyser der gøres på baggrund af simuleringerne, kan bruges i virkeligheden når lignende situationer opstår.
En branche, hvor simuleringer er et yderst vigtigt redskab, er i motorsporten. I Formel 1 benytter holdene sig af simulatorer, hvor de genskaber bilerne og derved kan teste nye dele inden de producerer dem i virkeligheden for at spare ressourcer, (F1 2020).
3.1 Pseudorandom number generator
I dette afsnit introduceres pseudo-tilfældige talgeneratorer, PRNG’er (fra engelsk pseudorandom number generators), og hvorledes disse kan bringes i anvendelse i forbindelse med simuleringer. I de tilhørende underafsnit beskrives først en type af PRNG kaldet lineær kongruens generator, og dernæst en metode til at omdanne uniformt fordelte talt til standard normalfordelte tal kaldet Box-Muller-transformation.
En computer fungerer ved, at den modtager et input, der bearbejdes af en algoritme, som derefter returnerer et output. Der findes ingen algoritmer, som er i stand til at generere faktisk tilfældige tal. Grunden til dette er, hvis der gives det samme input, til den samme algoritme, vil resultatet være det samme output som tidligere, fordi en computer fungerer på baggrund af matematik og derfor er deterministisk. Det er dog muligt ved hjælp af en beregningsmodel at skabe en illusion af ægte tilfældighed. En sådan model kaldes for en PRNG.
En PRNG beskrives ved nedenstående karakteristika, (Oxford 2015).
Et input, eller seed, på baggrund af hvilket algoritmen beregner et pseudo-tilfældigt output. Herefter fortsætter algoritmen rekursivt, hvor det forrige output anvendes som nyt input.
Cyklussen, som beskriver den talserie, algoritmen beregner.
Perioden, som beskriver hvor mange repetitioner algoritmen gennemløber, før cyklussen gentages. Jo kortere perioden er, des mere gennemskuelig vil algoritmen fremstå.
Fordelingen af cyklussen. Som det illustreres på figur 3.1 (genskabt ud fra figuren i (Math 2016, 3:07)), er det ideelt for en PRNG, at cyklussen er uniformt fordelt, mens andre typer af fordelinger ikke er ideelle.
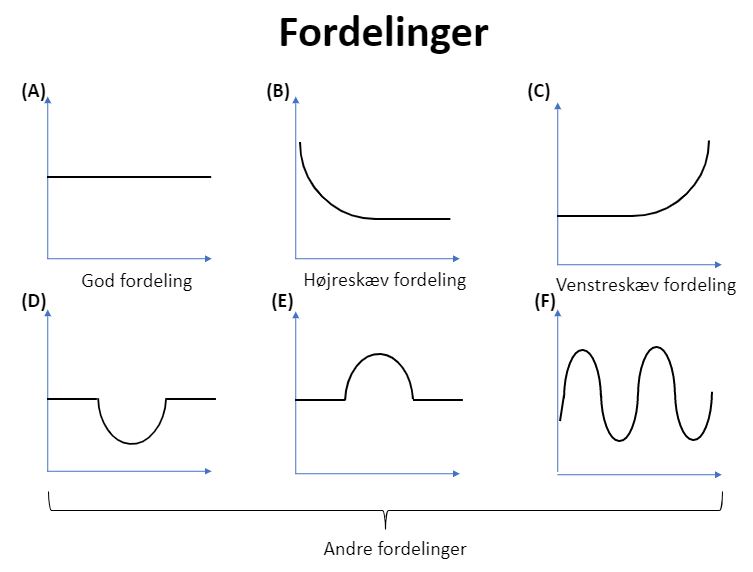
Figur 3.1: PRNG-fordelinger. (A) viser en uniform fordeling af cyklussen, hvilket er ideelt for en PRNG. (B) og (C) viser to skæve fordelinger, hvor der derfor er større sandsynlighed for lave (B) og store (C) værdier. (D), (E) og (F) viser andre typer af fordelinger, der heller ikke er ideelle for en PRNG.
I takt med udviklingen af de teknologiske hjælpemidler er der opstået mere effektive algoritmer til PRNG. En af de mere kendte og hyppigt anvendte algoritmer er lineær kongruens generator, som gennemgåes i det følgnede afsnit.
3.1.1 Lineær kongruens generator
Dette afsnit beskriver, hvorledes lineær kongruens generatorer, LCG (fra engelsk linear congruential generator), kan generere en cyklus af tilsyneladende tilfældige tal, som, ved valg af passende parametre, er uniformt fordelt. Det følgende afsnit er primært baseret på kilden (Radziwill 2015).
LCG danner en cyklus af tal ved iteration, og kræver kun få parametre. Helt specifikt er algoritmen givet ved
Definition 3.1 Givet \(a, c, m \in \mathbb{Z}\), hvor \(0 < m, 0 < a\) og \(0 \leq c \leq m\), genererer algoritmen lineær kongruens generator en talsekvens, \(X = [X_0, X_1, \ldots, X_n]\), givet ved \(X_i = (a \cdot X_{i-1} + c) \mod m.\)
Algoritmen fungerer således: Der startes ved et seed, angivet med \(X_0\), som bliver multipliceret med faktoren, \(a\), og konstantleddet, \(c\), adderes. Derefter tages modulus \(m\) af værdien.
På figur 3.2, fra (Cmglee 2015), ses tre eksempler på LCG. De to første eksempler har samme parametre, men forskelligt seed.
Figur 3.2: Tre eksempler på algoritmen lineær kongruens generator. De to første eksempler har samme parametre, men forskelligt seed.
I teorien er parametrene arbitrære, men i praksis bruges nogle værdier oftere end andre. Begrundelsen for dette er, at der findes værdier for parametrene, der vil returnere en åbentlyst ikke-tilfældig cyklus. Et eksempel på dette er ved parametrene \(m = 64, a = 33\) og \(c = 12\). Efter et antal iterationer vil der ses et mønster i værdierne, og det vil være åbenlyst, at denne cyklus i virkeligheden ikke er tilfældig. Dette eftervises i det følgende eksempel.
Eksempel
De følgende simuleringer er baseret på kilden (Trumbo 2005).
Først defineres en funktion for LCG-algoritmen, som tager de nødvendige parametre for algoritmen som inputs. Derudover angives også et argument, \(n\), der fortæller hvor mange iterationer algoritmen skal foretage.
lcg <- function(modulus, faktor, tilvaekst, seed, iterationer) {
r <- c()
r[1] <- seed
for (i in 1: (iterationer-1)) {
r[i + 1] <- (faktor * r[i] + tilvaekst) %% modulus
}
return(r)
}Det følgende er et eksempel på en LCG-cyklus med en periode på \(16\).
## [1] 57 37 17 61 41 21 1 45 25 5 49 29 9 53 33 13 57 37 17 61På figur 3.3 plottes denne cyklus. Det er åbenlyst at cyklussen ikke er tilfældig, da den danner et synligt mønster. Selv, hvis antallet af gange, LCG køres igennem, ændres, vil mønstret ikke ændres.
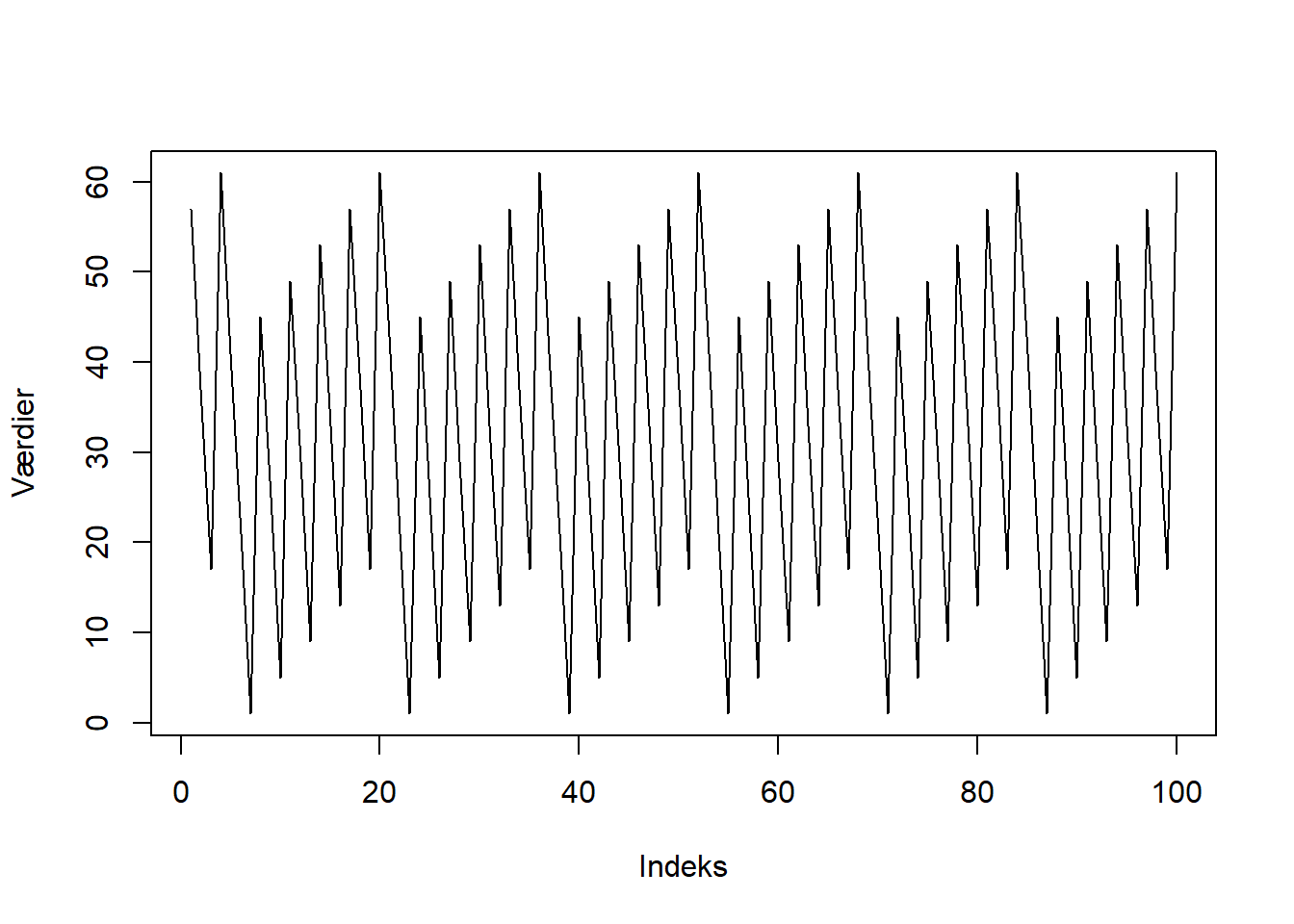
Figur 3.3: Et eksempel på en ikke-tilfældig LCG-cyklus.
På figur 3.4 vises et eksempel på, hvordan LCG-algoritmen kan bruges til at lave en uniform fordeling i intervallet \([0, 1]\). Når cyklussen er oprettet, divideres hvert element deri med den valgte modulus, hvilket gør, at hvert element bliver indeholdt i \([0, 1]\).
lcg2 <- lcg(modulus = 86436, faktor = 1093, tilvaekst = 0,
seed = 12, iterationer = 1000)
lcg2_uniform <- lcg2/86436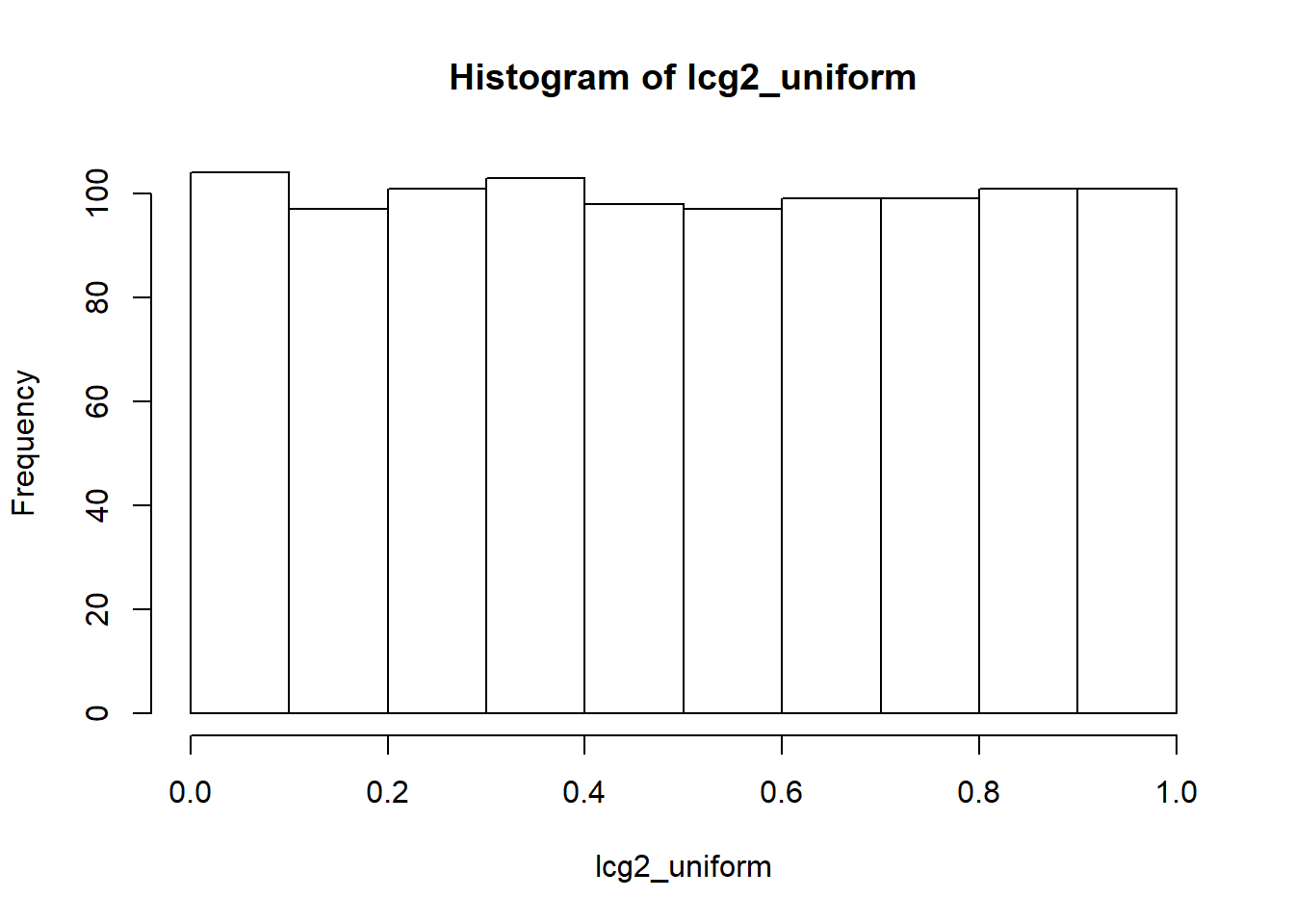
Figur 3.4: Et eksempel på en LCG-cyklus, der er uniformt fordelt.
Her kan det også nævnes, at hvis den cyklus, algoritmen returnerer, plottes i et 2d-punktplot, som på figur 3.5, vil der fremgå en mere tilfældig fordeling, dog vil der stadig kunne ses et mønster.
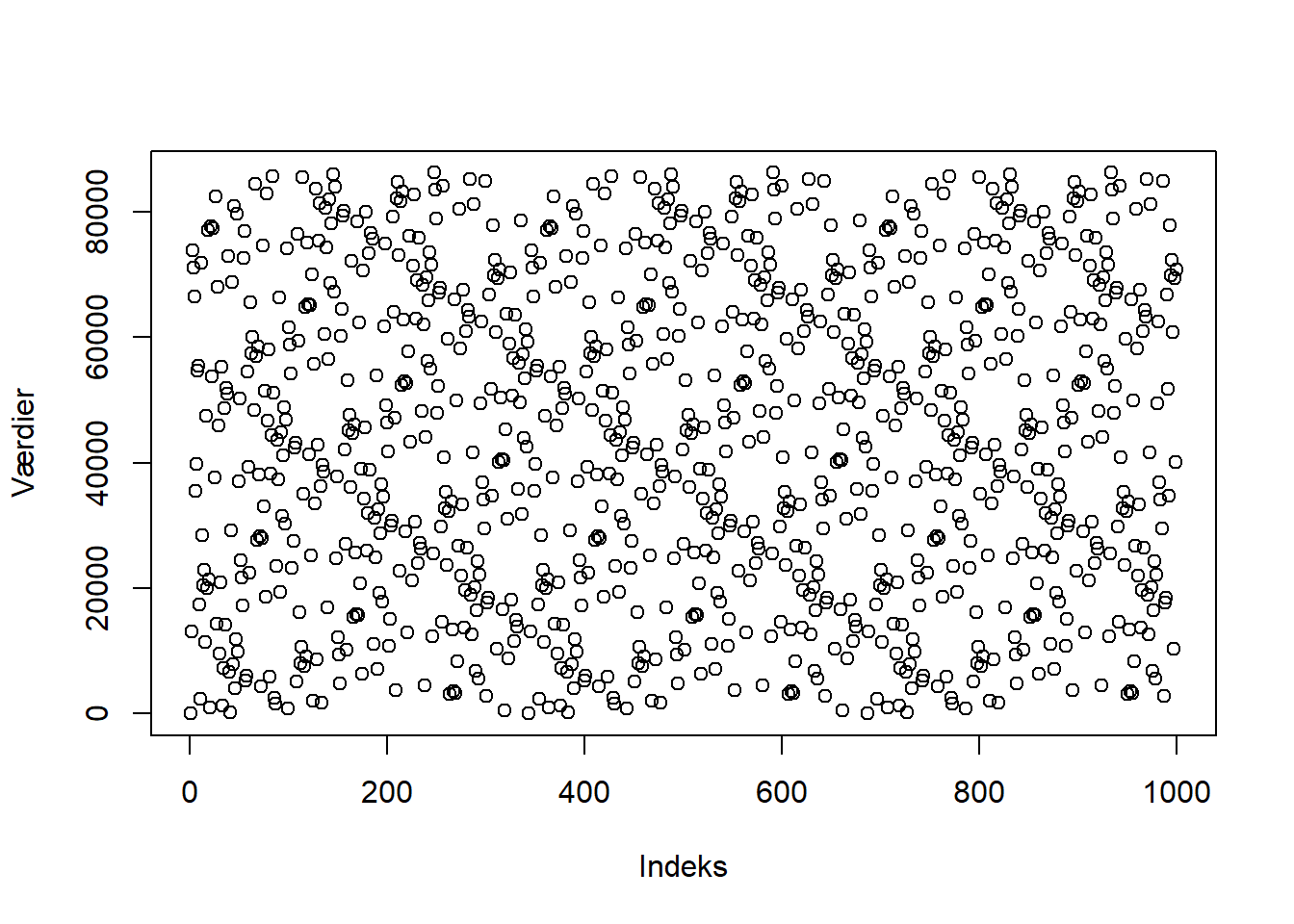
Figur 3.5: En 2d-graf af en LCG-cyklus, hvor der ses et svagt mønster.
Afslutningsvist vil der vises et eksempel, hvor der returneres en cyklus, der ser tilfældig ud. Denne cyklus kan ses på figur 3.6.
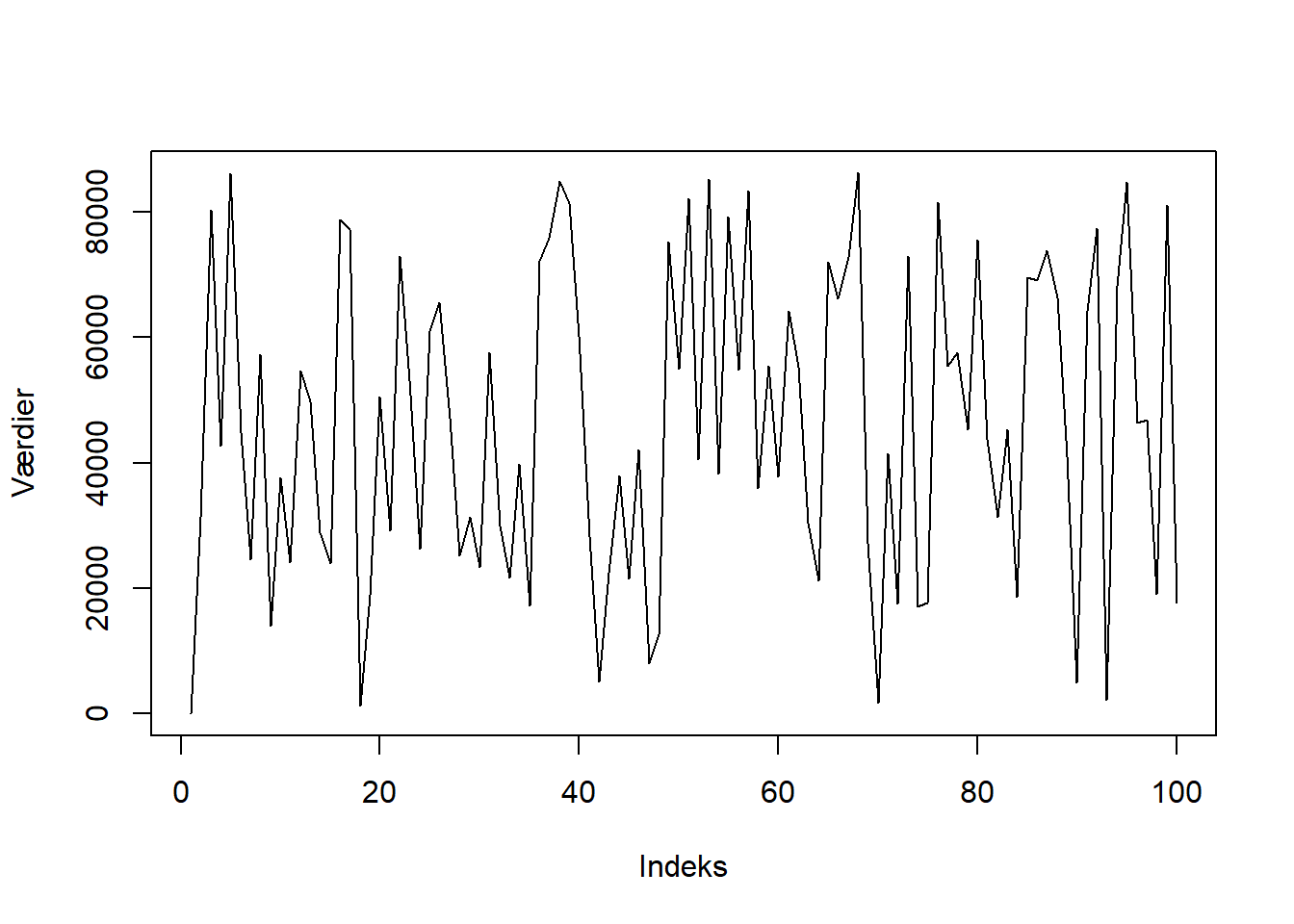
Figur 3.6: Et eksempel på en tilsyneladende tilfældig LCG-cyklus.
3.1.2 Box-Muller-transformation
I dette afsnit beskrives Box-Muller-transformation, hvilket er en metode til at generere standard normalfordelte tal ud fra uniformt fordelte tal. Dette gøres for at belyse, hvordan en computer kan generere tilsyneladende tilfældige tal, der er normalfordelte. Afsnittet er skrevet med inspiration fra (Weisstein 2020a). Metoden beskrives konkret i nedenstående sætning.
Sætning 3.1 Box-Muller-transformation
Antag, at \(U_1\) og \(U_2\) er uafhængige stokastiske variabler, der begge er uniformt fordelt på intervallet \([0, 1]\). Lad \[Z_1 = \sqrt{-2 \mathrm{ln} U_1} \mathrm{cos}(2\pi U_2)~ \wedge~ Z_2 = \sqrt{-2 \mathrm{ln} U_1} \mathrm{sin}(2\pi U_2).\] Så er \(Z_1\) og \(Z_2\) uafhængige stokastiske variabler, der er standard normalfordelte.
Eksempel
I dette afsnit oprettes to normalfordelinger ved hjælp af Box-Muller-transformationen i R.
Først simuleres to stokatiske variabler, U1 og U2, hvor \(\mathrm{U1 \sim unif(0,1)}\) og \(\mathrm{U2 \sim unif(0,1)}\).
Disse to stokatiske variabler benyttes nu til at oprette de to påstået standard normalfordelte stokatiske variabler, Z1 og Z2.
# Opretter Z1 vha. formlen for Box-Muller
Z1 <- sqrt(-2*log(U1))*cos(2*pi*U2)
# Opretter Z2 vha. formlen for Box-Muller
Z2 <- sqrt(-2*log(U1))*sin(2*pi*U2) Efterprøvning i R
I det følgende afsnit efterprøves de forventede karakteristika af de to stokastiske variabler \(Z_1\) og \(Z_2\), der blev oprettet ved hjælp af Box-Muller-transformationen.
Først undersøges deskriptivt, hvilken fordeling Z1 og Z2 har, ved at oprette et boksplot af de to stokastiske variabler, som ses på figur 3.7.
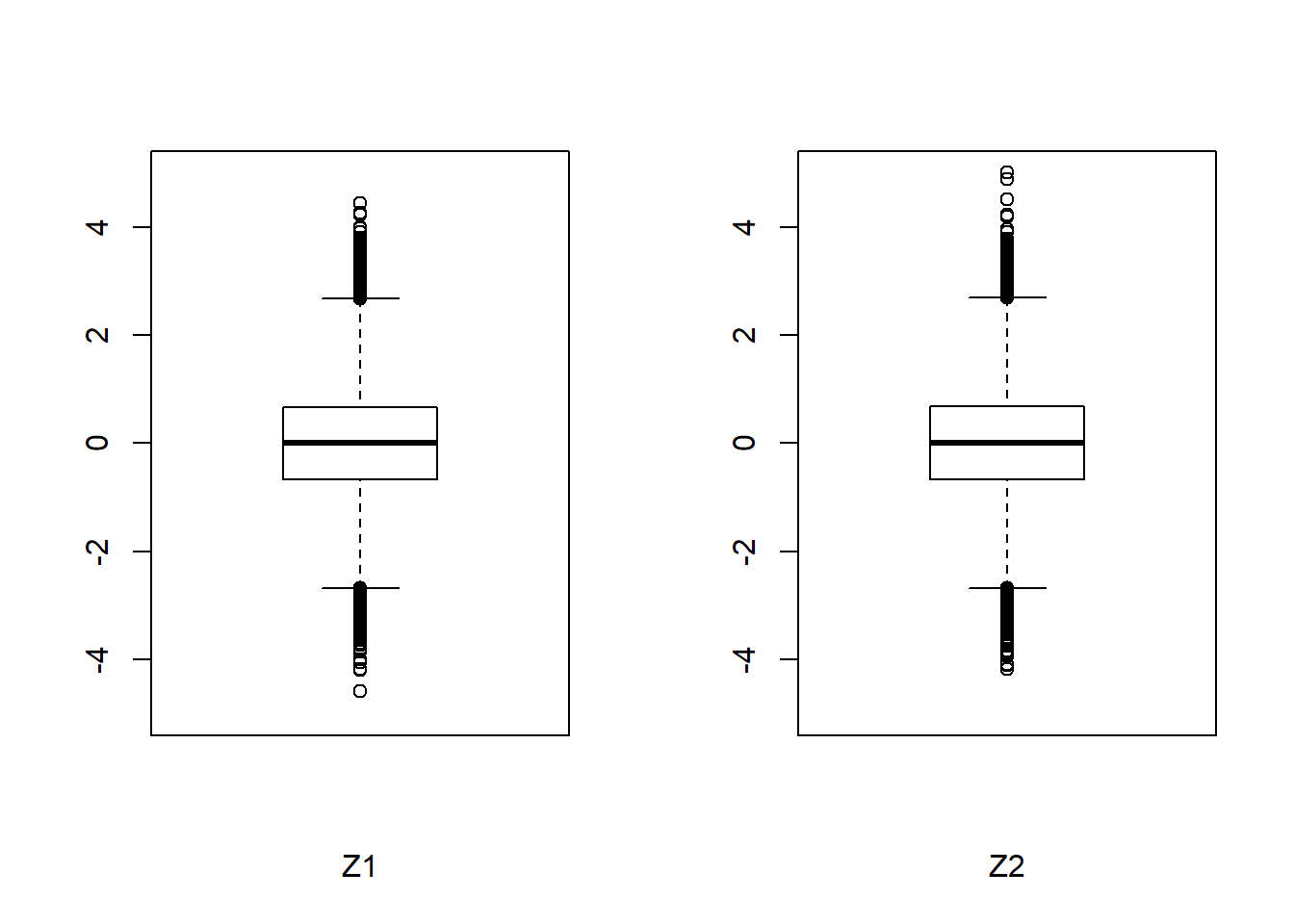
Figur 3.7: Et boksplot over Z1 og Z2
Det ses på boksplottet, at der er en indikation på normalfordeling med henvisning til de fire krav et boksplot af en normalfordeling opfylder. De fire krav er:
Idet en normalfordeling er symmetrisk fordelt omkring dens middelværdi, er medianen og middelværdien lig hinanden.
Grundet normalfordelingens symmetri, er øvre og nedre kvartil lige langt fra medianen.
På grund af symmetrien i en normalfordeling, er der lige mange outliers over øvre kvartil som under nedre kvartil.
Da en outlier i et boksplot identificeres som data, der ligger mere end \(1.5 \cdot \text{IQR}\) udover nedre og øvre kvartil, medfører det, at data, der ligger mere end \(2.68\) standardafvigelser fra middelværdien er outliers. Dermed følger, at \(0.7\%\) af observationerne ligger som outliers.
Punkterne 2 og 3 tjekkes ved at betragte boksplottet, hvor der ikke umiddelbart synes at være noget, der modbeviser en normalfordeling af Z1 og Z2.
For at tjekke punkt 1, beregnes medianen og middelværdien i kodestykket nedenfor.
Dette giver henholdsvis en middelværdi og median for Z1 på \(-7.9683876\times 10^{-4}\) og \(-0.0023288\), samt for Z2 på \(0.0014972\) og \(6.8522143\times 10^{-4}\). De meget lave værdi stemmer overens med forventningen om, at Z1 og Z2 er standard normalfordelte.
For at tjekke punkt \(4\), beregnes andelen af outliers i hvert boksplot i kodestykket nedenfor.
OutVals1 <- boxplot(Z1, plot = FALSE)$out # Outliers i Z1
outliers_Z1 <- length(OutVals1) # Tæller antal outliers i Z1
OutVals2 <- boxplot(Z2, plot = FALSE)$out # Outliers i Z2
outliers_Z2 <- length(OutVals2) # Tæller antal outliers i Z2
# Andelen af outliers i Z1 og Z2
outliers_andel_Z1 <- outliers_Z1/length(Z1)
outliers_andel_Z2 <- outliers_Z2/length(Z2) Dette giver en andel af outliers i Z1 på 0.0074 og i Z2 på 0.00745. Dette svarer til cirka \(0.7\%\) outliers i både Z1 og Z2, hvilket stemmer overens med punkt 4.
Der er altså ikke noget evidens imod, at Z1 og Z2 skulle være normalfordelte. Tværtimod underbygger beregningen af deres middelværdi, at de er standard normalfordelte, hvilket undersøges nærmere på figur 3.8, hvor fordelingerne sammenlignes med densiteten for en standard normalfordeling.
Hernest kigges der på histogrammerne for Z1 og Z2. På figur 3.8 sammenlignes histogrammerne for henholdsvis Z1 og Z2 med densiteten for standard normalfordeling.
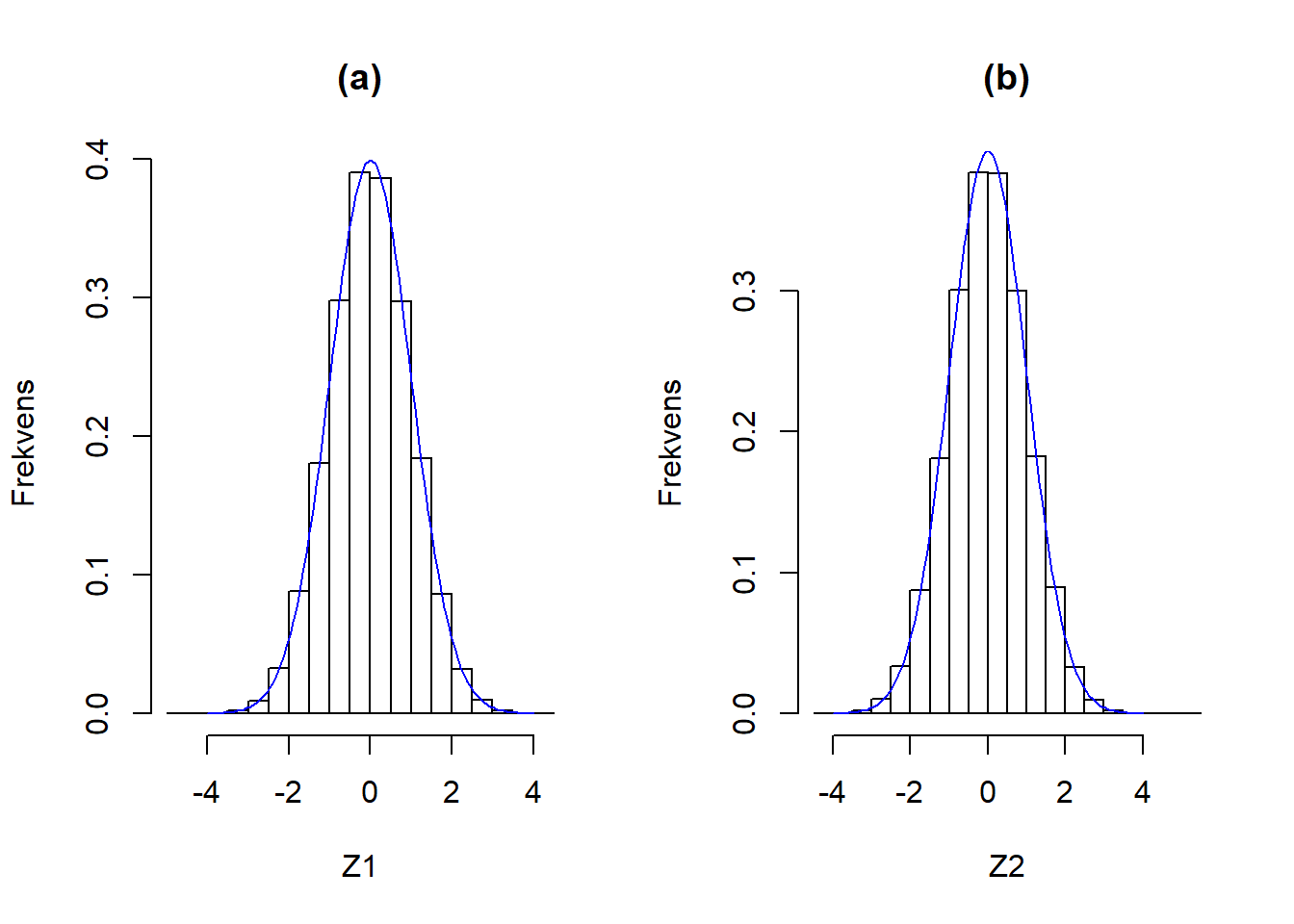
Figur 3.8: Sammenligning af histogrammerne for henholdsvis Z1 (a) og Z2 (b) med densiteten for standard normalfordeling, som er angivet med en blå linje.
Det ses på histogrammerne, at de tilnærmelsesvist er normalfordelte, samt at de har en middelværdi på \(\approx 0\) og en standardafvigelse på \(\approx 1\), og derved er Z1 og Z2 tilnærmelsesvist standard normalfordelte.
Desuden er det også en konsekvens af Box-Muller-transformationerne, at Z1 og Z2 er uafhængige. Dette undersøges på figur 3.9.
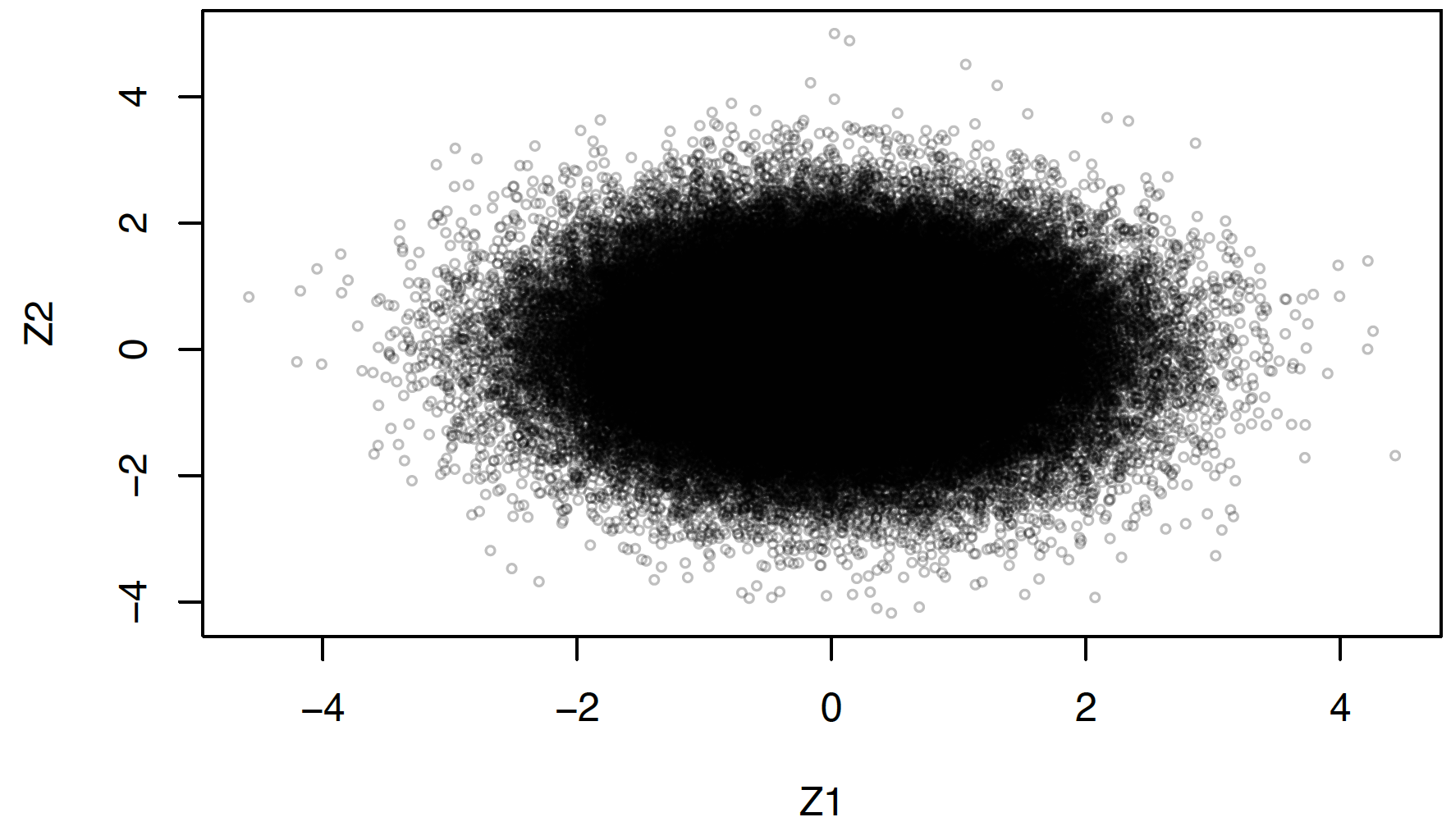
Figur 3.9: Graf for uafhængigheden mellem Z1 og Z2.
Udover at eftervise uafhængigheden af Z1 og Z2 grafisk, kan det også undersøges ved hjælp af funktionen cor i R, som giver en værdi for korrelationen af de to talsekvenser.
Korrelationen af to variabler udregnes ved formlen
\[ cor(X, Y) = \frac{cov(X, Y)}{sd(X) \cdot sd(Y)} \] Hvor \(cov\) angiver kovariansen og \(sd\) angiver standardafvigelsen.
Korrelation fortæller, hvor stor en lineær sammenhæng der er mellem to variabler. Denne værdi ligger i intervallet \([-1, 1]\), hvor \(-1\) påviser en perfekt negativ lineær sammenhæng, \(1\) påviser en perfekt positiv lineær sammenhæng, og \(0\) viser, at der ingen lineær sammenhæng er.
Et resultat på afrundet -0.0021, hvilket næsten er \(0\), viser altså også at der ingen lineær korrelation er mellem Z1 og Z2, hvilket giver en indiktion for, at de er uafhængige.
3.2 Simulering i R
I dette afsnit gives eksempler på, hvorledes der kan udføres simuleringer af forskellige fordelinger, således disse fordelinger kan anvendes til statistisk inferens. Afsnittet er primært baseret på kilden (Peng 2019).
I dataanalysen vil de viste fordelinger bruges som populationer, og stikprøver udtages så ved hjælp af forskellige funktioner. Idéen med denne fremgangsmåde er, at der derved udtages stikprøver fra teoretisk uendelige fordelinger.
Nogle af de fordelinger, der kan simuleres i R, er normal-, binomial-, uniforme-, beta- og gammafordelinger. Alle disse fordelinger har forskellige karateristika, som påvirker hvilke værdier de kan antage. Der vil nu vises eksempler på, hvordan disse fordelinger simuleres i R, og hvordan resultatet vil se ud.
3.2.1 Normalfordeling
I R simuleres en normalfordeling ved funktionen rnorm. At en stokastisk variabel, X, er normalfordelt med middelværdi \(\mu\) og standardafvigelse \(\sigma\) skrives \(X \sim N(\mu, \sigma)\). Fordelingen på figur 3.10 bliver genereret ud fra en middelværdi på \(0\) og en standardafvigelse på \(1\).
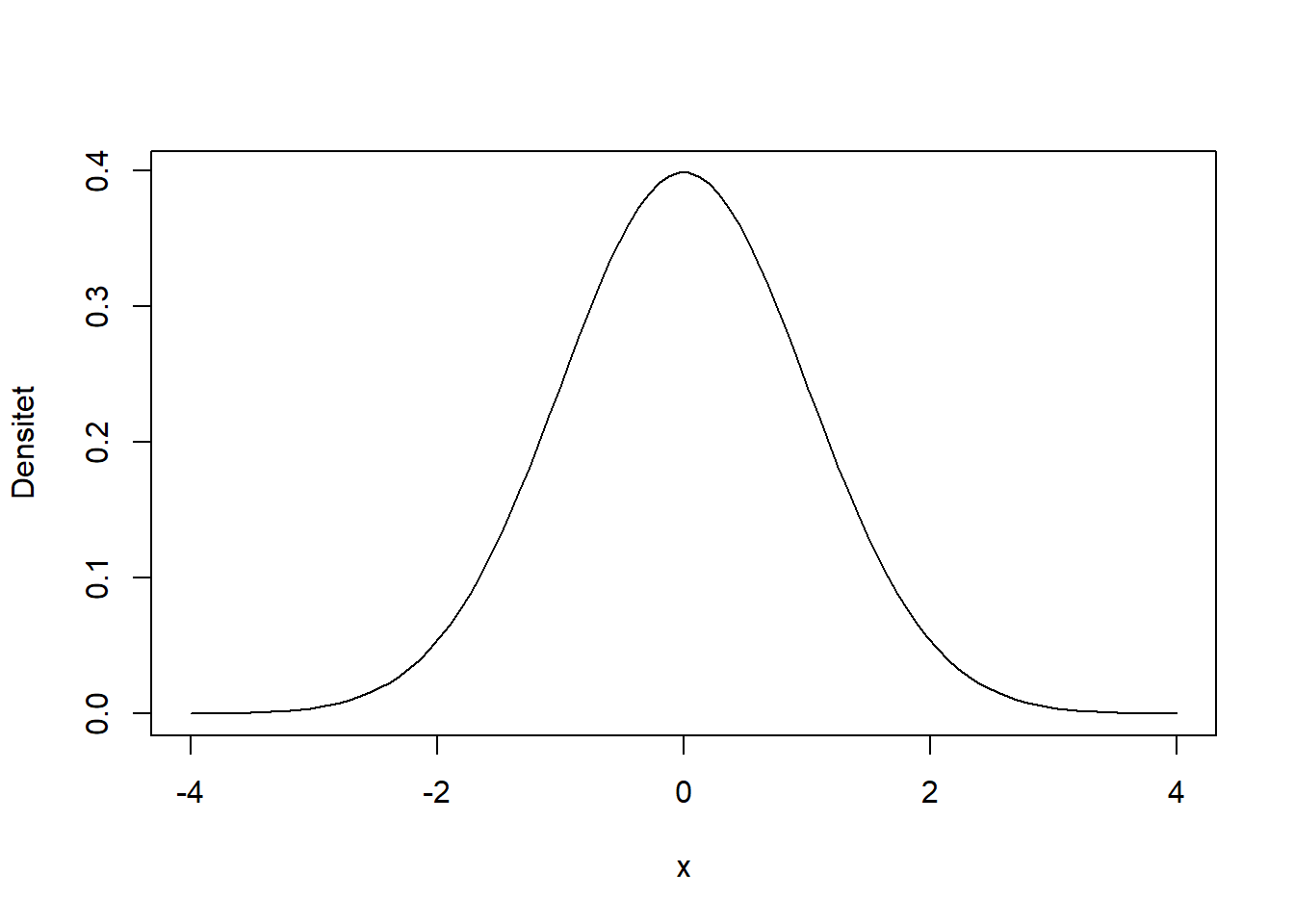
Figur 3.10: Densitetskurven for en standard normalfordeling.
3.2.2 Uniform fordeling
En uniform fordeling er defineret ud fra et interval, som der skal genereres et givent antal værdier indenfor. Alle disse værdier har lige stor sandsynlighed for at blive genereret. At en stokastisk variabel, X, er uniformt fordelt i intervallet \((a, b)\) skrives \(X \sim \text{unif}(a, b)\). På figur 3.11 ses densitetskurven for en uniform fordeling.
![En uniform fordeling, hvor alle tal har lige stor sandsynlighed for at optræde i intervallet [0 , 1].](P2-rapport_files/figure-html/unifordeling-1.png)
Figur 3.11: En uniform fordeling, hvor alle tal har lige stor sandsynlighed for at optræde i intervallet [0 , 1].
3.2.3 Binomialfordeling
En binomialfordeling bliver genereret ud fra sandsynligheder med to udfald, succes eller fiasko. I den binomiale fordeling gives en size som er størrelsen af et eksperiment, samt en sandsynlighed for succes, angivet med prob. For hver gentagelse af eksperimentet optælles andelen af successer, som minimalt kan være \(0\) og maksimalt \(1\). At en stokastisk variabel, X, er binomal fordelt med \(n\) antal eksperimenter og en sandsynlighed for sucess på \(p\), skrives \(X \sim \text{binom}(n, p)\). På figur 3.12 illustreres andelen af sucesser for en binomialfordeling.
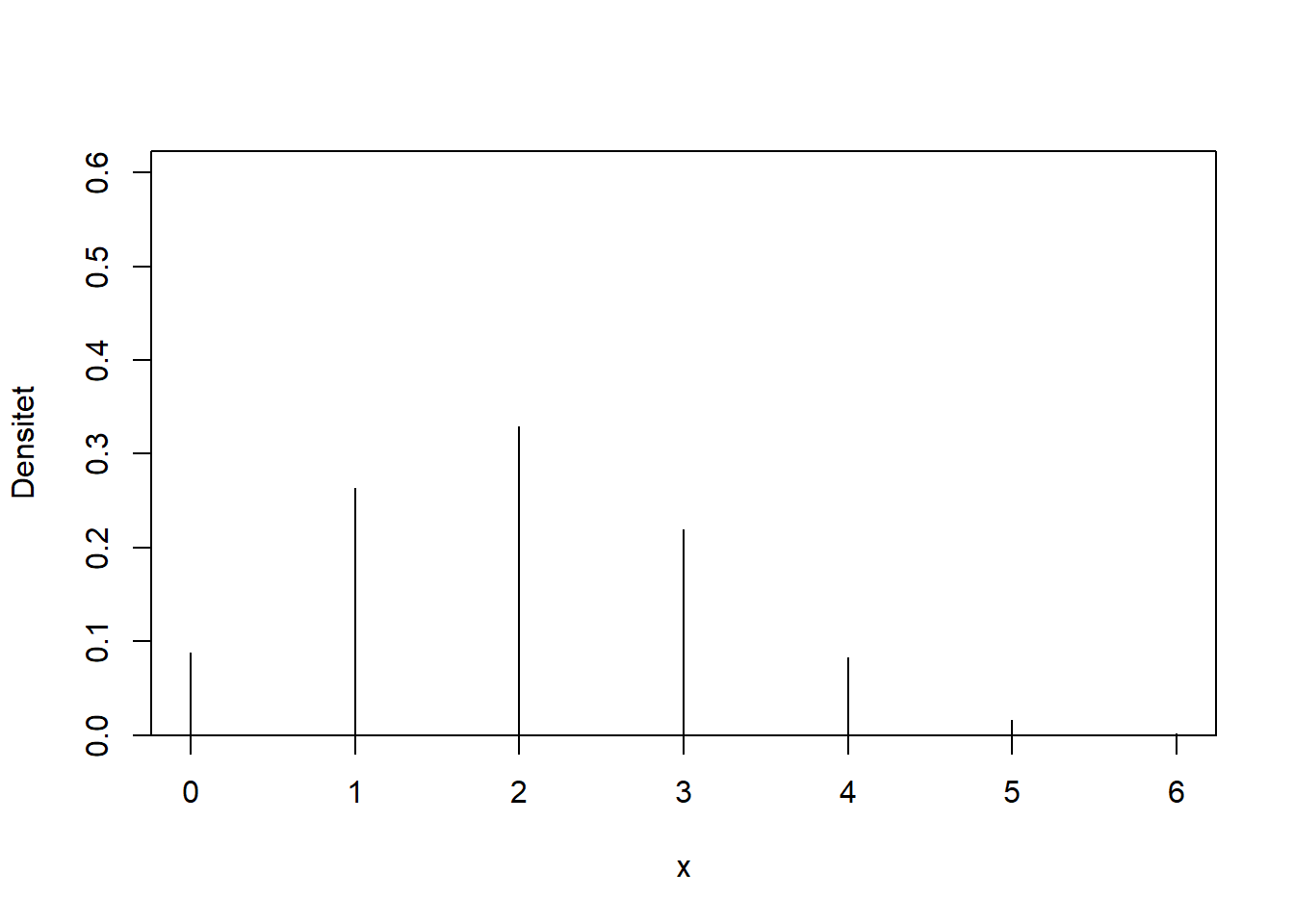
Figur 3.12: En binomialfordeling med size = 6 og en sandsynlighed for succes på prob = 1/3.
3.2.4 Skæve fordelinger
En skæv fordeling er kendetegnet ved, at størstedelen af observationerne er samlet omkring visse værdier, mens de resterende observationer fordeler sig ud til kun én af siderne. De resterende observationer kaldes for halen af fordelingen, og alt efter retningen af halen, kaldes den skæve fordeling for venstreskæv elller højreskæv.
3.2.4.1 Betafordeling
En skæv fordeling kan være en betafordeling. At en stokastisk variabel, \(X\) er betafordelt med parametrene \(\alpha\) og \(\beta\) skrives \(X \sim \text{Beta}(\alpha, \beta)\). I en betafordeling angiver \(\alpha - 1\) andelen af sucesser, og \(\beta - 1\) angiver andelen af fiaskoer, (Kim 2020).
En venstreskæv og en højreskæv betafordeling vil nu simuleres og vises på figur 3.13, hvor \(\alpha = 8\) og \(\beta = 2\) for den venstreskæve, mens \(\alpha = 2\) og \(\beta = 8\) for den højreskæve.
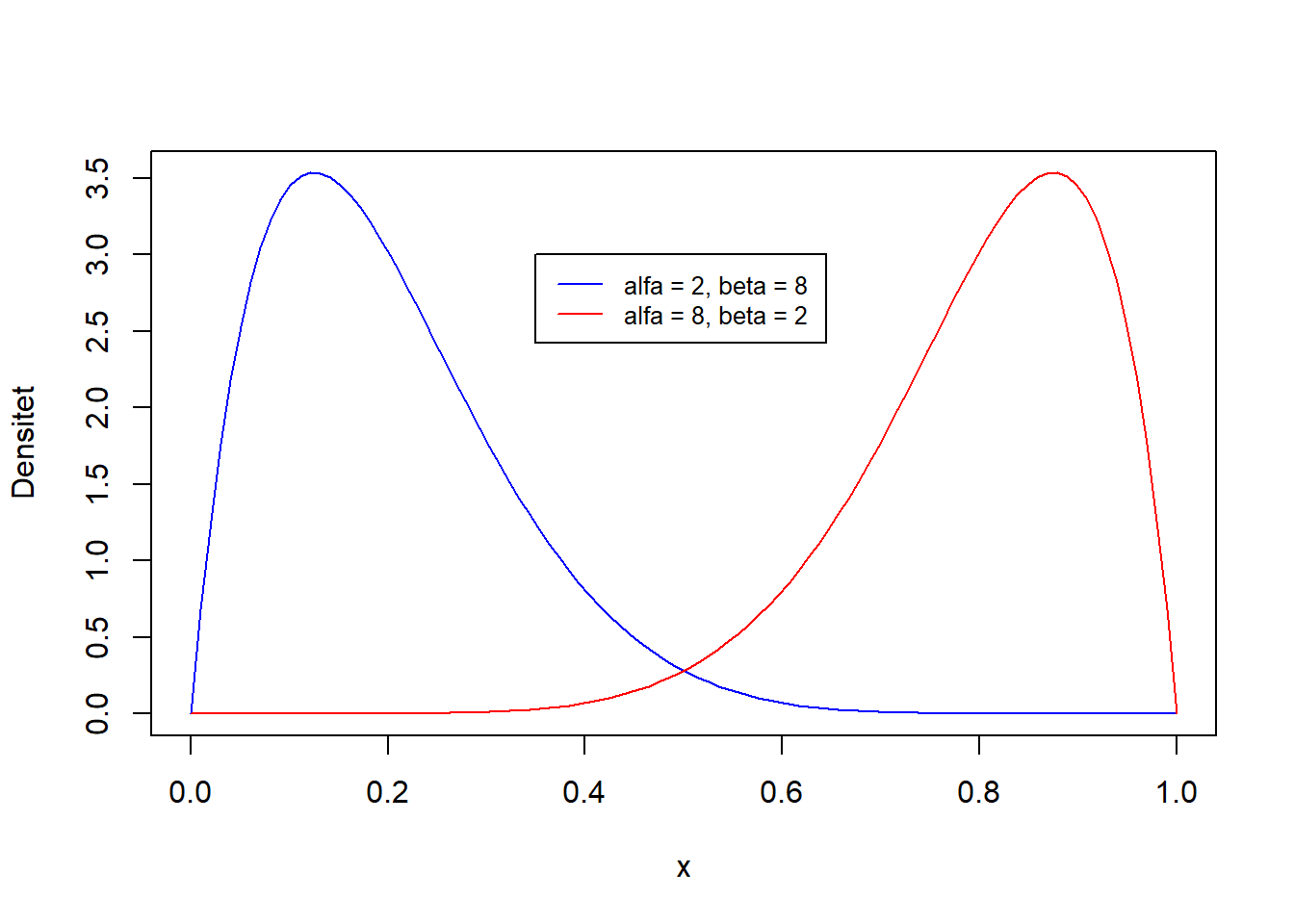
Figur 3.13: To betafordelinger med henholdsvis alfa = 8 og beta = 2, og alfa = 2 og beta = 8.
3.2.4.2 Gammafordeling
Gammafordelingen er ligeledes en skæv fordeling. Funktionaliteten af gammafordelingen er at forudsige ventetiden til den \(\alpha\)’te begivenhed. Tæthedsfunktionen for gammafordelingen, er beskrevet med to forskellige parametersæt, henholdsvis \((k,~\theta)\) og \((\alpha,~\beta)\). I denne rapport vil der fremefter blive anvendt parameterne \((\alpha,~\beta)\). Tæthedsfuktionen er givet ved \(f(x)=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x}\), hvor \(\alpha > 0\) er shape, \(\beta > 0\) er rate, \(\Gamma(\alpha) = (\alpha - 1)!\) og \(x \in ( 0, \infty)\). At en stokastisk variabel, X, er gammafordelt med shape \(\alpha\) og rate \(\beta\), skrives \(X \sim \text{Gamma}(\alpha, \beta)\), (Kim 2019). På figur 3.14 er vist tre forskellige højreskæve gammafordelinger.

Figur 3.14: Tre gammafordelinger hvor beta = 1 og alfa på henholdsvis 1, 5 og 10.
3.2.5 Repetitioner
I nogle statistiske metoder er det nødvendigt at arbejde med flere stikprøver end kun én enkelt. Med funktionen replicate i R, kan der genereres adskillige nye stikprøver ud fra den oprindelige. Processen med replicate vil nu vises. Først ses en stikprøve med tre observationer.
## Oprindelig stikprøve
## Observation 1 -0.3268578
## Observation 2 1.0451809
## Observation 3 0.3082858I følgende eksempel replikeres der fem gange, hvilket betyder, at der bliver oprettet fem nye stikprøver. I forbindelse med denne process anvendes funktionen sample, som er funktionen der resampler, enten med eller uden tilbagelægning fra stikprøven. I dette eksempel bruges funktionen med tilbagelægning. Fra den oprindelige stikprøve udtrækkes en observation, som indsættes i en ny stikprøve. Observationen bliver derefter lagt tilbage i den oprindelige stikprøve, hvilket medfører, at den samme observation kan udtages flere gange. Grunden til dette er, at stikprøven anses for at være repræsentativ for population, og to observationer af den samme værdi derfor ikke er utænkelig.
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1.0451809 -0.3268578 1.0451809 1.0451809 0.3082858
## [2,] -0.3268578 1.0451809 1.0451809 1.0451809 -0.3268578
## [3,] 0.3082858 1.0451809 -0.3268578 -0.3268578 -0.3268578Funktionen har nu resamplet fem nye repræsentative stikprøver udfra den oprindelige.
Bibliografi
Cmglee. 2015. “Linear Congruential Generator Visualisation.” 2015. https://commons.wikimedia.org/w/index.php?curid=38637545.
Dictonary, Cambridge. 2020. “Simulation.” 2020. https://dictionary.cambridge.org/dictionary/english/simulation.
F1, Mercedes AMG. 2020. “Simulator.” 2020. https://careers.mercedesamgf1.com/facilities/simulator/.
Kim, Aerin. 2019. “Gamma Distribution — Intuition, Derivation, and Examples.” 2019. https://towardsdatascience.com/gamma-distribution-intuition-derivation-and-examples-55f407423840.
Kim, Aerin. 2020. “Beta Distribution — Intuition, Examples, and Derivation.” 2020. https://towardsdatascience.com/beta-distribution-intuition-examples-and-derivation-cf00f4db57af.
Math, Coding. 2016. “Coding Math: Episode 51 - Pseudo Random Number Generators Part I.” 2016. https://www.youtube.com/watch?v=4sYawx70iP4.
Oxford, The Numerical Algorithms Group Ltd. 2015. “NAG Toolbox Chapter Introduction — Random Number Generators.” 2015. https://www.nag.co.uk/numeric/mb/nagdoc_mb/manual_25_1/html/g05/g05intro.html.
Peng, Roger D. 2019. “R Programming for Data Science.” 2019. https://bookdown.org/rdpeng/rprogdatascience/simulation.html.
Radziwill, Nicole. 2015. “A Linear Congruential Generator (Lcg) in R.” 2015. https://qualityandinnovation.com/2015/03/03/a-linear-congruential-generator-lcg-in-r.
Trumbo, Bruce E. 2005. “Congruential Generators of Pseudorandom Numbers.” 2005. http://www.sci.csueastbay.edu/~btrumbo/Stat3401/Hand3401/CongGenIntroB.pdf.
Weisstein, Eric W. 2020a. “Box-Muller Transformation.” 2020. https://mathworld.wolfram.com/Box-MullerTransformation.html.