Kapitel 5 Permutationer
I afsnit 2.3.2 blev der redegjort for, hvilke antagelser, der skal være opfyldt, for at en t-test giver retvisende resultater. Ligeledes blev der i kapitel 4 vist, hvorledes resultater for en t-test kan være misvisende, hvis stikprøverne ikke er normalfordelte. I dette kapitel vil der redegøres for en løsning til dette problem. Hvis antagelserne ikke er opfyldte, og en t-test derfor ikke kan anvendes, er det muligt at anvende permutationer.
Givet en ordnet liste, \(X = [x_1, x_2, \ldots, x_n ]\), er en permutation, \(\pi\), en omarrangering af listens elementer, \(X_\pi = [x_{\pi(1)}, x_{\pi(2)}, \ldots, x_{\pi(n)}]\). Antallet af mulige permutationer af en ordnet liste, \(X\), af længde \(n\), er givet ved \(n!\), (Weisstein 2020b).
Som eksempel, er en mulig permutation, \(\pi_1\), af \(A = [1, 2, 3]\) givet ved \(A_{\pi_1} = [2, 1, 3]\), og der er i alt \(|A|! = 3! = 1 \cdot 2 \cdot 3 = 6\) mulige permutationer af listen.
Ved hjælp af permutationer er det muligt at udføre en hypotesetest. En sådan hypotesetest kaldes for en permutationstest.
5.1 Permutationstest
I dette afsnit gives en forklaring af, hvad en permutationstest er. Afsnittet er skrevet på baggrund af (Chihara and Hesterberg 2019, side 54).
Antag, at en tilfældig stikprøveudtagning af en population kan udtrykkes ved \(X = [x_1, x_2, \ldots, x_n]\). Der opstilles en nulhypotese \(H_0\) og en alternativ hypotese, \(H_1\), der er relevante at undersøge. Der kan så vælges en teststørrelse at undersøge for at måle evidensen imod \(H_0\). Værdien af denne teststørrelse er givet ved \(t_{obs}\) for stikprøven.
En permutationstest går ud på at forsøge at måle evidens imod \(H_0\), som i en almindelig t-test. Dette gøres ved at beregne teststørrelsen for samtlige permutationer af \(X\). Denne mængde af permutationer er givet ved \(\Pi_X = \{X_{\pi_1}, X_{\pi_2}, \ldots X_{\pi_M} \}\), hvor \(M\) er antallet af mulige permutationer af \(X\). Teststørrelsen for den \(i\)’te permutation benævnes \(t_{\pi_i}\).
Selve beregningen af teststørrelsen afhænger af de specifikke hypoteser, men det er et krav, at store værdier for \(t_{\pi_i}\) indikerer evidens imod \(H_0\). Desuden er det kun nulhypoteser om ingen forskel, der kan testes ved hjælp af permutationer - eksempelvis kan evidensen imod \(H_0: \mu_1 \neq \mu_2\) ikke beregnes, (Chihara and Hesterberg 2019, s. 48).
P-værdien for en tosidet test beregnes som antal gange, den numeriske værdi af permutationsteststørrelsen, \(|t_{\pi_i}|\), er større end den observerede teststørrelse, \(t_{obs}\), divideret med antallet af mulige permuationer, \(M\). P-værdien beregnes på tilsvarende vis for en ensidet test, hvor \(|t_{\pi_i}|\) erstattes med \(t_{\pi_i}\), og uligheden erstattes med det tilsvarende passende, (Chihara and Hesterberg 2019 side 55).
\[p = \frac{\#(|t_{\pi_i}| \geq t_{obs}) + 1}{M + 1}\]
Permutationstest har den fordel, at den antager meget lidt omkring stikprøven. I særdeleshed antager den hverken tilfældig stikprøveudtagning, eller at populationen, fra hvilken stikprøven stammer, er normalfordelt. Desuden er permutationstest især fordelagtig, når fordelingen af teststørrelsen er ukendt.
Der er dog visse ulemper ved en permutationstest. For det første, skal det antages, at den del af data, der permuteres, er ombyttelig. For det andet er det ikke alle teststørrelser, der kan undersøges ved hjælp af en permutationstest - for eksempel vil middelværdien af samtlige permutationer være lig hinanden for en test for en enkelt stikprøve. For det tredje bliver antallet af mulige permutationer hurtigt meget stor, når størrelsen af stikprøven stiger. Hvis der for eksempel er \(n = 10\) datapunkter i stikprøven, vil der være \(10! = 3,628,800\) mulige permutationer af stikprøven.
Netop på grund af ombytteligheden af stikprøven fungerer permutationstests. Hvis stikprøven er ombyttelig, vil hver eneste permutation af stikprøven, inklusiv stikprøven selv, være lige sandsynlige. Dette medfører, at hvis \(H_0\) er sand, vil enhver difference imellem \(t_{obs}\) og \(t_{\pi_i}\) være lille og tilfældig. Hvis værdien for \(t_{\pi_i}\) på den måde konkluderes at være væsentlig anderledes end \(t_{obs}\), tyder det på, at \(H_0\) skal forkastes.
Det store antal af permutationer afhjælpes ved kun at beregne \(t_{\pi_i}\) for et passende antal, tilfældigt udvalgte, permutationer af stikprøven, og et acceptabelt resultat vil stadig blive opnået.
5.2 Uparret permutationstest
Der vil nu vises et eksempel på, hvordan permutationstest kan anvendes som en hypotesetest. Antag, at det ønskes undersøgt, om middelværdien af to stikprøver er signifikant forskellige. Den opstillede nulhypotese bliver \(H_0 : \mu_1 - \mu_2 = 0\), og den alternative hypotese bliver \(H_1 : \mu_1 - \mu_2 \neq 0\).
Der vil blive udtrukket to stikprøver, vist på figur 5.1, fra den samme betafordeling.
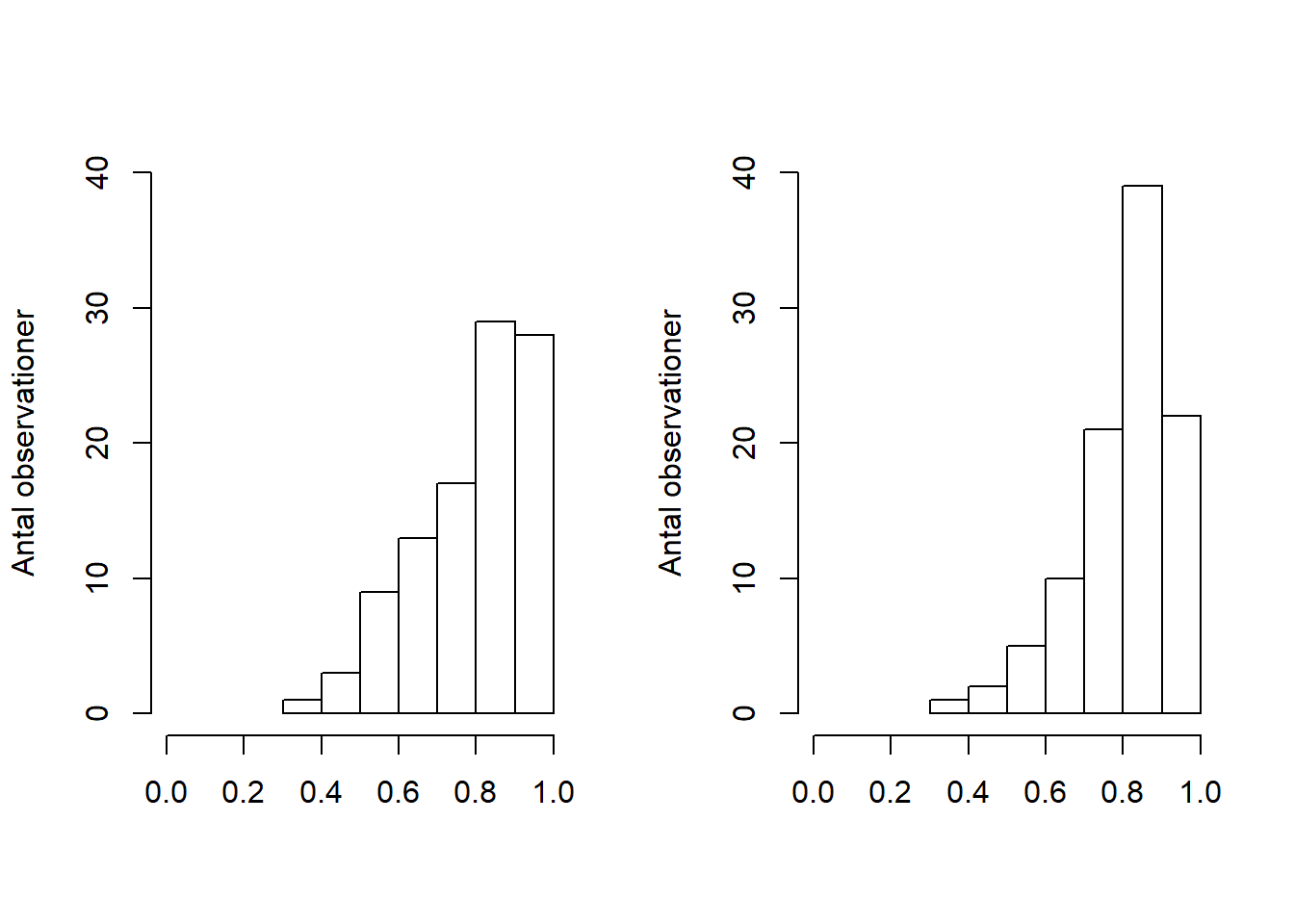
Figur 5.1: To stikprøver udtrukket fra den samme betafordeling med parametrene alfa = 8 og beta = 2.
Teststørrelsen vil i dette tilfælde være forskellen mellem stikprøvernes middelværdi, \(t_{obs} = |\hat{\mu}_1 - \hat{\mu}_2|\). Den observerede teststørrelse ses at være 0.0076034. Hvorvidt denne forskel er signifikant, kan nu undersøges ved at beregne forskellen i middelværdi for samtlige permutationer af stikprøverne. Observationerne fra hver stikprøve vil blive forenet i en enkelt stikprøve, som der vil permuteres udfra.
I nedenstående kode udføres der \(100\) permutationer på den forenede stikprøve. Den forenede stikprøve har en størrelse på \(N = 200\). I hver permutation udtrækkes de første \(100\) observationer til at være den permuterede stikprøve permuteret_stik1 , mens de sidste \(100\) observationer bliver til den permuterede stikprøve permuteret_stik2. Derefter udregnes den absolutte forskel i middelværdien mellem de nye permuterede stikprøver, i alt \(100\) gange, en for hver permutation. Denne difference kaldes den permuterede teststørrelse, \(S_{\pi}\).
t_obs <- abs(mean(stik1) - mean(stik2))
forenet_stik <- c(stik1, stik2)
t_pi <- c()
for(i in 1:100){
permuteret_forenet_stik <- sample(forenet_stik, size = (2 * 100))
permuteret_stik1 <- head(permuteret_forenet_stik, 100)
permuteret_stik2 <- tail(permuteret_forenet_stik, 100)
t_pi[i] <- abs(mean(permuteret_stik1) - mean(permuteret_stik2))
}
head(t_pi, 3)## [1] 0.018010076 0.006666829 0.012069227I outputtet head(t_pi, 3) ses et eksempel på tre af de permuterede teststørrelser. På figur 5.2 illusteres fordelingen af de permuterede teststørrelser.
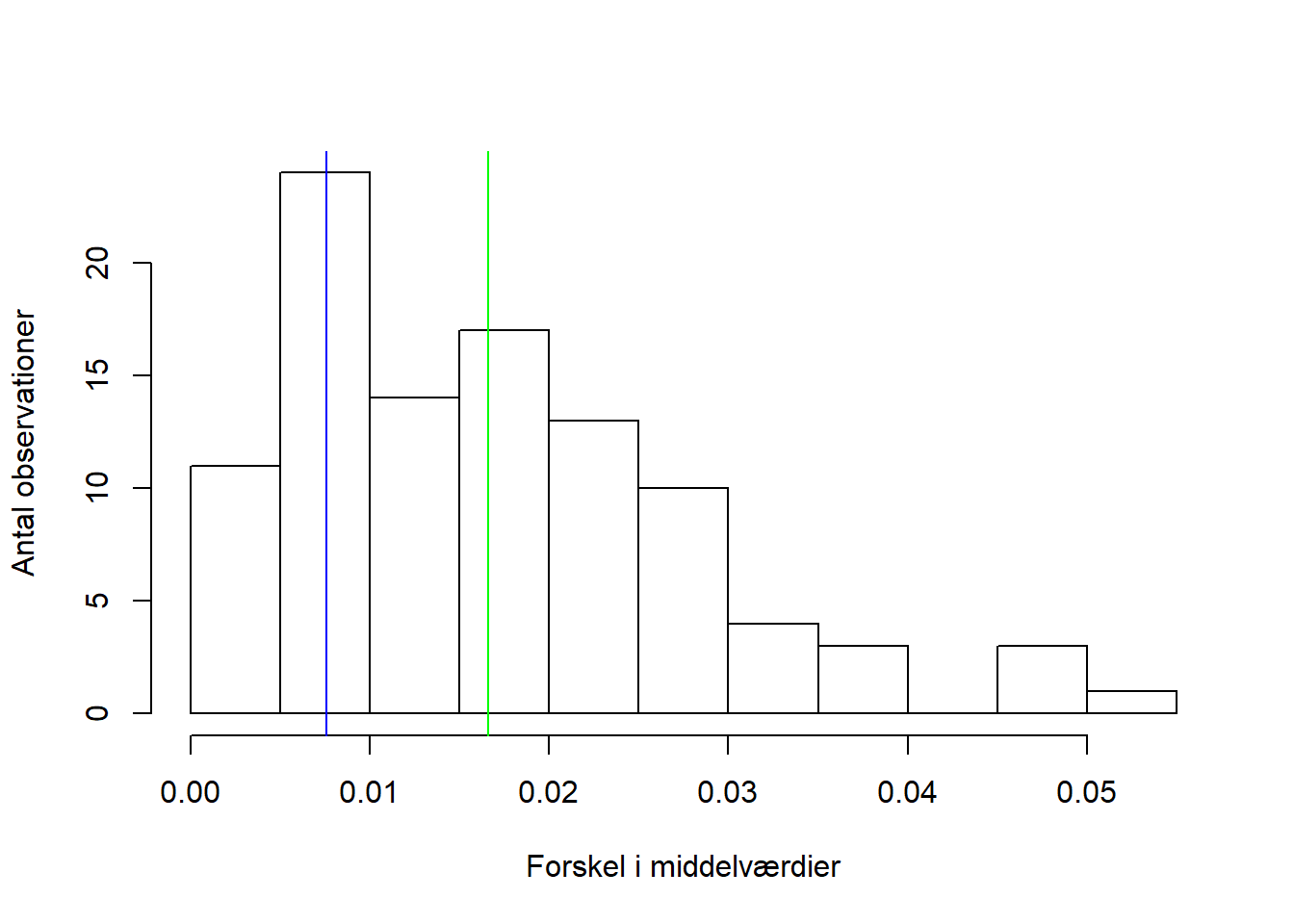
Figur 5.2: Permutationsfordelingen af teststørrelserne. Den blå linje viser den observerede forskel i middelværdierne, og den grønne viser middelværdien for samtlige permuterede teststørrelser.
Nu kan p-værdien beregnes, ved at udregne hvor mange gange de permuterede teststørrelser er større end den observerede teststørrelse. Denne værdi divideres derefter med antallet af permutationer. Dette gøres i nedenstående kodestykke.
antal_ekstreme_vaerdier <- table(abs(t_pi) >= t_obs)[2]
p_vaerdi <- unname(antal_ekstreme_vaerdier+1)/(length(t_pi)+1)
p_vaerdi## [1] 0.7425743Med en p-værdi på 0.7425743, er der ikke noget belæg for at forkaste nulhypotesen. For at undersøge korrektheden af en permutationstest, kan andelen af type-I fejl, som skal svare til signifikansniveauet, beregnes, (Agresti and Finlay 2014, s. 159-160).
Type-I fejl
Antallet af type-I fejl, der opstår i en uparret permutationstest kan undersøges ved at se, hvor mange gange \(H_0\) forkastes, selvom \(H_0\) er sand.
I koden nedenfor bestemmes antallet af type-I fejl for en uparret permutationstest.
konf_niveau <- 0.95
reps <- 1000
n <- 100
type_1_fejl <- replicate(n = reps, {
stik1 <- rbeta(n, shape1 = 8, shape2 = 2)
stik2 <- rbeta(n, shape1 = 8, shape2 = 2)
samlet_stik <- c(stik1, stik2)
t_obs <- abs(mean(stik1) - mean(stik2))
t_pi <- c()
for(i in 1:(n*2)){
permuteret_samlet_stik <- sample(samlet_stik, size = (2 * n))
permuteret_stik1 <- head(permuteret_samlet_stik, n)
permuteret_stik2 <- tail(permuteret_samlet_stik, n)
t_pi[i] <- abs(mean(permuteret_stik1) - mean(permuteret_stik2))
}
antal_ekstreme_vaerdier <- table(abs(t_pi) >= t_obs)[1]
p_vaerdi <- (200-sum(antal_ekstreme_vaerdier)+1)/(length(t_pi)+1)
type1fejl <- p_vaerdi > 1 - konf_niveau
return(type1fejl)
})
fejltable <- table(type_1_fejl)
fejltable## type_1_fejl
## FALSE TRUE
## 56 944I alt forkastes \(H_0\) fejlagtigt i 5.6\(\%\) af tilfældene, hvilket stemmer overens med det valgte signifikansniveau.
5.3 Parret permutationstest
Ligesom permutationstest kan bruges til at lave en uparret hypotesetest, kan den også bruges til en parret. Fremgangsmåden er den samme, bortset fra, at det er indgangene i hvert koordinatpar \((x_i, y_i)\) i stikprøven \(Z = ((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n))\), der permuteres.
I nedenstående kode, vises et eksempel på en parret permutations-test for forskel i middelværdi, der gør brug af pakken wPerm.
reps <- 100
n <- 100
permutationer <- 1000
p_reps <- replicate(n = reps, {
stik1 <- rgamma(n, shape = 10, rate = 2)
stik2 <- rgamma(n, shape = 4, rate = 13)
test <- wPerm::perm.paired.loc(x = stik1, y = stik2,
parameter = mean,
alternative = "two.sided",
R = permutationer)
p_vaerdi <- test$p.value
})
p_vaerdi_parret <- mean(p_reps)
p_vaerdi_parret## [1] 0.002Med en p-værdi på 0.002 kan nulhypotesen forkastes, da der er evidens for, at den ikke er korrekt.
Bibliografi
Agresti, Alan, and Barbara Finlay. 2014. Statistical Methods for the Social Sciences. 4th ed. Edinburgh Gate, England: Pearson.
Chihara, Laura M., and Tim C. Hesterberg. 2019. Mathematical Statistics with Resampling and R. 2nd ed. 111 River Street, Hoboken, NJ 07030, USA: John Wiley & Sons, Inc.
Weisstein, Eric W. 2020b. “Permutation.” 2020. https://mathworld.wolfram.com/Permutation.html.