Kapitel 2 Problemanalyse

2.1 Statistikkens udvikling

Ordet statistik stammer tilbage fra det latinske statisticum collegium (“statsrådgiver”) og det italienske statista (“statsmand” eller “politiker”), (Dictionary 2020). At statistik netop stammer derfra, giver god mening, under anskueelse af betydningen af disse to ord og den tidlige anvendelse af statistik. I takt med udviklingen af suverænitetsstaterne, steg behovet for at registrere befolkningen og dennes tilhørselsforhold. Derfor anvendte statsrådgivere og statsmænd statistik til at beskrive staten, særligt demografien. Senerere blev dette udvidet til at indsamle flere informationer, og ligeledes at analysere og fortolke disse ved hjælp af statistik, (Danske 2020).

En kendt statistiker, der har været med til at lægge grundlaget for moderne statistik, er Ronal Fisher, der introducerede princippet om randomisering. Det siger, at et eksperiment skal gentages på et antal kontrolgrupper, og de elementer der bruges i eksperimentet skal tilfældigt udvælges fra hele populationen. Dette gjorde data forventningsret, som mindsker variationen i et eksperiment, (Encyclopaedia Britannica 2020).

En anden statistiker, som har haft indflydelse på moderne statistik er William Sealy Gosset, som gik under aliasset Student. Gosset arbejdede på Guinness bryggeri, hvor han udviklede statistiske metoder til sit arbejde, der kunne håndtere små stikprøver. I denne forbindelse opfandt han t-fordelingen, samt den dertil tilhørende t-test, og arbejdede også på Monte Carlo simulering, (O’Connor and Robertson 2003).

Yderligere har udviklingen af computeren været med til at gøre anvendelsen af komplicerede statistiske beregninger hurtigere, mere præcise og mere tilgængelige. Anvendelsesområderne for statistik har ligeledes udviklet sig, fra i begyndelsen at være noget staten anvendte til styring af økonomi og befolkningsindblik, til stort set at være repræsenteret i alle større hverv i dag. Den moderne definition af statistik kan beskrives som evnen til at drage konklusioner om generelle tilfælde, populationer, på baggrund af enkelte tilfælde, stikprøver, (Agresti and Finlay 2014, s. 4).

2.2 Statistik

Statistik opdeles overordnet i to kategorier, deskriptiv statistisk og statistisk inferens.

Deskriptiv statistik

Det følgende afsnit er baseret på (AAU 2020 a) og (Agresti and Finlay 2014, s. 4-5)

Deskriptiv statistik drejer sig om at opsummere data, således at informationerne heri anskueliggøres og forståelsen af data styrkes, uden at fordreje eller miste den oprindelige information. Dette kan eksempelvis gøres ved at beregne middelværdien og spredningen, da det giver et bedre overblik, end at skulle overskue samtlige datapunkter. I nogle tilfælde kan det være tilstrækkeligt at lave en grafisk fremstilling af data, eventuelt i kombination med middelværdi og spredning.

Statistisk inferens

Det følgende afsnit er baseret på (AAU 2020 b), (AAU 2020 c) og (Agresti and Finlay 2014, s. 4-5).

På baggrund af informationen, som udtrykkes af deskriptiv statistik, er det således muligt ved hjælp af statistisk inferens at kommme med antagelser og drage konklusioner.

I statistisk inferens differentieres der mellem to metoder, estimering og hypotesetest. Når der estimeres på baggrund af en population, bruges stikprøven til at beskrive en ukendt del af populationen. Det kan eksempelvis være gennemsnitsindkomst hos en befolkning, \(\mu\), for hvilken der findes et estimat \(\hat{\mu}\), som bruges til at beskrive \(\mu\). Dette betegnes som et punktestimat, og vil oftest suppleres med et intervalestimat. Årsagen til dette er, at punktestimater er tilfældige, og derfor ændrer sig fra stikprøve til stikprøve. Da punktestimaters sandsynlighed for at være korrekt derfor er lig \(0\), tilstræbes det at anvende et intervalestimat, hvor det kan siges at \(\mu\) med \(95\%\) sikkerhed ligger, fremfor et punktestimat. Dette kaldes for et konfidensinterval.

Den anden form for statistisk infernes, hypotesetest, beskrives i det næste afsnit.

2.3 Hypotesetest

En hypotesetest baserer sig på det videnskabelige princip om falsificering. Der opstilles en indledende formodning om en population, kaldet nulhypotesen \(H_0\), og en alternativ, modsat hypotese \(H_1\). Er den indledende formodning ikke korrekt, må den alternative hypotese være gældende.

Ved en hypotesetest undersøges, hvorvidt der er en difference mellem observerede værdier og forventede værdier, hvis \(H_0\) er sand. Sandsynligheden for, at der er en difference, er stor, eftersom der arbejdes på en stikprøve og ikke selve populationen, og derfor benyttes et mål for, hvornår differencen er for stor, kaldet signifikansniveauet, \(\alpha\).

Når nulhypotesen og den alternative hypotese er blevet opstillet, kan stikprøvens resultat sammenlignes med det forventede resultat under nulhypotesen, ved hjælp af en teststørrelse. Teststørrelsen kan blandt andet bestemmes som antallet af standardafvigelser, den observerede værdi, \(\hat{\theta}\), ligger fra den forventede værdi \(\theta_0\), i retning af den alternative hypotese, (Editor 2015).

At \(\hat \theta\) ligger mere end \(3\) standardafvigelser fra \(\theta_0\), er højst usandsynligt, da \(\hat \theta\) i så fald er en outlier i populationen. I et sådan tilfælde er \(\theta_0\) højst sandsynligt ikke populationens korrekte værdi, hvorved nulhypotesen kan forkastes.

Derudover benyttes testtørrelsen til at udregne p-værdien, som er sandsynligheden for at få en teststørrelse, der er lige så eller mere ekstrem, hvis \(H_0\) er sand.

Værdien af teststørrelsen påvirker p-værdien på den måde, at når teststørrelsen bliver mere ekstrem, falder p-værdien. Jo mindre p-værdien er, des mindre stoles på \(H_0\), og hvis p-værdien er mindre end signifikansniveauet, \(\alpha\), forkastes \(H_0\). Er p-værdien derimod større end \(\alpha\), er der ikke belæg for at forkaste \(H_0\) - dette betyder dog ikke, at \(H_0\) givetvis er sand.

En illustration af teststørrelsens betydning ved en normalfordeling kan ses på Figur 2.1.

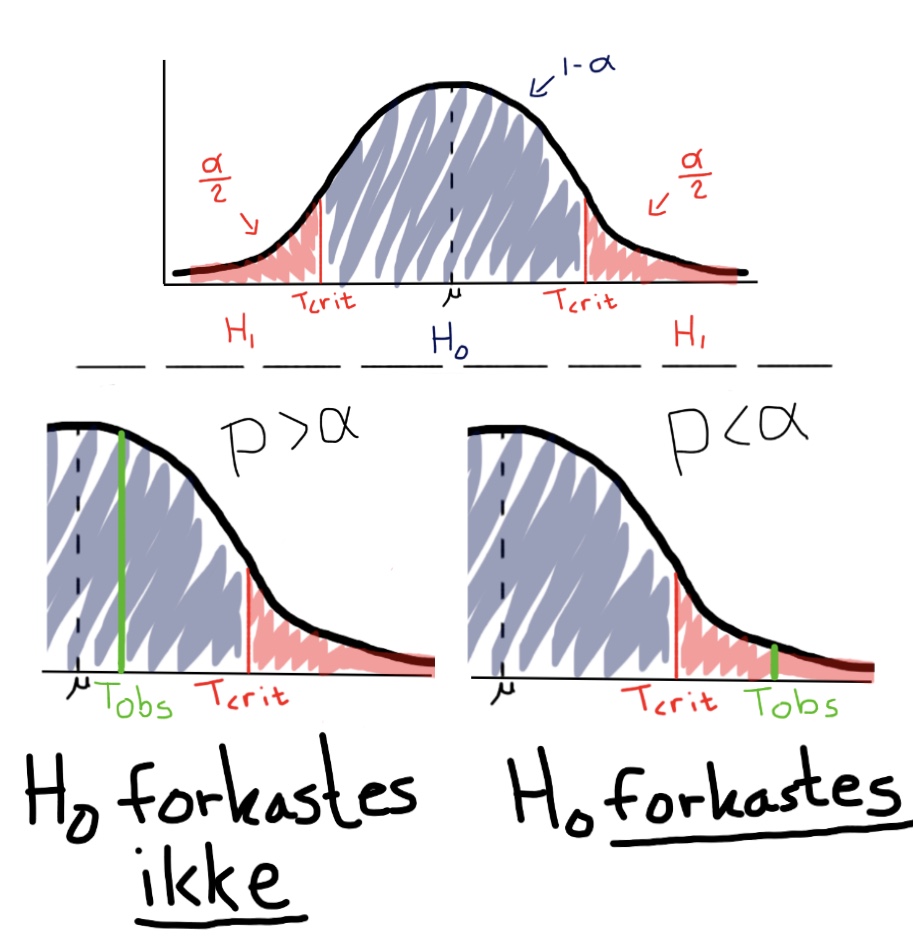
Teststørrelsens indflydelse på nulhypotesen. Er den observerede værdi mindre ekstrem end den kritiske værdi forkastes nulhypotesen ikke. Er den observerede værdi mere ekstrem end den kritiske værdi forkastes nulhypotesen og den alternative hypotese antages at være gældende.

Figur 2.1: Teststørrelsens indflydelse på nulhypotesen. Er den observerede værdi mindre ekstrem end den kritiske værdi forkastes nulhypotesen ikke. Er den observerede værdi mere ekstrem end den kritiske værdi forkastes nulhypotesen og den alternative hypotese antages at være gældende.

Normalt arbejdes der med et signifikansniveau på \(5\%\), \(\alpha=0.05\). Dog er der intet fast signifikansniveau og det kunne lige såvel være \(10\%\) eller \(1\%\). Betydningen heraf diskuteres i næste afsnit, (Team 2020).

2.3.1 Fejltyper

Der er risiko for to primære fejl når der foretages en hypotesetest. Den første, type-I fejl, er hvor \(H_0\) forkastes, men i virkeligheden er sand, og den anden, type-II fejl, er hvor \(H_0\) accepteres, men i realiteten er falsk. Dette er illustreret på figur 2.2.

En af de primære årsager til disse fejl er, hvor signifikansniveauet bliver sat, da dette i nogle tilfælde har stor betydning for, hvorvidt en hypotese bliver forkastet eller ej.

Sandsynligheden for type-I fejl er lig med det valgte signifikansniveau, \(\alpha\). Sandsynligheden for type-II fejl, \(\beta\), er derimod ikke let at præcisere. Dog er der stor sandsynlighed for type-II fejl, hvis den virkelige sandhed er tæt på nulhypotesen. Er den virkelige sandhed derimod langt fra nulhypotesen, vil sandsynligheden for type-II fejl være tilsvarende lille. Ligeledes har stikprøvens størrelse indflydelse, eftersom meget data mindsker risikoen for type-II fejl, hvor der er større risiko ved en mindre mængde data. Andelen af type-II fejl benyttes til at udregne hypotesetestens styrke, \(1-\beta\). Styrken beskriver andelen af gange, hvor \(H_1\) korrekt bliver forkastet, (Frydenberg 2001).

Figur 2.2: Tabel over fejltyper

Det vil påvises, hvilken betydning små differencer i middelværdien samt stikprøvestørrelsen har for andelen af type-II fejl.

##                          Stikprøvestørrelsen, n =
## Differencen i middelværdi     5    10    25    50   200  1000 10000
##                     0.001 0.959 0.950 0.947 0.949 0.956 0.952 0.946
##                     0.1   0.948 0.948 0.932 0.915 0.794 0.409 0.000
##                     1     0.731 0.472 0.068 0.001 0.000 0.000 0.000
##                     2     0.225 0.013 0.000 0.000 0.000 0.000 0.000
##                     5     0.000 0.000 0.000 0.000 0.000 0.000 0.000

Tabellen viser, at både stikprøvestørrelsen samt differencen i middelværdien, har stor betydning for andelen af af type-II fejl. Er differencen i middelværdierne \(0.001\) fremgår det, at stikprøvestørrelsen mellem \(5\) og \(10,000\) ikke giver signifikante forskelle, hvilket medfører, at stikprøvestørrelsen skal være meget større for at mindske andelen af type-II fejl. Derudover mindskes risikoen for type-II fejl som stikprøvestørrelsen øges, hvilket også er gældende hvis differencen i middelværdierne forøges.

2.3.2 Hypotesetest for middelværdier

I dette afsnit gennemgås fremgangsmåden for, hvordan en hypotesetest kan bruges til at bestemme middelværdien for en population. I dette afsnit kaldes en sådan hypotesetest for en t-test. Afsnittet er skrevet på baggrund af (AAU 2020 d).

Forud for gennemførelsen af en t-test, er der nogle antagelser, som skal være opfyldt, for at t-testen ikke giver misvisende resultater.

Stikprøven skal være repræsentativ for populationen.
Variablen skal være kvantitativ.
Stikprøveudtagning skal være udført med tilfældighed.
Populationen skal være normalfordelt.

I det følgende afsnit vil alle fire antagelser være opfyldt, og herefter er fremgangsmetoden som beskrevet i afsnit 2.3.

Eksempel

Der vil nu vises et eksempel på en t-test. Figur 2.3 viser en stikprøve af 10 observationer med en middelværdi på -0.1398759, udtaget fra en standard normalfordelt population.

Figur 2.3: Histogram over 10 simulerede standard normalfordelte tal.

I kodestykket nedenfor gennemgås den beskrevne fremgangsmåde for en t-test. I dette eksempel er \(H_0: \mu = 0\), og \(H_1: \mu \neq 0\).

forventet_middelvaerdi <- 0 

stik <- rnorm(n = 10, mean = 0, sd = 1)
middelvaerdi <- mean(stik)
standardafvigelse <- sd(stik)

estimeret_standardfejl <- standardafvigelse/sqrt(10) 

t_obs <- (abs(middelvaerdi-forventet_middelvaerdi))/
            estimeret_standardfejl

p_ensidet <-  1 - pdist("t", q = t_obs, df = 10-1, plot = FALSE)

p_tosidet <- 2 * p_ensidet
p_tosidet

## [1] 0.3784184

Eftersom p-værdien er 0.3784184 \(> \alpha=0.05\), forkastes \(H_0\) ikke. Der er altså ikke fundet nok evidens imod \(H_0\) til at kunne forkaste den. Havde p-værdien derimod været mindre end \(\alpha\) ville det medføre, at \(H_0\) forkastes og det ville formodes, at \(H_0\) ikke er korrekt for populationen.

2.4 Problemformulering

Kan det ses på resultatet af klassiske inferensmetoder, hvis deres antagelser ikke er overholdt? Og i så fald, hvorledes kan simuleringsstudier bidrage til at afdække dette problem?
Hvilke alternativer er der til klassiske inferensmetoder, såsom t-tests og konfidensintervaller, når deres antagelser ikke er overholdt, og hvor robuste er alternativerne?

Bibliografi

AAU, The Applied Statistics Team. 2020a. “ASTA - Lektion 1.1.” 2020. https://asta.math.aau.dk/course/asta/2020-1/std/lecture/1-1.

AAU, The Applied Statistics Team. 2020b. “ASTA - Lektion 1.2.” 2020. https://asta.math.aau.dk/course/asta/2020-1/std/lecture/1-2.

AAU, The Applied Statistics Team. 2020c. “ASTA - Lektion 1.3.” 2020. https://asta.math.aau.dk/course/asta/2020-1/std/lecture/1-3.

AAU, The Applied Statistics Team. 2020d. “ASTA - Lektion 2.1 Hypothesis Test.” 2020. https://asta.math.aau.dk/course/asta/2020-1/std/lecture/2-1?file=B/lecture-B-1.html#(1).

Agresti, Alan, and Barbara Finlay. 2014. Statistical Methods for the Social Sciences. 4th ed. Edinburgh Gate, England: Pearson.

Danske, Den Store. 2020. “Statistik.” 2020. http://denstoredanske.dk/Samfund,_jura_og_politik/Samfund/Samfund_og_statistik/statistik.

Dictionary, Online Etymology. 2020. “Statistics.” 2020. https://www.etymonline.com/word/statistics?fbclid=IwAR24xfhlEU8QlZQWFlc8zdzbupnl-HDFTIdr8y4HwH637e5yP1XO9Lh3dqs.

Editor, Minitab Blog. 2015. “Understanding Hypothesis Tests: Why We Need to Use Hypothesis Tests in Statistics.” 2015. https://blog.minitab.com/blog/adventures-in-statistics-2/understanding-hypothesis-tests-why-we-need-to-use-hypothesis-tests-in-statistics.

Encyclopaedia Britannica, The Editors of. 2020. “Sir Ronald Aylmer Fisher.” 2020. https://www.britannica.com/biography/Ronald-Aylmer-Fisher.

Frydenberg, Morten. 2001. “Epidemiologi Og Biostatistik.” 2001. https://www.biostat.au.dk/teaching/praegrad/for%C3%A5r2001/forelaesninger/biostatistik/uge2torsdag.pdf.

O’Connor, J. J., and E. F. Robertson. 2003. “William Sealy Gosset.” 2003. http://mathshistory.st-andrews.ac.uk/Biographies/Gosset.html.

Team, ASTA. 2020. “Hypothesis Test.” 2020. https://asta.math.aau.dk/course/asta/2020-1/std/lecture/2-1?file=B/lecture-B-1.pdf.