Kapitel 6 Bootstrap

I dette kapitel vil den teoretiske del af bootstrap blive beskrevet.

Der findes forskellige bootstrap-metoder, som varierer på forskellige punkter. Valget af bootstrap-metode afhænger af den individuelle situation, hvor der skal udføres statistisk inferens. Der gøres opmærksom på, at i den resterende del af rapporten, vil ordet bootstrap henvise til den ikke-parametriske bootstrap-metode. Ikke-parametrisk bootstrap, er når der ikke sættes specifikke antagelser eller en præcis model for populationen, når undersøgelsen udføres. Derimod antages det, at en stikprøve er repræsentativ for hele populationen, (Berrar 2019, side 3).

Der vil i kapitlet blive undersøgt, hvordan bootstrap kan anvendes i praksis til at udregne standardfejl for en estimator, hvordan hypotesetest kan udføres ved hjælp af bootstrap og hvordan bootstrap kan benyttes til at angive konfidensintervaller. Til hver anvendelse vil der også blive givet et eksempel på metoden.

6.1 Ikke-parametrisk bootstrap

Bootstrap er en resampling-metode, der bruges til at generere yderligere stikprøver, kaldet bootstrap-stikprøver, ud fra en given stikprøve, hvor målet er at udføre statistisk inferens for en valgt teststørrelse. For eksempel kan bootstrap give et indblik i tendenser for teststørrelsen, såsom standardfejlen og forventningsrethed, eller udregne konfidensintervaller. Der gøres opmærksom på, at bootstrap ikke kan bruges til at få et bedre estimat for parameteren, da bootstrap-fordelingen er centreret omkring stikprøvens estimat, se figur 6.1 (genskabt ud fra figur 5.2 i (Chihara and Hesterberg 2019, side 108)), for eksempel middelværdien \(\hat {\mu}\), og ikke populationens middelværdi, \(\mu\), (Chihara and Hesterberg 2019 s. 114).

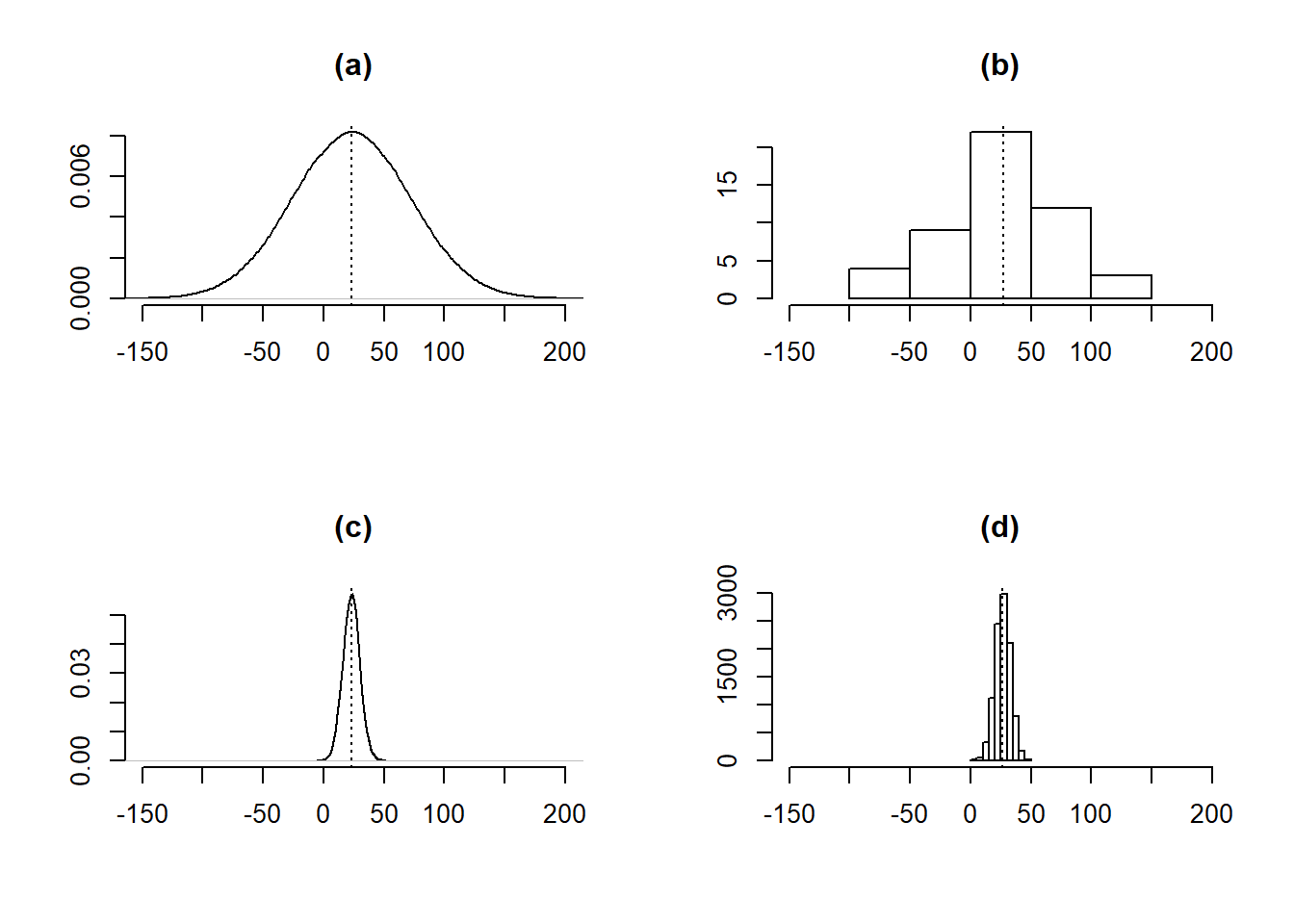
Figur 6.1: (a) Populationens fordeling, N(23, 49). (b) Fordelingen af en stikprøve af størrelsen 50. (c) Den teoretiske fordeling af stikprøvens middelværdi. (d) Fordelingen af bootstrap-stikprøvernes middelværdi. De stiplede linjer representerer middelværdien.

Hver bootstrap-stikprøve har samme størrelse som stikprøven. Bootstrap opererer med tilbagelægning, så der er en sandsynlighed for, at et givent datapunkt bliver udtaget mere end en gang. Samtidig er der en sandsynlighed for, at et datapunkt slet ikke bliver udvalgt. Det er relevant at undersøge, hvor mange af de oprindelige observationer, som i gennemsnit medtages i nye bootstrap-stikprøver, og ligeledes, hvor mange, som udelades.

Sandsynligheden for, at en specifik observation ikke udtages én gang fra de oprindelige \(n\) observationer, er \(1-1/n\), og sandsynligheden for, at denne observation ikke udtages \(n\) gange er \((1-1/n)^n\). Når stikprøvestørrelsen, \(n\), går mod uendeligt gælder, at \((1-1/n)^n~ \stackrel{n \rightarrow \infty}{=}~ 1/e \approx 0.368\). Derfor vil en bootstrap-stikprøve af tilpas stor størrelse indeholde \(\approx 63.2\%\) observationer fra den oprindelige stikprøve, og udelade \(\approx 36.8\%\), (Wicklin 2017).

I alt bliver der genereret \(B\) bootstrap-stikprøver, som der hver især udføres statistisk inferens på. Med den computerkraft der er tilgængelig i dag, anbefales der af kilden, (Marin 2018), mindst \(10,000\) resamples for at få et nøjagtigt estimat. Grunden til, at der ikke genereres et endnu større antal bootstrap-stikprøver end de \(10,000\) er, at bootstrap-stikprøven genereres ud fra den obseverede data, og et større \(B\) vil derfor ikke medføre yderligere information om populationen, (Marin 2018, 10:20).

Fordelen ved bootstrap er, at selvom der kun er én tilgængelig stikprøve fra den underliggende population, er der stadig mulighed for at estimere stikprøvefordelingen, uden at der kræves yderligere stikprøver fra populatonen, se figur 6.2. Dette skyldes netop antagelsen om, at stikprøven skal være repræsentativ for populationen.

Figur 6.2: Her er illustreret forskellen mellem at finde den teoretiske stikprøvefordeling ved hjælp af mange stikprøver fra populationen (orange), og måden hvorpå stikprøvefordelingen kan findes ved hjælp af kun én stikprøve, der udføres bootstrap på (grøn).

Der er to hovedårsager til at benytte bootstrap, som beskrevet i (Marin 2018). For det første, hvis stikprøven ikke er tilpas stor, og stikprøvefordelingen derfor heller ikke kan antages at være normalfordelt. For det andet, hvis metoden til at beregne teststørrelsens standardfejl er teoretisk avanceret. Eksempelvis er standardfejlen for middelværdien nem at løse, \(\hat{\text{se}}(\hat{\mu}) = \frac{S}{\sqrt{n}}\), mens det ikke er tilfældet, hvis det i stedet er afstanden mellem to percentiler, der estimeres.

6.2 Bootstrap-standardfejl

Der vil i dette afsnit beskrives, hvordan standardfejl af en stikprøve kan udregnes ved hjælp af bootstrap. Udregnes standardfejlen på denne måde, kaldes den for bootstrap-standardfejlen. Det følgende afsnit er primært skrevet på baggrund af (Yen 2019).

Standardafvigelsen for en estimator beskrives som estimatorens standardfejl. Standardfejlen er et udtryk for, hvor stor en afvigelse der er fra populationens parameter til stikprøvens estimat. Jo mindre standardfejlen er, desto mindre er afvigelsen mellem estimatet og parameteren. Som udgangspunkt vil en stikprøves estimat aldrig være lig populationens parameter, fordi der ved udtagning af en stikprøve, i hvert tilfælde vil være variabilitet.

Som eksempel vil standardfejlen for estimatet af middelværdien, \(\hat{\mu}\), være \(\text{se}(\hat{\mu}) = \frac{\sigma}{\sqrt{n}}\).

Når der arbejdes med data udover det teoretiske, vil standardafvigelsen for populationen, \(\sigma\), altid være ukendt. Derfor bruges stikprøvens estimat for standardafvigelsen, \(S\) til at beregne den estimerede standardfejl, \(\hat{\text{se}}\).

Som eksempel vil den estimerede standardfejl for estimatet af middelværdien, \(\hat{\mu}\), være \(\hat{\text{se}}(\hat{\mu}) = \frac{S}{\sqrt{n}}\), hvor \(S = \sum_{i=1}^{n} \frac{(x_i - \hat{\mu})^2}{n - 1}\) er stikprøvens standardafvigelse for middelværdien, og \(n\) er størrelsen på stikprøven.

Dog er dette ikke altid ligetil i virkeligheden. Oftest er der ikke tilstrækkelige informationer om populationen eller fordeligen af denne. Samtidig kræver det, at der er nogle specifikke krav, som er opfyldt. Disse problemer kan undgås ved at benytte bootstrap til at estimere bootstrap-standardfejlen, givet ved nedenstående formel.

\[se^*(\hat{\theta}) = \sqrt{\frac{1}{B-1}\sum_{b=1}^{B}(\hat{\theta_b^*} - \bar{\theta} )^2}\]

Hvor \(\hat{\theta}\) er stikprøvens estimat for den ønskede parameter, \(B\) er antal bootstrap-stikprøver, \(\hat\theta_b^*\) er estimatet for den \(b\)’te bootstrap-stikprøve og \(\bar{\theta} = (\frac{1}{B}) \sum_{b=1}^{B}\hat{\theta_b^*}\), (Bartlett 2013).

Eksempel

I kodestykket nedenfor udtages en tilfældig stikprøve fra en standard normalfordelt population. Først udregnes standardfejlen for stikprøven. Derefter laves \(10,000\) bootstrap-stikprøver, som benyttes til at beregne stikprøvens bootstrap-standardfejl. Til sidst sammenlignes disse to estimater. Pakken boot benyttes.

n <- 1000

stik <- rnorm(n, mean = 0, sd = 1)
SD_stik <- sd(stik)
SE_stik <- SD_stik/sqrt(n)

B <- 10000

middel_funk <- function(stik, i){mean(stik[i])} # Estimator

# Bootstrap-stikprøver
Boot_stik <- boot::boot(data = stik, statistic = middel_funk, R = B) 
# Standardfejlen for bootstrap-stikprøverne
SE_boot <- sd(Boot_stik$t) 

# Procentvis afvigelse mellem normal standardfejl og 
# bootstrap-standardfejl
diff_procent <- ((abs(SE_stik - SE_boot))/SE_stik) * 100

Fra eksemplet fås, at bootstrap-standardfejlen for stikprøven er \(se^*(\hat{\mu})=\)0.0325, hvilket approksimerer stikprøvens standardfejl på \(\text{se}(\hat{\mu})=\)0.0325, med en forskel i dette tilfælde på 0.064\(\%\). Hvis der opstår en situation, hvor der ikke er en simpel måde, hvorpå det er muligt at udregne standardfejlen, kan bootstrap-standardfejlen altså udnyttes, da en forskel på 0.064\(\%\) ikke er signifikant.

6.3 Bootstrap-hypotesetest

Som nævnt i afsnit 2.3.2, skal visse antagelser være opfyldt, for at garantere korrektheden af resultaterne af en t-test, og det efterfølgende resultat af overtrædelsen af disse antagelser, blev vist i kapitel 4.

Når disse antagelser ikke er opfyldt, kan bootstrap anvendes til at udføre hypotesetest, og i så fald kaldes det i det følgende for en bootstrap-test. I følgende to afsnit gennemgås først fremgangsmåden for en uparret bootstrap-test, og dernæst fremgangsmåden for en parret bootstrap-test.

6.3.1 Uparret bootstrap-test

I dette afsnit benyttes bootstrap til at lave en uparret hypotesetest på skæve stikprøver.

Lad to uafhængige uparrede stikprøver, \(X=[x_{1},~x_{2},~...,~x_{n}]\) og \(Y=[y_{1},~y_{2},~...,~y_{m}]\), hvor \(X \wedge Y \sim \text{Beta}(2, 8)\), med ens varians være givet på figur 6.3.

n <- 20
m <- 50

stik1 <- rbeta(n, shape1 = 2, shape2 = 8)
stik2 <- rbeta(m, shape1 = 2, shape2 = 8)

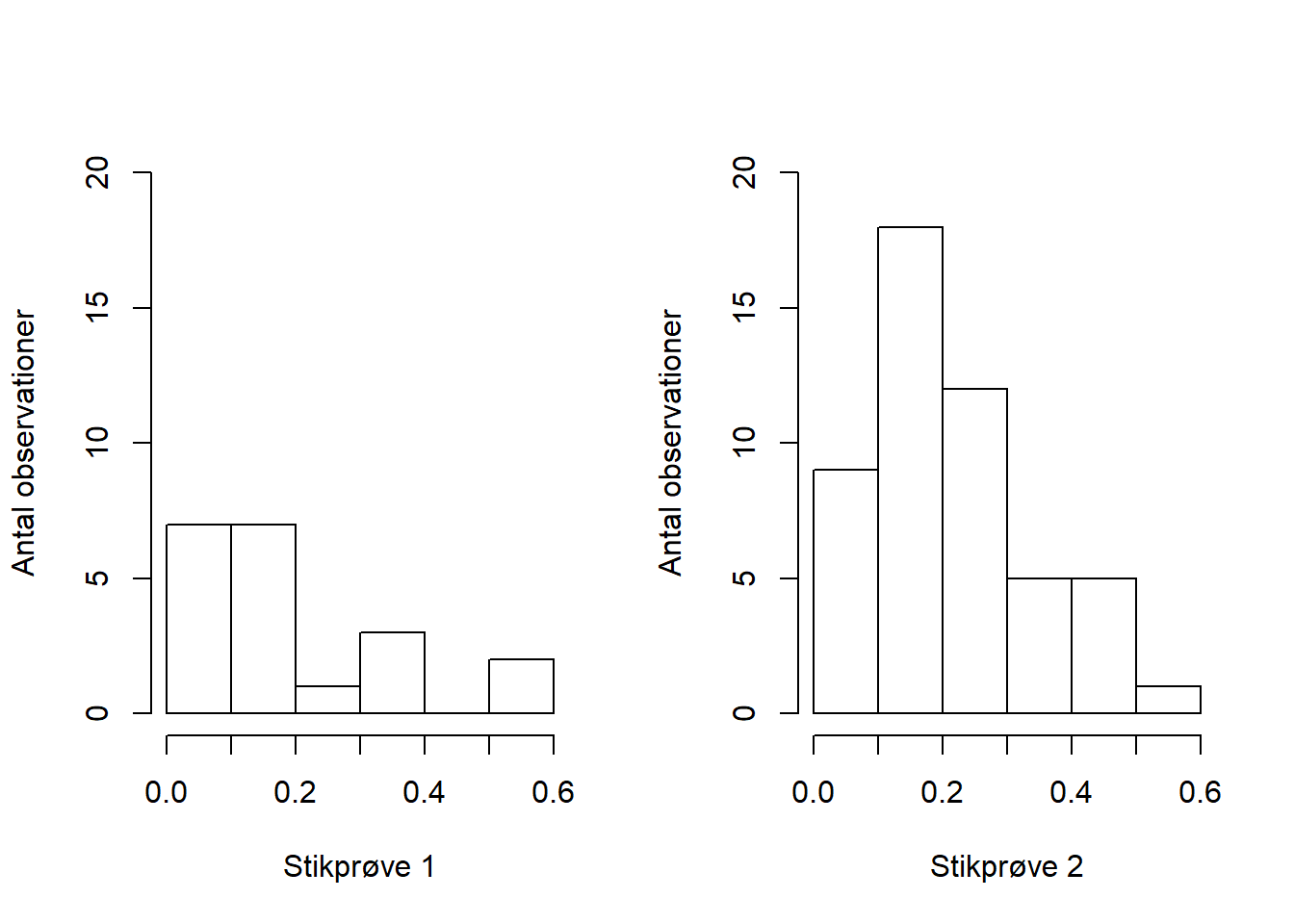
Figur 6.3: To uafhængige uparrede stikprøver

Så opstilles der en nulhypotese, \(H_0: \mu_{_X} - \mu_{_Y} = 0\), hvor \(\mu_{_X}\) og \(\mu_{_Y}\) er de sande middelværdier for populationerne, hvorfra stikprøverne blev udtrukket og en alternativ hypotese, \(H_1: \mu_{_X} - \mu_{_Y} \neq 0\), samt et signifikansniveau, \(\alpha = 0.05\).

På baggrund af forskellen i de to stikprøvers middelværdi, er det muligt at udregne en teststørrelse ved nedenstående formel.

\[t_{obs} = \frac{(\bar{X}-\bar{Y}) - (\bar{X_0} - \bar{Y_0})}{((s_X^2/n) + (s_Y^2/m))}\]

Hvor \(\bar{X_0}\) og \(\bar{Y_0}\) er middelværdien for \(X\) og \(Y\) under \(H_0\), og \(s\) er standardafvigelsen.

t_obs <- ((mean(stik1) - mean(stik2)) - (0)) /
            (sqrt(((sd(stik1))^2 / n)) +
              ((sd(stik2))^2 / m))
t_obs

## [1] -0.6280534

For at udføre bootstrap-testen, forenes de to stikprøver til en samlet stikprøve med størrelsen \(n + m\) observationer. Derefter laves en bootstrap-stikprøve af \(n + m\) observationer fra den samlede stikprøve. De første \(n\) indgange i bootstrap-stikprøven er bootstrap-stikprøven for \(X\), og kaldes \(X^*\). De resterende \(m\) indgange er bootstrap-stikprøven for \(Y\), og kaldes \(Y^*\). Til sidst udregnes bootstrap-teststørrelsen ved hjælp af nedenstående formel.

\[t^* = \frac{(\bar{X}^*-\bar{Y}^*) - (\bar{X} - \bar{Y})}{((s_{X^*}^2/n) + (s_{Y^*}^2/m))}\]

I alt beregnes der \(B\) bootstrap-teststørrelser, (Myung 2015). Et eksempel på dette udregnes i nedenstående kodestykke.

bootstraps <- 1000
boot_t <- replicate(n = bootstraps, {
    
    # Samlede bootstrap-stikprøve
    boot <- sample(x = c(stik1, stik2), replace = TRUE) 
  
    boot_x <- boot[1 : n] # Bootstrap-stikprøve 1
    boot_y <- boot[(n + 1) : (n + m)] # Bootstrap-stikprøve 2
  
    boot_test <- ((mean(boot_x) - mean(boot_y)) -
                    (mean(stik1) - mean(stik2))) /
                      (sqrt(((sd(boot_x))^2 / n)) +
                        ((sd(boot_y))^2 / m))
})
head(boot_t, 3)

## [1] -1.5835004  0.8703555 -0.3314820

Ovenfor ses tre af bootstrap-teststørrelserne, og fordelingen af dem kan ses på på figur 6.4, hvor den observerede teststørrelse er markeret med en blå linje, og bootstrap-teststørrelsernes middelværdi er markeret med en grøn linje.

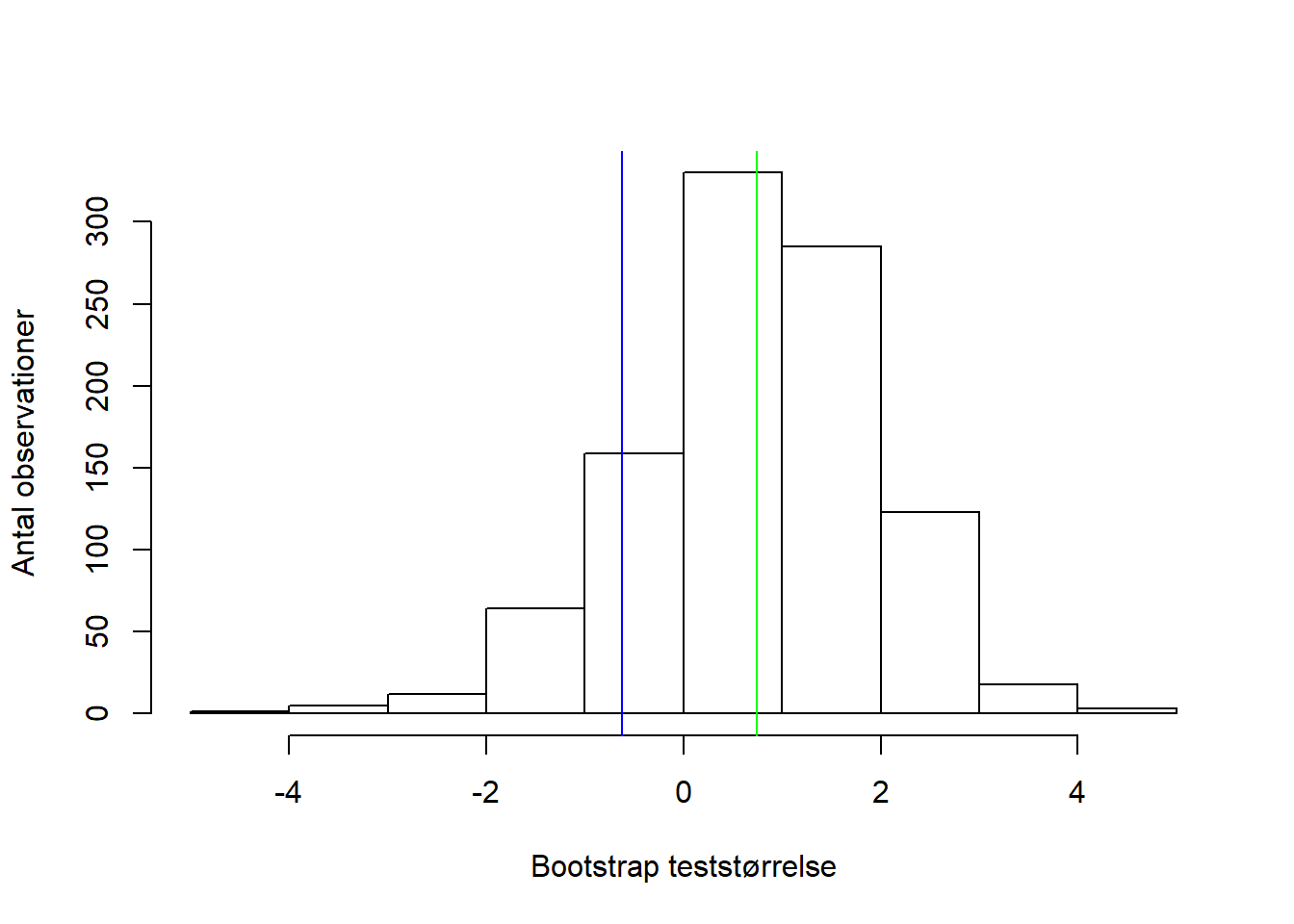
Figur 6.4: Fordelingen af bootstrap-teststørrelserne, hvor den blå linje markerer den observerede teststørrelse, og den grønne linje markerer fordelingens middelværdi.

Herefter kan p-værdien udregnes som ved permutationstest i afsnit 5.1.

antal_ekstreme <- abs(boot_t) >= t_obs

p_vaerdi <- (sum(antal_ekstreme) + 1) / (bootstraps + 1)
p_vaerdi

## [1] 1

Med en p-værdi på 1, kan \(H_0\) ikke forkastes, da der ikke er evidens for at middelværdierne for de to populationer er forskellige. Dette resultat stemmer overens med figur 6.4, da bootstrap-teststørrelsernes middelværdi er tæt på den observerede teststørrelse.

Eksempel

Den udførte test kan ved hjælp af R’s funktion replicate, gentages mange gange, for at undersøge om resultatet vil blive det samme, ved mange stikprøveudtagninger. Fremgangsmåden for den uparrede bootstrap-test er den samme. Den bliver blot gentaget \(100\) gange, og middelværdien af de \(100\) p-værdier findes.

res <- replicate(n = 100, {
  stik1 <- rbeta(n, shape1 = 2, shape2 = 8)
  stik2 <- rbeta(m, shape1 = 2, shape2 = 8)
  t_obs <- ((mean(stik1) - mean(stik2)) - (0)) /
              sqrt(((sd(stik1))^2 / n)) + ((sd(stik2))^2 / m)

  boot_t <- replicate(n = bootstraps, {
  
    boot <- sample(c(stik1, stik2), replace = TRUE)
  
    boot_x <- boot[1 : n]
    boot_y <- boot[(n+1) : (n+m)]
    boot_test <- ((mean(boot_x) - mean(boot_y)) -
                    (mean(stik1) - mean(stik2))) /
                      sqrt(((sd(boot_x))^2 / n)) +
                        ((sd(boot_y))^2 / m)
  })
  
  antal_ekstreme <- abs(boot_t) >= t_obs

  p_vaerdi <- (sum(antal_ekstreme)+1) / (bootstraps + 1)
})

p_vaerdi_uparret <- mean(res)
p_vaerdi_uparret

## [1] 0.7864935

Der ses, at gennemsnittet af p-værdierne er lig 0.7865, hvilket er større end signifikansniveauet. Dermed er der ikke evidens nok til at forkaste nulhypotesen.

6.3.2 Parret bootstrap-test

I dette afsnit benyttes bootstrap til at lave en parret hypotesetest på skæve stikprøver.

Lad to parrede stikprøver være givet, \(X=[x_{1},~x_{2},~...,~x_{n}]\) og \(Y=[y_{1},~y_{2},~...,~y_{n}]\). Der oprettes et tredje datasæt, \(Z\), som består af differencerne mellem \(x_i\) og \(y_i\), \(Z = [x_1-y_1,~ x_2-y_2,~...,~x_n-y_n] = [z_1,~z_2,~...,~z_n]\). Ved hjælp af det nye datasæt er det muligt at udregne teststørrelsen, \(t_{obs} = \frac{\bar{Z} - \mu_0}{\hat{SE}(Z)}\).

Så opstilles der en nulhypotese, \(H_0:~\mu_Z = 0\), hvor \(\mu_Z\) angiver den sande middelværdi for \(Z\), og en alternativ hypotese, \(H_1:~\mu_Z \neq 0\), samt et signifikansniveau, \(\alpha = 0.05\).

Der udtages en bootstrap-stikprøve for \(Z\), som betegnes \(Z^*\). På baggrund af bootstrap-stikprøven kan der nu udregnes \(B\) nye teststørrelser, \(t^*_i = \frac{\bar{Z}^*_i - \bar{Z}}{\hat{SE}(Z^*_i)}\), hvor \(Z^*_i\) er den \(i\)’te bootstrap-stikprøve, og \(i = 1, 2, \ldots, B\), (Chihara and Hesterberg 2019, s. 106, 124-127, 246).

Eksempel

I nedenstående kode, vises et eksempel på en parret bootstrap-test, hvor stikprøverne ikke er fra den samme fordeling.

n <- 15

p_reps <- replicate(n = 100, {
  stik1 <- rgamma(n, shape = 10, rate = 2)
  stik2 <- rgamma(n, shape = 4, rate = 13)
  stik_diff <- stik1 - stik2
  obs_t <- (mean(stik_diff)-0)/(sd(stik_diff)/sqrt(n))

  boot_t <- c()
  for(i in seq(1, bootstraps)){
    boot <- sample(stik_diff, n, replace = TRUE)
    boot_t[i] <- (mean(boot)-mean(stik_diff))/(sd(boot)/sqrt(n))
  }
  
  antal_ekstreme <- abs(boot_t) >= obs_t
  
  p_vaerdi <- (sum(antal_ekstreme) + 1) / (bootstraps + 1)
})

p_vaerdi_parret <- mean(p_reps)
p_vaerdi_parret

## [1] 0.001028971

Det ses, at p-værdien er lig 0.001029, hvilket er mindre end signifikansniveauet. Her vil nulhypotesen forkastes, da der er evidens for at differencen ikke er \(0\). For at undersøge korrektheden af en bootstrap-test, kan andelen af type-I fejl, som skal svare til signifikansniveauet, beregnes, (Agresti and Finlay 2014, s. 159-160).

Type-I fejl

Antallet af type-I fejl, der opstår i en parret bootstrap-test kan undersøges ved at se, hvor mange gange \(H_0\) forkastes, selvom \(H_0\) er sand.

I koden nedenfor bestemmes antallet af type-I fejl for en parret bootstrap-test.

n <- 20
konf_niveau <- 0.95
sand_middel <- 0

type_1_fejl_boot <- replicate(n = 500, {
  stik1 <- rgamma(n, shape = 8, rate = 2)
  stik2 <- rgamma(n, shape = 8, rate = 2)
  stik_diff <- stik1 - stik2
  obs_t <- (mean(stik_diff)-sand_middel)/(sd(stik_diff)/sqrt(n))

  boot_t <- c()
  for(i in seq(1, bootstraps)){
    boot <- sample(stik_diff, n, replace = TRUE)
    boot_t[i] <- (mean(boot)-mean(stik_diff))/(sd(boot)/sqrt(n))
  }

  antal_ekstreme <- abs(boot_t) >= obs_t

  p_vaerdi <- (sum(antal_ekstreme)+1) / (bootstraps + 1)
  
  andel <- p_vaerdi > 1 - konf_niveau
})

type_1_parret <- table(type_1_fejl_boot)
type_1_parret

## type_1_fejl_boot
## FALSE  TRUE 
##    18   482

I alt forkastes \(H_0\) fejlagtigt i 3.6\(\%\) af tilfældene, hvilket ikke stemmer overens med det valgte signifikansniveau.

Selvom det virker godt, at bootstrap laver færre type-I fejl end signifikansniveauet antyder, er det ikke nødvendigvis en fordel. Hvis der laves en hypotesetest, hvor det forventede antal type-I fejl er lig signifikansniveauet, men det faktiske antal er noget andet, kan det lede til forkerte konklusioner.

6.4 Bootstrap-konfidensintervaller

I dette afsnit beskrives, hvorledes et konfidensinterval kan beregnes ved hjælp af bootstrap. Der vises tre forskellige metoder, kaldet henholsvis percentil-, basic- og T-metoden. Til sidst sammenlignes de tre metoders dækningsgrader ved forskellige stikprøvestørrelser.

Et \(95\%\) konfidensinterval på en normalfordelt estimator, \(\Theta\), kan udregnes ved \(\text{KI} = [\hat\theta - 1.96\cdot \text{se}(\hat\theta),~\hat\theta + 1.96\cdot \text{se}(\hat\theta)]\), (Orloff and Bloom 2014). Hvis ikke fordelingen er kendt, er det ikke muligt at udregne et konfidensinterval således. Her er det i stedet muligt at benytte bootstrap til at udregne et konfidensinterval, hvilket kan gøres ved hjælp af forskellige metoder.

6.4.1 Percentilmetoden

En intuitiv fremgangsmåde til at bestemme et \((1-\alpha)100\%\) konfidensinterval ved percentiler, er at bruge det \((B(\frac{\alpha}{2}))\)’te og \((B(1-\frac{\alpha}{2}))\)’te percentil, hvor \(B\) er antallet af bootstrap-stikprøver Lad \(\Theta^* = [\vartheta_1,~ \ldots,~\vartheta_B]\) være en sorteret liste af bootstrap-estimater. Derved er formlen for et konfidensinterval på baggrund af percentiler:

\[\text{KI}_p = \left[q_{(\alpha/2)},~q_{(1-\alpha/2)}\right]\]

Hvor \(q_i\) er det \(i\)’te percentil i \(\Theta^*\). (Lau, Gonzalez, and Nolan n.d.)

Eksempel

I kodestykket nedenfor udtages en tilfældig stikprøve fra en standard normalfordeling. Herefter laves \(10,000\) bootstrap-stikprøver, som middelværdien udregnes på. Til sidst sorteres middelværdierne i en liste.

data <- rnorm(100, mean = 0, sd = 1)

n <- length(data)
bootstraps <- 10000

bootstrap_fordeling <- replicate(n = bootstraps, {
  x <- mean(sample(data, size = n, replace = TRUE))
})

SortedBoots <- sort(bootstrap_fordeling)

Dernæst vælges signifikansniveauet til \(\alpha = 0.05\), og konfidensintervallet ved hjælp af percentiler beregnes i nedenstående kodestykke.

KI_niveau <- 0.95
alpha <- 1 - KI_niveau

NedrePercentil <- round(bootstraps * alpha/2)
OevrePercentil <- round(bootstraps * (1-alpha/2))

KI_Percentil <- c(Nedre = SortedBoots[NedrePercentil], 
                  Oevre = SortedBoots[OevrePercentil])

KI_Percentil

##       Nedre       Oevre 
## -0.08445604  0.32382861

Percentilmetoden giver et konfidensinterval på \(\text{KI}_p = [\)-0.084 , 0.324\(]\).

6.4.2 Basic-metoden

Denne type konfidensinterval ud fra bootstrap er også kendt som reversed percentile interval, der benytter nedenstående formel til udregning af konfidensintervaller.

\[\text{KI}_b = \left[2\hat\theta- q_{(1-\alpha/2)}, ~ 2\hat\theta- q_{(\alpha/2)}\right]\]

Hvor \(q_i\) er det \(i\)’te percentil i \(\Theta^*\) og \(\hat\theta\) er middelværdien af stikprøven, (Duke n.d.). Hermed følger udledningen af basic-metoden:

Bevis. Fra percentilmetoden kendes følgende konfidensinterval.

\(0.95 \approx P[q_{(\alpha/2)} \leq \hat{\theta}^* \leq q_{(1-\alpha/2)}]\)

Der trækkes \(\hat{\theta}\) fra på alle sider af uligheden og der ganges igennem med \(-1\), så uligheden vendes om.

\(0.95 = P[q_{(\alpha/2)} - \hat\theta \leq \hat{\theta}^* - \hat\theta \leq q_{(1-\alpha/2)} - \hat\theta]\)

\(0.95 = P[\hat\theta - q_{(\alpha/2)} \geq \hat\theta - \hat{\theta}^* \geq \hat\theta - q_{(1-\alpha/2)}]\)

Differencen \(\theta - \hat\theta\) er tilnærmelsevist den samme som \(\hat\theta - \hat\theta^*\), hvilket nu indsættes i uligheden.

\(0.95 \approx P[\hat\theta - q_{(\alpha/2)} \geq \theta - \hat\theta \geq \hat\theta - q_{(1-\alpha/2)}]\)

Dernæst lægges \(\hat{\theta}\) til på alle sider af uligheden, og dermed fås konfidensintervallet.

\(0.95 = P[2\hat\theta - q_{(\alpha/2)} \geq \theta \geq 2\hat\theta - q_{(1-\alpha/2)}]\)

Eksempel

I kodestykket nedenfor beregnes middelværdien af stikprøven og benyttes i formlen.

theta_hat <- mean(data)

KI_Basic <- c(Nedre = 2*theta_hat-SortedBoots[OevrePercentil],
              Oevre = 2*theta_hat-SortedBoots[NedrePercentil])

KI_Basic

##       Nedre       Oevre 
## -0.08905211  0.31923255

Basic-metoden giver et konfidensinterval på \(\text{KI}_b = [\)-0.089 , 0.319\(]\).

6.4.3 T-metoden

Denne type bootstrap-konfidensinterval, benytter nedenstående formel.

\[\text{KI}_t=\left[\hat\theta-t^{*}_{(1-\alpha/2)}\cdot \hat{\text{se}}(\theta),~\hat\theta-t^{*}_{(\alpha/2)}\cdot\hat{\text{se}}(\theta)\right]\]

Hvor \(\hat\theta\) er middelværdien af stikprøven, \(t^{*}=\frac{\hat{\vartheta}-\hat\theta}{\hat{\text{se}}(\vartheta)}\) og \(\hat{\vartheta}\) er middelværdien for \(\Theta^*\), (Lau, Gonzalez, and Nolan n.d.).

Beviset for formlen til konfidensintervallet for T-metoden, følger samme metode som i afsnittet for basic-metoden.

Eksempel

I kodestykket forneden beregnes \(t^{*}\) for det nedre og øvre percentil. Dernæst beregnes konfidensintervallet ud fra formlen.

T_Nedre <- (SortedBoots[OevrePercentil]-theta_hat) /
  (sd(bootstrap_fordeling))

T_Oevre <- (SortedBoots[NedrePercentil]-theta_hat) /
  (sd(bootstrap_fordeling))

KI_T <- c(Nedre = theta_hat - T_Nedre * (sd(data)/sqrt(n)),
               Oevre = theta_hat - T_Oevre * (sd(data)/sqrt(n)))
KI_T

##       Nedre       Oevre 
## -0.09330652  0.32339224

T-metoden giver et konfidensinterval på \(\text{KI}_t = [\)-0.093 , 0.323\(]\).

6.4.4 Dækningsgrader

I dette afsnit vil der undersøges, hvor præcise metoderne for at udregne konfidensintervallerne med bootstrap er. Dette gøres ved at udregne dækningsgraden af konfidensintervallerne som de forskellige metoder har produceret.

Som det første oprettes en funktion, der udregner middelværdien for stikprøven, og tager en stikprøve og et indeks som input.

# Estimator for middelværdi
meanFunc <- function(stik, i) 
{    middel <- mean(stik$data[i])
     n <- length(i)
     varians <- (n-1) * var(stik$data[i]) / n^2
     c(middel, varians)
}

Det næste der udregnes er et konfidensinterval. Konfidensintervallet beregnes ved hjælp af funktionen boot.ci, der kommer fra pakken boot.

Der bliver først lavet 100 konfidensintervaller på baggrund af normalfordelte stikprøver. Så undersøges der om middelværdien af populationen er i konfidensintervallet. Hvis det er tilfældet, vil outputtet være TRUE, hvis ikke vil det være FALSE. Herefter indsættes disse output i en matrix.

Til sidst beregnes dækningsgraden som andelen af de intervaller, der indeholder den sande middelværdi. Der laves 100 konfidensintervaller for hver stikprøvestørrelse. Stikprøvestørrelsen er angivet i en sekvens fra 4 til 100 med spring på 4. Denne proces udføres for de tre metoder, percentil, basic og T.

Her udføres processen for beregning af dækningsgraden for alle tre metoder.

sand_middel <- 0

matriks_p <- matrix(ncol = 25, nrow = 100)
vector_p <- c()

matriks_b <- matrix(ncol = 25, nrow = 100)
vector_b <- c()

matriks_t <- matrix(ncol = 25, nrow = 100)
vector_t <- c()

for(n in seq(4, 100, 4)){
  res <- replicate(n = 100,{
    stik <- data.frame(data = rnorm(n))
    boot_stik <- boot::boot(data = stik, statistic = meanFunc, 
                            R = 100)
    
    # Beregner konfidensintervallerne, hvor typen "stud" betegner
    # T-metoden
    interval <- boot::boot.ci(boot.out = boot_stik, 
                              conf = KI_niveau, 
                              type = c("perc", "basic", "stud"))
    
    # Returnerer nedre og øvre grænse for konfidensintervallerne
    interval_p <- interval$percent[4:5]
    interval_b <- interval$basic[4:5]
    interval_t <- interval$student[4:5]
    
    # Undersøger om den sande middelværdi er i konfidensintervallet
    tf_p <- interval_p[1]<=sand_middel & interval_p[2]>=sand_middel
    tf_b <- interval_b[1]<=sand_middel & interval_b[2]>=sand_middel
    tf_t <- interval_t[1]<=sand_middel & interval_t[2]>=sand_middel
    return(c(tf_p, tf_b, tf_t))
  })
  
  # Dækningsgraden afhængigt af stikprøvestørrelsen
  matriks_p[,n/4] <- res[1,]
  vector_p <- append(vector_p, mean(matriks_p[,n/4]))
  
  matriks_b[,n/4] <- res[2,]
  vector_b <- append(vector_b, mean(matriks_b[,n/4]))
  
  matriks_t[,n/4] <- res[3,]
  vector_t <- append(vector_t, mean(matriks_t[,n/4]))
}

# Dækningsgraden for percentilmetoden
vector_p[1:5]

## [1] 0.78 0.84 0.89 0.89 0.96

I vector_p fremgår middelværdierne for dækningsgraden af 100 konfidensintervaller genereret ud fra percentilmetoden. Den første middelværdi er for stikprøvestørrelsen \(n = 4\), den næste er for stikprøvestørrelsen \(n = 8\) og så videre.

Dækningsgraderne for de tre metoder illustreres på figur 6.5.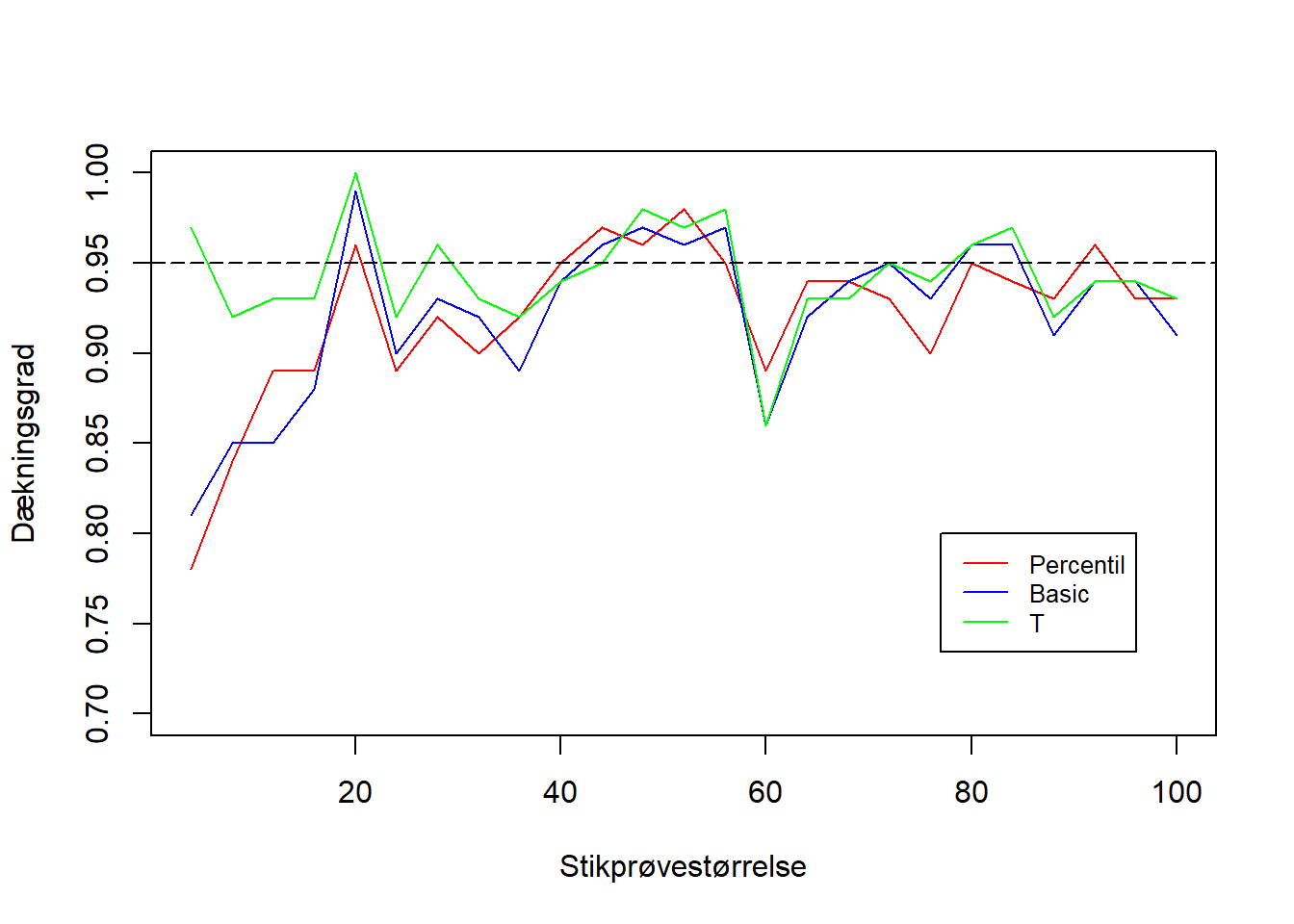

Figur 6.5: Dækningsgraden for de tre bootstrap-konfidensintervaller. På x-aksen ses stikprøvestørrelsen, mens på y-aksen ses dækningsgraden af konfidensintervallet på baggrund af den givne stikprøvestørrelse.

Her tyder det på, at T-metoden præsterer bedre ved mindre stikprøver end både percentilmetoden og basic-metoden. Ved tilpas stor stikprøvestørrelse opnår percentil- og basic-metodens konfidensinterval begge den samme dækningsgrad som T-metoden, og generelt kan der ses, at percentil- og basic-metoden har cirka den samme dækningsgrad. Både percentil- og basic-metoden ser ud til at have større udsvingninger end T-metoden. Desuden ser alle tre metoders dækningsgrader ud til at stabilisere sig omkring \(95\%\), når stikprøvestørrelsen bliver tilstrækkelig stor.

Bibliografi

Agresti, Alan, and Barbara Finlay. 2014. Statistical Methods for the Social Sciences. 4th ed. Edinburgh Gate, England: Pearson.

Bartlett, Jonathan. 2013. “The Miracle of the Bootstrap.” 2013. https://thestatsgeek.com/2013/07/02/the-miracle-of-the-bootstrap/.

Berrar, Daniel. 2019. “Introduction to the Non-Parametric Bootstrap.” 2019. https://www.researchgate.net/publication/332553015_Introduction_to_the_Non-Parametric_Bootstrap.

Chihara, Laura M., and Tim C. Hesterberg. 2019. Mathematical Statistics with Resampling and R. 2nd ed. 111 River Street, Hoboken, NJ 07030, USA: John Wiley & Sons, Inc.

Duke, Stat. n.d. “Bootstrap Confidence Intervals.” Accessed May 26, 2020. http://www2.stat.duke.edu/~banks/111-lectures.dir/lect13.pdf.

Lau, Sam, Joey Gonzalez, and Deb Nolan. n.d. “Principles and Techniques of Data Science.” Accessed May 26, 2020. https://www.textbook.ds100.org/ch/18/hyp_studentized.html.

Marin, Mike. 2018. “Bootstrapping and Resampling in Statistics with Example| Statistics Tutorial # 12 |MarinStatsLectures.” 2018. https://www.youtube.com/watch?v=O_Fj4q8lgmc&list=PLqzoL9-eJTNDp_bWyWBdw2ioA43B3dBrl&index=2&t=1s.

Myung, Jay. 2015. “Bootstrap Hypothesis Testing.” 2015. https://faculty.psy.ohio-state.edu/myung/personal/course/826/bootstrap_hypo.pdf.

Orloff, Jeremy, and Jonathan Bloom. 2014. “Bootstrap Confidence Intervals.” 2014. https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading24.pdf.

Wicklin, Rick. 2017. “The Average Bootstrap Sample Omits 36.8.” 2017. https://blogs.sas.com/content/iml/2017/06/28/average-bootstrap-sample-omits-data.html.

Yen, Lorna. 2019. “An Introduction to the Bootstrap Method.” 2019. https://towardsdatascience.com/an-introduction-to-the-bootstrap-method-58bcb51b4d60.