Chapter 8 R Lab 7 - 27/05/2022
In this lecture we will learn how to estimate non-linear regression models.
The following packages are required: MASS (included automatically in the R release), splines (included automatically in the R release) and tidyverse.
library(MASS) #for the Boston dataset
library(splines)
library(tidyverse)For this lab we will use the Boston dataset contained in the MASS library and already introduced in Lab 5. The data are named Boston and are already available as soon as you load the package.
glimpse(Boston)## Rows: 506
## Columns: 14
## $ crim <dbl> 0.00632, 0.02731, 0.02729, 0.03237, 0.06905, 0.02985, 0.08829,…
## $ zn <dbl> 18.0, 0.0, 0.0, 0.0, 0.0, 0.0, 12.5, 12.5, 12.5, 12.5, 12.5, 1…
## $ indus <dbl> 2.31, 7.07, 7.07, 2.18, 2.18, 2.18, 7.87, 7.87, 7.87, 7.87, 7.…
## $ chas <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
## $ nox <dbl> 0.538, 0.469, 0.469, 0.458, 0.458, 0.458, 0.524, 0.524, 0.524,…
## $ rm <dbl> 6.575, 6.421, 7.185, 6.998, 7.147, 6.430, 6.012, 6.172, 5.631,…
## $ age <dbl> 65.2, 78.9, 61.1, 45.8, 54.2, 58.7, 66.6, 96.1, 100.0, 85.9, 9…
## $ dis <dbl> 4.0900, 4.9671, 4.9671, 6.0622, 6.0622, 6.0622, 5.5605, 5.9505…
## $ rad <int> 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4,…
## $ tax <dbl> 296, 242, 242, 222, 222, 222, 311, 311, 311, 311, 311, 311, 31…
## $ ptratio <dbl> 15.3, 17.8, 17.8, 18.7, 18.7, 18.7, 15.2, 15.2, 15.2, 15.2, 15…
## $ black <dbl> 396.90, 396.90, 392.83, 394.63, 396.90, 394.12, 395.60, 396.90…
## $ lstat <dbl> 4.98, 9.14, 4.03, 2.94, 5.33, 5.21, 12.43, 19.15, 29.93, 17.10…
## $ medv <dbl> 24.0, 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15…We consider lstat (lower status of the population (percent)) as the only regressor/covariate and medv (median value of owner-occupied homes in $1000s) as response variable. The relationship between the two variables is shown in the following scatterplot:
Boston %>%
ggplot(aes(x=lstat, y=medv)) +
geom_point() +
geom_smooth()## `geom_smooth()` using method = 'loess' and formula 'y ~ x'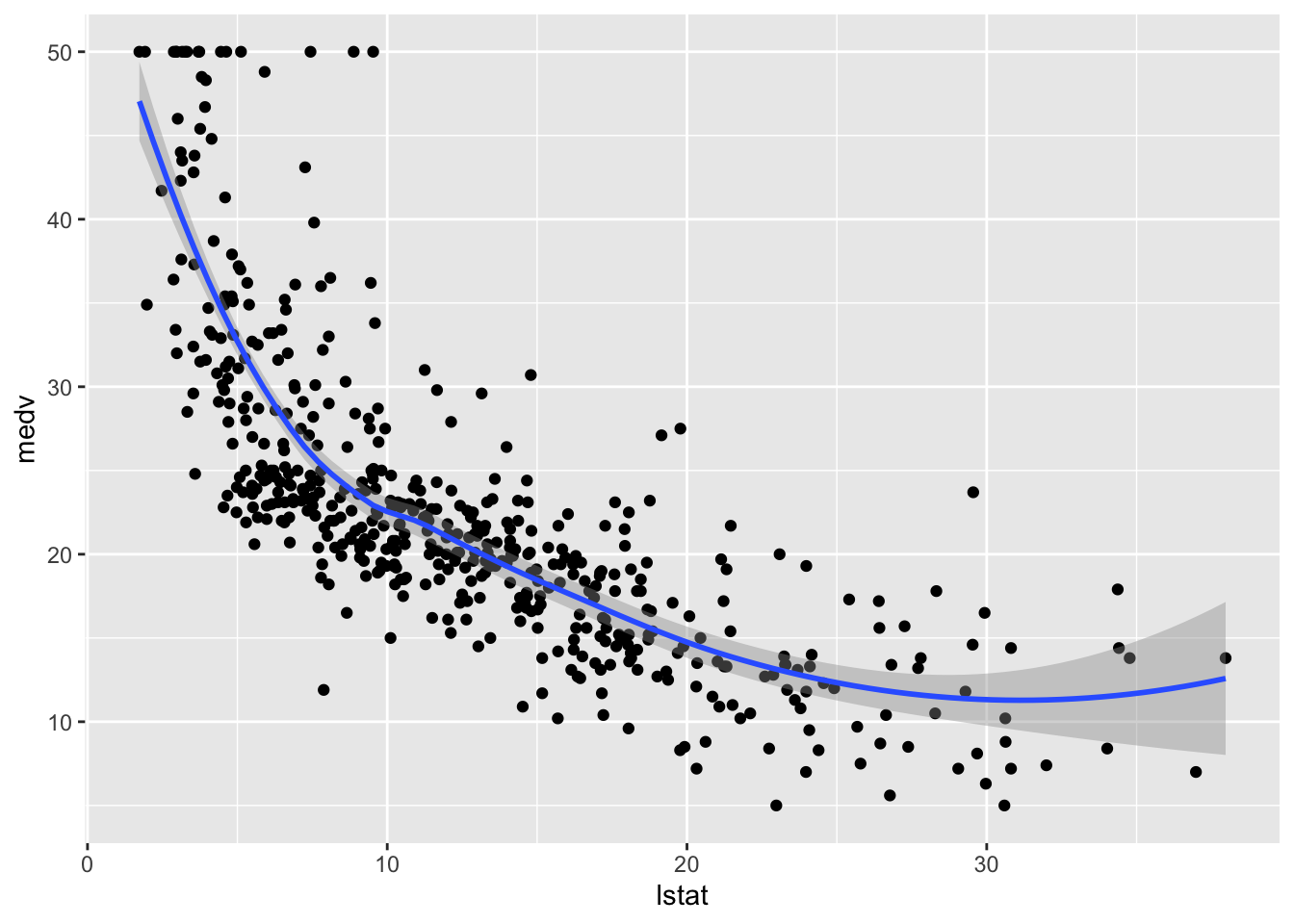
The plot suggests a non-linear relationship between the two variables. Note that the function geom_smooth includes by default a non linear model fitted by using the loess method.
We first create a new variable named lstat_ord obtained by transforming lstat into a categorical qualitative variable (known as factor in R) defined by 4 classes. To do this we use the function cut which divides the range of the variable into intervals and codes its values according to which interval they fall. With the option breaks of the cut function it is possible to specify how many classes we want or the cut-points to be used for defining the classes. In this case we ask for 4 classes that will be automatically created for having approximately the same length:
Boston$lstat_ord = cut(Boston$lstat, breaks = 4)
table(Boston$lstat_ord)##
## (1.69,10.8] (10.8,19.9] (19.9,28.9] (28.9,38]
## 243 187 57 19Note that now in Boston you have an additioal column named lstat_ord.
As usual we proceed by splitting the data into training (80%) and test set:
set.seed(123)
training.samples = sample(1:nrow(Boston),
0.8*nrow(Boston),
replace=F)
train.data= Boston[training.samples, ]
test.data = Boston[-training.samples, ]8.1 Linear regression model
We first estimate a linear regression model (using the training data) even if we know that the relationship between the two studied variables is not linear.
mod_lm = lm(medv ~ lstat, data = train.data)
summary(mod_lm)##
## Call:
## lm(formula = medv ~ lstat, data = train.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.073 -3.891 -1.401 1.761 24.602
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.49437 0.61789 55.83 <2e-16 ***
## lstat -0.95445 0.04275 -22.33 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.154 on 402 degrees of freedom
## Multiple R-squared: 0.5536, Adjusted R-squared: 0.5525
## F-statistic: 498.6 on 1 and 402 DF, p-value: < 2.2e-16We want now to include the fitted model in the scatterplot. The first way for doing this is to use the ggplot2::geom_smooth function by setting method="lm" (linear model):
train.data %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_smooth(method = "lm")## `geom_smooth()` using formula 'y ~ x'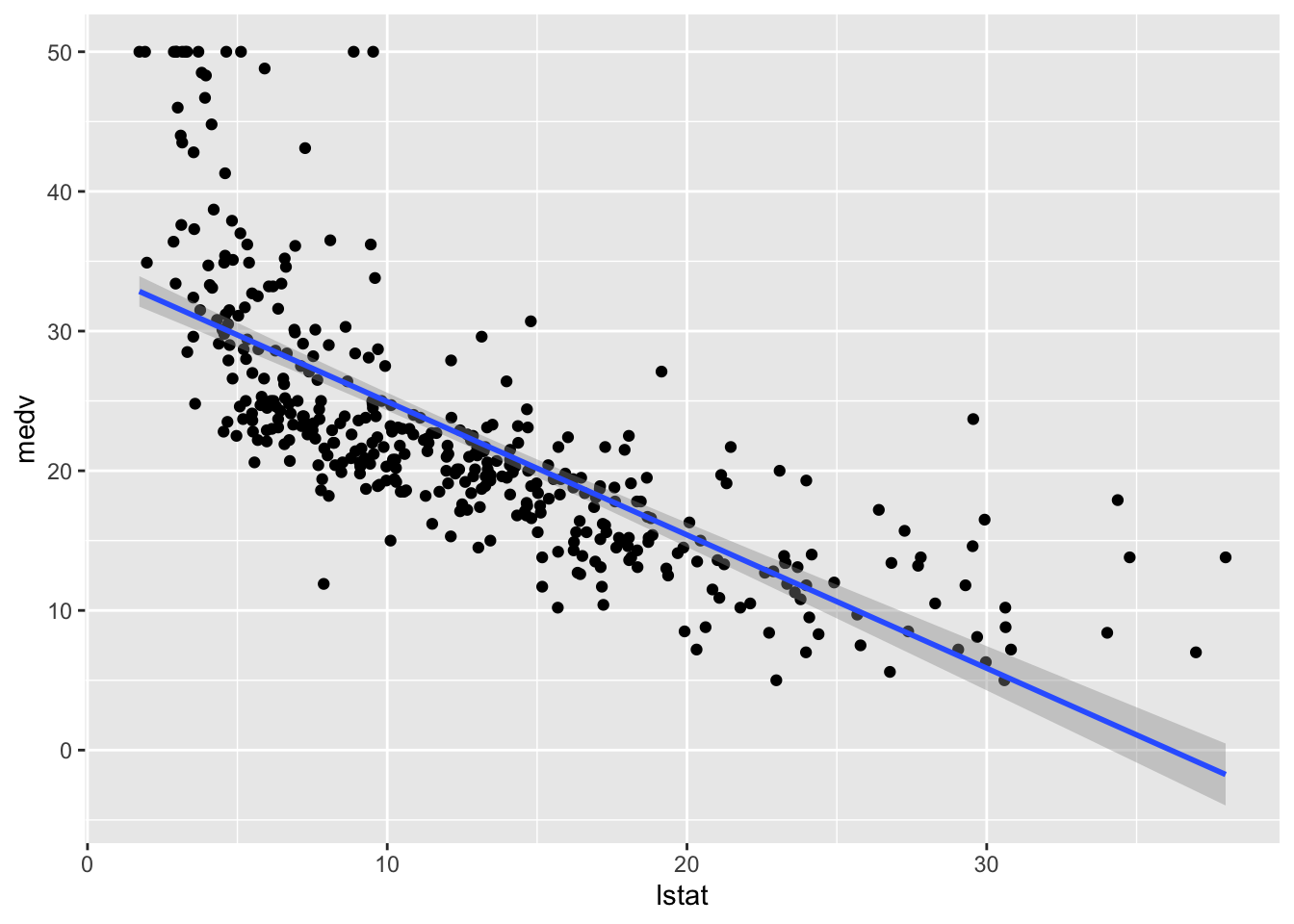
This approach is convenient is you want to display the 95% confidence interval around the fitted line (i.e. the estimated - pointwise - standard error of predictions measuring the uncertainty of the predictions).
Alternatively we can proceed as follows by adding, on the fly and not permanently, the predictions in a new column of the dataframe and then plot it using geom_line (remind that the predictions in this case refer to the training set):
train.data %>%
mutate(pred = mod_lm$fitted.values) %>% #temp column
ggplot(aes(lstat, medv)) +
geom_point() +
geom_line(aes(y=pred), col="blue",lwd=1.5)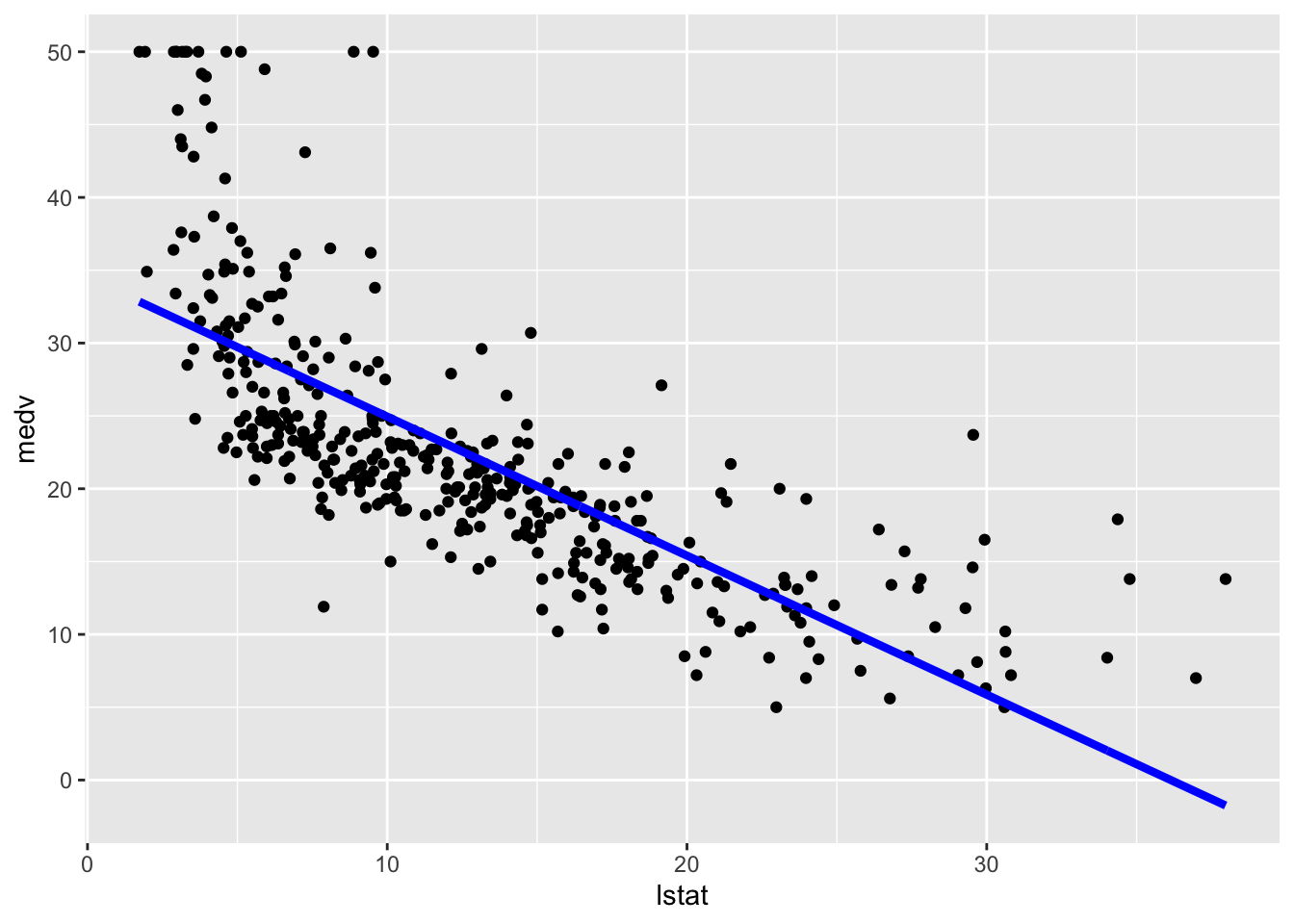
The option lwd specifies the line width. In this case obtaining the predictions confidence interval is a bit tricky and we are not going to do it.
We now compute the predictions for the test set. The model performance is assessed by means of the mean square error (MSE) and the correlation (COR) between observed and predicted values:
lm_pred = mod_lm %>% predict(test.data)
# Model performance
lm_perf =
data.frame(
MSE = mean((lm_pred - test.data$medv)^2),
COR = cor(lm_pred, test.data$medv)
)
lm_perf## MSE COR
## 1 41.70676 0.71400498.2 Linear regression model with step functions
We consider now the case of a linear regression model with step functions defined by the classes of lstat_ord. In this case a constant model will be estimated for each of the 4 regions. We don’t have to do anything special in this case apart from specifying a standard linear model where lstat_ord is the only regressor. R will take care of creating the corresponding three dummy variables (remember that the baseline category is absorbed by the intercept):
mod_cut = lm(medv ~ lstat_ord,
data = train.data)
summary(mod_cut)##
## Call:
## lm(formula = medv ~ lstat_ord, data = train.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.6452 -4.6452 -0.6312 2.7079 21.4548
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 28.5452 0.4807 59.38 <2e-16 ***
## lstat_ord(10.8,19.9] -9.8281 0.7368 -13.34 <2e-16 ***
## lstat_ord(19.9,28.9] -16.1452 1.1148 -14.48 <2e-16 ***
## lstat_ord(28.9,38] -17.2764 1.7540 -9.85 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.747 on 400 degrees of freedom
## Multiple R-squared: 0.4661, Adjusted R-squared: 0.4621
## F-statistic: 116.4 on 3 and 400 DF, p-value: < 2.2e-16The value 28.55 is the average predicted value of medv in the first class of lstat_ord; 28.55 -9.83 is the average predicted value of medv for the second category, and so on.
We plot the fitted model with the two methods. Note that for using geom_smooth it is necessary to specify by means of formula that we are using a transformation of x=lstat:
# Method 1
train.data %>%
ggplot(aes(x=lstat, y=medv)) +
geom_point() +
geom_smooth(method="lm", formula=y~cut(x,4))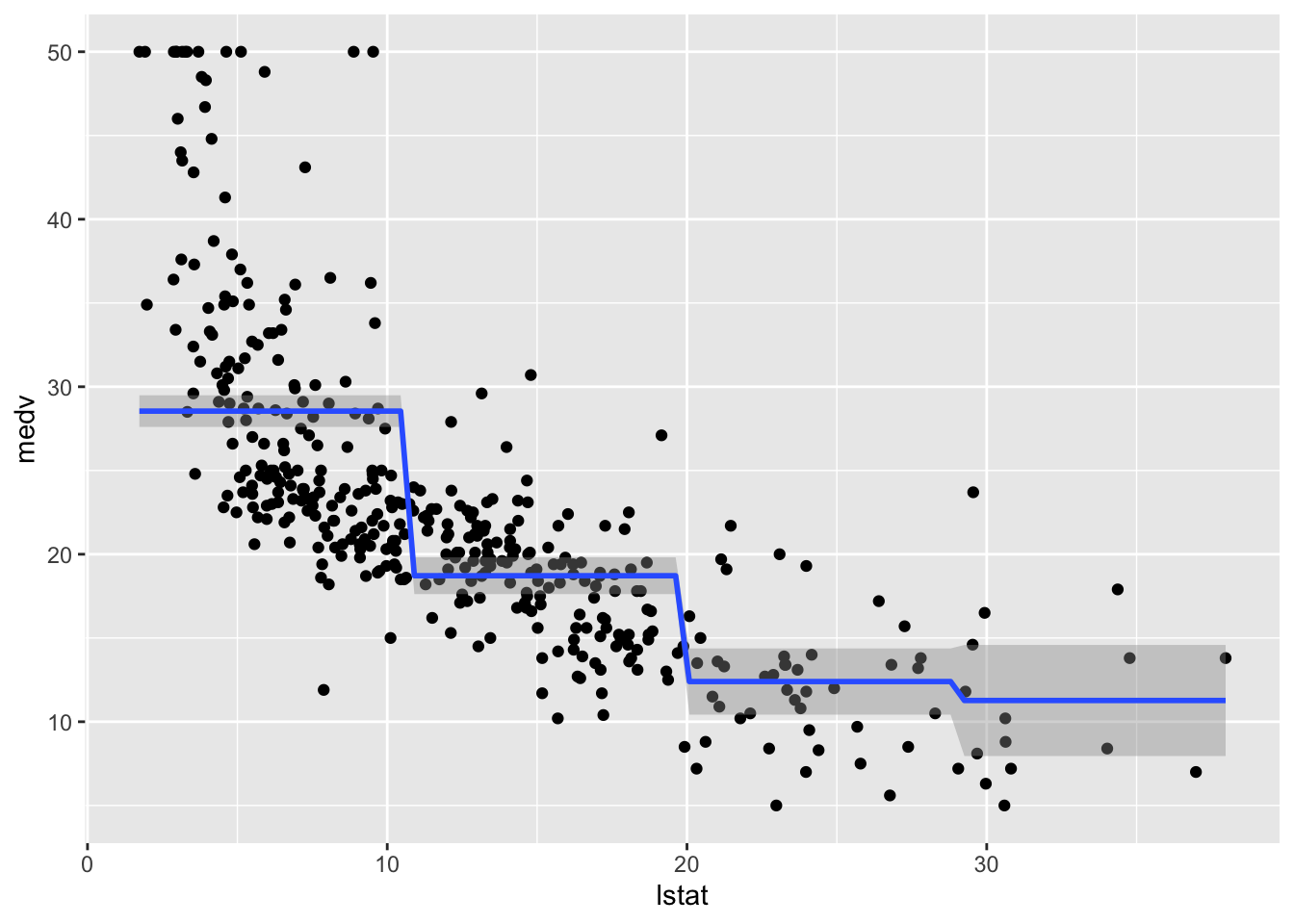
# Method 2
train.data %>%
mutate(pred = mod_cut$fitted.values) %>%
ggplot(aes(x=lstat, y=medv)) +
geom_point() +
geom_line(aes(y=pred),col="blue",lwd=1.5)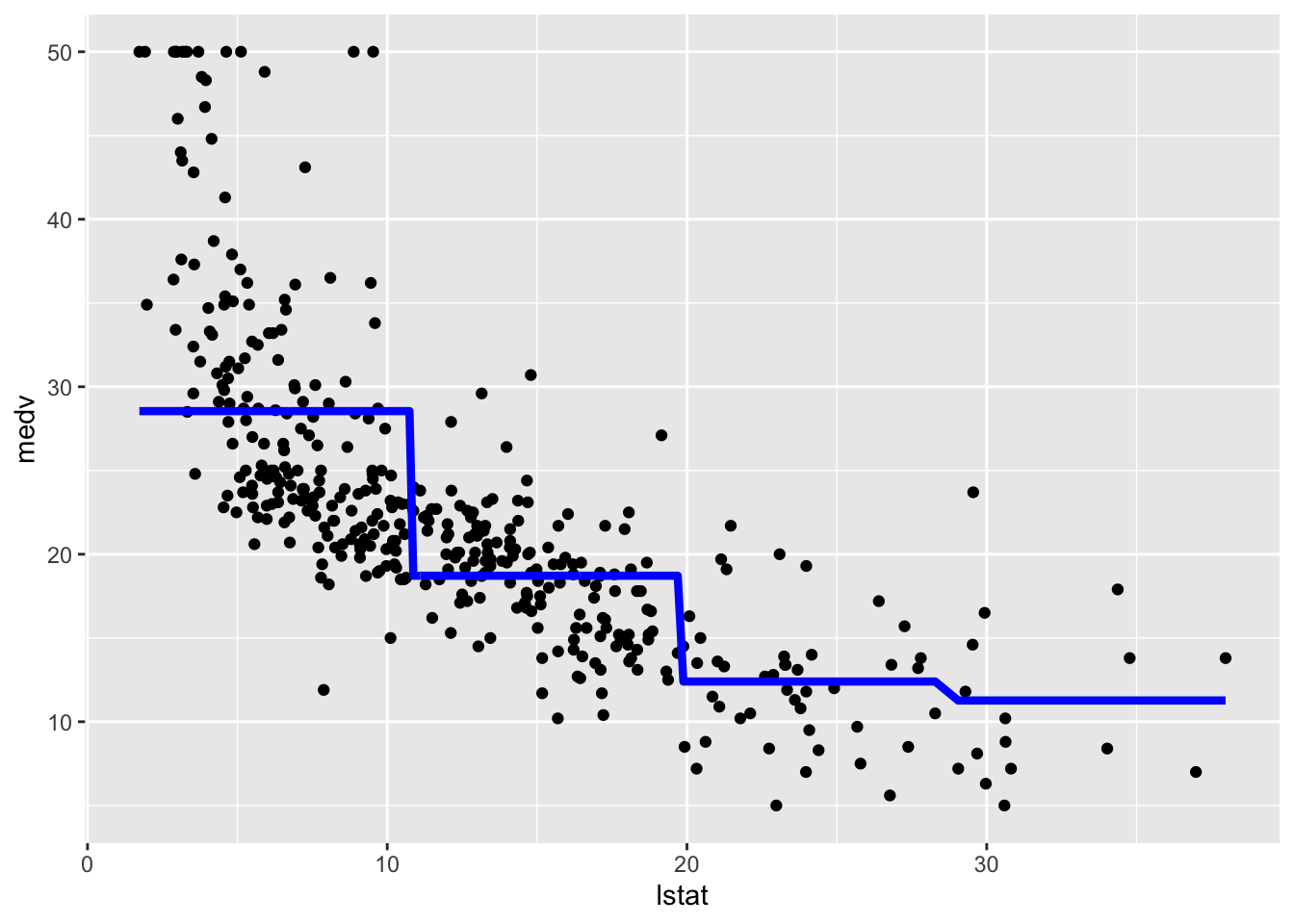
We now compute the predictions for the test set and the two performance indexes.
cut_pred = mod_cut %>% predict(test.data)
# Model performance
cut_perf =
data.frame(
MSE = mean((cut_pred - test.data$medv)^2),
COR = cor(cut_pred, test.data$medv)
)
cut_perf## MSE COR
## 1 49.53634 0.64482078.3 Polynomial regression
The polynomial regression model was already introduced in Lab 1. We implement here a model where \(d=5\) and then include the fitted model in the training data scatterplot:
mod_poly = lm(medv ~ poly(lstat, 5),
data = train.data)
summary(mod_poly)##
## Call:
## lm(formula = medv ~ poly(lstat, 5), data = train.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.9116 -2.9841 -0.6678 1.8604 27.2880
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.5109 0.2545 88.458 < 2e-16 ***
## poly(lstat, 5)1 -137.4146 5.1150 -26.865 < 2e-16 ***
## poly(lstat, 5)2 56.7147 5.1150 11.088 < 2e-16 ***
## poly(lstat, 5)3 -23.8206 5.1150 -4.657 4.38e-06 ***
## poly(lstat, 5)4 25.2578 5.1150 4.938 1.16e-06 ***
## poly(lstat, 5)5 -19.7620 5.1150 -3.864 0.00013 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.115 on 398 degrees of freedom
## Multiple R-squared: 0.6947, Adjusted R-squared: 0.6909
## F-statistic: 181.1 on 5 and 398 DF, p-value: < 2.2e-16# Method 1
ggplot(train.data, aes(lstat, medv) ) +
geom_point() +
stat_smooth(method = "lm",
formula = y ~ poly(x, 5))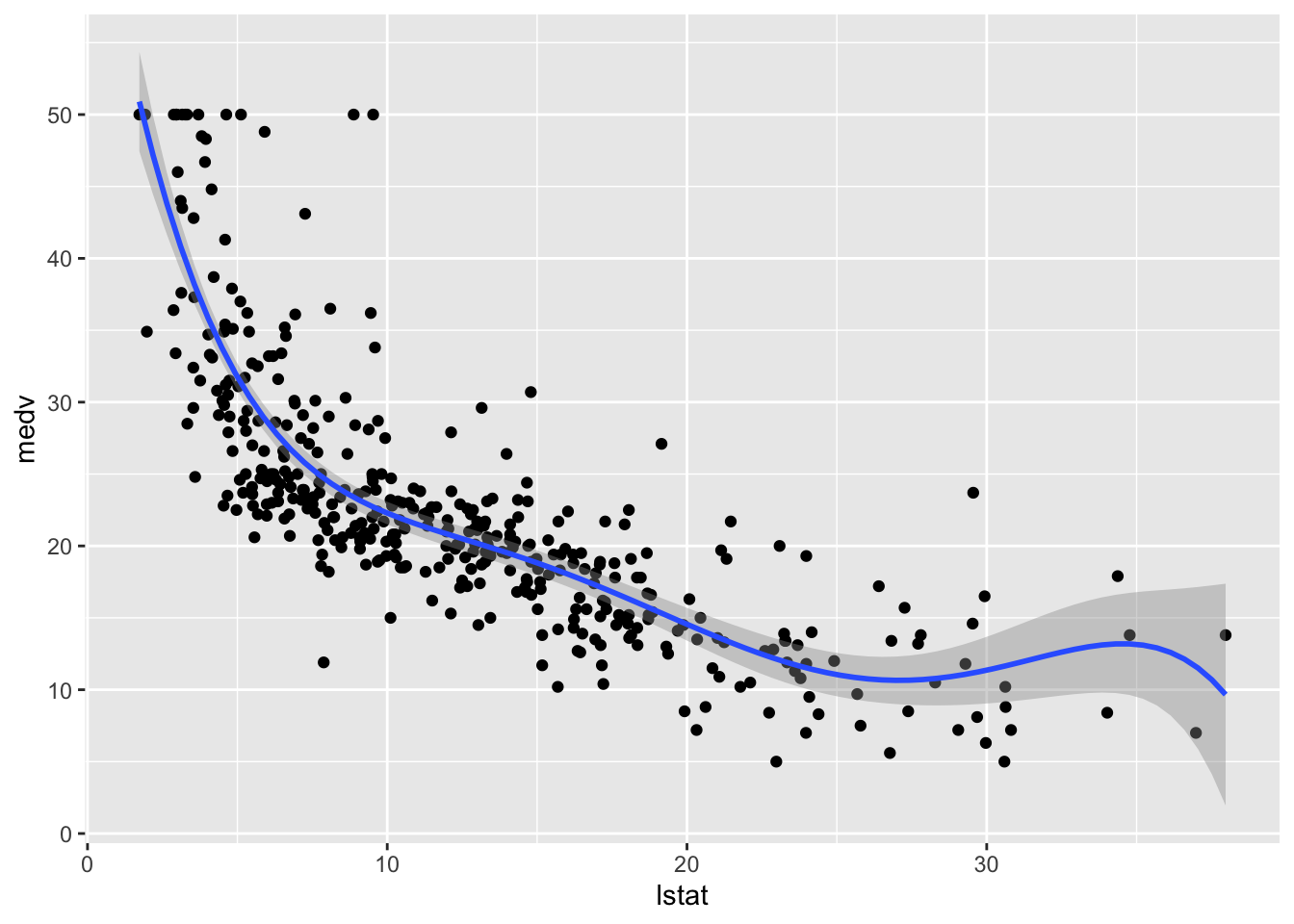
# Method 2
train.data %>%
mutate(pred = mod_poly$fitted.values) %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_line(aes(y=pred),col="blue",lwd=1.5)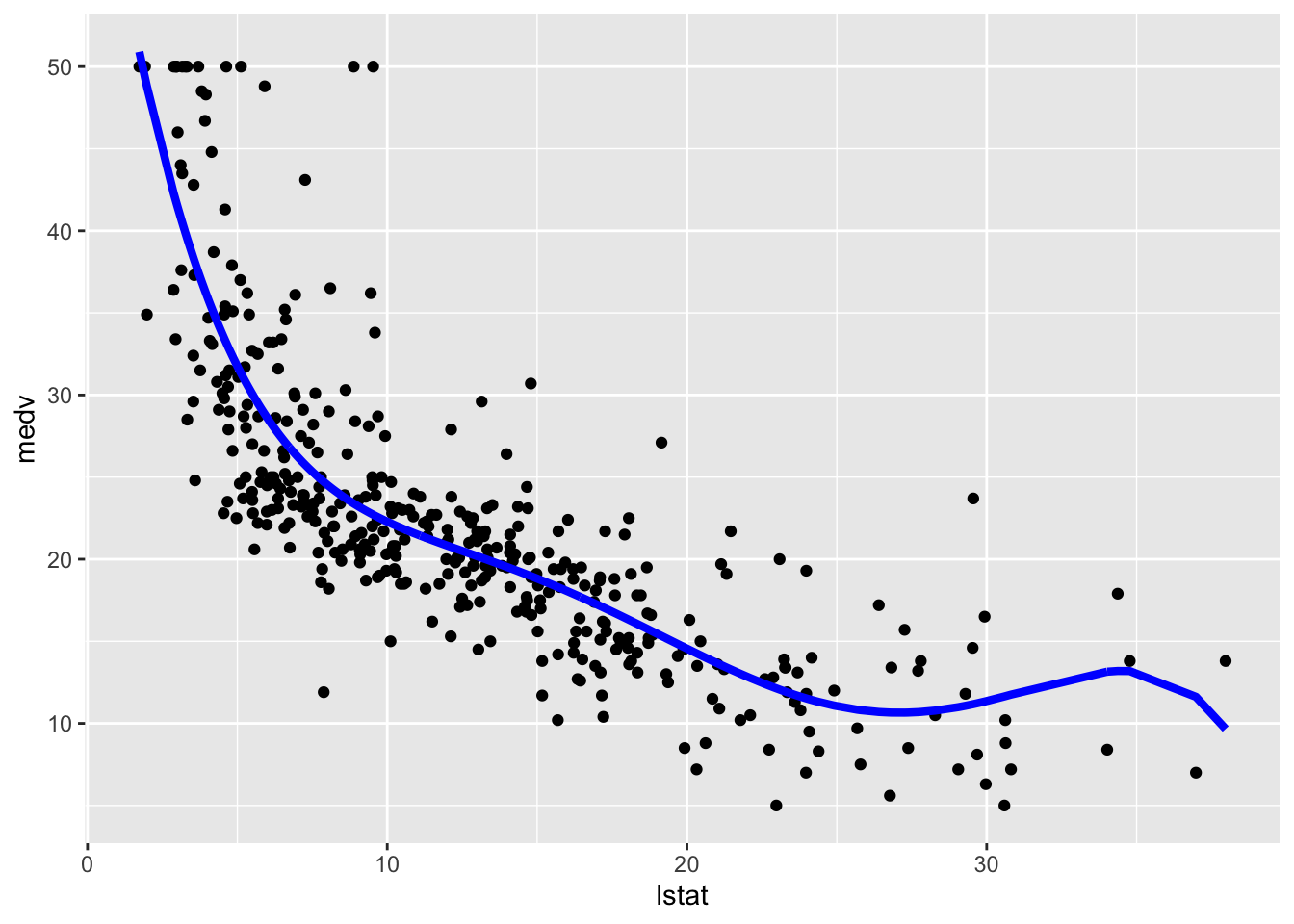
We then compute predictions for the test set together with the model performance indexes.
poly_pred = mod_poly %>% predict(test.data)
# Model performance
poly_perf =
data.frame(
MSE = mean((poly_pred - test.data$medv)^2),
COR = cor(poly_pred, test.data$medv)
)
poly_perf## MSE COR
## 1 31.47374 0.79665078.4 Regression spline
To estimate a cubic spline and a natural cubic spline regression model we use the function bs and ns from the library splines embedded in the lm function. We use as knots the 3 quartiles (corresponding to the quantiles of order 0.25, 0.5 and 0.75) of lstat. Note that the function bs can implement also splines with an order different from 3 (see the degree input argument). However the function ns doesn’t give this opportunity (it estimates only the natural cubic spline model). For this reason we consider deegree=3 aldo for the function bs (it is also the default specification you coul also not including it):
library(splines)
knots = quantile(train.data$lstat,
p = c(0.25, 0.5, 0.75))
mod_cs = lm(medv ~ bs(lstat, knots = knots, degree = 3),
data = train.data)
mod_ns = lm(medv ~ ns(lstat, knots = knots),
data = train.data)To plot the two fitted models we proceed as follows:
# Method 1
train.data %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_smooth(method = "lm",
formula = y ~ bs(x,knots = knots),col="blue") +
geom_smooth(method = "lm",
formula = y ~ ns(x,knots = knots),col="red", lty=2)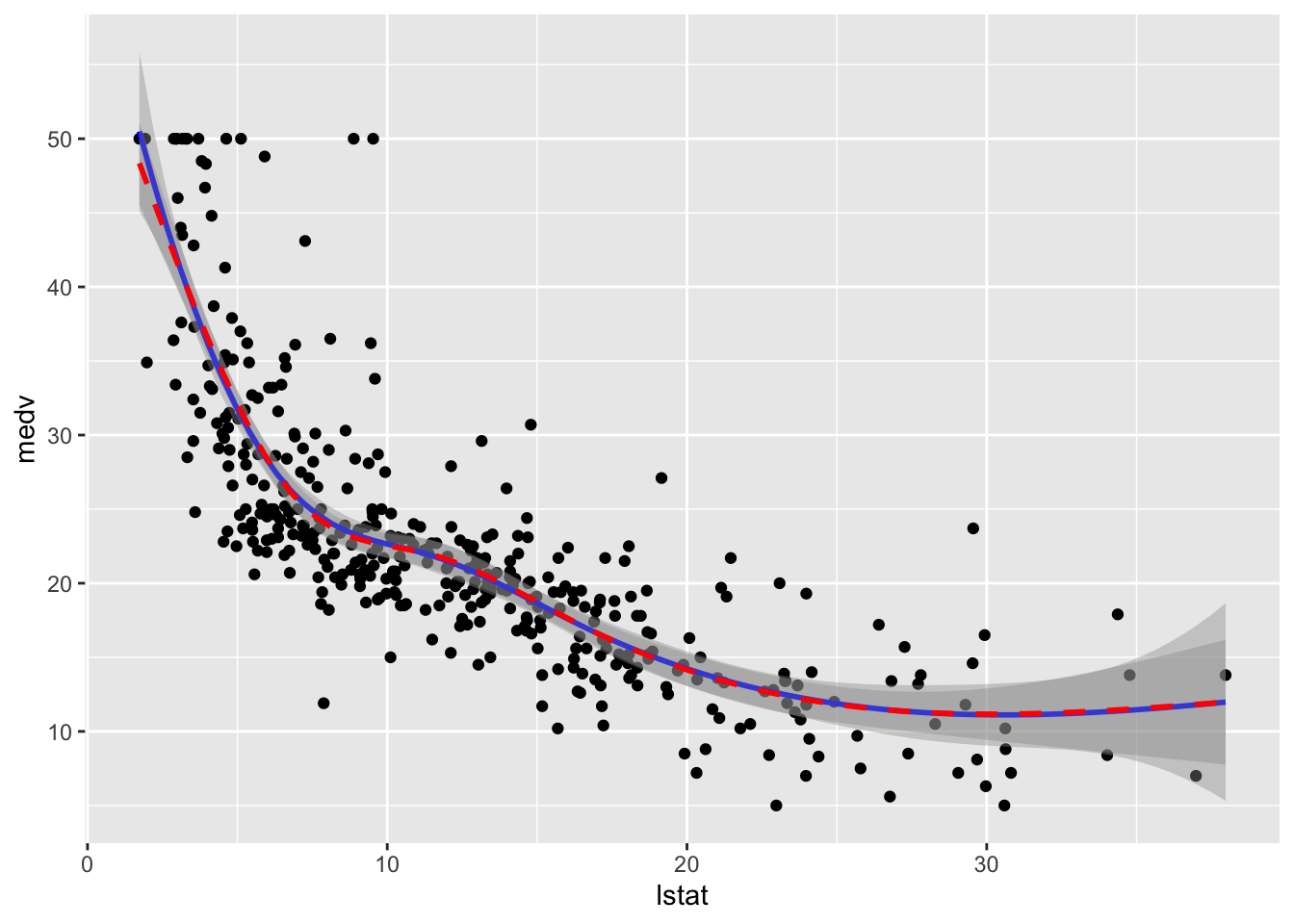
# Method 2
train.data %>%
mutate(pred1 = mod_cs$fitted.values,
pred2 = mod_ns$fitted.values) %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_line(aes(y=pred1),col="blue",lwd=1.5)+
geom_line(aes(y=pred2),col="red",lwd=1.5,lty=2)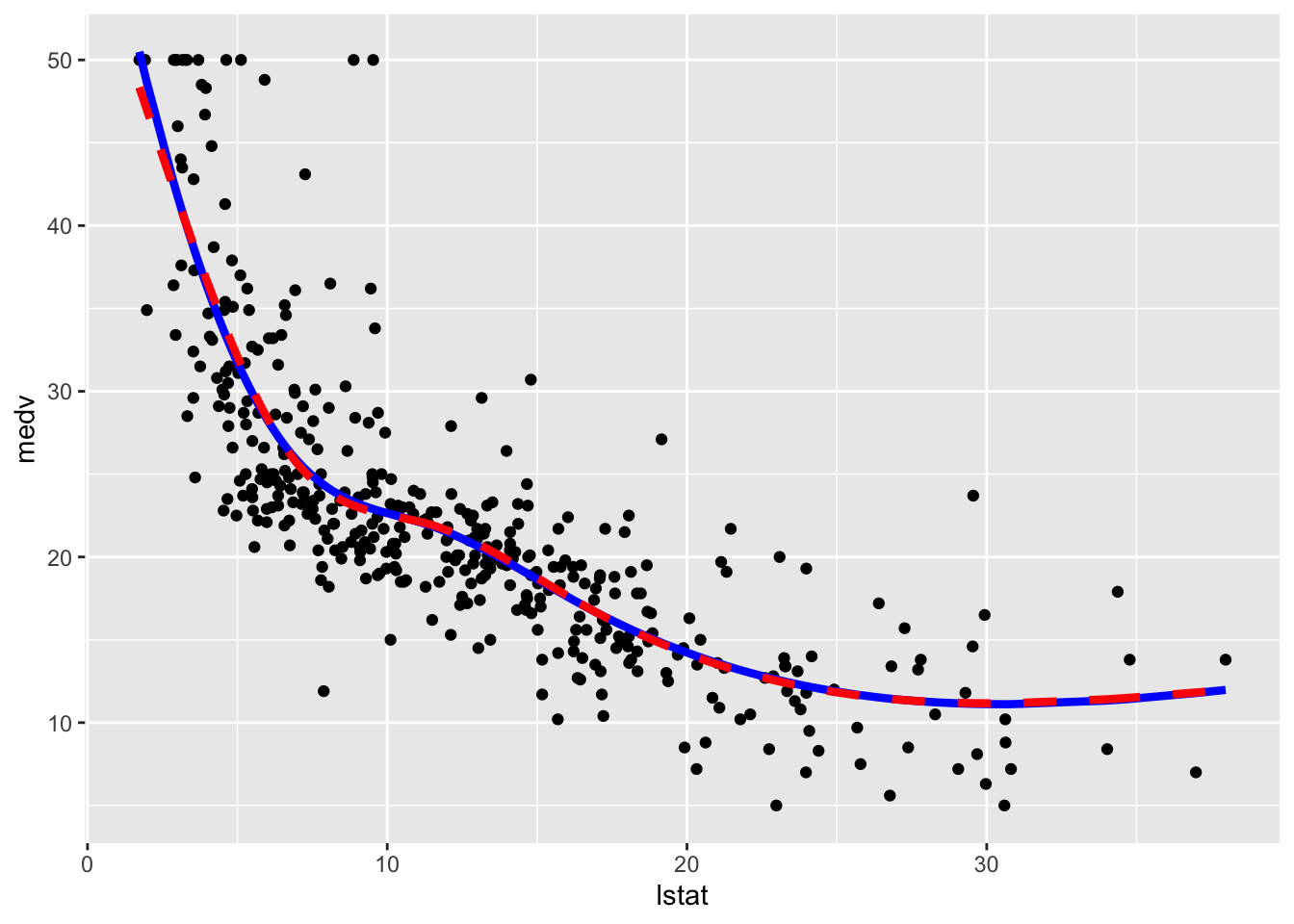
We observe that the two regression spline models are really very similar in terms of fitted lines.
We consider in the following the natural cubic spline model and compute the predictions for the test set and the usual performance indexes.
ns_pred = mod_ns %>% predict(test.data)
# Model performance
ns_perf = data.frame(
MSE = mean((ns_pred - test.data$medv)^2),
COR = cor(ns_pred, test.data$medv)
)
ns_perf## MSE COR
## 1 31.63657 0.79539698.5 Local regression (LOESS)
By using the function loess (see ?loess) it is possible to fit a local regression model (LOESS) to the training data. In this case we decide to use the 20% of the closest points (i.e. the neighborhood size) by means of span=0.2 and fit linear local models (degree=1). These two specifications should be subject to tuning.
mod_loess = loess(medv ~ lstat,
span = 0.2,
degree = 1,
data = train.data)
summary(mod_loess)## Call:
## loess(formula = medv ~ lstat, data = train.data, span = 0.2,
## degree = 1)
##
## Number of Observations: 404
## Equivalent Number of Parameters: 9.26
## Residual Standard Error: 5.071
## Trace of smoother matrix: 10.99 (exact)
##
## Control settings:
## span : 0.2
## degree : 1
## family : gaussian
## surface : interpolate cell = 0.2
## normalize: TRUE
## parametric: FALSE
## drop.square: FALSEGiven that now we are not using the lm function we don’t have any parameter estimates in the output. To plot the fitted model and evaluate its performance we use the following code:
# Method 1
train.data %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_smooth(method = "loess", span=0.2,
method.args = list(degree = 2))## `geom_smooth()` using formula 'y ~ x'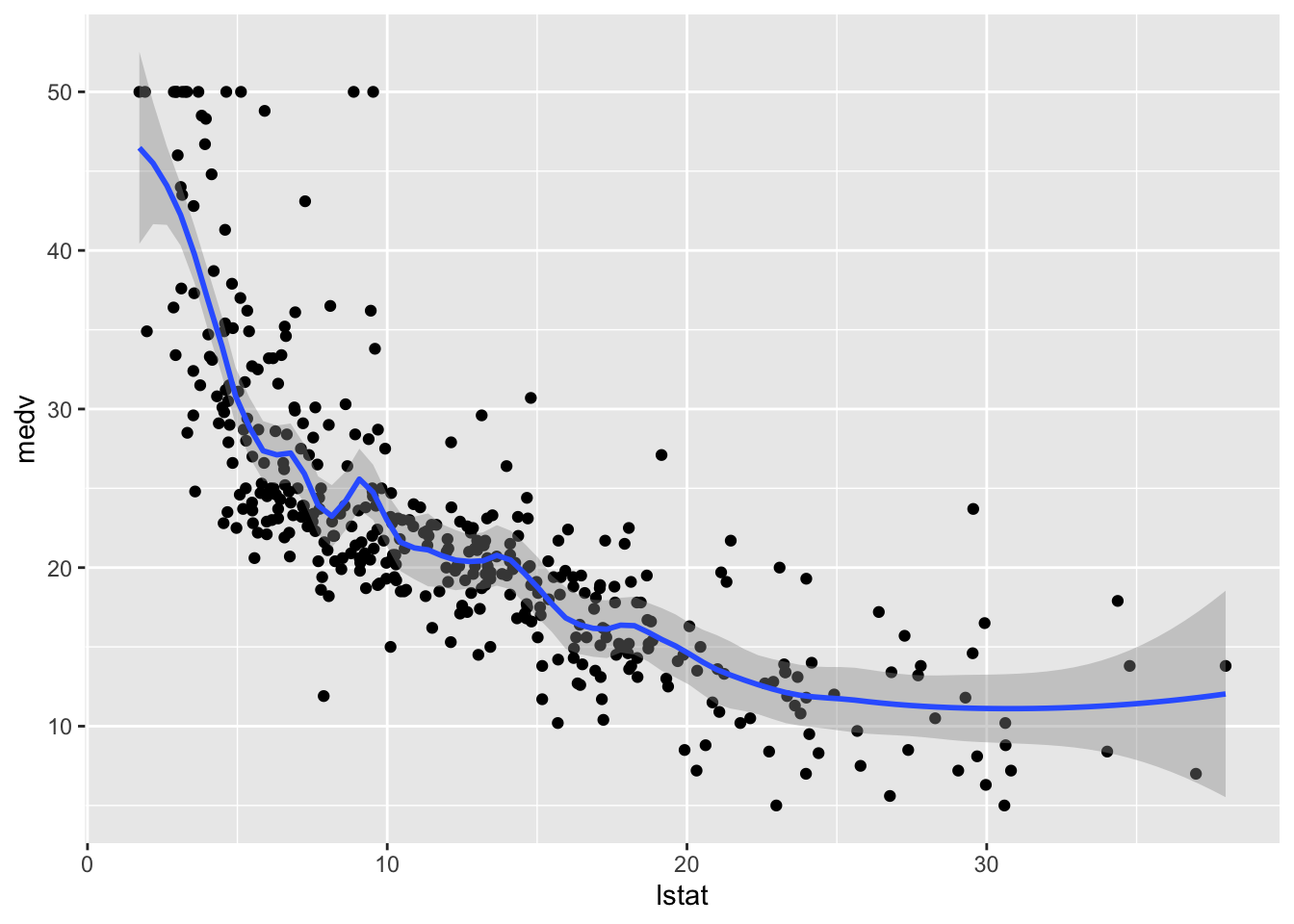
# Method 2
train.data %>%
mutate(pred = mod_loess$fitted) %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_line(aes(lstat,pred), col="red", lwd=1.5)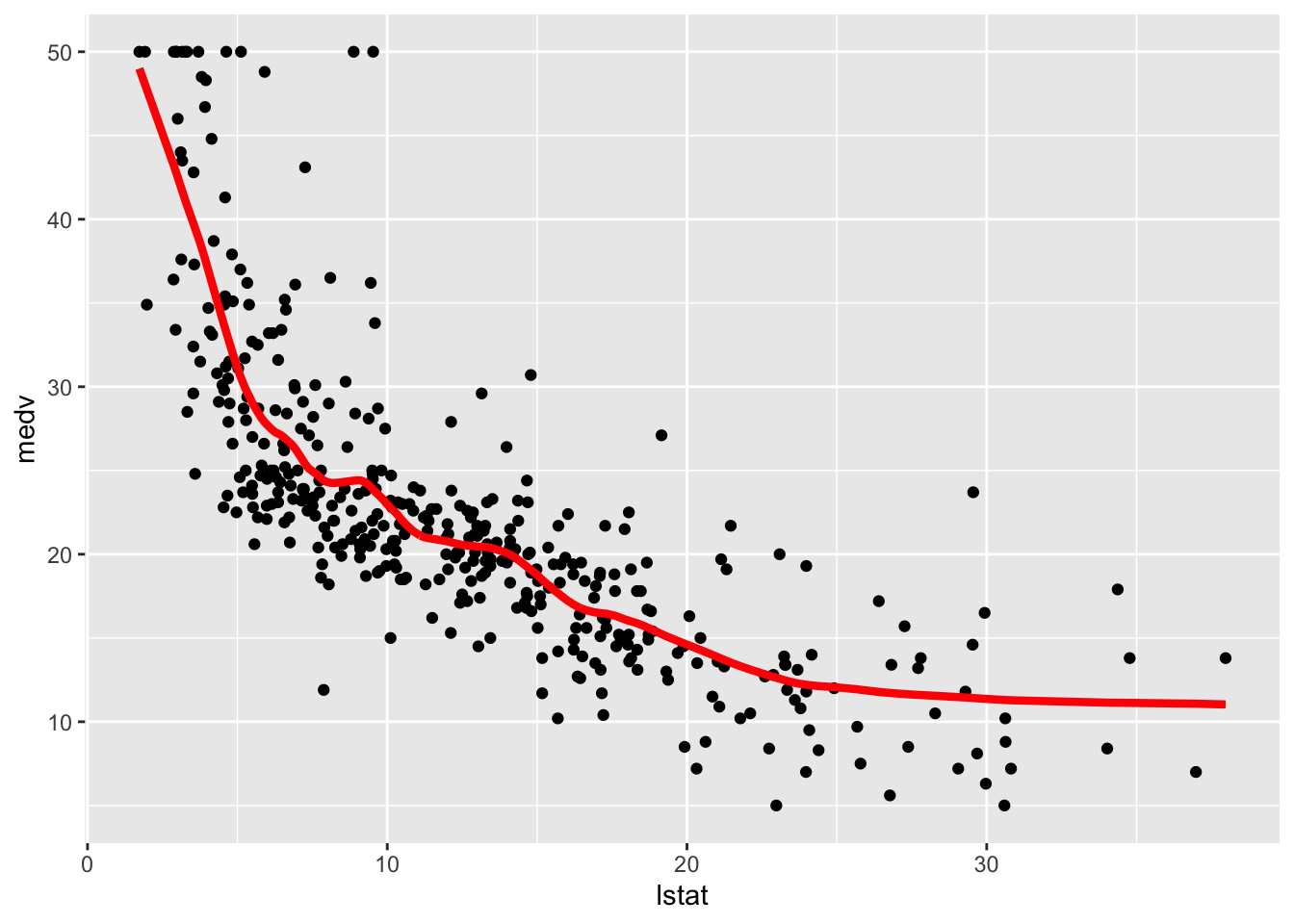 
We finally compute the test predictions and the two indexes:
# Compute predictions
loess_pred = mod_loess %>% predict(test.data)
# Model performance
loess_perf = data.frame(
MSE = mean((loess_pred - test.data$medv)^2),
COR = cor(loess_pred, test.data$medv)
)
loess_perf ## MSE COR
## 1 31.12398 0.79802488.6 Smoothing splines
We fit now two smoothing splines models by using the function smooth.spline. It works slightly differently from the previous function because it does not take in input the formula but x and y that have to be provided separately. The value of lambda is the smoothing parameter \(\lambda\). As an example we use two values: 0.0001 and 1 (in general the higher the value of lambda and the smoother the function).
mod_ss1 = smooth.spline(y = train.data$medv,
x = train.data$lstat,
lambda = 0.0001)
mod_ss1## Call:
## smooth.spline(x = train.data$lstat, y = train.data$medv, lambda = 1e-04)
##
## Smoothing Parameter spar= NA lambda= 1e-04
## Equivalent Degrees of Freedom (Df): 15.24549
## Penalized Criterion (RSS): 9463.225
## GCV: 26.78662mod_ss2 = smooth.spline(y = train.data$medv,
x = train.data$lstat,
lambda = 1)
mod_ss2## Call:
## smooth.spline(x = train.data$lstat, y = train.data$medv, lambda = 1)
##
## Smoothing Parameter spar= NA lambda= 1
## Equivalent Degrees of Freedom (Df): 2.380572
## Penalized Criterion (RSS): 13093.4
## GCV: 34.19045Note that the function returns the Equivalent/Effective Degrees of Freedom (Df) number which can be interpreted as a measure of model flexibility (in general the higher the Effective Degrees of Freedom and the more flexible/complex the model). In this case we observe that mod_ss2 is a less flexible model (lower number of Df) and so we expect mod_ss1 to be less smoother (this was also expected given the value of \(\lambda\)).
It is possible to let the function smooth.spline to determine by means of cross-validation the best model flexibility. To use this option we just have to include the option cv=T (and it is not necessary to specify the value of \(\lambda\)):
mod_ss3 = smooth.spline(y = train.data$medv,
x = train.data$lstat,
cv = T) ## Warning in smooth.spline(y = train.data$medv, x = train.data$lstat, cv = T):
## cross-validation with non-unique 'x' values seems doubtfulmod_ss3## Call:
## smooth.spline(x = train.data$lstat, y = train.data$medv, cv = T)
##
## Smoothing Parameter spar= 0.9148907 lambda= 0.0008700739 (12 iterations)
## Equivalent Degrees of Freedom (Df): 9.370943
## Penalized Criterion (RSS): 9684.976
## PRESS(l.o.o. CV): 26.5401The corresponding value of lambda can be retrieved by:
mod_ss3$lambda## [1] 0.0008700739We now plot the 3 fitted models. Note that in this case it is not possible to use the geom_smooth function, so we proceed with the second method for plotting. Moreover, note that in this case it is not possible to use the $fitted.values option because smooth.spline works differently. We have instead to apply the fitted function to the smooth.spline outputs in order to obtain the fitted values:
# Method 2
train.data %>%
mutate(pred1 = fitted(mod_ss1),
pred2 = fitted(mod_ss2),
pred3 = fitted(mod_ss3)) %>%
ggplot(aes(lstat, medv)) +
geom_point() +
geom_line(aes(y=pred1),col="blue",lwd=1.2) +
geom_line(aes(y=pred2),col="red",lwd=1.2) +
geom_line(aes(y=pred3),col="darkgreen",lwd=1.2)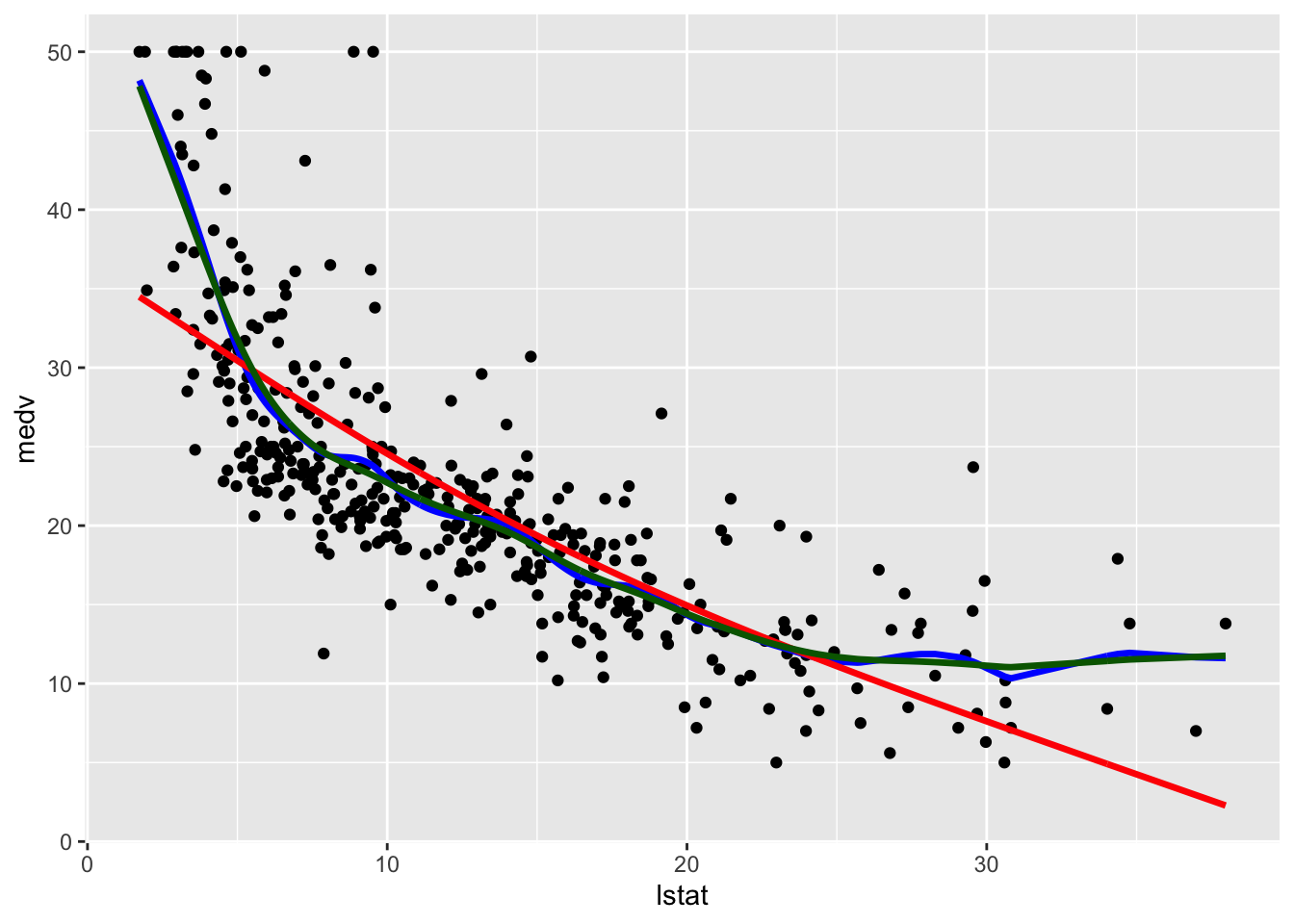 
Note that the line with the highest value of lambda (and the lowest value of effective degrees of freedom) is the smoothest one (red color, very similar to a straight line). The other two lines are very similar and have a non linear shape.
We use mod_ss3 (i.e. the tuned model) to compute the test predictions and evaluate model performance. Also the predict function works differently here: it takes as input not the entire data frame test.data but only the regressor values test.data$lstat. Additionally the predict argument is composed by two objects named x and y. We are obviously interested in the latter:
# Compute predictions
ss_pred = predict(mod_ss3, test.data$lstat)
# Model performance
ss_perf = data.frame(
MSE = mean((ss_pred$y- test.data$medv)^2),
COR = cor(ss_pred$y, test.data$medv)
)
ss_perf ## MSE COR
## 1 31.03266 0.79962718.7 Models comparison
It’s now time to compare all the implemented models in terms of MSE and correlation between predicted and observed values in the test set. By using the rbind function we combine (by rows) all the dataframes containing the performance indexes. By using arrange we also order the methods according to the correlation values (descending order):
rbind(lm = lm_perf,
poly = poly_perf,
cut = cut_perf,
loess = loess_perf,
ns = ns_perf,
ss = ss_perf) %>%
arrange(desc(COR))## MSE COR
## ss 31.03266 0.7996271
## loess 31.12398 0.7980248
## poly 31.47374 0.7966507
## ns 31.63657 0.7953969
## lm 41.70676 0.7140049
## cut 49.53634 0.6448207Smoothing splines (whose complexity is computed by using cross-validation) is the best method with also the lowest MSE. Local regression (LOESS), polynomial regression and natural spline regression have a similar performance, with a value of the correlation higher than 0.79. The linear model and the linear model with the step functions are the worst models.
We plot in the following the best three models. In order to include in the plot a legend with the model names we need to create a column containing the model names (then we will use this column in the aes specification of geom_line). This can be done by moving from a wide to a long dataset, by means of the function pivot_longer, described in the following picture:
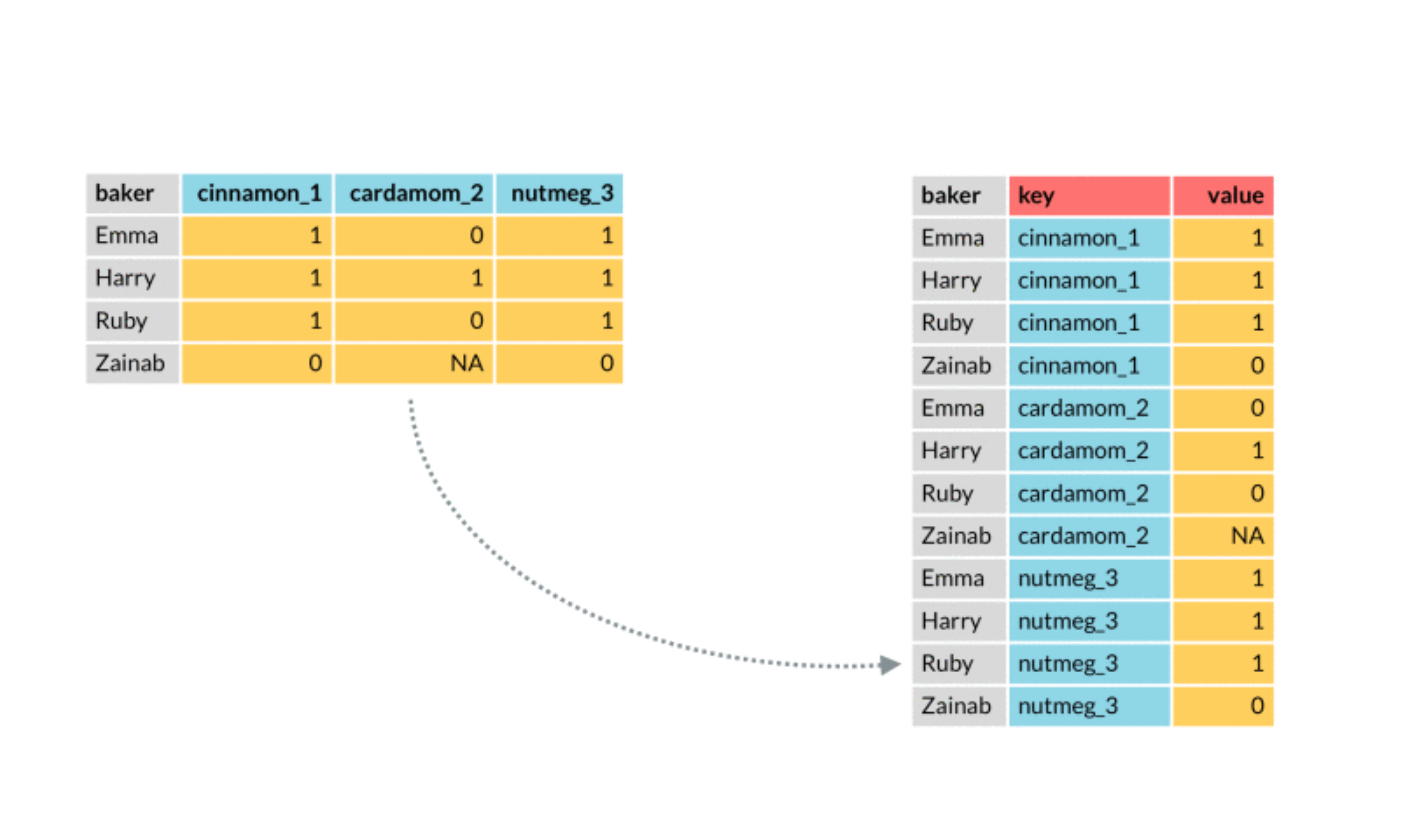
The observations (baker in the picture) correspond to our statistical units for which we have several predictions coming from different models. On the left (wide format) we have a column for each prediction method. On the right (long format) the observations are repeated for several lines and we have two new columns: one for the key (method in our case) and the value (the predictions in our case).
In the following code we first include in train.data 3 new columns referring to the predictions of the three best methods. This is the dataframe in the wide format with 404 rows:
widedata = train.data %>%
mutate(predss = fitted(mod_ss3),
predloess = mod_loess$fitted,
predpoly = mod_poly$fitted.values)
colnames(widedata)## [1] "crim" "zn" "indus" "chas" "nox" "rm"
## [7] "age" "dis" "rad" "tax" "ptratio" "black"
## [13] "lstat" "medv" "lstat_ord" "predss" "predloess" "predpoly"dim(widedata)## [1] 404 18We now move from the wide to the long format by using pivot_longer. We select the three columns to pivot into longer format (predss:predpoly) and specify with names_tot the name of the new column that will contain the model name (it is created from column names of the predictions columns). Finally, with values_to we define the name of the new column that will contain the predictions:
longdata = widedata %>%
pivot_longer(col = predss:predpoly,
names_to = "model",
values_to = "pred")
glimpse(longdata)## Rows: 1,212
## Columns: 17
## $ crim <dbl> 45.74610, 45.74610, 45.74610, 6.65492, 6.65492, 6.65492, 0.0…
## $ zn <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 60, 60, 60, 0, 0, 0, 33,…
## $ indus <dbl> 18.10, 18.10, 18.10, 18.10, 18.10, 18.10, 4.05, 4.05, 4.05, …
## $ chas <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ nox <dbl> 0.693, 0.693, 0.693, 0.713, 0.713, 0.713, 0.510, 0.510, 0.51…
## $ rm <dbl> 4.519, 4.519, 4.519, 6.317, 6.317, 6.317, 6.860, 6.860, 6.86…
## $ age <dbl> 100.0, 100.0, 100.0, 83.0, 83.0, 83.0, 74.4, 74.4, 74.4, 61.…
## $ dis <dbl> 1.6582, 1.6582, 1.6582, 2.7344, 2.7344, 2.7344, 2.9153, 2.91…
## $ rad <int> 24, 24, 24, 24, 24, 24, 5, 5, 5, 4, 4, 4, 1, 1, 1, 24, 24, 2…
## $ tax <dbl> 666, 666, 666, 666, 666, 666, 296, 296, 296, 307, 307, 307, …
## $ ptratio <dbl> 20.2, 20.2, 20.2, 20.2, 20.2, 20.2, 16.6, 16.6, 16.6, 21.0, …
## $ black <dbl> 88.27, 88.27, 88.27, 396.90, 396.90, 396.90, 391.27, 391.27,…
## $ lstat <dbl> 36.98, 36.98, 36.98, 13.99, 13.99, 13.99, 6.92, 6.92, 6.92, …
## $ medv <dbl> 7.0, 7.0, 7.0, 19.5, 19.5, 19.5, 29.9, 29.9, 29.9, 20.4, 20.…
## $ lstat_ord <fct> "(28.9,38]", "(28.9,38]", "(28.9,38]", "(10.8,19.9]", "(10.8…
## $ model <chr> "predss", "predloess", "predpoly", "predss", "predloess", "p…
## $ pred <dbl> 11.68768, 11.07657, 11.61738, 19.62469, 20.07383, 19.53149, …The new dataframe longdata has 1212 rows (the observations are repeated 3 times). There is also a new column in named model containing the names of the models:
table(longdata$model)##
## predloess predpoly predss
## 404 404 404This column will be used for setting the legend and the lines’ color. The predictions are all stacked in the pred column.
We plot can be obtained as follows:
longdata %>%
ggplot(aes(lstat, medv) ) +
geom_point(col="gray") +
geom_line(aes(lstat,pred, col=model),lwd=1.5)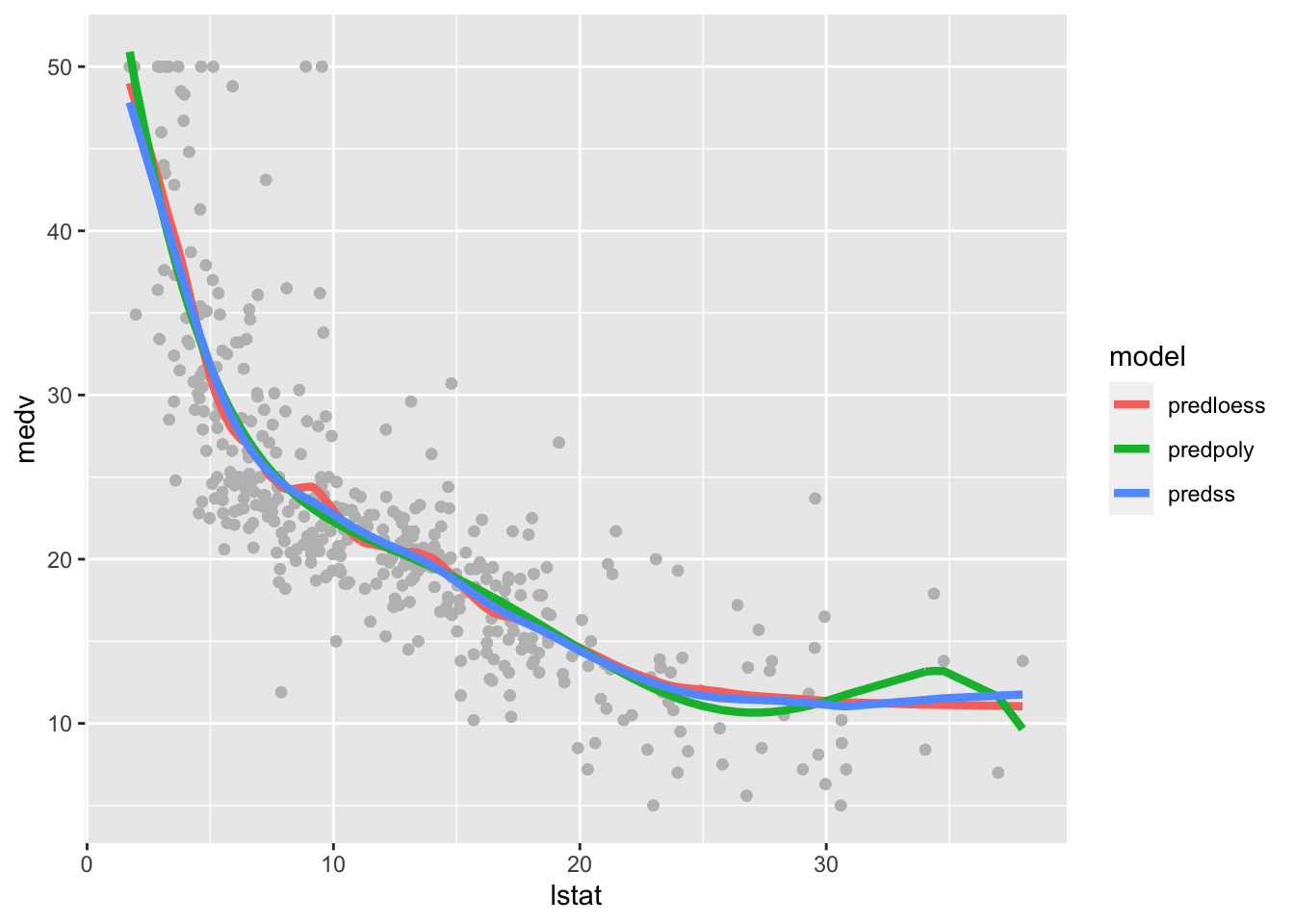
The polynomial fitted model has a weird bump in the right outer values of lstat. The loess and polynomial fitted models are very similar but the loess line is slightly wigglier.
8.8 Exercises Lab 7
The RMarkdown file Lab7_home_exercises_empty.Rmd contains the exercise for Lab. 7. Write your solutions in the RMarkdown file and produce the final html file containing your code, your comments and all the outputs.