Chapter 13 Analyse d’un médiateur en particulier
Ici, l’objectif est d’étudier la part médiée par l’un des médiateurs M spécifiquement. Cela veut dire faire des hypothèses sur les autres facteurs intermédiaires : sont-ils des médiateurs ou des facteurs de confusion du lien \(\small M \rightarrow Y\)?
Par exemple, si l’on veut étudier la part médiée par le fait de faire du sport à 23 ans, on va intégrer les variables socio-économiques et relatives au réseau social comme des facteurs de confusion intermédiaire. La place des autres variables comportementales est plus discutable : le fait de boire ou de fumer peuvent être des marqueurs d’un certains mode de vie qui va favoriser ou non le fait de faire du sport, mais l’inverse est aussi vrai. Le lien est bidirectionnel, ce qui ne peut pas être étudier ici.
On peut étudier les 2 scénariis et comparer les résultats.
13.1 Description
prop.sexe | prop.sport | prop.x | meanSBP |
Femme | Oui | 98 | 116.80 |
Homme | Oui | 211 | 129.40 |
Femme | Non | 228 | 122.81 |
Homme | Non | 111 | 137.61 |
13.2 Les autres comportements comme facteurs de confusion
exp1 <- cmest(
data = base3, # base
model = "gformula", # approach, defaut is rb (regression-based)
# if postc is not empty only gformula or msm
estimation = "imputation", # method of estimation. "imputation" is conterfactual estimation
inference = "bootstrap", # method for se and CI
nboot = 100, # defaut is 200
EMint = FALSE, # interaction exposure mediator
multimp = TRUE, # imputation multiple des DM
m = 10,
outcome = "t8_SBP",
exposure = "t0_baby_sex",
mediator = c("t4_act_sport"),
basec = c("t0_mother_scol_crt",
"t0_fathers_csp_defav"),# confusion baseline
postc = c("t4_tabac_2cl",
"t4_drink_everyday",
"t4_litteraciepbm",
"t4_numeraciepbm",
"t4_act_read",
"t4_O_level",
"t4_hadchildren",
"t4_married",
"t4_act_friend",
"t4_religious"), # confusion intermédiaire
yreg = "linear", # outcome regression model
a = "Homme", # "active" value of exposure
astar = "Femme", # "control" value of exposure
mreg = list("logistic"), # regression model for each mediator
mval = list("Non") , # ref for M
postcreg = list("logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic") # ref for M
) ; set.seed(28062022)type | effect | ci.low | ci.high |
cde | 12.81 | 10.66 | 16.32 |
rpnde | 12.81 | 10.66 | 16.32 |
rtnde | 12.81 | 10.66 | 16.32 |
rpnie | -2.12 | -4.17 | -1.35 |
rtnie | -2.12 | -4.17 | -1.35 |
te | 10.68 | 8.14 | 13.55 |
pm | -0.20 | -0.43 | -0.12 |
Si les hommes et les femmes avaient la même activité physique à 23 ans, des différences de TAS seraient augmentées de 19.94% (95CI = [11.5 to 42.75]).
13.3 Les autres comportements comme médiateurs
exp1 <- cmest(
data = base3, # base
model = "gformula", # approach, defaut is rb (regression-based)
# if postc is not empty only gformula or msm
estimation = "imputation", # method of estimation. "imputation" is conterfactual estimation
inference = "bootstrap", # method for se and CI
nboot = 100, # defaut is 200
EMint = FALSE, # interaction exposure mediator
multimp = TRUE, # imputation multiple des DM
m = 10,
outcome = "t8_SBP",
exposure = "t0_baby_sex",
mediator = c("t4_act_sport"),
basec = c("t0_mother_scol_crt",
"t0_fathers_csp_defav"),# confusion baseline
postc = c("t4_litteraciepbm",
"t4_numeraciepbm",
"t4_act_read",
"t4_O_level",
"t4_hadchildren",
"t4_married",
"t4_act_friend",
"t4_religious"), # confusion intermédiaire
yreg = "linear", # outcome regression model
a = "Homme", # "active" value of exposure
astar = "Femme", # "control" value of exposure
mreg = list("logistic"), # regression model for each mediator
mval = list("Non"), # ref for M
postcreg = list("logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic",
"logistic") # ref for M
) ; set.seed(28062022)type | effect | ci.low | ci.high |
cde | 12.72 | 10.56 | 16.32 |
rpnde | 12.72 | 10.56 | 16.32 |
rtnde | 12.72 | 10.56 | 16.32 |
rpnie | -2.09 | -4.09 | -1.28 |
rtnie | -2.09 | -4.09 | -1.28 |
te | 10.63 | 8.23 | 13.66 |
pm | -0.20 | -0.43 | -0.11 |
Les résultats sont quasiment identiques.
13.4 Une autre analyse : part médiée par la fait de lire souvent
Je peux étudier une autre variable pour laquelle je vais envisager un autre scénario :
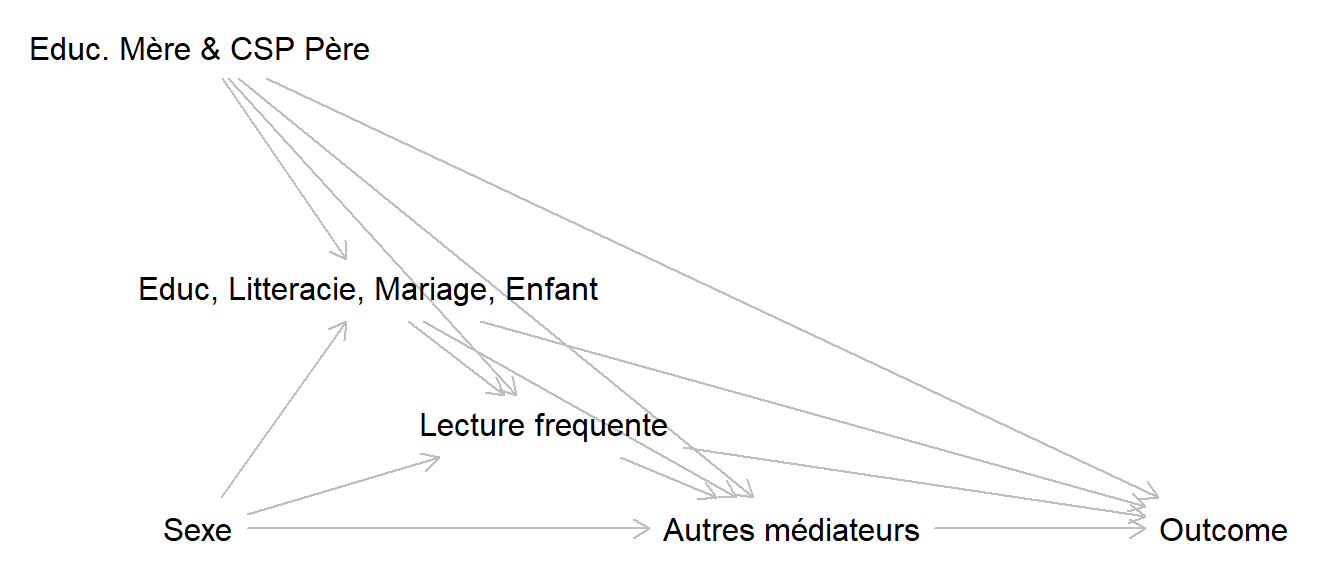
exp1 <- cmest(
data = base3, # base
model = "gformula", # approach, defaut is rb (regression-based)
# if postc is not empty only gformula or msm
estimation = "imputation", # method of estimation. "imputation" is conterfactual estimation
inference = "bootstrap", # method for se and CI
nboot = 100, # defaut is 200
EMint = FALSE, # interaction exposure mediator
multimp = TRUE, # imputation multiple des DM
m = 10,
outcome = "t8_SBP",
exposure = "t0_baby_sex",
mediator = c("t4_act_read"),
basec = c("t0_mother_scol_crt",
"t0_fathers_csp_defav"),# confusion baseline
postc = c("t4_litteraciepbm",
"t4_O_level",
"t4_hadchildren",
"t4_married"), # confusion intermédiaire
yreg = "linear", # outcome regression model
a = "Homme", # "active" value of exposure
astar = "Femme", # "control" value of exposure
mreg = list("logistic"), # regression model for each mediator
mval = list("Oui"), # ref for M
postcreg = list("logistic",
"logistic",
"logistic",
"logistic") # ref for M
) ; set.seed(28062022)type | effect | ci.low | ci.high |
cde | 10.13 | 7.95 | 13.02 |
rpnde | 10.13 | 7.95 | 13.02 |
rtnde | 10.13 | 7.95 | 13.02 |
rpnie | 0.56 | -0.12 | 1.40 |
rtnie | 0.56 | -0.12 | 1.40 |
te | 10.69 | 8.50 | 13.76 |
pm | 0.05 | -0.01 | 0.14 |
On explique 5.26% (95CI = [-1.16 to 13.71]) des différences de TAS entre les hommes et les femmes par des différences liés aux habitudes de lecture.