第23章非参数回归模型

23.1 概述

我们之前的线性回归设定自变量与因变量（或者经过链接函数处理后的因变量）呈线性关系，所获得的系数\(\beta\)也是对应自变量与因变量的整体关联。但是，有时我们的自变量与因变量并非线性关系。在这种情况下，我们可以考虑通过增加次方项（order）的方式增加模型的拟合度，此时我们有两个选择：（1）将次方项由小到大逐渐增加，直至新的次方项不显著；（2）将次方项由大到小逐渐减少，直至新的次方项显著。

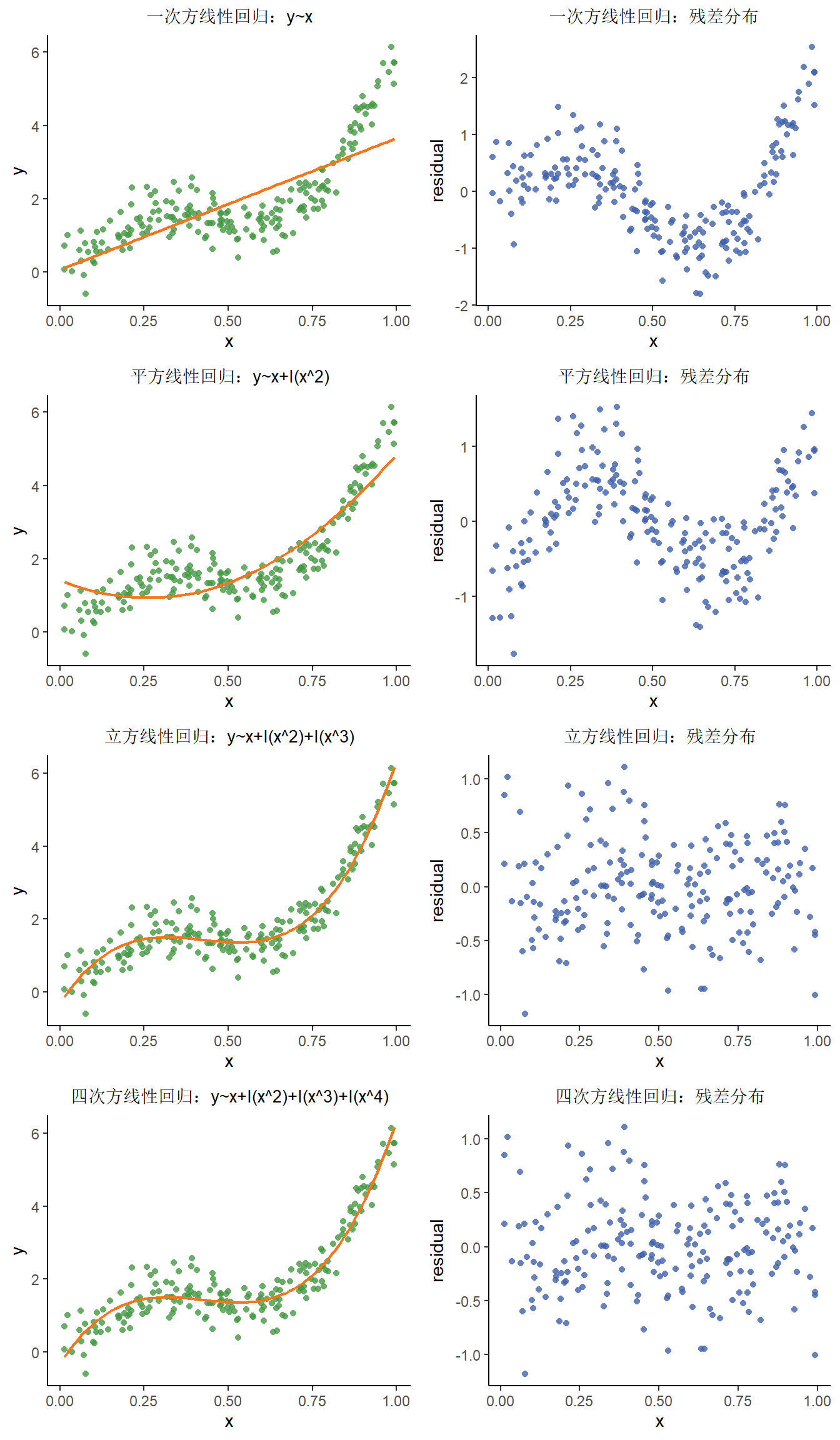
我们看各模型的各项变量的显著性，可以发现在四次方项时的变量是不显著的，所以模型构建时只囊括到立方项。

	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	0.054	0.125	0.434	0.665
x	3.599	0.215	16.755	0.000

	Estimate	Std. Error	t value
(Intercept)	1.415	0.162	8.721
x	-3.753	0.711	-5.277
I(x^2)	7.193	0.675	10.651

	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	-0.331	0.147	-2.246	0.026
x	14.441	1.178	12.255	0.000
I(x^2)	-36.453	2.641	-13.801	0.000
I(x^3)	28.710	1.714	16.753	0.000

	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	-0.331	0.196	-1.685	0.094
x	14.433	2.473	5.836	0.000
I(x^2)	-36.419	9.536	-3.819	0.000
I(x^3)	28.659	13.919	2.059	0.041
I(x^4)	0.025	6.797	0.004	0.997

在上面的多项式回归方程中，我们的假设是自变量x的多个次方项与因变量y（或经过函数转换的因变量y）之间存在线性关系，得到的是一个y与x的多项式方程。事实上，当我们面对更为复杂的数据分布时，其实并不清楚自变量x的分布情况，也不清楚自变量x与因变量y的关联性。同时，当自变量数目较多时，我们也无法通过调整次方项的方式确定模型与实际数据分布的最优拟合。此外，多项式回归很容易受到两端离群值的影响。因此，我们需要在变量分布未知的前提下构建回归方程，这种回归方法叫做非参数回归。非参数回归的优点为灵活且不需过多的数据关联性假设；缺点为计算复杂且结果不易解释。因此，在已知数据关联性结构（如正态分布，泊松分布）的前提下，推荐选择参数回归的方法。

23.2 核平滑

非线性回归的一种拟合方式是利用每个自变量x的局部区域中的\((x_i,y_i)\)观测点进行零次方、一次方乃至多次方的多项式的拟合，各个观测点依照特定的核（kernel）赋予权重，以此获得在x处估计的y值，这种方法叫做核平滑（kernel smoother），表示为

\[\begin{equation} \hat{f}_{\lambda}(x)=\frac{\frac{1}{n\lambda}\sum\limits_{i=1}^{N}K(\frac{x-x_{i}}{\lambda})f(x_i)}{\frac{1}{n\lambda}\sum\limits_{i=1}^{N}K(\frac{x-x_{i}}{\lambda})} \tag{23.1} \end{equation}\]

其中：

\(\frac{1}{n\lambda}\sum\limits_{i=1}^{N}K(\frac{x-x_{i}}{\lambda})\)为核估计方程（Kernel density estimation）。
\(K(·)\)为核函数，特点为：对称、非负、均值为0、积分为1。
平滑参数\(\lambda\)为正数，常被称为带宽（bandwidth）或窗口（window）。
\(f(x_i)\)为\(y_i\)与\(x_i\)的关系式。

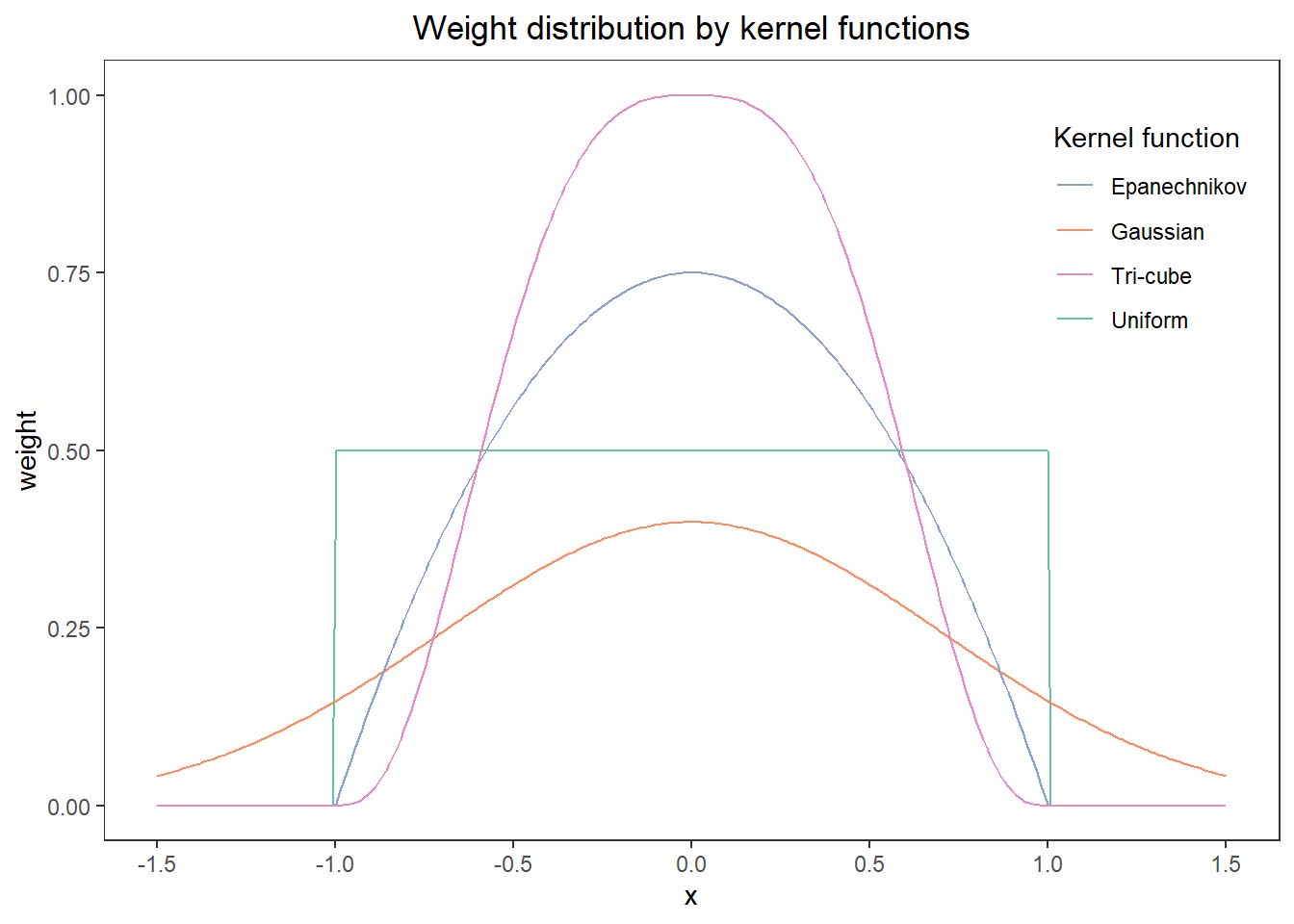
常用核函数包括：

均匀核（uniform）/矩形核（rectangular）：

\[\begin{equation} K(x)=\begin{cases} \frac{1}{2}&,\ -1\leq x \leq 1\\ 0&,\ 其它 \end{cases} \end{equation}\]

在\(\lambda\)范围内赋予均匀权重。

高斯核（Gaussian）：

\[\begin{equation} K(x)=\frac{1}{\sqrt{2\pi}}exp{(-\frac{x^2}{2})} \end{equation}\]

全范围内赋予权重且两端的权重衰减极快。

Epanechnikov核（二次核）：

\[\begin{equation} K(x)=\begin{cases} \frac{3}{4}(1-x^2)&,\ -1\leq x \leq 1\\ 0&,\ 其它 \end{cases} \end{equation}\]

\(\lambda\)范围内赋予权重，中心区域权重高，而后权重持续衰减。

双三次核（Tri-cube）

\[\begin{equation} K(x)=\begin{cases} (1-|x|^3)^3&,\ -1\leq x \leq 1\\ 0&,\ 其它 \end{cases} \end{equation}\]

上述核函数的权重分布图如下：

注意：

估计的y值并不会对核函数的选择非常敏感。
平滑参数\(\lambda\)的最优选择通常通过主观判断曲线的拟合度来确定。

在核平滑方程(23.1)中，\(f(x_i)\)关系式可以是x的零次方、一次方乃至多次方的多项式，其中最常用（也最为简洁）的关系式为x的零次方，我们将在这里做演示，其余次方项的关系式可以参考此链接。

x的零次方其实就意味着\(f(x_i)\)关系式就是\(y_i\)自身，我们要估计的\((x_0,y_0)\)处的值便是点\(x_0\)附近\(\lambda\)范围内\(y_i\)的加权值。以Epanechnikov核为例，我们来演示\(y_0\)值的估计。

# 生成模拟数据
set.seed(1)
x_sim <- runif(n=200) # 生成x值
y_true <- sin(2*pi*x_sim**2)**3 # 生成y值
y_sim <- y_true + rnorm(length(x_sim), mean=0, sd=0.08) # 添加y值随机误差项

# 构建Epanechnikov核函数
func_e <- function(x){
  y <- numeric(length(x))
  idx <- abs(x)<=1
  y[idx] <- (3/4)*(1-x[idx]**2)
  return (y)
}

# 创建核平滑函数
func_smooth <- function(x,y,lambda,func){
  y_smooth <- numeric(length(x))
  if(lambda>0){
    for (i in seq(length(x))){
      dist <- (x-x[i])/lambda # 计算距离
      weight <- func(dist) # 计算权重
      y_smooth[i] <- sum(weight*y)/sum(weight)
    }
    return (y_smooth)
  }
  else{print("Error! Lambda should be a positive value.")}
}

y_smooth_1 <- func_smooth(x_sim, y_sim, 0.5, func_e)
y_mse_1 <- sum((y_sim-y_smooth_1)**2)/length(y_sim)
y_smooth_2 <- func_smooth(x_sim, y_sim, 0.1, func_e)
y_mse_2 <- sum((y_sim-y_smooth_2)**2)/length(y_sim)
y_smooth_3 <- func_smooth(x_sim, y_sim, 0.05, func_e)
y_mse_3 <- sum((y_sim-y_smooth_3)**2)/length(y_sim)
y_smooth_4 <- func_smooth(x_sim, y_sim, 0.001, func_e)
y_mse_4 <- sum((y_sim-y_smooth_4)**2)/length(y_sim)

p1 <- ggplot() +
  geom_point(aes(x=x_sim, y=y_sim), color="#459943", alpha=0.8) +
  geom_line(aes(x=x_sim, y=y_smooth_1), color="#d95f02", linewidth=0.8) +
  labs(x="x", y="y") +
  annotate(geom="text", x=0.8, y=0.9, label="lambda=0.5") +
  annotate(geom="text", x=0.8, y=0.8, label=paste0("MSE=", round(y_mse_1,3)))

p2 <- ggplot() +
  geom_point(aes(x=x_sim, y=y_sim), color="#459943", alpha=0.8) +
  geom_line(aes(x=x_sim, y=y_smooth_2), color="#d95f02", linewidth=0.8) +
  labs(x="x", y="y") +
  annotate(geom="text", x=0.8, y=0.9, label="lambda=0.1") +
  annotate(geom="text", x=0.8, y=0.8, label=paste0("MSE=", round(y_mse_2,3)))

p3 <- ggplot() +
  geom_point(aes(x=x_sim, y=y_sim), color="#459943", alpha=0.8) +
  geom_line(aes(x=x_sim, y=y_smooth_3), color="#d95f02", linewidth=0.8) +
  labs(x="x", y="y") +
  annotate(geom="text", x=0.8, y=0.9, label="lambda=0.05") +
  annotate(geom="text", x=0.8, y=0.8, label=paste0("MSE=", round(y_mse_3,3)))

p4 <- ggplot() +
  geom_point(aes(x=x_sim, y=y_sim), color="#459943", alpha=0.8) +
  geom_line(aes(x=x_sim, y=y_smooth_4), color="#d95f02", linewidth=0.8) +
  labs(x="x", y="y") +
  annotate(geom="text", x=0.8, y=0.9, label="lambda=0.001") +
  annotate(geom="text", x=0.8, y=0.8, label=paste0("MSE=", round(y_mse_4,3)))

plot_grid(p1,p2,p3,p4, ncol=2)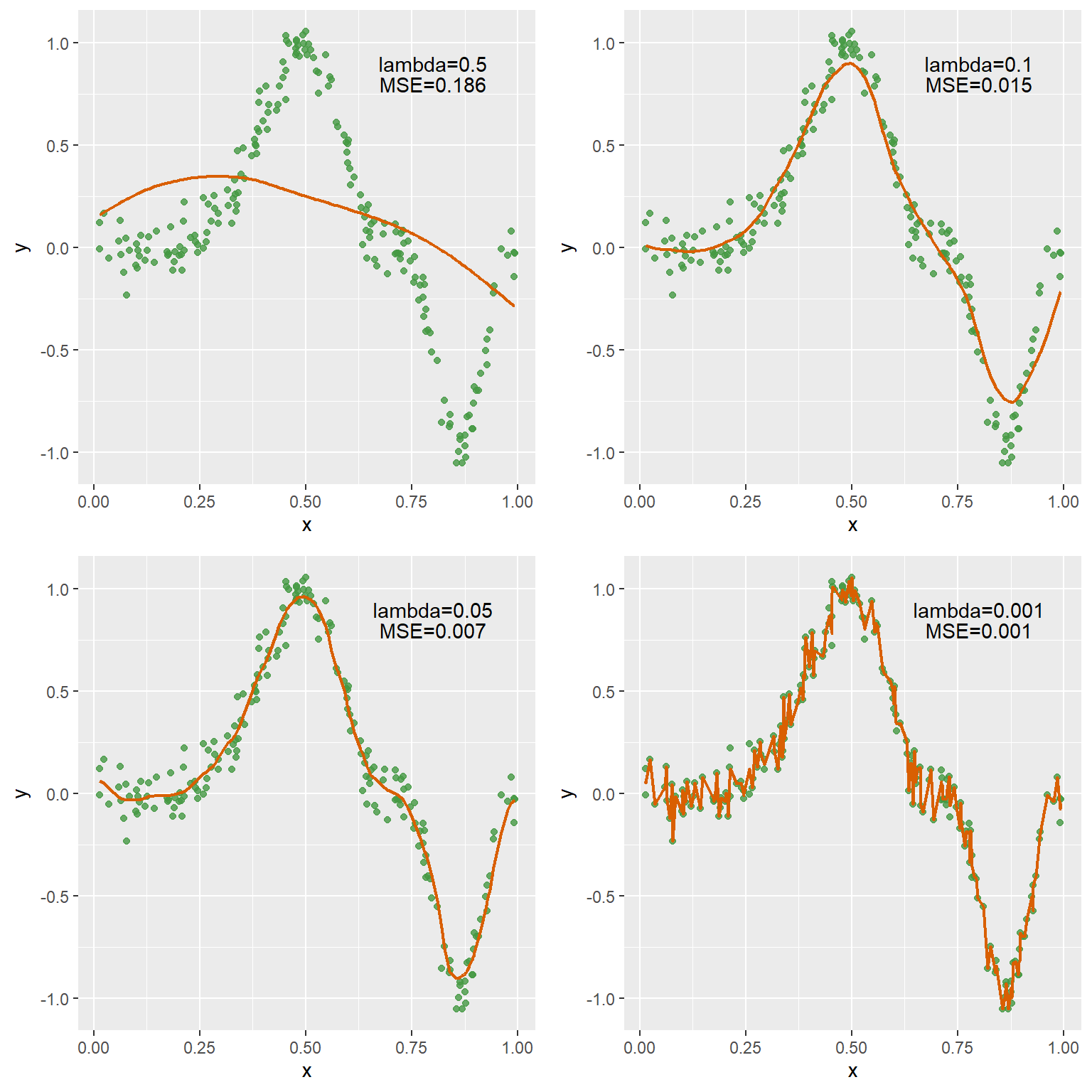

在R中可以使用ksmooth()函数实现，但是可选的核只有均匀核box和高斯核normal两种。所以，如果想要个性化编写核，可以基于上面的代码进行调整。

23.3 样条平滑

在上面的核平滑例子中，我们可以看到，随着平滑参数\(\lambda\)的减小，构建的回归方程也更能拟合原先的数据分布，表现为均方误差（MSE）逐渐减小，但是这也会导致回归方程过拟合的现象，表现为曲线不再平滑（即曲线的二阶导数[曲率]将变大）。因此需要将平滑参数\(\lambda\)作为权重系数以平衡MSE与曲线的平滑性，此方程可以表示为：

\[\begin{equation} \frac{1}{N}\sum\limits_{i=1}^{N}(Y_{i}-f(x_{i}))^{2} + \lambda\int[f^{''}(x)]^{2}dx \end{equation}\]

我们的目标是通过调节平滑参数\(\lambda\)，使上述方程的值尽可能最小。当\(\lambda\)增大时，拟合的曲线会向直线逼近，即模型会趋于简单；反之，模型将更为复杂。

splines包的smooth.spline()函数可以用于样条平滑，最优平滑参数\(\lambda\)通常使用广义交叉验证法（GCV）判断，GCV最小的值即为最优平滑参数\(\lambda\)。

# 生成模拟数据
set.seed(1)
x_sim <- runif(n=200) # 生成x值
y_true <- x_sim + 2*x_sim**2 + 3*x_sim**3 + sin(2*pi*x_sim) # 生成y值
y_sim <- y_true + rnorm(200, mean=0, sd=0.4)

# 设置平衡参数范围
allspar = seq(0,1,length.out = 200)
s = length(allspar)

n = length(x_sim)
k = 99
RSS = rep(0,s)
df = rep(0,s)

# 遍历平滑参数
for(i in 1:s)
{
  yhat = smooth.spline(y_sim, df = k, spar = allspar[i])
  df[i] = yhat$df
  yhat = yhat$y
  RSS[i] = sum((yhat-y_sim)^2)
}

# 计算GCV 
GCV = (RSS/n)/((1-df/n)^2)

spar_opt = allspar[which.min(GCV)]

ggplot() +
  geom_line(aes(x=allspar, y=GCV)) +
  geom_point(aes(x=spar_opt, y=GCV[which.min(GCV)]), color="#459943")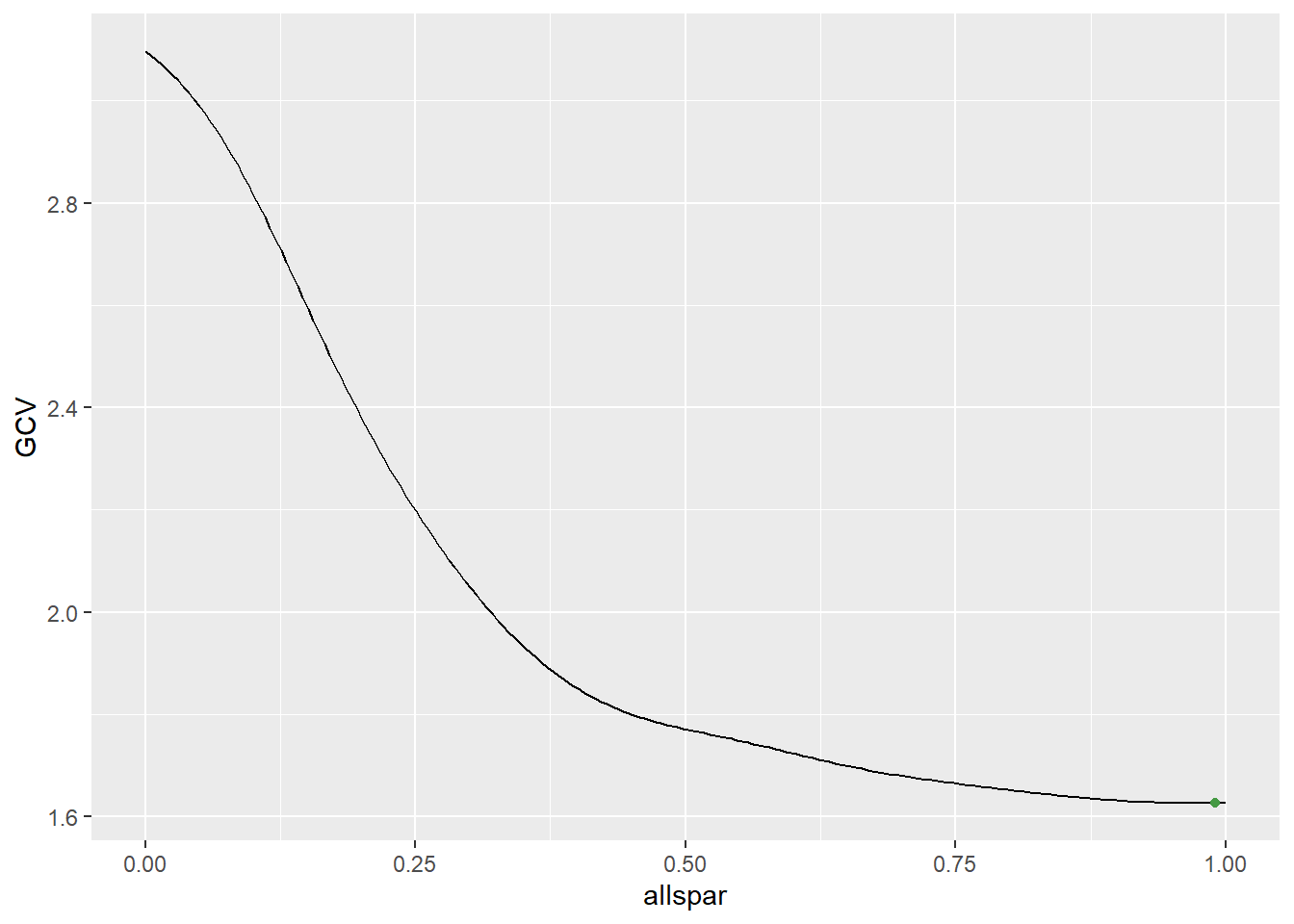

23.4 立方样条

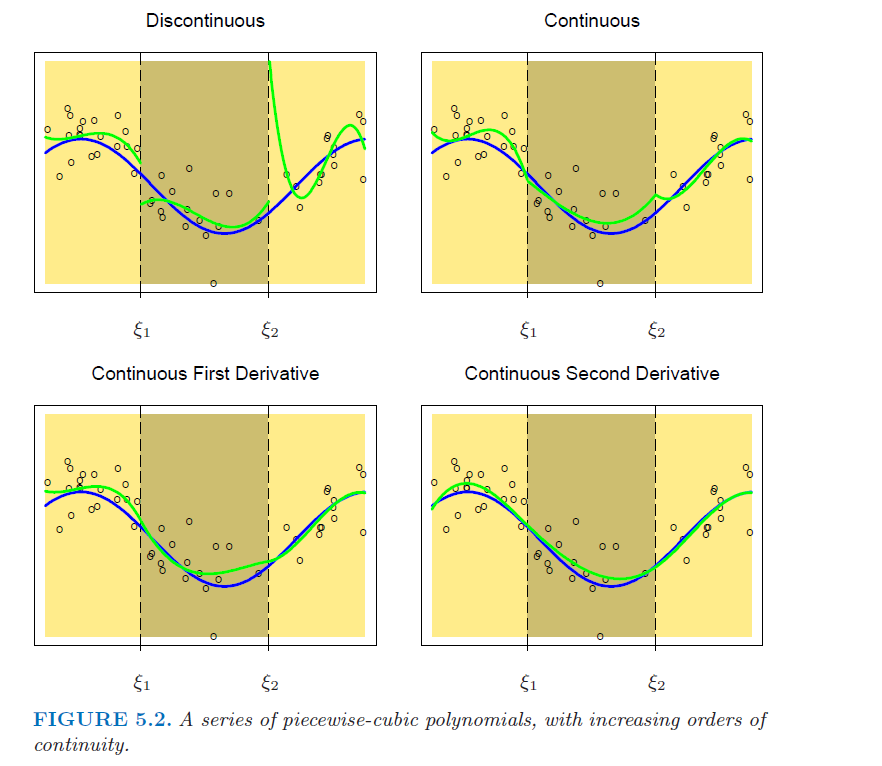
样条（spline）指的是多段平滑连续的多项式函数。我们将数据X分为\(I\)段，每一段的区间范围为[\(\xi_{i-1}\),\(\xi_{i}\))。则在第1段区间，我们可以构建一个多项式函数\(C_{1}(x)=h(\xi_{0}\leq x <\xi_{1})\)；在第2段区间，我们可以构建一个多项式函数\(C_{2}(x)=h(\xi_{1}\leq x <\xi_{2})\)；以此类推，直到最后一段区间，我们可以构建多项式函数\(C_{I}(x)=h(\xi_{I-1}\leq x <\xi_{I})\)。最后，构建拟合的样条函数\(f(x)=\sum\limits_{i=1}^{I}\beta_{i}C_{i}(x)\)。而我们要做的就是求出各段多项式的系数\(\beta\)使得\(\sum\limits_{j=1}^{N}(Y_{j}-f(x_{j}))^2\)最小，在求解的过程中，我们需要解决两个大问题：

连续性，即截点两侧的函数在截点的值相等：\(f(\xi_{i}^{-})=f(\xi_{i}^{+})\)
平滑线，即截点两侧的函数在截点处的连接是平滑的，由于二阶导数已经能够使得连接肉眼可见地平滑，因此样条中每个自变量的最高次方通常设为立方项，需要满足的条件为：\(f^{'}(\xi_{i}^{-})=f^{'}(\xi_{i}^{+})\)，\(f^{''}(\xi_{i}^{-})=f^{''}(\xi_{i}^{+})\)。参考链接

以j为次方项，p为次方（即阶数为p+1），k为节点数，可构建如下函数：

\[\begin{equation} \begin{aligned} &h_{j}(x)=x^{j-1}, j=1,2,...,p+1 \\[2em] &h_{i+p+1}(x)=(x-\xi_{i})_{+}^{p}, i=1,2,...,k\\[2em] &其中，(x-\xi_{i})_{+}^{p}=\begin{cases} (x-\xi_{i})^{p}&,\ x \geq \xi_{i}\\ 0&,\ 其它 \end{cases} \end{aligned} \end{equation}\]

在上式中，p=0为常数样条，p=1为一次方样条，p=2为二次方样条，p=3为三次方样条。

令\(H=[h_{1}(X)\ h_{2}(X)\ ...\ h_{k+p+1}(X)]\)，\(\hat\beta\)为H各项对应的系数，根据最小二乘法可知，\(\hat\beta=(H^{T}H)^{-1}H^{T}Y\)，估计Y值为\(\hat Y=H(H^{T}H)^{-1}H^{T}Y=SY\)，自由度为\(df=trace(S)\)。

下面，我们来演示样条拟合的代码实现过程。

# 依旧以上例中的x_sim和y_sim为例进行演示
# 创建节点：5个点，中间3个为节点
k_5 <- seq(min(x_sim),max(x_sim),length.out=5)

# 创建节点：10个点，中间8个为节点
k_10 <- seq(min(x_sim),max(x_sim),length.out=10)

# # 手动创建样条函数
# h1 <- rep(1, length(x_sim))
# h2 <- x_sim
# h3 <- x_sim**2
# h4 <- x_sim**3
# h5 <- (x_sim-k_5[2])**3
# h5[h5<0] <- 0
# h6 <- (x_sim-k_5[3])**3
# h6[h6<0] <- 0
# h7 <- (x_sim-k_5[4])**3
# h7[h7<0] <- 0
# 
# # 创建H矩阵
# H <- cbind(h1,h2,h3,h4,h5,h6,h7)

# H矩阵函数
func_h <- function(x,k){
  # 获取节点数
  nk <- length(k)-2
  # 创建样条函数
  h1 <- rep(1, length(x))
  h2 <- x
  h3 <- x**2
  h4 <- x**3
  # 创建H矩阵
  H <- cbind(h1,h2,h3,h4)
  # 自动创建节点处样条函数
  for(i in seq(from=2, to=nk+1)){
    h <- (x-k[i])**3
    h[h<0] <- 0
    assign(paste0("h_k",i), h) # 使用assign()函数给自动生成变量赋值
    H <- eval(parse(text=paste0("cbind(H,h_k",i,")"))) # 对自动生成变量进行列合并
  }
  return (H)
}

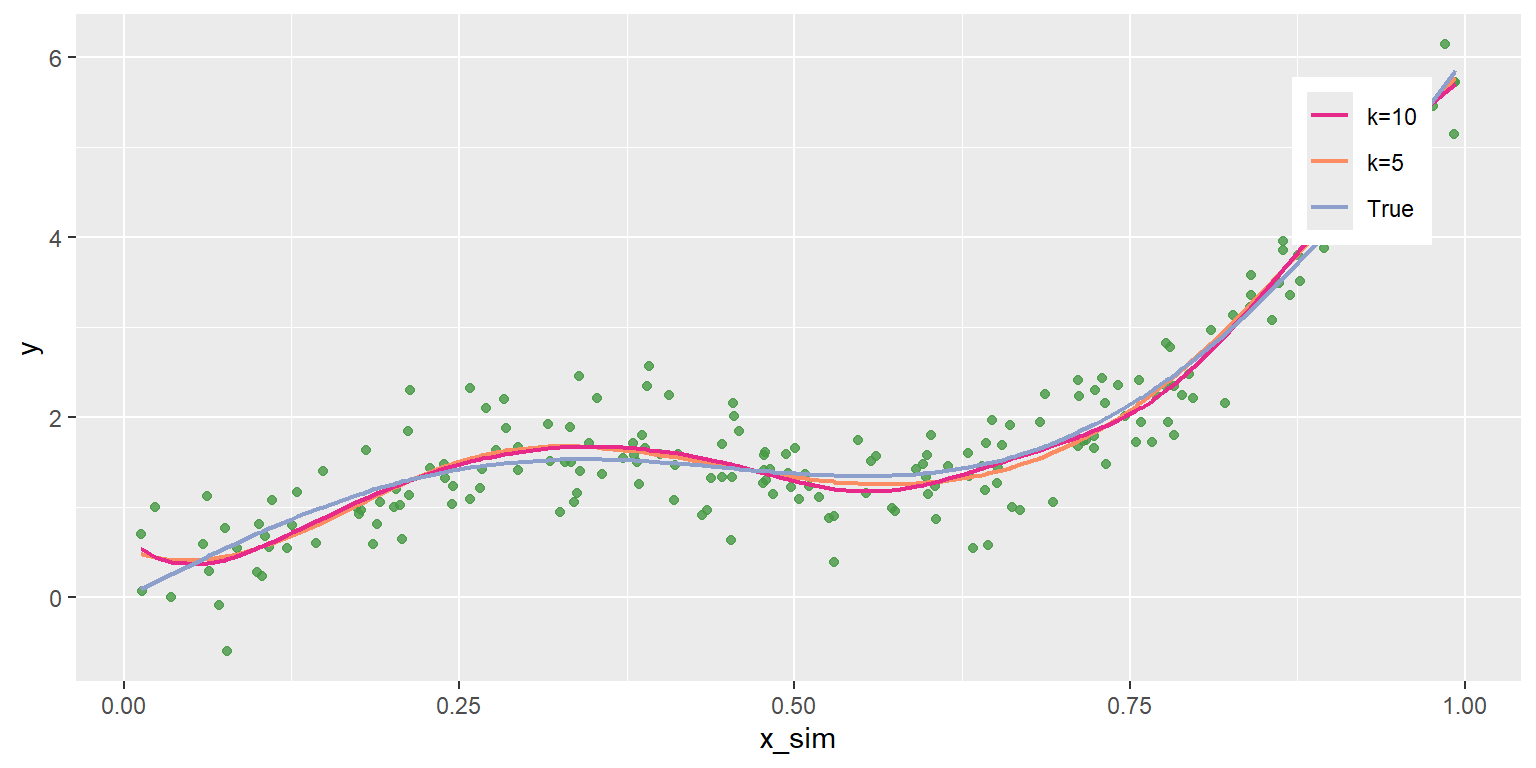
H_5 <- func_h(x_sim,k_5)
H_10 <- func_h(x_sim,k_10)

# 构建线性回归模型
lm_b_5 <- lm(y_sim~H_5 - 1) # 不要截距
lm_b_10 <- lm(y_sim~H_10 - 1) # 不要截距

# Y预测值
y_pred_5 <- predict(lm_b_5)
y_pred_10 <- predict(lm_b_10)

ggplot() +
  geom_point(
    aes(x=x_sim, y=y_sim), color="#459943", alpha=0.8
  ) +
  geom_line(aes(x=x_sim, y=y_pred_5, color="k=5"), linewidth=0.8) +
  geom_line(aes(x=x_sim, y=y_pred_10, color="k=10"), linewidth=0.8) +
  geom_line(aes(x=x_sim, y=y_true, color="True"), linewidth=0.8) +
  scale_color_manual(
    values = c("k=5"="#fc8d62","k=10"="#e7298a", "True"="#8da0cb")
  ) +
  labs(y="y") +
  theme(
    legend.title = element_blank(),
    legend.position = c(0.89, 0.78)
  )

# 查看各项系数
knitr::kable(round(coef(summary(lm_b_5)),3))

	Estimate	Std. Error	t value	Pr(>\|t\|)
H_5h1	0.543	0.254	2.139	0.034
H_5h2	-6.102	4.950	-1.233	0.219
H_5h3	76.253	26.808	2.844	0.005
H_5h4	-145.658	42.386	-3.436	0.001
H_5h_k2	210.706	55.781	3.777	0.000
H_5h_k3	-28.493	28.834	-0.988	0.324
H_5h_k4	-107.617	49.716	-2.165	0.032

knitr::kable(round(coef(summary(lm_b_10)),3))

	Estimate	Std. Error	t value	Pr(>\|t\|)
H_10h1	0.684	0.411	1.666	0.097
H_10h2	-13.765	17.562	-0.784	0.434
H_10h3	170.042	207.293	0.820	0.413
H_10h4	-461.993	703.684	-0.657	0.512
H_10h_k2	392.561	942.119	0.417	0.677
H_10h_k3	75.099	427.864	0.176	0.861
H_10h_k4	5.334	325.236	0.016	0.987
H_10h_k5	193.311	312.873	0.618	0.537
H_10h_k6	-385.140	322.914	-1.193	0.234
H_10h_k7	410.268	327.668	1.252	0.212
H_10h_k8	-443.690	382.064	-1.161	0.247
H_10h_k9	63.631	837.552	0.076	0.940

23.5 B样条拟合

在上例中，我们通过在自变量x的全范围内构建多项式用于模型拟合，但是需要注意的是，其中的一次方、二次方和三次方项时在全范围内都普适的，存在共线性的问题，表现为\(det(H)\simeq 0\)。为了解决这一问题，我们可以基于各个节点，在特定范围内分别构建样条基函数（basis function），这些基函数组合在一起就形成B样条（B spline）拟合函数。关于B样条基函数的计算，可以参考这两个链接：参考链接1和参考链接2。

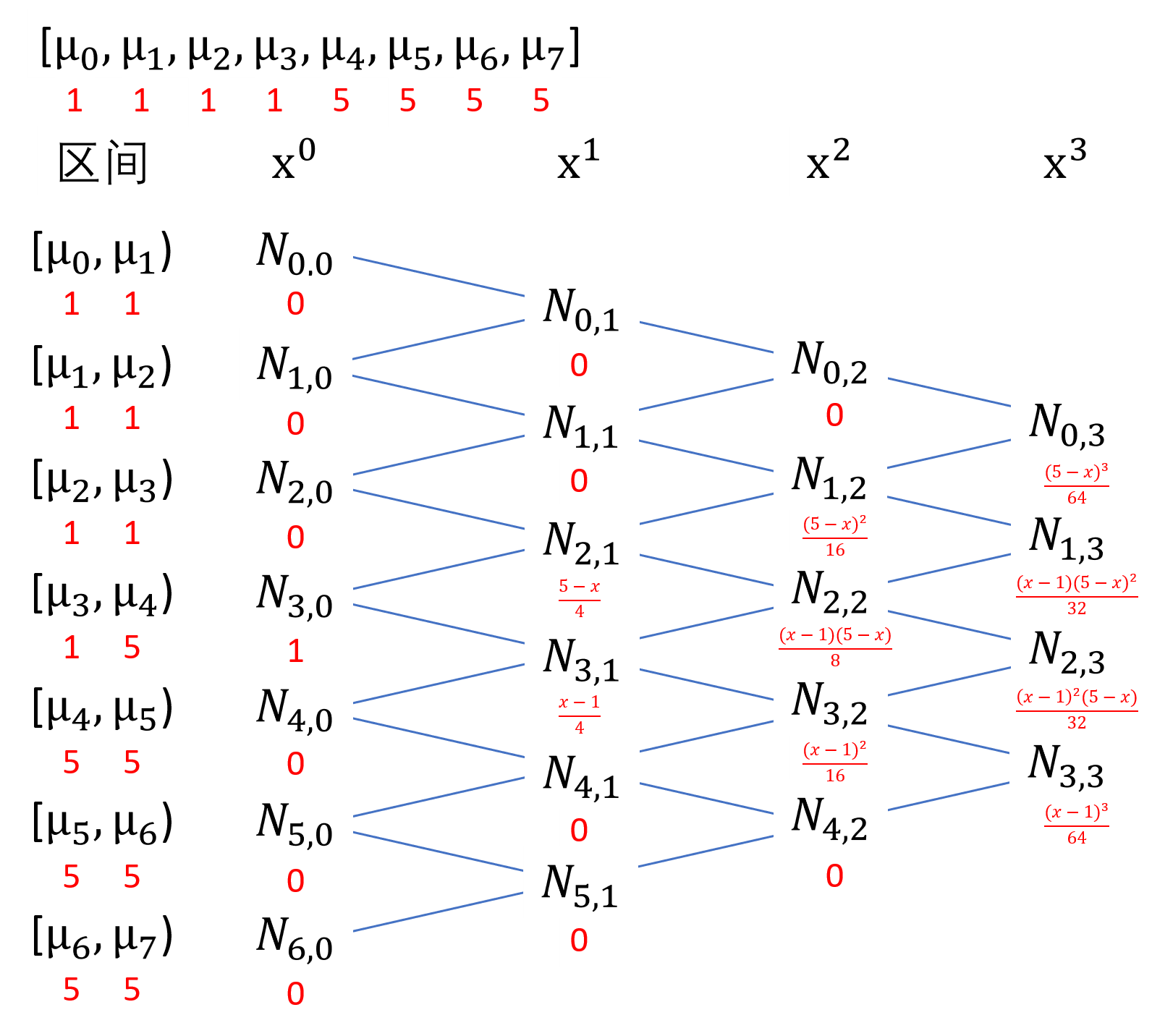
我们以\(N_{i,p}(x)\)表示第\(i\)个\(p\)次方的B样条基函数（自变量为x），以\(\mu_{i}\)表示第\(i\)个节点，那么，B样条基函数公式（又被称为Cox-de Boor递归公式）可以表示为：

\[\begin{equation} \begin{aligned} &N_{i,0}(x)=\begin{cases} 1&,\ \mu_{i} \leq x < \mu_{i+1}\\ 0&,\ 其它 \end{cases}\\ &N_{i,p}(x)=\frac{x-\mu_{i}}{\mu_{i+p}-\mu_{i}}N_{i,p-1}(x) + \frac{\mu_{i+p+1}-x}{\mu_{i+p+1}-\mu_{i+1}}N_{i+1,p-1}(x) \end{aligned} \end{equation}\]

当p=1时，第\(i\)个1次方的B样条基函数可以表示为：

\[\begin{equation} \begin{split} N_{i,1}(x)&=\frac{x-\mu_{i}}{\mu_{i+1}-\mu_{i}}N_{i,0}(x) + \frac{\mu_{i+2}-x}{\mu_{i+2}-\mu_{i+1}}N_{i+1,0}(x)\\ &=\begin{cases} \frac{x-\mu_{i}}{\mu_{i+1}-\mu_{i}}&,\ \mu_{i} \leq x < \mu_{i+1}\\ \frac{\mu_{i+2}-x}{\mu_{i+2}-\mu_{i+1}}&,\ \mu_{i+1} \leq x < \mu_{i+2}\\ 0&,\ 其它 \end{cases} \end{split} \end{equation}\]

当p=2时，第\(i\)个2次方的B样条基函数可以表示为：

\[\begin{equation} \begin{split} N_{i,2}(x)&=\frac{x-\mu_{i}}{\mu_{i+2}-\mu_{i}}N_{i,1}(x) + \frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+1}}N_{i+1,1}(x)\\ &=\begin{cases} \frac{x-\mu_{i}}{\mu_{i+2}-\mu_{i}}\frac{x-\mu_{i}}{\mu_{i+1}-\mu_{i}}&,\ \mu_{i} \leq x < \mu_{i+1}\\ \frac{x-\mu_{i}}{\mu_{i+2}-\mu_{i}}\frac{\mu_{i+2}-x}{\mu_{i+2}-\mu_{i+1}}+\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+1}}\frac{x-\mu_{i+1}}{\mu_{i+2}-\mu_{i+1}}&,\ \mu_{i+1} \leq x < \mu_{i+2}\\ \frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+1}}\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+2}}&,\ \mu_{i+2} \leq x < \mu_{i+3}\\ 0&,\ 其它 \end{cases} \end{split} \end{equation}\]

当p=3时，第\(i\)个3次方的B样条基函数可以表示为：

\[\begin{equation} \begin{split} N_{i,3}(x)&=\frac{x-\mu_{i}}{\mu_{i+3}-\mu_{i}}N_{i,2}(x) + \frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+1}}N_{i+1,2}(x)\\ &=\begin{cases} \frac{x-\mu_{i}}{\mu_{i+3}-\mu_{i}}\frac{x-\mu_{i}}{\mu_{i+2}-\mu_{i}}\frac{x-\mu_{i}}{\mu_{i+1}-\mu_{i}},\ \mu_{i} \leq x < \mu_{i+1}\\[2ex] \frac{x-\mu_{i}}{\mu_{i+3}-\mu_{i}}(\frac{x-\mu_{i}}{\mu_{i+2}-\mu_{i}}\frac{\mu_{i+2}-x}{\mu_{i+2}-\mu_{i+1}}+\frac{x-\mu_{i+1}}{\mu_{i+2}-\mu_{i+1}}\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+1}})+\frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+1}}\frac{x-\mu_{i+1}}{\mu_{i+3}-\mu_{i+1}}\frac{x-\mu_{i+1}}{\mu_{i+2}-\mu_{i+1}},\\ \mu_{i+1} \leq x < \mu_{i+2}\\[2ex] \frac{x-\mu_{i}}{\mu_{i+3}-\mu_{i}}\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+1}}\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+2}}+\frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+1}}(\frac{x-\mu_{i+1}}{\mu_{i+3}-\mu_{i+1}}\frac{\mu_{i+3}-x}{\mu_{i+3}-\mu_{i+2}}+\frac{x-\mu_{i+2}}{\mu_{i+3}-\mu_{i+2}}\frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+2}}),\\ \mu_{i+2} \leq x < \mu_{i+3}\\[2ex] \frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+1}}\frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+2}}\frac{\mu_{i+4}-x}{\mu_{i+4}-\mu_{i+3}},\ \mu_{i+3} \leq x < \mu_{i+4}\\[2ex] 0,\ 其它 \end{cases} \end{split} \end{equation}\]

综合上面的式子，我们可以得到如下规律：

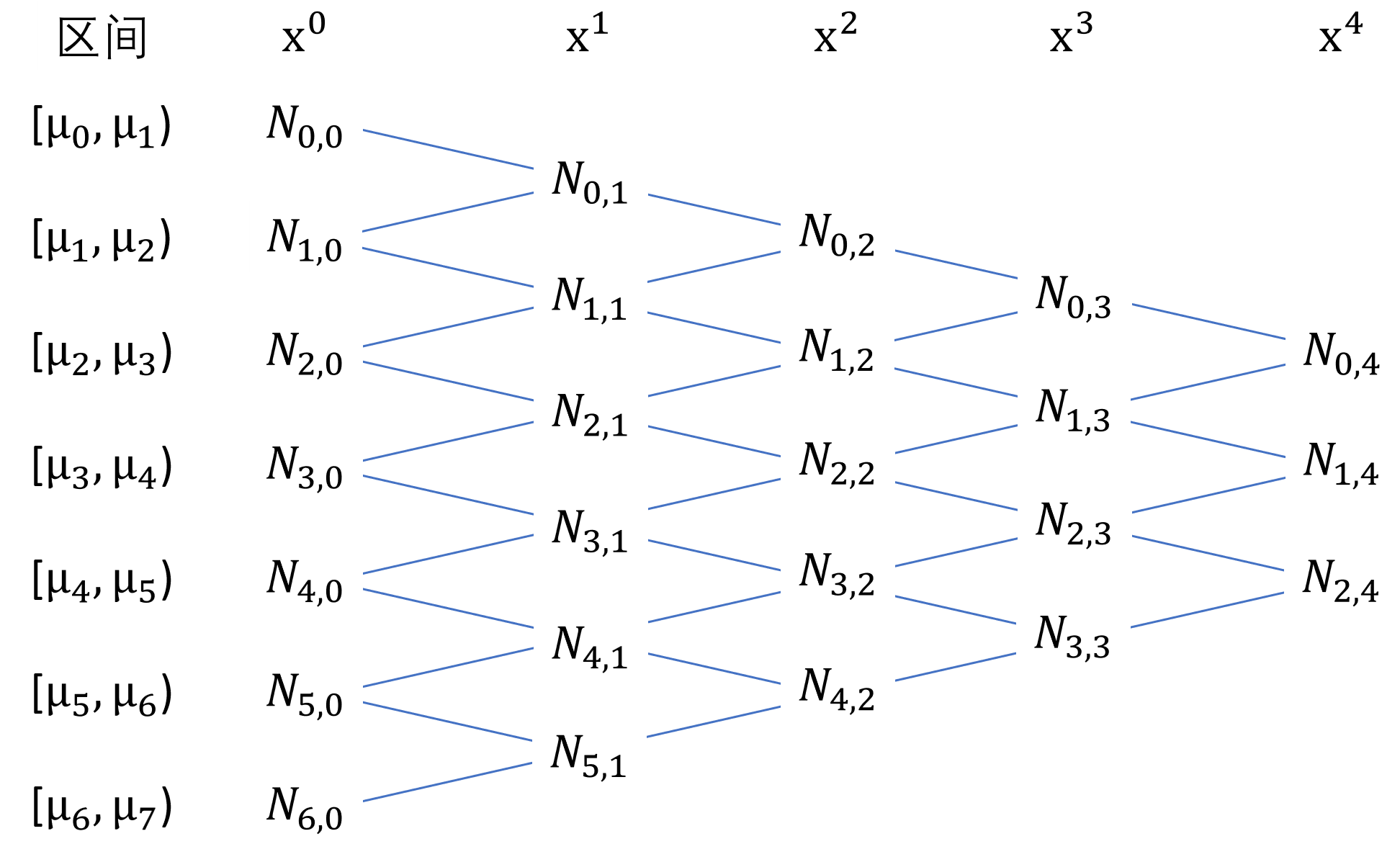
第i个\(p\)次方样条基函数的取数区间为[\(\mu_{i}\),\(\mu_{i+p+1}\))，一共p+1个节段，p+2个控制点（节段点）。而m个\(p\)次方样条基函数的取数区间为[\(\mu_{0}\),\(\mu_{m+p+1}\))，一共\(p+1+m-1=p+m\)个节段，p+m+1个控制点。为了确保m能存在，通常会先根据输入数据分别生成\(p+1\)个最小值和最大值生成\(2×(p+1)\)个控制点，这样\(m=2×(p+1)-p-1=p+1\)，其中的1为截距项，剩下的p为各个节段。当最小值与最大值之间设定了新的k个控制点时，\(m=2×(p+1)+k-p-1=p+k+1\)。

为更好地了解B样条基函数的生成过程，我们手写代码生成B样条基函数（参考链接）。

basis <- function(x, degree, i, knots) {
  if(degree == 0){
    B <- ifelse((x >= knots[i]) & (x < knots[i+1]), 1, 0)
  } else {
    if((knots[degree+i] - knots[i]) == 0) {
      alpha1 <- 0
    } else {
      alpha1 <- (x - knots[i])/(knots[degree+i] - knots[i])
    }
    if((knots[i+degree+1] - knots[i+1]) == 0) {
      alpha2 <- 0
    } else {
      alpha2 <- (knots[i+degree+1] - x)/(knots[i+degree+1] - knots[i+1])
    }
    B <- alpha1*basis(x, (degree-1), i, knots) + alpha2*basis(x, (degree-1), (i+1), knots)
  } 
  return(B)
}

bs_own <- function(x, degree=3, interior.knots=NULL, intercept=FALSE, Boundary.knots = range(x)) {
  if(missing(x)) stop("You must provide x")
  if(degree < 1) stop("The spline degree must be at least 1")
  if(!is.null(interior.knots)) {
    interior.knots.sorted <- sort(interior.knots)
  }else{
    interior.knots.sorted <- NULL
  }
  knots <- c(rep(Boundary.knots[1], (degree+1)), interior.knots.sorted, rep(Boundary.knots[2], (degree+1)))
  K <- length(interior.knots) + degree + 1 # 对应bs()函数中的df

  B.mat <- matrix(0,length(x),K)
  for(j in 1:K) {B.mat[,j] <- basis(x, degree, j, knots)}
  if(any(x == Boundary.knots[2])) {B.mat[x == Boundary.knots[2], K] <- 1} # 最大值时返回1
  if(intercept == FALSE) {
    return(B.mat[,-1])
  } else {
    return(B.mat)
  }
}

# 以c(1,2,3,4,5)向量进行演示
x_5 <- seq(1,5)
bs_own(x_5, intercept = TRUE)

##          [,1]     [,2]     [,3]     [,4]
## [1,] 1.000000 0.000000 0.000000 0.000000
## [2,] 0.421875 0.421875 0.140625 0.015625
## [3,] 0.125000 0.375000 0.375000 0.125000
## [4,] 0.015625 0.140625 0.421875 0.421875
## [5,] 0.000000 0.000000 0.000000 1.000000

我们以c(1,2,3,4,5)数字向量为例，了解一下三次方B样条基函数的实现过程。

在R中，可以使用splines包中的bs()函数进行B样条基函数的生成。bs()函数中的主要参数有：

x：输入数据。
df：自由度，为最终生成的变量个数，计算公式为\(df=length(knots)+degree\)，当计算的df小于length(knots)或者degree时，返回degree值。
knots：节点，可以传入数字向量自定义节点。
degree：次方，默认为3。
intercept：是否包含截距项，默认为FALSE。
Boundary.knots：区间的起始点，默认为输入数据x的最小值与最大值。

bs()函数返回的是N×M的矩阵，其中N为记录数目（即样本量），M为自由度df：当intercept为FALSE时，实际的中间节点数（不包括两端的起始点）为\(df-degree\)；当intercept为TRUE时，由于第一列为截距项，实际的中间节点数为\(df-1-degree\)。在生成的结果中，可以使用attributes()函数查看信息。通过声明knots可以获得节点位置信息。

样条函数通常跟广义线性模型联合使用，以此控制自变量与因变量之间可能存在的多次方关联性，其方程可以写成\(g(y) = \beta_{0} + \sum\limits_{i=1}^{df}\beta_{i}N_{i,p}(x) + 协变量\)，其中的df就是自由度。关于节点数目的选择，我们可以通过所构建的回归方程的AIC来判断，选择AIC最小时对应的节点数。

library(splines)

# 使用bs()函数进行计算
bs_k4 <- bs(x_5, df=3, intercept=FALSE)

# 结果与上面手动写的代码一致
bs_k4

##             1        2        3
## [1,] 0.000000 0.000000 0.000000
## [2,] 0.421875 0.140625 0.015625
## [3,] 0.375000 0.375000 0.125000
## [4,] 0.140625 0.421875 0.421875
## [5,] 0.000000 0.000000 1.000000
## attr(,"degree")
## [1] 3
## attr(,"knots")
## numeric(0)
## attr(,"Boundary.knots")
## [1] 1 5
## attr(,"intercept")
## [1] FALSE
## attr(,"class")
## [1] "bs"     "basis"  "matrix"

# 使用x_sim与y_sim数据，进行线性回归
df_sim <- data.frame(x=x_sim, y=y_sim)
lm_bs <- lm(y~bs(x, df=5), data=df_sim)
summary(lm_bs)

## 
## Call:
## lm(formula = y ~ bs(x, df = 5), data = df_sim)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.14799 -0.23504 -0.03946  0.26373  1.05778 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)     0.23229    0.17333   1.340    0.182    
## bs(x, df = 5)1  0.55464    0.32241   1.720    0.087 .  
## bs(x, df = 5)2  2.19034    0.19964  10.972   <2e-16 ***
## bs(x, df = 5)3 -0.02233    0.27125  -0.082    0.934    
## bs(x, df = 5)4  3.67468    0.22967  16.000   <2e-16 ***
## bs(x, df = 5)5  5.56362    0.24219  22.972   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3946 on 194 degrees of freedom
## Multiple R-squared:  0.905,  Adjusted R-squared:  0.9026 
## F-statistic: 369.8 on 5 and 194 DF,  p-value: < 2.2e-16

# 预测
set.seed(1)
x_test <- runif(5)
predict(object=lm_bs, newdata=data.frame(x=x_test))

##        1        2        3        4        5 
## 1.458080 1.648290 1.248474 4.354624 1.194660

23.6 限制性立方样条

数据拟合过程中，由于两端的数据较稀疏，如果在两端用立方样条，容易出现置信区间偏大的情况，因此，我们通常会把两端设定成线性回归，中间仍然设定成立方样条。假设自变量x的范围为[\(\mu_{0}=x_{min}\),\(\mu_{k+1}=x_{max}\)]，k为节点数，把x分为k+1个区间。那么，在[\(\mu_{0}\),\(\mu_{1}\)]区间和[\(\mu_{k}\),\(\mu_{k+1}\)]区间，自变量x与因变量y为线性关系；在其余区间，则为三次方关系。将限制性立方样条样条跟广义线性模型联合使用，其方程可以写成\(g(y) = \beta_{0} + \beta_{1}x + \sum\limits_{i=2}^{k-1}\beta_{i}C_{i}(x) + 协变量\)。其中，\(C_{i}(x)\)可以表示为：

\[\begin{equation} \begin{aligned} &C_{i}(x) = (x-\mu_{i-1})_{+}^{3} - (x-\mu_{k-1})_{+}^{3}\frac{\mu_{k}-\mu_{i-1}}{\mu_{k}-\mu_{k-1}} + (x-\mu_{k})_{+}^{3}\frac{\mu_{k-1}-\mu_{i-1}}{\mu_{k}-\mu_{k-1}}, i=2,3,...,k-1\\[2em] &(x-\mu_{i-1})_{+}^{3}=\begin{cases} (x-\mu_{i-1})^{3}&,\ x \geq \mu_{i-1}\\ 0&,\ x < \mu_{i-1} \end{cases} \end{aligned} \end{equation}\]

由上式可知，当k=3时，有1个额外项（对应\(\beta_{2}\)）\(C_{2}(x) = (x-\mu_{1})_{+}^{3} - (x-\mu_{2})_{+}^{3}\frac{\mu_{3}-\mu_{1}}{\mu_{3}-\mu_{2}} + (x-\mu_{3})_{+}^{3}\frac{\mu_{2}-\mu_{1}}{\mu_{3}-\mu_{2}}\)，这时

\[\begin{equation} f(x)=\begin{cases} \beta_{0} + \beta_{1}x&, \mu_{0} \leq x < \mu_{1}\\ \beta_{0} + \beta_{1}x + \beta_{2}(x-\mu_{1})^3&, \mu_{1} \leq x < \mu_{2}\\ \beta_{0} + \beta_{1}x + \beta_{2}[(x-\mu_{1})^3- (x-\mu_{2})^{3}\frac{\mu_{3}-\mu_{1}}{\mu_{3}-\mu_{2}}]&, \mu_{2} \leq x < \mu_{3}\\ \beta_{0} + \beta_{1}x + \beta_{2}[(x-\mu_{1})^3- (x-\mu_{2})^{3}\frac{\mu_{3}-\mu_{1}}{\mu_{3}-\mu_{2}} + (x-\mu_{3})^{3}\frac{\mu_{2}-\mu_{1}}{\mu_{3}-\mu_{2}}]&, \mu_{3} \leq x \leq \mu_{4} \end{cases} \end{equation}\]

当k=4时，有2个额外项（对应\(\beta_{2}\)和\(\beta_{3}\)），分别为：

\[\begin{equation} C_{2}(x) = (x-\mu_{1})_{+}^{3} - (x-\mu_{3})_{+}^{3}\frac{\mu_{4}-\mu_{1}}{\mu_{4}-\mu_{3}} + (x-\mu_{4})_{+}^{3}\frac{\mu_{3}-\mu_{1}}{\mu_{4}-\mu_{3}}\\[2em] C_{3}(x) = (x-\mu_{2})_{+}^{3} - (x-\mu_{3})_{+}^{3}\frac{\mu_{4}-\mu_{2}}{\mu_{4}-\mu_{3}} + (x-\mu_{4})_{+}^{3}\frac{\mu_{3}-\mu_{2}}{\mu_{4}-\mu_{3}} \end{equation}\]

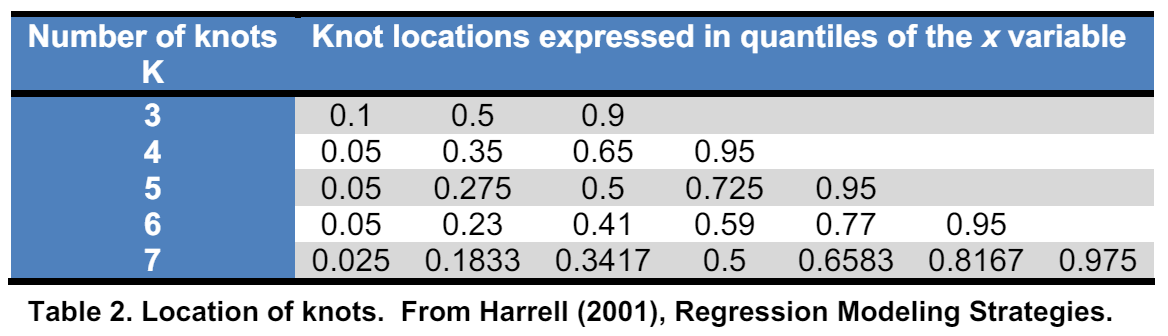
R中限制性立方样条可以使用rms包的rcs()函数实现。相较于节点位置，节点数目对限制性立方样条的结果影响更大。节点数目通常被设定在3-5之间，我们也可以通过AIC或者交叉验证的方式找到合适的节点数目。节点数目与位置的设定如下（参考链接)）：

限制性立方样条在逻辑回归和生存分析中有着广泛的应用，下面我们以survival包中的colon数据为例，介绍限制性立方样条在生存分析中的应用。

23.6.1 初步生存分析

# 加载包
library(survival) # 生存分析包
library(survminer) # 生存分析作图包
library(rms) # 限制性立方样条分析包
library(tidyverse)
library(cowplot)

# 数据预处理
df_colon <- colon # 读取数据
df_colon$sex <- as.factor(df_colon$sex)

dd_colon <- datadist(df_colon)
options(datadist="dd_colon")

# 通过AIC找到最优节点数
aic_vector <- c()
for(knot in seq(3,10)){
  coxph_colon <- cph(
    Surv(time, etype) ~ rcs(age,knot) + sex,
    data = df_colon
  )
  aic_colon <- extractAIC(coxph_colon)
  aic_vector <- c(aic_vector, aic_colon[2])
}

print(paste0("最优节点数为 ", seq(3,10)[which.min(aic_vector)],", AIC为 ", round(aic_vector[which.min(aic_vector)],3)))

## [1] "最优节点数为 3, AIC为 11983.713"

接着，我们使用最优节点数进行生存分析并展示模型

# 使用最优节点数构建模型
coxph_colon <- cph(
  Surv(time, etype) ~ rcs(age,3) + sex,
  data = df_colon
)

# 展示模型
summary(coxph_colon)

##              Effects              Response : Surv(time, etype) 
## 
##  Factor        Low High Diff. Effect    S.E.     Lower 0.95 Upper 0.95
##  age           53  69   16     0.103590 0.052179  0.00132   0.205860  
##   Hazard Ratio 53  69   16     1.109100       NA  1.00130   1.228600  
##  sex - 0:1      2   1   NA    -0.072813 0.066458 -0.20307   0.057441  
##   Hazard Ratio  2   1   NA     0.929770       NA  0.81622   1.059100

# coxph检验
cox.zph(coxph_colon, transform="rank") # p>0.05 符合coxph假设

##             chisq df    p
## rcs(age, 3) 0.464  2 0.79
## sex         2.416  1 0.12
## GLOBAL      2.761  3 0.43

# 确定年龄与生存风险存在线性及非线性关系
anova(coxph_colon)

##                 Wald Statistics          Response: Surv(time, etype) 
## 
##  Factor     Chi-Square d.f. P     
##  age        6.90       2    0.0317
##   Nonlinear 6.32       1    0.0120
##  sex        1.20       1    0.2732
##  TOTAL      7.54       3    0.0565

23.6.2 模型结果可视化

# 全人群，在特定范围内预测风险比并可视化
hr_full <- rms::Predict( # 使用rms包的Predict函数
  coxph_colon,
  age = seq(from=18, to=85, length.out=200), # 总样本的年龄范围为18-85
  fun = exp,
  ref.zero = TRUE
)

# 显示前6行预测风险比
head(hr_full)

##        age sex     yhat     lower    upper
## 1 18.00000   1 1.415352 0.9363055 2.139496
## 2 18.33668   1 1.410370 0.9365194 2.123974
## 3 18.67337   1 1.405405 0.9367332 2.108566
## 4 19.01005   1 1.400458 0.9369466 2.093271
## 5 19.34673   1 1.395528 0.9371599 2.078086
## 6 19.68342   1 1.390616 0.9373728 2.063013
## 
## Response variable (y):  
## 
## Adjust to: sex=1  
## 
## Limits are 0.95 confidence limits

g1 <- ggplot(data=hr_full) +
  geom_ribbon(aes(x=age, ymin=lower, ymax=upper), fill="#c6dbef", alpha=0.5) +
  geom_line(aes(x=age, y=yhat), color="#08519c", linetype="solid", size=0.8) +
  geom_hline(yintercept=1, linetype="dashed", size=0.7) +
  labs(x="age", y="HR") +
  theme_classic()

# 分性别，在特定范围内预测风险比并可视化
hr_sex <- rms::Predict( 
  coxph_colon,
  age=seq(from=18, to=85, length.out=200), # 总样本的年龄范围为18-85
  sex=c("0","1"),
  fun = exp,
  ref.zero = TRUE
)

# 显示前6行预测风险比
head(hr_sex)

##        age sex     yhat     lower    upper
## 1 18.00000   0 1.315959 0.8645847 2.002982
## 2 18.33668   0 1.311326 0.8646166 1.988832
## 3 18.67337   0 1.306710 0.8646452 1.974789
## 4 19.01005   0 1.302111 0.8646706 1.960853
## 5 19.34673   0 1.297527 0.8646926 1.947023
## 6 19.68342   0 1.292960 0.8647112 1.933298
## 
## Response variable (y):  
## 
## Limits are 0.95 confidence limits

g2 <- ggplot(data=hr_sex) +
  geom_ribbon(aes(x=age, ymin=lower, ymax=upper, fill=sex), alpha=0.5, color=NA) +
  geom_line(aes(x=age, y=yhat, color=sex), linetype="solid", size=0.8) +
  geom_hline(yintercept=1, linetype="dashed", size=0.7) +
  scale_fill_manual(values=c("#c6dbef", "#d4b9da")) +
  scale_color_manual(values=c("#08519c", "#dd1c77")) +
  scale_y_continuous(breaks=seq(0.75, 1.75, 0.25)) +
  labs(x="age", y="HR") +
  theme_classic() +
  theme(legend.position = c(0.8,0.9))

plot_grid(g1,g2, ncol=2)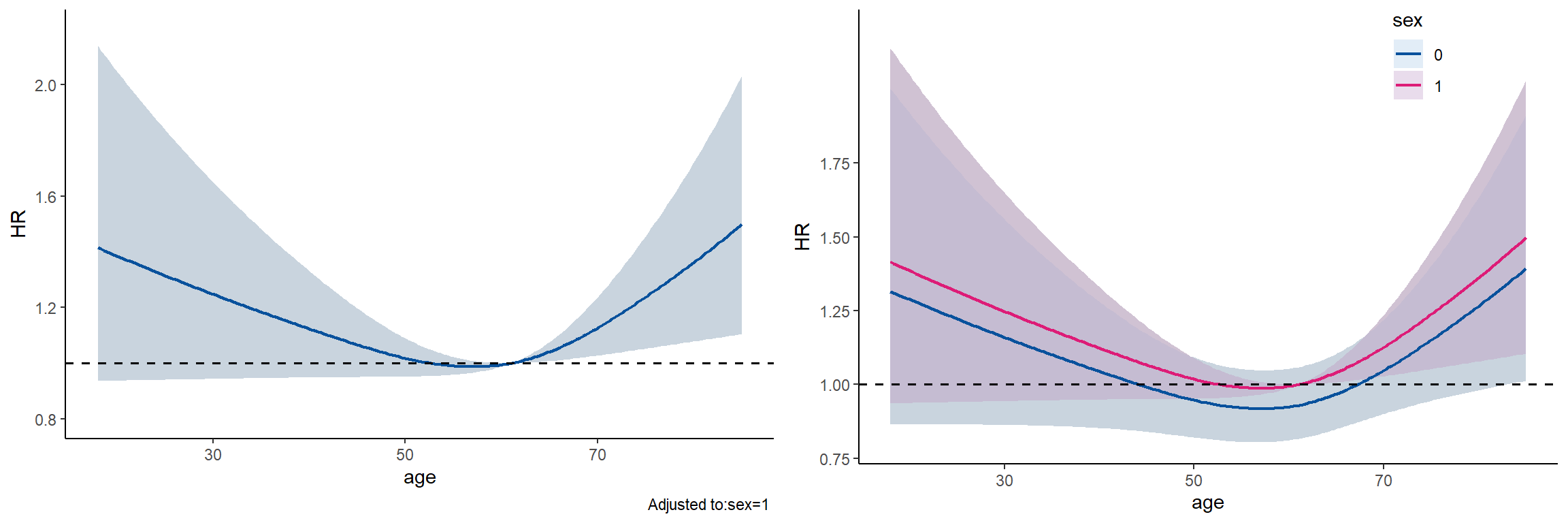

23.6.3 拐点以及临界点

除了可视化，我们还关心图像上面的几个特殊位置：拐点以及HR为1的临界点。我们可以使用bootstrap的方法得到这些点的位置和95%的置信区间。我们只需要求得最小值的位置，就能知道拐点。由上图可知，HR为1的点有两个，我们可以通过预测风险比中，HR在某一点前后分别大于和小于1，确定这两个位置对应的两个点（即1个位置有2个点对应，一个HR大于1，一个HR小于1），然后求这两点的均值来获得。

我们先来看最初方程中的拐点以及HR为1的临界点的位置。

min_hr <- hr_full$age[which.min(hr_full$yhat)]
print(paste0("年龄拐点为 ", round(min_hr,1), " 岁"))

## [1] "年龄拐点为 57.1 岁"

hr_cutoff <- hr_full %>% 
  select(age, yhat) %>% 
  mutate(
    yhat_lag = lag(yhat),
    yhat_process = yhat-1,
    yhat_lag_process = yhat_lag-1,
    yhat_sign = yhat_process*yhat_lag_process
  ) 

cutoff_point <- c(
  mean(hr_full$age[which(hr_cutoff$yhat_sign<=0)[1]], hr_full$age[which(hr_cutoff$yhat_sign<=0)[1]-1]),
  mean(hr_full$age[which(hr_cutoff$yhat_sign<=0)[2]], hr_full$age[which(hr_cutoff$yhat_sign<=0)[2]-1])
)
  
print(paste0("HR=1时的年龄为 ", round(cutoff_point[1],1),"和", round(cutoff_point[2],1)," 岁"))

## [1] "HR=1时的年龄为 53和61.1 岁"

boot_func <- function(df){
  df_1 <- df %>% filter(etype==1) %>% sample_n(size=n(), replace=TRUE)
  df_2 <- df %>% filter(etype==2) %>% sample_n(size=n(), replace=TRUE)

  return(rbind(df_1, df_2))
}

point_func <- function(df, n=1000, seed=1){
  # 设置随机种子
  set.seed(seed)
  point_vec <- c()
  
  for (i in seq(n)){
    # 生成bootstrap数据框
    boot_df <- boot_func(df)
    
    # 构建方程
    coxph_boot <- cph(
      Surv(time, etype) ~ rcs(age,3) + sex,
      data = boot_df
    )

    # 预测风险比
    hr_boot <- rms::Predict(
      coxph_boot,
      age = seq(from=27, to=81, length.out=200), # 总样本的年龄范围为27-81
      fun = exp,
      ref.zero = TRUE
    )

    # 获取拐点及临界点
    min_hr <- hr_boot$age[which.min(hr_boot$yhat)]

    hr_cutoff <- hr_boot %>%
      select(age, yhat) %>%
      mutate(
        yhat_lag = lag(yhat),
        yhat_process = yhat-1,
        yhat_lag_process = yhat_lag-1,
        yhat_sign = yhat_process*yhat_lag_process
      )

    if (length(which(hr_cutoff$yhat_sign<=0))==1) {
      cutoff_point <- c(
      mean(hr_boot$age[which(hr_cutoff$yhat_sign<=0)[1]], hr_boot$age[which(hr_cutoff$yhat_sign<=0)[1]-1]),
      NA)
      cutoff_count <- 1
    } else if(length(which(hr_cutoff$yhat_sign<=0))==2){
      cutoff_point <- c(
      mean(hr_boot$age[which(hr_cutoff$yhat_sign<=0)[1]], hr_boot$age[which(hr_cutoff$yhat_sign<=0)[1]-1]),
      mean(hr_boot$age[which(hr_cutoff$yhat_sign<=0)[2]], hr_boot$age[which(hr_cutoff$yhat_sign<=0)[2]-1]))
      cutoff_count <- 2
    } else{
      cutoff_point <- NA
      cutoff_count <- 0
    }
    point_vec <- rbind(point_vec, c(min_hr, cutoff_point, cutoff_count))
  }
  return(point_vec)
}

point_boot <- point_func(df_colon, n=50) # 演示bootstrap 50次的结果

# 获取95%ci
apply(point_boot[point_boot[,4]==2,c(1,2,3)], MARGIN=2, FUN=function(x){quantile(x, probs=c(0.025, 0.975))})

##           [,1]     [,2]     [,3]
## 2.5%  52.29045 38.55980 61.19095
## 97.5% 61.13668 60.75678 61.84221

最后一个apply()函数依次列出了拐点、第一个临界点和第二个临界点的95%置信区间。

23.7 广义可加模型

有时，我们在对因变量进行分析时，有些自变量跟因变量之间呈现非线性关系，我们要做的只是控制这些非线性的自变量，并分析其它自变量跟因变量的线性关系，这可以通过广义可加模型实现，其原理就是在线性模型的基础上，声明哪些自变量是非线性的。mgcv包中的gam()函数可以实现这一功能。

library(mgcv)
df_heart <- read.csv("data/heart.csv")
df_heart$sex <- as.factor(df_heart$sex)

gam_heart <- gam(trestbps ~ s(age) + chol + sex, data=df_heart, family=gaussian)

summary(gam_heart)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## trestbps ~ s(age) + chol + sex
## 
## Parametric coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 127.37996    2.91055  43.765   <2e-16 ***
## chol          0.02177    0.01057   2.059   0.0397 *  
## sex1         -1.61445    1.16084  -1.391   0.1646    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##          edf Ref.df     F p-value    
## s(age) 4.378  5.452 16.32  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.096   Deviance explained = 10.2%
## GCV = 279.39  Scale est. = 277.38    n = 1025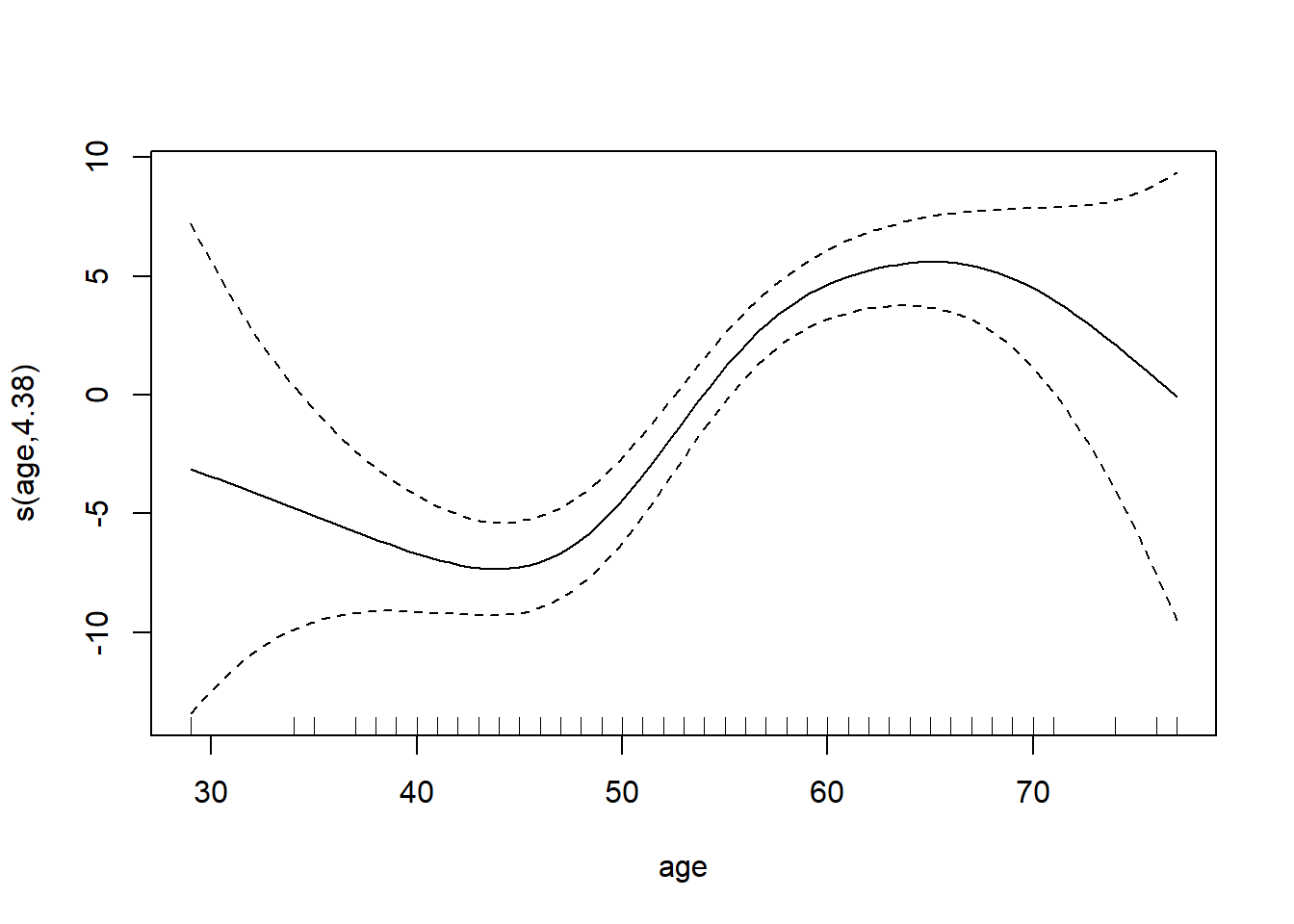

plot(gam_heart)

我们认为age变量与trestbps变量是非线性关联的，所以在构建方程时声明s(age)，结果也显示s(age)是显著的，说明age变量与trestbps变量是非线性关联的，这种关联可以使用plot(模型) 展示。如果s()项是非显著的，意味着此自变量跟因变量是线性关系，直接将此自变量放入线性模型中即可。

第23章 非参数回归模型