第22章 广义线性模型
22.1 概述
线性回归即分析因变量与自变量之间是否存在线性关系。传统的线性回归(即简单线性回归)需要假设因变量y为正态分布。但是在真实世界里,因变量y的分布可以是多样的,比如为伯努利分布、泊松分布、伽马分布等等,广义线性模型就是能将线性回归套用到各种y分布中的模型。
广义线性模型本质是原始数据中每个记录\(i\)的因变量\(y_i\)的分布可以用自然参数\(\theta_i\)来表示,而\(\theta_i\)经过特定函数(链接函数)转换后可以与自变量\(X_i\)存在线性关联。广义线性模型模型包含三个基本元素:系统成分(systematic component)(即自变量)、随机成分(random component)(即因变量)和链接函数(link function)。其中,系统成分是线性组合形式\(X\beta\);随机成分必须服从指数族分布,可以用自然参数\(\theta_i\)表示出来,比如正态分布中,\(\theta_i\)即为\(\mu_i\),因为当方差\(\sigma^2\)恒定的情况下,\(y_i\)的概率密度函数可以表示为\(f(y_i;\mu_i,\sigma) = \frac{1}{\sqrt{2\pi}\sigma}exp\{-\frac{(y_i-\mu_i)^2}{2\sigma^2}\}\), 伯努利分布中,\(\theta_i\)即为\(p_i\),因为\(y_i\)的概率密度函数可以表示为\(f(y_i;p_i) =p_{i}^{y_{i}}(1-p_{i})^{1-y{i}}\);链接函数则是需要推算出的包含\(\theta_i\)的函数部分。
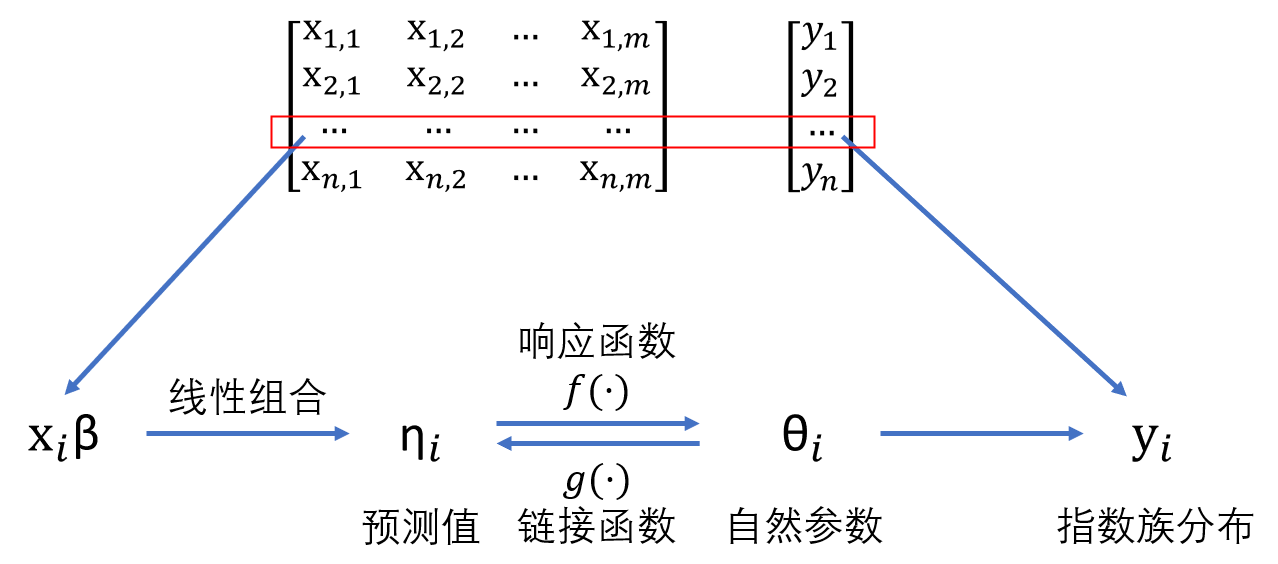
如果因变量服从指数族分布,则其分布公式可以写成:
\[\begin{align} f(y;\theta,\phi) = exp({\frac{y\theta-b(\theta)}{a(\phi)}+c(y,\phi)}) \tag{22.1} \end{align}\]在上述公式中,我们需要知道的是:
- \(\theta\)就是包含\(\theta_i\)的链接函数g(·)。
- 此分布的均值为\(E(y) = b^{'}(\theta)\),方差为\(Var(y) = b^{''}(\theta)a(\phi)\)。
22.2 简单线性回归
22.2.1 模型构建
使用简单线性回归的前提条件为:
- 线性相关(linearity):自变量(X)和因变量(Y)的关系可表示为\(Y = X\beta\),其中Y为n×1的列矩阵(n为样本量),X为n×(m+1)的矩阵(m为变量数目,1为截距项),\(\beta\)为(m+1)×1的列矩阵。
- 残差相互独立(independence):即各观测值残差的协方差为0,以\(\varepsilon_i\)表示第i个观测值的残差,则有\(\forall_{i\neq j}\ Cov(i,j)=0\)。
- 残差的方差恒定(homoscedasticity):即各观测值的残差不会随着自变量X的改变而发生一致性的变化(比如不会随着X的增大而增大),可以表示为\(\forall_{i \in n}\ Var(\varepsilon_i)=\sigma^2\)。
- 残差服从正态分布(Normality):可以表示为\(\forall_{i \in n}\ \varepsilon_i \overset{\mathrm{iid}}{\sim} N(0,\sigma^2)\)。通常来说,如果第4个条件满足,那么第2和第3个条件也会满足。
如果原始数据中的因变量服从正态分布,我们可以直接使用lm()函数进行简单线性回归分析,其中的参数设置为因变量~自变量1+自变量2+...,如果需要囊括除因变量以外的所有变量,可以设置为因变量~.。以darwin数据集为例,我们进行mean_gmrt1和mean_acc_in_air1变量的线性回归分析。
22.2.2 结果输出
在上例中,我们已经构建了一个名为lm1的简单线性回归模型,这个模型的输出格式为列表,包含12个元素,部分元素内容的截图如下:

我们可以使用模型$元素名称的方式调用感兴趣的元素内容(如通过ml1$residuals调用残差),或者使用summary()函数和broom包的tidy()函数查看模型的主要结果。
##
## Call:
## lm(formula = mean_gmrt1 ~ mean_acc_in_air1, data = df_darwin)
##
## Residuals:
## Min 1Q Median 3Q Max
## -183.77 -77.72 -27.78 48.01 572.42
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 196.78 13.94 14.117 < 2e-16 ***
## mean_acc_in_air1 125.61 24.71 5.084 9.58e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 124.1 on 172 degrees of freedom
## Multiple R-squared: 0.1306, Adjusted R-squared: 0.1256
## F-statistic: 25.85 on 1 and 172 DF, p-value: 9.578e-07## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 197. 13.9 14.1 1.51e-30
## 2 mean_acc_in_air1 126. 24.7 5.08 9.58e- 7## (Intercept) mean_acc_in_air1
## 196.7841 125.6117## 2.5 % 97.5 %
## (Intercept) 169.26879 224.2995
## mean_acc_in_air1 76.84351 174.379922.2.3 残差分析图
我们接着可以对残差进行可视化分析。
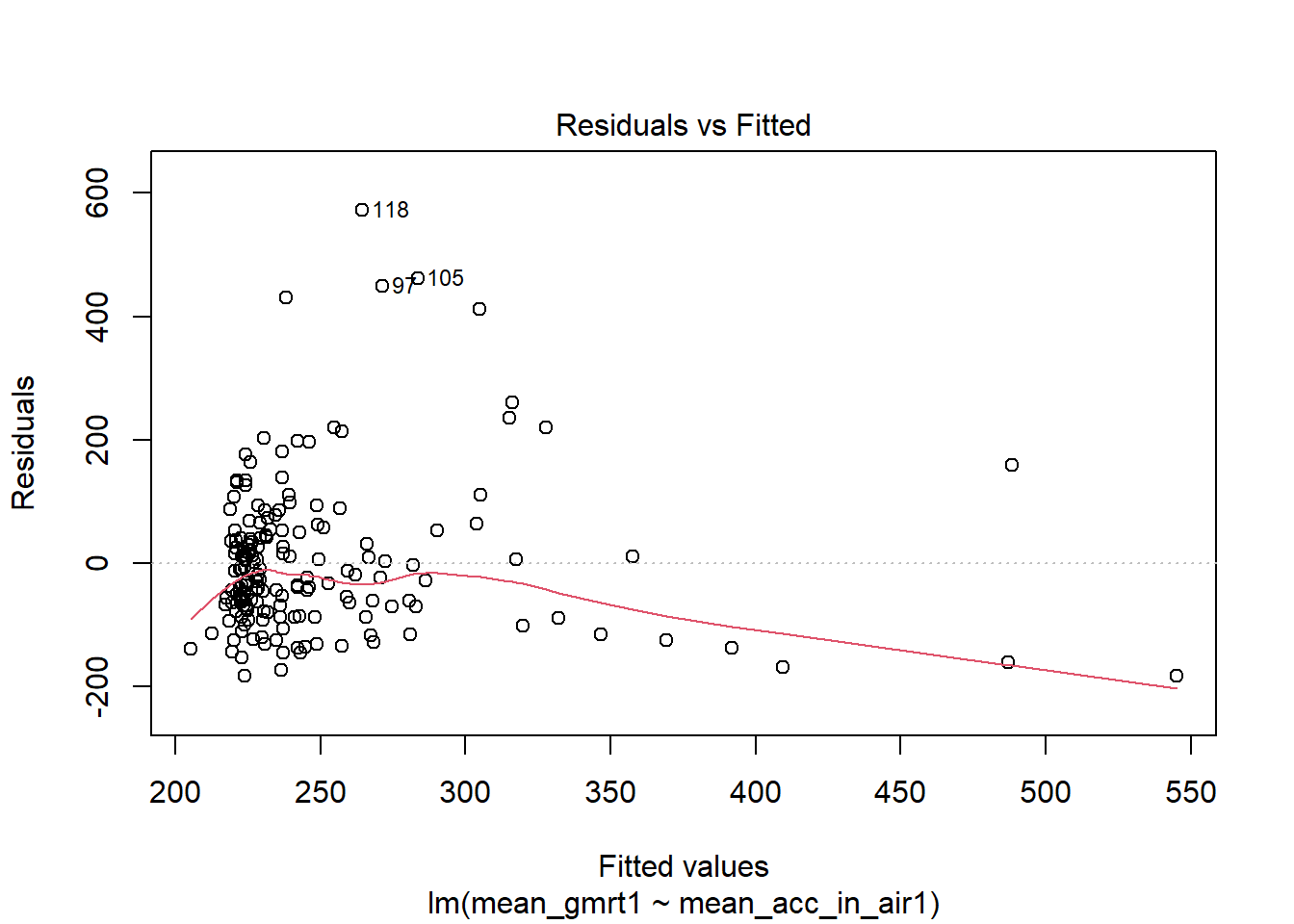
第一张图(Residuals vs Fitted),横轴为因变量Y的值,纵轴为残差。如果残差分布比较均匀,说明模型的误差是随机分布的(即符合Guaasian-Markov条件)。如果残差随着因变量的增加而增大(或减小)或者呈现二次曲线分布,提示原始数据可能并不是线性关系,这时可以有两种处理方式:方式1为先通过对数、指数或平方根等变换,然后再进行线性回归;方式2为选用加权线性回归的方法进行分析[小节22.3]。
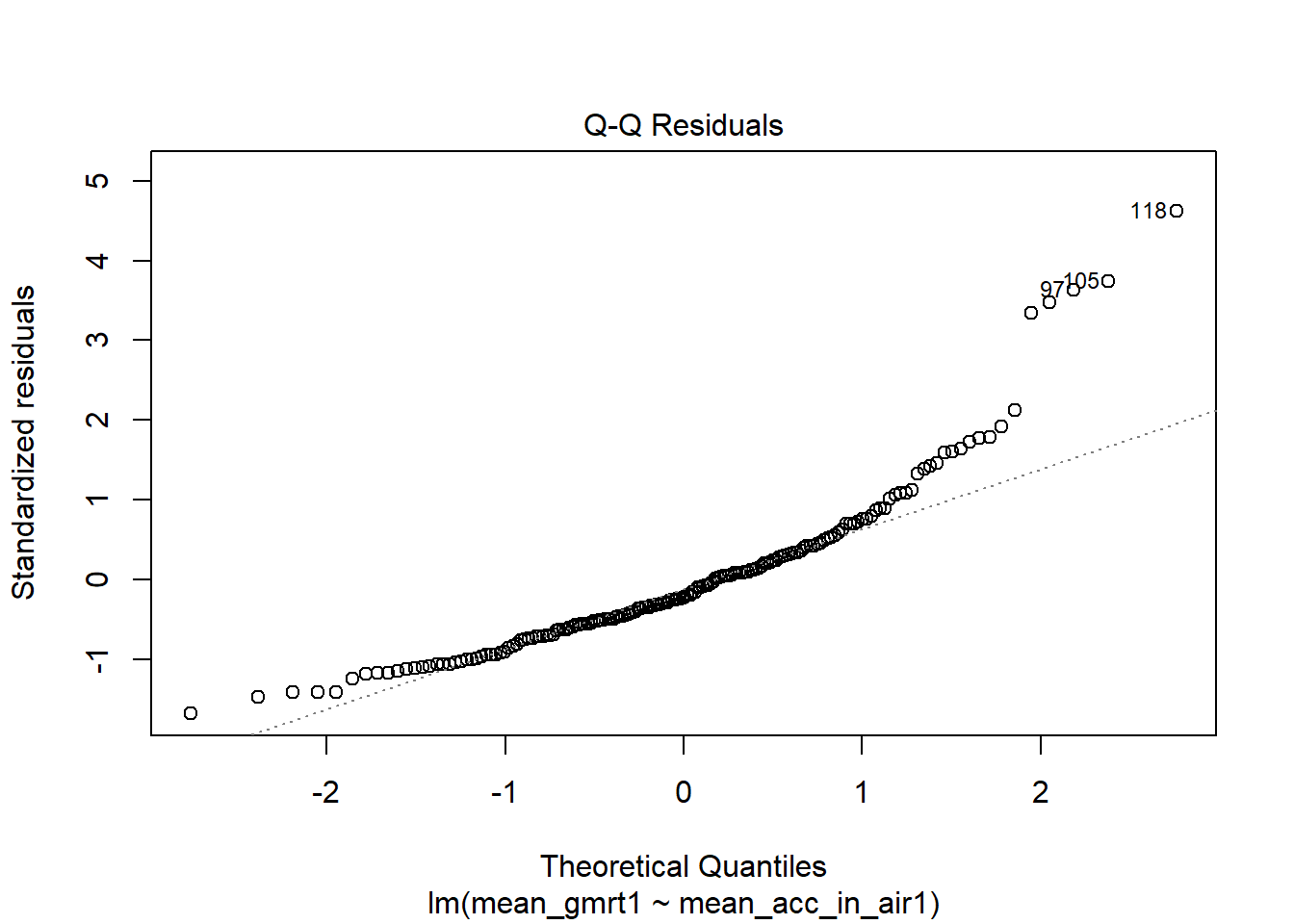
第二张图为Q-Q图,用于检验残差的正态分布情况[小节20.1]。
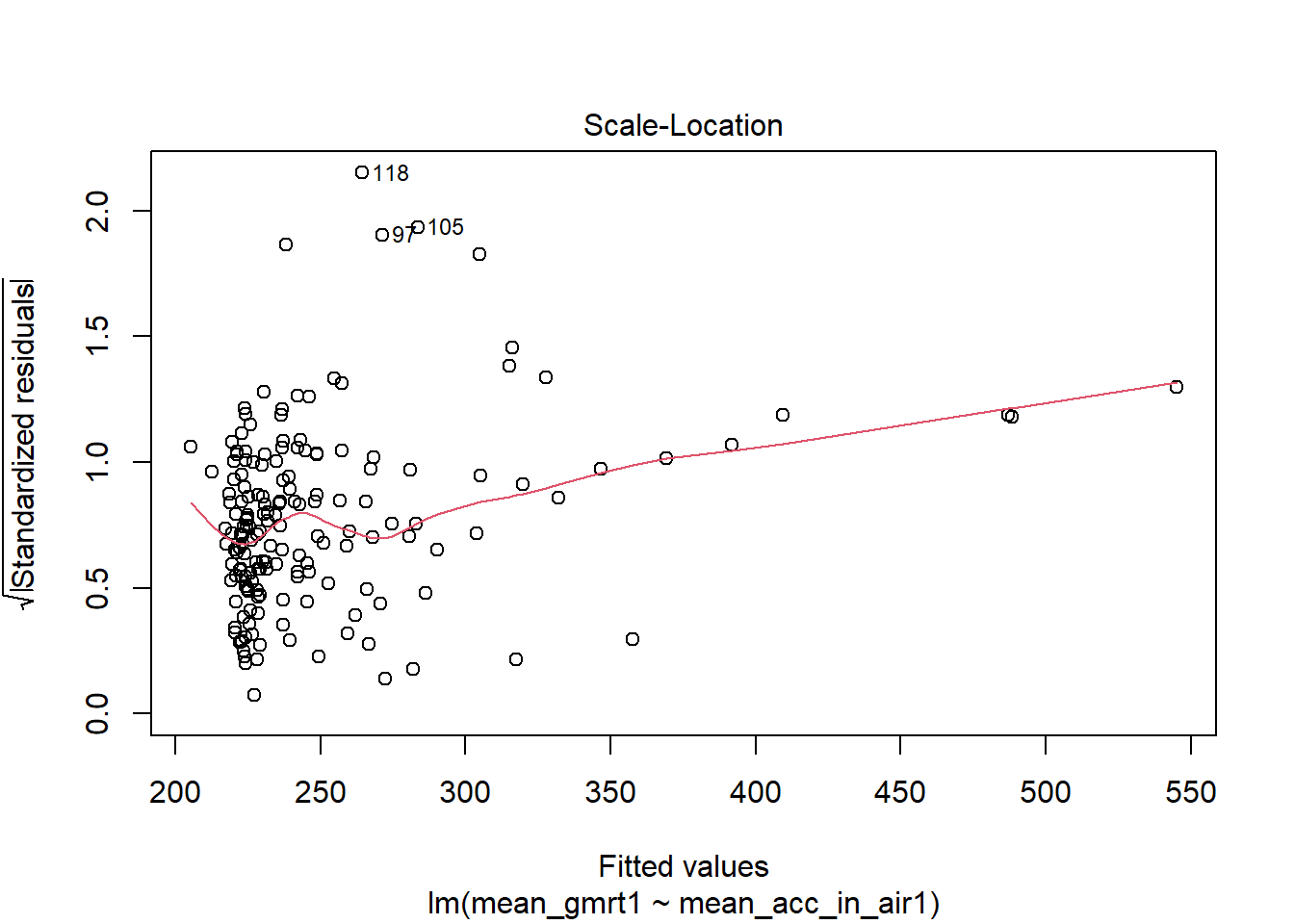
第三张图与第一张图类似,将残差进行了标准化处理,可以更好地观察残差的偏离情况。
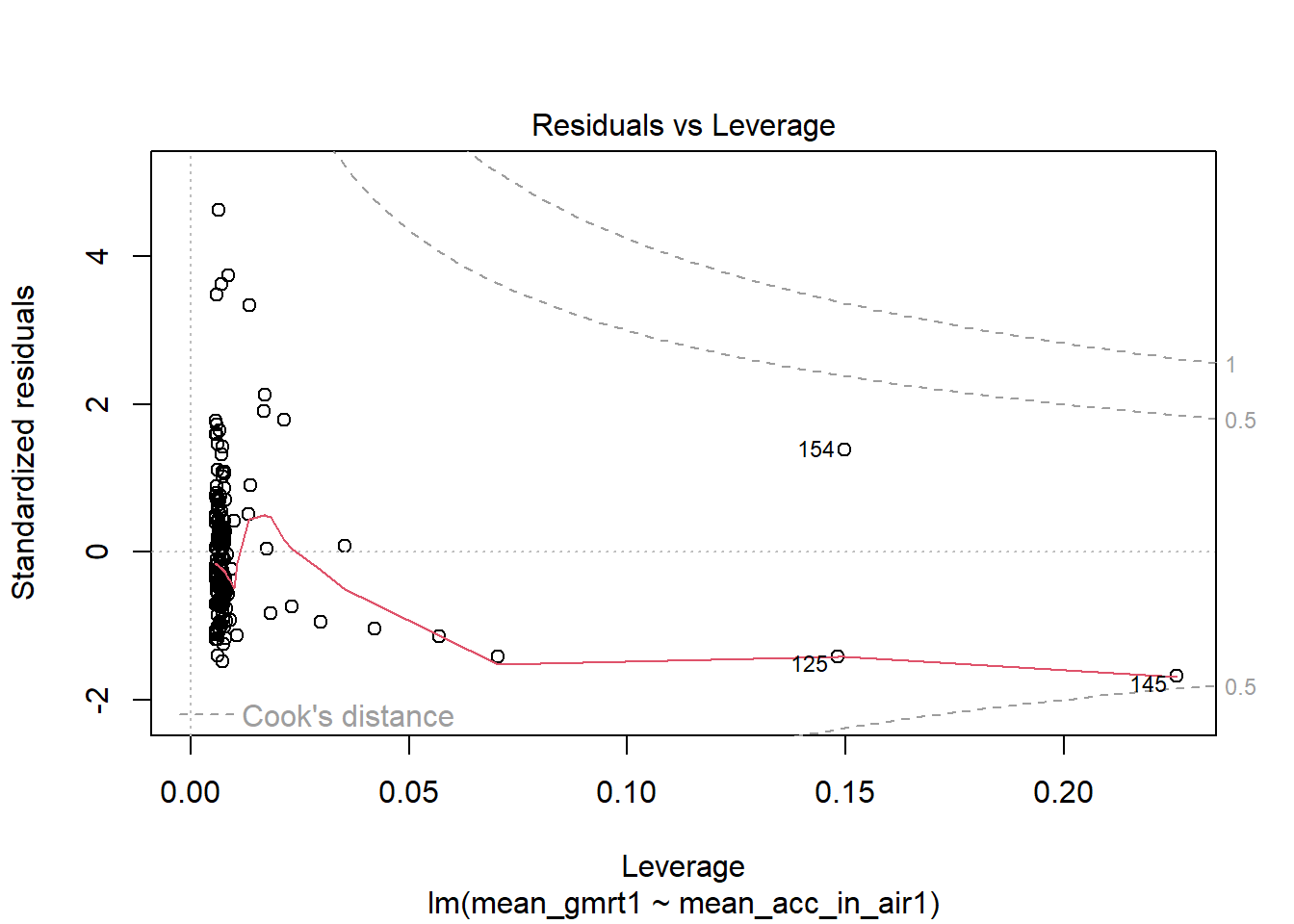
第四张图用于判断极端值。横轴为杠杆效力(leverage),指的是某个观测值对于回归模型的影响(即对决定系数\(R^2\)的影响)。杠杆效力越大,说明该观测值对回归模型的影响越强。纵轴为残差,用于表示模型与观测值的实际匹配程度,残差绝对值越大,说明模型预测值与实际观测值相差越远,提示该观测值有欠拟合的风险。杠杆效力与残差的阈值通常用Cook’s distance来判断(图中标注为虚线)。通常Cook’s distance的阈值为\(\frac{4}{n}\)(n为样本量)。当一个观测值有很强的杠杆效力同时残差绝对值也很大时,提示此观测值可能是极端值,会对模型的稳定性造成较大的影响,此时需要对此观测值进行检查,看是否存在数据录入错误或者其它造成该数据出现极端状况的因素。如果数据异常情况无法解释,可以考虑将异常值删除再重新建模。
第四张图中仅标注了Cook’s distance为0.5和1的情况,不足以辅助我们进行模型判断,此时我们可以使用cooks.distance()函数进行更详细的探索。
# 基于模型计算Cook's distance
cooksD_lm1 <- cooks.distance(model=lm1) # 返回一个数值向量
# 可视化Cook's distance
plot( # 对向量进行可视化,横轴为索引值,纵轴为数值
cooksD_lm1, # 目标向量
main = "Cook's distance" # 设置图片名称
)
abline(h=4/length(cooksD_lm1), lty=2, col="red") # 添加Cook's distance水平阈值线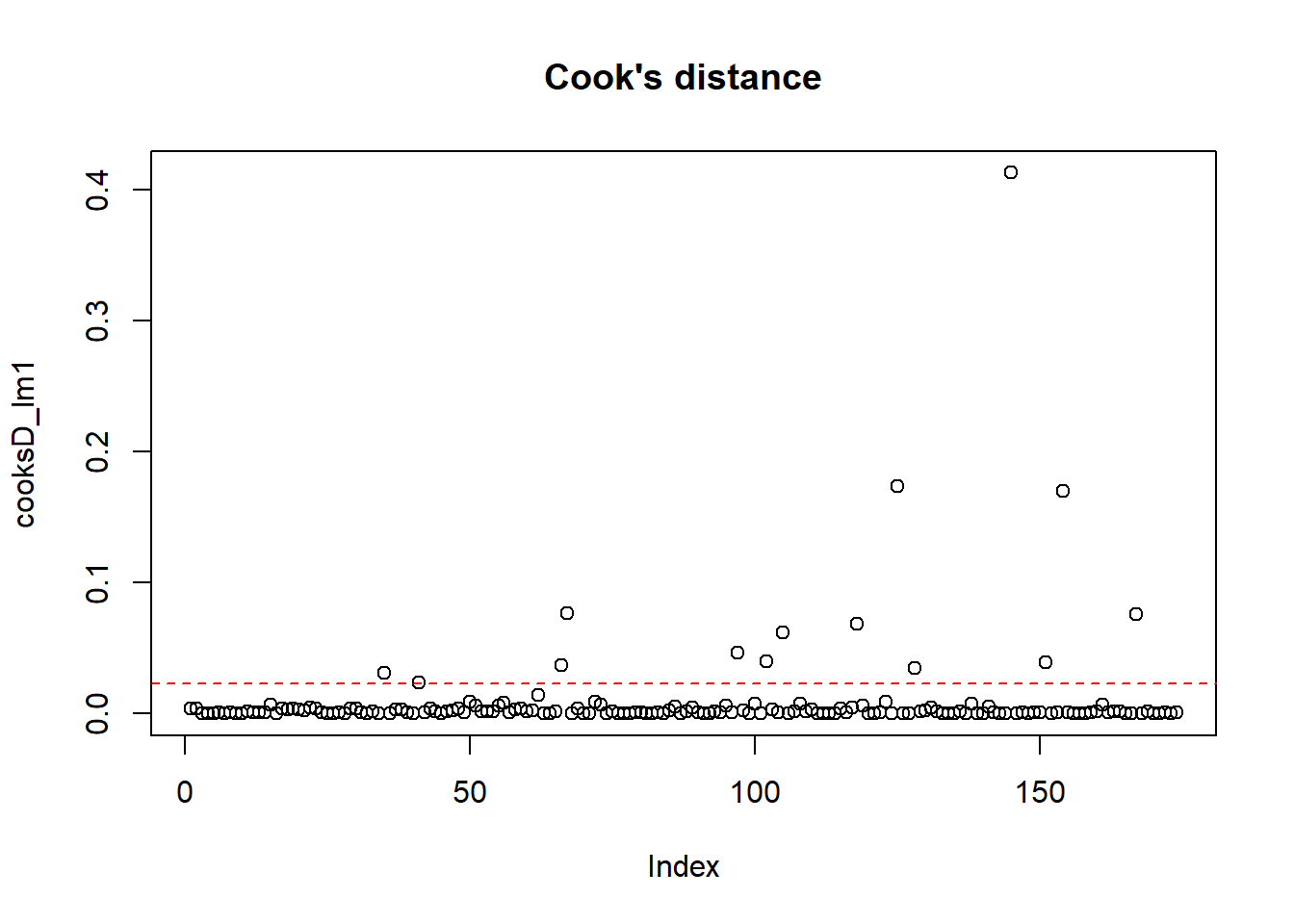
22.2.4 模型比较
有时我们需要构建多个回归模型并对这些模型进行比较,这时会遇到两种情况:
参与比较的模型是嵌套关系,比如模型A为
Y~X1,模型B为Y~X1+X2,模型C为Y~X1+X2+X3,我们可以使用anova()函数进行模型间的卡方比较(Chi-Square Comparison)。当P值显著时,选择自变量数目更多的模型;反之,选择自变量数目更少的模型。第二种情况为参与比较的模型是非嵌套关系,比如模型A为
Y~X1+X2,模型B为Y~X1+X3,模型C为Y~X4,我们可以综合考虑adj.r.squared、AIC和BIC指标,选择adj.r.squared值大、AIC和BIC值小的模型。需要指出的是,AIC的计算公式为\(AIC=-2*ln(L)+2*k\),BIC的计算公式为\(BIC=-2*ln(L)+ln(n)*k\),其中L为似然函数,n为样本量,k为自变量数目。相比AIC,BIC在样本量较大时(n≥100)对模型参数惩罚更大,导致BIC更倾向于选择参数少的简单模型。
22.2.4.1 嵌套模型比较
# 创建新模型(lm1的嵌套模型)
lm2 <- lm(mean_gmrt1~mean_acc_in_air1+max_x_extension1, data=df_darwin)
# 模型lm1与lm2的比较
anova(lm1, lm2)## Analysis of Variance Table
##
## Model 1: mean_gmrt1 ~ mean_acc_in_air1
## Model 2: mean_gmrt1 ~ mean_acc_in_air1 + max_x_extension1
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 172 2648354
## 2 171 2583537 1 64817 4.2901 0.03984 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 122.2.4.2 非嵌套模型比较
# 创建新模型(lm1的非嵌套模型)
lm3 <- lm(mean_gmrt1~max_x_extension1, data=df_darwin)
# 比较两个模型的AIC与BIC值
summary(lm1)##
## Call:
## lm(formula = mean_gmrt1 ~ mean_acc_in_air1, data = df_darwin)
##
## Residuals:
## Min 1Q Median 3Q Max
## -183.77 -77.72 -27.78 48.01 572.42
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 196.78 13.94 14.117 < 2e-16 ***
## mean_acc_in_air1 125.61 24.71 5.084 9.58e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 124.1 on 172 degrees of freedom
## Multiple R-squared: 0.1306, Adjusted R-squared: 0.1256
## F-statistic: 25.85 on 1 and 172 DF, p-value: 9.578e-07##
## Call:
## lm(formula = mean_gmrt1 ~ max_x_extension1, data = df_darwin)
##
## Residuals:
## Min 1Q Median 3Q Max
## -333.18 -83.69 -19.33 51.31 559.77
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 217.92774 15.48129 14.077 < 2e-16 ***
## max_x_extension1 0.01575 0.00602 2.617 0.00967 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 130.5 on 172 degrees of freedom
## Multiple R-squared: 0.03829, Adjusted R-squared: 0.03269
## F-statistic: 6.847 on 1 and 172 DF, p-value: 0.009668## [[1]]
## [1] 2175.479
##
## [[2]]
## [1] 2193.047## [[1]]
## [1] 2184.956
##
## [[2]]
## [1] 2202.52422.2.5 模型预测
当我们需要使用构建的模型对新数据进行预测时,可以使用predict()函数。
# 新数据的格式需要与模型创建时的数据格式一致
df_newdata <- data.frame( # 创建新两个观测值,变量名称必须与模型构建数据的变量名一致
mean_acc_in_air1 = c(99, 100),
max_x_extension1 = c(1500, 1700)
)
# 进行预测
predict(object=lm2, newdata=df_newdata)## 1 2
## 11910.46 12031.1822.2.7 多重共线性检验
当模型中包含多个自变量时,我们需要对自变量进行多重共线性检验,以保证自变量间的相互独立。这个检验可以通过car包的vif()函数实现。
# 加载包
library(car)
# 构建多元线性回归模型
lm_full <- df_darwin %>%
select(ends_with("1")) %>%
lm(formula = mean_gmrt1 ~.)
# 多重共线性检验
vif(lm_full)## air_time1 gmrt_in_air1 max_x_extension1 max_y_extension1 mean_acc_in_air1
## 1.187575 1.325397 1.110168 1.061823 1.194585通常认为,当VIF>10时,对应自变量存在多重共线性问题,需要被删除。
22.3 加权线性回归
当某些观测值异常,导致残差不呈正态分布时,可以考虑对观测值添加不同的权重,降低异常值对残差的影响,使得线性模型更加拟合。其本质是在原有的最小二乘法基础上给每个观测值添加一个权重\(w_{i}\),使得\(\frac{1}{N}\sum\limits_{i=1}^{N}w_{i}(y_{i}-\beta x_{i})^2\)最小。权重\(w_{i}\)的赋值方式可以有以下两种情况:
下面我们以heart数据集中的age,sex和trestbps为自变量,chol为因变量进行演示。
# 读取数据
df_heart <- read_csv("data/heart.csv", col_select=c("age","sex","trestbps","chol"))
df_heart <- df_heart %>%
mutate(sex=as.factor(sex))
#### 以分类变量sex构建权重 ####
sex_weight <- df_heart %>%
group_by(sex) %>% # 按sex分组
summarise(var(chol)) # 计算方差
# 将权重加入原数据框
df_heart_sw <- df_heart %>%
mutate(
weight = case_when(
sex == "0" ~ 1/as.numeric(sex_weight[1,2]), # 注意此处为方差的倒数
sex == "1" ~ 1/as.numeric(sex_weight[2,2]),
)
)
# 构建加权线性模型
chol_wls_sex <- lm(chol~., weights=weight, data=df_heart_sw)
# 查看模型
summary(chol_wls_sex)##
## Call:
## lm(formula = chol ~ ., data = df_heart_sw, weights = weight)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -2.7631 -0.6774 -0.0896 0.6035 4.5735
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 187.76702 13.49851 13.910 < 2e-16 ***
## age 0.94979 0.16767 5.665 1.91e-08 ***
## sex1 -19.82182 3.93122 -5.042 5.44e-07 ***
## trestbps 0.15439 0.08828 1.749 0.0806 .
## weight NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9804 on 1021 degrees of freedom
## Multiple R-squared: 0.06884, Adjusted R-squared: 0.0661
## F-statistic: 25.16 on 3 and 1021 DF, p-value: 1.043e-15#### 以连续变量trestbps构建权重 ####
# 遍历次方项
weight_residual <- function(n){
# 添加权重
df_new <- df_heart %>%
mutate(weight = 1/trestbps**n)
# 构建加权模型
chol_wls <- lm(chol~., weights=weight, data=df_new)
# 获取残差平方和
return(sum(chol_wls$residuals)**2)
}
order_list <- seq(from=1, to=5, by=0.5)
residual_list <- c()
for (n in order_list){
residual_list <- c(residual_list, weight_residual(n))
}
# 选择最佳次方项
opt_order <- order_list[which.min(residual_list)] # 1
# 将权重加入原数据
df_heart_tw <- df_heart %>%
mutate(weight = 1/trestbps**opt_order)
# 构建加权线性模型
chol_wls_trestbps <- lm(chol~., weights=weight, data=df_heart_tw)
# 查看模型
summary(chol_wls_trestbps)##
## Call:
## lm(formula = chol ~ ., data = df_heart_tw, weights = weight)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -11.7682 -3.0127 -0.3242 2.4188 27.4165
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 274.0369 130.0201 2.108 0.0353 *
## age 1.1271 0.1764 6.390 2.52e-10 ***
## sex1 -18.6964 3.4014 -5.497 4.89e-08 ***
## trestbps -0.1932 0.4966 -0.389 0.6974
## weight -6594.9717 8454.8562 -0.780 0.4356
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.353 on 1020 degrees of freedom
## Multiple R-squared: 0.08406, Adjusted R-squared: 0.08047
## F-statistic: 23.4 on 4 and 1020 DF, p-value: < 2.2e-16以上就是如果进行加权线性回归的方法。在实际应用中,选择哪个变量进行权重计算,具体需要将残差与对应的自变量进行散点图可视化,看在哪个自变量的情况下,残差的分布最不恒定,便选择该自变量进行权重计算。
22.4 Logistic回归
22.4.1 二分类的Logistic回归
22.4.1.1 模型构建
当每个记录的因变量\(y_i\)呈现伯努利分布(\(y_i\sim bern(p_i)\)),\(p_i\)为事件发生概率。如果我们按照公式(22.1)的形式进行转换,将有如下结果:
\(\begin{align} f(y_i;p_i) &= p_{i}^{y_{i}} (1-p_i)^{1-y_i}\\ &= exp{[ln(p_{i}^{y_{i}} (1-p_i)^{1-y_i})]}\\ &= exp{(y_i ln\frac{p_i}{1-p_i} + ln(1-p_i))} \end{align}\)
通过上面的公式,我们可以发现,链接函数为\(\theta_{i} = ln\frac{p_i}{1-p_i}\),进而可以推出\(p_i = \frac{e^{\theta_i}}{1+e^{\theta_i}}\)。
下面我们就能利用最大似然估计(maximum likelihood estimation)来进行参数估计,具体步骤为:
- 写出边缘概率质量函数(marginal pmf)。
- 写出联合概率质量函数(joint pmf)。
- 写出包含参数的似然方程。
- 写出包含参数的log转换似然方程。
- 求第4步方程最大值时的参数。
在Logistic回归中,我们来看一下参数是如何估计的。
- 由于每个记录的因变量\(y_i\)呈现伯努利分布(\(y_i\sim bern(p_i)\)),因此该因变量的边缘概率质量函数为\(f(y_i;p_i) = p_{i}^{y_{i}} (1-p_i)^{1-y_i}\)
- 样本量为n时的联合概率质量函数为\(F(y_i;p_i) = \prod\limits_{i=1}^{n}p_{i}^{y_{i}} (1-p_i)^{1-y_i}\)
- 由于\(X_i\beta = \theta_{i} = ln\frac{p_i}{1-p_i}\),将\(p_i\)用\(\theta_{i}\)替代可得包含参数的似然方程为\(L(y_i;\theta_{i}) = \prod\limits_{i=1}^{n} (\frac{1}{1+e^{-\theta_i}})^{y_i}(\frac{1}{1+e^{\theta_i}})^{1-y_i}\)
- log转换似然方程为\(LL(y_{i};\theta_{i}) = \sum\limits_{i=1}^{n}(y_{i}\theta_{i}-ln(1+e^{\theta_{i}}))\)
- 求第4步方程关于\(\beta\)的偏导数,得出参数值。
在R中,可以使用glm()函数并声明family=binomial(link="logit")参数进行Logistic回归分析。我们继续以UCI心脏病数据集为例,分析age(年龄),sex(性别),chol(胆固醇),exang(运动诱发心绞痛)与target(心脏病)的关系。
22.4.1.2 结果输出
构建完logistic回归模型后,我们可以通过summary()函数查看模型的主要参数或使用coef()函数查看特定变量的系数。如果需要计算特定变量改变对比值比(OR)的影响,还需要在coef()函数的基础上添加exp()自然指数函数。
##
## Call:
## glm(formula = target ~ age + sex + chol + exang, family = binomial(link = "logit"),
## data = df_heart)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 6.599456 0.653895 10.093 < 2e-16 ***
## age -0.065606 0.009012 -7.280 3.34e-13 ***
## sex1 -1.634551 0.181844 -8.989 < 2e-16 ***
## chol -0.004717 0.001497 -3.151 0.00162 **
## exang1 -2.031718 0.169163 -12.010 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1420.2 on 1024 degrees of freedom
## Residual deviance: 1074.4 on 1020 degrees of freedom
## AIC: 1084.4
##
## Number of Fisher Scoring iterations: 4## age
## -0.06560621## age
## 0.936499622.4.1.3 设置参照水平
R默认将分类变量的第一个水平当做参照,如果想更改参照水平,可以使用relevel()函数声明参数ref来设置参照水平,注意此时声明的参数需要时分类变量的水平标签。
# 将sex的参照水平改为"1"
df_heart$sex <- relevel(
df_heart$sex,
ref = "1"
)
# 构建logistic回归方程
heart_lr_ref <- glm(
formula = target ~ age + sex + chol + exang,
data = df_heart,
family = "binomial"
)
summary(heart_lr_ref)##
## Call:
## glm(formula = target ~ age + sex + chol + exang, family = "binomial",
## data = df_heart)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.964905 0.577910 8.591 < 2e-16 ***
## age -0.065606 0.009012 -7.280 3.34e-13 ***
## sex0 1.634551 0.181844 8.989 < 2e-16 ***
## chol -0.004717 0.001497 -3.151 0.00162 **
## exang1 -2.031718 0.169163 -12.010 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1420.2 on 1024 degrees of freedom
## Residual deviance: 1074.4 on 1020 degrees of freedom
## AIC: 1084.4
##
## Number of Fisher Scoring iterations: 422.4.1.4 模型预测
我们可以使用predict()函数进行模型预测,需要注意的是,计算结果默认返回为线性模型(即\(X\beta\)部分)的计算结果。如果想要获取患病的概率,需要声明参数type="response"。
# 构建新数据,格式需要与模型创建时的数据格式一致
df_newdata <- data.frame(
age = 60,
sex = "1", # 注意:如果变量为分类变量,此时的输入数据类型应当为字符型,否则会报错;如果原始变量对应标签,则需输入标签
chol = 250,
exang = "0" # 注意:如果变量为分类变量,此时的输入数据类型应当为字符型,否则会报错
)
# predict()函数预测值,logistic回归中返回logit值
predict(object=heart_lr, newdata=df_newdata)## 1
## -0.1506097# predict(type="response")函数预测值,logistic回归中返回概率值
predict(object=heart_lr, newdata=df_newdata, type="response")## 1
## 0.462418622.4.1.5 模型检验
我们可以通过拟合优度(goodness of fit)检验或过度离势(overdispersion)检验。
我们可以通过偏差残差(residual deviance)的自由度为n-m+1(n为样本量,m为变量数目)的卡方分布概率进行判断,当P>0.05时,说明拟合良好;反之,则拟合不良。
如果方差\(Var(y)\)大于期望值\(E(y)\)[小节22.1],则有过度离势的风险,也就是说预测值与实际值存在偏差过大的风险。过度离势检验可以通过残差偏差与残差自由度的比值进行判断:当比值接近1时,说明不存在过度离势,模型可以给出较好地预测结果;若比值偏离1过多,说明存在过度离势。
当拟合不良或者存在过度离势风险时,可以进行调整的方法有:
- 使用类二项分布,即声明
family=quasibinomial(link="logit")。 - 检查是否有离群值。
- 调整变量数目,构建新模型。
## [1] 0.8846252## [1] 1.05333622.4.2 多分类的Logistic回归
22.4.2.1 模型构建
当因变量包含多个水平且这些水平之间没有顺序之分,我们可以使用nnet包的multinom()函数进行多分类的Logistic回归。依旧以UCI心脏病数据集为例,分析age(年龄),sex(性别),chol(胆固醇),exang(运动诱发心绞痛)与slope(心电图ST段的抬高、水平或下降)的关联。
library(nnet)
df_heart$slope <- factor(
df_heart$slope,
levels = c(0,1,2), # 声明变量水平
labels = c("upsloping", "flat", "downsloping") # 声明变量水平对应的标签
)
df_heart$slope <- relevel(
df_heart$slope,
ref = "flat" # 设置参照水平
)
heart_multinorm <- multinom(
formula = slope ~ age + sex + chol + exang,
data = df_heart
)## # weights: 18 (10 variable)
## initial value 1126.077596
## iter 10 value 868.786660
## final value 860.912099
## converged22.4.2.2 结果输出
## Call:
## multinom(formula = slope ~ age + sex + chol + exang, data = df_heart)
##
## Coefficients:
## (Intercept) age sex0 chol exang1
## upsloping -0.6764409 -0.001693713 -0.3395789 -0.0040698972 -0.04503808
## downsloping 2.5966568 -0.041799508 -0.1145905 0.0004102111 -1.32626176
##
## Std. Errors:
## (Intercept) age sex0 chol exang1
## upsloping 0.9584007 0.01461531 0.3025586 0.002703241 0.2557647
## downsloping 0.4917123 0.00795408 0.1535345 0.001375784 0.1540684
##
## Residual Deviance: 1721.824
## AIC: 1741.824## , , upsloping
##
## 2.5 % 97.5 %
## (Intercept) -2.554871792 1.201989959
## age -0.030339187 0.026951760
## sex0 -0.932582868 0.253425157
## chol -0.009368153 0.001228358
## exang1 -0.546327751 0.456251595
##
## , , downsloping
##
## 2.5 % 97.5 %
## (Intercept) 1.632918421 3.560395168
## age -0.057389217 -0.026209798
## sex0 -0.415512652 0.186331709
## chol -0.002286277 0.003106699
## exang1 -1.628230241 -1.024293282注意,此时的结果没有输出P值,所以我们需要通过t值计算
# 计算t值
t <- summary(heart_multinorm)$coefficients / summary(heart_multinorm)$standard.errors
# 计算P值
p <- pnorm(abs(t), mean=0, sd=1, lower.tail=FALSE) * 2
# 呈现P值
p## (Intercept) age sex0 chol exang1
## upsloping 4.803114e-01 9.077427e-01 0.2617106 0.1321797 8.602218e-01
## downsloping 1.285888e-07 1.479416e-07 0.4554562 0.7655770 7.417336e-18我们可以看到,以slope变量的flat水平为参照时,upsloping水平与age变量显著相关,downsloping水平与age和exang变量显著相关。
22.4.2.3 模型预测
参照上例,多分类的Logistic回归公式为:
\(ln(\frac{P(upsloping)}{P(flat)}) = Intercept_{1} + \beta_{age_{1}}*age + \beta_{sex0_{1}}*sex + \beta_{chol_{1}}*chol + \beta_{exang1_{1}}*exang\)
\(ln(\frac{P(downsloping)}{P(flat)}) = Intercept_{2} + \beta_{age_{2}}*age + \beta_{sex0_{2}}*sex + \beta_{chol_{2}}*chol + \beta_{exang1_{2}}*exang\)
这里我们可以得到在对应数据下,各个水平的概率比:
\(P(upsloping) = e^{Intercept_{1} + \beta_{age_{1}}*age + \beta_{sex0_{1}}*sex + \beta_{chol_{1}}*chol + \beta_{exang1_{1}}*exang} \ P(flat)\)
\(P(downsloping) = e^{Intercept_{2} + \beta_{age_{2}}*age + \beta_{sex0_{2}}*sex + \beta_{chol_{2}}*chol + \beta_{exang1_{2}}*exang} \ P(flat)\)
由于\(P(flat) + P(upsloping) + P(downsloping) = 1\),可以求出各个水平的概率。在R中,我们可以通过声明predict()函数的type="probs"参数得到各个水平的概率。
# 构建新数据,格式需要与模型创建时的数据格式一致
df_newdata <- data.frame(
age = c(60,60),
sex = c("1","0"),
chol = c(250,250),
exang = c("0","0")
)
# 获得各个水平的概率
predict(
object = heart_multinorm,
newdata = df_newdata,
type = "probs"
)## flat upsloping downsloping
## 1 0.4207361 0.06985821 0.5094057
## 2 0.4549811 0.05379277 0.491226122.4.3 有序分类的Logistic回归
22.4.3.1 模型构建
如果一个因变量包含多个水平且这些水平是有序的(如某疾病的I期、II期和III期,疗效的好、中和差),我们就需采用有序分类的Logistic回归。其原理是将各个水平按顺序依次分割为二元Logistic回归,比如疾病三期分期的分析时,需要拆分为I期与(II、III)期的Logistic回归以及(I、II)期与III期的Logistic回归。
有序分类的Logistic回归的前提假设为,在拆分的多个二分类Logistic回归中,除了截距不同,自变量的系数均相等,也即假定自变量在多个模型中对累计概率的比值比影响相同(比例优势假设)。
有序分类的Logistic回归有多种计算公式,在R中,用\(i\)表示分类变量的第\(i\)个水平,该Logistic回归的公式为:
\(\begin{align} logit[P(Y \leq i|X)] &= ln[\frac{P(Y \leq i|X)}{1-P(Y \leq i|X)}]\\ &= \beta_{0i} - (X_{1}\beta_{1} + X_{2}\beta_{2} ...) \end{align}\)
分类变量的第\(i\)个水平的概率为:
\(\begin{align} P(Y = i|X) &= P(Y \leq i|X) - P(Y \leq i-1|X)\\ &= \frac{1}{1+e^{-(\beta_{0i} - (X_{1}\beta_{1} + X_{2}\beta_{2} ...))}} - \frac{1}{1+e^{-(\beta_{0i-1} - (X_{1}\beta_{1} + X_{2}\beta_{2} ...))}} \end{align}\)
使用有序分类的Logistic回归时,需要满足以下条件:
- 只有一个因变量且因变量水平为有序水平
- 模型包含至少一个自变量。
- 因变量的观察结果相互独立。
- 自变量之间无多重共线性。
- 满足平行线检验(即比例优势假设),即不同因变量水平的自变量系数相等;如果不满足此检验,则可采用多分类的Logistic回归[小节22.4.2]。
依旧以UCI心脏病数据集为例,分析age(年龄),sex(性别),chol(胆固醇),exang(运动诱发心绞痛)与restecg(安静心电图等级0-2)的关联。需要用到MASS包的polr()函数进行建模,brant包的brant()函数进行平行线检验。
# 加载包
library(MASS)
df_heart$restecg <- factor(
df_heart$restecg,
levels = c(0,1,2), # 声明变量水平
labels = c("normal", "abnormal", "definite") # 声明变量水平对应的标签
)
# 构建有序分类的Logistic回归
heart_lr_ordered <- polr(
formula = ordered(restecg) ~ age + sex + chol + exang,
data = df_heart,
Hess = TRUE,
method = "logistic"
)22.4.3.2 结果输出
## Call:
## polr(formula = ordered(restecg) ~ age + sex + chol + exang, data = df_heart,
## Hess = TRUE, method = "logistic")
##
## Coefficients:
## Value Std. Error t value
## age -0.026495 0.007290 -3.635
## sex0 0.357080 0.144737 2.467
## chol -0.005977 0.001358 -4.400
## exang1 -0.171215 0.137261 -1.247
##
## Intercepts:
## Value Std. Error t value
## normal|abnormal -2.9196 0.4675 -6.2450
## abnormal|definite 1.4521 0.5134 2.8283
##
## Residual Deviance: 1507.732
## AIC: 1519.732## 2.5 % 97.5 %
## age -0.040862635 -0.012277577
## sex0 0.074248137 0.641960508
## chol -0.008661442 -0.003359093
## exang1 -0.440539053 0.097790937# 整合OR值与95%置信区间
cbind(
OR=exp(coef(heart_lr_ordered)), # 将系数进行自然指数转换并将结果命名为OR
exp(confint(heart_lr_ordered))
)## OR 2.5 % 97.5 %
## age 0.9738525 0.9599610 0.9877975
## sex0 1.4291503 1.0770740 1.9002026
## chol 0.9940408 0.9913760 0.9966465
## exang1 0.8426406 0.6436893 1.1027322对于上述结果,对于连续变量age,我们可以解读为,在其余变量不变的情况下,年龄每增加1年,在restecg任何水平中观察到对应事件的概率都比原先下降了2.6%;对于分类变量sex,我们可以解读为,在其余变量不变的情况下,在restecg任何水平中,女性发生对应事件的概率都是男性的1.43倍。
此时的结果没有输出P值,所以我们需要通过t值计算
# 获取系数
coef_table <- coef(summary(heart_lr_ordered))
# 计算P值
p <- pnorm(abs(coef_table[, "t value"]), mean=0, sd=1, lower.tail=FALSE) * 2
# 整合P值
cbind(coef_table, p)## Value Std. Error t value p
## age -0.026495472 0.007289554 -3.634718 2.782853e-04
## sex0 0.357080067 0.144737369 2.467090 1.362162e-02
## chol -0.005977034 0.001358487 -4.399773 1.083641e-05
## exang1 -0.171214742 0.137261230 -1.247364 2.122640e-01
## normal|abnormal -2.919643828 0.467520446 -6.244954 4.239240e-10
## abnormal|definite 1.452055475 0.513406107 2.828279 4.679907e-0322.4.3.3 共线性检验
## age sex0 chol exang1 normal|abnormal
## 40.166490 1.536197 28.508204 1.559544 54.099268
## abnormal|definite
## 3.932806结果显示,变量间无共线性。
22.4.3.4 平行线检验
## --------------------------------------------
## Test for X2 df probability
## --------------------------------------------
## Omnibus 25.52 4 0
## age 7.93 1 0
## sex0 7.22 1 0.01
## chol 3.05 1 0.08
## exang1 6.56 1 0.01
## --------------------------------------------
##
## H0: Parallel Regression Assumption holds结果显示,自变量中存在P<0.05的情况,所以本例倾向用多分类的Logistic回归分析。(由于没有找到合适的例子,我们先勉强分析下去)
22.4.3.5 模型预测
# 构建新数据,格式需要与模型创建时的数据格式一致
df_newdata <- data.frame(
age = c(60,60),
sex = c("1","0"),
chol = c(250,250),
exang = c("0","0")
)
# 获得各个水平的概率
predict(
object = heart_lr_ordered,
newdata = df_newdata,
type = "probs"
)## normal abnormal definite
## 1 0.5409935 0.4484044 0.01060212
## 2 0.4519643 0.5329523 0.01508340各水平概率的计算方法为:
\(P(y=normal) = \frac{1}{1+e^{-(Intercept_{(normal|abnormal)}-(\beta_{age_{1}}*age + \beta_{sex0_{1}}*sex + \beta_{chol_{1}}*chol + \beta_{exang1_{1}}*exang))}}\)
\(P(y=abnormal) = \frac{1}{1+e^{-(Intercept_{(abnormal|definite)}-(\beta_{age_{1}}*age + \beta_{sex0_{1}}*sex + \beta_{chol_{1}}*chol + \beta_{exang1_{1}}*exang))}} - P(y=normal)\)
\(P(y=definite) = 1 - P(y=normal) - P(y=abnormal)\)
22.4.4 条件Logistic回归
在观察性研究中,我们有时会将具有特定属性的观察对象(病例组)与没有该条件的对象(对照组)按照1:n的比例匹配,此时如果采用二分类的Logistic回归分析,会高估OR值,因此需要选用条件Logistic回归。在R中可以用survival包的clogit()函数实现,其模型构建与其它Logistic回归类似,只是需要额外使用strata()声明分层变量。我们来看下面的例子,为了分析某治疗方案的治疗效果,我们将病人按照种族和年龄以1:3的比例匹配对照组,利用所得数据进行分析。
# 加载包
library(survival)
set.seed(1)
# 创建数据框
df_condition <- data.frame(
ID = rep(1:100, each=4),
race = rep(c("A","B","C","D"), each=100),
treatment = rep(c(1,0,0,0), time=100),
age = rep(round(rnorm(n=100, mean=75, sd=6)), each=4),
case = sample(c(0,1), size=400, replace=TRUE)
)
# 设置分类变量
df_condition$treatment <- factor(df_condition$treatment)
df_condition$race <- factor(df_condition$race)
# 构建模型
condition_logit <- clogit(
formula = case ~ treatment + strata(ID),
data = df_condition
)
# 查看结果
summary(condition_logit)## Call:
## coxph(formula = Surv(rep(1, 400L), case) ~ treatment + strata(ID),
## data = df_condition, method = "exact")
##
## n= 400, number of events= 194
##
## coef exp(coef) se(coef) z Pr(>|z|)
## treatment1 0.08395 1.08757 0.23666 0.355 0.723
##
## exp(coef) exp(-coef) lower .95 upper .95
## treatment1 1.088 0.9195 0.6839 1.729
##
## Concordance= 0.51 (se = 0.036 )
## Likelihood ratio test= 0.13 on 1 df, p=0.7
## Wald test = 0.13 on 1 df, p=0.7
## Score (logrank) test = 0.13 on 1 df, p=0.722.5 泊松分布
22.5.1 模型构建
当因变量为特定时间段的离散型的计数(如每周某疾病的发病数、每天特定时刻的车流量)时,我们通常认为其符合泊松分布。根据之前关于链接函数的推导,我们很容就知道,泊松分布的链接函数为log()。此时需要在glm()函数中声明参数poisson(link = "log")。在下面的例子中,我们来分析age和treatment与一段时间内某疾病发生例数count的关联。
set.seed(1)
# 创建数据框
df_poisson <- data.frame(
ID = 1:400,
treatment = sample(c(1,2,3), size=400, replace=TRUE, prob=c(0.1,0.3,0.6)),
age = round(rnorm(n=400, mean=75, sd=5)),
count = rpois(n=400, lambda=4)
)
# 设置分类变量
df_poisson$treatment <- factor(
df_poisson$treatment,
levels = c(1,2,3),
labels = c("ctr","trtA","trtB")
)
# 构建模型
poisson_reg <- glm(
formula = count ~ treatment + age,
data = df_poisson,
family = poisson(link="log")
)22.5.2 结果输出
##
## Call:
## glm(formula = count ~ treatment + age, family = poisson(link = "log"),
## data = df_poisson)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.914037 0.369845 2.471 0.0135 *
## treatmenttrtA -0.132652 0.089796 -1.477 0.1396
## treatmenttrtB -0.179513 0.082606 -2.173 0.0298 *
## age 0.008069 0.004846 1.665 0.0959 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 440.66 on 399 degrees of freedom
## Residual deviance: 433.30 on 396 degrees of freedom
## AIC: 1674.9
##
## Number of Fisher Scoring iterations: 422.5.3 模型预测
# 新数据的格式需要与模型创建时的数据格式一致
df_newdata <- data.frame(
treatment = c("ctr","trtA","trtB"), # 注意这里的输入值为对应的标签值
age = c(70, 70, 70)
)
# 预测发生例数
predict(object=poisson_reg, newdata=df_newdata, type="response")## 1 2 3
## 4.387930 3.842816 3.66689322.5.4 模型检验
与小节22.4.1.5一样,当模型不佳时,可以考虑使用类泊松分布,即声明family=quasipoisson(link="log")。
22.5.5 时间段变化的泊松分布
上面的例子是时间段固定的泊松分布。在实际生活中,我们可能会遇到时间段不固定的泊松分布情况,比如对不同病人观察了不同的时间长度(T),记录了某疾病的发病次数。此时,我们需要添加自变量log(T)并使用offset()函数将该变量的系数固定为1。
set.seed(1)
# 创建数据框
df_poisson2 <- data.frame(
ID = 1:400,
treatment = sample(c(1,2,3), size=400, replace=TRUE, prob=c(0.1,0.3,0.6)),
time = round(runif(n=400, min=1, max=2)*10),
age = round(rnorm(n=400, mean=75, sd=5)),
count = rpois(n=400, lambda=4)
)
# 设置分类变量
df_poisson2$treatment <- factor(
df_poisson2$treatment,
levels = c(1,2,3),
labels = c("ctr","trtA","trtB")
)
# 构建模型
poisson_reg2 <- glm(
formula = count ~ treatment + age + offset(log(time)),
data = df_poisson2,
family = poisson(link="log")
)
# 结果呈现
summary(poisson_reg2)##
## Call:
## glm(formula = count ~ treatment + age + offset(log(time)), family = poisson(link = "log"),
## data = df_poisson2)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.999534 0.352866 -2.833 0.00462 **
## treatmenttrtA 0.164334 0.098108 1.675 0.09393 .
## treatmenttrtB 0.133367 0.091128 1.464 0.14333
## age -0.006285 0.004660 -1.349 0.17735
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 535.13 on 399 degrees of freedom
## Residual deviance: 530.70 on 396 degrees of freedom
## AIC: 1768.8
##
## Number of Fisher Scoring iterations: 5# 新数据的格式需要与模型创建时的数据格式一致
df_newdata <- data.frame(
treatment = "ctr", # 注意这里的输入值为对应的标签值
time = 10,
age = 70
)
# 预测time=10时间段内的发生例数
predict(object=poisson_reg2, newdata=df_newdata, type="response")## 1
## 2.37042222.6 总结
22.6.1 应用场景
关于各分布形式的介绍,可以参考此链接。
| 因变量分布形式 | 链接函数 | 场景 |
|---|---|---|
| 正态分布 (Gaussian) | Identity (恒等函数) | 身高 |
| 逆高斯分布 (Inverse Gaussian) | Inverse squared (平方的倒数) | 数据呈正偏态分布,如某商品的销量 |
| 伽马分布 (Gamma) | Inverse (倒数) | 等待服务的时间 |
| 二项分布 (Binomial) | Logit, Probit, clog-log | 用于两种结局的选择,比如是否发病 |
| 泊松分布 (Poisson) | Log (对数) | 用于计数事件,比如单位时间内发生某事件的次数 |
22.6.2 表格呈现
我们依然可以使用gtsummary包对模型结果进行汇总。
22.6.2.1 简单线性回归
library(gtsummary)
# 单变量简单线性回归
linear_uv <- df_darwin %>%
select(ends_with("1")) %>%
tbl_uvregression(
method = lm, # 设置回归模型
y = mean_gmrt1, # 设置因变量
estimate_fun = function(x){style_ratio(x, digits = 3)}, # 设置显示小数点位数
pvalue_fun = function(x){style_pvalue(x, digits = 3)}, # 设置小数点位数
hide_n = TRUE # 不显示计数
) %>%
add_global_p() %>%
bold_p()
# 显示结果
linear_uv| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| air_time1 | -0.003 | -0.004, -0.001 | <0.001 |
| gmrt_in_air1 | 0.678 | 0.641, 0.715 | <0.001 |
| max_x_extension1 | 0.016 | 0.004, 0.028 | 0.010 |
| max_y_extension1 | 0.014 | 0.005, 0.023 | 0.002 |
| mean_acc_in_air1 | 125.6 | 76.84, 174.4 | <0.001 |
| Abbreviation: CI = Confidence Interval | |||
# 多变量变量简单线性回归
linear_mv <- df_darwin %>%
select(ends_with("1")) %>%
glm(formula = mean_gmrt1~., family="gaussian") %>%
tbl_regression(
estimate_fun = function(x){style_ratio(x, digits = 3)}, # 设置显示小数点位数
pvalue_fun = function(x){style_pvalue(x, digits = 3)} # 设置小数点位数
) %>%
add_global_p() %>%
bold_p()
# 显示结果
linear_mv| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| air_time1 | -0.001 | -0.001, 0.000 | 0.015 |
| gmrt_in_air1 | 0.642 | 0.601, 0.683 | <0.001 |
| max_x_extension1 | 0.006 | 0.002, 0.011 | 0.002 |
| max_y_extension1 | 0.002 | -0.001, 0.005 | 0.214 |
| mean_acc_in_air1 | 17.93 | -0.686, 36.55 | 0.059 |
| Abbreviation: CI = Confidence Interval | |||
# 将两张表格结合
tbl_merge(
list(linear_uv, linear_mv),
tab_spanner = c("**Univariable**", "**Multivariable**") # 调整回归分析名称
) %>%
modify_footnote(
everything() ~ NA, # 移除表注
abbreviation = TRUE # 移除缩写的表注
) %>%
modify_header(
label ~ "**Variable**" # 调整变量栏名称
) %>%
modify_caption(
"**Linear regression results**" # 添加表题
)| Variable |
Univariable
|
Multivariable
|
||||
|---|---|---|---|---|---|---|
| Beta | 95% CI | p-value | Beta | 95% CI | p-value | |
| air_time1 | -0.003 | -0.004, -0.001 | <0.001 | -0.001 | -0.001, 0.000 | 0.015 |
| gmrt_in_air1 | 0.678 | 0.641, 0.715 | <0.001 | 0.642 | 0.601, 0.683 | <0.001 |
| max_x_extension1 | 0.016 | 0.004, 0.028 | 0.010 | 0.006 | 0.002, 0.011 | 0.002 |
| max_y_extension1 | 0.014 | 0.005, 0.023 | 0.002 | 0.002 | -0.001, 0.005 | 0.214 |
| mean_acc_in_air1 | 125.6 | 76.84, 174.4 | <0.001 | 17.93 | -0.686, 36.55 | 0.059 |
| Abbreviations: CI = Confidence Interval, NA | ||||||
22.6.2.2 二分类的Logistic回归
# 单变量简单线性回归
logreg_uv <- df_heart %>%
select(age,sex,chol,exang,target) %>%
tbl_uvregression(
method = glm, # 设置回归模型
y = target, # 设置因变量
method.args = list(family = binomial(link='logit')), # 设置glm参数
exponentiate = TRUE, # 将系数进行自然指数转换
estimate_fun = function(x){style_ratio(x, digits = 3)}, # 设置显示小数点位数
pvalue_fun = function(x){style_pvalue(x, digits = 3)}, # 设置小数点位数
hide_n = TRUE # 不显示计数
) %>%
add_global_p() %>%
bold_p()
# 显示结果
logreg_uv| Characteristic | OR | 95% CI | p-value |
|---|---|---|---|
| age | 0.948 | 0.935, 0.962 | <0.001 |
| sex | <0.001 | ||
| 1 | — | — | |
| 0 | 3.618 | 2.718, 4.851 | |
| chol | 0.996 | 0.994, 0.998 | 0.001 |
| exang | <0.001 | ||
| 0 | — | — | |
| 1 | 0.128 | 0.094, 0.173 | |
| Abbreviations: CI = Confidence Interval, OR = Odds Ratio | |||
# 多变量变量简单线性回归
logreg_mv <- df_heart %>%
select(age,sex,chol,exang,target) %>%
glm(formula = target~., family=binomial(link='logit')) %>%
tbl_regression(
exponentiate = TRUE, # 将系数进行自然指数转换
estimate_fun = function(x){style_ratio(x, digits = 3)}, # 设置显示小数点位数
pvalue_fun = function(x){style_pvalue(x, digits = 3)} # 设置小数点位数
) %>%
add_global_p() %>%
bold_p()
# 显示结果
logreg_mv| Characteristic | OR | 95% CI | p-value |
|---|---|---|---|
| age | 0.936 | 0.920, 0.953 | <0.001 |
| sex | <0.001 | ||
| 1 | — | — | |
| 0 | 5.127 | 3.611, 7.370 | |
| chol | 0.995 | 0.992, 0.998 | 0.001 |
| exang | <0.001 | ||
| 0 | — | — | |
| 1 | 0.131 | 0.094, 0.182 | |
| Abbreviations: CI = Confidence Interval, OR = Odds Ratio | |||
# 将两张表格结合
tbl_merge(
list(logreg_uv, logreg_mv),
tab_spanner = c("**Univariable**", "**Multivariable**") # 调整回归分析名称
) %>%
modify_footnote(
everything() ~ NA, # 移除表注
abbreviation = TRUE # 移除缩写的表注
) %>%
modify_header(
label ~ "**Variable**" # 调整变量栏名称
) %>%
modify_caption(
"**Logistic regression results**" # 添加表题
)| Variable |
Univariable
|
Multivariable
|
||||
|---|---|---|---|---|---|---|
| OR | 95% CI | p-value | OR | 95% CI | p-value | |
| age | 0.948 | 0.935, 0.962 | <0.001 | 0.936 | 0.920, 0.953 | <0.001 |
| sex | <0.001 | <0.001 | ||||
| 1 | — | — | — | — | ||
| 0 | 3.618 | 2.718, 4.851 | 5.127 | 3.611, 7.370 | ||
| chol | 0.996 | 0.994, 0.998 | 0.001 | 0.995 | 0.992, 0.998 | 0.001 |
| exang | <0.001 | <0.001 | ||||
| 0 | — | — | — | — | ||
| 1 | 0.128 | 0.094, 0.173 | 0.131 | 0.094, 0.182 | ||
| Abbreviations: CI = Confidence Interval, OR = Odds Ratio, NA | ||||||