第19章相关性分析

19.1 分类变量的相关性分析

19.1.1 概述

分类变量的相关性分析本质是分析实际观测值和理论推断值之间的偏离程度。在完成分类变量的相关性分析（独立性检验）后，对于有相关性的变量，我们还会对相关性的具体程度感兴趣，因此也会进行相关性的度量。具体的分析方法与列联表类型[小节18.1.3]有关：

列联表类型	独立性检验	相关性度量
独立样本四格表	卡方检验 Fisher’s精确检验	Pearson列联系数 \(\varphi\)系数
配对样本四格表	McNemar检验
单向有序列联表（分组有序）	卡方检验	Pearson列联系数 Cramer’s V系数
单向有序列联表（结果有序）	秩和检验	Gamma系数 Kendall’s tau-b相关系数 Kendall’s tau-c相关系数
双向无序列联表	卡方检验 Fisher’s精确检验	Pearson列联系数 Cramer’s V系数
双向有序列联表（不同属性）	Spearman相关分析 Kendall’s \(\tau\)相关分析	Spearman秩相关系数 Gamma系数 Kendall’s tau-b相关系数 Kendall’s tau-c相关系数
双向有序列联表（属性相同）	McNemar-Bowker检验

卡方检验（\(\chi^2\) test）和Fisher’s精确检验（Fisher’s exact test）的选择与列联表类型[小节18.1.3]、样本总量和期望频数有关：

列联表类型	应用条件	检验方法	函数语法
四格表	样本总量≥40 且期望频数≥5	Pearson卡方检验	chisq.test(correct=FALSE)
	样本总量≥40 且 1≤期望频数＜5	连续性校正的卡方检验	chisq.test(correct=TRUE)(默认参数)
	样本总量＜40 或任意格子期望频数＜1	Fisher’s精确检验	fisher.test()
RC列联表	期望频数＜5的格子不超过总格子数的\(\frac{1}{5}\) 且所有格子的期望频数≥1	Pearson卡方检验	chisq.test(correct=FALSE)
RC列联表	期望频数＜5的格子超过总格子数的\(\frac{1}{5}\) 或任意格子的期望频数＜1	Fisher’s精确检验	fisher.test()

有时两个分类变量的关联可能受到第三个变量的影响，因此当我们在分析两个分类变量的相关性时，有时需要控制其它的分类变量，这时需要用Cochran-Mantel-Haenszel检验（CMH检验）。

19.1.2 卡方检验

卡方检验的通用公式为： \[ \chi^2 = \sum \frac{|观察频数 - 期望频数|^2}{期望频数} \]

四格表卡方值的快速计算公式（即拟合度公式）为： \[ \chi^2 = \frac{n(ad - bc)^2}{(a + b)(c + d)(a + c)(b + d)} \] 其中，n = a + b + c + d

卡方值（\(\chi^2\)）越大，代表实际观测值和理论推断值的偏离程度越大；反之亦然。当两者完全相等时，卡方值为0。

卡方检验可以用来进行：

拟合优度检验：即检验一组给定数据与指定分布的拟合程度。比如，我们想要知道数据的分布是否符合某种分布类型；特定人群对若干种干预方案的喜好是否有差异。
独立性检验：即同一个样本中的两个分类变量之间是否具有相关性。

19.1.2.1 拟合优度检验

例假设我们收集了90名老年人对A、B、C三种运动干预方案的选择，我们想知道老年人对这三种干预方案的选择是否有差异。这时可以使用chisq.test()函数来实现。

# 创建数据框
preference_df <- data.frame(
  ID = 1:90,
  preference = c(rep("A",45), rep("B",20), rep("C",25))
)

# 生成频数分布表
pref_tab <- xtabs(formula = ~preference, data = preference_df)

# 拟合优度检验
chisq.test(pref_tab)

## 
##  Chi-squared test for given probabilities
## 
## data:  pref_tab
## X-squared = 11.667, df = 2, p-value = 0.002928

在汇报卡方检验结果时，需要写成 \(\chi^2\)(自由度,样本量) = 卡方值，P值的形式。

例如，上例的结果需要表达为：\(\chi^2\)(2,90) = 11.667, P = 0.003。

根据上例的结果，我们可以发现P值小于0.05，因此认为老年人对这三种干预方案的选择是有差异的。

要进一步比较是哪两种干预方案之间的选择有差异，我们可以进行两两比较。

library(tidyverse)
# 获取preference水平
preference_unique <- unique(preference_df$preference)

# 使用循环语句进行配对比较
for (i in seq(length(preference_unique))) {
  # 生成不包含第i个preference水平的子数据
  subset_df <- preference_df %>% filter(preference != preference_unique[i])
  
  # 生成频数分布表
  subset_pref_tab <- xtabs(formula = ~preference, data = subset_df)
  
  # 拟合优度检验
  chisq_result <- chisq.test(subset_pref_tab)
  
  # 报告结果
  print(
    paste0(
      "P value of comparison between level ", 
      paste(preference_unique[-i], collapse = " and "), # 合并剩下的preference水平
      " is: ",
      round(chisq_result$p.value, 4) # 报告P值
    )
  )
}

## [1] "P value of comparison between level B and C is: 0.4561"
## [1] "P value of comparison between level A and C is: 0.0168"
## [1] "P value of comparison between level A and B is: 0.0019"

可以看到，A方案的选择人数与剩下两个方案的选择人数之间是有显著差异的。

注意：

拟合优度检验使用了大样本的性质，要求样本容量足够大，一般来说样本量≥30。

各区间的理论频数不能太小，至少为5。如果未达到标准，可以重新调整划分区间。

19.1.2.2 独立性检验

例我们将以UCI心脏病数据集为例，分析exang（运动诱发心绞痛）与target（心脏病）的相关性。

# 读取数据
heart_df <- read_csv("data/heart.csv")

## Rows: 1025 Columns: 14
## ── Column specification ─────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (14): age, sex, cp, trestbps, chol, fbs, restecg, thalach, exang, oldpeak...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

# 建立列联表
cross_table <- xtabs(formula = ~exang+target, data = heart_df)

# 卡方检验
chisq_result <- chisq.test(cross_table)

在生成的结果列表chisq_result中一共包含9个元素，其中名为expected的元素便是期望频数。

# 查看期望频数
chisq_result$expected

##      target
## exang        0        1
##     0 331.0439 348.9561
##     1 167.9561 177.0439

由于样本总量≥40且期望频数≥5，所以选择Pearson卡方检验，声明参数correct=FALSE。

chisq.test(cross_table, correct=FALSE)

## 
##  Pearson's Chi-squared test
## 
## data:  cross_table
## X-squared = 196.67, df = 1, p-value < 2.2e-16

19.1.3 Fisher’s精确检验

Fisher’s精确检验的基本思想是在四格表周边合计数（a+b）、(c+d)、(a+c)、(b+d)不变的条件下，计算表内a、b、c、d，4个频数变动时的各种组合的概率\(P_i\)；再按检验假设用单侧或双侧的累计概率P，依据所取的检验水准α进行判断。

各组合的概率\(P_i\)服从超几何分布： \[ p_i = \frac{(a + b)!(c + d)!(a + c)!(b + d)!}{a!b!c!d!n!} \] 其中，n = a + b + c + d

还是以四格表为例，我们简要说明一下\(P_i\)公式是如何得来的：

	变量1：水平1	变量1：水平2	列合计
变量2：水平1	a	b	a+b
变量2：水平2	c	d	c+d
行合计	a+c	b+d	n

首先，我们需要保证在变量1：水平1这一列的总数a+c不变的情况下，满足变量1：水平1和变量2：水平1的样本数为a，则有\(C_{a+c}^a\)种方法。接着，我们需要保证在变量1：水平2这一列的总数b+d不变的情况下，满足变量1：水平2和变量2：水平1的样本数为b，则有\(C_{b+d}^b\)种方法。最后，在变量2：水平1这一行的样本可以随机组合，有(a+b)!种方法；在变量2：水平2这一行的样本可以随机组合，有(c+d)!种方法。这就是满足当前样本分布的组合数。而n个样本随机组合一共有n!种方法，所以最终出现当前样本分布的概率为： \[ \frac{C_{a+c}^aC_{b+d}^b(a + b)!(c + d)!}{n!} = \frac{(a + b)!(c + d)!(a + c)!(b + d)!}{a!b!c!d!n!} \]

需要注意的是，卡方检验是右侧单尾检验，而Fisher’s精确检验可以是单尾或者双尾检验。当我们将a由小到大排列时，会得到不同取值下的组合概率\(P_i\)。如果我们实际观察到的组合中满足变量1：水平1和变量2：水平1的样本数为A，Fisher’s精确检验的左侧单尾指的是所有不大于A的组合的累积概率，即\(\sum P_{(i|a \leq A)}\)。同理，Fisher’s精确检验的右侧单尾指的是所有不小于A的组合的累积概率，即\(\sum P_{(i|a \geq A)}\)。而Fisher’s精确检验的双尾指的是所有不等于A的组合的累积概率，即\(\sum P_{(i|a \neq A)}\)。

同时我们也可以看到，虽然Fisher’s精确检验更加准确，但计算成本更高。因此，与卡方检验相比，Fisher’s精确检验更适用于样本量较小情况下的两个分类变量间的相关性检验。

Fisher’s精确检验可以使用fisher.test()函数来实现，默认为双尾检验，如果需要调整假设检验方式，可以声明alternative参数。

例某机构为研究某药物A对I级高血压的控制效果，将32例I级高血压的患者随机分成用药组（17人）和非用药组（15人），得到药物A的控制效果数据如下：

组别	血压已控制	血压未控制	合计
用药组	13	4	17
非用药组	7	8	15
合计	20	12	32

由于样本量小于40，所以我们需要用Fisher’s精确检验来检验药物A是否有效。

# 创建列联表
bp_cross_table <- matrix(c(13,7,4,8), nrow = 2) # 注意matrix默认为"Fortran"排列，即纵向排列

# 设置列联表行列名
rownames(bp_cross_table) <- c("drug", "no-drug")
colnames(bp_cross_table) <- c("controlled", "not-controlled")

# 运行Fisher's精确检验
fisher.test(bp_cross_table)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  bp_cross_table
## p-value = 0.1437
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##   0.6614127 22.5856041
## sample estimates:
## odds ratio 
##   3.554873

所得P = 0.144＞0.05，所以认为用药组与非用药组的效果相等，即药物A对血压的控制效果并不显著。

19.1.4 Cochran-Mantel-Haenszel检验

在进行分类变量的关联性分析时，有时候会出现两个分类变量（变量A和变量B）的总体关联性是一种情况，但是当基于第三个分类变量（变量C）分层后，在进行分类变量的关联性分析，这时的关联性消失或者出现跟之前总体关联性结果相反的情况，这种现象被称为辛普森悖论（Simpson’s Paradox）。

例我们来看一个例子，现在有两种药物对肺癌的总体治愈率数据，如下所示：

药物类型	治愈人数	未治愈人数	治愈率
药物A	900	100	90%
药物B	800	200	80%

我们可以看到，药物A的治愈率为90%，高于药物B的治愈率，所以药物A的对肺癌的治疗效果比药物B似乎更胜一筹。但是如果我们将患者按照性别进行划分后，重新计算各药物对肺癌的治愈率，会得到如下结果：

药物类型	性别	治愈人数	未治愈人数	治愈率
药物A	男性	870	30	96.7%
药物A	女性	30	70	30%
药物B	男性	680	20	97.1%
药物B	女性	120	180	40%

这样看来，不论是在男性还是在女性患者中，药物B对肺癌的治愈率都高于药物A，这与总体治愈率数据相矛盾。

为什么会出现这种情况呢？我们来剖析一下总体和性别分层的治愈率是怎样计算的：

药物类型	男性	女性	总治愈率
药物A	\(\frac{870}{900}\) \(\frac{q_1}{p_1}\)	\(\frac{30}{100}\) \(\frac{q_3}{p_3}\)	\(\frac{870 + 30}{900 + 100}\) \(\frac{q_1 + q_3}{p_1 + p_3}\)
药物B	\(\frac{680}{700}\) \(\frac{q_2}{p_2}\)	\(\frac{120}{300}\) \(\frac{q_4}{p_4}\)	\(\frac{680 + 120}{700 + 300}\) \(\frac{q_2 + q_4}{p_2 + p_4}\)

我们可以发现，各性别分层的权重不同会影响总治愈率，因此如果要使总治愈率出现反转，需要有三个特征：

各分层的分母（即药物A中的\(p_1\)与\(p_3\)、药物B中的\(p_2\)与\(p_4\)）相差较大，这就保证了总治愈率主要基于分母较大的分层治愈率。
各个分层治愈率之间有较大差异，这就保证了分层治愈率的权重改变对总治愈率的影响程度。如果分层治愈率之间无太大差异，则药物A、B中各分层权重的差异对总治愈率不会有太大影响。
各分层的分母比率（即药物A中的\(p_1\):\(p_3\)、药物B中的\(p_2\):\(p_4\)）有明显差异，这就保证了分层治愈率对总治愈率的实际影响程度。分母较大一方的占比越高，则总治愈率越接近分母较大一方的分层治愈率；反之，总治愈率会向分母较小一方的分层治愈率倾斜。

上面的例子告诉我们，总体的关联性趋势不一定能反映分层后的关联性分析趋势，这是因为存在一些混杂因素的影响。因此我们在进行数据分析的过程中需要警惕辛普森悖论的存在，不仅要关注数据的整体趋势，还要注意到各个子集内部的趋势。

虽然我们可以按照变量C的各个水平，分别进行变量A和变量B的卡方检验。但是，有时我们只是想在控制变量C的情况下去看变量A与B的关联性，这时就需要用到Cochran-Mantel-Haenszel检验（CMH检验）。CMH检验假设在变量C的各个水平上，变量A和B都是条件独立的，也即变量C的各个水平上的变量A之间以及各个水平上的变量B之间不会相互影响。CMH检验的是基于公共的优势比进行的，具体计算可参考此链接。

我们继续根据上面的例子，使用mantelhaen.test()函数完成CMH检验。这时需要生成三变量的列联表。在制备列联表时，需要将控制变量C放在最外层。如果是使用xtabs()函数生成列联表时，控制变量C应该放在formula参数的最后一位，即formula = ~变量A+变量B+变量C。

values <- c(870,680,30,20,30,120,70,180) # 计数向量
row.names <- c("drug A", "drug B") # 行标题
col.names <- c("cured", "uncured") # 列标题
matrix.names <- c("male", "female") # 第三个维度的标题

lung_cancer <- array(values, dim = c(2,2,2), dimnames = list(row.names,col.names,matrix.names)) # 创建列联表

# 查看列联表
lung_cancer

## , , male
## 
##        cured uncured
## drug A   870      30
## drug B   680      20
## 
## , , female
## 
##        cured uncured
## drug A    30      70
## drug B   120     180

# CMH检验
mantelhaen.test(lung_cancer)

## 
##  Mantel-Haenszel chi-squared test with continuity correction
## 
## data:  lung_cancer
## Mantel-Haenszel X-squared = 2.6655, df = 1, p-value = 0.1025
## alternative hypothesis: true common odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.4985488 1.0462466
## sample estimates:
## common odds ratio 
##         0.7222222

所得P = 0.1025大于0.05，因此认为药物A、B对肺癌治疗效果无显著性差异。

19.1.5 相关性的度量

当我们知道了分类变量之间有相关性后，也会对相关性的强弱感兴趣。相关性的强弱便是相关性度量，常用指标包括：

Phi(\(\varphi\))系数：

只适用于四格表，范围为[0,1]。计算公式为 \(\varphi = \sqrt{\frac{\chi^2}{n}}\) 。phi系数小于0.3时，相关性较弱；phi系数大于0.6时，表示相关较强。

Pearson列联系数（C系数）：

计算公式为 \(C = \sqrt{\frac{\chi^2}{\chi^2 + n}}\) 。范围为[0,1]，值越大表明两变量之间的相关性越强；适合行、列数相同的列联表。

Cramer’s V系数：

是对Pearson列联系数的修正，计算公式为 \(V = \sqrt{\frac{\chi^2}{n \times \min[(r-1),(c-1)]}}\) 。范围为[0,1]，值越大表明两变量之间的相关性越强；适用于行、列数不同的列联表。

我们可以使用vcd包中的assocstats()函数完成对列联表中两个分类变量相关性的度量。

library(vcd)
# 以卡方检验的列联表为例做演示
assocstats(cross_table)

##                     X^2 df P(> X^2)
## Likelihood Ratio 206.16  1        0
## Pearson          196.67  1        0
## 
## Phi-Coefficient   : 0.438 
## Contingency Coeff.: 0.401 
## Cramer's V        : 0.438

19.1.6 McNemar检验

我们有时需要对同一研究对象（如同一患者的肿瘤细胞）或两两匹配对象（如同胎、同体重的小鼠）分别予以两种不同的处理方式，亦或进行某处理方式前后的效果比较。前者用于推断两种处理方式的效果是否有差别，后者用于推断特定的处理方式是否有效果。这时我们可以使用McNemar检验。

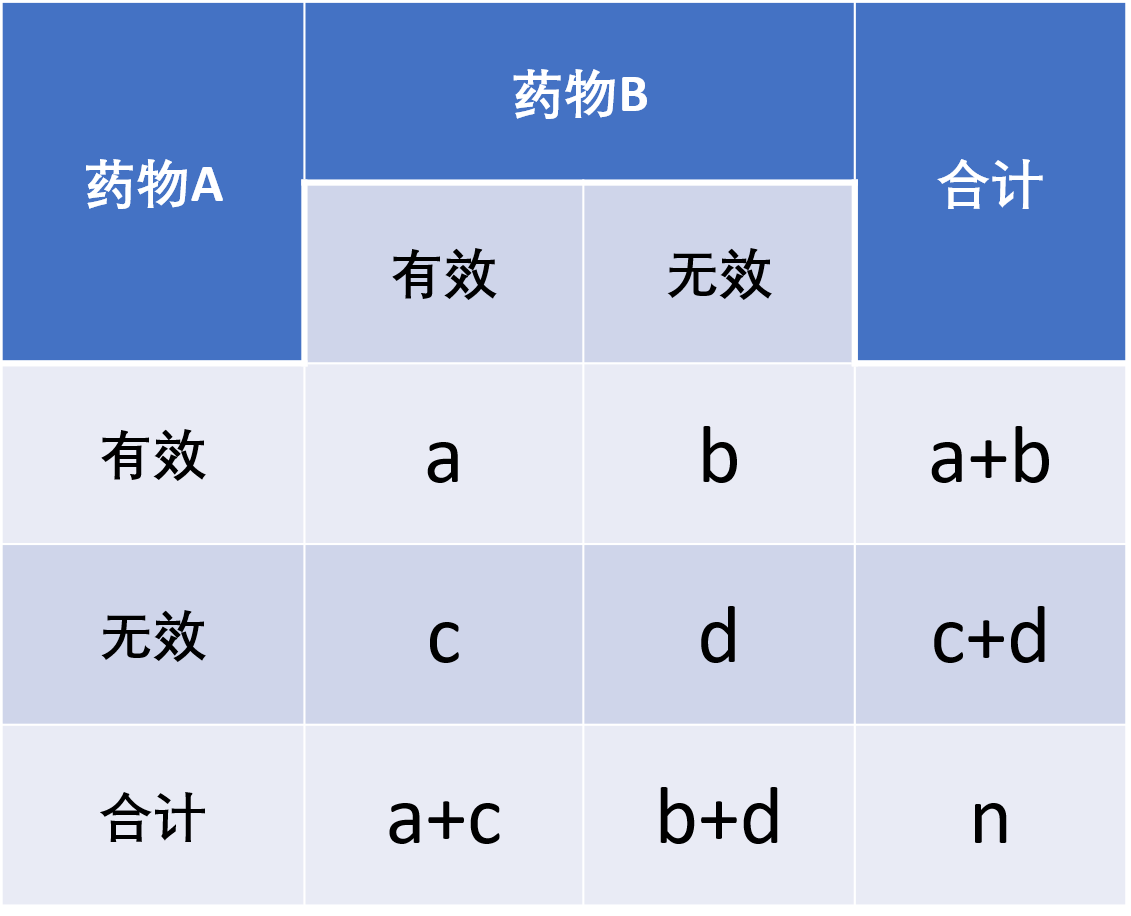
McNemar检验主要关注两种处理方式（或某种处理方式前后）的不一致数目（b和c）是否有很大的差异。其卡方值计算公式为：

\[ \chi^2 = \frac{(b - c)^2}{b + c}, \nu = 1 \]

McNemar检验可以通过mcnemar.test()函数实现。此函数默认使用校正，当b+c≥40时，不需要使用校正，此时需要声明参数correct=FALSE。

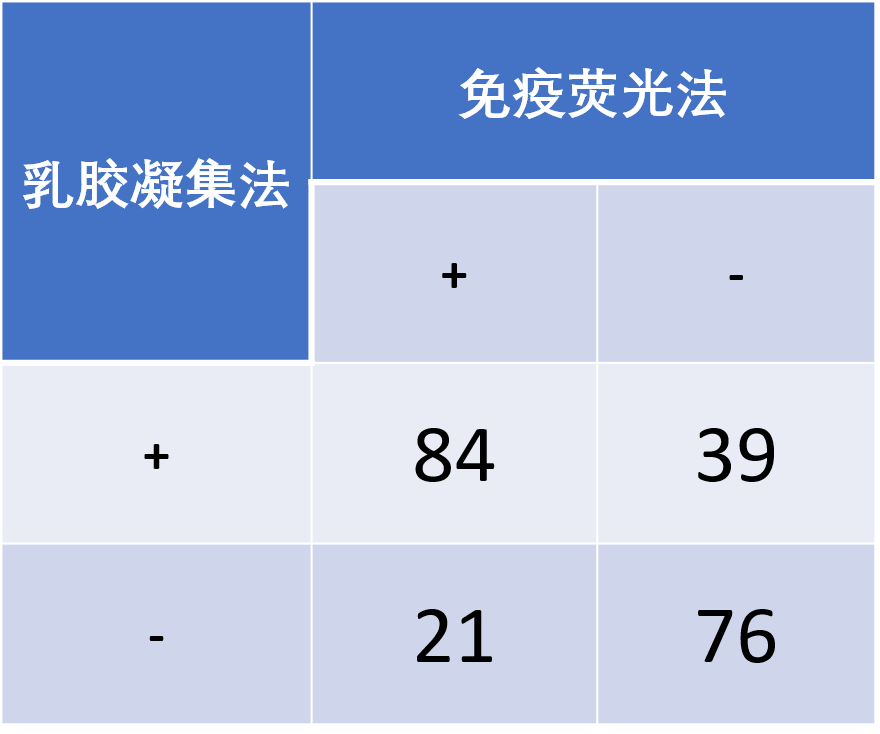
例某实验室分别用乳胶凝集法和免疫荧光法对220名疑似系统性红斑狼疮患者血清中核抗体进行测定，结果如下，分析两种方法的检测结果是否有差别。

# 创建数据框
mcnemar_df <- data.frame(
  LAT = rep(c(1,0), times=c(123,97)),
  IF = c(rep(c(1,0), times=c(84,39)), rep(c(1,0), times=c(21,76)))
)

# 创建列联表
mcnemar_crosstab <- xtabs(formula = ~ LAT + IF, data = mcnemar_df)

# 进行mcnemar检验
mcnemar.test(mcnemar_crosstab, correct = FALSE)

## 
##  McNemar's Chi-squared test
## 
## data:  mcnemar_crosstab
## McNemar's chi-squared = 5.4, df = 1, p-value = 0.02014

结果显示P=0.02＜0.05，因此这两种方法的检测结果是有显著差别的。

注意：

McNemar检验的两组变量必须是无序分类变量。对于配对样本多水平有序分类变量的检验可以考虑Wilcoxon符号秩和检验。

由于McNemar检验只关注两个分类变量的不一致结果，当a、d的量级显著高于b、c的量级时，也有可能出现检验结果不显著的情况，此时需要引起警惕。

19.1.7 一致性检验

对于配对样本而言，有时我们不光想知道两种处理方式是否具有相关性，我们还想知道这两种处理方式的结果是否是一致的，这时就需要一致性检验。一致性与相关性的区别如下：

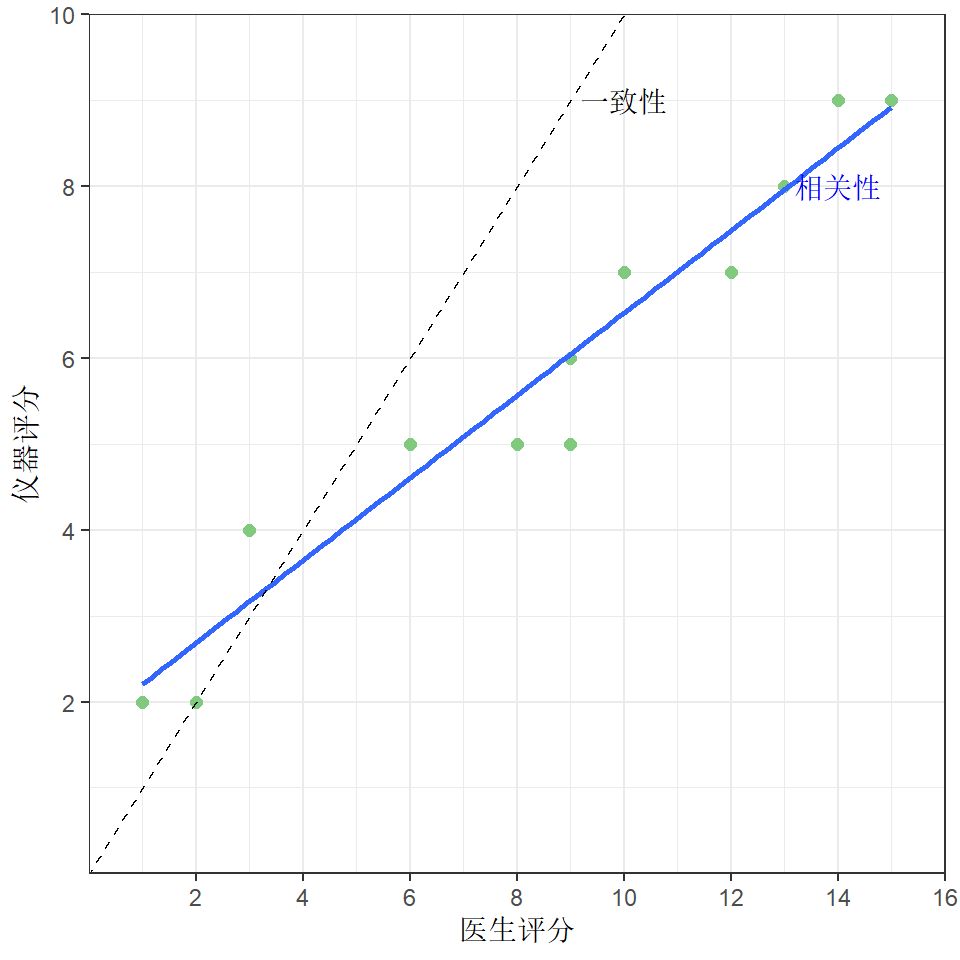
Cohen’s Kappa分析常被用于配对样本四格表的一致性检验，Kappa值的范围为[-1,1]。比如我们根据实际的观测值[小节19.1.6]，可以计算出要比较的两种处理方式（或特定处理方式的处理前后效果）的实际结果一致的比率：\(P_0 = \frac{a + d}{n}\)

但是，这里面的一致比率还包括在完全随机的情况下会出现的结果一致的比率，即\(P_e = \frac{(a + b)(a + c) + (c + d)(b + d)}{n^2}\)

这时，如果我们计算\(P_0\)与\(P_e\)的差值在最理想状态（即结果完全一致）与\(P_e\)的差值的占比，就能够较好地反映实际结果一致性，这个计算出来的比值就是Kappa值，即\(\kappa = \frac{P_0 - P_e}{1 - P_e}\)

Kappa值为-1，代表结果完全不一致；为0，代表结果是随机出现的；为1，代表结果完全一致。一般而言，Kappa值≤0.4时，表明一致性较差；在(0.4,0.6]范围时，表明一致性中等；在(0.6,0.8]范围时，表明一致性较好；＞0.8时，表明一致性极好。

对于双向有序列联表（属性相同）的一致性检验，通常采用Fleiss’ Kappa分析。

例依旧基于McNemar检验[小节19.1.6]中乳胶凝集法和免疫荧光法评价的例子，我们来进行Cohen’s Kappa分析，这时需要用到irr包的kappa2()函数。

library(irr)

# 直接使用数据框即可计算
kappa2(mcnemar_df)

##  Cohen's Kappa for 2 Raters (Weights: unweighted)
## 
##  Subjects = 220 
##    Raters = 2 
##     Kappa = 0.457 
## 
##         z = 6.88 
##   p-value = 6.12e-12

计算得到的Kappa值为0.457，Z值小于0.05，说明两种方法的结果是不一致的。

19.2 连续变量的相关性分析

当两个连续变量均服从正态分布[小节20.1]时，可以使用Pearson相关性分析获得两个变量的相关系数，注意此时分析的是两个变量的线性相关系数。通常情况下，Pearson相关系数绝对值位于[0,0.2)区间为极弱相关，位于[0.2,0.4)区间为弱相关，位于[0.4,0.6)区间为中等相关，位于[0.6,0.8)区间为强相关，位于[0.8,1]区间为极强相关。

当至少有一个变量不服从正态分布时，可以使用Spearman或者Kendall’s \(\tau\)相关性分析进行非参数的相关系数度量。当样本量较大（n＞30)时，使用Spearman或者Kendall’s \(\tau\)得出的结论会类似（注意：数值不一定一样）；当样本量较小时，使用Kendall’s \(\tau\)较为可靠。

可以cor()函数计算相关系数或cor.test()函数来计算相关系数和显著性水平。

19.2.1 Pearson相关性分析

# 加载数据集
data(diamonds)

# 选取diamonds数据集中的前5000个观测值进行后续演示
diamonds <- diamonds[1:5000,]

# Pearson相关性分析
cor(x = diamonds$depth, y = diamonds$price, method = "pearson") # 仅显示相关系数

## [1] 0.02181933

cor.test(x = diamonds$depth, y = diamonds$price, method = "pearson") # 显示相关系数及显著性

## 
##  Pearson's product-moment correlation
## 
## data:  diamonds$depth and diamonds$price
## t = 1.5429, df = 4998, p-value = 0.1229
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.005903537  0.049508676
## sample estimates:
##        cor 
## 0.02181933

19.2.2 Spearman相关性分析

# Spearman相关性分析
cor(x = diamonds$depth, y = diamonds$price, method = "spearman") # 仅显示相关系数

## [1] 0.03809354

cor.test(x = diamonds$depth, y = diamonds$price, method = "spearman") # 显示相关系数及显著性

## 
##  Spearman's rank correlation rho
## 
## data:  diamonds$depth and diamonds$price
## S = 2.004e+10, p-value = 0.007062
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##        rho 
## 0.03809354

19.2.3 Kendall相关性分析

# Kendall相关性分析
cor(x = diamonds$depth, y = diamonds$price, method = "kendall") # 仅显示相关系数

## [1] 0.02551886

cor.test(x = diamonds$depth, y = diamonds$price, method = "kendall") # 显示相关系数及显著性

## 
##  Kendall's rank correlation tau
## 
## data:  diamonds$depth and diamonds$price
## z = 2.6754, p-value = 0.007464
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##        tau 
## 0.02551886

19.3 连续变量的相关性矩阵图

我们可以借助PerformanceAnalytics包直观快速地对多个连续变量的相关性进行可视化展示。

# 加载包
library(PerformanceAnalytics)

# 对diamonds数据集中的连续变量进行相关性矩阵图演示
chart.Correlation(diamonds[,c(1,5:10)], histogram=TRUE, pch=19)

生成的相关性矩阵图中： 1. 对角线为该变量数据的分布图。 2. 下三角为两个变量的散点图。红色为拟合趋势线。 3. 上三角显示两个变量的相关系数，*表示显著性：* P＜0.05，** P＜0.01，*** P＜0.001.

注意：

如果想要个性化设置相关性矩阵，可以参考此链接。需要注意的是，如果要修改函数，使用fix()函数可以直接修改后覆盖，使用edit()函数只能用于另存为新函数，原函数不会改变。

我们也可以使用corrplot包将相关性矩阵制作成热图。

# 加载包
library(corrplot)

# 计算diamonds数据集中的连续变量的相关系数
diamonds_corr <- cor(diamonds[,c(1,5:10)])

# 制作热图
corrplot(
  corr = diamonds_corr,
  method = "color", # 设置热图类型
  type = "lower", # 设置热图显示方式
  order = "AOE", # 设置热图变量显示顺序
  addCoef.col = "gray" # 设置相关系数的显示颜色
)

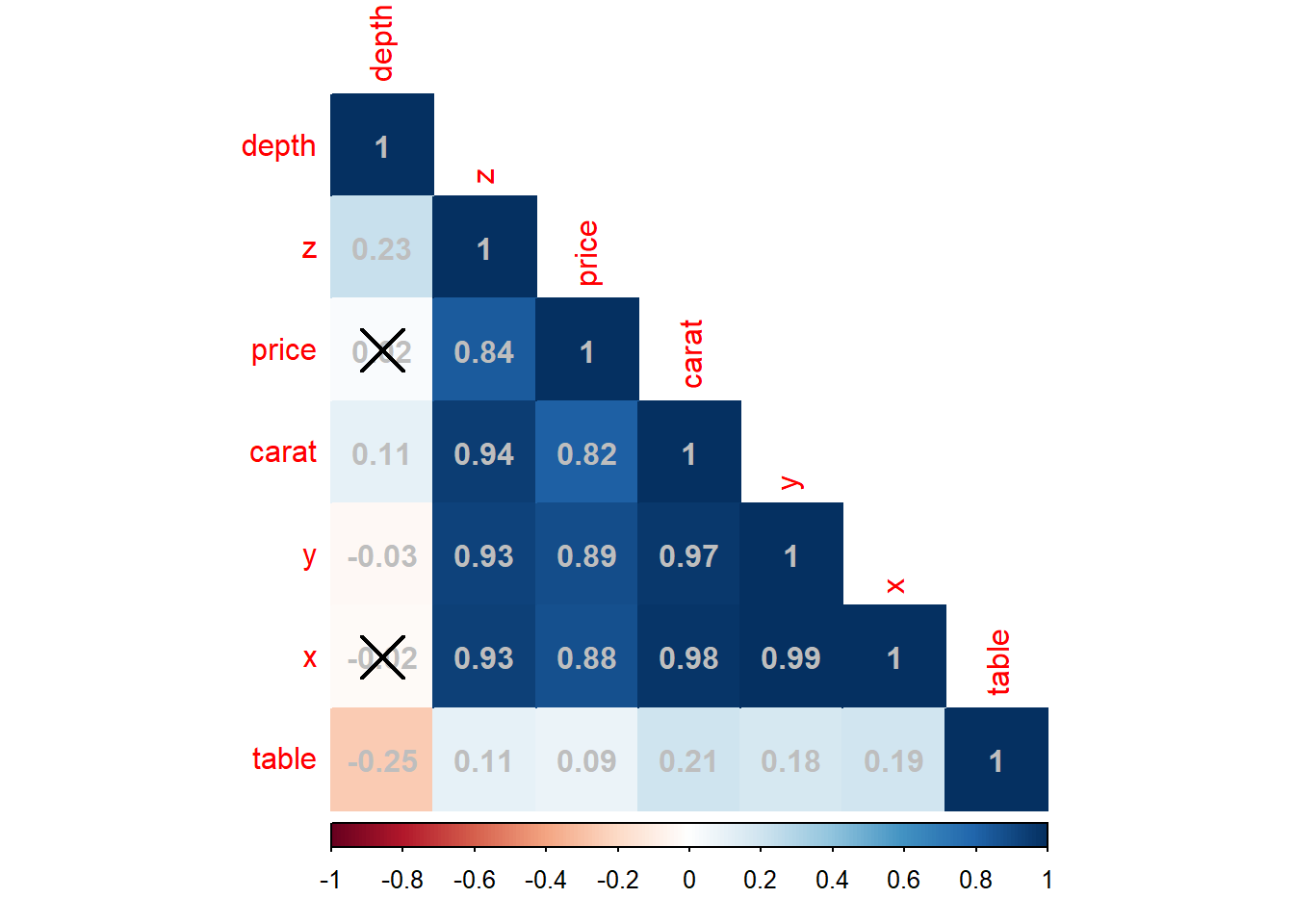
我们还可以结合相关系数显著性矩阵将热图中不显著相关的变量进行标记。

# 计算diamonds数据集中的连续变量的相关系数
diamonds_corr <- cor(diamonds[,c(1,5:10)])

# 计算diamonds数据集中的连续变量的相关系数的显著性
diamonds_p <- cor.mtest(diamonds[,c(1,5:10)])$p

# 制作热图
corrplot(
  corr = diamonds_corr, # 设置相关系数矩阵
  p.mat = diamonds_p, # 设置相关性系数显著性矩阵
  method = "color", # 设置热图类型
  type = "lower", # 设置热图显示方式
  order = "AOE", # 设置热图变量显示顺序
  addCoef.col = "gray" # 设置相关系数的显示颜色
)

第19章 相关性分析