第20章 连续型变量组间差异比较

20.1 正态分布

许多连续型变量的组间差异比较需要根据数据是否遵循正态分布来选择合适的检验方法。因此，在进行数据统计之前，需要对数据进行正态性检验。

如果数据为非正态分布，优先考虑能否通过对数或平方根转换将数据转为正态分布。如果经过转换后，数据仍无法达到正态分布的要求，可以选择对原数据进行非参数检验。

下面我们将以R自带的diamonds数据集为例，进行正态分布检验的演示。

20.1.1 密度图

密度图（density plot）能够直观地展示数据的分布情况。当如果图形呈对称钟形，我们可以初步判断数据呈正态分布。若图形出现小部分的偏斜，当样本量足够大（＞30）时，根据中心极限定理（central limit theorem），我们也可以认为该数据符合正态分布。

library(tidyverse)

# 加载数据集
data(diamonds)

# 选取diamonds数据集中的前5000个观测值进行后续演示
diamonds <- diamonds[1:5000,]

# 生成密度图
ggplot(
  data = diamonds,
  aes(depth, color=cut, fill=cut) # 按照不同的cut生成密度图
) +
geom_density(alpha=0.1)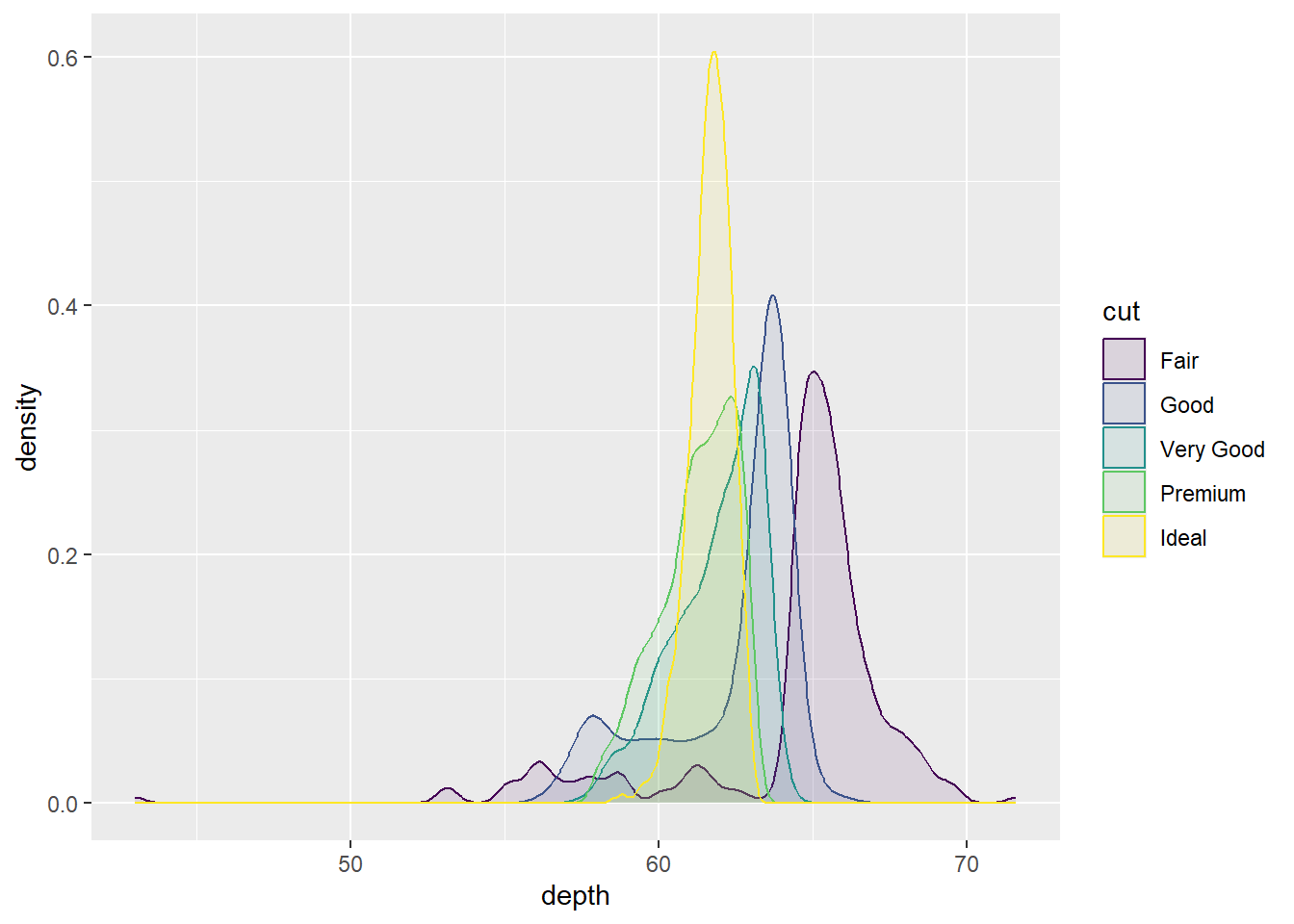

20.1.2 Q-Q图

Q-Q图（Q-Q plot）的原理是则将假定为正态分布时的Z值（或分位数）作为x坐标，将实际观测值作为y坐标制作散点图。如果样本数据近似正态分布，则这些点大致落在一条直线上，该直线的斜率为标准差，截距为均值。

ggplot(data = diamonds, aes(sample=depth)) +
  geom_qq() +
  geom_qq_line() +
  facet_wrap(vars(cut))

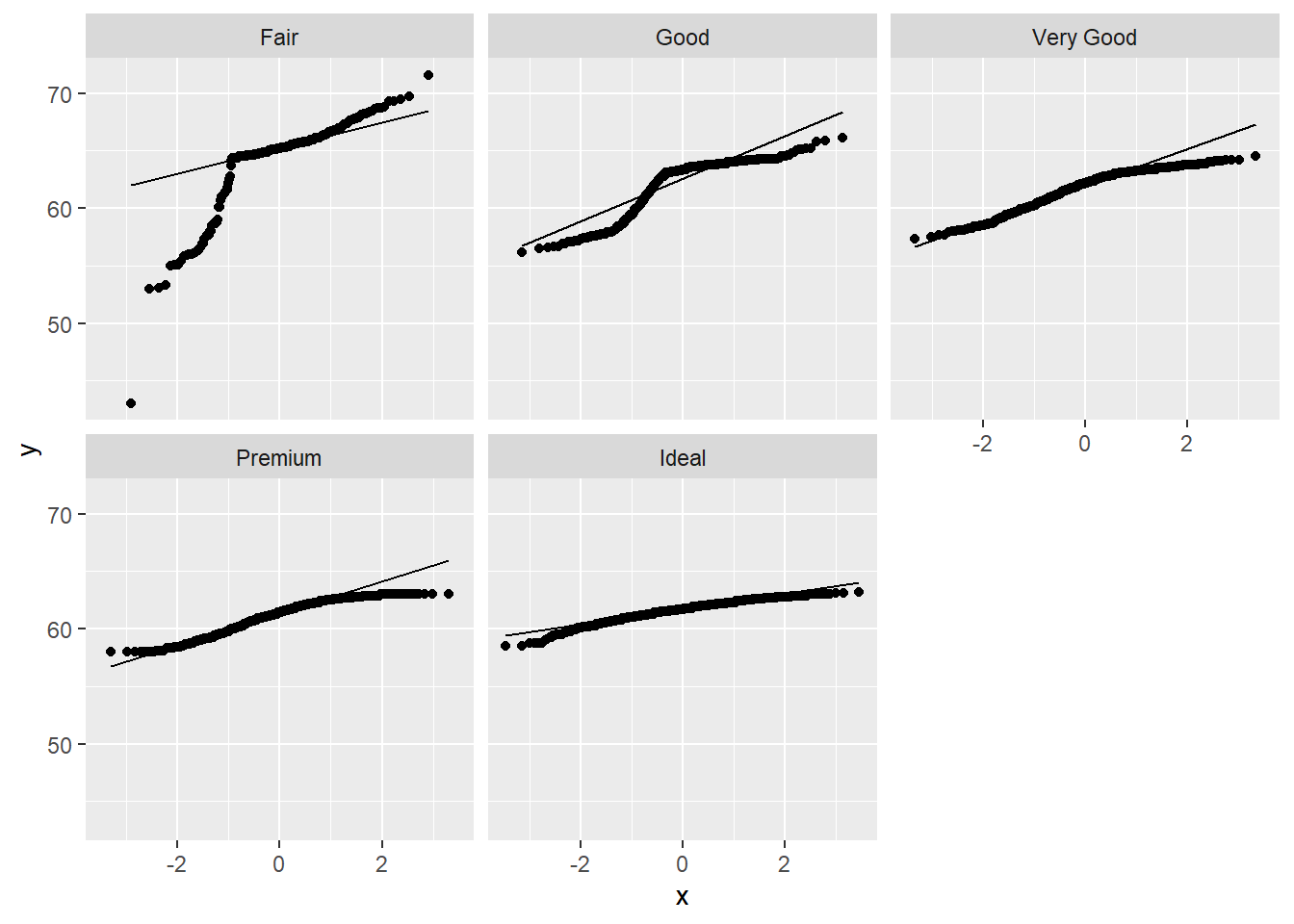
20.1.3 正态性检验

Shapiro-Wilk检验和Kolmogorov–Smirnov检验是常用的正态性检验方法。Shapiro-Wilk检验的原理是基于样本数据与对应正态分布概率之间的相关性，可以使用shapiro.test()函数实现。Kolmogorov–Smirnov检验则根据样本数据的累计概率与预期概率的差值，推断样本来自的总体是否服从某一理论分布，是一种拟合优度的检验方法，适用于大样本的情况，可以使用ks.test()函数实现。当样本量不超过50时，倾向使用Shapiro-Wilk检验；当样本量大于50时，倾向使用Kolmogorov–Smirnov检验。shapiro.test()函数接受的样本量上限为5000，当样本量大于5000时，只能用ks.test()函数。

# 创建一个样本量为1000的数据框用于shapiro-wilk检验演示
diamonds_sample <- diamonds %>% sample_n(size=1000, replace=FALSE)

# shapiro-wilk检验
shapiro.test(diamonds_sample$depth)

## 
##  Shapiro-Wilk normality test
## 
## data:  diamonds_sample$depth
## W = 0.98146, p-value = 5.676e-10

# 使用diamonds数据框进行Kolmogorov–Smirnov检验
# ks.test()可以进行单样本的特定分布检验，也可以进行双样本的分布比较，需要在y中说明
# y="pnorm"默认进行比较的正态分布为N(0,1)
ks.test(x=diamonds$depth, y="pnorm")

## Warning in ks.test.default(x = diamonds$depth, y = "pnorm"): Kolmogorov -
## Smirnov检验里不应该有连结

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  diamonds$depth
## D = 1, p-value < 2.2e-16
## alternative hypothesis: two-sided

# 如果要使用ks.test()检验数据是否特定正态分布，可以额外说明
ks.test(
  x = diamonds$depth, # 设置目标数据
  y = "pnorm", # 设置预期数据分布类型
  mean = mean(diamonds$depth), # 预期数据分布参数，这里为预期正态分布均值
  sd = sd(diamonds$depth) # 预期数据分布参数，这里为预期正态分布标准差
)

## Warning in ks.test.default(x = diamonds$depth, y = "pnorm", mean =
## mean(diamonds$depth), : Kolmogorov - Smirnov检验里不应该有连结

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  diamonds$depth
## D = 0.073766, p-value < 2.2e-16
## alternative hypothesis: two-sided

注意： 如果出现Warning: ties should not be present for the Kolmogorov-Smirnov的警告，是因为Kolmogorov–Smirnov检验假设数据是连续的，不存在同一个数值重复出现的情况，当数据中出现重复数值时，就会出现该警告，此时可以增加一个均匀扰动项x+runif(length(x),-0.05,0.05)参考链接，统计结果不会收到影响。

20.2 参数检验

20.2.1 独立样本t检验

当我们对两组相互独立的连续型数据进行比较时，如果这两组数据符合正态分布，可以通过独立样本t检验（参数检验）比较两组数据的总体均值是否有显著的差异；如果这两组数据不符合正态分布，则需要选择Mann-Whitney U检验（非参数检验）。对于符合正态分布的数据，方差齐性或方差不齐会影响检验方式的选择，当方差齐性时，选择Student’s t检验，当方差不齐时，选择Welch t检验，具体说明可参考此链接。两组数据的独立样本检验的具体流程如下：

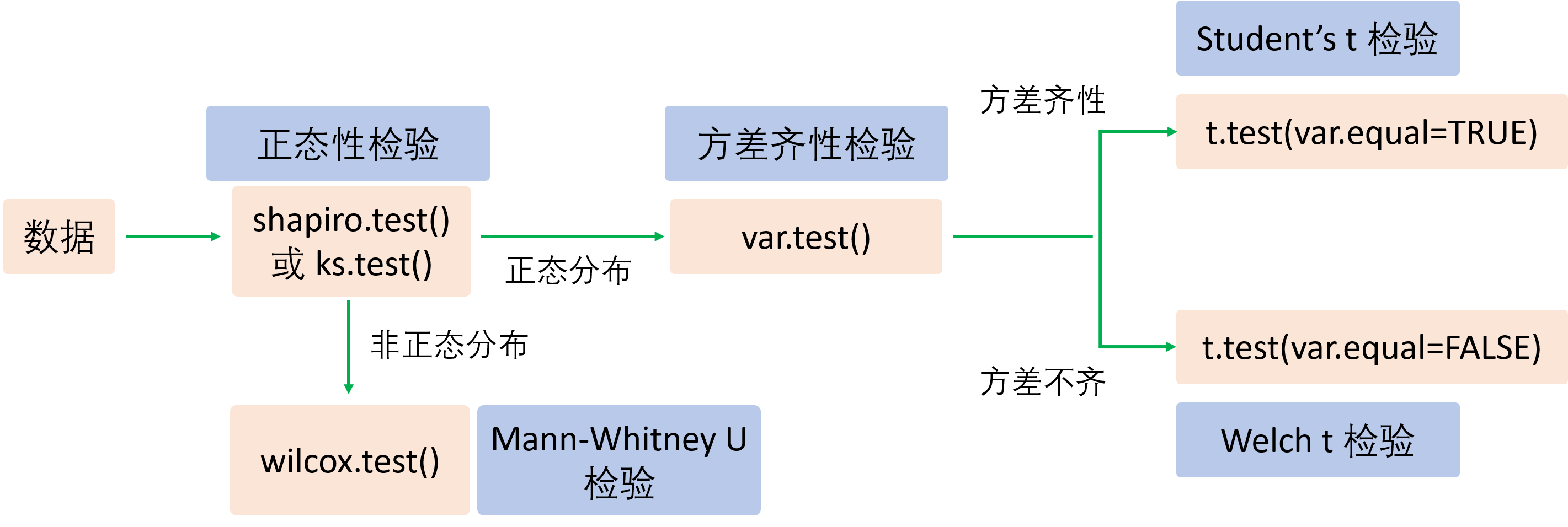
如果我们要对两所学校某次数学统考的成绩进行比较，就可以考虑独立样本检验。

library(tidyverse)
library(purrr) # 正常情况下只需要tidyverse，电子书生成需要调用
library(broom) # 正常情况下只需要tidyverse，电子书生成需要调用

# 创建数据框
set.seed(1)
df_ind <- data.frame(
  school1 = rnorm(n=2000, mean=75, sd=15),
  school2 = rnorm(n=2000, mean=80, sd=20)
)

# 批量进行正态分布检验
df_ind %>%
  pivot_longer( # 将宽数据转为长数据
    cols = starts_with("school"), # 选择需要进行数据转换的变量
    names_to = "school", # 设置存储目标变量的变量名
    values_to = "score" # 设置存储目标数据的变量名
  ) %>%
  nest( # 对数据按group打包成子数据框
    .by = school, # 设置打包分组
    .key = "score_value" # 设置存储新生成子数据框的变量名
  ) %>%
  mutate(
    t_model = map( # 使用map()函数创建新变量model用于存储正态性检验结果
      score_value, # 设置map()函数的目标变量
      ~ks.test( # 设置目标函数ks.test()进行正态性检验
        x=.x$score, # 设置目标数据
        y="pnorm", # 设置预期数据分布类型
        mean=mean(.x$score), # 设置预期正态分布均值
        sd=sd(.x$score) # 设置预期正态分布标准差
      )
    ),
    t_results = map( # 使用map()函数创建新变量results用于整理检验结果
      t_model, # 设置map()函数的目标变量
      ~tidy(.x) # 设置目标函数tidy()整理检验结果
    )
  ) %>%
  unnest(t_results) # 拆解results变量

## # A tibble: 2 × 7
##   school  score_value          t_model   statistic p.value method     alternative
##   <chr>   <list>               <list>        <dbl>   <dbl> <chr>      <chr>      
## 1 school1 <tibble [2,000 × 1]> <ks.test>    0.0147   0.781 Asymptoti… two-sided  
## 2 school2 <tibble [2,000 × 1]> <ks.test>    0.0153   0.739 Asymptoti… two-sided

# 方差齐性检验
var.test(x=df_ind$school1, y=df_ind$school2)

## 
##  F test to compare two variances
## 
## data:  df_ind$school1 and df_ind$school2
## F = 0.56529, num df = 1999, denom df = 1999, p-value < 2.2e-16
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.5178297 0.6171085
## sample estimates:
## ratio of variances 
##          0.5652939

# 方差不齐，采用 Welch t 检验
t.test(x=df_ind$school1, y=df_ind$school2, var.equal=FALSE)

## 
##  Welch Two Sample t-test
## 
## data:  df_ind$school1 and df_ind$school2
## t = -9.5521, df = 3711.7, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -6.664615 -4.394661
## sample estimates:
## mean of x mean of y 
##  74.79067  80.32031

对两所学校的数学成绩进行正态性检验发现，两组数据均呈现正态分布（P值分别为0.781和0.739）。方差齐性结果显示，两组数据方差不齐（P＜2.2e-16）。因此选择Welch t检验比较两组数据，结果显示两组数据之间有显著性差异（P＜2.2e-16）。

20.2.2 配对样本t检验

当我们需要对同一个样本的两次重复测试或同一对象经过两种不同处理后的结果进行比较时，可以采用配对检验。在进行配对检验之前，需要对两次测试的差值进行正态性检验，当差值符合正态分布时，采用t.test()函数进行配对样本t检验（参数检验）；当差值不符合正态分布时，采用wilcox.test()函数进行Wilcoxon符号秩和检验（非参数检验）。不论那种函数，都需要声明参数paired=TRUE。配对样本检验的具体流程如下：

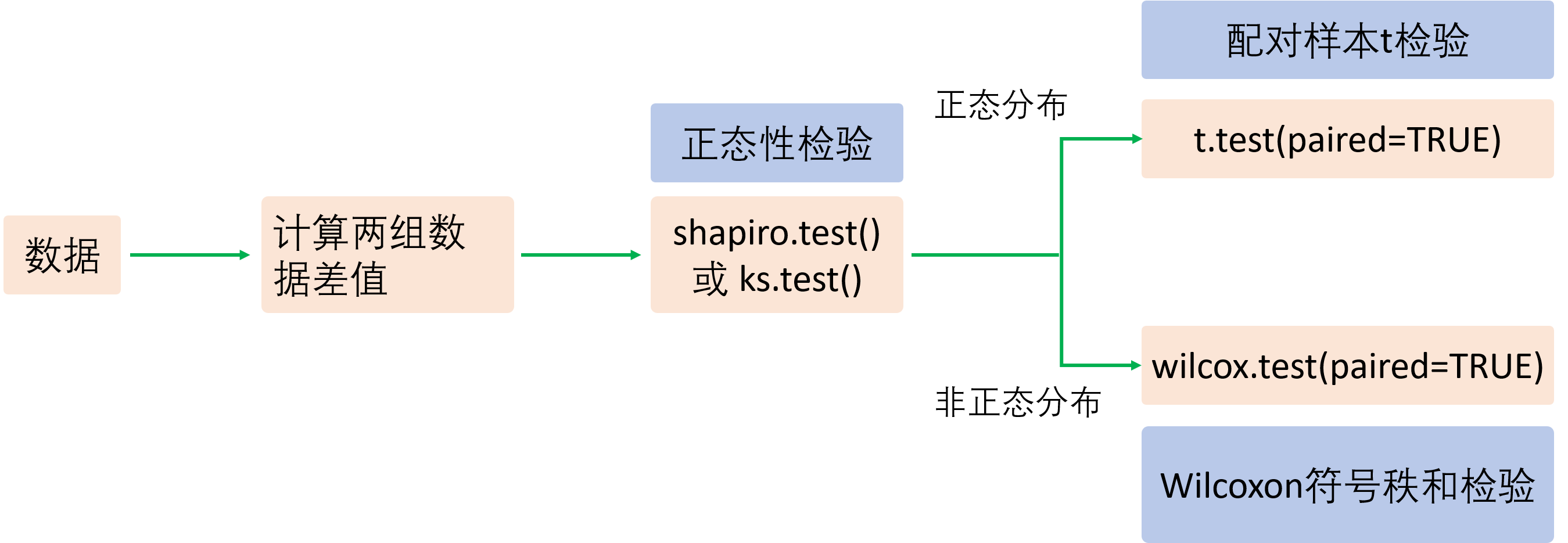
当我们想对同一个班期中与期末的数学考试成绩进行比较，看数学考试成绩是否有提高时，可以使用配对样本检验。

# 创建数据框
set.seed(1)
df_pair <- data.frame(
  t0 = rnorm(n=300, mean=50, sd=10)
)
df_pair <- df_pair %>% 
  rowwise() %>% # 逐行进行运算
  mutate(
    t1 = t0+rnorm(1, mean=10, sd=2), # 在t0基础上加一个符合N(10,4)正态分布的随机数
    t_delta = t1-t0
  ) 

# 对t1-t0差值进行正态性检验
shapiro.test(df_pair$t_delta)

## 
##  Shapiro-Wilk normality test
## 
## data:  df_pair$t_delta
## W = 0.99645, p-value = 0.7431

# 差值显著性>0.05，说明差值符合正态分布，进行配对样本t检验
t.test(x=df_pair$t0, y=df_pair$t1, paired=TRUE)

## 
##  Paired t-test
## 
## data:  df_pair$t0 and df_pair$t1
## t = -82.788, df = 299, p-value < 2.2e-16
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -10.215831  -9.741433
## sample estimates:
## mean difference 
##       -9.978632

配对样本t检验的显著性P＜0.05，说明期中与期末的数学考试成绩是有显著性差异的。再看Paired t-test结果里的mean difference（第一项t0减第二项t1）为负，说明期末成绩显著高于期中成绩。

20.2.3 单因素方差分析

当我们对两组以上相互独立的连续型数据进行比较时，如果不同组的数据均符合正态分布且满足方差齐性检验，则使用oneway.test()函数同时声明参数var.equal=TRUE进行单因素方差分析（参数检验）；如果不同组的数据均符合正态分布但不满足方差齐性时，则使用oneway.test()函数同时声明参数var.equal=FALSE进行Welch’s ANOVA检验；如果数据不符合正态分布，则需要使用kruskal.test()函数进行Kruskal-Wallis检验（非参数检验）。

单因素方差分析的方差齐性检验汇总如下：

检验方法	函数	包	描述	说明
Bartlett \(\chi^2\)检验	bartlett.test()	stats（R自带）	所检验的数据需要服从正态分布	当P＞0.05时，说明方差齐性
Levene检验	leveneTest()	car	所检验的数据可以不服从正态分布，结果更为稳健	当P＞0.05时，说明方差齐性

比如我们想对三所学校某次数学统考的成绩进行比较，看总体上的数学成绩是否有差异，如果有，我们想知道哪些班之间的成绩有差异，就可以用单因素方差分析。

library(car)

# 创建数据框
set.seed(1)
df_anova <- data.frame(
  school1 = rnorm(n=1000, mean=85, sd=4),
  school2 = rnorm(n=1000, mean=70, sd=10),
  school3 = rnorm(n=1000, mean=75, sd=30)
)

# 将数据转为长格式
df_anova_long <- df_anova %>% 
  pivot_longer(
    cols = starts_with("school"),
    names_to = "school",
    values_to = "score"
  )

# 批量进行正态性检验
df_anova_long %>%
  nest(
    .by = "school",
    .key = "score_value"
  ) %>%
  mutate(
    t_model = map(
      score_value,
      ~ks.test(x=.x$score, y="pnorm", mean=mean(.x$score), sd=sd(.x$score))
    ),
    t_results = map(
      t_model,
      ~tidy(.x)
    )
  ) %>%
  unnest(t_results)

## # A tibble: 3 × 7
##   school  score_value          t_model   statistic p.value method     alternative
##   <chr>   <list>               <list>        <dbl>   <dbl> <chr>      <chr>      
## 1 school1 <tibble [1,000 × 1]> <ks.test>    0.0178   0.911 Asymptoti… two-sided  
## 2 school2 <tibble [1,000 × 1]> <ks.test>    0.0186   0.878 Asymptoti… two-sided  
## 3 school3 <tibble [1,000 × 1]> <ks.test>    0.0204   0.797 Asymptoti… two-sided

# 各组数据均符合正态分布
# 进一步进行方差齐性检验，使用car包的leveneTest()函数
leveneTest(score~school, data=df_anova_long)

## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value    Pr(>F)    
## group    2  924.26 < 2.2e-16 ***
##       2997                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# 方差不齐，选择 Welch anova 检验
anova_group <- oneway.test(score~school, data=df_anova_long, var.equal=FALSE)
anova_group

## 
##  One-way analysis of means (not assuming equal variances)
## 
## data:  score and school
## F = 939.81, num df = 2.0, denom df = 1530.1, p-value < 2.2e-16

由于三所学校的数学分数均符合正态分布但是方差不齐，所以选择Welch anova检验进行组间差异分析，结果显示组间存在显著差异（P＜2.2e-16）。为进一步探究哪些学校的数学分数之间有显著差异，我们需要对学校进行两两比较（即事后检验）。常见检验方式的说明如下：

检验方法	函数	包	适用场景
Fisher’s LSD检验	LSD.test()	agricolae	组别较少时使用，使用最为广泛
Scheffe检验	ScheffeTest()	DescTools	各组样本量不同时使用
Tukey检验	TukeyHSD()	stats（R自带）	各组样本量相同时使用
Tamhane T2检验	pairwise.t.test(var.equal=FALSE)	stats（R自带）	数据符合正态分布但方差不齐时进行事后检验
BWS检验	bwsAllPairsTest()	PMCMRplus	非参数检验结果显著时的组间比较

由于多次检验会增加I类错误的概率，因此需要对组间比较所得的P值进行校正，常见的方法如下：

校正方法	函数	校正公式
Bonferroni校正	pairwise.t.test(p.adjust.method=‘bonferroni’)	\(\frac{\alpha}{n}\) \(\alpha\)为显著性水平 n为检验次数
Holm校正	pairwise.t.test(p.adjust.method=‘holm’)	\(\frac{\alpha}{n-i+1}\) \(\alpha\)为显著性水平 n为检验次数 i为原始P值从小到大排列的序号
fdr校正	pairwise.t.test(p.adjust.method=‘fdr’)	\(p^{adjusted}_{i} = min\{1,min_{j≥i}\{\frac{np_{j}}{j}\}\}\) i和j为原始P值从小到大排列的序号 \(p_j\)为排序为j的原始P值

多次检验校正的示意图如下：

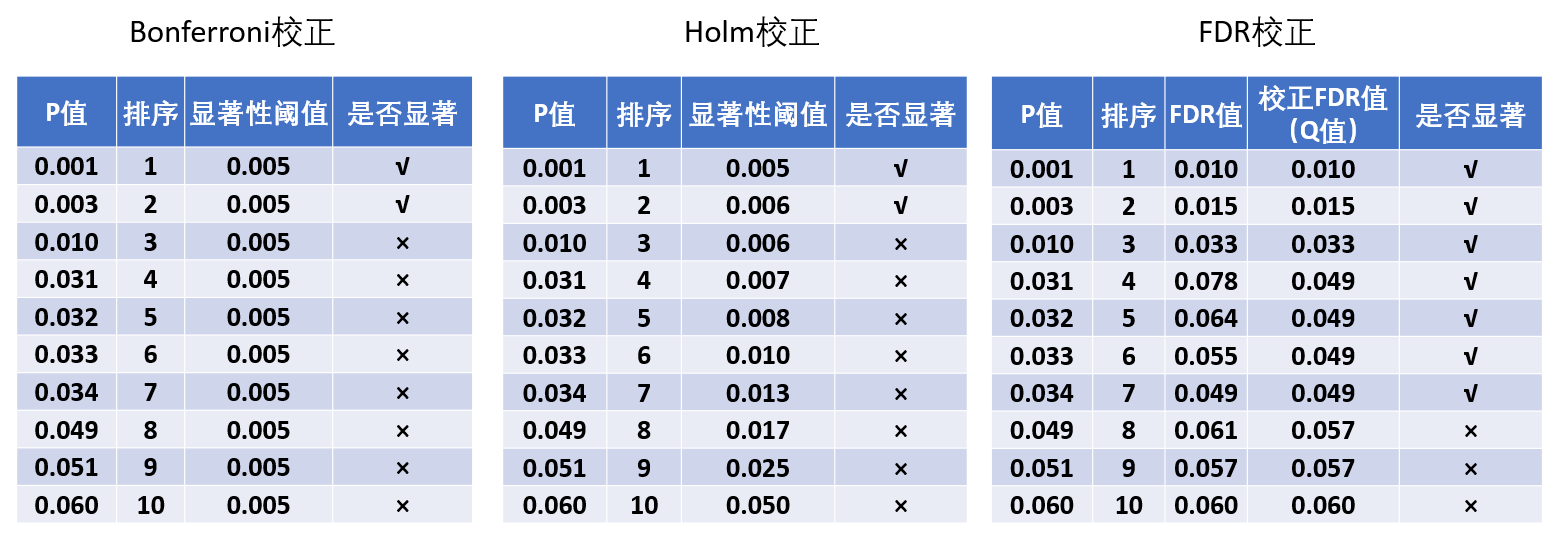
由于三所学校的数学分数均符合正态分布但是方差不齐，我们将使用Tamhane T2检验进行事后检验。

pairwise.t.test(
  x = df_anova_long$score,
  g = df_anova_long$school,
  var.equal=FALSE
)

## 
##  Pairwise comparisons using t tests with pooled SD 
## 
## data:  df_anova_long$score and df_anova_long$school 
## 
##         school1 school2
## school2 < 2e-16 -      
## school3 < 2e-16 4.3e-11
## 
## P value adjustment method: holm

结果显示，三所学校的数学分数之间均有显著性差异。

20.2.4 多因素方差分析

当我们需要对多个变量的多组独立数据进行分析时，可以采用多因素方差分析。比如，我们想要研究不同身高水平（“short”,“normal”,“tall”三个水平)的男女生（各600名）的数学得分之间是否有差异，就可以用多因素方差分析。

# 创建数据框
set.seed(1)
df_multi_anova <- data.frame(
  score = rnorm(n=1200, mean=80, sd=5),
  gender = rep(c("M","F"), each=600),
  height = rep(c("short", "normal", "tall"), times=400)
)

df_multi_anova <- df_multi_anova %>% 
  mutate(
    across(c(gender,height), ~as_factor(.x))
  )

# 对gender各组批量进行正态性检验
df_multi_anova %>%
  nest(
    .by = c("gender","height"),
    .key = "score_value"
  ) %>%
  mutate(
    t_model = map(
      score_value,
      ~ks.test(x=.x$score, y="pnorm", mean=mean(.x$score), sd=sd(.x$score))
    ),
    t_results = map(
      t_model,
      ~tidy(.x)
    )
  ) %>%
  unnest(t_results)

## # A tibble: 6 × 8
##   gender height score_value        t_model   statistic p.value method alternative
##   <fct>  <fct>  <list>             <list>        <dbl>   <dbl> <chr>  <chr>      
## 1 M      short  <tibble [200 × 1]> <ks.test>    0.0451   0.811 Asymp… two-sided  
## 2 M      normal <tibble [200 × 1]> <ks.test>    0.0414   0.882 Asymp… two-sided  
## 3 M      tall   <tibble [200 × 1]> <ks.test>    0.0458   0.796 Asymp… two-sided  
## 4 F      short  <tibble [200 × 1]> <ks.test>    0.0450   0.814 Asymp… two-sided  
## 5 F      normal <tibble [200 × 1]> <ks.test>    0.0396   0.913 Asymp… two-sided  
## 6 F      tall   <tibble [200 × 1]> <ks.test>    0.0524   0.642 Asymp… two-sided

# 各组数据均符合正态分布
# 对gender和height两个变量的数据进行方差齐性检验
leveneTest(score~gender, data=df_multi_anova)

## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value Pr(>F)
## group    1  2.2011 0.1382
##       1198

leveneTest(score~height, data=df_multi_anova)

## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value  Pr(>F)  
## group    2  2.4783 0.08432 .
##       1197                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# 数据正态分布，方差齐性均满足，进行多因素方差分析
multi_anova <- aov(score~gender+height, data=df_multi_anova)
knitr::kable(tidy(multi_anova)) # 通常使用summary(multi_anova)即可，此为电子书显示美观而用

term	df	sumsq	meansq	statistic	p.value
gender	1	36.075704	36.075704	1.3574245	0.2442167
height	2	4.639306	2.319653	0.0872818	0.9164246
Residuals	1196	31785.593490	26.576583	NA	NA

# 查看交互效应
inter_anova <- aov(score~gender*height, data=df_multi_anova)
knitr::kable(tidy(inter_anova)) # 通常使用summary(inter_anova)即可，此为电子书显示美观而用

term	df	sumsq	meansq	statistic	p.value
gender	1	36.075704	36.075704	1.3603964	0.2437017
height	2	4.639306	2.319653	0.0874729	0.9162495
gender:height	2	122.476825	61.238413	2.3092693	0.0997773
Residuals	1194	31663.116665	26.518523	NA	NA

20.2.5 重复测试方差分析

现有一项减肥药物的研究招募了1400名I度肥胖者，随机分成2组，1组使用A减肥药，1组使用B减肥药。受试者坚持服药6个月并在第0、3、6个月进行一次称重，数据记录在weight.csv文件中。现在我们想要分析：

1. 减肥药A和B的效果是否有不同？
2. 受试者服药后的体重是否有显著改变？
3. 减肥药与时间是否有交互作用？

要回答以上问题，我们可以使用重复测试方差分析。重复测试方差分析需要各组各水平的数据分布为正态分布。在进行分析之前，还需要对数据进行球形假设检验，已确定不同重复测试水平之间的协方差是否相等（相等则球形检验P值＞0.05）。如果球形假设检验不成立，则需要选择Greenhouse-Geisser（GG）或Huynh-Feldt（HF）校正的单因素分析或多因素分析。

如果用R自带包，需要分别进行球形假设检验与重复测试方差分析，过程较为繁琐。我们也可以使用ez包中的ezANOVA()函数完成此分析。

library(ez)

# 导入数据
weight_df <- read_csv("data/weight.csv")

# 显示前6行数据
weight_df %>% head() 

## # A tibble: 6 × 5
##      ID group    t0    t1    t2
##   <dbl> <chr> <dbl> <dbl> <dbl>
## 1     1 A      87.8  72    69.5
## 2     2 A      90.5  89.2  86.1
## 3     3 A     101.   93    88.4
## 4     4 A     107   101   100. 
## 5     5 A     107.  109   103. 
## 6     6 A     113.  100.   96.1

# 将数据转为长格式
weight_df_long <- weight_df %>% 
  pivot_longer(
    cols = c("t0","t1", "t2"),
    names_to = "time",
    values_to = "weight"
  )

# 显示前6行数据
weight_df_long %>% head()

## # A tibble: 6 × 4
##      ID group time  weight
##   <dbl> <chr> <chr>  <dbl>
## 1     1 A     t0      87.8
## 2     1 A     t1      72  
## 3     1 A     t2      69.5
## 4     2 A     t0      90.5
## 5     2 A     t1      89.2
## 6     2 A     t2      86.1

# 检验各水平数据是否符合正态分布
weight_df_long %>%
  nest(
    .by = c("group", "time"),
    .key = "weight_data"
  ) %>%
  mutate(
    t_model = map(
      weight_data,
      ~ks.test(x=.x$weight, y="pnorm", mean=mean(.x$weight), sd=sd(.x$weight))
    ),
    t_results = map(
      t_model,
      ~tidy(.x)
    )
  ) %>%
  unnest(t_results)

## # A tibble: 6 × 8
##   group time  weight_data        t_model   statistic p.value method   alternative
##   <chr> <chr> <list>             <list>        <dbl>   <dbl> <chr>    <chr>      
## 1 A     t0    <tibble [700 × 2]> <ks.test>    0.0332   0.422 Asympto… two-sided  
## 2 A     t1    <tibble [700 × 2]> <ks.test>    0.0233   0.842 Asympto… two-sided  
## 3 A     t2    <tibble [700 × 2]> <ks.test>    0.0220   0.887 Asympto… two-sided  
## 4 B     t0    <tibble [700 × 2]> <ks.test>    0.0250   0.775 Asympto… two-sided  
## 5 B     t1    <tibble [700 × 2]> <ks.test>    0.0270   0.689 Asympto… two-sided  
## 6 B     t2    <tibble [700 × 2]> <ks.test>    0.0226   0.868 Asympto… two-sided

# 进行重复测试方差分析
repeat_anova <- ezANOVA(
  data = weight_df_long, # 设置目标数据框（长数据）
  dv = weight, # 设置因变量
  wid = ID, # 设置受试者编号
  within = time, # 设置组内变量
  between = group # 设置组间变量
)

# 呈现重复测试方差分析结果
repeat_anova

## $ANOVA
##       Effect DFn  DFd          F            p p<.05        ges
## 2      group   1 1398   26.28103 3.365441e-07     * 0.01658596
## 3       time   2 2796 2686.77709 0.000000e+00     * 0.16503038
## 4 group:time   2 2796  148.47595 5.215233e-62     * 0.01080438
## 
## $`Mauchly's Test for Sphericity`
##       Effect         W            p p<.05
## 3       time 0.6884479 5.66169e-114     *
## 4 group:time 0.6884479 5.66169e-114     *
## 
## $`Sphericity Corrections`
##       Effect       GGe       p[GG] p[GG]<.05       HFe        p[HF] p[HF]<.05
## 3       time 0.7624554 0.00000e+00         * 0.7631179 0.000000e+00         *
## 4 group:time 0.7624554 5.17306e-48         * 0.7631179 4.728223e-48         *

输出结果一共包含三个表格。第一个表格为重复测试方差分析的结果。第二个表格为球形假设检验结果，当P值＜0.05时，说明各水平不符合球形假设，此时需要参考第三个表格进行自由度df校正，当e（epsilon）＜0.75时，建议使用Greenhouse-Geisser（GG）校正，反之，建议使用Huynh-Feldt（HF）校正。

根据表二的球形假设检验结果，time以及group-time的交互均不符合球形假设，所以需要参照表三进行df校正，此时由于表中的e＞0.75，所以选择HFe校正。

# time的组间自由度DFn校正
repeat_anova$ANOVA$DFn[2] * repeat_anova$`Sphericity Corrections`$HFe[1]

## [1] 1.526236

# time的组内自由度DFd校正
repeat_anova$ANOVA$DFd[2] * repeat_anova$`Sphericity Corrections`$HFe[1]

## [1] 2133.678

# group-time的组间自由度DFn校正
repeat_anova$ANOVA$DFn[3] * repeat_anova$`Sphericity Corrections`$HFe[2]

## [1] 1.526236

# group-time的组内自由度DFd校正
repeat_anova$ANOVA$DFd[3] * repeat_anova$`Sphericity Corrections`$HFe[2]

## [1] 2133.678

综合上述结果，我们来回答开头的问题：

1. 减肥药A和B的效果有显著不同，因为group项\(F_{(1,1398)}\)=26.28，P＜0.05。
2. 受试者服药后的体重有显著改变，因为time项\(F_{(1.53,2133.68)}\)=2686.78，P＜0.05。
3. 减肥药与时间存在有交互作用，因为group:time项\(F_{(1.53,2133.68)}\)=148.48，P＜0.05。

20.3 小结

检验方法	函数	描述	条件
Student’s t检验	t.test(paired=FALSE, var.equal=TRUE)	比较单个变量的两组独立数据（参数检验）	数据符合正态分布且方差齐性
Welch t检验	t.test(paired=FALSE, var.equal=FALSE)	比较单个变量的两组独立数据（参数检验）	各组数据符合正态分布且方差不齐
配对样本t检验	t.test(paired=TRUE)	比较单个变量的两组配对数据（参数检验）	数据差值符合正态分布
单因素方差分析	aov(Y~X)或oneway.test(Y~X) X为自变量 Y为因变量	比较单个变量的多水平独立数据（参数检验）	各组数据符合正态分布且方差齐性
多因素方差分析	aov(Y~X1+X2…) X为自变量 Y为因变量	比较多个变量的多组独立数据（参数检验）	各变量的各组数据符合正态分布且方差齐性
重复测试方差分析	aov(Y~B*W+Error(ID/W)) Y为因变量 B为组间变量 W为组内变量 ID为受试者ID 或使用ezANOVA()	比较单个变量的多组配对数据（参数检验）	单个变量各水平的重复测试数据符合正态分布
Mann-Whitney U检验	wilcox.test(paired=FALSE)	比较单个变量的两组独立数据（非参数检验）	数据不符合正态分布或方差不齐
Wilcoxon符号秩和检验	wilcox.test(paired=TRUE)	比较单个变量的两组配对数据（非参数检验）	数据差值不符合正态分布
Kruskal-Wallis检验	kruskal.test(paired=FALSE)	比较单个变量的多组独立数据（非参数检验）	数据不符合正态分布或方差不齐
Friedman M检验	kruskal.test(paired=TRUE)	比较单个变量的多组配对数据（非参数检验）	单个变量一些水平的重复测试数据不符合正态分布