Practical 4 Modelling with Regression and GWR

4.1 Part 1. Main Practical

4.1.1 Introduction

This session covers the following topics on regression modelling with data and spatial data:

• Ordinary Least Squares (OLS) regression
• Generalized Linear Model (GLM) regression
• Geographically Weighted Regression (GWR)

OLS and GLM are global regressions, in which the model coefficient estimates are fixed, or in statistical terminology, non-stationary. These assume the relationships between the response variable and predictor variables are the same everywhere. They return a single coefficient estimate to describe the relationship between the target variable and teach predictor variable. The GWR models are spatially varying coefficient models and generate coefficient estimates at each location for each predictor variable. As such they allow the spatial heterogeneity in modelled relationships to be explored and mapped (i.e. the model coefficient estimates vary locally).

The code below installs some packages. It does this by testing for the presence of each packages and installing the ones that are not present:

packages <- c("sf", "tidyverse", "tmap", "car", "GWmodel", "MASS")
# check which packages are not installed
not_installed <- packages[!packages %in% installed.packages()[, "Package"]]
# install missing packages
if (length(not_installed) > 0) {
  install.packages(not_installed, repos = "https://cran.rstudio.com/", dep = T)
}
# load the packages
library(sf)         # for spatial data
library(tidyverse)  # for data wrangling
library(tmap)       # for mapping
library(car)        # for outlier and regression tools
library(GWmodel)    # for GWR
# we will load MASS later!
# remove unwanted variables
rm(list = c("packages", "not_installed"))

And you will need to load the georgia data. This is a commonly used dataset in R. It has census data for the counties in Georgia, USA.

georgia <- st_read("georgia.gpkg", quiet = T)

You should examine this in the usual way:

# spatial data
georgia
summary(georgia)
# maps
tm_shape(georgia) + tm_borders()
tm_shape(georgia) + tm_polygons("MedInc")

You will see that georgia contains a number of variables for the counties including the percentage of the population in each County that:

• is Rural (PctRural)
• have a college degree (PctBach)
• are elderly (PctEld)
• that are foreign born (PctFB)
• that are classed as being in poverty (PctPov)
• that are black (PctBlack)

It also include the median income of the county (MedInc in dollars) which will be the target variable of the models of the OLS and GWR models.

The code below converts the MedInc variable to 1000s of USD:

# convert MedInc to 1000s of $
georgia %>%  mutate(MedInc = MedInc/1000) -> georgia

And as we have done some EDA now, you might want to explore the properties of the attributes in georgia layer. Do these summaries tell us anything useful? (Answer: yes they do!)

Note the use of dplyr::select below to force R to use the select function in dplyr (other functions called select may have been loaded by other packages).

## Plot 1. variable histograms
# set the pipe and drop the sf geometry
georgia %>% st_drop_geometry() %>% 
  # select the numerical variables of interest
  dplyr::select(ID, TotPop90:PctBlack, MedInc) %>%
  # convert to long format
  pivot_longer(-ID) %>%
  # pass to a faceted ggplot 
  ggplot(aes(x = value)) + geom_histogram(bins = 30, col = "red", fill = "salmon") + 
  facet_wrap(~name, scales = "free", ncol = 4)
## Correlations
cor.tab = georgia %>% st_drop_geometry() %>% 
  dplyr::select(MedInc, TotPop90:PctBlack) %>% cor() 
round(cor.tab, 3)
# Plot 2. paired scatterplots
plot(st_drop_geometry(georgia[, c(14, 3:8)]), 
     pch = 1, cex = 0.7, col = "grey30", upper.panel=panel.smooth)

4.1.2 OLS regression for continuous variables

In this first sub-section, we will fit an OLS estimated linear regression and interrogate its fit in terms of R-squared, predictor variable significance, and the strength of the relationships through the coefficient estimates.

In R we can construct a regression model using the function lm which stands for linear model. This is a standard ordinary regression function, and although simple it is very powerful. There are many variants and functions for manipulating lm outputs: remember R was originally a stats package.

The equation for a regression is:

\[y_i = \beta_{0} + \sum_{m}^{k=1}\beta_{k}x_{ik} + \epsilon_i\]

where \(y_i\) is the response variable for observation \(i\), \(x_{ik}\) is the value of the \(k^{\textsf{th}}\) predictor variable for observation \(i\), \(m\) is the number of predictor variables, \(\beta_{0}\) is the intercept term, \(\beta_{k}\) is the regression coefficient for the \(k^{th}\) predictor variable and \(\epsilon_i\) is the random error term for observation \(i\).

The basic formula in R to specify a linear regression model, lm is as follows:

model = lm(variable_we_are_trying_to_predict ~ predictor_variable1 +
              predictor_variable2...)

For illustration, we will fit the following OLS regression, to model median income:

ols_mod1 = lm(formula = MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
              data = georgia)

The OLS regression can be inspected using summary:

summary(ols_mod1)

## 
## Call:
## lm(formula = MedInc ~ PctRural + PctBach + PctEld + PctFB + PctPov + 
##     PctBlack, data = georgia)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -12.4203  -2.9897  -0.6163   2.2095  25.8201 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 52.59895    3.10893  16.919  < 2e-16 ***
## PctRural     0.07377    0.02043   3.611 0.000414 ***
## PctBach      0.69726    0.11221   6.214 4.73e-09 ***
## PctEld      -0.78862    0.17979  -4.386 2.14e-05 ***
## PctFB       -1.29030    0.47388  -2.723 0.007229 ** 
## PctPov      -0.95400    0.10459  -9.121 4.19e-16 ***
## PctBlack     0.03313    0.03717   0.891 0.374140    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.155 on 152 degrees of freedom
## Multiple R-squared:  0.7685, Adjusted R-squared:  0.7593 
## F-statistic: 84.09 on 6 and 152 DF,  p-value: < 2.2e-16

4.1.2.1 Interpreting a regression model

There are lots of things to look at in the summary of the model but we will focus on 3 aspects:

First, Significance. If we examine the model we can see that nearly all are significant predictors of median income. The level of significance is indicated by the p-value in the column \(Pr(>|t|)\) and the asterisks \(*\). For each coefficient \(\beta_k\) these are the significance levels associated with the NULL hypothesis \(\textsf{H}_0 : \beta_k = 0\) against the alternative \(\textsf{H}_0 : \beta_k \ne 0\). This corresponds to the probability that one would obtain a \(t\)-statistic for \(\beta_k\) at least as large as the one observed given \(\textsf{H}_0\) is true.

The p-value provides a measure of how surprising the relationship is and indicative of whether the relationship between \(x_k\) and \(y\) found in this data could have been found by chance. Very small p-values suggest that the level of association found here could have come from a random sample of data if \(\beta_k\) really is zero. Cutting to the chase, small p-values mean strong evidence for a non-zero regression coefficient (i.e. significance), So in this case we can say:

• ‘changes in PctFB are significantly associated with changes in MedInc at the \(0.01\) level’. This means that the association between the predictor and the response variables is not one that would be found by chance in a series of random samples \(99\%\) of the time. Formally we can reject the Null hypothesis that there is no relationship between changes in MedInc and PctFB
• ‘changes in PctRural, PctBach, PctEld, and PctPov are significantly associated with changes in MedInc at the at the \(<0.001\) level’, which is actually an indicator of less than \(0.001\). So were are even more confident that the observed relationship between these variables and MedInc are not by chance and can again confidently reject the Null hypotheses.
• PctBlack was not found to be significantly associated with MedInc.

Second, the Coefficient Estimates. These are the \(\beta_{k}\) values that tell you the rate of change between \(x_k\) and \(y\) in the column ‘Estimate’ in the summary table. The first of these is the Intercept - this is \(\beta_0\) in the regression equation and tells you the value of \(y\) if \(x_1 \cdots x_k\) are all zero.

For the dependent or predictor variables, \(x_k\), we can now see how changes of 1 unit for the different predictor variables are associated with changes in MedInc:

• The association of PctRural is positive but small: each increase in 1% of PctRural is associated with an increase of $73.7 in median income (0.0737 x $1000);
• The association of PctBach is positive, with each additional 1% of the population with a bachelors degree associated with an in increase of $697;
• each increase of 1% of PctEld is associated with a decrease in median income of $789;
• each increase of 1% of PctFB is associated with a decrease in median income of $1290;
• each increase of 1% of PctPov is associated with a decrease in median income of $954;

So the regression model m gives us an idea of how different factors are associated with the target variable for Median Income in the counties of the state of Georgia and their interaction.

Third, the model fit given by the \(R^2\) value. This provides a measure of model fit. This is calculated as the difference between the actual values of \(y\) (e.g. of MedInc) and the values predicted by the model - sometimes written as \(\hat{y\ }\) (called ‘\(y\)-hat’). A good description is here http://blog.minitab.com/blog/adventures-in-statistics-2/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-goodness-of-fit

Generally \(R^2\)’s of greater than 0.7 indicate a reasonably well fitting model. Some researchers describe low \(R^2\) as ‘bad’ - they are not - it just means you a have a more imprecise model - the predictions are a bit wrong-er! Essentially there is a sliding scale of reliability of the predictions - based on the relative amounts of deterministic and random variability in the system being analysed - and \(R^2\) is a measure of this.

4.1.2.2 Investigating the residuals

We are particularly interested in residual outliers - these are records that the model does not describe very well, either vastly over-predicting or under-predicting the target variable (MedInc).

For this situation, a useful diagnostic is the studentised residual. For different values of predictors, the expected difference between the actual and fitted \(y\) values has a different variance even if the theoretic model gives \(\epsilon_i\) a constant variance. This discrepancy is due to issues such as collinear predictors. Standardised variables attempt to compensate for this. Plotting these and looking for notably high or low values is a helpful way of spotting outliers in the regression model.

The residuals can be summarised:

summary(ols_mod1$residuals)

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -12.4203  -2.9897  -0.6163   0.0000   2.2095  25.8201

And a simple way of examining is just to plot the standardised residuals in order:

s.resids <- rstudent(ols_mod1)
plot(s.resids,type='h')
abline(h=c(-2,2),col='lightskyblue')

Here we see some residuals for some counties are relatively high. Normally, one might expect standardised residuals to lie between -2 and 2. Adding lines to this plot helps to identify when this is not the case - as is done above.

Finally, we need to check another model assumption in lm - that the error term \(\epsilon_i\) are normally distributed. The best way to do this is via a qq-plot which plots the empirical quantiles of a variable whose distribution we are interested in against the theoretical distribution we are testing for. If the variable is from this distribution, the results should yield a straight line - frequently a reference line is provided to test this. Here s.resids is the variable of interest - the studentised residuals, and these are compared to the \(t\) distribution. Although \(\epsilon_i\) have a normal distribution, theory shows that the studentised residuals derived from a sample coming from this model have a \(t\) distribution. However, the qqPlot function from the package car does all the work, and requires only the regression model object to create a plot:

qqPlot(ols_mod1)

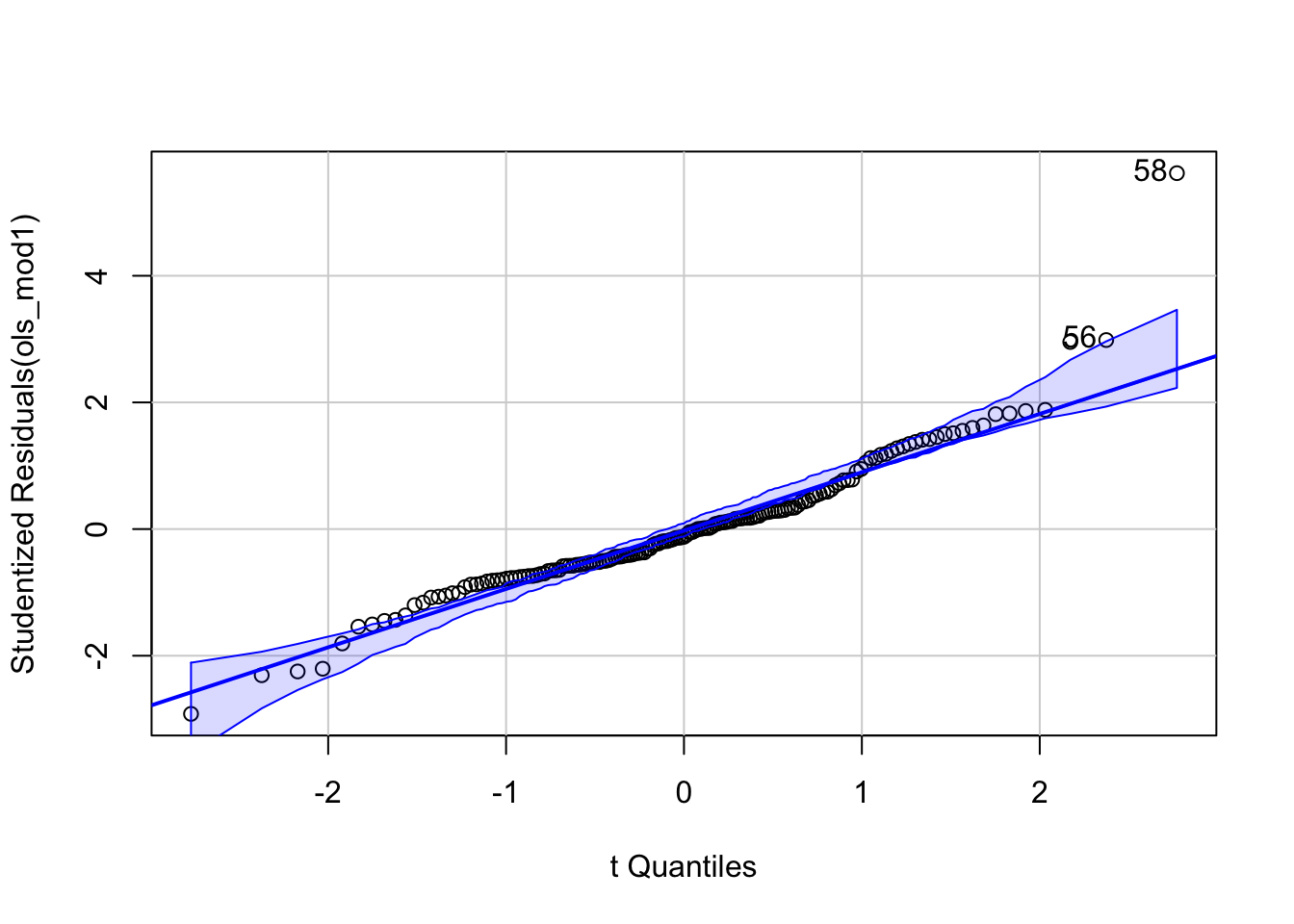
Figure 4.1: A qqplot, showing the outliers.

This demonstrates that mostly, the residuals do conform to this, but with a number of extreme outliers at the higher end - some of them are labelled in the plot. The optional analyses in Part 2 describes how these could be addressed if they were thought to be a problem.

4.1.2.3 Using the model to predict

Back to the model. There are 2 other things to note:

First, the phrasing of the interpretation of the model outputs is key:

• “each additional 1% of the population that has a degree is associated with an increase of $69.7 in median income”
• “each additional 1% of the population that is elderly is associated with an increase of $-789 in median income” (i.e. a decrease)
• etc

This is inference. These enhance our understanding of the process being investigated. We are not as yet able to say anything about what is causing these variations in Median Income as we have no theoretical model to infer causality.

Second, the model can be used for Prediction, either manually or using the predict function. In this case, the aim is to predict county level Median Income given new values for the model factors (dependent or predictor variables). The table below shows some hypothetical data for hypothetical Counties and the predicted Median Income for these:

# create some test data 
test = data.frame(
  PctRural = c(10, 70, 50, 70, 10),
  PctBach  = c(5, 5, 10, 10, 25),
  PctEld   = c(2, 5, 5, 12, 15),
  PctFB    = c(1, 1, 1, 5, 5),
  PctPov   = c(20, 10, 8, 25, 25),  
  PctBlack = c(5, 75, 20, 30, 75)) 
# predict using the model
predIncome = round(predict(ols_mod1, newdata = test), 3)
# display
data.frame(test, Predicted.Income = predIncome)

Table 4.1: Predicted Median Income values from the model ‘m’

PctRural	PctBach	PctEld	PctFB	PctPov	PctBlack	Predicted.Income
10	5	2	1	20	5	35.041
70	5	5	1	10	75	48.961
50	10	5	1	8	20	51.057
70	10	12	5	25	30	25.964
10	25	15	5	25	75	31.122

Prediction will be returned to in later weeks. But you should know that this is an important function of regression models.

4.1.3 Generalised Linear Models (GLMs)

An important assumption in OLS is that the \(y_i\) variable is assumed to have a normal distribution, whose mean is determined by the predictor variables (as \(\beta_0 + \sum_k \beta_kx_{ik}\) ) and whose variance is \(\sigma^2\). For many data, this is not the case: counts, binary responses (Yes/No, True/False, etc). These cases are briefly considered in this section.

4.1.3.1 Poisson Regression for count variables

Suppose the value of \(y_i\) was a count of some phenomenon - for example the number of crimes committed in a month, or the number of houses sold (rather than the price). Then, the normal distribution is not a sensible model because:

• \(y_i\) can only take integer values
• \(y_i\) takes a minimum value of zero

or, more bluntly, \(y_i\) is not normally distributed! Typically count data are modelled by the Poisson distribution:

\[ \textsf{Prob}(y_i=j) = \frac{e^{-\lambda}\lambda^j}{j!} \] where \(\lambda\) is the mean value of \(y_i\). There is a constraint that \(\lambda > 0\). Here \(\lambda\) is a constant parameter, but if this depended on some predictor variables, we would have a prediction model similar to OLS, but with \(y_i\) as a Poisson distributed count variable rather than a normally distributed continuous one. In principal, one could specify the model so that \(\lambda_i\), the mean value for observation \(i\), is given by \(\lambda_i = \beta_0 + \sum_k\beta_kx_{ij}\) however, this could lead to problems if a negative value of \(\lambda_i\) were predicted. One way of overcoming this is to specify a log-transformed relationship:

\[ \log(\lambda_i) = \beta_0 + \sum_{k=1}^{k=m} \beta_k x_{ik} \]

which is the standard form for Poisson regression.

Taking antilogs on both sides, the effect on the expected value is a multiplicative one:

\[ \lambda_i = e^{\beta_0} \times e^{\beta_1 x_{i1}} \times \cdots e^{\beta_k x_{ik}} \]

so that the expected number of observations changes by a scale factor (i.e. a ratio) for a unit change in a predictor variable. In particular for a coefficient \(\beta_k\), the factor is \(e^{\beta_k}\) - this is useful in interpreting the model.

A final - and extra - feature found in some Poisson regression model is the idea of an offset. For many geographical count-based regressions, there is a ‘population at risk’ - for example the total population of an area when counting people having a particular illness. In this case an expected count is essentially a rate of occurrence multiplied by the population at risk. The model can be written as

\[ \lambda_i = P_i \times e^{\beta_0} \times e^{\beta_1 x_{i1}} \times \cdots e^{\beta_k x_{ik}} \] where \(P_i\) is the population at risk. Writing \(P_i\) as \(e^{\log(P_i)}\) this is really just another predictor term (in \(\log(P_i)\)) but with the coefficient being fixed at the value 1, rather than being calibrated. Such a term can be specified in R - and is referred to as an offset term.

Here, we will use a data set based on UK crime reporting data - as made available via the police.uk web site. The code below loads a sf object called lsoa_imd, loaded from the R binary format file:

load('lsoa_imd.RData')

And you could examine this:

lsoa_imd

In this case, burglary reports for a one month period in Newcastle upon Tyne are counted for the geographical lower-level super output areas (LSOAs). The response variable is burgs, the count of reported burglaries. This is the \(y\)-variable. A number of variables are used as predictor variables:

• IMD_score: the Index of Multiple Deprivation - an index of economic and social deprivation. Higher values correspond to more deprived areas.
• dens: the population density of each LSOA (people per hectare) - this is a measure of degree of rurality/urban-ness
• popn: the population at risk - the log of this will be the offset variable here.

The regression is set out below:

crime_model <- glm(formula = burgs~dens + IMD_score + offset(log(popn)),
                   data=lsoa_imd, 
                   family=poisson())
summary(crime_model)

## 
## Call:
## glm(formula = burgs ~ dens + IMD_score + offset(log(popn)), family = poisson(), 
##     data = lsoa_imd)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.9792  -1.3341  -0.1743   0.2937   5.7159  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -7.611e+00  1.760e-01 -43.232  < 2e-16 ***
## dens         6.727e-05  2.020e-03   0.033  0.97344    
## IMD_score    1.080e-02  3.293e-03   3.280  0.00104 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 274.86  on 174  degrees of freedom
## Residual deviance: 264.40  on 172  degrees of freedom
## AIC: 519.14
## 
## Number of Fisher Scoring iterations: 5

The density coefficient, although positive, is not significant. The index of multiple deprivation is significant, suggesting a strong linkage between burglary risk and higher levels of deprivation. The value of the coefficient is 0.0108 - and the antilog of this is 1.0109 suggesting that if the IMD increases by one unit, this corresponds to around 1% rise in the risk of burglary. The code for extracting such statements is below - note the use of the antilog function, exp to interpret the coefficients:

# coefficients
beta <- coef(crime_model)
beta

##   (Intercept)          dens     IMD_score 
## -7.610940e+00  6.726884e-05  1.079957e-02

# antilogs 
exp(beta) 

##  (Intercept)         dens    IMD_score 
## 0.0004950064 1.0000672711 1.0108580958

This shows that an increase of one unit of IMD corresponds to 1% rise in the risk of burglary.

Finally we can use the antilog of the coefficient estimates to generate confidence intervals that show the range of plausible values (i.e. within a 95% probability of not being found by chance), in absence of a model fit statistic. This shows that an increase in 1 of IMD corresponds to a increases in crime that potentially range from 0.4% to 1.7%:

# confidence intervals
exp(confint(crime_model, level = 0.95))

## Waiting for profiling to be done...

##                   2.5 %       97.5 %
## (Intercept) 0.000348045 0.0006942827
## dens        0.995965750 1.0038902772
## IMD_score   1.004299656 1.0173621388

4.1.3.2 Binomial Logistic Regression for binary variables

The final part of the practical undertakes a logistic regression using a GLM. Remember, GLMs allow models to be specified in situations where the response and / or the predictor variables do not have a normal distribution. An example is where the response is a True / False, Yes / No or 1 / 0.

The practical replicates some of the results from A. J. Comber, Brunsdon, and Radburn (2011), evaluating geographic and perceived access to health facilities. It develops an analysis of a binary response variable describing perceptions of difficulty in GP access using data collected via a survey.

You should load some new data :

data.pt = st_read("place_survey_pts.gpkg", quiet = T)

Have a look at this data and its attributes in the usual way:

summary(data.pt)
tmap_mode("view")
tm_shape(data.pt)+
  tm_dots(col = "#FB6A4A80")+
  tm_basemap('OpenStreetMap')
tmap_mode("plot")
data.pt

You should see that the 8530 data points are distributed around Leicestershire and that there are a number of attributes of potential interest.

What we are interested in this analysis is the degree to which different factors can examine respondent perceptions of their difficulty in accessing GP surgeries. The following variables will be used in this analysis: GP, Health, Illness, Doc and Cars. These relate to the respondent characteristics:

• GP: perceptions of difficulty in their access to GPs;
• Health: their declared health status;
• Illness: whether they have a limiting long term illness;
• Doc: distance from the respondent’s home postcode to the nearest GP surgery - this was calculated after the survey;
• cars: the number of cars they own, specifically we can use this to determine non-car ownership.

A bit of pre-processing is needed to get these into a format that is suitable for analysis. First the data is subsetted to include the variables of interest.

data.pt <- data.pt %>% dplyr::select(GP, Health, Illness, Doc, cars) 

The text descriptions for GP, Health, Illness and cars need to be converted to binary variables and the piping syntax with transmute can be used to wrangle our data into a suitable format:

# convert the data 
data.pt %>% 
  transmute(
    DocDiff = (GP == "Fairly difficult" | GP == "Very difficult")+0,
    BadHealth = (Health == "Bad" | Health ==    "Very bad")+0,
    Illness = (Illness == "Do have")+0,
    NoCar = (cars == 0)+0,
    DocDist = Doc/1000) -> data.pt

Note that the code snippet above has converted the logical TRUE and FALSE values to 1s and 0s by adding the +0 to the end of the logical tests, and that distance has been converted to km.

data.pt

## Simple feature collection with 8530 features and 5 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 428996.3 ymin: 278160.6 xmax: 488368.7 ymax: 339447.7
## Projected CRS: OSGB36 / British National Grid
## First 10 features:
##    DocDiff BadHealth Illness NoCar   DocDist                      geom
## 1        0         0       0     0 4.0977625 POINT (440376.8 300305.5)
## 2        0         0       0     0 3.3847649 POINT (440376.8 300305.5)
## 3        0         0       0     0 3.5586326 POINT (440376.8 300305.5)
## 4        0         0       0     0 3.1351070   POINT (439700 305037.9)
## 5        1         0       0     0 3.0747871   POINT (439700 305037.9)
## 6        1         0       0     0 2.7230989   POINT (439700 305037.9)
## 7        0         0       0     0 3.6944257 POINT (439571.9 306769.6)
## 8        0         0       0     0 3.8510225 POINT (439571.9 306769.6)
## 9        0         0       0     0 1.1882823 POINT (443344.2 305529.1)
## 10       0         0       0     0 0.4131231 POINT (442862.8 305615.2)

We are now in a position to create a logistic regression model and have a look at the results - note the specification of the family as binomial with a specified link. Logistic regression should be used when modelling a binary outcome from a set of continuous and / or binary predictor variables:

#create the model
m.glm = glm(formula = DocDiff~Illness + BadHealth + DocDist + NoCar, 
            data = data.pt, 
            family= binomial(link = "logit"))
# inspect the results
summary(m.glm) 

## 
## Call:
## glm(formula = DocDiff ~ Illness + BadHealth + DocDist + NoCar, 
##     family = binomial(link = "logit"), data = data.pt)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.4904  -0.3166  -0.2418  -0.2055   2.8609  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -4.10048    0.10373 -39.530  < 2e-16 ***
## Illness      0.58943    0.11042   5.338 9.39e-08 ***
## BadHealth    0.52257    0.17616   2.966  0.00301 ** 
## DocDist      0.29524    0.02988   9.879  < 2e-16 ***
## NoCar        1.33701    0.11031  12.121  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3318.6  on 8529  degrees of freedom
## Residual deviance: 3039.5  on 8525  degrees of freedom
## AIC: 3049.5
## 
## Number of Fisher Scoring iterations: 6

This shows that all of the inputs are significant predictors of experiencing difficulty over GP access. This model is of the form:

\[\begin{equation} pr(y_1 = 1) = logit(\beta_0 + \beta_{1}x_{1}+\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{4}) \label{eq:eglm} \end{equation}\]

where \(y_1\) is a 0/1 indicator showing whether the respondent expressed difficulty in their access to GPs, \(x_1\) is an 0/1 indicator variable showing whether the respondent said they had a Long Term Illness, \(x_2\) is an indicator variable stating whether the respondent considered they were in Bad Health, \(x_3\) is the distance from the respondent to their nearest GP surgery based on road network distance and \(x_4\) is a 0/1 indication of car ownership.

So what does the model say? We can use the exponential of the coefficient estimates to generate probabilities (odds ratios) and confidence intervals that show the range of plausible values (i.e. within a 95% probability of not being found by chance), in absence of a model fit statistic.

# odds ratios
exp(coef(m.glm)) 

## (Intercept)     Illness   BadHealth     DocDist       NoCar 
##  0.01656477  1.80295494  1.68634808  1.34344909  3.80765553

# confidence intervals
exp(confint(m.glm, level = 0.95)) 

## Waiting for profiling to be done...

##                  2.5 %    97.5 %
## (Intercept) 0.01346685 0.0202271
## Illness     1.45106558 2.2376869
## BadHealth   1.18425653 2.3651566
## DocDist     1.26583777 1.4233458
## NoCar       3.06412578 4.7230562

What these show is that there are significant statistical relationships between a number of variables and experiencing difficulty in access to GPs. Specifically the proportion of respondents experiencing GP access difficulty…

• increases with Long Term Illness (1.8x more likely, with a CI or likely range of between 1.5 and 2.2 than without it);
• increases with a lack of car ownership (3.8x more likely than for those who own a car);
• increases if the respondent has Bad Health (1.7x more likely);
• increases by 34% (1.34) per extra km distance to the nearest GP surgery.

These show how these factors are associated with experiencing difficulty in accessing GPs and particularly that distance as well as the other factors, is a good predictor of experiencing access difficulty to GPs. The paper by A. J. Comber, Brunsdon, and Radburn (2011) has very slightly different results due to some data cleaning differences. It also shows how these odds ratio (likelihoods) vary spatially and demonstrates that distance does not work in this way for hospitals (one of the main aims of the paper was to unpick access and accessibility in the health and geography literature).

4.1.4 Geographically Weighted Regression

Regression of some kind underpins many statistical models. However often they make one massive assumption: that the relationships between the \(x_k\)’s and \(y\) are the same everywhere. Regression models (and most other models) are aspatial and because they consider all of the data in the study area in one universal model, they are referred to as Global models. For example, in the models seen in this session so far the assumption is that the contributions made by the different variables in predicting the target variable are the same across the study area. In reality this assumption of spatial invariance is violated in many instances when geographic phenomena are considered.

For these reasons, as a geographer….

• I do not expect things to be the same everywhere
• I expect to find clusters, hotspots etc
• I am interested in how and where processes, relationships, and other phenomena vary spatially**

In statistical terminology… I am interested in spatial non-stationarity in relationships and process spatial heterogeneity.

What this means is that instead of just one general relationship for, for example, the association between changes in MedInc and PctBach in the OLS model in Section 2, I might expect that relationship (as described in the coefficient estimate for \(\beta_k\)) to be different in different places. This is a core concept for geographical data analysis.

This idea informs the technique known as Geographically Weighted Regression or GWR (Brunsdon, Fotheringham, and Charlton 1996). If the relationships between the \(x_k\)’s and \(y\) vary spatially, one might at least expect that the relationship between nearby sets of observations should be consistent.

Recall that the equation for an OLS regression is:

\[y_i = \beta_{0} + \sum_{m}^{k=1}\beta_{k}x_{ik} + \epsilon_i \]

as above.

Suppose we assign a value of each regression coefficient to a location \((u,v)\) in space (e.g. \(u\) is an easting and \(v\) a northing), so that we denote it \(\beta_{k(u,v)}\). Thus we could estimate each \(\beta_{k(u,v)}\) by calibrating a weighted regression model where \(w_i\) was 1 if an observation was within some radius \(h\) of \((u,v)\) and 0 otherwise.

In this way, an entire surface of coefficients could be estimated. It may be imagined as being generated by a moving circular window, scanning across a map of the locations of the observations. However, 0/1 weighting is quite crude, and one might expect data from the periphery of the circular window to have less spatial influence than data near the middle.

This is a Geographically weighted regression that examines how that relationships between \(y\) and \(x\) vary spatially:

\[y = \beta_{0_(u_i, v_i)} + \sum_{m}^{k=1}\beta_{k}x_{ik_{(u_i, v_i)}} + \epsilon_{(u_i, v_i)}\]

Thus, critical to the operation of GW models is a moving window or kernel, that downweights peripheral observations. The kernel moves through the study area and at each location computes a local model. It uses data under the kernel to construct a (local) model at that location with data points further away from the kernel centre weighted to that they contribute less to the solution. Hence the weighted element in the GW framework. Thus, the kernel defines the data and weights that are used to calibrate the model at each location. The weight, \(w_i\), associated with each location \((u_i, v_i)\) is a decreasing function of \(d_i\), the distance from the centre of the kernel to \((u_i, v_i)\):

A typical kernel function for example is the bisquare kernel. For a given size or bandwidth \(h\), this is defined by \[ f(d) = \left\{ \begin{array}{cl} \left(1 - \left( \frac{d}{h} \right)^2 \right)^2 & \mbox{ if $d < h$}; \\ & \\ 0 & \mbox{ otherwise.} \end{array} \right. \] Here \(h\) may be defined as a fixed value, or in an adaptive way. Gollini et al. (2015) provide a description of common kernels shape used in GW models. Generally larger values of \(h\) result in a greater degree of spatial smoothing - having a larger window around \(\mathbf{u}\) in which cross tabulations have non-zero weighting. As \(h \rightarrow \infty\) the coefficients converge to the global OLS model.

4.1.4.1 Creating a GWR

Here we will use the GWmodel package to undertake a GWR of the georgia data, replicating the OLS model, but this time allowing the coefficient estimates to vary over space.

There are 2 basic steps to any GW approach:

1. Determine the optimal kernel bandwidth \(h\) (i.e. how many data points - or which size window - to include in each local model). Here an AIC approach is used. This is the recommended fit measure - see Comber et al (2022) for discussion of this.
2. Fit the GWR model.

Note that the code below uses the sp version of the data.

# convert the georgia data to sp format
georgia_sp = as(georgia, "Spatial")
# determine the kernel bandwidth
bw <- bw.gwr(formula = MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
             approach = "AIC",
             adaptive = T, 
             data = georgia_sp) 
# fit the GWR model
gwr.mod <- gwr.basic(formula = MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
                     adaptive = T,
                     data = georgia_sp, 
                     bw = bw)  

You should have a look at the bandwidth: it has a value of 81 indicating that the nearest 81 data points (51% of the data - there are 159 records) will be used in each local regression.

bw

## [1] 81

You should have a look at the GWR outputs:

gwr.mod

The code above prints out the whole model summary. You should compare the Summary of GWR coefficient estimates with the outputs of the ordinary regression model coefficient estimates, also included in the GWR print out:

# table of GWR coefficients
t1 = apply(gwr.mod$SDF@data[, 1:7], 2, summary)
# OLS coefficients
t2 = coef(ols_mod1)
# joint together with a row bind
tab <- rbind(t1, t2)
# add name to last row of tab
rownames(tab)[7] <- "Global"
# transpose tab
tab <- t(round(tab, 3))
tab

Table 4.2: Comparison of Global and Local model coefficients.

	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.	Global
Intercept	42.686	48.206	52.833	52.948	56.936	63.306	52.599
PctRural	0.015	0.052	0.070	0.079	0.112	0.160	0.074
PctBach	0.262	0.553	0.649	0.712	0.899	1.362	0.697
PctEld	-1.275	-0.991	-0.864	-0.889	-0.781	-0.509	-0.789
PctFB	-3.465	-2.343	-1.312	-1.440	-0.627	1.013	-1.290
PctPov	-1.744	-1.269	-0.866	-0.928	-0.507	-0.415	-0.954
PctBlack	-0.226	-0.059	0.033	0.011	0.071	0.187	0.033

So the Global coefficient estimates are similar to the Mean and Median values of the GWR output. But you can see the variation in the association between the target variable (MedInc) and the different coefficient estimates.

4.1.4.2 Mapping GWR outputs

The GWmodel outputs have a number of components. Of interest is the SDF which is spatial object of the same class as the input - in this case a SpatialPolygonsDataFrame.

The variation in the GWR coefficient estimates can be mapped to show how different factors are varyingly associated with MedInc in different parts of study area. The maps show how the variation in the relationship between the predictor variables and unemployment was found:

tm_shape(gwr.mod$SDF) +
  tm_fill(c("PctBach", "PctEld"), size = 0.2) +
  tm_layout(legend.position = c("right", "top"))

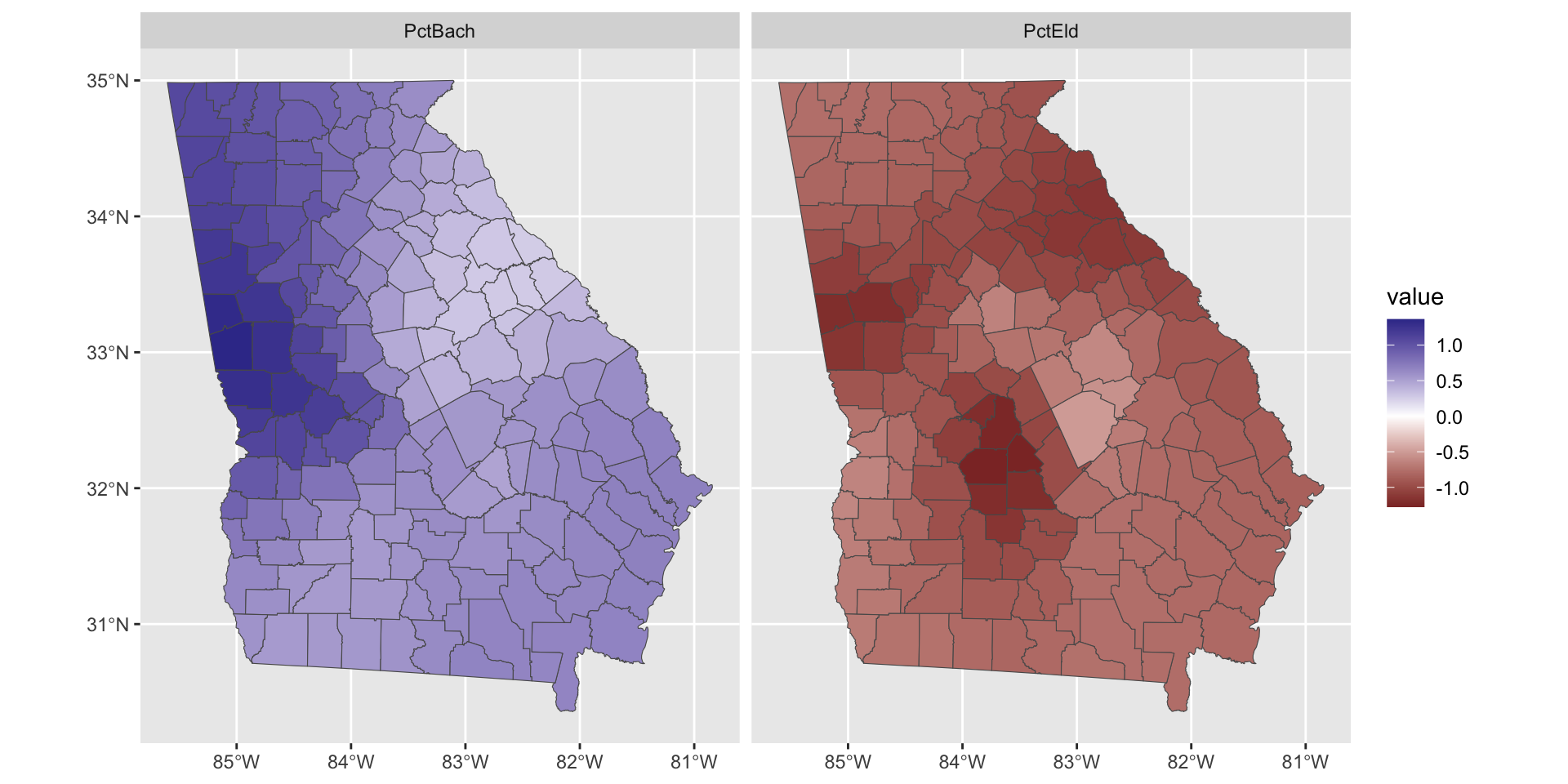
Figure 4.2: Maps of 2 of the coefficient estimates.

Note that some of the coefficients have values that flip from positive to negative in different parts of the study area. We may want to plot those with a different colour scheme as in the figure below:

tm_shape(gwr.mod$SDF) +
  tm_fill(c("PctFB", "PctBlack"), midpoint = 0) +
  tm_style("col_blind")+ 
  tm_layout(legend.position = c("right", "top"))

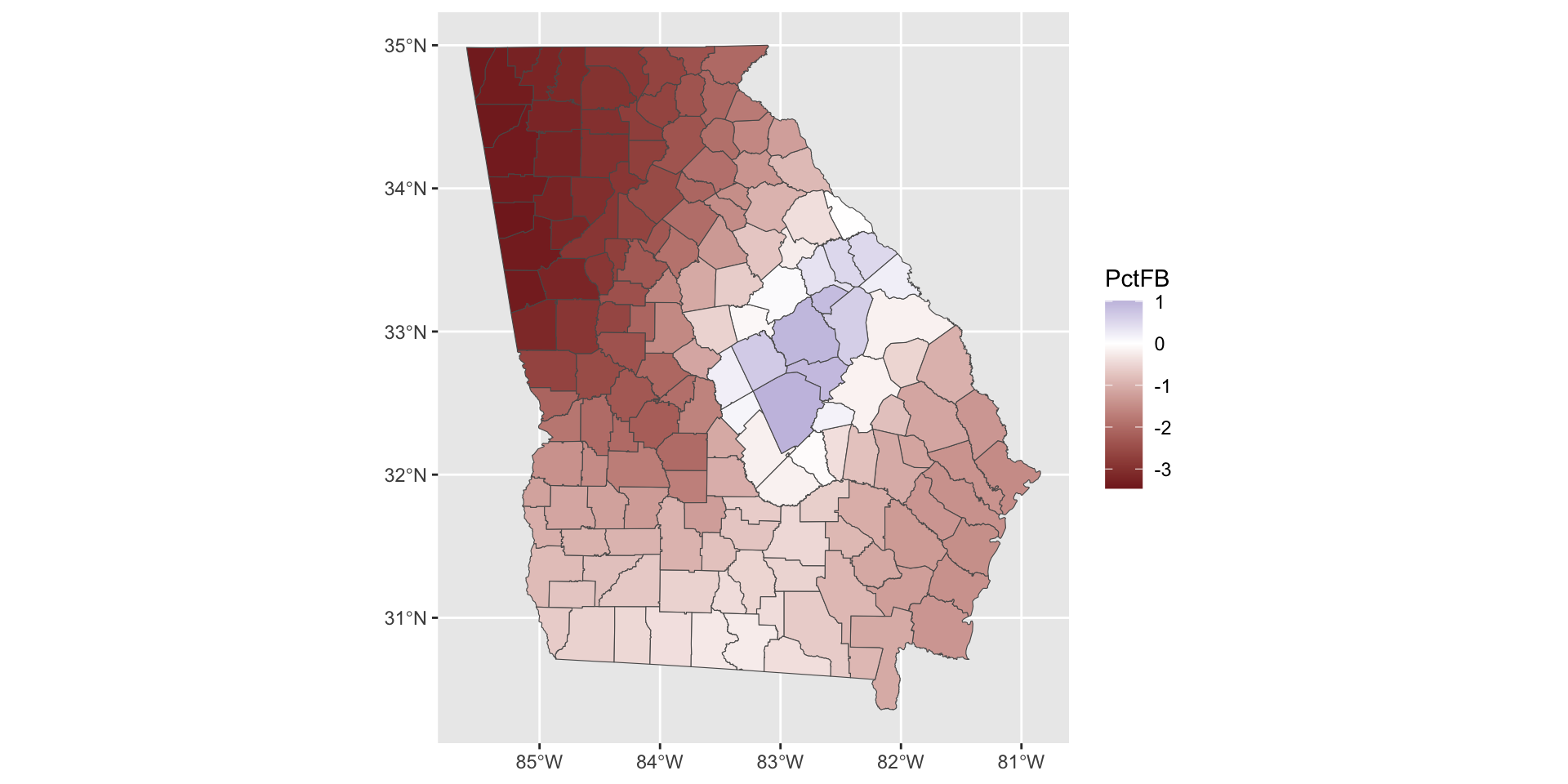
Figure 4.3: Maps of coefficients that flip from negative to positive.

So what we see here are the local variations in the degree to which changes in different variables are associated with changes in Median Income. The maps above are not simply maps of the input predictor variable, but instead highly localised trends in the variation of the relationship of these with the response variable.

Of interest here, and linking back to the coefficient estimates summaries in Table 1, what we can see are how the relationship between the target and predictor variables vary geographically in both the figures above (this is and indication process spatial heterogeneity and spatial non-stationarity to put it into statistical terms). Additionally we also see how and where the relationships between the covariates and the response variable change sign - where the relationship flips between a positive association and a negative one. This indicate that any causal process between median Income and the predictor variables may not be spatially consistent.

4.1.4.3 Mapping significant GWR outputs

A final refinement is to identify where the relationships between the covariates and the target variable are significant. The GWmodel output includes t-values from which statistically significant local models can be identified, by identify t-values less than -1.96 and greater than +1.96. These are included in the GWR spatial outputs (named with a _TV suffix). The spatial outputs are in the gwr.mod$SDF object.

First for values that do not flip sign:

# determine significant t-values
tval = gwr.mod$SDF$PctRural_TV
signif = tval < -1.96 | tval > 1.96
# create the map 
tm_shape(gwr.mod$SDF) +
  tm_fill("PctRural") +
  tm_layout(legend.position = c("right","top"))+
  # now add the significant t-values layer
  tm_shape(gwr.mod$SDF[signif,]) +
        tm_borders(col = "black", lwd = 0.5) 

Then for those covariates that do flip sign, using the colour blind style in tmap:

tval = gwr.mod$SDF$PctBlack_TV
signif = tval < -1.96 | tval > 1.96
# create the map 
tm_shape(gwr.mod$SDF) +
  tm_fill("PctBlack", midpoint = 0) +
  tm_style("col_blind")+ 
  tm_layout(legend.position = c("right","top"))+
  # now add the t-values layer
  tm_shape(gwr.mod$SDF[signif,]) +
        tm_borders(col = "black", lwd = 0.5) 

Interrogation of the coefficient maps from GWR and the coefficient summary table is key to investigating spatial heterogeneity. The maps can be used to examine spatial variation of the local coefficient estimates and where the coefficients are significant.

4.2 Part 2. Optional analyses

4.2.1 Outliers and Robust (‘bomb-proof’) Regression

You will need to install an additional package:

library(MASS)

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

In the earlier section we looked at basic regression, which assumes that the relationship between the predictor variables (\(x_m\)) and the response variable (\(y\)) is linear plus a random error term. However the assumption that the relationship is linear, and that the error terms have identical and independent normal distributions is quite often a consequence of wishful thinking, rather than a rigorously derived conclusion. Although quite often these assumptions are resemble reality enough to allow inference (understanding and predictions) to be of some use, changing some of the model assumptions would certainly result in more plausible results.

To take a step closer to reality, it is a good idea to look beyond these assumptions to obtain more reliable predictions, or gain a better theoretical understanding. To mediate the problems caused by the inappropriate use of simple OLS regression, two general approaches are used:

1. Making the model calibration more robust - so that minor deviations (such as extreme outliers) - do not negatively influence the modelling process.
2. Allowing different assumptions in the model or the error term.

In this section we will look at some examples of these.

Earlier, in the main practical, the model residuals were examined (the code is repeated below). There were a few outliers:

s.resids <- rstudent(ols_mod1)
plot(s.resids,type='h')
abline(h=c(-2,2),col='lightskyblue')

This outliers might ‘throw’ the regression. One way to investigate this is to remove the outlying observations and re-fit the model. The removal is best done using the dplyr approach and the filter function, and then re-fitting the model.

georgia %>% filter(abs(rstudent(ols_mod1)) <= 2) -> georgia_NoOut
ols_mod2 <- lm(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
              data = georgia_NoOut)

Then the compareCoefs function in the car package compares the models:

compareCoefs(ols_mod1, ols_mod2)

Some of the values alter notably between the models with and without outliers, with some differences greater than others: outliers do have an influence!

However, it could be argued that the approach of removing them entirely is misleading - essentially trying to pass off a model as universal but intentionally ignoring observations that contradict it. Although that might be quite extreme, the point holds to some extent. Those counties do have those statistics, and so should perhaps not be ignored entirely.

Robust regression offers a more nuanced approach. Here, instead of simply ignoring the outliers, it is assumed that for whatever reason, they are subject to much more variance than the remaining observations - possibly due to some characteristic of the sampling process, or - more likely here - due to some unusual circumstances in the geographical locality (for example the presence of a large university skewing income figures compared to most of the State). Rather than totally ignoring such observations, they are downweighted to allow for this. This is less extreme than removing outliers - which in a sense is extreme downweighting to the value zero!

There are a number of approaches to robust regression - here we will use one proposed by Huber (1981). This uses an algorithm as below:

1. Fit a standard regression model and note the residuals.
2. Compute the weight for each observation as a function of absolute residual size. A number of possible weight functions could be used, but Huber’s is
   \[ w_i(z_i) = \left\{ \begin{array}{ll} 1, & \textsf{if } |z_i| < c; \\ c/|z|, & \textsf{if } |z_i| \ge c; \\ \end{array} \right. \] where \(c \approx 1.345\) and \(z_i\) is a scaled residual for observation \(i\). If actual residual is \(e_i\), then \(z_i = e_i/\tau\) where \(\tau\) is the median of \(\frac{|e_i|}{0.6745}\). After residuals reach a value \(c\) weighting gradually decreases - in accordance with the idea that higher residuals come from processes with greater variance.
3. Refit the regression model with these weights. Update the residual values.
4. Repeat from step 2 until regression coefficient estimates converge.

This is all implemented in the rlm function in the package MASS. It is very easy to use - once you have loaded MASS it just works like lm:

ols_mod3 <- rlm(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack,
                data = georgia)
ols_mod3

## Call:
## rlm(formula = MedInc ~ PctRural + PctBach + PctEld + PctFB + 
##     PctPov + PctBlack, data = georgia)
## Converged in 9 iterations
## 
## Coefficients:
## (Intercept)    PctRural     PctBach      PctEld       PctFB      PctPov 
## 51.60773916  0.06337478  0.67787963 -0.77778234 -1.22469054 -0.88053199 
##    PctBlack 
##  0.03179542 
## 
## Degrees of freedom: 159 total; 152 residual
## Scale estimate: 4.19

Here the coefficient estimates are printed out, and it may also be seen that the model converged in 8 iterations, and that the scale factor \(\tau\) was estimated as 4.4. As with lm you can print out a summary:

summary(ols_mod3)

Finally, coefficients from all three models can be compared:

coef_tab <- data.frame(OLS=coef(ols_mod1),
                       OutliersDeleted=coef(ols_mod2),Robust=coef(ols_mod3))
round(coef_tab, 3)      

Table 4.3: Comparison of coefficients across 3 regression models.

	OLS	OutliersDeleted	Robust
(Intercept)	52.599	52.905	51.608
PctRural	0.074	0.067	0.063
PctBach	0.697	0.728	0.678
PctEld	-0.789	-0.925	-0.778
PctFB	-1.290	-1.485	-1.225
PctPov	-0.954	-0.887	-0.881
PctBlack	0.033	0.043	0.032

For some coefficients, the robust estimate is closer to the standard OLS and for others it is closer to the outliers deleted estimate. Additionally for some it differs from OLS, but not in the same direction as the ‘outliers deleted’ case. As a precautionary approach, I suggest working with the robust approach if there are some notable outliers.

4.2.2 Multi-scale GWR

In the standard form, a single bandwidth is used in GWR under the assumption that the response-to-predictor relationships operate over the same scales for all of the variables contained in the model. This may be unrealistic because some relationships can operate at larger scales and others at smaller ones. A standard GWR will nullify these differences and find a ‘best-on-average’ scale of relationship non-stationarity (geographical variation). To address this, multiscale GWR (MGWR) (Yang 2014; Fotheringham, Yang, and Kang 2017) can be used. In this, the bandwidth for each relationship is determined separately, allowing the scale of individual response-to-predictor relationships to vary.

MGWR is now recognised as the default GWR with a standard GWR only being appropriate on very specific circumstances. A. Comber et al. (2020) describe GWR developments and provide a comprehensive route map through the different flavours of OLS regression, spatial regression (not covered here), GWR and MGWR.

The first stage in any GWR is to fit the bandwidths. For MGWR this is done using the gwr.multiscale function in GWmodel and can take some time.

gw.ms <- gwr.multiscale(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
                        data = georgia_sp,
                        adaptive = T, max.iterations = 1000,
                        criterion="CVR",
                        kernel = "bisquare",
                        bws0=c(1000,1000,1000,1000,1000,1000,1000),
                        verbose = F, predictor.centered=rep(T, 6))

You can inspect the results

gw.ms

A particularly the bandwidths as this is what we are after here:

gw.ms[[2]]$bws

## [1]  31 120  67 157  43  18  80

Perhaps this can be more intuitively presented in a data table:

data.frame(VarName = names(gw.ms$SDF)[1:length(gw.ms[[2]]$bws)], 
           MSGWR_bw = gw.ms[[2]]$bws)

##     VarName MSGWR_bw
## 1 Intercept       31
## 2  PctRural      120
## 3   PctBach       67
## 4    PctEld      157
## 5     PctFB       43
## 6    PctPov       18
## 7  PctBlack       80

This shows that the Intercept, PctPov and PctFB have highly localised relationships with MedInc (with adaptive bandwidths of the 31, 18 and 43 nearest data points, respectively). The PctRural and PctEld bandwidths tend towards the global relationship (of 159 observations), and PctBach and PctBlack are somewhere in between.

These bandwidths can now be plugged back into a MGWR, changing a few of the input parameters to indicate that bandwidths have been determined:

gw.res = gwr.multiscale(MedInc~PctRural+PctBach+PctEld+PctFB+PctPov+PctBlack, 
               data = georgia_sp,
               adaptive = T,
               criterion="CVR", kernel = "bisquare", 
               bws0=gw.ms[[2]]$bws,
               bw.seled=rep(T, 6),
               verbose = F, predictor.centered=rep(F, 6))

Now if we inspect the coefficient table fo the MGWR model we should see these same varying scales of relationship with MedInc. The tab object below shows, for example, very little variation in the coefficient estimates for PctEld and much larger variation in PctPov.

# table of MGWR coefficients
t1 = apply(gw.res$SDF@data[, 1:7], 2, summary)
# MGWR bandwidths
t2 = gw.ms[[2]]$bws
# joint together with a row bind
tab <- rbind(t1, t2)
# add name to last row of tab
rownames(tab)[7] <- "BW"
# transpose tab
tab <- t(round(tab, 3))
tab

##             Min. 1st Qu. Median   Mean 3rd Qu.   Max.  BW
## Intercept 53.080  55.744 57.477 58.251  61.512 64.920  31
## PctRural   0.044   0.048  0.053  0.053   0.058  0.061 120
## PctBach    0.569   0.629  0.670  0.689   0.759  0.817  67
## PctEld    -1.124  -1.121 -1.119 -1.119  -1.116 -1.115 157
## PctFB     -3.724  -3.021 -2.509 -2.372  -1.696 -0.714  43
## PctPov    -1.380  -0.708 -0.554 -0.658  -0.484 -0.366  18
## PctBlack  -0.181  -0.177 -0.166 -0.168  -0.160 -0.153  80

Finally these can be mapped in the same way as with a standard GWR. The code below maps the coefficient estimate from the MGWR model and compares the result with that from a standard GWR.

# 1. standard GWR
tval = gwr.mod$SDF$PctBlack_TV
signif = tval < -1.96 | tval > 1.96
# create the map
p1 = tm_shape(gwr.mod$SDF) +
  tm_fill("PctBlack", midpoint = 0) +
  tm_style("col_blind")+ 
  tm_layout(legend.position = c("right","top"), , title = "GWR")+
  # now add the t-values layer
  tm_shape(gwr.mod$SDF[signif,]) +
  tm_borders(col = "black", lwd = 0.5) 
# 2. MGWR
tval = gw.ms$SDF$PctBlack_TV
signif = tval < -1.96 | tval > 1.96
# create the map 
p2 = tm_shape(gw.ms$SDF) +
  tm_fill("PctBlack", midpoint = 0) +
  tm_style("col_blind")+ 
  tm_layout(legend.position = c("right","top"), title = "MGWR")+
  # now add the t-values layer
  tm_shape(gwr.mod$SDF[signif,]) +
  tm_borders(col = "black", lwd = 0.5)
tmap_arrange(p1, p2)

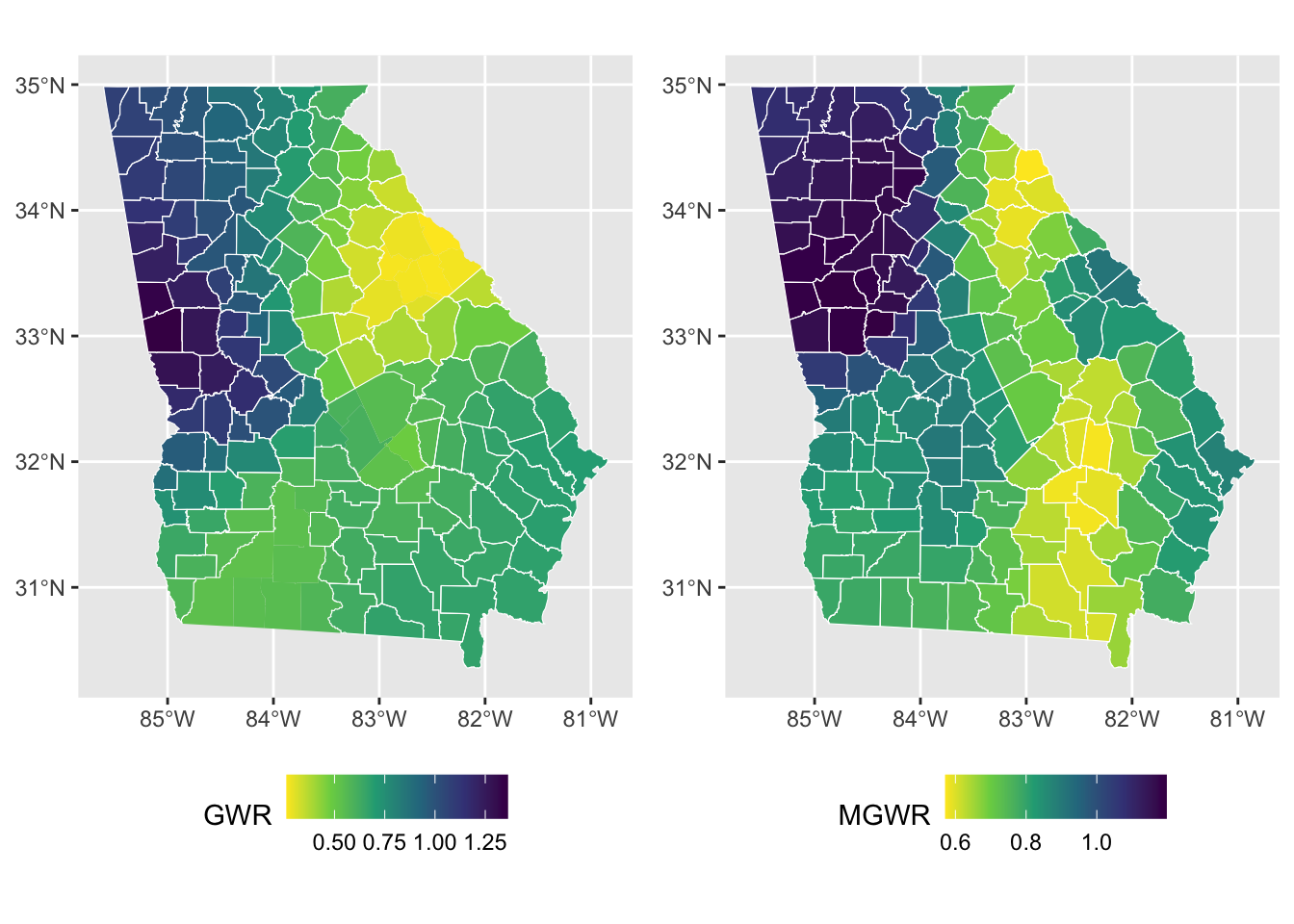
Figure 4.4: A comparison of spatially varying coefficiecnt estimates using GWR and MGWR, with local significance indicated.

There is a lot more to GWR and MGWR. Gollini et al. (2015) provide a comprehensive (if somewhat chaotically organised ) descriptions of these. They are summarised at length in A. Comber et al. (2020) and succinctly in A. Comber et al. (2020).

References

Brunsdon, Chris, A Stewart Fotheringham, and Martin E Charlton. 1996. “Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity.” Geographical Analysis 28 (4): 281–98.

Comber, Alexis J, Chris Brunsdon, and Robert Radburn. 2011. “A Spatial Analysis of Variations in Health Access: Linking Geography, Socio-Economic Status and Access Perceptions.” International Journal of Health Geographics 10 (1): 1–11.

Comber, Alexis, Chris Brunsdon, Martin Charlton, Guanpeng Dong, Rich Harris, Binbin Lu, Yihe Lü, et al. 2020. “The GWR Route Map: A Guide to the Informed Application of Geographically Weighted Regression.” arXiv Preprint arXiv:2004.06070.

Fotheringham, A Stewart, Wenbai Yang, and Wei Kang. 2017. “Multiscale Geographically Weighted Regression (MGWR).” Annals of the American Association of Geographers 107 (6): 1247–65.

Gollini, Isabella, Binbin Lu, Martin Charlton, Christopher Brunsdon, Paul Harris, et al. 2015. “GWmodel: An r Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models.” Journal of Statistical Software 63 (i17).

Yang, Wenbai. 2014. “An Extension of Geographically Weighted Regression with Flexible Bandwidths.” PhD thesis, University of St Andrews.