Practical 5 Machine Learning

5.1 Machine Learning in caret

This practical is based on Chapter 7 in Comber and Brunsdon (2021). The assignment for this module will be a Machine Learning problem.

The session introduces and illustrates a number of important aspects of what is commonly called Machine Learning but historically has simply been regarded as non-linear regression.

Some house price and socio-economic data for Liverpool in the UK is introduced and used to illustrate the key considerations in the mechanics of machine learning and then used to generate different predictive and inferential models contained with the caret package - a wrapper for hundreds of machine learning algorithms.

You will need to load the some packages. The code below installs some packages. It does this by testing for the presence of each packages and installing the ones that are not present:

packages <- c("sf", "tidyverse", "tmap", "caret", "gbm", "GGally")
# check which packages are not installed
not_installed <- packages[!packages %in% installed.packages()[, "Package"]]
# install missing packages
if (length(not_installed) > 0) {
  install.packages(not_installed, repos = "https://cran.rstudio.com/", dep = T)
}
library(sf)         # for spatial data
library(tidyverse)  # for data wrangling
library(tmap)       # for mapping
library(caret)      # for Machine Learning
library(gbm)        # for Gradient Boosting
library(GGally)     # for fancy graphics
# remove unwanted variables
rm(list = c("packages", "not_installed"))

This practical illustrates a few different approaches for Machine Learning. There are number of R packages that support Machine Learning and probably the best developed of these is the caret package (Classification And REgression Training) (Kuhn 2015), as used in the illustrations above. The advantage of caret is that it provides a consistent environment and integrated interface to many Machine Learning algorithms (see https://topepo.github.io/caret/available-models.html or enter the following in the R console names(getModelInfo()) to see the full list). The functions for different algorithms are contained in other R packages and caret provides a bridge to them and standardizes a number of common tasks. It contains tools for data splitting and pre-processing, model tuning, determining estimates of variable importance and related functionality. Details of the caret package (Kuhn 2015) can be found at http://topepo.github.io/caret/ and in the book by the package author (Kuhn and Johnson 2013). Note that caret does not load all the functions and packages on installation, but instead assumes that they are present and loads them as needed: if a package is not present caret provides a prompt to install it.

A number of different algorithms (approaches) are used for prediction and inference (and classification not covered here):

• Standard linear regression
• \(k\)-Nearest Neighbour
• Bagged Regression Trees
• Gradient Boosting Machines
• Support Vector Machine

These are all applied to the same data, the creation of which is described in the next sub-section.

5.2 Data

Socio-economic data for the Liverpool area are used to illustrate the specific machine learning consideration. The ml.RData R binary file includes 3 sf objects with population census data at 2 different scales and data of residential properties for sale for the Liverpool area.

Load the ml.RData file to your R / RStudio session and examine the result:

load("ml.RData")
ls()

## [1] "lsoa"       "oa"         "properties" "select"

The 3 spatial datasets in sf format are as follows:

• oa: a multipolygon object of Output Areas (OAs)
• lsoa: a multipolygon object of Lower Super Output Areas (LSOAs)
• properties: a multipoint object of houses for sale in the Liverpool area

The oa and lsoa represent Output Areas (~300 people) and Lower Super Output Areas (~1500 people) respectively. They each contain census data of economic well-being (unemployment and percentages - unmplyd), life-stage indicators (percentage of under 16 years (u16), 16-24 years (u25), 25-44 years (u45), 45-64 years (u65) and over 65 years (o65) and an environmental variable of the percentage of the census area containing greenspaces. The unemployment and age data were from the 2011 UK population census (https://www.nomisweb.co.uk) and the greenspace proportions were extracted from the Ordnance Survey Open Greenspace layer (https://www.ordnancesurvey.co.uk/opendatadownload/products.html). The spatial frameworks were from the EDINA data library (https://borders.ukdataservice.ac.uk). The OAs and LSOAs are both projected to the OSGB projection (EPSG 27700). The OA layer also has a geo-demographic class label (spgrpnm) from the OAC (see Gale et al. (2016)) of 8 classes.

The properties data was scraped from Nestoria (https://www.nestoria.co.uk) on 30th May 2019 using their API (https://www.programmableweb.com/api/nestoria). It contains latitude and longitude in decimal degrees, giving location, price in 1000s of pounds (£), the number of bedrooms and 38 binary variables indicating the presence of different keywords in the property listing such as Conservatory, Garage, Wood Floor etc. The code below lists these:

properties %>% st_drop_geometry() %>% select_if(is_logical) %>% 
  colnames() %>% paste(" - ",.) %>% paste(collapse='\n') %>% cat()

Some EDA can provide an initial understanding of the data. For example the code below creates a ggpairs plot of the oa data, and you should modify this to create a similar plot of the lsoa data:

# OA pairs plot
oa %>% st_drop_geometry() %>% select_if(is.numeric)  %>% 
  ggpairs(lower = list(continuous = wrap("points", alpha = 0.5, size=0.1)))+
  theme(axis.line=element_blank(),
        axis.text=element_blank(),
        axis.ticks=element_blank())  

If you examine the oa and lsoa correlations you should note a number of things

1. the broad similarity of the distribution of values across the 2 scales;
2. the extremely skewed distributions of the greenspace attribute (gs_area) at both scales, but with less skew at the coarser LSOA scale;
3. that these are correlations are stronger at OA level.

Alternative visualisations are possible with the properties data:

ggplot(properties,aes(x=Beds,y=Price, group=Beds)) + geom_boxplot()

We can also use tmap to see the geographical distribution of houses with different numbers of bedrooms, which has a geographical pattern:

tmap_mode('view')
tm_shape(properties) + tm_dots(col='Beds', size = 0.03, palette = "PuBu")
tmap_mode('plot')

Finally, the properties data can be linked to to the socio-economic data in the Output Area layer (oa) by location (actually a point-in-polygon operation - see see Brunsdon and Comber (2018) for a full description of such spatial operations). The result is that the census data attributes are attached to each record in properties based on the record’s location. An alternative would be to pool the house price data over the census areas, but this would require the house price data to be averaged in some way (e.g. average house price or the percentage of house with \(n\) bedrooms), and would lose much of the nuance in the data such as the keywords indicating whether the property had a garage, a conservatory or was semi-detached, etc.

To spatially intersect spatial data layers they need to be in the same geographic projection. The code below converts the properties data to the OSGB projection,with Easting and Northing in metres replacing Lon and Lat variables in degrees. The 2 datasets are then spatially intersected and a few unwanted variables are removed (census area codes, latitude, longitude) and the final dataset for analysis is created (data_anal).

properties %>% st_transform(27700) %>% 
  # add Easting and Northing as variables
  mutate(Easting =  (properties %>% st_coordinates() %>% .[,1])  ) %>%
  mutate(Northing = (properties %>% st_coordinates() %>% .[,2])  ) %>%
  # intersect with OA data and drop unwanted variables
  st_intersection(st_transform(oa, 27700))  %>% 
  # drop Lat, Lon OAC code, LSOA ID and sf geometry
  dplyr::select(-Lon, -Lat, -spgrpnm, -code) %>% 
  st_drop_geometry() %>% 
  # remove NAs and pipe to a data.frame
  drop_na() -> data_anal

## Warning: attribute variables are assumed to be spatially constant throughout
## all geometries

This contains only the observations in properties that intersect with the oa layer and has the attributes from the oa layer attached. You should examine the data:

head(data_anal)

## # A tibble: 6 × 49
##   Kitchen Garden Modern Gas.Central.Heating No.Chain Parking Shared.Garden
##   <lgl>   <lgl>  <lgl>  <lgl>               <lgl>    <lgl>   <lgl>        
## 1 TRUE    FALSE  FALSE  FALSE               FALSE    FALSE   FALSE        
## 2 FALSE   FALSE  FALSE  FALSE               FALSE    FALSE   FALSE        
## 3 FALSE   FALSE  TRUE   FALSE               FALSE    FALSE   FALSE        
## 4 FALSE   FALSE  FALSE  FALSE               FALSE    TRUE    FALSE        
## 5 FALSE   FALSE  FALSE  TRUE                FALSE    TRUE    FALSE        
## 6 TRUE    FALSE  FALSE  FALSE               TRUE     TRUE    FALSE        
## # ℹ 42 more variables: Double.Bedroom <lgl>, Balcony <lgl>, New.Build <lgl>,
## #   Lift <lgl>, Gym <lgl>, Porter <lgl>, Price <dbl>, Beds <ord>,
## #   Terraced <lgl>, Detached <lgl>, Semi.Detached <lgl>, Conservatory <lgl>,
## #   Cul.de.Sac <lgl>, Bungalow <lgl>, Garage <lgl>, Reception <lgl>,
## #   En.suite <lgl>, Conversion <lgl>, Dishwasher <lgl>, Refurbished <lgl>,
## #   Patio <lgl>, Cottage <lgl>, Listed <lgl>, Fireplace <lgl>, Victorian <lgl>,
## #   Penthouse <lgl>, Purpose.Built <lgl>, Wood.Floor <lgl>, Loft <lgl>, …

5.3 Prediction vs. Inference

Statistical models are constructed for 2 primary purposes: to predict something or to understand some process (also known as inference). The distinction between the two activities has sometimes been blurred as the volume of activities in data analytics has increased, and the background training of those involved these activities has diversified. Sometimes the terminology is confusing, the word inference is used to mean both prediction and understanding. This is because analyses for prediction and understanding both seek to infer \(y\) from \(x\) in some way, through some function \(f\), where \(x\) represents the input (predictor, independent, etc) variables and \(y\) is the target (or dependent) variable and \(\epsilon\) is some random error term:

\[ y = f(x) + \epsilon{}\]

Here the word inference is associated with process understanding.

It is always useful to return to core knowledge to (re-)establish fundamental paradigms, and in this case to consider how others regard the distinction between prediction and other kinds of inference:

…in a real estate setting, one may seek to relate values of homes to inputs such as crime rate, zoning, distance from a river, air quality, schools, income level of community, size of houses, and so forth. In this case one might be interested in how the individual input variables affect the prices—that is, how much extra will a house be worth if it has a view of the river? This is an inference problem. Alternatively, one may simply be interested in predicting the value of a home given its characteristics: is this house under- or over-valued? This is a prediction problem. (James et al. (2013) p20, bold emphasis added).

Viewed through this lens, prediction and inference can be distinguished as follows:

Prediction uses the estimated function \(f\) to forecast \(y\), for example over unsampled areas when data for those areas becomes available, into the future, given different future states.

Inference uses estimated function \(f\) to understand the impact of the the inputs \(x\) on the outcome \(y\). It is often associated with process understanding, with the aim of, for example, determining how much of \(y\) is explained by a particular \(x\), for example \(x_i\), through its partial derivative \(\partial{f} / \partial{x_i}\).

The aim in both cases is to identify the function \(f\) that best approximates the relationships or structure in the data. And, although Prediction and Inference are both in a sense inferential with one focusing on forecasting and the other on process understanding, and both may use the same estimation procedure to determine \(f\), the major difference is that they have different procedural considerations. This is especially the case for how the issues around independence and collinearity amongst predictor variables are considered for example: highly correlated input variables may make it difficult to separate variable effects in when the objective is inference, whereas this does not matter for prediction, which is concerned only with the accuracy and reliability of the forecast.

5.4 The Mechanics of Machine Learning

Recall that the basic objectives of machine learning are for process understanding (inference) and prediction. Machine learning achieves these by determining data structure (relationships) and identifying the functions that best approximates these relationships.

There are 2 general approaches to machine learning: supervised and unsupervised learning.

Supervised learning is undertaken when the outcomes are are known, that prior knowledge exists of what the model or function output values should be. More formally, for each observation of the predictor variables \(x_{i}\) there the associated response \(y_i\) is known. In this situation, the aim is determine the function \(f\) that best approximates the relationship between the observed outputs and inputs, by predicting the known response variable as accurately as possible in order to best predict future or unknown responses. The overall approach is to split the data into training and validation data subsets, to construct the model using the training data, to then apply (test) the model over the validation data for which the actual observed outcomes are known and finally to compare the observed with predicted values to determine the model reliability or fit (see below).

Unsupervised learning describes the situation when the response is unknown. That is, for each observation, \(x_i\) is observed but not the response \(y_i\). It is unsupervised because the there is no response to supervise the fitting of a function. This limits the statistical analyses that are possible to those that seek to understand the relationships between the variables over observations, such as cluster analysis or classification. Here all the data are used as inputs to construct the model rather and measures of model fit describe the in-sample prediction accuracy. In classification models, model fit is determined by evaluating the within-class homogeneity - that is the closeness (similarity) of each of observation (record) to the class to which it allocated in the clustering process.

In both supervised and unsupervised approaches the goal is to identify specific relationships or structure in the predictor variables data in order to generate a robust and powerful statistical model. There are additional data considerations such as whether to rescale the data or not, which variables to use as inputs, although the latter is more important for inference in supervised approaches, model specification (variable selection) in supervised approaches, determining the number of clusters \(k\) in unsupervised approaches, model evaluation, etc. Much of the actual development and application of of machine learning is concerned with these considerations rather then actually running the algorithm. These are illustrated in the sub-sections below.

5.4.1 Data rescaling and normalisation

Many statistical machine learning models use some form of multi-variate distance measure to determine how far apart different observations are from each other. A multi-variate feature space is defined by the predictor variables passed to the model. Consider linear regression. It determines the hyper-plane with the minimum summed distance between each observation and the plane. By way of example, consider a very simple linear regression model of Price in the properties data can be constructed from Beds and Lat.

df <- properties %>% st_drop_geometry() %>%
  select(Price, Beds, Lat) %>% 
  mutate(Beds = as.numeric(as.character(Beds)))
summary(lm(Price~Beds+Lat, data = df))

However, the problem in this case (and in most others) is that the variables are in different units of measurement: Lat is in degrees, Beds is a count of beds and Price is in 1000s of pounds. Floor area, if present, would be in square metres, etc. The danger is that models constructed on the raw data can be dominated by variables with large numerical values. For example if Price were in pounds rather than 1000s of pounds then this domination would be greatly enhanced. Similarly, the relative influence of Lat would change if it was expressed as an Easting in metres, as in the OSGB projections of oa and lsoa. However, this seems to be a somewhat arbitrary way to proceed - the houses have the same physical size, and the same location regardless of units of measurement, and it seems nonsensical for the notion of closeness to change with any change in these units.

For this reason, data is often re-scaled (or scaled) prior to applying ML algorithms. Usually this is done either by computing \(z\)-scores, or rescaling by minimum and maximum values. For any variable \(x\), re-scaling by \(z\)-score is as follows:

\[z = \frac{x - \bar{x} }{\sigma_x}\]

where \(\bar{x}\) is the mean of \(x\) and \(\sigma_x\) is the standard deviation of \(x\). The result is that \(z\) has a mean of zero and a standard deviation of one, regardless of the units of \(x\). Additionally, the distributions of the \(z\)-scores are the same as those of \(x\).

R has a number of in-built functions for re-scaling data, including the scale function in the base R installation which re-scales via \(z\)-scores. This changes the data values but not their distribution:

df <- properties %>% st_drop_geometry() %>%
  select(Price, Beds, Lat) %>% 
  mutate(Beds = as.numeric(as.character(Beds)))

X <- df %>% scale()

The object X now contains \(z\)-score rescaled columns from df - you can check the first six observations and compare with the original data.

head(df)
head(X)

You can also check that this has been applied individually to each variable and not in a ’group-wise` way across all of the numeric variables using a single pooled mean and standard deviation across all variables

apply(X, 2, mean)
apply(X, 2, sd)

5.4.2 Training and Validation data splits

Supervised machine learning especially for prediction, requires the input data to be split into 2 subsets: one to create the model and the other test or evaluate its performance.

In supervised machine learning, the data contains the target variable (output) and this allows the model to be evaluated using a quantifiable and objective metric. Recall that the aim is to use a matrix of predictor variables \(x_{i...n}\), now denoted as \(X\) and a response variable to be predicted \(y\) in order to determine some function \(f(X)\) such that \(f(X)\) generates outputs that are as close to \(y\) as possible.

Thus, one of the critical issues in supervised machine learning and the associated training and validation splits, is that any given split of the data may be not be representative of the dataset as a whole (and therefore our knowledge of the problem) and models constructed on such a subset may lead to erroneous prediction.

The caret package includes the createDataPartition function that splits data into two sets for training and validation and ensures that the distribution of outcome variable classes is similar in both. This is because is uses bootstrapping approach (random sampling with replacement) to create a stratified random split. A set is set below to ensure reproducibility.

set.seed(1234) # for reproducibility
train.index = createDataPartition(data_anal$Price, p = 0.7, list = F)

The distributions of the target variable Price are similar across the 2 splits:

summary(data_anal$Price[train.index])
summary(data_anal$Price[-train.index])

The data needs to be split into training and validation (testing) subsets:

train_anal = data_anal[train.index,] 
test_anal = data_anal[-train.index,] 

The numeric attributes of the training and validation subsets can be re-scaled, remembering to keep the target variable in its original form:

train_z = 
  train_anal %>% select(-Price) %>% 
  mutate_if(is_logical,as.character) %>% 
  mutate_if(is_double,scale) %>%  data.frame()
test_z = 
  test_anal %>% select(-Price) %>% 
  mutate_if(is_logical,as.character) %>% 
  mutate_if(is_double,scale) %>%  data.frame()
# add unscale price back
train_z$Price = train_anal$Price
test_z$Price = test_anal$Price

Note that it is important to rescale the data with \(z\)-scores, after subsetting the data. The danger of normalising / rescaling the data before the split then information about the future is being introduced into the training explanatory variables.

These data will be used in the prediction models below, inference models will use the full data.

5.4.3 Measures of fit

The function \(f\) in the equation \(f(X)\) depends not only on some training data, but also on the tuning parameters. Varying the tuning parameters will alter how close \(f(X)\) is to \(y\) with the aim of identifying which combination of parameters get the closest. A key tuning parameter is the choice over the measure of fit that will be used to evaluate the model as it created.

The general method of evaluating model performance using this split is called cross-validation or CV. This is an out-of-sample testing to validate the model using some fitness measure to determine how well the model will generalise - i.e. predict using an independent dataset.

So the general method of evaluating model performance is to split the data into a training set and a test set, denoted as \(S = {X, y}\) and \(S' = {X', y'}\) respectively, and calibrate \(f\) using \(S\), with a given set of tuning parameters. Then \(X'\) are used compute \(f(X')\) and the results are compared to \(y'\). This CV procedure returns a measure of how close the predictions of \(y'\) are to the observed values of \(y'\) when \(f(X')\) is applied.

There are a number of ways of measuring this. Two commonly used methods (for regression) are the root mean square error (RMSE), defined by squaring the errors, or residual differences between \(y'\) and \(f(X')\), finding their mean and taking square root of the resulting mean:

\[\text{RMSE} = \sqrt{ \sum{ \frac{ (y' - f(X') )^2}{n} }}\]

Essentially RMSE tells us how far the data are from the line of best fit. An alternative is the mean absolute error (MAE), defined by

\[\text{MAE} = \sum \frac{ \vert{y' - f(X')} \vert{} } {n}\]

MAE describes the average absolute difference between observed (\(y\)) and predicted or modelled \(y\) (generated by \(f(X)\) or \(f(X')\)). Perhaps the most common accuracy measure for regression model fit is \(R^2\), the coefficient of determination, calculated from the residual sum of squares over the total sum of squares:

\[\text{R}^2 = 1- \frac{ \sum{ (y' - f(X') )^2} } { \sum{ (y' - \bar{y'} )^2} }\]

All of these essentially measure the degree to which the predicted responses differ from the actual ones in the test data set. For the MAE and RMSE measures, smaller values imply better prediction performance and \(R^2\) works in the opposite way (larger values are better). For many Machine Learning applications MAE is commonly uised to evaluate model fit. For categorical prediction, the proportion of correctly predicted categories is a useful score and again larger values imply better performance.

Of course the descriptions above apply to data split into training and test (validation) subsets, typically in the context of prediction. Models are also evaluated during their construction using Leave-One-Out Cross Validation and \(k\)-fold Cross-Validation. These procedures include a resampling process that splits the data into \(k\) groups or ‘folds’. The approach in outline is to randomly split the data into \(k\) folds, such that each observation is included once in each fold. Then for each fold, keep one as the hold-out or test data, train the model the rest and evaluate it on the test, retaining the evaluation score. The retained evaluation scores are summarised to give an overall measure of fit. In this process each individual observation is uniquely assigned to a single fold, used in the hold out set once and is used to train the model \(k-1\) times. It takes longer than fitting a single model as it effectively undertakes \(k+1\) model fits, but is important for generating reliable models, whether for prediction or inference.

The caret package includes a large number of options for evaluating model fit that can be specified using the trainControl function. You should examine the method parameters that can be passed to trainControl in the help. The trainControl function essentially defines the specifies the type of ‘in-model’ sampling and evaluation that is undertaken to iteratively refine the model. It generates a list of parameters that are passed to the train function that creates the model.

ctrl1 <- trainControl(method = "cv",
                      number = 10) # a 10-fold CV

Others are available, such as repeated \(k\)-fold cross-validation, leave-one-out etc. The function trainControl can be used to specify the type of resampling:

ctrl2 <- trainControl(method = "repeatedcv",
                      number = 10,
                      repeats = 10) # a 10-fold repeated CV, repeated 10 times

The outputs of these could be examined one by one but in this case only the first three values are different:

# there are many settings  
names(ctrl1)
# compare the ones that have been specified
c(ctrl1[1], ctrl1[2], ctrl1[3])  
c(ctrl2[1], ctrl2[2], ctrl2[3])  

5.4.4 Model Tuning

So far, we have considered a number aspects associated with the mechanics of Machine Learning (data preparation, training data, measures of fit) and in each case we have noted that there is a caret function to do this, or a parameter that can be specified and passed to function that creates the model (the train function in caret has not been introduced yet).

Different machine learning approaches require different tuning parameters. Some relate to the input data as described above (fit, training, validation etc.), other hyper-parameters relate to the model configuration and control the model training process. For example in a neural network these include the number of layers, the number of nodes in each layer, as well as specifying the fitness measures and other parameters in trainControl.

The final choice of tuning parameters for any specific model can be optimised (tuned) by adjustment until the best fit is found through the aggregate accuracy of the trained model. In all cases the objective of tuning is modify the model and find the best combination of parameters for the task in hand. The caret vignette has a nice overview of tuning. You should examine this after the practical session.

vignette("caret")

The specific tuning parameters for any given caret machine learning model can be listed using the modelLookup function.

The code below does for a \(k\)-Nearest Neighbour (kNN) model:

modelLookup("knn")

##   model parameter      label forReg forClass probModel
## 1   knn         k #Neighbors   TRUE     TRUE      TRUE

This tells us that there is one tuning parameter, the parameter \(k\) for the number of nearest neighbours. Note that confusingly this is a different \(k\) to the one used to refer to CV folds.

Again an initial model can be generated and the results evaluated (the model may take a minute or 2 to train):

# default model
set.seed(123)
ctrl <- trainControl(method="repeatedcv", repeats=10)
knnFit <- train(Price ~ ., data = train_z, method = "knn", 
                trControl = ctrl, verbose = FALSE)

knnFit

This indicates that the final model had used 7 nearest neighbours, but that only 3 values were evaluated. This is because the default setting in caret is to evaluate a tuning set size of \(3^{paramters}\). In the case of kNN it is 3 (\(3^1\)).

There are 2 ways of tuning the model:

• specify a tune length and pass that to the train function;
• set up a tuning grid and pass that to the train function.

These are both illustrated below and should each take about 2 minutes each to run:

ctrl <- trainControl(method="repeatedcv", repeats=10)
# 1. using tune length
set.seed(123)
knnFit2 <- train(Price ~ ., data = train_z, method = "knn", tuneLength = 20, 
                 trControl = ctrl, verbose = FALSE)
# 2. using a tuning grid 
params = data.frame(k = seq(5, 43, 2))
set.seed(123)
knnFit3 <- train(Price ~ ., data = train_z, method = "knn", 
                trControl = ctrl, 
                tuneGrid = params, verbose = FALSE)

The results can be examined by printing out the whole model or just the best tuning combinations of those evaluated under the default settings. If you inspect the outputs you should see that they have achieved the same results through the different routes.

knnFit3
knnFit2

Here we see that for both final models \(k = 7\).

The best models can be accessed directly using the which.min and which.max functions as below, to interrogate the different accuracy measures:

# RMSE
knnFit2$results[which.min(knnFit2$results$RMSE),]
knnFit3$results[which.min(knnFit3$results$RMSE),]
# R2
knnFit2$results[which.max(knnFit2$results$Rsquared),]
knnFit3$results[which.max(knnFit3$results$Rsquared),]
# MAE
knnFit2$results[which.min(knnFit2$results$MAE),]
knnFit3$results[which.min(knnFit3$results$MAE),]

Examine the outputs and notice that in this case the different measures suggest subtly different optimal parameters depending on the error measurement. The value of \(k\) is now different indicating the differences between the measures of model fit given by the different metrics. The train argument metric defaults to RMSE but others can be specified.

The different fits can be visualized and note that the curves for RMSE, MAE and Rsquared (\(R^2\)) potentially suggest a different value (Figure 5.1) for \(k\).

knnFit2$results %>% select(k, RMSE, MAE, Rsquared) %>% 
  pivot_longer(-k) %>%
  ggplot(aes(x = k, y = value)) +
  geom_point() +
  geom_line()+ ylab("Accuracy") +
  facet_wrap("name", scales = "free")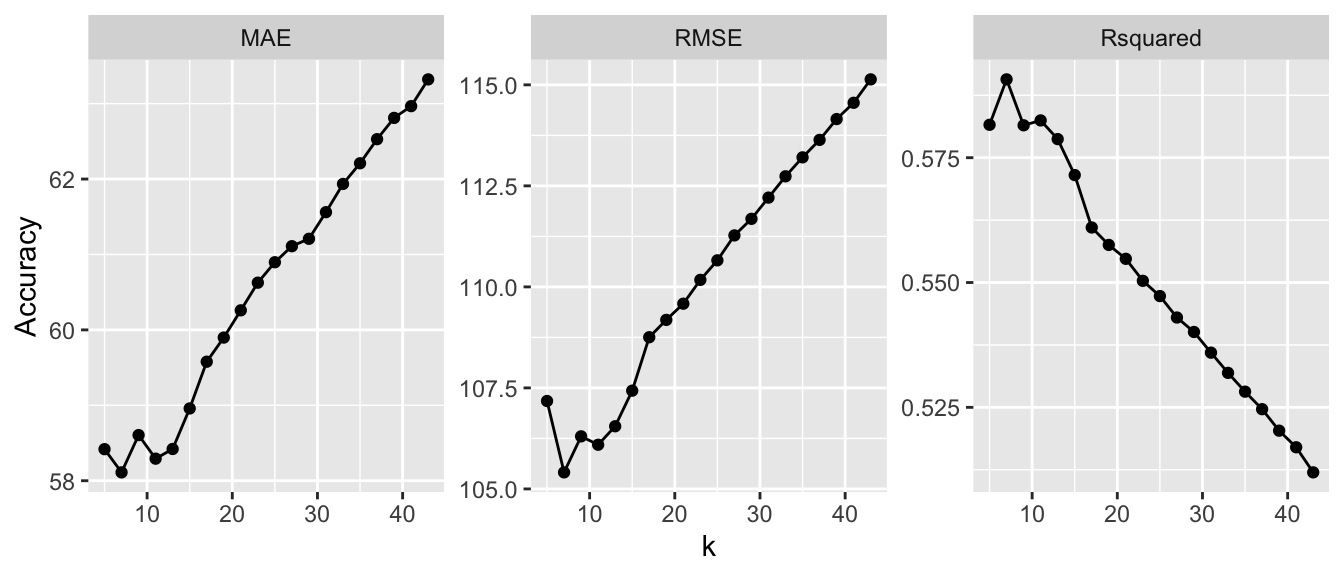

Figure 5.1: Model fits under different metrics with different numbers of neighbours.

Machine Learning models often have more than 1 parameter to tune. The code below describes these for a gradient boosted machine model:

modelLookup("gbm")

##   model         parameter                   label forReg forClass probModel
## 1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE      TRUE
## 2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE      TRUE
## 3   gbm         shrinkage               Shrinkage   TRUE     TRUE      TRUE
## 4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE      TRUE

This tells us that there are four tuning parameters for a gradient boosting machine: - n_trees - the number of trees - interaction.depth - a tree complexity parameter - shrinkage - the learning / adaptation rate - n.minobsinnode - the minimum number of samples in a node for splitting

An initial model can be generated and the results evaluated (the model will take ~2 minutes to train, even with just the defaults):

set.seed(123)
ctrl <- trainControl(method="repeatedcv", repeats=10)
gbmFit <- train(Price ~ ., data = train_z, method = "gbm", 
                trControl = ctrl, verbose = FALSE)

gbmFit

This indicates that the final model values n.trees = 150, interaction.depth = 3, shrinkage = 0.1 and n.minobsinnode = 10. However, they also indicate that the default implementation of GBM in caret evaluates different values for only 2 tuning parameter (interaction.depth and n.tree) and uses only a single value for shrinkage (0.1) and n.minobsinnode (10). Recall that caret defines a tuning set size of \(3^{paramters}\). In the case of GBM it is 9 (\(3^2\)).

We may be able to improve the model fit by letting it tune for a bit longer by passing a longer value of tuneLength than the default \(3^{paramters}\). The Appendix demonstrates how to do this using a tuning grid.

The final aspect of tuning is to increase the cross-validation splits passed to the trControl parameter in train.

The code above generating the kNN and GBM models is reproducible because of the use of the set.seed function. The potential for ambiguity and variation in the results of the train function arises because of the random element of the processing: where in the data the algorithm starts etc when fitting the data. The set.seed function ensures repeatable results. Try running the code snippet defining gbmFit above without set.seed(123) and examine the optimal values of \(k\) that are determined in different runs. The results will be similar but with some small differences

Robust training and validation splits within the training are needed to ensure that the model is not a function of the split but of the general patterns in the data. As well as being done outside of the train function to set up training and validation subsets, it is also possible within the function, through the trainControl function which specifies training parameters and stabilises the results. As a rule of thumb \(k=10\) with 10 repeats should result in a robust model. This takes a bit longer to run as it is a 10-fold repeated CV, repeated 10 times, but the outputs should be more stable, avoiding the need to (arbitrarily) pass a value to set.seed in order to generate reproducible results.

ctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 10) 
knnFit4 <- train(Price ~ ., data = train_z, method = "knn", tuneLength = 20,
                 trControl = ctrl, verbose = FALSE)

knnFit4

5.4.5 Validation

Finally, having trained a well tuned model, it can be applied to the hold out data to test it using the predict function. This gives an indication of the generalizability of the model - the degree to which it is specific to the training / validation split. Theoretically the split was optimised such that the properties of the response variable (Price) were the same in both subsets. The code below goes back to the last GBM model and applies this to the test data and compared the predicted house price values with the actual observed house price values. The scatter plot of these with some trendlines are shown in Figure 5.2.

pred = predict(gbmFit,newdata = test_z)
data.frame(Predicted = pred, Observed = test_z$Price) %>% 
  ggplot(aes(x = Observed, y = Predicted))+
  geom_point(size = 1, alpha = 0.5)+
  geom_smooth(method = "loess", col = "red")+
  geom_smooth(method = "lm")

## `geom_smooth()` using formula = 'y ~ x'
## `geom_smooth()` using formula = 'y ~ x'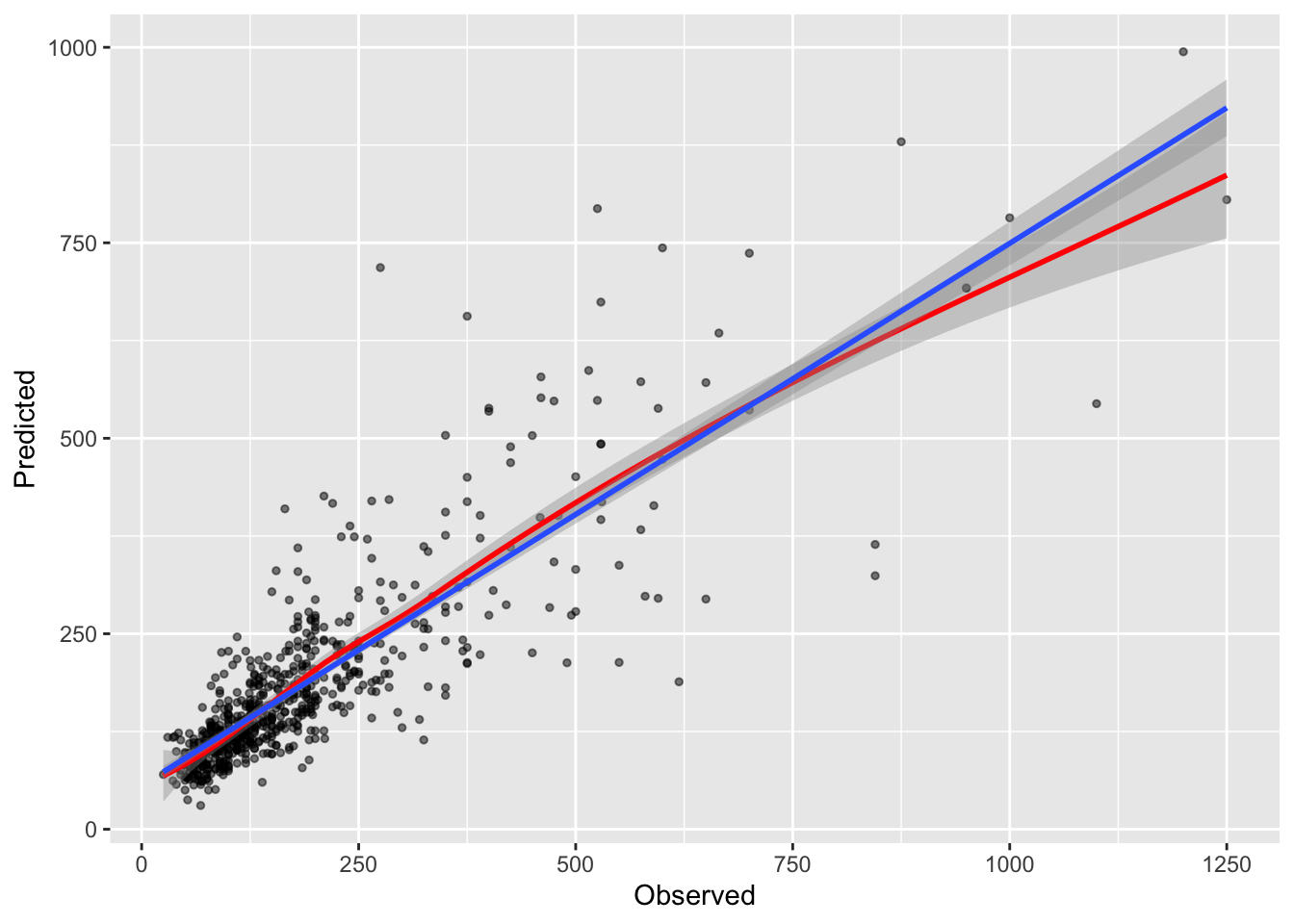

Figure 5.2: Predicted against Observed house Price values from the GBM model, with the model fit indicated by the blue linear trend line and the loess trend in red giving an indication of the variation in prediction from this.

A loess trend line is included in Figure 5.2. We have not fitted a non-linear regression but this trend line reflects the variation in the predicted and observed data, point by point. The loess inflections suggest that model does reasonable well at predicting house prices in the lower middle of the range of values, where both the loess and lm (linear model) trend lines are parallel, it does less well at predicting higher observed values.

A measure of overall model fit can be obtained, which essentially summarises the comparison of the observed values of Price against the predicted ones:

postResample(pred = pred, obs = test_z$Price)

##       RMSE   Rsquared        MAE 
## 83.6676724  0.7125818 50.7697005

5.4.6 Summary

The basic objectives of machine learning are for process understanding (inference) and prediction. These are pursued using 2 general approaches:

• Supervised learning which is typically used for prediction using data split in to training and testing (validation) subsets
• Unsupervised learning is typically used for inference (understanding) or classification and uses the full dataset with model fit measures describing in-sample accuracy.

Input data should be rescaled (normalised) in order to minimise the scale differences between different units of measurements in fitting the model (variables with large values can unreasonably dominate model fitting). There are different ways to do this but the stand approach is use \(z-scores\) that transform the data to have mean of zero and a standard deviation of one, regardless of the units of \(x\).

For supervised approaches to prediction, input data need to be split into 2 subsets (one to create the model, the other evaluate its performance) and there are functions for ensuring that the target variable has a similar distribution in both subsets.

A number of different measures of fit can be used to evaluate model performance including \(R^2\), root mean square error (RMSE) and mean absolute error (MAE). They all measure the degree to which the predicted values differ from actual ones in the test data set.

Models fitting uses different in-sample (i.e. training data) cross-validation folding procedures in which individual data observations are repeatedly held-out and predicted to generate the model. In the caret package trainControl function specifies the of ‘in-model’ sampling and evaluation.

Models should be tuned by exploring a number of combinations of model parameters. The model implementations in the caret package automatically examines a small subset of tuning parameters. However, a larger tuning grid can be specified.

The aim of validation is to determine the generalizability of a predictive model - how well it predicts! It is undertaken by applying the model to data whose results are known and comparing the predicted value with the observed value

5.5 Comparing different Machine Learning approaches

A sample of the many possible machine learning and models for classification and regression are illustrated. These have been selected to represent a spectrum of increasing non-linear complexity through ensemble approaches such as bagged regression trees and random forests as well as learning approaches (Support Vector Machines), as well as classic approaches such as \(k\)-Nearest Neighbour and Discriminant Analysis. This section provides a (very) brief overview of these. In subsequent sections and sub-sections their strengths of prediction, inference and classification are compared with standard linear regression / linear discriminant analysis. Recall that caret will evaluate a small range of tuning parameters, but these can also be specified in a tuning grid as describe above.

Linear Regression

Linear regression seeks to identify (fit) the hyper-plane in multivariate space that minimises the difference between the observed target variable and that predicted by the model. The linear nature of the model relates to this (as illustrated below) and is applied for prediction and inference.

\(k\)-Nearest Neighbour

The \(k\)-Nearest Neighbour algorithm operates under the assumption that records with similar values of, for example Price in the properties data have similar attributes - they are expected to be close in the multidimensional feature space described earlier. In this sense it seeks to model continuous variables or classes given other nearby values. The algorithm is relatively straightforward: for each \(y_i\), select the \(k\) observations closest to observation \(i\) and predict \(y_i\) to be the arithmetic mean of \(y\) of these observations. In this example, use compute the average of the \(k\) nearest observations. Thus the KNN algorithm is based on feature similarity to the number of neighbours (\(k\)) in attribute rather than geographical space.

Bagged Regression Trees

Bootstrap aggregating (bagging) (Breiman 1996) seek to overcome the high variance in regression trees by generating multiple models with the same parameters. The variance issue with regression trees is that although the initial partitions at the top of the tree will be similar between runs and sampled data, there can be large with differences in the branches lower down between individual trees. This is because later (deeper) nodes tend to overfit to specific sample data attributes in order to further partition the data. As a result, samples that are only slightly different can result in variable models and differences in predicted values. This high variance problem causes model instability. The models (and their predictions) can be sensitive to the initial training data sample and thus regression trees suffer from poor predictive accuracy.

To overcome this Bootstrap aggregating (bagging) was proposed by Breiman (1996) to improve regression tree performance. Bagging, as the name suggests, generates multiple models with the same parameters and averages the results from multiple tress. This reduces the chance of over-fitting as might arise with a single model and improves model prediction. The bootstrap sample in bagging will on average contain 63% of the training data, with about 37% left out of the bootstrapped sample. This is the out-of-bag (OOB) sample which are used to determine the model’s accuracy through a cross-validation process.

There are three steps to Bagging:

1. Create a number of samples from the training data. These are termed Bootstrapped samples because they are repeatedly sampled from a training set, before the model is computed from them. These samples contain slightly different data but with the same distribution properties of the full dataset.
2. For each bootstrap sample create (train) a regression tree.
3. Determine the average predictions from each tree, to generate an overall average predicted value.

Gradient Boosted Machine

Boosting seeks to convert weak learning trees into strong learning ones, with each tree fit on a slightly modified version of the original data. Gradient boosting machines (Friedman 2001) uses a loss function to indicate how good a model coefficient estimates are at fitting the underlying data. It trains many trees (models) in a gradual, additive and sequential manner, and parameterises subsequent trees by evaluated losses in previous ones. The loss function is specific to the model objectives. For the house price models here, the loss function quantifies the error between true and predicted (modelled) house prices. GBMs have some advantages for inference as the results from the boosted regression trees are easily explainable and the importance of the inputs can easily be retrieved.

Support Vector Machine

Support vector machine (SVM) analyses for classification and regression (Vapnik 1995). SVM is a non-parametric approach that relies on kernel functions. For regression SVM model outputs do not depend on distributions of input variables (unlike ordinary linear regression). Rather it uses kernel functions, that allow non-linear models to be constructed under the principle of maximal margin, which focuses on keeping the error below a certain value rather than prediction. The kernel functions undertake complex data transformations and then determine the process (hyperplanes) that separate the transformed data. The support vectors are the data points that are closer to the hyperplane influencing its position and orientation. These support vectors allow the margins to be maximised and removing support vectors changes the position of the hyperplane, allowing the SVM to be built.

5.5.1 Prediction

The code below creates 5 prediction models using Standard linear regression (lmFit in the code below), \(k\)-Nearest Neighbour (knnFit) Bagged Regression Trees (tbFit), Gradient Boosting Machines (gbmFit) and Support Vector Machine (svmFit). Each is of these models are run with the rescaled training data (train_z), the control parameters defined below (a 10-fold cross-validated model) with the default tuning parameters in order to create predictive models. These are then applied to the normalized test data (test_z) to generate predictions of known house price values which are then evaluated. Finally, the predictions from the different models are compared.

The following control parameters are used in all models:

# the control parameters 
ctrl <- trainControl(method = "repeatedcv", number = 10, repeats = 10)

The code below creates each of the models, with some of them taking some time to run:

lmFit  = train(Price~.,data=train_z,method="lm", trControl=ctrl,verbose=FALSE)
knnFit = train(Price~.,data=train_z,method="knn",trControl=ctrl,verbose=FALSE)
tbFit  = train(Price~.,data=train_z,method="treebag",trControl=ctrl,verbose=FALSE)
gbmFit = train(Price~.,data=train_z,method="gbm",trControl=ctrl,verbose=FALSE)
svmFit = train(Price~.,data=train_z,method="svmLinear",trControl=ctrl,verbose=FALSE)

For all of the models, the outputs can be examined in the same way (with a model named xxFit):

• tuning parameters can be examined using modelLookup;
• the model results can be examined through xxFit$results;
• the best fitted model is reported in xxFit$finalModel;
• predictions can be made using the predict function, which automatically takes the best model: pred.xx = predict(xxFit, newdata = test_z);
• the prediction can then be evaluated using the postResample function to compare the known test values of Price with the predicted ones: postResample(pred = pred.xx, obs = test_z$Price).

The prediction results can be compared with each other, using the postResample function in caret with the generic predict function. The below shows the accuracy of the predicted house price values when compared against the known, observed house price values in the test data for each model.

Considering MAE, it looks like the Support Vector Machine (SVM) approach is generating the model with the strongest fit, although when applied to unseen data to predict known values the Gradient Boosting Machine (GBM) is best:

# Extract the model validations
df_tab = rbind(
      lmFit$results[which.min(lmFit$results$RMSE),2:4], 
      knnFit$results[which.min(knnFit$results$RMSE),2:4], 
      tbFit$results[which.min(tbFit$results$RMSE),2:4], 
      gbmFit$results[which.min(gbmFit$results$RMSE),5:7],
      svmFit$results[which.min(svmFit$results$RMSE),2:4])
colnames(df_tab) = paste0("Model ", colnames(df_tab))
# Generate the predictions for each model
pred.lm  = postResample(pred = predict(lmFit, newdata = test_z), obs = test_z$Price)

## Warning in predict.lm(modelFit, newdata): prediction from a rank-deficient fit
## may be misleading

pred.knn = postResample(pred = predict(knnFit, newdata = test_z), obs = test_z$Price)
pred.tb  = postResample(pred = predict(tbFit, newdata = test_z), obs = test_z$Price)
pred.gbm = postResample(pred = predict(gbmFit, newdata = test_z), obs = test_z$Price)
pred.svm = postResample(pred = predict(svmFit, newdata = test_z), obs = test_z$Price)
# Extract the prediction validations
df_tab2 = t(cbind(pred.lm, pred.knn, pred.tb, pred.gbm, pred.svm))
colnames(df_tab2) = paste0("Prediction ", colnames(df_tab2))
# Combine 
df_tab = data.frame(df_tab, df_tab2)
rownames(df_tab) = c("SLR", "kNN","BRT", "GBM", "SVM")

# print out
df_tab

Table 5.1: The Model and Prediction accuracies of different machine learning models.

	Model RMSE	Model R2	Model MAE	Prediction RMSE	Prediction R2	Prediction MAE
SLR	107.604	0.571	63.351	95.508	0.625	59.753
kNN	105.616	0.586	58.109	104.918	0.565	60.904
BRT	99.507	0.627	59.452	95.233	0.635	58.858
GBM	91.550	0.686	51.779	84.157	0.709	51.466
SVM	111.743	0.565	56.253	103.978	0.601	56.255

So, if you were given some information about a house and about the local area, the gbmFit could be used to predict the price: you would know whether a house for sale was good value, or what the price for any given house should be.

The kinds of information you need is shown in the test_z or test_anal layers - trying examining this:

head(test_anal)
head(test_z)

The function below makes data.frame of observations generated randomly from a data table, in order to apply to the model to predict price:

# define the function
create_random_obs = function(n.obs = 10, data.table = train_z){
  # a nested function to generate random data
  make_data_row = function(data.table) {
    # for each of the columns in  data.table
    row_index = sample(1:nrow(data.table), ncol(data.table))
    # bind with a column index 1:ncol
    row_index = cbind(1:ncol(data.table), row_index)
    # create a observation row
    vec = data.table[1,]
    # for each column insert the randomly selected row / column value
    for(j in 1:nrow(row_index)){
      vec[1,j] = data.table[row_index[j,2], row_index[j,1]]
    }
    names(vec) = names(data.table)
    return(vec)
  }
  # loop to generate n.obs random observations
  res = vector()
  for(i in 1:n.obs){
    res = rbind(res, make_data_row(data.table))
  }
  return(res)
}

The function can be applied to the rescaled data, train_z:

test_df = create_random_obs(n.obs = 10, data.table = train_z)

You could examine what is created, noting that data in test_df will be different each time it is created:

test_df

And then this can be used as input to the model to generate predicted house prices (in £1000s), noting that your results will be different because your version of test_df will be different: :

predict(gbmFit, newdata = test_df)

##  [1] 308.11136 146.37018 157.47482 256.60449 252.52416 328.64469 130.98272
##  [8]  62.03806 279.30244 136.51271

This can also be done with unscaled data to predict prices as long as all the numeric variables are unscaled. The code below uses data from the the original data table (data_anal) but does some conversions (converting TRUE / FALSE logical values to character and the numeric data to a matrix - this was the effect of the mutate_if(is_double,scale) operation in the creation of train_z above, which was used to construct the models:

test_df = 
  create_random_obs(n.obs = 10, 
                    data.table = data_anal %>% 
                      mutate_if(is_logical,as.character) %>% 
                      mutate_if(is_double,as.matrix))
predict(gbmFit, newdata = test_df)

In summary, there are a large number of possible refinements and choices in the models used for prediction:

• different models will be better suited to the input data than others, suggesting the need to explore a number of model types and families;
• the model predictions can be evaluated by the degree to which they predict observed, known values in the test data;
• the model algorithms can be tuned beyond the caret defaults through a tuning grid, and details of the tuning parameters are listed using the modelLookup("<method>") function;
• the models could be run outside of caret to improve their speed and tuning options as some take a long time to run with even modest data dimensions.

You may wish to save the results of this section (e.g. save.image(file = "prac4_5.3.RData")).

5.5.2 Inference

In contrast to prediction, where the aim is to create a model able to reliably predict the response variable given a set of input variables, the aim of inference is understanding, specifically, process understanding.

The data considerations for inference are slightly different than for prediction because the aims are different. First data do not have to be split. In fact they should not be split as there is danger that some of the potential for understanding will be lost through the split and there is no need to hold data back for training and validation. This means that the full structure of the data can be exploited by the model. Second, theRE is a critical need to consider variable selection (also known as model selection) particularity in the context of collinearity. Model selection is an important component of any regression analysis, but more so for understanding as indicated above: simply if the aim is understanding and 2 variables are correlated (i.e. they essentially have the same relationship with the target variable), then identifying the variable effects on the outcome may be difficult. Determining which predictor variables to include in the analysis is not so important for prediction where the aim is simply to identify the model with the strongest prediction accuracy.

The code below defines X and Y to illustrate a different caret syntax for illustration only, dropping one of the lifestage/ age variables (u25) because groups of variables adding to 1, 100 etc across all records can confound some statistical models, converting the logical True or False values to characters and the Beds variable from an ordered factor to numeric values:

X = data_anal %>% dplyr::select(-Price, -u25) %>% 
  mutate_if(is_logical,as.character) %>% 
  mutate(Beds = as.numeric(Beds)) %>%
  mutate_if(is_double,scale) %>%  data.frame()
Y = data_anal["Price"]

The code below creates 5 inference models using Standard linear regression (lmFit in the code below), \(k\)-Nearest Neighbour (knnFit) Bagged Regression Trees (tbFit), Gradient Boosting Machines (gbmFit) and Support Vector Machine (svmFit). None of these are tuned beyond the defaults in caret. However tuning has been heavily illustrated in previous sections. The aim here is to illustrate how the different types of models can be compared and evaluated and used to generate understanding of the factors associated with house price. The code below creates each of the models:

ctrl= trainControl(method="repeatedcv",number=10,repeats=5)
set.seed(123)
lmFit  = train(Price~.,data=cbind(X,Y),method="lm",trControl=ctrl, trace = F)
knnFit = train(Price~.,data=cbind(X,Y),method="knn",trControl=ctrl,trace=F)
tbFit  = train(Price~.,data=cbind(X,Y),method="treebag",trControl=ctrl)
gbmFit = train(Price~.,data=cbind(X,Y),method="gbm",trControl=ctrl,verbose=F)
svmFit = train(Price~.,data=cbind(X,Y),method="svmLinear",trControl=ctrl,verbose=F)

For inference and understanding, the aim is to understand how each of the different inputs are related to Price, the target variable. However, each approach generates different kinds of results. For example coefficient estimates can be extracted from the glmnet as with standard regression models with lm, but not from the other models.

Examining the variable importance allows the different model inferences to be explored. Figure 5.3 compares these for these different models. Each model defines variable importance in different ways, and so the specific mechanism for each model should be examined outside of caret. In this case the results show that the Beds covariate is generally the variable that is associated most strongly with the response (Price), but some models identify others as well: green space area (gs_area) for kNN and SVM, Northing (all models) and the proportion of the population under 45 (u45), unemployed (unmplyd) are also generally important. Notice, also the different profiles of the variables in the different models: TB has many similarly salient variables. whereas the other models have similar gradients / profiles of importance (although with different variables in each model).

# define a print function 
# this was modified from here: 
# https://github.com/topepo/caret/blob/master/pkg/caret/R/print.varImp.train.R
print.varImp.10 <- function(x = vimp, top = 10) {
   printObj <- data.frame(as.matrix(sortImp(x, top)))
   printObj$name = rownames(printObj)
   printObj
}   
# use this extract the top 10 variables to a data.frame - df
df = data.frame(print.varImp.10(varImp(lmFit)), method = "LM") 
df = rbind(df, data.frame(print.varImp.10(varImp(knnFit)), method = "kNN")) 
df = rbind(df, data.frame(print.varImp.10(varImp(tbFit)), method = "TB")) 
df = rbind(df, data.frame(print.varImp.10(varImp(gbmFit)), method = "GBM")) 
df = rbind(df, data.frame(print.varImp.10(varImp(svmFit)), method = "SVM")) 
df %>% 
  ggplot(aes(reorder(name, Overall), Overall)) +
  geom_col(fill = "tomato") +
  facet_wrap( ~ method, ncol = 3, scales = "fixed") +
  coord_flip() + xlab("") + ylab("Variable Importance") +
  theme(axis.text.y = element_text(size = 7))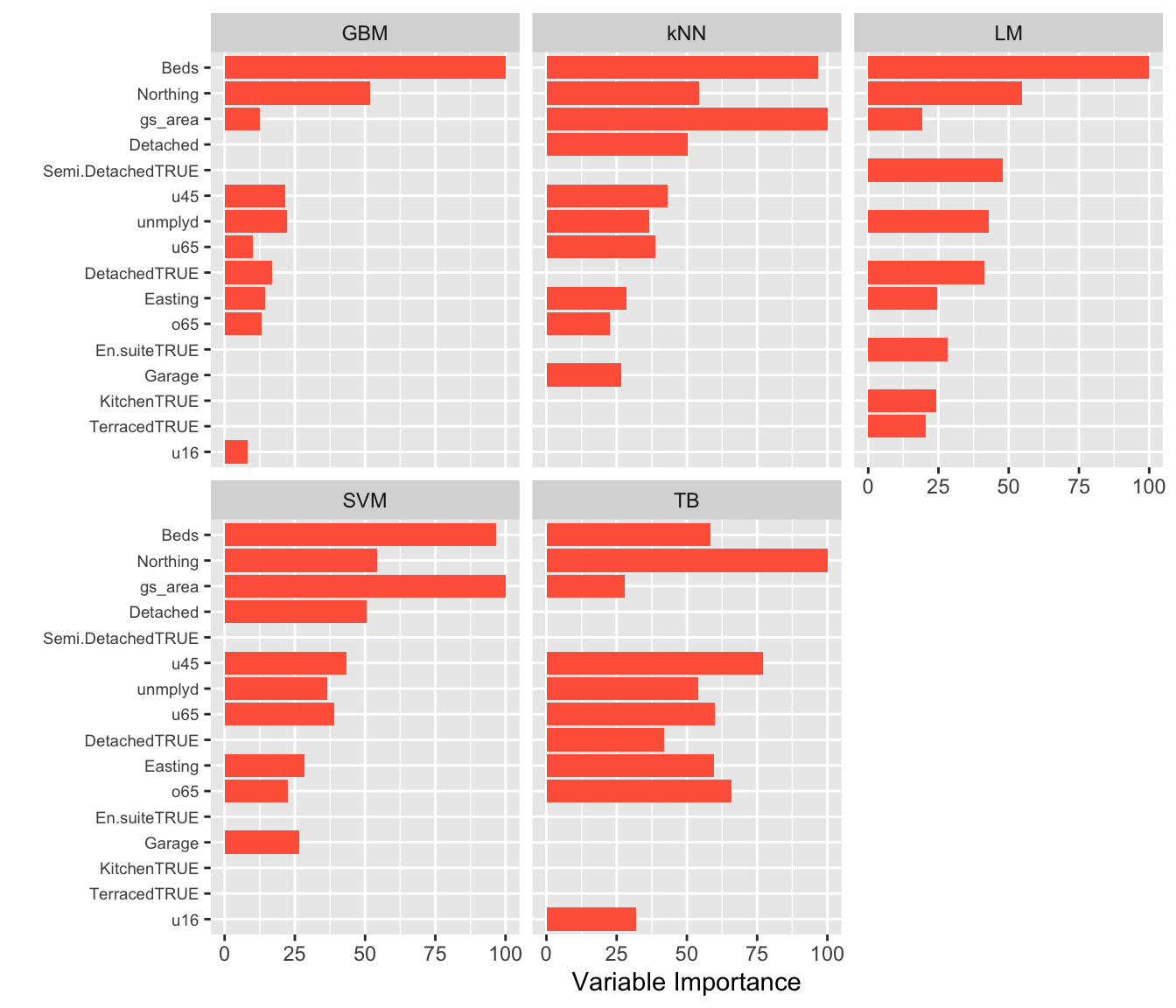

Figure 5.3: The Variable Importance associated with diffrerent inference models.

There is much more that could be done here. The data were not scaled, none of the approaches was tuned, in-sample accuracies have not been reported, tune lengths could be increased, alternative controls could be evaluated. It is however, worth examining the individual models in more detail. The above code ran the caret implementation but greater control and analytical nuance can be exercised using the gbm, knn, etc packages directly. Changes to all of these default settings could be explored.

You may wish to save the results of this practical (e.g. save.image(file = "prac4.RData")).

Appendix: Creating and evaluating a tuning grid

The code below creates a data frame to be passed to the tuneGrid parameter in train, with columns for each tuning parameter, named in the same way as arguments required by the function. In the example below a grid of contains 270 combinations of parameters - these will take at least an hour or 2 to evaluate SO DO IT OUTSIDE OF THE PRACTICAL!

The code snippet below defines a grid that contains 270 combinations of parameters - these will take an hour or 2 to evaluate.

params <- expand.grid(n.trees = seq(50, 300, by = 50),
                      interaction.depth  = seq(1, 5, by = 1),
                      shrinkage = seq(0.1, 0.3, by = 0.1),
                      n.minobsinnode = seq(5,15,5))
dim(params)
head(params)
set.seed(123)
gbmFit_t <- train(Price ~ ., data = train_z, method = "gbm", 
                trControl = ctrl,
                tuneGrid = params, verbose = FALSE)

The results can be examined:

gbmFit_t$bestTune

or the whole model can be printed:

gbmFit_t

The best model can be accessed directly using the which.min and which.max functions as below to interrogate the different accuracy measures. Notice that the MAE provides slightly different optimal parameters:

gbmFit_t$results[which.min(gbmFit$results$RMSE),]
gbmFit_t$results[which.max(gbmFit$results$Rsquared),]
gbmFit_t$results[which.min(gbmFit$results$MAE),]

If you are unsure whether the full range of tuning parameters have been evaluated you could define a grid containing even more combinations of parameters, perhaps leaving this run overnight. the code below sets up a tuning grid with 1000 combinations of parameters.

params <- expand.grid(n.trees = seq(50, 400, by = 50),
                      interaction.depth  = seq(1, 5, by = 1),
                      shrinkage = seq(0.1, 0.5, by = 0.1),
                      n.minobsinnode = seq(10,50,10))
dim(params)
head(params)

References

Breiman, Leo. 1996. “Bagging Predictors.” Machine Learning 24 (2): 123–40.

Brunsdon, Chris, and Lex Comber. 2018. An Introduction to r for Spatial Analysis and Mapping (2e). Sage.

Comber, Lex, and Chris Brunsdon. 2021. Geographical Data Science and Spatial Data Analysis: An Introduction in r. Sage.

Friedman, Jerome H. 2001. “Greedy Function Approximation: A Gradient Boosting Machine.” Annals of Statistics, 1189–1232.

Gale, Christopher G, A Singleton, Andrew G Bates, and Paul A Longley. 2016. “Creating the 2011 Area Classification for Output Areas (2011 OAC).” Journal of Spatial Information Science 12: 1–27.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. Vol. 112. Springer.

Kuhn, Max. 2015. “Caret: Classification and Regression Training.” Astrophysics Source Code Library.

Kuhn, Max, and Kjell Johnson. 2013. Applied Predictive Modeling. Vol. 26. Springer.

Vapnik, Vladimir. 1995. The Nature of Statistical Learning Theory. Springer science & business media.