7 Zusammenhangsmaße
7.1 Abstandsmaßen und Zusammenhangsmaße
Wir haben gelernt, was der statistische Signifikanztest ist. NHST hilft uns, zu erkennen, wenn der Unterschied von einer Stichprobe zur anderen nicht zufällig ist (not random). Allerdings hat dies einen Haken (bzw. zwei Haken).
- Keine Effektstärke wird gemessen
- Stichprobengröße beeinflusst unser Ergebniss.
Effektgröße gibt es für Mittelwertunterschiede (man spricht von Abstandsmaßen) und für Zusammenhänge (Zusammenhangsmaße). Beides wurde in der letzten Einheit besprochen.
Wir haben allerdings noch ein Maß ausgelassen und zwar Chi-Square/Chi-Quadrat.
CHI-QUADRAT vergleicht die erwarteten Häufigkeiten mit den tatsächlichen Häufigkeiten.
Auch hier starten wir wieder bei einer Kreuztabelle.
Wir müssen zuerst die erwarteten Häufigkeiten ausrechnen. Die erwarteten Häufigkeit für ein bestimmtes Feld berechnen wir, indem wir die Randsumme mal der Reihensumme nehmen und dies durch die totale Anzahl an Beobachtungen dividieren. Danach können wir diese mit den tatsächlichen Häufigkeiten vergleichen. Sie erinnern sich bestimmt an das Konzept des Fehlerterms. Auch hier berechnen wir diesen:
\(Fehlerterm=\text{Tatsächliche Häufigkeit}-\text{Erwartete Häufigkeit}\)
… dann können wir die Summe der quadrierten Fehlerterme ausrechnen:
\(\text{Summe der quadrierten Fehlerterme}=\sum_{i=1}^n(\text{Tatsächliche Häufigkeit}-\text{Erwartete Häufigkeit})^2\)
Von dem können wir dann das Chi-Quadrat berechnen. Dafür müssen wir noch durch die erwarteten Häufikgeiten dividieren (wir standardisieren quasi durch die erwarteten Häufigkeiten - e.g. prozentuale Abweichung zu den erwarteten Häufigkeiten)
\(\text{Chi-Quadrat}=\mathcal{X}^2=\sum_{i=1}^n\frac{(\text{Tatsächliche Häufigkeit}-\text{Erwartete Häufigkeit})^2}{\text{Erwartete Häufigkeit}}\)
Die Chi-Verteilung beschreibt die Wahrscheinlichkeit der Chi-Quadrat Werte, wenn die Null-Hypothese wahr ist. Diese verändert sich mit der Anzahl der Freiheitsgraden.
Dass die Chi-Quadrat-Verteilung linkssteil bzw. rechtsschief ist, macht Sinn: Wir würden ja erwarten, dass wenn die Nullhypothese richtig ist, dass wir mehr niedrige Chi-Quadrat Werte erhalten würden (sprich der Unterschied zwischen den erwarteten und den tatsächlichen Häufigkeiten ist sehr klein).
Ein wichtiges Fakt dieser Verteilung ist, dass der Erwartungswert der Chi-Quadrat-Verteilung mit n Freiheitsgraden gleich der Anzahl der Freiheitsgrade ist. Der Mittelwert entspricht also der Anzahl der Freiheitsgrade und die Abweichung ist die doppelte Anzahl der Freiheitsgrade.
Diese Verteilung, präziser gesagt die Quantile der Chi-Quadrat Verteilung, ist auch in der Tabelle aufgezeichnet, welche Sie auch als Klausurunterlage zur Verfügung haben. Wenn das berechnete Chi-Quadrat größer ist als der Wert in der Tabelle, haben wir eine größere Abweichung als jene, welche noch im Bereich der Nullhypothese ist, sprich wir haben ein signifikantes Ergebnis. Achten Sie darauf, dass Sie bei einer gerichteten Hypothese und einer Wahrscheinlichkeit von 95 Prozent in der Spalte mit 0.975 nachsehen und bei einer ungerichteten Hypothese und einer Wahrscheinlichkeit von 95 Prozent in der Spalte mit 0.95.
Die Berechnung des Chi-Quadrates verlangt einige Annahmen, die getroffen werden müssen:
Kategorien sind exklusiv (e.g. eine Beobachtung kann nicht in mehreren Zellen gelistet sein)
N ist groß genug (2x2 Tabelle: mindestens 5 Beobachtungen pro Zelle, größere Tabellen: mindestens 1 pro Zelle und mindestens 5 in 20 Prozent der Zellen) Wenn die Beobachtungsanzahl zu klein ist, haben wir keine Annäherung zur Chi-Verteilung. Das heißt, wir würden den P-Wert falsch einschätzen.
In diesem Fall müssen wir auf Alternativen zurückgreifen:
- Fischer’s exact text
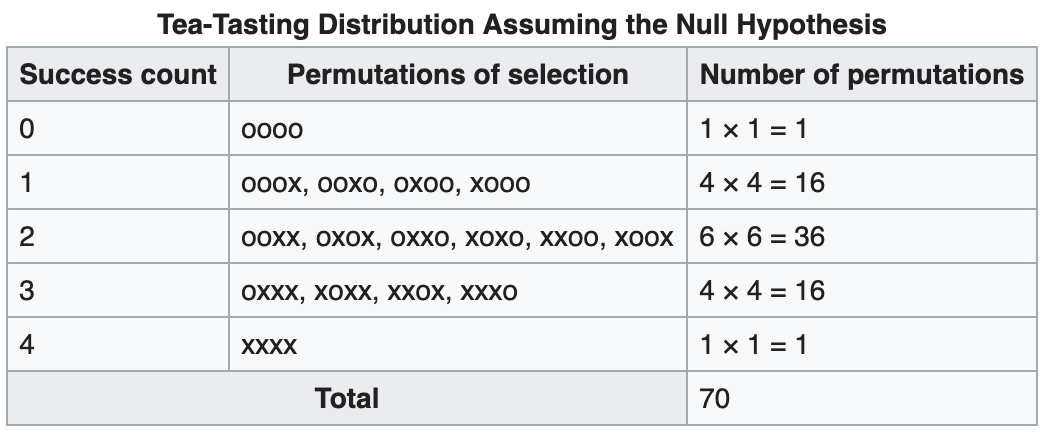
1/70 = Wahrscheinlichkeit für die Situation dass alle richtig sind
gegeben die Null-Hypothese ist richtig.
Wahrscheinlichkeit = 0.01428 bei drei Richtigen wäre das schon nicht mehr signifikant. Daher haben wir hier wenig Power.
- Kontinuierliche Anpassung: Hier wird ein konstanter Betrag abgezogen.
\(\text{Chi-Quadrat}=\mathcal{X}^2=\sum_{i=1}^n\frac{(|\text{Tatsächliche Häufigkeit}-\text{Erwartete Häufigkeit}|-0.5)^2}{\text{Erwartete Häufigkeit}}\)
- Likelihood-Quotienten-Test (Als Logarithmus einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl zu erhalten.)
\(L\mathcal{X}^2=2\sum \text{Tatsächliche Häufigkeit} * ln(\frac{\text{Tatsächliche Häufigkeit}}{\text{Erwartete Häufigkeit}})\)
Allerdings haben wir uns jetzt immer mit dem generellen Zusammenhang beschäftigt. Was ist, wenn wir uns für ein spezielles Ereignis interessieren.
Hierzu können wir den standardisierten Fehlerterm berechnen:
\(\text{Standardisierter Fehlerterm}=\frac{\text{Tatsächliche Häufigkeit}-\text{Erwartete Häufigkeit}}{\sqrt{\text{Erwartete Häufigkeit}}}\)
Warum haben wir hier kein Quadrat? Weil wir dies ja gemacht haben, um die Werte aufzusummieren (sodass sich diese nicht gegenseitig aufheben).
Chancenverhältnis ist eine andere Möglichkeit, diese Verhältnisse auszurechnen (siehe letzte Einheit).
Bei kontinuierlichen Variablen verwenden wir Pearsons R, welches auf der Kovarianz aufbaut:
\(Kovarianz=\frac{\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})}{n-1}\)
Problem der Kovarianz: Diese hängt von der Skalierung der Variablen ab. Daher standardisieren wir dies mit der Standardabweichung.
\(Korrelation=r=\frac{Kovarianz}{s_xs_y}=\frac{\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})}{(n-1)*s_xs_y}\)
Wir haben allerdings noch nicht gelernt, die Signifikanz für dieses Zusammenhangsmaß zu berechnen.
Um dies umzusetzen, müssen wir zuerst r standardisieren (bzw. so transformieren dass wir einen z-standardisierten Korrelationskoeffizienten erhalten).
- r z-transformieren
\(z_r=\frac{1}{2}log[\frac{1+r}{1-r}]\)
\(z_{r=0.25}=\frac{1}{2}log[\frac{1+0.25}{1-0.25}] = 0.256\)
- Standardfehler von \(z_r\) berechnen
\(SE_{z_r}=\frac{1}{\sqrt{n-3}}\)
\(SE_{z_r}=\frac{1}{\sqrt{8216}}=0.01083633\)
(n-3, da 2 Parameter (\(\bar{x},\bar{y}\)) nicht variieren können, weiterer Grund ist die Herleitung der Formel.)
- Test Statistik berechnen (Effekt über Fehler)
\(z=\frac{z_r}{SE_{z_r}}=\frac{0.256}{0.01083633}=23.57\)
\(\rightarrow\) weit außerhalb der Nullhypothesenverteilung (signifikant mit p<0.001)
Bei kleinen Stichproben:
\(t_r=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\)
- Konfidenzintervalle
\(KI_{\text{unteres, z-transformiert}}=z_{r}-1.96*SE_{z_r}\)
\(= 0.234\)
\(KI_{\text{oberes, z-transformiert}}=z_{r}+1.96*SE_{z_r}\)
\(= 0.276\)
\(Transformation=\frac{e^{2z_r}-1}{e^{2z_r}+1}\)
\(KI_{\text{unteres, nicht-z-transformiert}}=\frac{e^{2*0.234}-1}{e^{2*0.234}+1}=0.2291085\)
\(KI_{\text{oberes, nicht-z-transformiert}}=\frac{e^{2*0.276}-1}{e^{2*0.276}+1}=0.2689448\)
7.2 Regressionsanalyse
Die folgende Formel kommt Ihnen vielleicht bekannt vor. Diese repräsentiert die Standardformel der Regression:
\(Y_i=\beta_0+\beta_1X_1+\epsilon_i\)
Beta 0 sagt uns, wo das Modell startet (exakt der Mittelwert, wenn wir keine zusätzlichen Schätzer haben) und Beta 1 sagt uns die Steigung (die Form des Modelles des Zusammenhanges).
WIE berechnen wir jetzt diese betas?
ZIEL eines Regressionsmodells ist es, die Koeffizienten so zu bestimmen, dass die Summe der quadrierten Fehlerterme minimiert wird.
\(\text{Summe der quadrierten Fehlerterme}=SS_R\text{(Residual sum of squares)}=\sum_{i=1}^n(\text{Tatsächlicher Wert}_i-\text{Vorhersage}_i)^2=\sum_{i=1}^n(Y_i-\hat{Y}_i)^2\)
Beta 1-Berechnung
Ein Zusammenhang kann gemessen werden, indem wir uns ansehen, inwiefern die Abweichung vom Mittelwert der erklärenden Variable mit der Abweichung des Mittelwertes der abhängigen Variable einhergeht.
\(\beta_1=\frac{Kovarianz_{x,y}}{Varianz_x}\)
Wir teilen hier den totalen Zusammenhang von X und Y durch die Varianz in X (wir standardisieren durch die Varianz in X). Sprich beta1 sagt uns den Effekt gemessen in Einheiten von X. Es ist wichtig zu verstehen, dass es sich um einen gerichteten Effekt handelt (X auf Y).
Standard Fehler von \(\beta_1\)
Um die Signifikanz von Beta zu berechnen, starten wir mit dem durchschnittlichen Standardfehler (SE) im Modell:
\(\text{Durchschnittlicher SE im Modell (Y)}=\sqrt{\frac{\sum^n_{i=1} (Y_i-\hat{Y_i})^2}{N-2}}\)
danach nehmen wir den durchschnittlichen Standardfehler im Modell und dividieren diesen durch die Wurzel aus der Summe der Abweichungen in X (\(\sqrt{SS_x}\)).
\(SE_b=\frac{SE_{Modell}}{\sqrt{SS_x}}\)
Mit Hilfe des Standardfehlers von Beta und Beta selbst können wir das Konfidenzintervall von Beta berechnen:
\(KI_{\beta, unteres}=\beta - z * SE\) (bei kleinen Stichproben t)
\(KI_{\beta, oberes}=\beta + z * SE\) (bei kleinen Stichproben t)
Des Weiteren können wir die Test Statistik berechnen (wir erinnern uns Effekt durch Fehler):
\(\text{Test Statistik}=\frac{\text{Tatsächliches Beta}-\text{Erwartetes Beta}}{SE_b}\)
Wir setzen das erwartete Beta 1 als 0, da wir keinen Effekt erwarten:
\(=\frac{\text{Tatsächliches Beta}-0}{SE_{\beta}} = \frac{\beta}{SE_{\beta}}\)
Noch verstehen wir nicht alle Parameter eines typischen Regressionsoutputs (siehe Beispiel auf den Folien). Wir wissen noch nicht, was die F-Statistik bedeutet und was uns das R-square sagt. Beide beschreiben die Qualität des Modells, sprich wie gut das Modell die Varianz in den Daten repräsentiert.
Die F-Statistik sagt uns, um wieviel besser unsere Schätzung (\(Y_i=\beta_0+\beta_1X_1\)) ist als wenn wir nur den Mittelwert von Y als Schätzung verwenden würden.
\(\text{F-Statistik}=\frac{\text{Erklärte Varianz}}{\text{Unerklärte Varianz}}\)
\(\text{Erklärte Varianz}= \frac{\text{Summe der Modell-Quadrate}=\sum^n_{i=1} (\hat{y_i}-\bar{y_i})^2}{\text{Freiheitsgrade des Modelles}}\)
\(\text{Unerklärte Varianz}= \frac{\text{Summe der Fehler-Quadrate}=\sum^n_{i=1} (y_i-\bar{y_i})^2}{\text{Freiheitsgrade für Fehlerterm}}\)
\(\text{Freiheitsgrade des Modelles}=\text{Parameter}-1\)
\(\text{Freiheitsgrade für Fehlerterm}=n-\text{Parameter}\)
\(\text{Parameter}=\text{Anzahl der erklärenden Variablen}+1\)
Eine F-Statistik größer 1 sagt uns, dass das Modell besser ist als die Schätzung rein durch den Mittelwert.
R-Quadrat ist auch ein Maß der Modellqualität und gibt den Anteil der Varianz von Y, welcher durch die erklärende Variablen erklärt werden kann, an.
\(R^2=1-\frac{\text{Summe der quardrierten Fehlerterme in der Regression}}{\text{Summe der quardrierten Fehlerterme im Modell }\bar{Y}}=\frac{Residual Sum of Squares (RSS)}{Total Sum of Squares (TSS)}\)
\(=1-\frac{\sum^n_{i=1}(y_i-\hat{y})}{\sum^n_{i=1}(y_i-\bar{y})}\)
Das R-Quadrat lässt sich sehr gut interpretieren. Es reicht von 0 (keine Verbesserung vom Modell vis a Vis dem Nullmodell) bis zu 1 (100 Prozent der Varianz in Y werden erklärt). Das heißt, ein R-Quadrat von 0.81 würde bedeuten, dass 81 Prozent der Y-Varianz erklärt werden können. Ein R-Quadrat von 0.24 würde bedeuten, dass 24 Prozent der Y-Varianz erklärt werden können. Mit einem R-Quadrat ab ca. 0.30 haben Sie bereits ein recht passables Modell geschätzt.
Wie ein Korrelationskoeffizient verlangt auch die Regressionsanalyse, dass gewisse Annahmen getroffen worden sind:
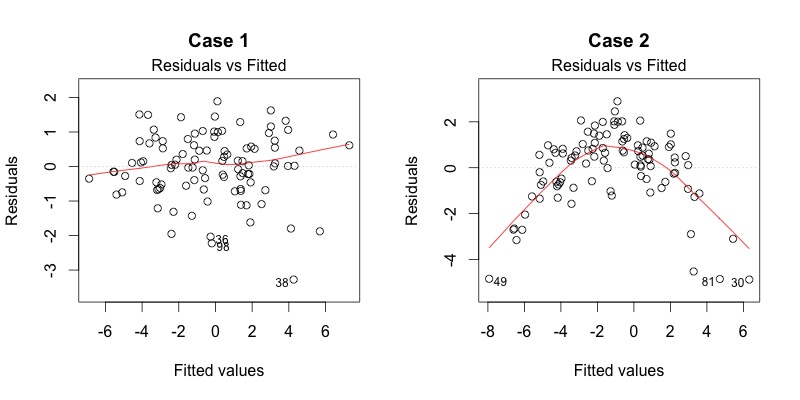
- Linearität: Um dies zu überprüfen, können wir die Residuen versus der Vorhersagewerte darstellen. Die Punkte sollten möglichst eine Gerade bilden (siehe Folie 51). Bei Nicht-Linearität können wir die Variablen log-transformieren.
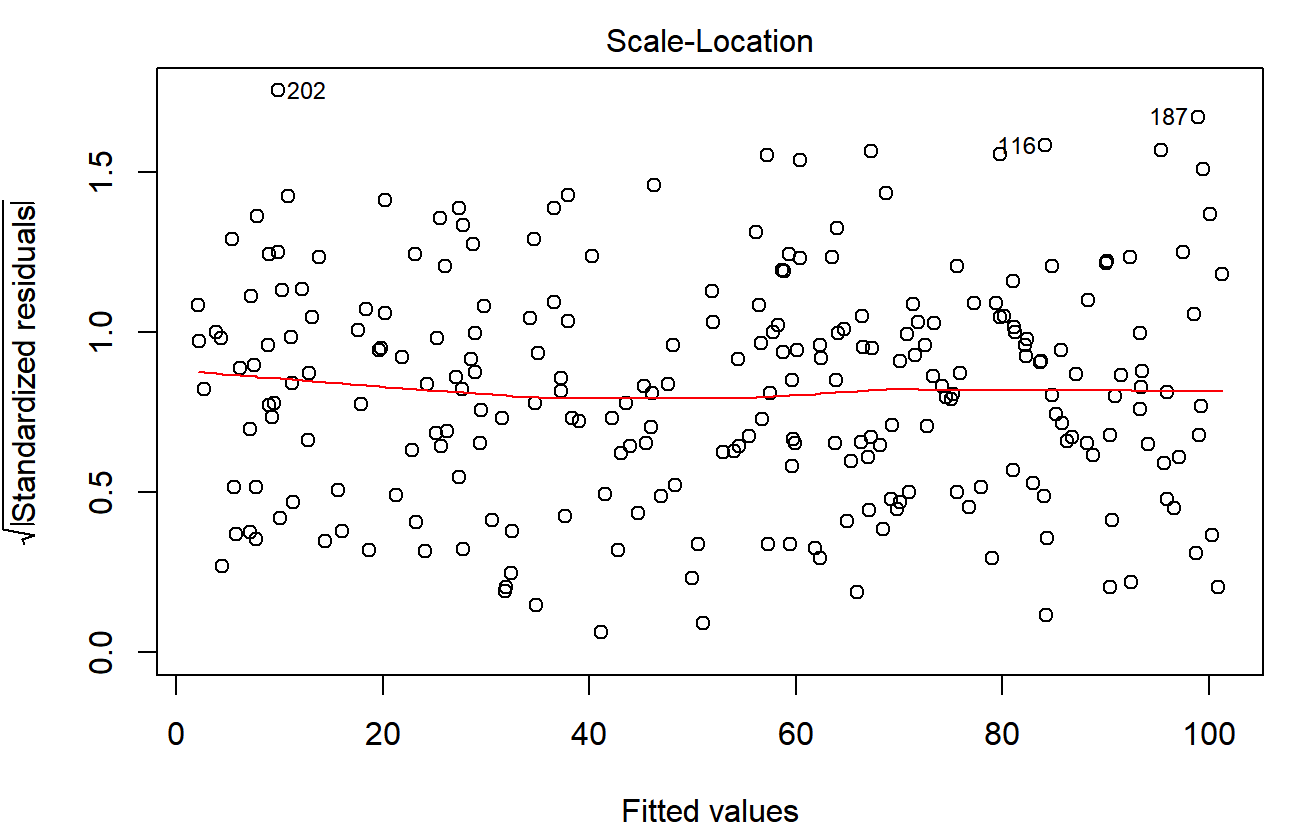
- Homoskedastizität: Um Homoskedastizität zu prüfen, können wir die fitted values vs Varianz darstellen. Wenn dies verletzt ist, können wir eine Log-Transformation der Y-Variable durchführen oder eine sogenannte weighted least square regression (Methode der gewichteten kleinsten Quadrate) schätzen.
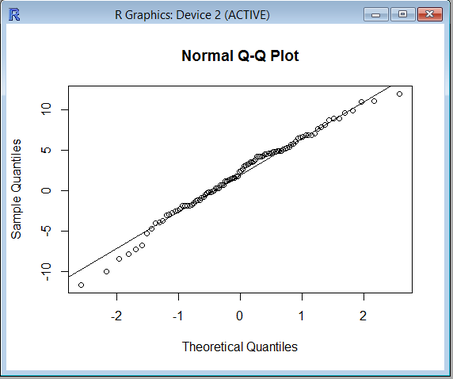
- Normalverteilung der Residuen: Um die Normalverteilung der Residuen zu überprüfen, können wir ein Quantil-Quantil Diagramm darstellen und wiederum sollten wir die meisten Punkte auf der Linie sehen.
 . Auch hier, wenn diese Annahme verletzt ist, können wir die Variablen transformieren (sqrt, log,…)
. Auch hier, wenn diese Annahme verletzt ist, können wir die Variablen transformieren (sqrt, log,…) - Keine Ausreißer: Wenn wir den Einfluss von Beobachtungen versus Fehlerterme darstellen, können wir Ausreißer identifizieren. Dies könnten wir versuchen auszuschließen.
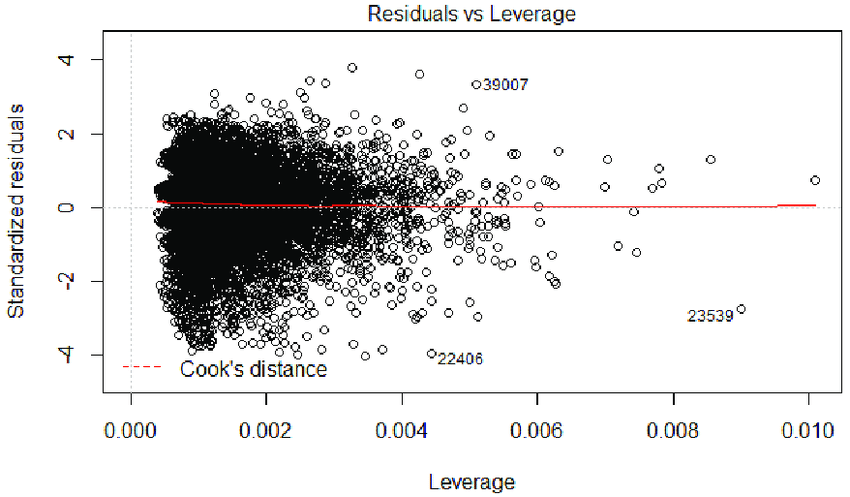
- Keine Autokorrelation: Der Durbon Watson Test sagt uns, ob wir eine Autokorrelation vorliegen haben oder nicht. Wenn ja, könnten wir versuchen, ein Modell mit fixen Effekten schätzen oder ein Modell mit gruppierten Standardfehlern rechnen.
- Keinen Omitted Variable Bias (kein Vergessen zentraler Variablen): Die Frage, ob wichtige Variablen ingoriert wurden, ist mehr eine theoretische als mathematische Frage.
Jetzt stellen Sie sich vielleicht die Frage, warum wir nicht einfach ein Pearson’s R berechnen können. Dies hat zwei Gründe:
- Korrelation misst den Zusammenhang von zwei Variablen, OLS misst, inwiefern die Varianz in Y durch die Varianz in X erklärt werden kann.
- Regressionsanalyse kann mehrere erklärende Variablen beinhalten. … MULTIVARIATE REGRESSIONSANALYSE/MULTIPLE REGRESSION}
Wie interpretieren wir also die multivariate Regression: Wir interpretieren einen Koeffizienten gleich wie in einer bivariaten Regression, müssen aber annehmen, dass alle anderen Variablen konstant bleiben (CETERIS PARIBUS).
Zu beachten gilt generell folgendes:
- Möglichst große Anzahl an Beobachtungen
- gut für die Normalverteilung der Residuen
- gut, wenn wir viele erklärende Variablen haben.
- Annahmen, welche wir zuvor besprochen haben
- Zusätzlich soll überprüft werden, dass keine Multikollinearität vorliegt
- Korrelation zwischen Variablen berechnen und VIF (variance inflator factors) berechnen (diese sollten nicht höher als 10 sein)