4 Wahrscheinlichkeit

Wir unterscheiden zwischen den folgenden drei Szenarien:

  • Deterministisch (X folgt ganz bestimmt Z)
  • Wahrscheinlich (X folgt mit einer gewissen Wahrscheinlichkeit Z)
  • Zufällig (Wenn X Z folgt ist dies rein zufällig)

WAHRSCHEINLICHKEIT ist eine Einstufung von Aussagen und Urteilen nach dem Grad der Gewissheit (Sicherheit).

4.1 Wichtige Begrifflichkeiten

4.1.1 Empirische und theoretische Wahrscheinlichkeit

Die theoretische Wahrscheinlichkeit ist jene Wahrscheinlichkeit, welche wir theoretisch a priori definieren. Die empirische Wahrscheinlichkeit ist die Wahrscheinlichkeit der tatsächlichen Beobachtungen. Bei einem Münzwurf ist theoretisch die Wahrscheinlichkeit Kopf zu werfen ebenso hoch wie die Wahrscheinlichkeit Zahl zu werfen, sprich die theoretische Wahrscheinlichkeit beträgt je 50 Prozent. Die empirische Wahrscheinlichkeit leitet sich aus den tatsächlichen Wurfresultaten ab. Werfen Sie zum Beispiel 40 Mal Kopf und 60 Mal Zahl, ist die empirische Wahrscheinlichkeit für Kopf 40 Prozent und die empirische Wahrscheinlichkeit für Zahl 60 Prozent.

4.1.2 Ergebnismenge

Als ERGEBNISMENGE bzw. ERGEBNISRAUM \(\Omega\) bezeichnet man die Menge aller möglichen Ergebnisse eines Zufallsvorgangs.

Beispiel für Ergebnismengen:

\(\Omega_{exit}=\{\text{Kopf}, \text{Zahl}\}\)

Wir können die Ergebnismenge und die tatsächlich beobachteten Ereignisse auch mit Hilfe eines Histogrammes darstellen. Dies wird dann Wahrscheinlichkeitsverteilung genannt. Jeder Balken übernimmt hier einen genau definierten Wert und die Verteilung kann selbstverständlich unterschiedlich aussehen.

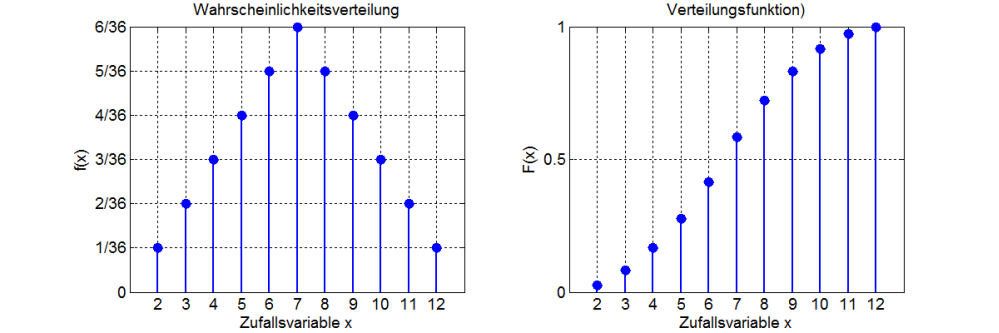
4.1.3 Dichtefunktion

Da Häufigkeiten die Grundlage von Wahrscheinlichkeit bietet, stellt sich erneut die Frage, wie wir mit metrischen Variablen umgehen. Bei metrischen Variablen können wir die DICHTEFUNKTION verwenden. Sie ist das Analogon zur Wahrscheinlichkeitsfunktion bei diskreten Wahrscheinlichkeiten.

Wir berechnen die Wahrscheinlichkeit für metrische Variable durch folgende Schritte:

  1. Überprüfen, ob eine Normalverteilung vorliegt. (Bei einer Verteilung, welche nicht normal ist, muss mit der Funktion oben ferechnet werden. Keine Sorge: Jedes Statistikprogramm kann dies für Sie erledigen.)
  2. Wenn ja, Transformation in z-Werte bzw Umwandlung in eine Standardnormalverteilung.
  3. Verteilungstabelle der Standardnormalverteilung konsultieren.

Was ist also eine Normalverteilung?

Normalverteilung ist eine der wichtigesten Verteilungen der Statistik. Sie wurde von Carl Friedrich Gauß beschrieben und wird deshalb auch oft als Gauß-Verteilung bezeichnet. Wegen der charakteristischen Form nennt man die Verteilung auch oft Glockenkurve. Sehr viele Variablen sind tatsächlich normalverteilt. Körpergröße (eines Geschlechts) zum Beispiel oder Intelligenz sind normalverteilt. Ganz viele Menschen sind durchschnittlich groß und durchschnittlich intelligent. Nur wenige Menschen sind sehr klein oder sehr groß oder haben einen besonders hohen Intelligenzkoeffizienten oder einen extrem niedrigen. Auch Variablen wie Einkommen oder Bevölkerungsgröße sind normalverteilt, wenn diese vorher logarithmiert werden.

Eine Sonderform der Normalverteilung ist die Standardnormalverteilung. Dies ist der Fall, wenn der Mittelwert 0 ist und die Standardabweichung bei 1 liegt.

Transformation von Normalverteilung zur Standardnormalverteilung funktioniert durch eine sogenannte Z-Transformation:

Stichprobe:

\[z_i=\frac{x_i-\bar{x}}{s}\]

Grundpopulation:

\[z_i=\frac{x_i-\mu}{\delta}\]

Vorteile von dieser Z-Transformation sind folgende:

  1. Werte können in den Kontext gesetzt werden. Wir können so Zahlen z-transformieren und dann abfragen wie weit diese über bzw. unter dem Mittelwert liegen. Wenn wir die Wahlbeteiligung zu den US-Präsidentschaftswahlen hernehmen, wo der Mittelwert bei 62 Prozent und die Standardabweichung bei 14 Prozent liegt, können wir uns zum Beispiel fragen, wie eine Wahlbeteiligung von 66 Prozent zu interpretieren ist. Wir nehmen dazu die 66 Prozent substrahieren 62 und dividieren dies durch 13. Wir bekommen einen Wert von 0.3. Dies bedeutet, dass der Wert 0.3 Standardabweichungen über dem Mittelwert liegt. Wenn wir dasselbe für 30 Prozent Wahlbeteiligung machen, bekommen wir einen z-Wert von -2.37 und wissen, dass 30 Prozent Wahlbeteiligung 2.37 Standardabweichungen unter dem Mittelwert liegt.

  2. Standardisierung aller Normalverteilungen. Der zweite Vorteil ist, dass wir durch die Transformation, die Integrale für die Wahrscheinlichkeitsberechnung aus einer Tabelle ablesen können und nicht selbst berechnen müssen. Eine solche Tabelle sieht wie folgt aus:

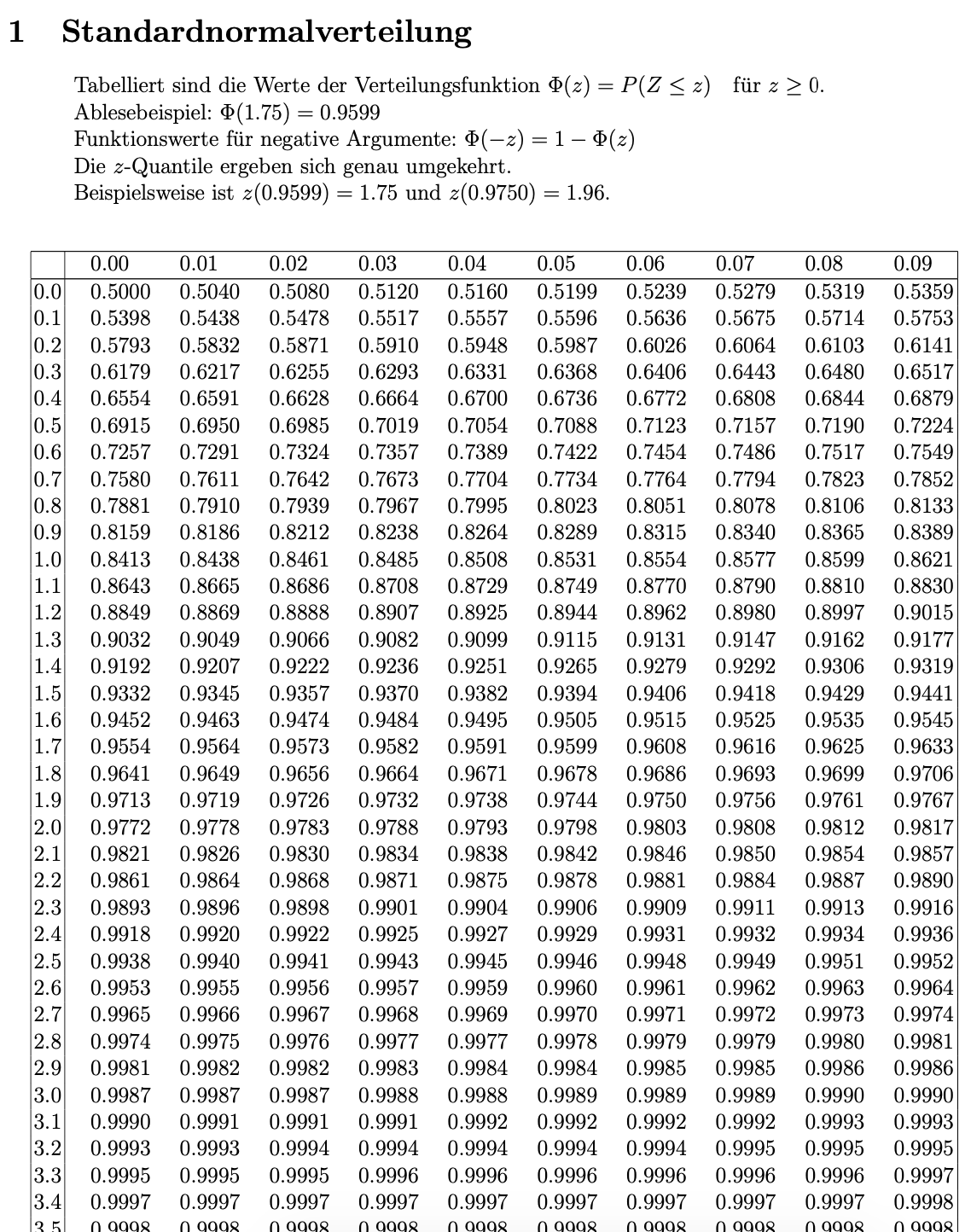## Bedingte Wahrscheinlichkeiten

BEDINGTE WAHRSCHEINLICHKEIT ist die Wahrscheinlichkeit des Eintretens eines Ereignisses unter der Bedingung, dass das Eintreten eines anderen Ereignisses bereits bekannt ist.

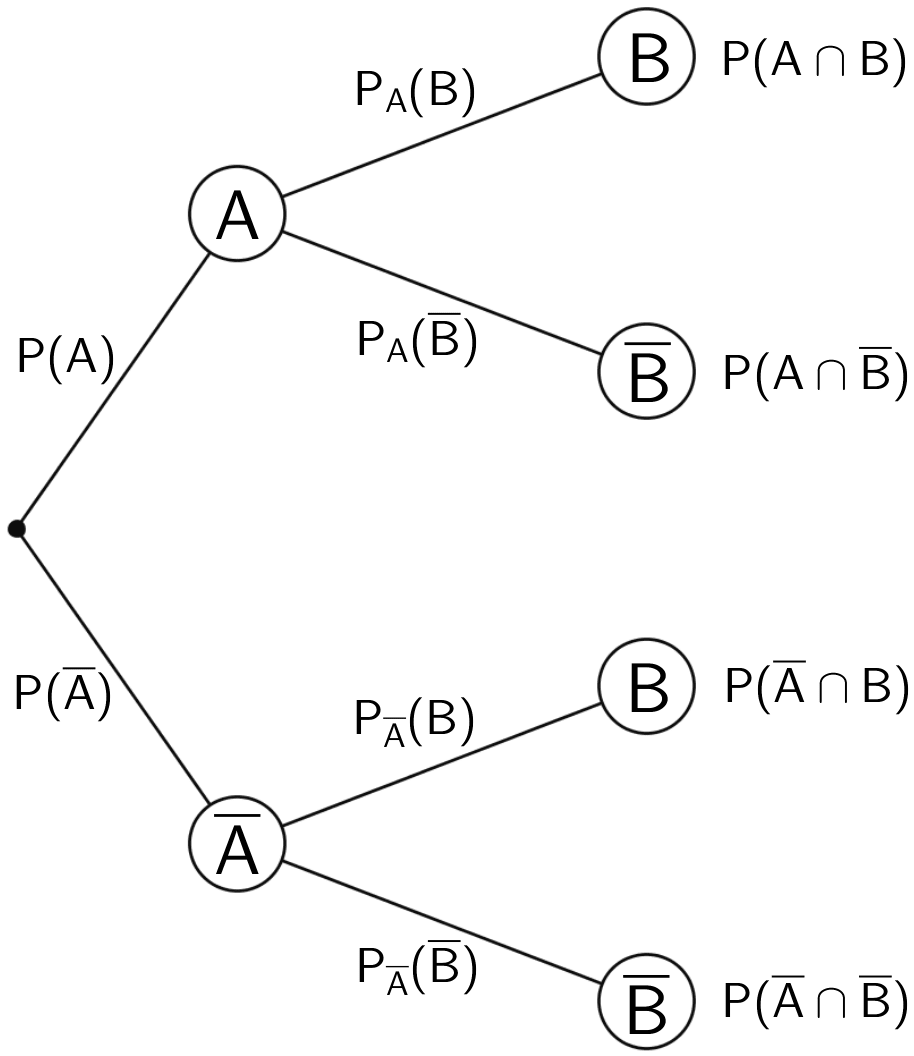
Wie können wir nun die Wahrscheinlichkeit ausrechnen \(P(A\cap B)\)? Indem wir folgendes multiplizieren: \(P(A)*P(A|B)\)

Das heißt dann \(P(A)*P(A|B)=P(A\cap B)\) also \(P(A|B)=\frac{P(A\cap B)}{P(A)}\)

4.1.4 Satz von Bayes

Der Satz von Bayes erlaubt in gewissem Sinn das Umkehren von Schlussfolgerungen: Man geht von einem bekannten Wert \(P(B|A)\) aus, ist aber eigentlich an dem Wert \(P(A | B)\) interessiert.

Der Satz von Bayes ist nützlich, wenn wir eine Komponente nicht wissen, wie zB die

\(P(A|B)=\frac{P(B|A)P(A)}{P(B)}\)