6 Hypothesen und Variablenzusammenhang
6.1 Null Hypothesis Significance Test
NULL HYPOTHESIS SIGNIFICANCE TEST (NHST), auch STATISTISCHER SIGNIFIKANZTEST, dient dazu anhand vorliegender Beobachtungen eine begründete Entscheidung über die Glültigkeit oder Ungültigkeit einer Hypothese zu treffen. Man versucht hierbei für die Wahrscheinlichkeit einer Fehlentscheidung zu kontrollieren.
NHST hat zwei Charakteristika:
- Daten werden anhand von konkurrierenden Hypothesen evaluiert.
- Wahrscheinlichkeitsrechnungen werden verwendet, um diese Evaluation durchzuführen.
Was sind also diese konkurrierenden Hypothesen?
Wir haben zum einen die sogenannte Null Hypothese und zum anderen die Alternativhypothese, sprich es gibt zwei Typen von Hypothesen, welche sich gegenüberstehen:
NULL HYPOTHESE (auch H0 genannt): Es besteht kein Effekt von X auf Y.
ALTERNATIVE HYPOTHESE (auch H1 oder HA genannt): Es besteht ein Effekt von X auf Y.
Die PHILOSOPHIE hinter dem statistischen Signifikanztest ist, dass wir niemals die Alternativhypothese beweisen können.
Wichtig also: wir gehen von der Nullhypothese aus und sehen wie wahrscheinlich diese richtig ist. Wir können aber niemals die Alternativhypothese direkt überprüfen, sondern müssen dies immer über den Umweg der Nullhypothese machen.
Falls wir also Evidenz gegen die Nullhypothese finden, können wir eher davon ausgehen, dass die Alternativhypothese richtig ist. Um diese Evidenz gegen/für die Nullhypothese zu finden, können wir WAHRSCHEINLICHKEIT verwenden.
Stellen Sie sich vor, wir hätten eine Statistikklausur mit 100 Fragen, wobei jede Frage mit richtig oder falsch beantwortet wird. Nur per Zufall könnte es sein, dass zB 50 Prozent der Fragen richtig geraten wurden. Ab wann könnte man annehmen, dass jemand Statistik exzellent beherrscht? Wenn wir dies umforumulieren, könnten wir auch fragen, mit welcher Anzahl an richtig-beantworteten Fragen, würden Sie glauben, dass die Studierende/der Studierende nicht nur zufällig ratet. Was würden Sie zB sagen, wenn die Studierende/der Studierende 95 der 100 Fragen richtig beantworten würde? Ist dies mit Raten möglich? Wahrscheinlich nicht. Hier könnten wir sagen, dass die Nullhypothese verworfen werden kann, sprich wir haben genug Evidenz gegen das Argument, dass die Studierende/der Studierende nichts weiß und geraten hat. Genauer gesagt, haben wir 95 Prozent Wahrscheinlichkeit, dass Studierende nicht geraten haben.
Auch hier ist es wichtig zu wissen, dass wir eine Nullhypothese zwar verwerfen, aber nicht annehmen können. Wenn die Studierende/der Studierende 56 der 100 Fragen richtig beantwortet hat, können wir zwar sagen, dass nicht ausreichend Evidenz vorliegt, um sicher zu gehen, dass die Studierende/der Studierende Statistik kennt bzw. nicht geraten hat. Wir können aber nicht sagen, die Studierende/der Studierende hat geraten. Wir haben also nicht genug Evidenz, um zu behaupten, dass die Nullhypothese falsch ist, aber wir können auch nicht sagen, dass diese richtig ist.
Somit gibt es zwei mögliche Resultate nach dem Hypothesentest:
A. Nullhypothese kann abgelehnt werden. B. Nullhypothese kann nicht abgelehnt werden.
Dies können wir auch in der Dichtefunktion der Normalverteilung so einzeichnen (siehe folgende Abbildung): Die Fläche in der Mitte umfasst die Wahrscheinlichkeit, wo die Nullhypothese nicht verworfen werden kann. Die strichlierten Flächen sind jene Flächen wo die Nullhypothese verworfen werden kann. Hierbei gibt es einen einseitigen und einen zweiseitigen Test gegen die Nullhypothese bzw. zwei Typen der Alternativhypothese:
- Zweiseitigen Test (\(X_1 \neq X_2\)) - sprich wir testen ob \(X_1\) ungleich \(X_2\) ist.
- Einseitigen Test (\(X_1 > X_2\) oder \(X_1 < X_2\) ) - sprich wir testen ob \(X_1\) größer bzw. kleiner \(X_2\) ist.
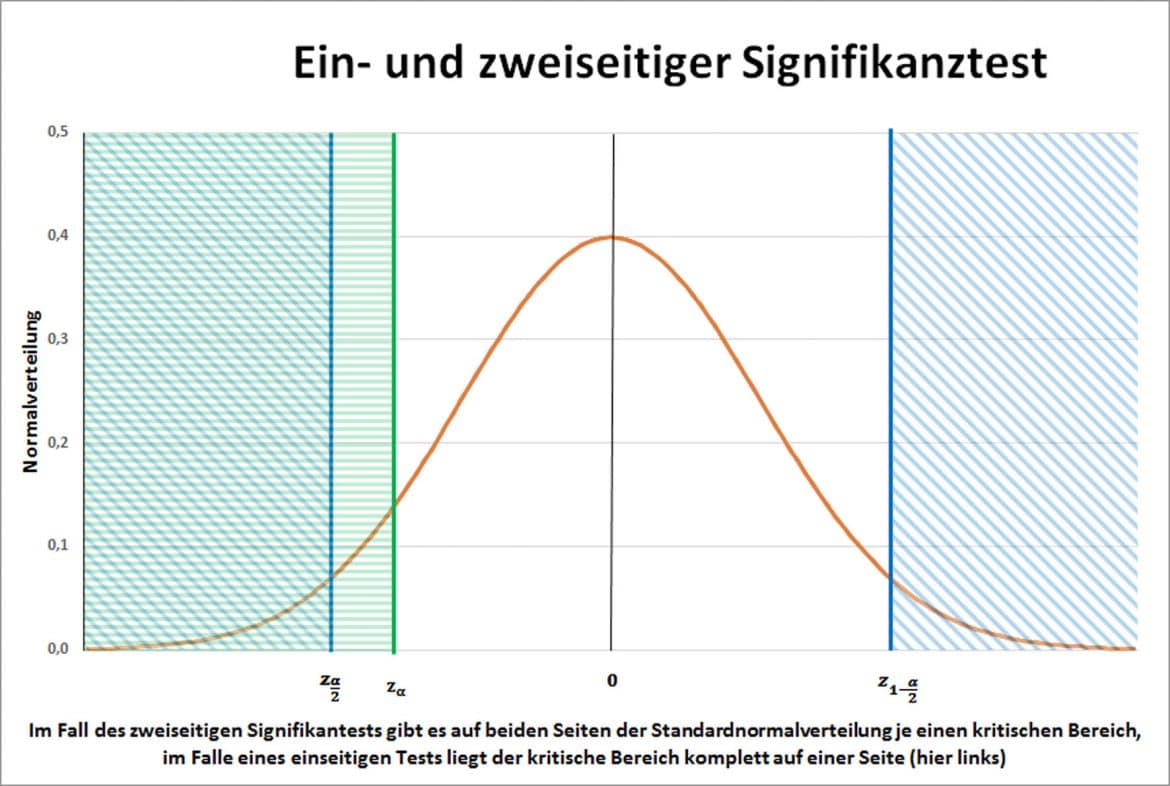
Das typische Vorgehen bei einem Hypothesentest ist folgendes:
- Vorhersagen auf Basis der Theorie treffen (Hypothesen definieren)
- Daten sammeln
- Annehmen, dass die Null-Hypothese nicht verworfen werden kann.
- Ein statistisches Modell schätzen, welches die alternative Hypothese repräsentiert.
- Die Wahrscheinlichkeit (p-Wert), welche angibt wie wahrscheinlich es ist das unter 4. definierte Modell zu bekommen, wenn die H0 nicht verworfen werden kann, berechnen.
- Wenn die Wahrscheinlichkeit sehr klein ist (p<0.05), dann können wir davon ausgehen, dass die H0 unwahrscheinlich ist und die HA eher wahrscheinlich ist.
Ad. 4: Hier müssen wir ein passendes Modell schätzen. Dazu verwenden wir das Wissen der letzten Einheiten und schätzen folgendes Modell:
\(Ergebnis_i=\beta_0+\beta_1 X_i+Fehlerterm\)
Effekt (\(\beta_1\)) = Wie oft hat X zu Y geführt?
Fehler = Wie oft hat X nicht zu Y geführt?
Daraus können wir auch die sogenannte Teststatisitk formulieren:
\(\frac{Effekt}{Fehler}\) \(\rightarrow\) TEST STATISTIK
TEST STATISTIK sagt uns, wieviel Effekt wir von der erklärenden Variable auf die abhängige Variable sehen wollen, um zu akzeptieren, dass die Null-Hypothese abgelehnt werden kann.
Ad. 5. Hier müssen wir den sogenannten P-Wert definieren, welcher angibt, wie wahrscheinlich es ist HA, zu finden, wenn H0 nicht verworfen werden kann. Im Beispiel oben könnten wir fragen, wie wahrscheinlich es ist, dass Studierende exzellent in der Statistikklausur abschneiden, wenn sie bei der Klausur raten würden. P-Wert ist eine bedingte Wahrscheinlichkeit, nämlich die Wahrscheinlichkeit ein bestimmtes Ergebnis bzw. ein Ergebnis welches größer dessen, ist zu erreichen \(P(Obs>=t|H0)\). Dies ist daher eine kumulierte Wahrscheinlichkeit und keine Punktschätzung.
Hier stellt sich folgende Frage: Wie klein sollte die Wahrscheinlichkeit sein, sodass die Nullhypothese unwahrscheinlich ist?
“it is OPEN TO THE EXPERIMENTER to be more or less exacting in respect of the smallness of the probability he would require […]” (Fischer, 1971, p. 13)
Aber es gibt ein paar gängige P-Werte, welche häufig verwendet werden:
Standard:
- p<0.01
- p<0.05
- p<0.1
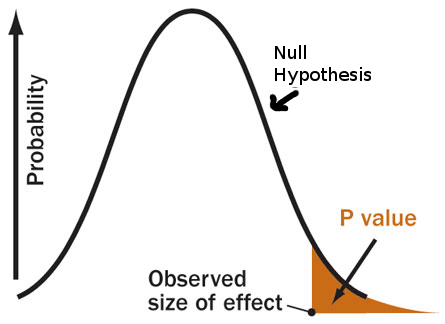
Warum 0.5? Das ist nicht so klar. Fischer verwendete dies nur deshalb weil das bei der Kurve ca. 2 Standardabweichungen weg liegt.
Wir können bei diesem Prozess zwei Fehler machen. Wir arbeiten mit Wahrscheinlichkeiten, aber können uns verschätzen, ob es tatsächlich einen Effekt in der Grundpopulation gibt oder nicht. Wir können den Typ 1 Fehler und den Typ II Fehler machen.
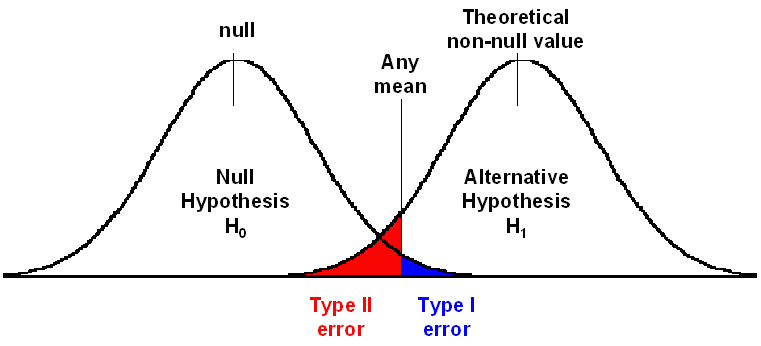
Typ 1 Fehler (falsch positiv und auch alpha-Fehler genannt): Wir lehnen die H0 ab, obwohl sie richtig ist bzw. wir glauben es gibt einen Effekt in der Population, obwohl es keinen gibt.
Typ 2 Fehler (falsch negativ und auch beta-Fehler genannt): Wir nehmen die H0 an, obwohl Sie unwahrscheinlich ist bzw. wir glauben, es gibt keinen Effekt in der Population, obwohl es tatsächlich einen gibt.
Was beeinflusst die Größe dieser Fehler?
Was beeinflusst die Größe von alpha (Fehler I)?
- Die Höhe der festgelegten Teststatistik beeinflusst \(\alpha\). Je größer alpha, desto höher das Risiko für einen Typ 1 Fehler.
Was beeinflusst die Größe von beta (Fehler II)?
- Die Höhe der festgelegten Teststatistik beeinflusst auch \(\beta\). Je kleiner alpha, desto höher das Risiko für einen Typ 2 Fehler.
- Die Größe des Effektes: Je größer der Effekt, desto geringer ist das Risiko eines Typ 2 Fehlers.
- Die Größe der Stichprobe: Je größer die Stichprobe, desto geringer ist das Risiko eines Typ 2 Fehlers.
Warum brauchen wir das Ganze?
Weil wir damit statistische Signifikanz bestimmen können. Wir benötigen dazu wieder die Konfidenzintervalle und es hilft uns, zu sagen, ob der Unterschied signifikant ist.
Ab wann ist das Ergebnis signifikant?
Bis jetzt hatten wir gesagt, dass bei keiner Überlappung der Konfidenzintervalle ein signifikantes Ergebnis vorliegt. Allerdings hatten wir da die Idee des P-Wertes und des NHST noch nicht gekannt. Hierzu benötigen wir ein neues Konzept, welches die mittlere Fehlerspanne genannt wird. Hierzu summieren wir die Reichweite der Konfidenzintervalle und dividieren dies durch zwei (bei zwei Gruppen), dann nehmen wir davon ein Viertel. Dies darf überlappen, um mit 0.05 Prozent signifikant zu sein.
Obwohl NHST ein sehr bekanntes und weit-verbreitetes Konzept ist, haben wir noch zwei wesentliche Probleme:
Stichprobengröße erhöht die Wahrscheinlichkeit eines signifikanten Ergebnisses.
Effektgröße wird ignoriert.
6.2 Effektgröße
COHEN’S D wird verwendet, um den Effekt über verschiedene Studien hinweg zu vergleichen, selbst wenn die abhängige Variable auf unterschiedliche Weise gemessen wurde. Diese Formel entspricht relativ genau der Formel für die z-Standardisierung, daher sprechen einige Autoren auch von einer STANDARDISIERTEN EFFEKTSTÄRKE.
Grundpopulation
\(d=\frac{\bar{\mu_1}-\bar{\mu_2}}{\sigma}\)
Stichprobe
\(\hat{d}=\frac{\bar{X_1}-\bar{X_2}}{s}\)
Wir haben zwei Gruppen und folglich zwei Standardabweichungen. Welche Standardabweichung sollten wir verwenden?
Wenn die Standardabweichungen der zwei Gruppen GLEICH sind…
… dann kann eine der zwei verwendet werden
Wenn die Standardabweichung der zwei Gruppen UNGLEICH sind…
… die Standardabweichung der Experiment-Gruppe (treatment group) verwenden
… die Standardabweichungen poolen (wobei wir nichts anderes machen als das gewichtete Mittel der Standardabweichung zu berechnen - die Standardabweichung der größeren Gruppe bekommt mehr Gewicht (das ist deshalb weil ja die Schätzer einer größeren Stichprobe präziser sind))
\(s_p=\sqrt{\frac{(N_1-1)*s_1^2+(N_2-1)*s_2^2}{N_1+N_2+2}}\)
Interpretation Cohen’s d ist die Effektgröße, gemessen in Einheiten der Standardabweichung. Dazu nehmen wir dann die Z-tabelle und können die Prozent ablesen.
Was ist allerdings, wenn wir nicht Gruppen haben, sondern eine kontinuierliche Variable? Müssen wir dann die kontunierliche Variable in Gruppen zwängen?
Nein müssen wir nicht, sondern wir verwenden das Pearson’s R bzw. den Korrelationskoeffizienten.
Population
\(p_{X,Y}=\frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X \sigma_Y}\)
Stichprobe
\(r_{xy}=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^n(y_i-\bar{y})^2}}\)
Pearson’s R: Interpretation
- \(-1\): Perfekt negative Korrelation
- \(-0.8\): Stark negative Korrelation
- \(-0.5\): Moderate negative Korrelation
- \(-0.2\): Schwach negative Korrelation
- \(0\): Keine Korrelation
- \(0.2\): Schwach positive Korrelation
- \(0.5\): Moderat positive Korrelation
- \(0.8\): Stark positive Korrelation
- \(1\): Perfekt positive Korrelation
Was wir bis jetzt wissen:
- Was tun, wenn wir eine kategorische und eine metrische Variable haben. - Cohen’s d
- Was tun, wenn wir zwei metrische Variablen haben. - Pearson’s R
- Was ist, wenn beide Variablen kategorisch sind? Odd’s Ratio
Die Berechnung des Odd’s Ratio geht wie folgt:
- Berechnung der bedingten Wahrscheinlichkeit von Kategorie A, wenn X vorliegt (\((P(A|X))\)) versus bedingte Wahrscheinlichkeit von A wenn X nicht vorliegt (\((P(A|\bar{X}))\))
- Berechnung der bedingten Wahrscheinlichkeit von Kategorie B, wenn X vorliegt (\((P(B|X))\)) versus bedingte Wahrscheinlichkeit von B wenn X nicht vorliegt (\((P(B|\bar{X}))\))
- Die zwei Chancen dividieren:
\(\frac{P(A|X)/P(A|\bar{X})}{P(B|X)/P(B|\bar{X})}\)
6.3 Annahmen Hypothesentest
- Daten sammeln
- Modell schätzen (\(Ergebnis_i = Modell + Fehlerterm_i\))
- Parameter ablesen
- Interpretation (was ist die Größe des Effektes, die Signifikanz, etc.)
Annahme 1: Additive und Lineare Effekte
Additive Effekte
Arbeitsstandard=\(\beta_0+\beta_1*\text{Globalisierung}+\beta_2 * \text{Regime Typ}+\beta_3 \text{NGO Aktivität}+\epsilon_i\)
Additiv bedeutet, dass die Arbeitsstandards am besten erklärt werden, wenn man die Effekte der verschiedenen erklärenden Variable zusammenzählt.
Linearität
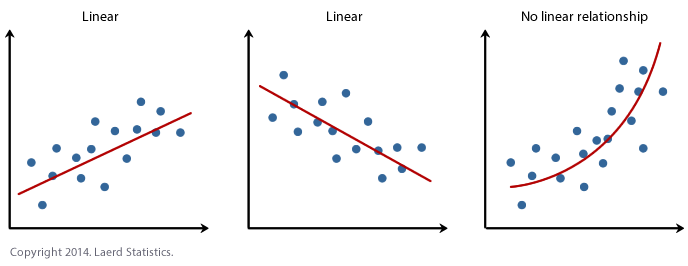
Was ist, wenn dies nicht hält? Dann tun wir uns schwer bei der Interpretation der Ergebnisse. Wir haben einen Faktor, der den Zusammenhang erklärt, aber dies wird sehr kompliziert wenn dies nicht linear ist.
Annahme 2: Unabhängige Fehlerterme
\(Kundenzufriedenheit=\beta_0+\beta_1*Speedyboarding_i+\epsilon_i\)
Die Standardabweichung und das Konfidenzintervall wird falsch geschätzt, da sich der Effekt auf Beobachtung A den Effekt von Beobachtung B beeinflusst. Daher haben wir hier zu geringe Fehlerterme.
Annahme 3: Homoskedaszität (keine Heteroskedaszität)
Bei der Homoskedaszität geht es darum, dass die Variablen eine ähnliche Varianz aufzeigen.
Warum ist das wichtig?
Die Schätzung selbst wird korrekt sein, auch wenn diese Annahme verletzt ist. Allerdings sind die Standardfehler inkonsistent.
Annahme 4: Normalverteilung
Problem ist, dass wir da dann viele Residuen im unteren oder oberen Bereich der Verteilung liegen. Diese sind also ungleich verteilt. Keine Normalverteilung hat einen ähnlichen Effekt wie Homoskedaszität, sprich die Fehlerterme sind nicht wirklich konstant. Dies ist allerdings wieder kein Problem, wenn die Stichprobengröße erhöht wird (Grund ist der zentraler Grenzwertsatz).
Annahme 5: Externe Variablen haben keinen Einfluss auf den Effekt
Bei einem statistischen Modell nehmen wir an, dass es keine zusätzlichen Variablen gibt, welche den Effekt beeinflussen. Wenn es diese gibt, müssen wir dafür auch im Modell Rechnung tragen. Tun wir dies nicht, unter- bzw. überschätzen wir den geschätzten Effekt von erklärenden Variablen auf die abhängige Variable.
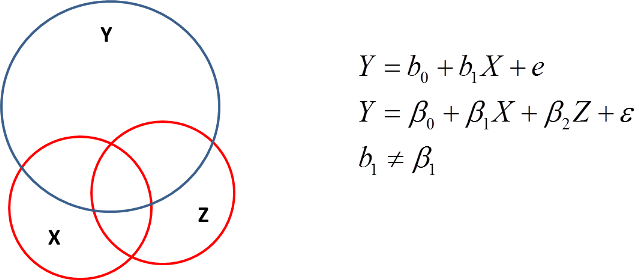
Annahme 5: Keine Multikollinearität
Allerdings bringt die Inklusion von möglichst vielen Variablen eine andere Gefahr mit sich. Wenn die Variablen zu stark miteinander korrelieren, können wir nicht mehr sagen was den Effekt verursacht hat, sprich die Effekte korrelieren miteinander. Was passiert da? Unsere Schätzer sind weniger vertrauenswürdig.