5 Inferenz

Inferenz erlaubt uns von einer Stichprobe auf die Grundgesamtheit zu schließen. Dazu müssen wir aber zuerst verstehen, warum wir Stichproben verwenden. Stellen Sie sich vor Sie wollen das Wahlverhalten von Tiroler_innen untersuchen. Grundsätzlich müssten Sie alle wahlberechtigten Personen in Tirol befragen. Dies wird aber kaum realisierbar sein. Was Sie stattdessen tun können, ist eine Stichprobe zu ziehen. Das heißt Sie befragen nur einen Bruchteil der Tiroler_innen und unersuchen das Wahlverhalten der befragten Personen (der Stichprobe). Jetzt kommt Inferenz ins Spiel. Es hilft Ihnen die Klarheit der Muster in der Stichprobe zu beschreiben und dadurch mit einer gewissen Sicherheit angeben zu können, dass dieses Muster auch in der Grundpopulation (alle Wahlberechtigte in Tirol) zu finden wäre.

Wir beginnen wieder mit der Idee des Modelles. Dies hatten wir in der Einheit der deskriptiven Statistik bereits besprochen: Ein Modell hilft uns eine Vorhersage zu Datenpunkten zu treffen. Dabei unterschätzen wir den Wert mancher Datenpunkte und überschätzen den Wert anderer Datenpunkte. Diese Abweichungen (diese Verschätzung) nennen wir Fehlerterm.

Wir verwendeten den Mittelwert als Beispiel für ein Modell, aber stellen Sie sich vor, wir wüssten nicht wie wir einen Mittelwert berechnen müssen. Wie würden wir den Wert finden, welcher die beste Vorhersage für unsere Datenpunkte macht finden?

Was wir machen könnten, ist uns dem optimalen Wert anzunähern. Dazu beginnen wir mal eine beliebige Zahl zu schätzen und dann die Summe der Fehlerterme zu berechnen. Jetzt schätzen wir einen anderen Wert und errechnen wiederum die Summe der Fehlerterme und wählen dann den geschätzten Wert, welcher eine niedrigere Summe der Fehlerterme aufweist. Dies können wir für ganz viele Schätzungen machen und uns so dem optimalen Wert annähern. Diesen Prozess nennen wir auch die Methode der kleinsten Quadrate (brauchen wir dann wieder bei der Regressionsanalyse - Einheit 6).

Dies haben wir jetzt für die Stichprobe gemacht. Es lässt sich daher nicht zwingend sagen, dass dieser optimale Wert, welchen wir auf Basis der Stichprobe berechnet haben, auch für die Grundpopulation den optimalen Wert darstellt.

5.1 Stichprobenverteilung

Die Abweichung der Schätzung aus der Stichprobe vom optimalen Wert der Grundpopulation nennen wir Stichprobenfehler. Mit einer Stichprobe unterschätzen wir den tatsächlchen Wert in der Grundpopulation, mit einer anderen Stichprobe überschätzen wir den tatsächlichen Wert in der Grundpopulation. Es gibt also eine Varianz in der Stichprobe. Der Mittelwert von optimalen Werten von ganz vielen Stichproben kommt wiederum dem tatsächlichen Wert der Grundgesamtheit sehr nahe (da wir uns eben mit manchen Stichproben überschätzen und mit manchen unterschätzen gleicht sich dies irgendwann wieder aus.). Wir können die Werte, welche wir von den Stichproben berechnet haben, in einer Häufigkeitsverteilung darstellen - mit Hilfe eines Histograms. Dies nennt man die Stichprobenverteilung:

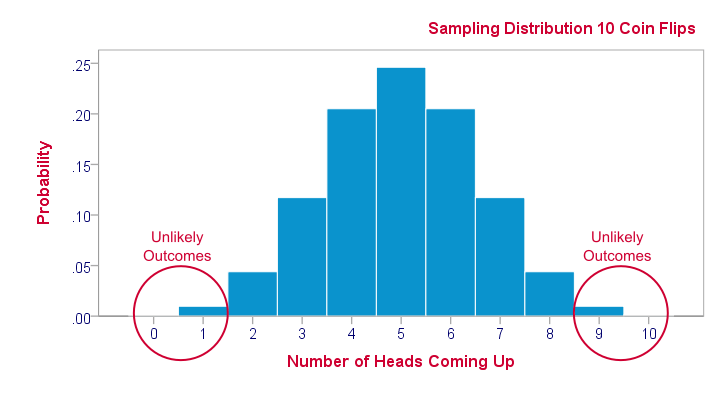Im Bild sehen Sie die Stichprobenverteilung von Münzwürfen. Es wurden 10 Münzen pro Runde (Stichprobe) geworfen. Dieser Vorgang wurde 100 Mal wiederholt und aufgeschrieben wie oft Kopf geworfen wurde. Das Mittel in dieser Verteilung liegt bei 5, sprich die Hälfte der Würfe liefern Kopf und die andere Hälfte Zahl. Dies entspricht auch der theorethischen Wahrscheinlichkeit.

Eine derartige Stichprobenverteilung ist eher ein theoretisches Konzept als dass wir diese tatsächlich messen und aufzeichnen. Aber es hilft uns im Folgenden zu verstehen, wovon unsere Stichprobe gezogen wurde.

5.2 Standardfehler

Es gibt noch einen weiteren Punkt, welcher in diesem Zusammenhang wichtig ist: Manchmal ist eine derartige Stichprobenverteilung enger, sprich Stichproben ähneln sich mehr in ihren Werten, und manchmal weiter, sprich Parameter aus Stichproben sind unterschiedlicher voneinander. Die Weite/Enge der Stichprobenverteilung können wir durch den Standardfehler definieren. Dieser Standardfehler wird für jede Statistik unterschiedlich berechnet. Der Standardfehler des Mittelwertes berechnet sich wie folgt:

\[\sigma_{\bar{x}}=\frac{s}{\sqrt{N}}\]

Sprich der Standardfehler des Mittelwertes ist die Standardabweichung der Stichprobe dividiert durch die Wurzel der Größe der Stichprobe (e.g. Anzahl der Beobachtungen in der Stichprobe).

5.3 Zentrale Grenzwertsatz

Allerdings ist die Vorraussetzung für die Berechung des Standardfehlers des Mittelwertes, dass unsere Stichprobe viele Beobachtungen hat. Viele deshalb da mit mehr Beobachtungen eine Normalverteilung der Beobachtungen erreicht werden kann. Wenn die Anzahl der Beobachtungen zu klein ist, haben wir keine Normalverteilung sondern eine t-Verteilung (kommt später).

Dieser Regel liegt der Zentrale Grenzwertsatz zu Grunde. Der Zentrale Grenzwertsatz besagt, dass mit steigender Anzahl an Beobachtungen in Stichproben die Stichprobenverteilung normaler wird.

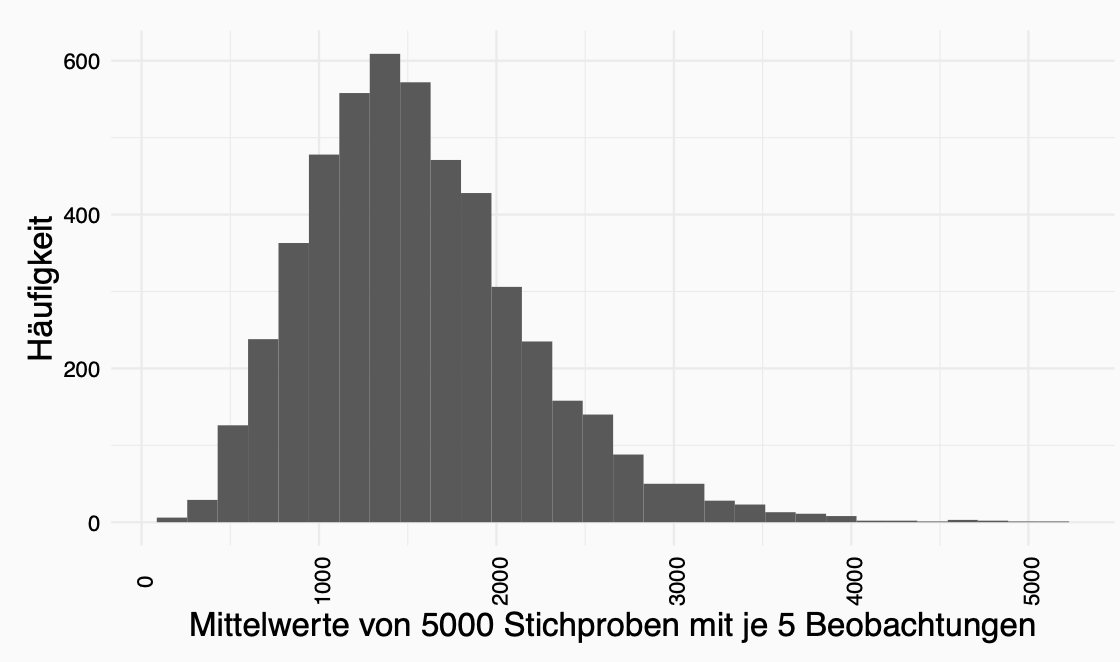
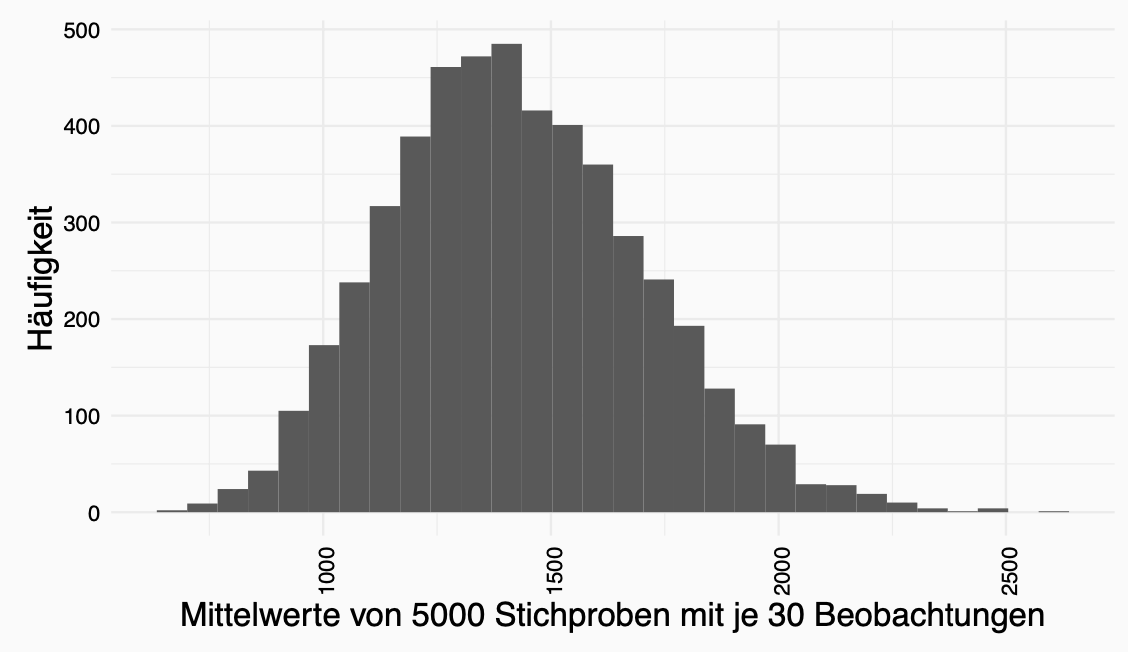
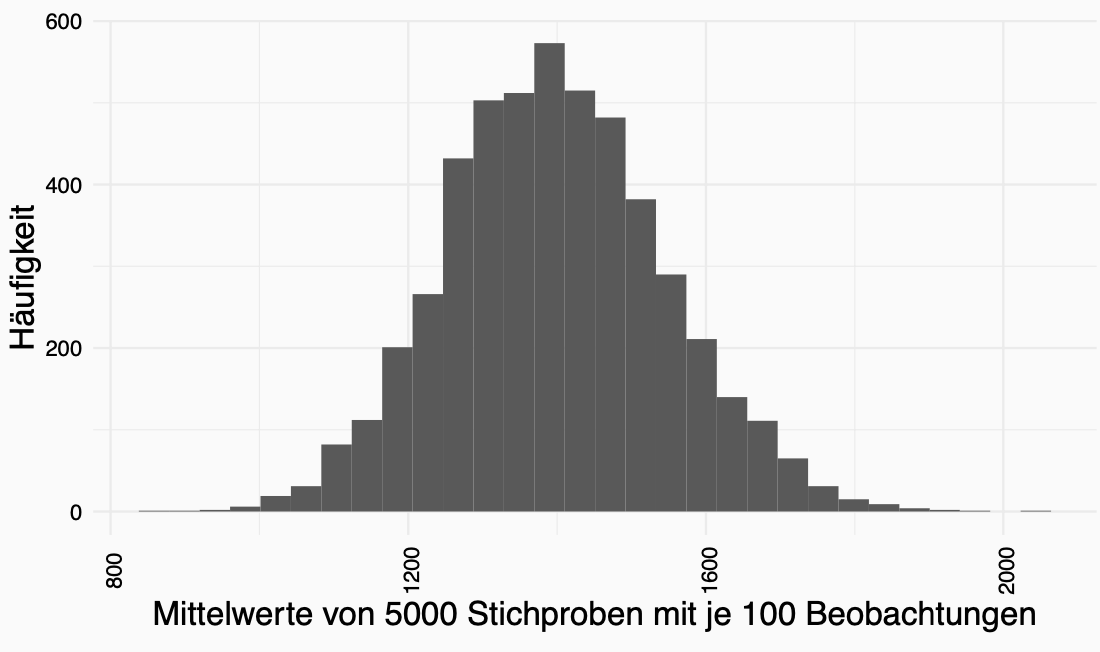
Warum ist das alles wichtig?

Wir nehmen zwei wichtige Punkte zu Stichprobenverteilungen mit:

Die Weite der Stichprobenverteilung informiert uns über die Wahrscheinlichkeit, dass eine Statistik der Stichprobe nahe dem Parameter der Grundpopulation liegt. \(\rightarrow\) STANDARDFEHLER (DES MITTELWERTES)
Wenn die Anzahl der Observationen erhöht wird, dann nähert sich die Verteilung einer Normalverteilung an. \(\rightarrow\) ZENTRALER GRENZWERTSATZ

5.4 Konfidenzintervall

Mit Hilfe dieser beiden Erkenntnisse können wir Konfidenzintervalle berechnen.

In der Statistik wollen wir aufgrund von einer Stichprobe gewisse Kenngrößen wie Mittelwert oder Standardabweichung schätzen. Wie wir diese Größen schätzen haben wir bereits in der deskriptiven Statistik kennengelernt. Es stellt sich nun die Frage, wie genau diese Schätzer sind. Konfidenzintervalle sind dazu eine Möglichkeit. Sie liefern ein Intervall, in dem der geschätzte Parameter mit einer vorgegebenen Wahrscheinlichkeit (typischerweise 95%) liegt.

Ein Konfidenzintervall ist also ein Intervall, welches den gesuchten Parameter einer Grundgesamtheit mit einer vorgegebenen Wahrscheinlichkeit (d.h. Konfidenzniveau oder Vertrauenswahrscheinlichkeit) enthält.

Die Idee eines Konfidenzintervalles ist es, dass mit 95 Prozent Wahrscheinlichkeit der wahre Wert der Grundpopulation im Konfidenzintervall enthalten ist. Würden Sie also 100 Konfidenzintervalle berechnen, wäre der wahre Wert in 95 der 100 Konfidenzintervalle enthalten.

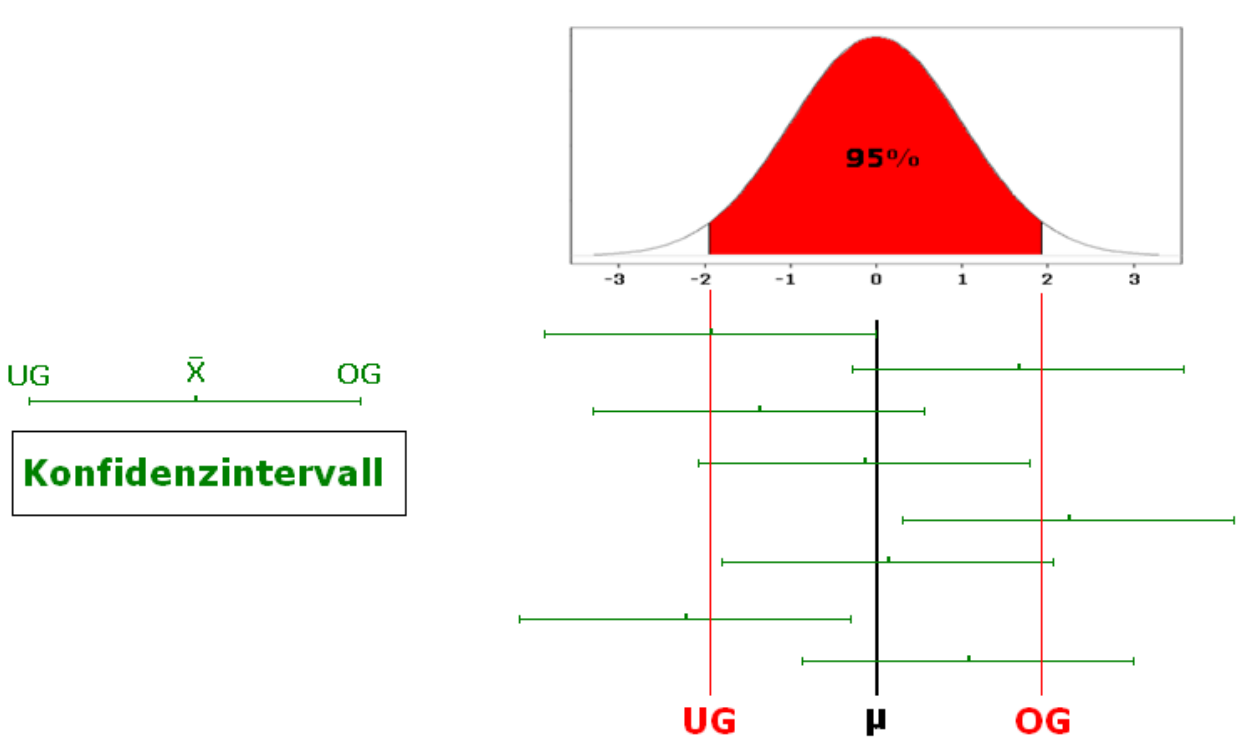Wir können hier selbstverständlich auch andere Wahrscheinlichkeiten als 95 Prozent definieren. 95 Prozent ist ein gängiges Maß. Wir beschreiben diese Wahrscheinlichkeit mithilfe von \(1-\alpha\). Alpha umfasst die Prozent, welche wir erlauben, dass nicht den wahren Parameter enthalten, sprich \(1-\alpha\) Prozentpunkte enthalten den wahren Werte und \(\alpha\) Prozentpunkte nicht. Man könnte sich dies wie folgt aufzeichnen:

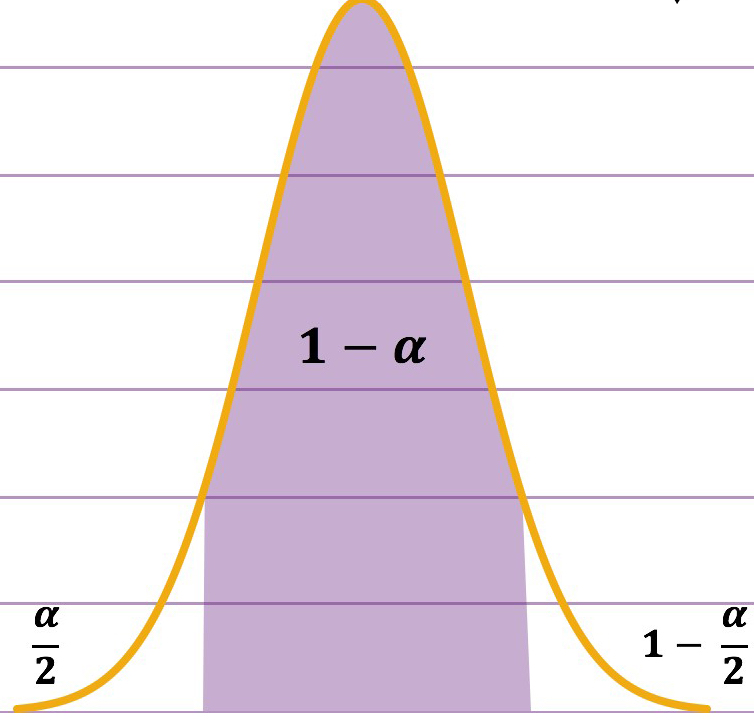
Für die Berechung des Konfidenzintervalles müssen wir die untere Grenze und die obere Grenze des Konfidenzintervalles berechnen. Dazu nehmen wir folgende Formeln:

\(\text{Obere Grenze (OG)}= \bar{X} + SE*z_{1-\frac{\alpha}{2}}\)

\(\text{Untere Grenze (UG)}= \bar{X} - SE*z_{1-\frac{\alpha}{2}}\)

hier ist es wichtig zu wissen, dass \(SE\) den Standardfehler des Mittelwertes darstellt, \(z_{\frac{\alpha}{2}}\) beschreibt die Wahrscheinlichkeit der Standardnormalverteilung zum Punkt, wo die wahren Werte wahrscheinlich noch nicht bzw. nicht mehr enthalten sind.

5.5 T-Verteilung

Was ist wenn wir kleinere Stichproben haben (sprich keine Normalverteilung)?

Wir wissen, dass bei der Erhöhung der Stichprobenzahl die Streuung geringer wird. Das heißt wenn wir eine niedrige Stichprobenzahl haben haben wir eine andere Verteilung mit breiteren “Tails” und einer flacheren Mitte.

Daher hat man eine zweite Verteilungstabelle eingeführt, nämlich die Student-t-Verteilung. Der Chefbrauer von Guinness, welcher unter dem Namen “Student” publizierte, hat diese Verteilung berechnet und veröffentlicht.

Hier haben wir eine andere Tabelle als die Standardnormalverteilungstabelle zu Grunde liegen und müssen in Berücksichtung der Fallzahl die Wahrscheinlichkeiten aus der T-Tabelle rauslesen.

All dies machen wir, um Inferenz herzustellen, sprich die Schlussfolgerung von der Stichprobe auf die Grundgesamtheit mit einer gewissen Sicherheit angeben zu können.

5.6 Robuste Schätzer

Wir haben noch zwei Dinge IGNORIERT:

Ausreißer
schiefe Verteilungen

Wie wirken sich Ausreißer auf die Standardabweichung aus? Die Standardabweichung nimmt exponentiell zu, weil wir ja einen Teil darin quadrieren. Die Standardabweichung ist Basis des Standardfehlers und der Standardfehler dient der Berechnung des Konfidenzintervalles, daher haben wir auch hier einen zunehmend großen Effekt.

Bei schiefen Verteilungen haben wir das Problem, dass wir mehr als 5 Prozent der Samples rausziehen, die nicht den Mittelwert enthalten.

Was können wir tun?

Die Daten ändern
Die Methode der Schätzung ändern

Zum Daten ändern: hier ist es wichtig, dass wir immer das Gleiche tun mit den Daten. Das was uns interessiert, ist der Unterschied zwischen den Datenpunkten und solange dieser relativ gleich, bleibt solange können wir Daten manipulieren. Was können wir also konkret tun?

Transformation - Logarithmus (\(ln(x_i)\)): Verringert den Effekt von hohen Ausreißern und positive Verzerrung. (Achtung: Null und negative Werte können nicht logarithmiert werden)

Wurzel (\(\sqrt{x_i}\)): Verringert hohe Werte mehr als niedrige Werte und positive Verzerrung. (Achtung: Funktioniert nur mit positiven Werten)
\(\frac{1}{x_i}\): Verringert hohe Werte und positive Verzerrung. (Achtung: Kehrt die Werte um)
\((x_{\text{Höchster Wert}}+x_{\text{Niedrigster Wert}}) - x_i\): Umkehrung von Werten. (Anmerkung: Ist auch nützlich in Kombination mit einer der oben genannten Methoden, um eine negative Verzerrung zu korrigieren)
Für große Stichproben sind schiefe Verteilungen kein großes Problem mehr.
Die Transformation hat einen Effekt, wie wir die Daten interpretieren.
Wenn wir die “falsche” Transformation ausführen, hat das schlimmere Konsequenzen auf das Ergebnis als wenn wir nicht transformieren.

Die zweite Möglichkeit wie wir Daten “ändern” können ist das Trimmen.

Daten sortieren
Die Anzahl der zu kürzenden Observationen berechnen:

\(\text{Anzahl Observationen}*\text{Prozent}_{trim} = \text{Die Anzahl der zu kürzenden Observationen (auf jeder Seite)}\)

Observationen streichen.
Statistiken neu berechnen.

Aber WIEVIEL der Daten sollte man denn kürzen?

Diese Entscheidung ist zugegebenermaßen etwas krude. Was auch noch krude ist, ist, dass wir Daten löschen. Daher haben wir hier andere Methoden.

Winsorizing ist die Transformation von Daten durch die Begrenzung von Extremwerten in den statistischen Daten, um den Effekt von potenziell falschen Ausreißern zu reduzieren. Benannt ist sie nach dem Ingenieur und Biostatistiker Charles P. Winsor (1895–1951).

Anstatt die oberen und unteren zB 5 Prozent der Daten zu löschen, ersetzen wir diese mit dem nächsten Wert.

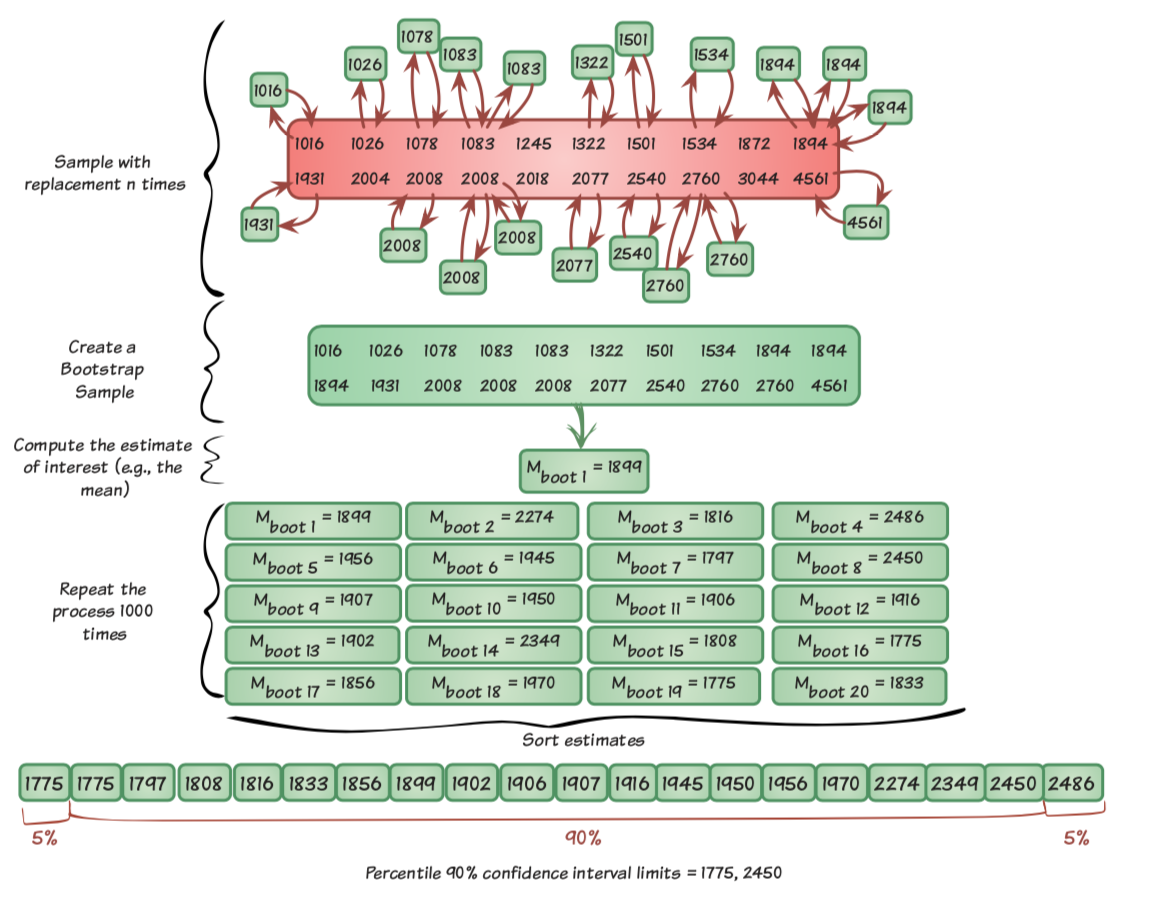
Bootstrapping

BOOTSTRAPPING beinhaltet wiederholtes Ziehen von Stichproben aus der Stichprobe und Berechnung der Statistik. Daraus können Konfidenzintervalle berechnet werden.