Chapter 5 统合模型分析

统合模型，就是同时包括了测量模型与结构模型的SEM模型。

  • 如果结构模型中，每一个变量都是潜在变量，则该模型为完全潜在模型。
  • 如果结构模型中，有任何一个变量是单一指标的测量变量，则该模型为部分潜在模型。

一般来说，统合模型的分析最好分为两阶段完成：

  • 阶段一：确定因素结果的拟合性（也就是CFA分析），这是后续结构模型分析的重要基础。
  • 阶段二：在不改变测量模型的前提下，增加结构模型的设定，并评估结构模型界定之后的拟合性。
library(tidyverse)
library(lavaan)
library(modelsummary)
library(semPlot)
library(corrplot)
# https://cran.r-project.org/web/packages/semptools/vignettes/semptools.html
library(semptools) # 给路径图标记显著性

5.1 假设模型

图5.1是原书242页的图8.3，即假设的统合模型，其中的潜变量：

  • Person为教师的创造人格特质
  • Crea为教学创新
  • Socialized为组织社会化程度
  • Efficacy为创意教学的自我效能感
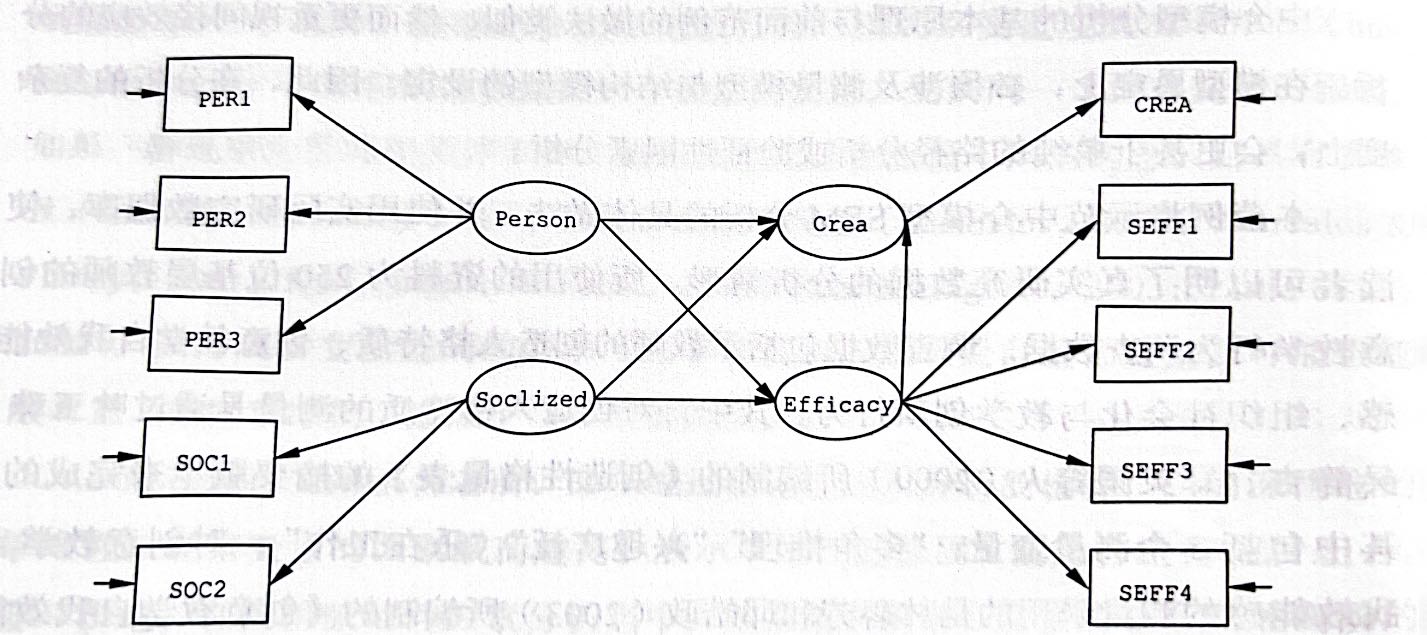
教师创意教学行为研究的SEM统合模型的概念图示

Figure 5.1: 教师创意教学行为研究的SEM统合模型的概念图示

数据是以协方差矩阵的形式给出的:

N <- 250 # 样本量
# 协方差矩阵
COV <- structure(c(17.711, 1.843, 0.801, 1.243, 1.692, 7.518, 7.585, 
6.499, 3.02, 2.663, 1.843, 0.404, 0.146, 0.227, 0.226, 1.074, 
1.062, 0.906, 0.369, 0.318, 0.801, 0.146, 0.374, 0.11, 0.115, 
0.301, 0.538, 0.388, 0.237, 0.307, 1.243, 0.227, 0.11, 0.589, 
0.208, 0.531, 0.609, 0.434, 0.322, 0.335, 1.692, 0.226, 0.115, 
0.208, 0.393, 0.741, 0.806, 0.664, 0.196, 0.326, 7.518, 1.074, 
0.301, 0.531, 0.741, 7.565, 5.202, 4.53, 1.947, 2.092, 7.585, 
1.062, 0.538, 0.609, 0.806, 5.202, 7.046, 4.626, 1.524, 1.824, 
6.499, 0.906, 0.388, 0.434, 0.664, 4.53, 4.626, 6.335, 1.649, 
1.662, 3.02, 0.369, 0.237, 0.322, 0.196, 1.947, 1.524, 1.649, 
4.482, 2.335, 2.663, 0.318, 0.307, 0.335, 0.326, 2.092, 1.824, 
1.662, 2.335, 2.982), dim = c(10L, 10L), dimnames = list(c("CREAT", 
"SEFF1", "SEFF2", "SEFF3", "SEFF4", "PER1", "PER2", "PER3", "SOC1", 
"SOC2"), c("CREAT", "SEFF1", "SEFF2", "SEFF3", "SEFF4", "PER1", 
"PER2", "PER3", "SOC1", "SOC2")))

我们可以绘制出相关系数的热力图矩阵，参见图：

# X和Y相关系数，等于二者的协方差除以二者标准差的积：
COR <- COV / (sqrt(diag(COV) %*% t(diag(COV))))

# 调用corrplot命令，绘制热力图
# Generate a lighter palette
col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF", "#77AADD", "#4477AA"))

corrplot(COR, method = "shade", shade.col = NA, tl.col = "black", tl.srt = 45,
         col = col(200), addCoef.col = "black", cl.pos = "n")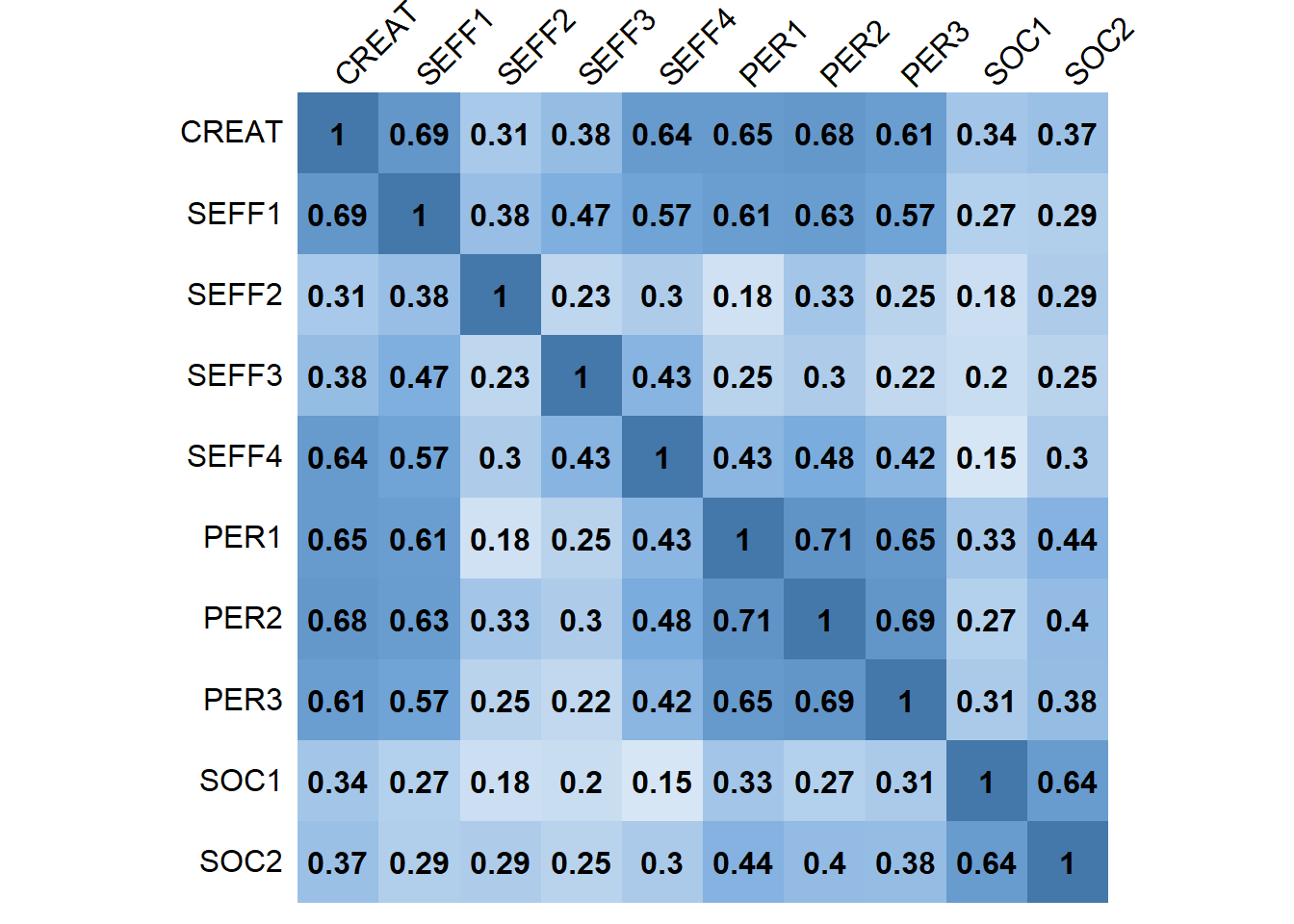
各测量变量的相关系数

Figure 5.2: 各测量变量的相关系数

5.2 模型界定

由于该模型有\(10\)个测量变量，根据公式(1.1)，测量数据的数目为\(10 \times 11 / 2 = 55\)个。

待估计的参数有\(25\)个，分别为：

  • \(10-4=6\)个因子载荷，因为\(4\)个潜变量各有一个因子载荷被限定为1。
  • \(10-1=9\)个测量变量的残差方差，因为CREA只有一个指标，需要将指标方差限制为0。
  • \(2\)个外生潜在变量的方差。
  • \(2\)个内生潜在变量的残差方差。
  • \(5\)个路径系数。
  • \(1\)个外源潜在变量的协方差（即Person和Soclized之间，图5.1没有画出来）。

5.3 阶段一：CFA

模型设定和拟合结果如下。可以看到，虽然\(\chi^2=80.964(df = 30, p <0.01)\)，拒绝了模型假设，但是，参照图1.1的结果，RMSEA为0.082. NNFI = 0.937，拟合程度还是不错的。

cfa_mod <- '
# measurement model
    CREA =~ 1*CREAT # 由于CREA只有一个测量变量，因此默认测量变量残差方差为0
    SEFF =~ SEFF1 + SEFF2 + SEFF3 + SEFF4
    PER  =~ PER1  + PER2  + PER3
    SOC  =~ SOC1  + SOC2'

cfa_fit <- cfa(model = cfa_mod, sample.cov = COV, sample.nobs = 250)
fitmeasures(cfa_fit)[c('chisq', 'df', 'pvalue', 'nfi', 'nnfi', 'rmsea')] |> round(3)
##  chisq     df pvalue    nfi   nnfi  rmsea 
## 80.964 30.000  0.000  0.936  0.937  0.082

图5.3展示了因素载荷，情况也大致良好，因此可以继续进行第二阶段的结构模型的估计。

semPaths(cfa_fit, 
         what = "std", 
         fade = F, # 关闭路径颜色渐变
         rotation = 2,
         edge.color = "darkgrey",
         esize = 3,
         curve = 2,
         edge.label.cex = 1.1)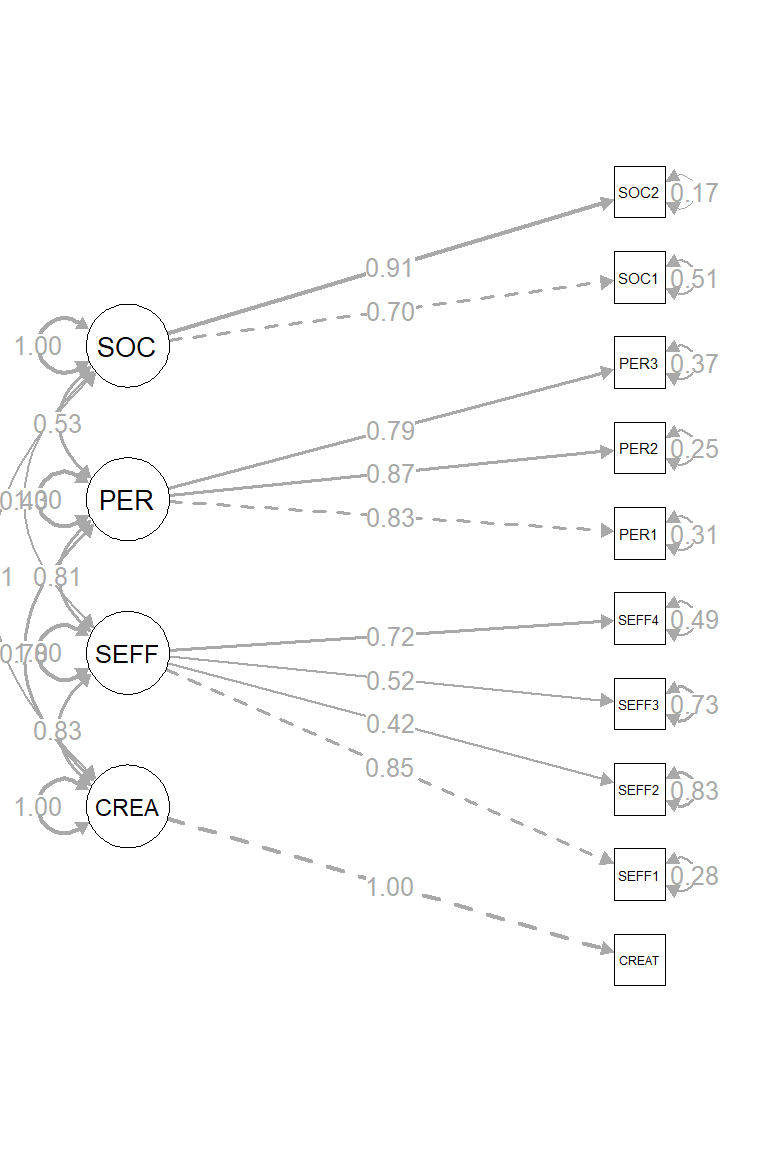
一阶段CFA的结果

Figure 5.3: 一阶段CFA的结果

5.4 阶段二：结构模型分析

模型设定和拟合情况如下，可以看到，模型的拟合程度还是不错的，但仍有修正空间。

sem_mod<-'
# measurement model
    CREA =~ 1*CREAT
    SEFF =~ SEFF1 + SEFF2 + SEFF3 + SEFF4
    PER  =~ PER1  + PER2  + PER3
    SOC  =~ SOC1  + SOC2
# structural model
    SEFF ~ a1*PER + c1*SOC
    CREA ~ a2*PER + b1*SEFF + c2*SOC
#set the correlation between variables to free
    SOC  ~~ PER # 外源潜在变量间的协方差
#define indirect effect (a*b)
    a1b1 := a1*b1
    c1b1 := c1*b1'


sem_fit <- sem(model = sem_mod, sample.cov = COV, sample.nobs = 250)
fitmeasures(sem_fit)[c('chisq', 'df', 'pvalue', 'nfi', 'nnfi', 'rmsea')] |> round(3) # 查看拟合结果
##  chisq     df pvalue    nfi   nnfi  rmsea 
## 80.964 30.000  0.000  0.936  0.937  0.082

图5.4绘制了整个模型（参见原书252页的图8.5），并添加了显著性水平。可以看到，所有的因素载荷都在统计学上具有显著意义。但是，SOC对SEFF和CREA都没有显著意义。换句话说，社会化因素在结构模型中的角色不太明显，几乎可以忽略。

for p less than .05, ** for p less than .01, and *** for p less than .001

p1 <- semPaths(sem_fit, 
         what = "std", 
         fade = F, # 关闭路径颜色渐变
         rotation = 2,
         layout = "tree2",
         edge.color = "darkgrey",
         esize = 3,
         edge.label.cex = 1.1,
         ask = FALSE)

p2 <- mark_sig(p1, sem_fit) # add asterisks
plot(p2)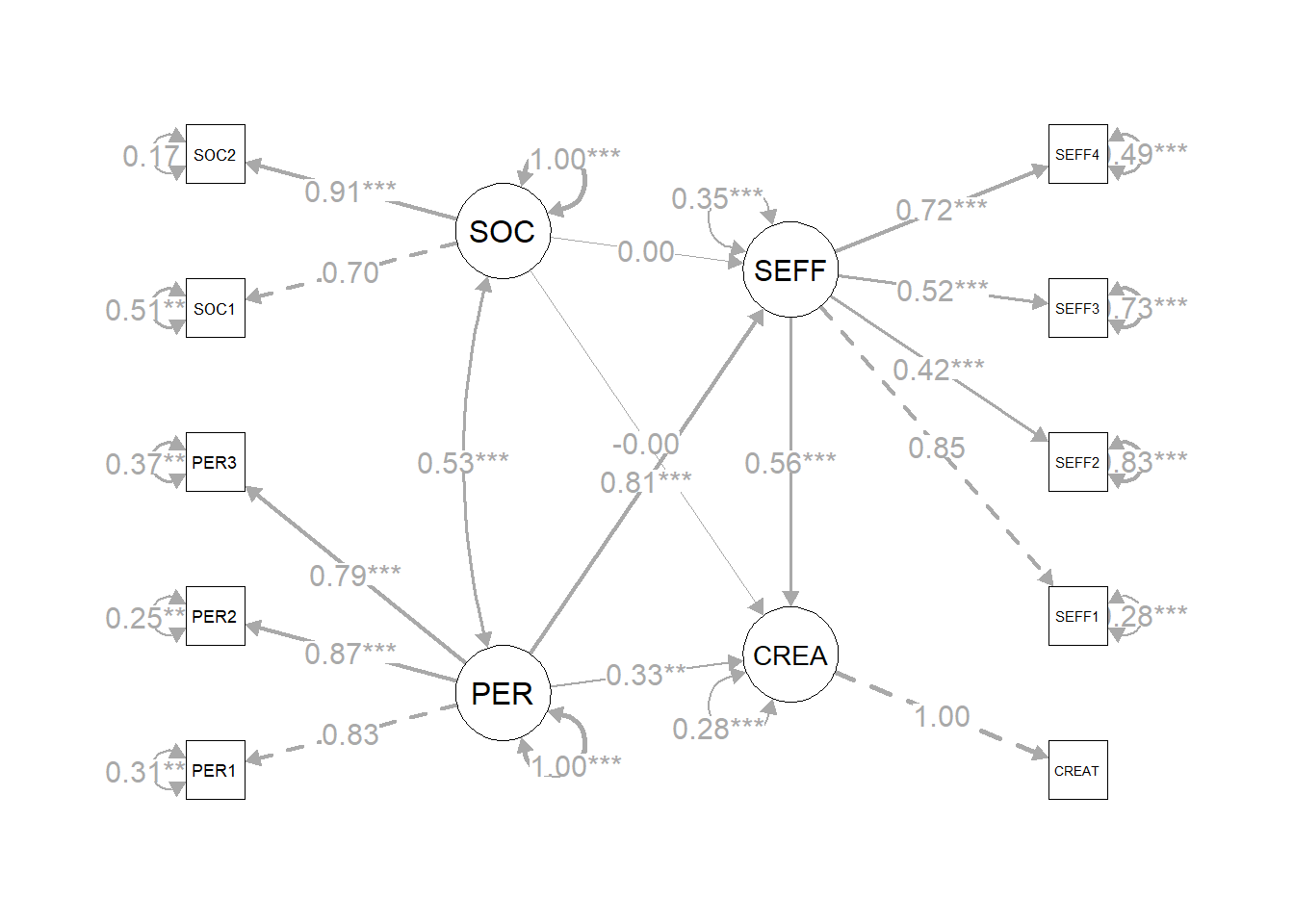
统合模型阶段二结构模型估计结果

Figure 5.4: 统合模型阶段二结构模型估计结果

5.5 模型修饰

模型修饰指数(MI)最高的五项如表5.1所示。一般来说，基于MI修饰模型时，必须考虑到切实的理论意义。

从给出的建议看，可采纳一下几条（具体思考历程，请参见原书253-254页）：

  1. 遵照第三行，增加CREA到SEFF4的测量因素载荷（原书253强调，不要轻易改动测量模型，因此，这里的改动只是出于示范目的）。
  2. 增加SEFF3和SEFF4的残差相关性。
modificationIndices(sem_fit) |>
  select(1:5) |>
  arrange(desc(mi)) |>
  head(5) |>
  knitr::kable(caption = "排名前五的模型修饰指数")
Table 5.1: 排名前五的模型修饰指数
lhs op rhs mi epc
PER =~ SEFF1 13.127181 0.1543965
CREAT ~~ SEFF4 13.031960 0.3288959
CREA =~ SEFF4 12.759405 0.0733377
SEFF1 ~~ SEFF4 11.869383 -0.0678181
SEFF2 ~~ PER1 9.984666 -0.1958852

拟合模型，并绘制路径图，如图5.5所示：

final_mod <- '
# measurement model
    CREA =~ CREAT + SEFF4 # 修饰1
    SEFF =~ SEFF1 + SEFF2 + SEFF3 + SEFF4
    PER  =~ PER1  + PER2  + PER3
    SOC  =~ SOC1  + SOC2
    CREAT ~~ 0 * CREAT 
# structural model
    SEFF ~ a1*PER + c1*SOC
    CREA ~ a2*PER + b1*SEFF + c2*SOC
#set the correlation between variables to free
    SOC  ~~ PER # 外源潜在变量间的协方差
    SEFF3 ~~ SEFF4 # 修饰2
#define indirect effect (a*b)
    PERindiCREA := a1*b1
    SOCindiCREA := c1*b1
# define total effect
    PERtotCREA := PERindiCREA + a2
    SOCtotCREA := SOCindiCREA + c2
'

final_fit <- sem(model = final_mod, sample.cov = COV, sample.nobs = 250)

p1 <- semPaths(final_fit, 
         what = "std", 
         fade = F, # 关闭路径颜色渐变
         rotation = 2,
         layout = "tree2",
         edge.color = "darkgrey",
         esize = 3,
         edge.label.cex = 1.1,
         ask = FALSE)

p2 <- mark_sig(p1, final_fit) # add asterisks
plot(p2)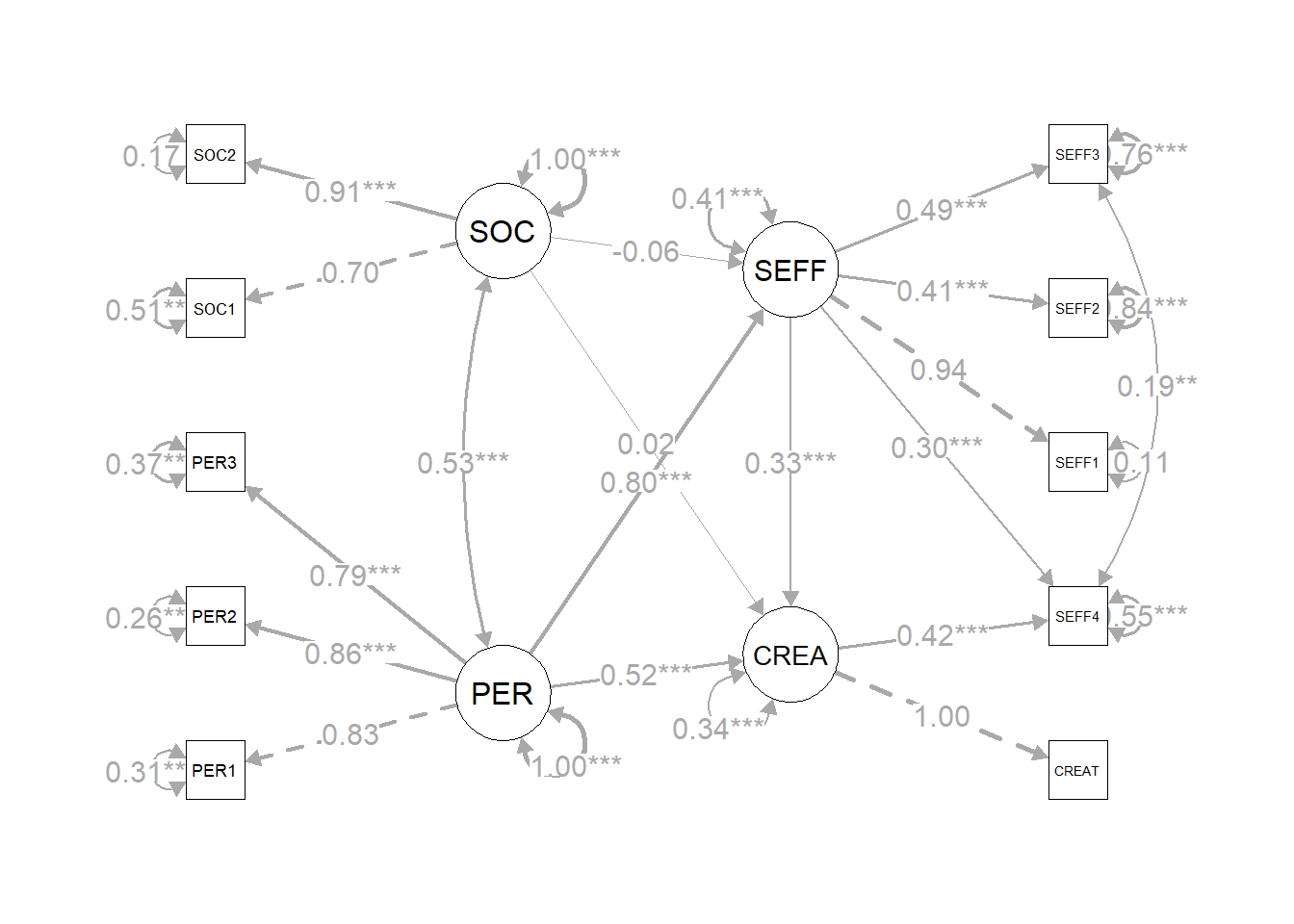
修正后统合模型最终解路径图示

Figure 5.5: 修正后统合模型最终解路径图示

由于最终模型和原模型有嵌套关系，因此可以进行卡方检验，显示模型具有显著改进。

anova(final_fit, sem_fit)
## 
## Chi-Squared Difference Test
## 
##           Df    AIC    BIC  Chisq Chisq diff   RMSEA Df diff Pr(>Chisq)    
## final_fit 28 7919.1 8014.2 59.089                                          
## sem_fit   30 7937.0 8025.0 80.964     21.875 0.19937       2  1.778e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

查看最终模型的拟合结果：

fitmeasures(final_fit)[c('chisq', 'df', 'pvalue', 'nfi', 'nnfi', 'rmsea')] |> round(3)
##  chisq     df pvalue    nfi   nnfi  rmsea 
## 59.089 28.000  0.001  0.953  0.959  0.067

5.6 直接效应和间接效应

表5.2给出了创造性格PER和组织社会化SOC，对于创意教学行为CREA的间接效应和总效应量及其统计检验。

summary(final_fit, standard = T)$pe |>
  filter(op == ":=") |>
  select(label, est, se, z, pvalue, std.all) |>
  mutate(across(where(is.numeric), ~round(., 3))) |>
  arrange(label) |>
  knitr::kable(caption = "潜在变量路径分析的部分复杂效应量")
Table 5.2: 潜在变量路径分析的部分复杂效应量
label est se z pvalue std.all
PERindiCREA 0.481 0.142 3.396 0.001 0.262
PERtotCREA 1.441 0.123 11.681 0.000 0.783
SOCindiCREA -0.053 0.064 -0.835 0.404 -0.019
SOCtotCREA -0.006 0.168 -0.034 0.973 -0.002