Chapter 2 验证性因素分析
验证性因素分析(CFA),主要是用来检验对某一潜变量的测量架构的设置是否合理。譬如,某一概念的测量由多个子题目构成,此时CFA可以确认,数据模型是否为研究者所预期的形式。
2.1 操作步骤概览
- 建立一个测量模型假设。
- 进行模型的识别,包括检查模型的可识别性,以及输入模型指令。
- 执行CFA分析。
- 进行结果分析。
- 进行模型的修正。
- 完成SEM分析,并给出报告。
该演示用到的软件包为:
library(tidyverse)
library(modelsummary)
library(lavaan)
library(semPlot)
# 绘图风格
theme_set(cowplot::theme_minimal_hgrid())2.2 模型界定
我们首先读入《组织创新气氛量表》数据,可以看到,该数据包含313个观测对象,以及18个变量。
dat <- read_csv("data/ch05.csv")
dim(dat) # 样本量和变量数## [1] 313 18计算原书中的表5.2,也就是对不同题项进行描述统计。这里可以用到modelsummary包,结果见表2.1。其中,第一列为题项名称,第二列为取值个数,第三列为缺失值比例,此后依次为均值、标准差、最小值、中位数、最大值和条形图展现的分布情况。
datasummary_skim(dat,
title = "组织创新气氛量表18题短版本的描述统计量",
fmt = fmt_sprintf("%.2f"))| Unique (#) | Missing (%) | Mean | SD | Min | Median | Max | ||
|---|---|---|---|---|---|---|---|---|
| A1 | 6 | 0 | 4.42 | 0.98 | 1.00 | 5.00 | 6.00 | |
| A2 | 6 | 0 | 4.31 | 1.02 | 1.00 | 4.00 | 6.00 | |
| A3 | 6 | 0 | 4.07 | 0.97 | 1.00 | 4.00 | 6.00 | |
| B1 | 6 | 0 | 4.02 | 1.16 | 1.00 | 4.00 | 6.00 | |
| B2 | 6 | 0 | 4.25 | 1.16 | 1.00 | 4.00 | 6.00 | |
| B3 | 6 | 0 | 4.24 | 1.09 | 1.00 | 4.00 | 6.00 | |
| C1 | 6 | 0 | 4.37 | 0.98 | 1.00 | 4.00 | 6.00 | |
| C2 | 6 | 0 | 4.34 | 1.03 | 1.00 | 4.00 | 6.00 | |
| C3 | 6 | 0 | 4.31 | 1.05 | 1.00 | 4.00 | 6.00 | |
| D1 | 6 | 0 | 4.83 | 0.94 | 1.00 | 5.00 | 6.00 | |
| D2 | 5 | 0 | 4.95 | 0.84 | 2.00 | 5.00 | 6.00 | |
| D3 | 5 | 0 | 4.83 | 0.91 | 2.00 | 5.00 | 6.00 | |
| E1 | 6 | 0 | 4.63 | 0.97 | 1.00 | 5.00 | 6.00 | |
| E2 | 6 | 0 | 4.73 | 1.01 | 1.00 | 5.00 | 6.00 | |
| E3 | 6 | 0 | 4.70 | 0.98 | 1.00 | 5.00 | 6.00 | |
| F1 | 6 | 0 | 4.23 | 1.17 | 1.00 | 4.00 | 6.00 | |
| F2 | 6 | 0 | 4.63 | 1.09 | 1.00 | 5.00 | 6.00 | |
| F3 | 6 | 0 | 4.49 | 0.94 | 1.00 | 5.00 | 6.00 |
模型设定为,不同字母开头的题项分别对应各自的潜变量(一共\(6\)个),每对潜变量之间存在相关性,测量残差不存在相关性。具体设置参见原书99页的图5.4。
2.3 模型识别
- 根据公式(1.1),测量数据数为\(\text{DP} = 18 \times (18 + 1) / 2 = 171\)个。
- 模型的待估参数为:
- \(18\)个因子载荷。
- \(18\)个测量残差。
- \(6-6=0\)个潜变量方差(为了确定潜变量的量纲,我们设定其方差都等于1,因此不需要被估计)。
- \(\left(\begin{array}{l}6 \\2\end{array}\right)=\frac{5 \times 6}{2} = 15\)个潜变量的协方差。
- 总共有\(18 + 18 + 15 = 51<171\)个待估参数,因此可以识别。
2.4 执行CFA分析并报告
lavaan包的模型设定是以字符串形式完成的。其中,=~表示测量模型中潜变量和测量变量之间的关系。程序默认(1)不同潜变量之间具有相关性;(2)不同测量残差之间不具有相关性,因此不再用手动设定这些细节了。如果我们想让潜变量之间不具有相关性,可以用orthogonal = T来关闭潜变量间的协方差估计(或者说将其统统约束为\(0\))。
原书用LISREL进行估计时,为了确定潜变量的量纲,使用的是将其方差固定为\(1\),而lavaan默认的是将第一个因子的载荷固定为\(1\)。为了复现书中LISREL给出的结果,需要用到std.lv = TRUE参数来手动设置,也就是使用固定方差为\(1\)的方法。
用cfa()命令进行拟合就可以了。
cfa_model <-'
#define the measurement model
FA =~ L11*A1 + L21*A2 + L31*A3
FB =~ L12*B1 + L22*B2 + L32*B3
FC =~ L13*C1 + L23*C2 + L33*C3
FD =~ L14*D1 + L24*D2 + L34*D3
FE =~ L15*E1 + L25*E2 + L35*E3
FF =~ L16*F1 + L26*F2 + L36*F3'
cfa_fit <- cfa(model = cfa_model,
data = dat,
std.lv = TRUE) # 固定潜变量方差为1最后,我们查看拟合的结果,对于拟合指标的解读,可以参见本册的1.4。而对于其他参数的估计,有两点值得特别说明一下:
- 当我们在
summary中添加standard = TRUE之后,因子载荷会多了Std.lv,Std.all两列,前者为只有潜变量被标准化时的载荷,后者为所有变量都被标准化时的载荷。 summary输出的倒数第二项为Covariances。由于该模型限定潜变量的方差都为1,所以这里的协方差就等于相关系数。summary输出的最后一项为Variances。注意,前面带.的方差指的是残差的方差,也就是内生变量不能被解释的那部分。不带.的方差就是该变量的方差。
cfa_res <- summary(cfa_fit,
fit.measures = T, # 输出拟合指标
standard = T) # 输出标准化解
print(cfa_res)## lavaan 0.6.15 ended normally after 31 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 51
##
## Number of observations 313
##
## Model Test User Model:
##
## Test statistic 241.755
## Degrees of freedom 120
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 2842.819
## Degrees of freedom 153
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.955
## Tucker-Lewis Index (TLI) 0.942
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -6751.785
## Loglikelihood unrestricted model (H1) -6630.907
##
## Akaike (AIC) 13605.569
## Bayesian (BIC) 13796.626
## Sample-size adjusted Bayesian (SABIC) 13634.870
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.057
## 90 Percent confidence interval - lower 0.047
## 90 Percent confidence interval - upper 0.067
## P-value H_0: RMSEA <= 0.050 0.132
## P-value H_0: RMSEA >= 0.080 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.052
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## FA =~
## A1 (L11) 0.815 0.051 15.967 0.000 0.815 0.830
## A2 (L21) 0.706 0.055 12.733 0.000 0.706 0.692
## A3 (L31) 0.614 0.054 11.430 0.000 0.614 0.634
## FB =~
## B1 (L12) 0.789 0.062 12.759 0.000 0.789 0.682
## B2 (L22) 0.961 0.058 16.591 0.000 0.961 0.833
## B3 (L32) 0.856 0.056 15.406 0.000 0.856 0.788
## FC =~
## C1 (L13) 0.699 0.053 13.178 0.000 0.699 0.717
## C2 (L23) 0.736 0.056 13.119 0.000 0.736 0.715
## C3 (L33) 0.696 0.058 11.950 0.000 0.696 0.663
## FD =~
## D1 (L14) 0.810 0.045 18.177 0.000 0.810 0.867
## D2 (L24) 0.741 0.040 18.750 0.000 0.741 0.886
## D3 (L34) 0.655 0.047 14.086 0.000 0.655 0.720
## FE =~
## E1 (L15) 0.806 0.046 17.392 0.000 0.806 0.830
## E2 (L25) 0.912 0.046 19.851 0.000 0.912 0.906
## E3 (L35) 0.791 0.047 16.810 0.000 0.791 0.811
## FF =~
## F1 (L16) 0.641 0.066 9.663 0.000 0.641 0.550
## F2 (L26) 0.828 0.058 14.296 0.000 0.828 0.758
## F3 (L36) 0.786 0.049 16.142 0.000 0.786 0.837
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## FA ~~
## FB 0.542 0.054 9.989 0.000 0.542 0.542
## FC 0.494 0.061 8.102 0.000 0.494 0.494
## FD 0.417 0.058 7.176 0.000 0.417 0.417
## FE 0.526 0.052 10.080 0.000 0.526 0.526
## FF 0.695 0.046 15.148 0.000 0.695 0.695
## FB ~~
## FC 0.697 0.047 14.906 0.000 0.697 0.697
## FD 0.447 0.055 8.127 0.000 0.447 0.447
## FE 0.575 0.048 12.091 0.000 0.575 0.575
## FF 0.391 0.061 6.403 0.000 0.391 0.391
## FC ~~
## FD 0.522 0.055 9.493 0.000 0.522 0.522
## FE 0.603 0.050 12.127 0.000 0.603 0.603
## FF 0.600 0.054 11.032 0.000 0.600 0.600
## FD ~~
## FE 0.557 0.046 12.046 0.000 0.557 0.557
## FF 0.316 0.062 5.137 0.000 0.316 0.316
## FE ~~
## FF 0.443 0.056 7.944 0.000 0.443 0.443
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .A1 0.300 0.046 6.509 0.000 0.300 0.311
## .A2 0.544 0.055 9.980 0.000 0.544 0.522
## .A3 0.561 0.052 10.700 0.000 0.561 0.598
## .B1 0.716 0.068 10.525 0.000 0.716 0.535
## .B2 0.408 0.057 7.211 0.000 0.408 0.306
## .B3 0.447 0.052 8.602 0.000 0.447 0.379
## .C1 0.461 0.050 9.305 0.000 0.461 0.485
## .C2 0.519 0.055 9.354 0.000 0.519 0.489
## .C3 0.618 0.061 10.173 0.000 0.618 0.560
## .D1 0.217 0.031 7.055 0.000 0.217 0.248
## .D2 0.151 0.024 6.204 0.000 0.151 0.215
## .D3 0.399 0.037 10.799 0.000 0.399 0.482
## .E1 0.292 0.032 9.243 0.000 0.292 0.311
## .E2 0.181 0.030 6.113 0.000 0.181 0.179
## .E3 0.325 0.033 9.733 0.000 0.325 0.342
## .F1 0.948 0.083 11.400 0.000 0.948 0.698
## .F2 0.507 0.058 8.700 0.000 0.507 0.425
## .F3 0.265 0.042 6.276 0.000 0.265 0.300
## FA 1.000 1.000 1.000
## FB 1.000 1.000 1.000
## FC 1.000 1.000 1.000
## FD 1.000 1.000 1.000
## FE 1.000 1.000 1.000
## FF 1.000 1.000 1.000特别的,如果我们想要检视哪些参数得到了估计,可以:
inspect(cfa_fit)## $lambda
## FA FB FC FD FE FF
## A1 1 0 0 0 0 0
## A2 2 0 0 0 0 0
## A3 3 0 0 0 0 0
## B1 0 4 0 0 0 0
## B2 0 5 0 0 0 0
## B3 0 6 0 0 0 0
## C1 0 0 7 0 0 0
## C2 0 0 8 0 0 0
## C3 0 0 9 0 0 0
## D1 0 0 0 10 0 0
## D2 0 0 0 11 0 0
## D3 0 0 0 12 0 0
## E1 0 0 0 0 13 0
## E2 0 0 0 0 14 0
## E3 0 0 0 0 15 0
## F1 0 0 0 0 0 16
## F2 0 0 0 0 0 17
## F3 0 0 0 0 0 18
##
## $theta
## A1 A2 A3 B1 B2 B3 C1 C2 C3 D1 D2 D3 E1 E2 E3 F1 F2 F3
## A1 19
## A2 0 20
## A3 0 0 21
## B1 0 0 0 22
## B2 0 0 0 0 23
## B3 0 0 0 0 0 24
## C1 0 0 0 0 0 0 25
## C2 0 0 0 0 0 0 0 26
## C3 0 0 0 0 0 0 0 0 27
## D1 0 0 0 0 0 0 0 0 0 28
## D2 0 0 0 0 0 0 0 0 0 0 29
## D3 0 0 0 0 0 0 0 0 0 0 0 30
## E1 0 0 0 0 0 0 0 0 0 0 0 0 31
## E2 0 0 0 0 0 0 0 0 0 0 0 0 0 32
## E3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 33
## F1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 34
## F2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 35
## F3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 36
##
## $psi
## FA FB FC FD FE FF
## FA 0
## FB 37 0
## FC 38 42 0
## FD 39 43 46 0
## FE 40 44 47 49 0
## FF 41 45 48 50 51 02.5 路径图
绘图是展示SEM分析结果最重要且最直观的方式,这里需要用到semplot包,结果参见图 2.1。
semPaths(cfa_fit,
what = "std") # 输出标准化的各项系数,也就是之前的Std.all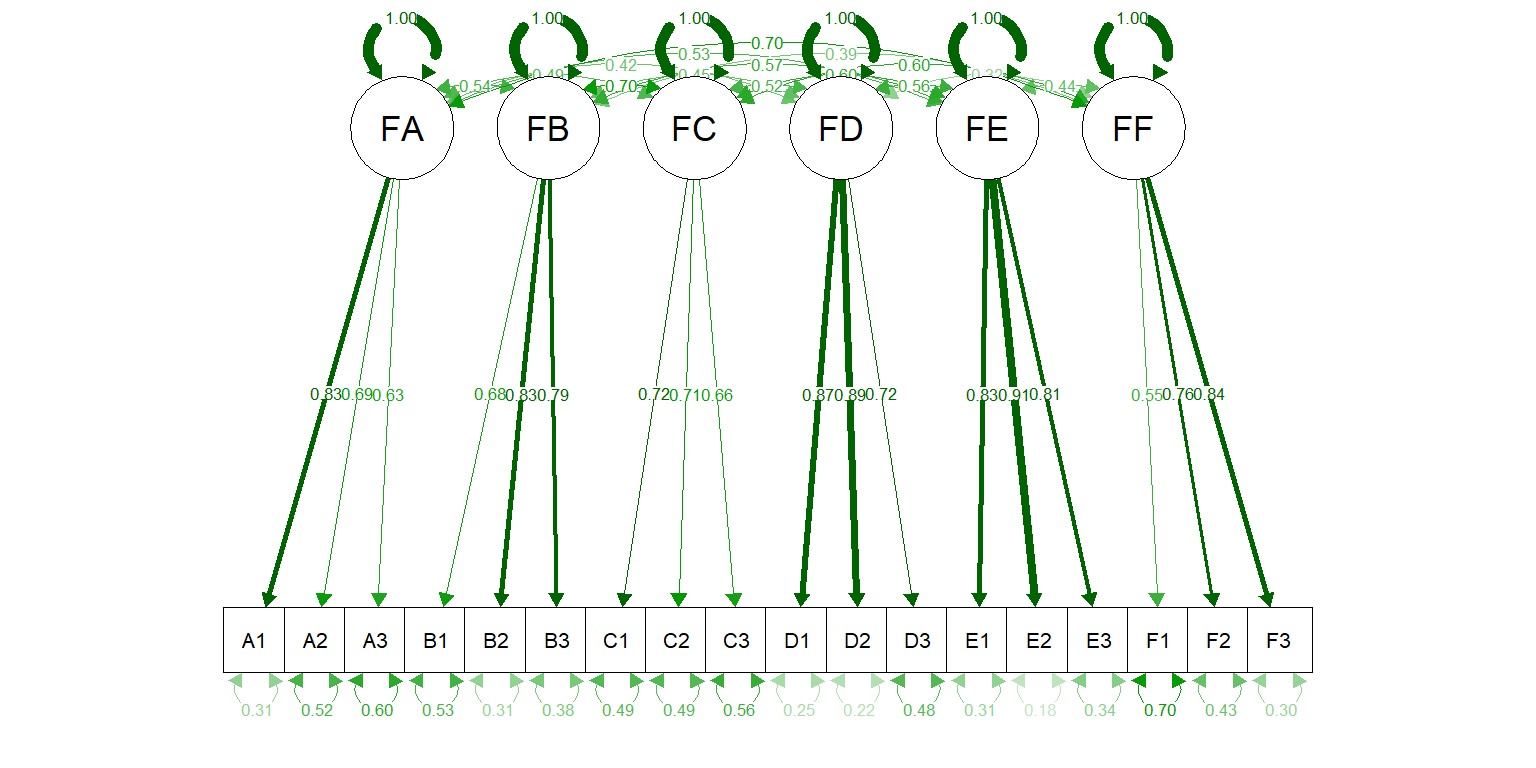
Figure 2.1: 以R进行CFA的结果图示
2.6 残差分析
通过估计得到的CFA模型,可以导出一个观测变量间的协方差矩阵,也称导出矩阵(reproduced matrix,记为\(\mathbf{\Sigma}\)),用实际观测到的协方差矩阵(记为\(\mathbf{S}\))减去这个矩阵,就是拟合的残差矩阵,通过分析残差的分布情况,可以对拟合优度进行检验。
下面计算了计算残差分布,残差最大值为0.187,最小值为-0.122,和原书112页的结果基本一致。
resid(cfa_fit, type = "raw")$cov |>
range() |>
round(3)## [1] -0.122 0.187考虑到各变量的量纲上的差异,可以对残差进行标准化。得到的标准化残差的绝对值大于\(1.96\)时,可以认为模型推导出的该协方差与实际协方差的差异,在\(0.05\)的水平上显著存在。
lavaan 对于resid命令的说明上说:If type=“standardized”, the residuals are divided by the square root of the asymptotic variance of these residuals. The resulting standardized residuals elements can be interpreted as z-scores.感觉应该和原书上所说的标准化残差是一个意思,但是不知道出于什么原因,这里的结果和书上的差距有些大。
resid(cfa_fit, type = "standardized")$cov |>
range() |>
round(3)## [1] -4.148 3.832通过绘制标准化残差的QQ图,可以帮助我们了解残差的分布情况,见图2.2。
# 提取标准化残差
res_std <- resid(cfa_fit, type = "standardized")$cov |>
unclass()
# 转化为向量形式
res_std <- res_std[lower.tri(res_std, diag = F)]
# 绘图
ggplot(mapping = aes(sample = res_std)) +
geom_qq() +
geom_qq_line() +
labs(x = "Standardized Residuals", y = "Normal Quantiles")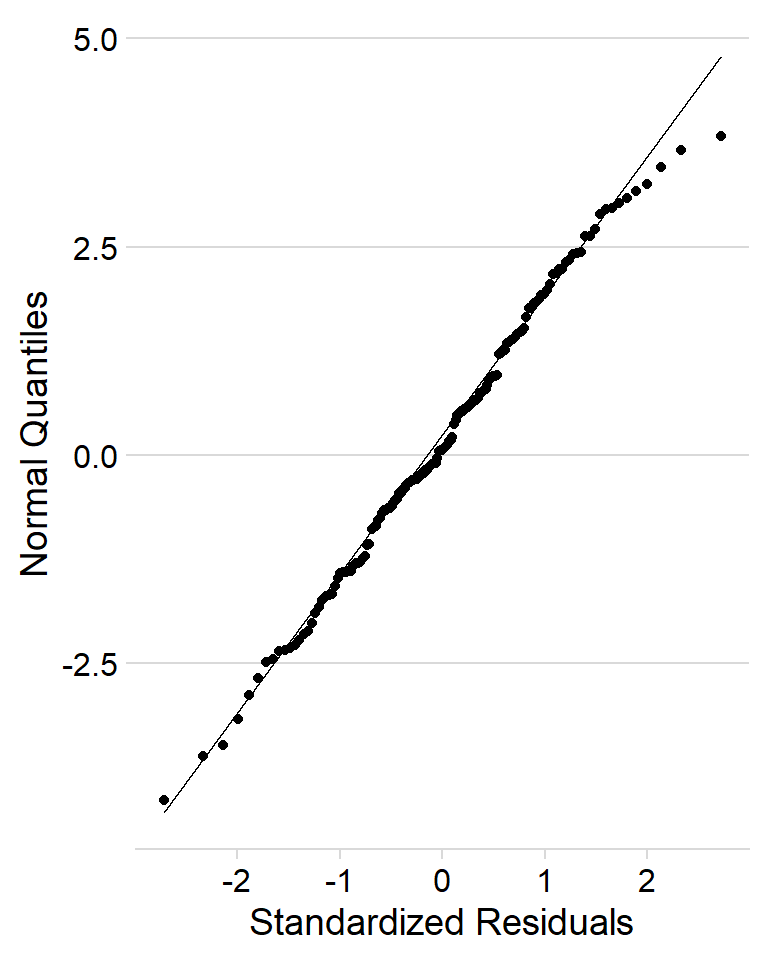
Figure 2.2: Qplot of standardized residuals
2.7 模型修饰指数的检查
当MI指数高于\(5\),意味着该残差有修正的必要,也就是测量变量还可能受到对应潜变量的影响。
表2.2给出了MI指数最高的5个潜变量-测量变量对。
modificationIndices(cfa_fit) |>
as_tibble() |>
select(1:4) |>
filter(mi >= 5) |>
arrange(desc(mi)) |>
head(5) |>
knitr::kable(
caption = "MI指数最高的5个潜变量测量变量对"
)| lhs | op | rhs | mi |
|---|---|---|---|
| FC | =~ | D3 | 19.83763 |
| FA | =~ | C3 | 14.82648 |
| FE | =~ | A1 | 14.04803 |
| D1 | ~~ | D2 | 13.88987 |
| D1 | ~~ | D3 | 13.42555 |
2.8 内在拟合检测
原书的内在拟合检测结果为123页的表5.5,这里对其进行复现,结果见表 2.3。
# 首先提取完全标准化的因子载荷
lambda <- cfa_res$pe |>
select(1:3, std.all) |>
filter(op == "=~")
# 然后提取完全标准化的残差
resi <- cfa_res$pe |>
filter(lhs == rhs & str_detect(lhs, pattern = "\\d")) |>
select(std.all) |>
pull()
# 合并
tab5_5 <- lambda |>
mutate(resi = resi) |>
mutate(across(.cols = is.numeric, .fns = ~round(., 3)))
# 计算rho_c,即组合信度composite reliability
# 代表测量变量的变异量能够被潜在变量解释的百分比
# 注意,下面的算式只适用于残差项不相关的情况
rho_c <- tab5_5 |>
group_by(lhs) |>
summarise(
CR = sum(std.all)^2 / ( sum(std.all)^2 + sum(resi) )
) |>
pull(CR)
# 计算rho_v,即平均变异萃取量
# 代表潜在变量对每个测量变量的变异量的平均解释程度
rho_v <- tab5_5 |>
group_by(lhs) |>
summarise(
AVE = sum(std.all^2) / ( sum(std.all^2) + sum(resi) )
) |>
pull(AVE)
# 合并结果
tibble(
lv = unique(tab5_5$lhs),
CR = round(rho_c, 3),
AVE = round(rho_v,3)) |>
knitr::kable(
caption = "验证性因分析结果摘要"
)| lv | CR | AVE |
|---|---|---|
| FA | 0.765 | 0.523 |
| FB | 0.813 | 0.593 |
| FC | 0.741 | 0.488 |
| FD | 0.866 | 0.685 |
| FE | 0.886 | 0.723 |
| FF | 0.764 | 0.526 |
2.9 模型修饰
但理论模型的参数估计或拟合情况不理想,需要对模型进行修正,以求改进,这一过程即为模型修饰。
原书128页,基于MI指标和模型可解释性,建立了第一个因子F1和C3变量之间的联系。结果如图 @ref(fig:new_fit)所示。
new_model <-'
#define the measurement model
FA =~ L11*A1 + L21*A2 + L31*A3 + L37 * C3
FB =~ L12*B1 + L22*B2 + L32*B3
FC =~ L13*C1 + L23*C2 + L33*C3
FD =~ L14*D1 + L24*D2 + L34*D3
FE =~ L15*E1 + L25*E2 + L35*E3
FF =~ L16*F1 + L26*F2 + L36*F3'
new_fit <- cfa(new_model,
data = dat,
std.lv = TRUE)
semPaths(new_fit,
what = "std") 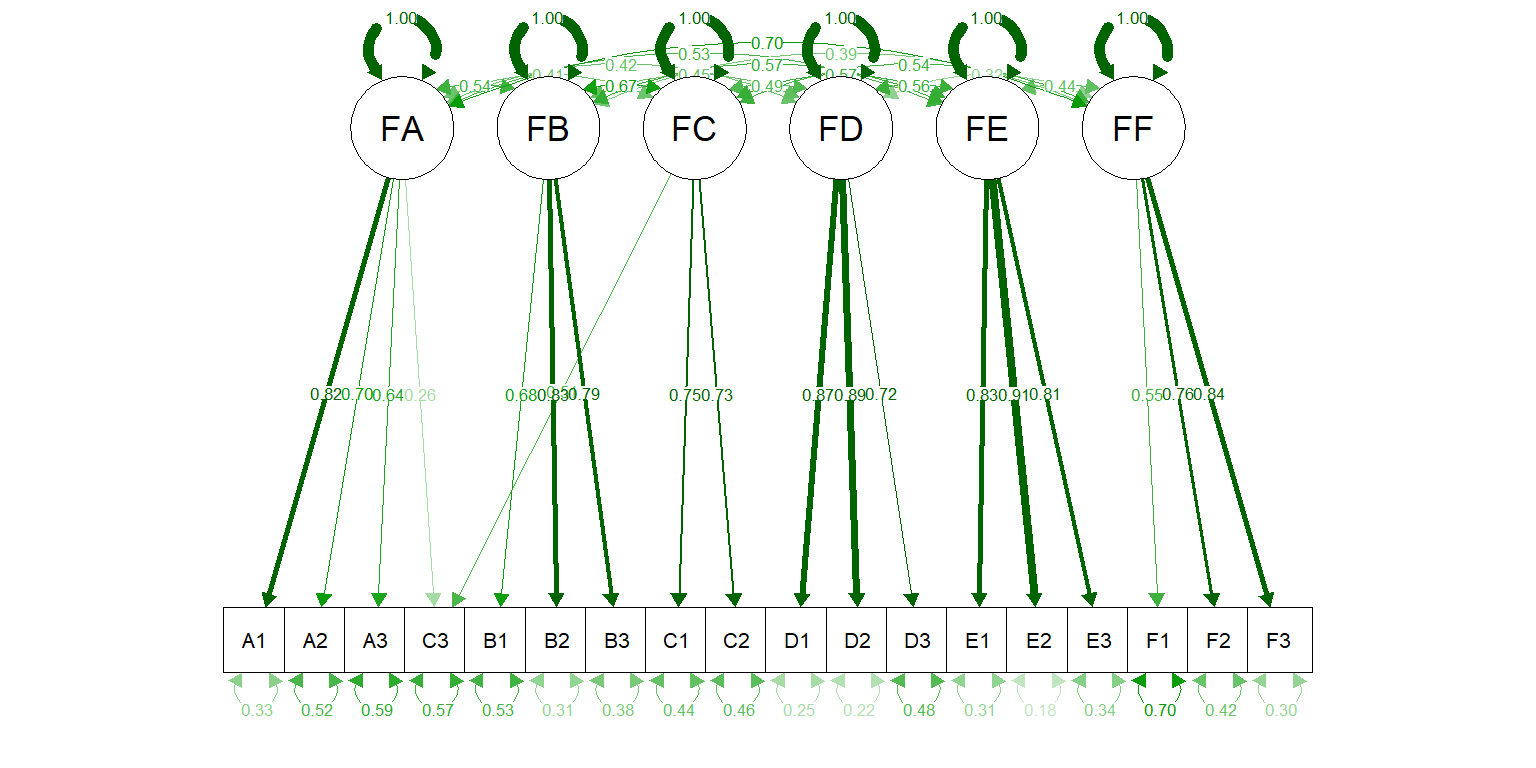
Figure 2.3: 修饰后的新模型
原书136页表5.9给出了修饰前后因素间相关系数的比较,我们可以用图2.4以更直观的形式来展现:
new_res <- summary(new_fit,
fit.measures = T, # 输出拟合指标
standard = T)
#修饰模型的因子间协方差(相关系数)
new_fit_est <- new_res$pe |>
filter(op == "~~") |>
filter(!str_detect(lhs, "\\d") & !str_detect(rhs, "\\d")) |>
filter(lhs != rhs) |>
select(1:3, est)
# 原模型的因子间协方差
cfa_fit_est <- cfa_res$pe |>
filter(op == "~~") |>
filter(!str_detect(lhs, "\\d") & !str_detect(rhs, "\\d")) |>
filter(lhs != rhs) |>
select(1:3, est)
# 合并
res <- new_fit_est |>
left_join(cfa_fit_est, by = join_by(lhs == lhs, rhs == rhs),
suffix = c(".new", ".old")) |>
select(1:3, 4, 6) |>
mutate(label = str_c(lhs, "-", rhs),
diff = abs(est.new - est.old)) |> # 新的系数减去老系数的差值
select(label, est.new, est.old, diff) |>
pivot_longer(-c(1, 4))
# 绘制结果(按变化的绝对值大小排序)
ggplot(data = res, aes(y = reorder(label, diff))) +
geom_point(aes(x = value, color = name), size = 5, alpha = .3) +
labs(x = "Covariance", y = NULL, color = NULL)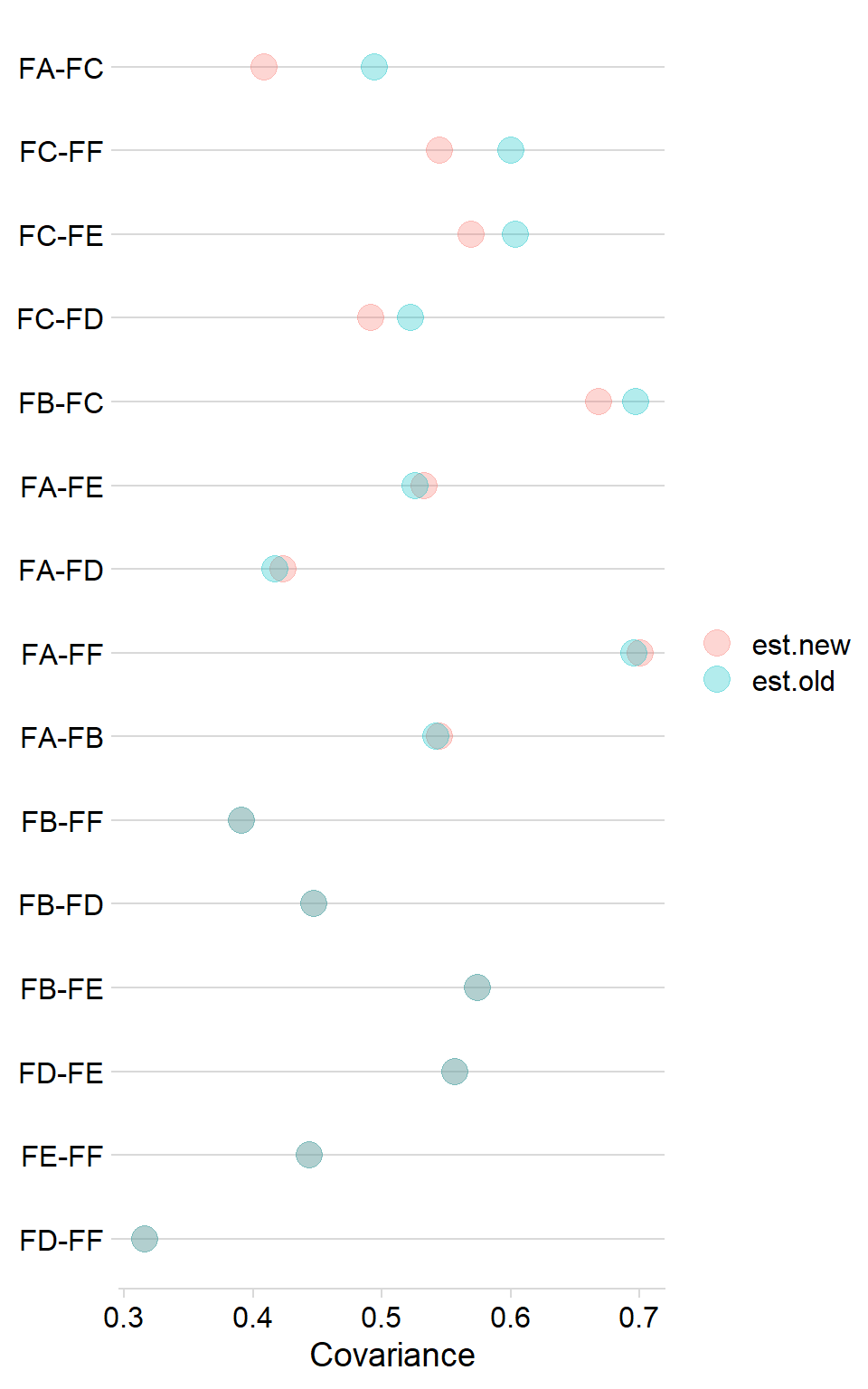
Figure 2.4: 修饰后与修饰前的因子协方差变化