Chapter 3 Chapter 3: Categorical and Ordinal Data

3.1 Models for Categorical Data

3.1.1 Introduction: Categorical Data may be nominal or ordinal

  1. Nominal outcome: When the dependent variable can take more than two values (non-binary outcome).
    1. Examples:
      1. Self-rated health: Poor/Fair/Good/Very good/Excellent
      2. Choice of social contact: Email/Face-to-face/Both methods/Neither
      3. Contraceptive usage: None/Pills/Condom/Sterilization
    2. How can we generalize from binary outcome to polytomous outcomes?
      1. We need to transform the model \[ \log\left(\frac{P(Y_i=1)}{P(Y_i=0)}\right)=X_i\beta \] in some manner that allows for \(Y_i=2,3,4,\ldots\), where these numbers may simply represent nominal (unordered) levels of an outcome. Think: red, blue, yellow as codes 1,2,3. Clearly, the numbers have no meaning other than to represent the data values. We will start outcomes at ``1’’ although this is arbitrary.
    3. Order can matter
      1. When the categories are nominal/unordered, we will use a multinomial logistic regression model.
      2. When the categories are ordered, we can use a more parsimonious logit model called the ordinal logistic regression model.

3.1.1.1 Exercise 1

Exercise: Consider some other multinomial outcomes and discuss whether they are truly nominal categories. 
Hint is visible here

3.1.2 Multinomial Logit Model

  1. Given \(J\) nominal (distinct, non-overlapping) categories, numbered 1,2,…,J, we associate a probability with each of them: \(p_1,p_2,\ldots,p_J\).

  2. The multinomial distribution provides the probability of specific realizations or counts \(\vec Y=(Y_1,Y_2,\ldots,Y_J)\) from a sample of size \(n\) to be:
    \[ P(Y_1=n_1,Y_2=n_2,\ldots,Y_J=n_J)=\frac{n!}{{n_1}!{n_2}!\ldots n_{J-1}!n_J!}p_1^{n_1}p_2^{n_2}\ldots p_J^{n_J} \]

    with \(n=\sum_j n_j\) and \(\sum_j p_j=1\).

  3. We can use the same ideas from binary data modeling, which is to take log-odds, but we have to do this differently, expanding the notion of odds to be the comparison (ratio) of two probabilities.

\[\begin{eqnarray*} \log\left(\frac{p_1}{p_J}\right)& = & b_{10}+b_{11}X_1+\ldots + b_{1p}X_p \\ \log\left(\frac{p_2}{p_J}\right) & = & b_{20}+b_{21}X_1+\ldots + b_{2p}X_p \\ & \cdots & \\ \log\left(\frac{p_{J-1}}{p_J}\right) & = & b_{(J-1)0}+b_{(J-1)1}X_1+\ldots + b_{(J-1)p}X_p \end{eqnarray*}\]

  • The reference category is \(J\) not \(0\) (and response 0 has been replaced).
  • The subscripts are important – they identify the relative log-odds of interest, since there are now so many.
  • When J=2, the multinomial model is same as the logistic model.
  • We can also use the probit link function to build a multinomial probit model.

3.1.3 Multinomial logit as a GLM

It is not simple to write the multinomial logit model as a GLM. First, define \(Y_i=(Y_{1i},Y_{2i},\dots,Y_{Ji})\). For the sake of simplicity, we will assume this is one draw, although when there are identical covariate patterns, the number of draws for that pattern could be used. This “grouped data” conceptualization is important in other contexts. Defining things in terms of one observation essentially means that one of the \(Y_{ji}\) will be 1 and the rest will be 0 – you just don’t know which one!

  1. \(Y_i \sim \mbox{MN}(p_{1i},p_{2i},\ldots,p_{Ji})\). A single multinomial draw.
  2. \(H_i=(\eta_{1i},\eta_{2i},\ldots,\eta_{(J-1)i}) = (X_i\beta_{1\cdot},X_i\beta_{2\cdot},\ldots,X_i\beta_{(J-1)\cdot})\), where \(\beta_{j\cdot}=(b_{j0},b_{j1},\ldots,b_{jp})'\) are a set of regression coefficients, one set for each of \(J-1\) nominal outcomes (none for the reference category). The dot (\(\cdot\)) signifies that it is a vector. As well, there are \(J-1\) \(\eta\)’s for each \(i\) in this formulation.
  3. Let \(\log\lambda_{ji}=\eta_{ji}\), for \(j=1,\ldots,(J-1)\), where \(\lambda_{ji}=\left(\frac{p_j}{p_J}\right)_i\) (the \(j^{th}\) odds ratio for subject \(i\)). Thus \(g(\lambda_{ji})=\log\lambda_{ji}\) is one component of a multivariate link function. Each \(\lambda_{ji}\) is a function of two probabilities, one of which is repeatedly in the denominator, so this is a truly multivariate implicit definition.
    a. The \(g^{-1}\) function is harder; we will show the components of \(g^{-1}\) and again define it implicitly. It is \[ p_{ji} = \frac{\lambda_{ji}}{1+\sum_{k=1}^{J-1}\lambda_{ki}},\ \mbox{ for }j=1,\ldots,J-1 \] Since \(p_{ji}\) depends on all \(\lambda\) which depend on all \(\eta\), the \(g\) and \(g^{-1}\) functions are clearly multivariate. Of course, \(\lambda_{ji}=\exp(\eta_{ji})\). What may be less obvious is that for reference category \(J\): \[ p_{Ji} = \frac{1}{1+\sum_{k=1}^{J-1}\lambda_{ki}}, \] which also insures that \(\sum_{j=1}^{J}p_{ji}=1\).

3.1.4 Multinomial logistic regression example

We will use the General Social Survey from 2002. In this example, the dependent variable is the form of social contact. The question is ``Do you contact other people via email or based on face-to-face meeting?’’ The responses are:

1:    Neither
2:    Mostly email
3:    Mostly face-to-face
4:    Both

What type of dependent variable this is? Continuous? Ordinal? Nominal?

Consider these predictors of contact type:

Gender:       Male (1) / Female (2)
Age:          (years-45)
Educ:         (years-12)
Income:       (<25K, 25-50K, >50K)

Age is “centered” at 45 and education at 12 years. These aid in interpretability of the constant in more complex models. Income is an ordinal predictor (you will code it with indicator variables, most likely)

3.1.5 Defining Odds for Multiple Categories

We can use the frequencies of each outcome category to express relative odds.

Code 
gss <- read.csv("./Data/GSS2002b.csv") %>%
    mutate_all(function(x) {
        x[x %in% c(98, 99, 998, 999, 9999)] <- NA
        return(x)
    }) %>%
    mutate(health = case_when(health == 1 ~ "Excellent", health == 2 ~ "Very good", health == 3 ~ "Fair", health ==
        4 ~ "Poor"), health = ordered(health, levels = c("Poor", "Fair", "Very good", "Excellent")), black = race_2 ==
        2, sex = case_when(sex == 1 ~ "Male", sex == 2 ~ "Female"), sex = ordered(sex, levels = c("Male", "Female")),
        age = age - 45, educ = educ - 12, )
gss$inc <- factor(gss$income3, levels = 1:3, labels = c("<25K", "25-50K", ">50K"))
gss$contact <- factor(gss$contact, levels = 1:4, labels = c("Neither", "Mostly by email", "Mostly face-to-face",
    "Both"))

freq <- table(gss$contact, useNA = "no")
percent <- round(100 * prop.table(freq), 2)
knitr::kable(cbind(freq, percent))
freq percent
Neither 817 30.56
Mostly by email 457 17.10
Mostly face-to-face 690 25.81
Both 709 26.52

From the table, we can construct odds, always relative to the same reference category, which is “Neither”:

Outcome Pr(Outcome) P(Neither) odds log-odds
Email 0.17 0.31 0.56 -0.58
Face 0.26 0.31 0.84 -0.17
Both 0.27 0.31 0.87 -0.14
  • The interpretation of odds is similar to odds.
    • When odds are greater than 1, the probability of belonging to the comparison group is greater than the probability of belonging to the reference group, and vice versa.
  • Similarly, an odds ratio (OR) for an effect can be defined in this context.
    • If the OR is greater than 1, it means the relative odds are larger.

We run our first multinomial logit model in R without covariates:

Code 
fit.null <- nnet::multinom(contact ~ 1, data = gss)
## # weights:  8 (3 variable)
## initial  value 3705.564827 
## final  value 3650.949081 
## converged
Code 
coefs <- summary(fit.null)$coefficients
print(summary(fit.null), digits = 3)
## Call:
## nnet::multinom(formula = contact ~ 1, data = gss)
## 
## Coefficients:
##                     (Intercept)
## Mostly by email          -0.581
## Mostly face-to-face      -0.169
## Both                     -0.142
## 
## Std. Errors:
##                     (Intercept)
## Mostly by email          0.0584
## Mostly face-to-face      0.0517
## Both                     0.0513
## 
## Residual Deviance: 7301.898 
## AIC: 7307.898

  • This R function provides coefficients \(\hat b_{10}=\)-0.58, \(\hat b_{20}=\)-0.17, \(\hat b_{30}=\)-0.14.
  • Each is the “constant” in the linear equation for log-relative-odds comparing one outcome to the reference (“neither”).
  • Thus all of the coefficients match the log-odds in the prior table.

To interpret a coefficient from a multinomial logistic regression, one “inverts” the log-odds to become odds. Thus, the odds of certain form of social contact relative to “neither” are:

  • P(email)/P(neither)=exp(-0.581)=0.56
  • P(face)/P(neither)=exp(-0.169)=0.845
  • P(both)/P(neither)=exp(-0.142)=0.87

Since the log-odds are all negative, the odds are all less than one (the reference category has the highest prevalence).

3.1.6 Adding covariates

As is common in regression modeling, the expectation varies conditional on characteristics, such as sex. We can examine the three sets of odds conditional on sex in a table:

Code 
DescTools::PercTable(xt <- xtabs(~contact + sex, data = gss), rfrq = "001")
##                                            
##                       sex     Male   Female
## contact                                    
##                                            
## Neither               freq     376      441
##                       p.col  31.8%    29.6%
##                                            
## Mostly by email       freq     211      246
##                       p.col  17.9%    16.5%
##                                            
## Mostly face-to-face   freq     293      397
##                       p.col  24.8%    26.6%
##                                            
## Both                  freq     302      407
##                       p.col  25.5%    27.3%
##

We can construct the relative odds, always with respect to the reference category for female and male separately using the column percentages, or even the raw counts [think about why this is true]:

Code 
print(ftable(xt[2:4, ]/xt[rep(1, 3), ]), digits = 3)
##                     sex  Male Female
## contact                             
## Mostly by email         0.561  0.558
## Mostly face-to-face     0.779  0.900
## Both                    0.803  0.923
  • We see that there are big differences in the odds of face-to-face contact (relative to neither), with males at 0.779 and females at 0.9.
  • We can construct the odds ratio by taking the ratio of these two odds
    • with females having 1.155 the odds of face-to-face contact as compared to males, and in reference to “neither.”

We already have described the way we add predictors to a multinomial logit model. Essentially, we have a series of equations, each with parallel form (for the \(K^{th}\) outcome, \(K<J\)):

\[\begin{eqnarray*} \log\left(\frac{p_K}{p_J}\right) & = & b_{K0}+b_{K1}X_1+\ldots + b_{Kp}X_p \\ & = & X\beta_K \end{eqnarray*}\] with the second equation in matrix notation and \(\beta_K=(b_{K0},b_{K1},\ldots,b_{Kp})'\).

  • There are \(J-1\) of these equations.
  • By having so many equations we are allowing a different relationship between the predictor and each outcome level.
    • That is, differences between sex groups may have a different relationship for face-to-face contact (relative to “neither”) as compared to email contact.

With single, nominal predictors, we can reproduce exactly the conditional log-relative-odds in our tables. We do so now for the predictor sex:

Code 
fit.sex <- nnet::multinom(contact ~ I(sex == "Female"), data = gss)
## # weights:  12 (6 variable)
## initial  value 3705.564827 
## iter  10 value 3649.248017
## iter  10 value 3649.248016
## iter  10 value 3649.248016
## final  value 3649.248016 
## converged
Code 
coefs <- summary(fit.sex)$coefficients
print(summary(fit.sex), digits = 3)
## Call:
## nnet::multinom(formula = contact ~ I(sex == "Female"), data = gss)
## 
## Coefficients:
##                     (Intercept) I(sex == "Female")TRUE
## Mostly by email          -0.578               -0.00598
## Mostly face-to-face      -0.249                0.14431
## Both                     -0.219                0.13893
## 
## Std. Errors:
##                     (Intercept) I(sex == "Female")TRUE
## Mostly by email          0.0860                  0.117
## Mostly face-to-face      0.0779                  0.104
## Both                     0.0773                  0.103
## 
## Residual Deviance: 7298.496 
## AIC: 7310.496

3.1.7 Interpretation

How do we interpret the components of this model?

  • For males, Log(P(email)/P(neither)) = -0.578.
  • For females, Log(P(email)/P(neither)) = -0.578 + -0.006 = -0.584.
  • Exponentiating, the two values become 0.561 and 0.558, respectively, which matches our table, above.
  1. Females are slightly less likely than males to use email, relative to “neither.”
  2. The comparison between females and males is being made relative to each other and to a common alternative outcome.
  3. The ratio of female to male odds would be called relative-odds (a ratio of ratios).
  4. Considering all of the three comparisons, females have greater odds of using face-to-face or both, relative to neither, as compared to males.

It’s a lot to keep track of, but there is one last point that must be made.

  1. Just because females have greater odds to use face-to-face contact, doesn’t mean that males use face-to-face less often than females.
    1. The problem lies in the denominators of these compared odds:
Males Females
P(face|M)/P(neither|M) < P(face|F)/P(neither|F)
    1. This does not imply P(face|M) < P(face|F)!
  2. The denominators P(Neither|Sex) may not be the same, since they are conditional on sex.
    1. There are two different “moving parts” for the two different groups.

3.1.8 Recovering the probability

It might not seem obvious at first that one can recover probabilities from odds for various scenarios, but it just takes a little algebra.

Given the scenario described by predictor vector \(X\), the model predicts a set of odds: \(P(Y=1|X)/P(Y=J|X),P(Y=2|X)/P(Y=J|X),\ldots,P(Y=J-1|X)/P(Y=J|X)\), take the sum of these, multiplied by the common denominator (to remove it): \[ P(Y=J|X)\sum_{j=1}^{J-1}P(Y=j|X)/P(Y=J|X) = \sum_{j=1}^{J-1}P(Y=j|X) \] But we also know that: \[ 1=P(Y=J) + \sum_{j=1}^{J-1}P(Y=j|X) \] by the law of total probability. We can rewrite this as:

\[ 1=P(Y=J) + P(Y=J)\sum_{j=1}^{J-1}P(Y=j|X)/P(Y=J) \] The right-hand summation is the sum of the odds predicted by the model. Solve for \(P(Y=J)\) and you get: \[ P(Y=J)=\frac{1}{1+ \sum_{j=1}^{J-1}P(Y=j|X)/P(Y=J)} \]

  • So if we sum the odds (call it \(S_{odds}\)), \(\frac{1}{1+S_{odds}}\) is the probability of the reference category (conditional on \(X\)).
  • Once we have \(P(Y=J)\), we can recover \(P(Y=j)=P(Y=J)\cdot P(Y=j)/P(Y=J)\), with the rightmost ratio simply being the odds predicted by the model.
  • The key observation here is that we need to use all of the odds to find a single probability.

3.1.8.1 Exercise 2

Exercise: using the multinomial coefficients for contact (above, with female as the predictor), find the probability of “both” for males and females. 
Hint is visible here

3.1.9 Example (cont.)

Just as in regression, we can include multiple, simultaneous predictors.

Code 
fit.full <- nnet::multinom(contact ~ I(sex == "Female") + age + educ + inc, data = gss)
## # weights:  28 (18 variable)
## initial  value 3331.265350 
## iter  10 value 3083.164064
## iter  20 value 2952.930124
## final  value 2939.423908 
## converged
Code 
print(displayMN(fit.full), digits = 3)
## $`Mostly by email`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)             -1.5832    0.14882 -10.638 0.00e+00 -1.8749 -1.2915
## I(sex == "Female")TRUE   0.0995    0.13066   0.761 4.46e-01 -0.1566  0.3556
## age                     -0.0292    0.00443  -6.586 4.51e-11 -0.0379 -0.0205
## educ                     0.3088    0.02775  11.130 0.00e+00  0.2544  0.3632
## inc25-50K                0.2457    0.17154   1.432 1.52e-01 -0.0905  0.5819
## inc>50K                  1.0577    0.16392   6.453 1.10e-10  0.7365  1.3790
## 
## $`Mostly face-to-face`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)             -0.5838    0.11236   -5.20 2.04e-07 -0.8040 -0.3636
## I(sex == "Female")TRUE   0.1241    0.11304    1.10 2.72e-01 -0.0974  0.3457
## age                      0.0191    0.00317    6.04 1.56e-09  0.0129  0.0253
## educ                     0.0552    0.02109    2.62 8.91e-03  0.0138  0.0965
## inc25-50K                0.3716    0.13525    2.75 6.01e-03  0.1065  0.6367
## inc>50K                  0.4397    0.14564    3.02 2.54e-03  0.1542  0.7251
## 
## $Both
##                        Estimate Std. Error z-value Pr(>|z|) lower95  upper95
## (Intercept)            -1.72080    0.14661  -11.74 0.00e+00 -2.0082 -1.43345
## I(sex == "Female")TRUE  0.28367    0.12009    2.36 1.82e-02  0.0483  0.51905
## age                    -0.00844    0.00377   -2.24 2.53e-02 -0.0158 -0.00104
## educ                    0.33062    0.02534   13.05 0.00e+00  0.2810  0.38029
## inc25-50K               0.82816    0.16279    5.09 3.63e-07  0.5091  1.14723
## inc>50K                 1.63750    0.15885   10.31 0.00e+00  1.3262  1.94885

You can read the results as if they are three separate logistic regression models, with the caveat that you are not comparing the nominal outcome, such as “email,” to its complement, “not email,” but rather to the common reference category, “neither.”

Rough summary of findings (focusing on stat. sig.), all else equal:

  1. for outcome email (relative to neither):
    • Older respondents are less likely to contact in this manner
    • More educated respondents are more likely to contact in this manner
    • Higher income respondents are more likely to contact in this manner
  2. for outcome face-to-face (relative to neither):
    • Older respondents are more likely to contact in this manner
    • More educated respondents are more likely to contact in this manner
    • Higher income respondents are more likely to contact in this manner
  3. for outcome both (relative to neither):
    • Females are more likely to contact in this manner
    • Older respondents are less likely to contact in this manner
    • More educated respondents are more likely to contact in this manner
    • Higher income respondents are more likely to contact in this manner

3.1.10 Relative odds ratio

  1. As in logit modeling, you might find that the coefficients lack clear interpretation, other than being positive or negative.
  2. However, when exponentiated, they reflect odds ratios, and these are multiplicative effects.
  3. Values greater than one are associated with greater odds (risk), and vice versa.
  4. Some texts refer to these as Relative Risk Ratios (RRRs), but we know that they are relative odds (ratios).

Here is the above table, for which estimates and confidence intervals are in terms of odds.

  • The table does not adjust s.e., z- or p-values; they are based on log-odds.
Code 
print(displayMN(fit.full, rrr = T), digits = 3)
## $`Mostly by email`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)               0.205    0.14882 -10.638 0.00e+00   0.153   0.275
## I(sex == "Female")TRUE    1.105    0.13066   0.761 4.46e-01   0.855   1.427
## age                       0.971    0.00443  -6.586 4.51e-11   0.963   0.980
## educ                      1.362    0.02775  11.130 0.00e+00   1.290   1.438
## inc25-50K                 1.279    0.17154   1.432 1.52e-01   0.913   1.789
## inc>50K                   2.880    0.16392   6.453 1.10e-10   2.089   3.971
## 
## $`Mostly face-to-face`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)               0.558    0.11236   -5.20 2.04e-07   0.448   0.695
## I(sex == "Female")TRUE    1.132    0.11304    1.10 2.72e-01   0.907   1.413
## age                       1.019    0.00317    6.04 1.56e-09   1.013   1.026
## educ                      1.057    0.02109    2.62 8.91e-03   1.014   1.101
## inc25-50K                 1.450    0.13525    2.75 6.01e-03   1.112   1.890
## inc>50K                   1.552    0.14564    3.02 2.54e-03   1.167   2.065
## 
## $Both
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)               0.179    0.14661  -11.74 0.00e+00   0.134   0.238
## I(sex == "Female")TRUE    1.328    0.12009    2.36 1.82e-02   1.049   1.680
## age                       0.992    0.00377   -2.24 2.53e-02   0.984   0.999
## educ                      1.392    0.02534   13.05 0.00e+00   1.324   1.463
## inc25-50K                 2.289    0.16279    5.09 3.63e-07   1.664   3.149
## inc>50K                   5.142    0.15885   10.31 0.00e+00   3.767   7.021

  • The reference group in all of these results is a male age 45 with 12 years of education and income < 25K.

  • The intercept is also more interpretable: for the reference group just mentioned, the relative odds of face-to-face is 0.6, so its probability is that fraction of the “neither” category’s.

  • Again, you need to know the probability of the neither category to deduce any other probability from the odds.

  • Interpreting the odds ratio for face-to-face contact, females are expected to have 13.2% greater odds of this method (odds with respect to “neither”) than males.

  • Interpreting the odds ratio for age, respondents in the population one year older than others, all else equal are expected to have 1.9% greater relative odds of using this method.

3.1.11 Predicting probabilities associated with different covariate patterns

To predict the probabilities of each category, we can use the post-estimation predict command:

Code 
head(predict(fit.full, type = "probs"))
##     Neither Mostly by email Mostly face-to-face       Both
## 1 0.2558265      0.24659442           0.1784756 0.31910341
## 2 0.1297616      0.27974428           0.1348249 0.45566917
## 3 0.3127636      0.19132388           0.2271968 0.26871575
## 4 0.5724270      0.01272941           0.3912813 0.02356234
## 5 0.5947183      0.04209615           0.3132954 0.04989015
## 6 0.2974463      0.16590487           0.2675552 0.26909366
  • These are probabilities of each record being one of the four categorical outcomes.
  • If we want to assign the most likely of the four, we can do this with the same command and a different option for type.

Below, we display the probabilities merged with the choice:

Code 
head(cbind(predict(fit.full, type = "probs"), prediction = predict(fit.full, type = "class")))
##     Neither Mostly by email Mostly face-to-face       Both prediction
## 1 0.2558265      0.24659442           0.1784756 0.31910341          4
## 2 0.1297616      0.27974428           0.1348249 0.45566917          4
## 3 0.3127636      0.19132388           0.2271968 0.26871575          1
## 4 0.5724270      0.01272941           0.3912813 0.02356234          1
## 5 0.5947183      0.04209615           0.3132954 0.04989015          1
## 6 0.2974463      0.16590487           0.2675552 0.26909366          1

The levels of the contact type are in the column order, so predicting a ‘4’ is equivalent to predicting “both.”

  1. We can compare these most likely category predictions to the actual response, in what is sometimes called the confusion matrix.
  2. It identifies the cases that are more or less well classified/predicted:
Code 
b <- apply(is.na(model.frame(~contact + sex + age + educ + inc, data = gss, na.action = "na.pass")), 1, sum) ==
    0
xt <- xtabs(~gss$contact[b] + predict(fit.full))
pctCorrect <- diag(xt)/apply(xt, 1, sum)
overallCorrect <- sum(diag(xt))/sum(xt)
print(xt, digits = 2)
##                      predict(fit.full)
## gss$contact[b]        Neither Mostly by email Mostly face-to-face Both
##   Neither                 422              12                 121  174
##   Mostly by email         131              30                  31  234
##   Mostly face-to-face     277               7                 153  163
##   Both                    134              18                  72  424
Code 
print(pctCorrect, digits = 2)
##             Neither     Mostly by email Mostly face-to-face                Both 
##                0.58                0.07                0.26                0.65
  • In this instance, we are able to classify 42.8% of the responses correctly, although there is some variability depending on the actual outcome.
  • This could be good or bad depending on the difficulty of the problem.
  • Some nominal outcomes are notoriously hard to predict, while others are not.
    • It depends on the subject domain and the number and quality of the predictor set.

Note that the percent correct in this instance is above chance. The best you could (by chance) do is guess the most frequent category all of the time. That category is “neither” and it is just a bit above 30%.

3.1.11.1 Exercise 3

Exercise: Explain how we seem to be doing better than chance. What would the ‘null’ model predict? 
Hint is visible here
  1. Let’s construct the probabilities of using the four forms of contact for a female, across a wide age range, 18 years of education, and with high income.
  2. We have to build an R data frame for these values.
    1. This table of probabilities (plotted) can be viewed as a set of competing risks that change as we look at individuals with different ages.
Code 
newdata <- data.frame(sex = "Female", age = 18:59 - 45, educ = 18 - 12, inc = ">50K")
probs <- predict(fit.full, newdata = newdata, type = "prob")
matplot(18:59, probs, type = "l", xlab = "age", ylab = "prob", col = c(2:4, 6), lty = c(1, 2, 3, 4), lwd = 3)
legend(50, 0.54, col = c(2:4, 6), lwd = 3, lty = c(1, 2, 3, 4), legend = colnames(probs), cex = 0.6, bty = "n")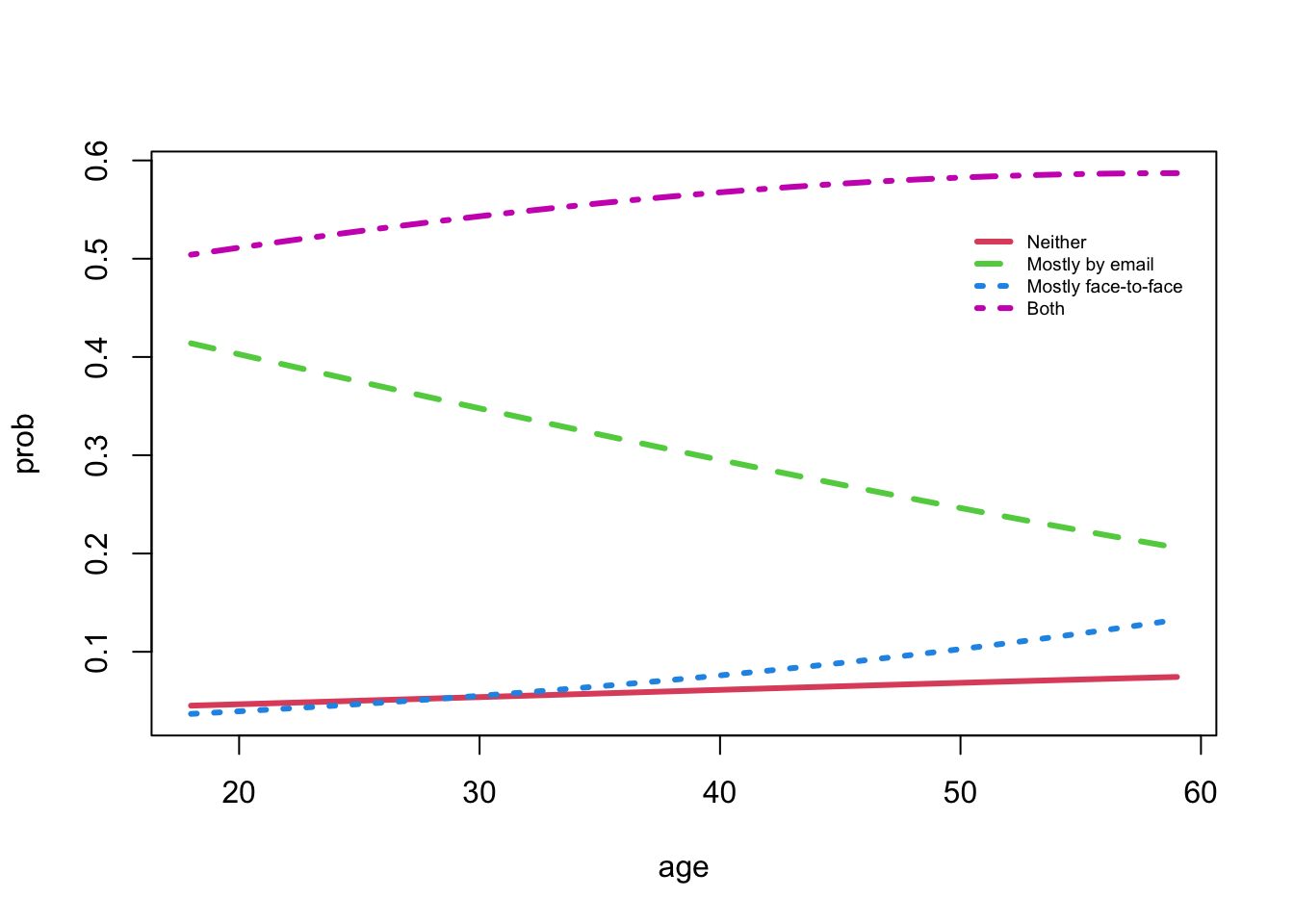

  • The two modes of contact (both and face-to-face) are expected to be larger for older respondents
  • However, email is decreasing with age.
  • What is not immediately apparent from the model fits is that the contact type “neither” shows a slightly increasing trend with age.
    • The probability of an omitted category can change over time as a by-product of the other contact type proportions.

Important takeaway messages:

  1. The model predicts probability of different nominal types.
    1. You can use it to assign the most likely type under a given scenario, but this masks the great uncertainty and variability in what happens in practice.
  2. The confusion matrix makes it fairly clear that a single prediction is only a part of the story.
    1. If we were to predict “fractional” occurrence of each nominal type, we might have a different picture of our predictive power. We do that now.
Code 
pred <- predict(fit.full, type = "prob")
actual <- model.matrix(~-1 + factor(gss$contact[b]))  # a way to code indicator vars
colnames(actual) <- sapply(strsplit(colnames(actual), ")"), "[", 2)
pctCorrect <- apply(pred * actual, 2, sum)/apply(actual, 2, sum)  #what does pred*actual do (think about the matrices)?
print(pctCorrect, digits = 2)
##             Neither     Mostly by email Mostly face-to-face                Both 
##                0.38                0.23                0.30                0.36
  • The fraction correct for each actual outcome is quite different using this ‘partial’ assignment to categories approach.
    • We do better with rarer categories, worse with more prevalent ones.
  • If we were to guess the outcome using a probabilistic draw from the predicted probabilities, we would be “wrong” more often.
    • In this example, our success rate drops to 33%.
    • This is more pronounced, clearly, when the predictive probabilities are far from 0 or 1.
    • This method reflects the uncertainty a bit better.

3.1.11.2 Exercise 4

Exercise: With a probabilistic approach to guessing, you can be wrong quite often. Can you think of real-world decision problems for which incorrect classification should be a rare or non-existent event? 
Hint is visible here

3.2 Ordinal Data

3.2.1 Ordinal Logit Model

Consider the outcome variable self-rated health:

4:    Excellent
3:    Good
2:    Fair
1:    Poor

There is a clear ordering with this outcome (better is larger in this case, and the variable type ordered enforces this). We examine its distribution now, but in reverse order, which will be helpful when we construct relative odds:

Code 
freq <- table(gss$health, useNA = "no")
percent <- round(100 * prop.table(freq), 2)
cumul <- cumsum(percent)
knitr::kable(cbind(freq, percent, cumul))
freq percent cumul
Poor 103 5.58 5.58
Fair 322 17.43 23.01
Very good 854 46.24 69.25
Excellent 568 30.75 100.00
  1. With ordinal data, a different form of relative odds is more appropriate.
    1. Rather than always compare to a reference level, we compare being below or at a threshold to being above it.
  2. We call these the odds of cumulative categories.

For health outcome \(Y\) with four levels (1,2,3,4), corresponding to the above descriptions, the three natural comparisons are: \[\begin{eqnarray*} \mbox{\em Comparison} & \mbox{\em Formula} & \mbox{\em odds} \\ \mbox{poor/fair+} & \frac{P(Y\leq 1)}{P(Y>1)} & 0.06 \\ \mbox{fair-/good+} & \frac{P(Y\leq 2)}{P(Y>2)} & 0.3 \\ \mbox{good-/excellent} & \frac{P(Y\leq 3)}{P(Y>3)} & 2.25 \end{eqnarray*}\]

  • We can say from these constructed odds that poor health is less common
    • This is because the odds are so low and there is nothing less than poor health.
  • However, the odds for good-/excellent reflect (poor, fair, or good) versus excellent.
    • So the larger odds simply implies that excellent health is not as common as the other three combined.
    • The reciprocal, 1/2.25=0.44, suggests that excellent health is somewhat common, because those odds correspond to the probability 0.31, and there’s nothing above this level of health.

3.2.2 Models based on odds of cumulative probabilities

It is possible to mimic the multinomial regression model, but use log-odds of cumulative probabilities as just described.

\[\begin{eqnarray*} \log\frac{P(Y\leq 1)}{P(Y>1)} & = & b_{10} + b_{11}X_1 + \cdots + b_{1p}X_p \\ \log\frac{P(Y\leq 2)}{P(Y>2)} & = & b_{20} + b_{21}X_1 + \cdots + b_{2p}X_p \\ \log\frac{P(Y\leq 3)}{P(Y>3)} & = & b_{30} + b_{31}X_1 + \cdots + b_{3p}X_p \end{eqnarray*}\]

For full generality, we allow each set of log-odds to have their own linear model. We will soon consider more restrictive models that exploit the ordinality more fully.

A simple model with no predictors should reproduce the relative odds just presented, as the intercepts \(b_{10},b_{20},b_{30}\) represent the log relative odds. These will be exponentiated separately to compare them to those constructed from the frequency table, above.

Code 
fit.ologit0 <- VGAM::vglm(factor(health) ~ 1, family = cumulative(parallel = FALSE, reverse = FALSE), data = gss)
summary(fit.ologit0)
## 
## Call:
## VGAM::vglm(formula = factor(health) ~ 1, family = cumulative(parallel = FALSE, 
##     reverse = FALSE), data = gss)
## 
## Coefficients: 
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1 -2.82921    0.09083  -31.15   <2e-16 ***
## (Intercept):2 -1.20773    0.04673  -25.84   <2e-16 ***
## (Intercept):3  0.81171    0.04696   17.29   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), logitlink(P[Y<=3])
## 
## Residual deviance: 4376.651 on 5538 degrees of freedom
## 
## Log-likelihood: -2188.325 on 5538 degrees of freedom
## 
## Number of Fisher scoring iterations: 1 
## 
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1'
Code 
interc <- exp(coef(fit.ologit0))
nms <- levels(gss$health)  #outcome nominal types          
names(interc) <- paste(nms[-length(nms)], nms[-1], sep = "|")
round(interc, 2)
##           Poor|Fair      Fair|Very good Very good|Excellent 
##                0.06                0.30                2.25
  • You can see that a bit of R code was needed to convert the three intercepts to recognizable odds, but it is possible.
  • We can think of the intercepts as implicitly setting cutoff points for a latent variable.
    • As that latent variable gets larger, the realized values of the ordinal outcome increase, crossing higher and higher thresholds.

Now we consider a model with a single predictor, sex. Again, there will be separate linear models for each odds, so the number of parameters is still identical to that for a multinomial logit model.

Code 
fit.ologit1.sex <- VGAM::vglm(factor(health) ~ I(sex == "Female"), family = cumulative(parallel = FALSE, reverse = FALSE),
    data = gss)
summary(fit.ologit1.sex)
## 
## Call:
## VGAM::vglm(formula = factor(health) ~ I(sex == "Female"), family = cumulative(parallel = FALSE, 
##     reverse = FALSE), data = gss)
## 
## Coefficients: 
##                          Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1            -2.87116    0.13847 -20.735   <2e-16 ***
## (Intercept):2            -1.27009    0.07168 -17.718   <2e-16 ***
## (Intercept):3             0.87826    0.07203  12.193   <2e-16 ***
## I(sex == "Female")TRUE:1  0.07442    0.18346   0.406    0.685    
## I(sex == "Female")TRUE:2  0.11080    0.09451   1.172    0.241    
## I(sex == "Female")TRUE:3 -0.11861    0.09496  -1.249    0.212    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), logitlink(P[Y<=3])
## 
## Residual deviance: 4372.975 on 5535 degrees of freedom
## 
## Log-likelihood: -2186.488 on 5535 degrees of freedom
## 
## Number of Fisher scoring iterations: 11 
## 
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1'
## 
## 
## Exponentiated coefficients:
## I(sex == "Female")TRUE:1 I(sex == "Female")TRUE:2 I(sex == "Female")TRUE:3 
##                1.0772599                1.1171686                0.8881551
  1. Given that all of the effects for sex are non-significant, we can easily argue that nothing is gained by having a different effect for each odds.
  2. We test this idea more formally beginning with a simpler model that assumes homogeneous effects of covariates regardless of the outcome on which the odds are based.
    1. This is called the proportional odds assumption.
    2. The name derives from the fact that all exponentiated effects are the same, up to a multiplicative constant that depends on the intercepts (the only thing allowed to vary).

\[\begin{eqnarray*} \log\frac{P(Y\leq 1)}{P(Y>1)} & = & b_{10} + b_{1}X_1 + \cdots + b_{p}X_p \\ \log\frac{P(Y\leq 2)}{P(Y>2)} & = & b_{20} + b_{1}X_1 + \cdots + b_{p}X_p \\ \log\frac{P(Y\leq 3)}{P(Y>3)} & = & b_{30} + b_{1}X_1 + \cdots + b_{p}X_p \end{eqnarray*}\]

Note the use of multiple intercepts.

If there are \(J\) ordinal categories, the more general form of the above is:

\[\begin{eqnarray*} \log\frac{P(Y\leq 1)}{P(Y>1)} & = & b_{10} + b_{1}X_1 + \cdots + b_{p}X_p \\ \log\frac{P(Y\leq 2)}{P(Y>2)} & = & b_{20} + b_{1}X_1 + \cdots + b_{p}X_p \\ & \cdots & \\ \log\frac{P(Y\leq (J-1))}{P(Y=J)} & = & b_{(J-1)0} + b_{1}X_1 + \cdots + b_{p}X_p \end{eqnarray*}\]

What’s different about this model?

  • The constants vary with the particular set of odds being modeled, as before, but now the effects for predictors are identical across the models.
  • This is parsimonious and thus preferred, as long as the homogeneity assumption is warranted.
  • We can check this with a likelihood ratio test.

The R polr function presents the results from this type of model a bit more cleanly, so we will use it for the proportional odds model fit.

Important note: polr inverts the sign of the covariate effects, so it fits this model: \[\begin{eqnarray*} \log\frac{P(Y\leq 1)}{P(Y>1)} & = & b_{10} - ( b_{1}X_1 + \cdots + b_{p}X_p ) \\ \log\frac{P(Y\leq 2)}{P(Y>2)} & = & b_{20} - ( b_{1}X_1 + \cdots + b_{p}X_p ) \\ & \cdots & \\ \log\frac{P(Y\leq (J-1))}{P(Y=J)} & = & b_{(J-1)0} - ( b_{1}X_1 + \cdots + b_{p}X_p ) \end{eqnarray*}\]

Code 
fit.ologit2.sex <- MASS::polr(health ~ I(sex == "Female"), data = gss)
summary(fit.ologit2.sex)
## 
## Re-fitting to get Hessian
## Call:
## MASS::polr(formula = health ~ I(sex == "Female"), data = gss)
## 
## Coefficients:
##                          Value Std. Error t value
## I(sex == "Female")TRUE 0.02082    0.08699  0.2393
## 
## Intercepts:
##                     Value    Std. Error t value 
## Poor|Fair            -2.8177   0.1122   -25.1232
## Fair|Very good       -1.1964   0.0729   -16.4122
## Very good|Excellent   0.8231   0.0695    11.8466
## 
## Residual Deviance: 4376.594 
## AIC: 4384.594 
## (918 observations deleted due to missingness)
  • One advantage to this function is the presentation of the intercept terms as reflecting cut point differences.
  • Beyond that, the advantages are limited.
  • The sign inversion suggests that positive effects are associated with more positive outcomes (whereas the odds in the equation are in terms of a more negative outcome)
  • We should test whether simplifying the model was warranted by comparing likelihoods.
  • This works better if we fit nested models using the same package, so we revert to vglm.
Code 
# refit using VGLM for LR comparisons
fit.ologit1b.sex <- VGAM::vglm(factor(health) ~ I(sex == "Female"), family = cumulative(parallel = TRUE, reverse = FALSE),
    data = gss)
anova(fit.ologit1b.sex, fit.ologit1.sex, type = "I")
## Analysis of Deviance Table
## 
## Model 1: factor(health) ~ I(sex == "Female")
## Model 2: factor(health) ~ I(sex == "Female")
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1      5537     4376.6                     
## 2      5535     4373.0  2   3.6185   0.1638
  • Models 1 and 2 look the same, but they are not.
    • The anova comparison function does not list all of the model fit parameters, and one model allowed the effect for sex to vary across different outcome odds.
  • The p-value is large enough that we do not reject the null hypothesis that the additional parameters are (jointly) zero.
    • In simpler terms, the simpler model fits well.

3.2.3 Multivariate models:

Now we fit a model with the same predictors as we used for the contact outcome. We first assume proportional odds:

Code 
fit.ologit3.full <- MASS::polr(health ~ I(sex == "Female") + age + educ + inc, data = gss)
summary(fit.ologit3.full)
## 
## Re-fitting to get Hessian
## Call:
## MASS::polr(formula = health ~ I(sex == "Female") + age + educ + 
##     inc, data = gss)
## 
## Coefficients:
##                          Value Std. Error t value
## I(sex == "Female")TRUE  0.1192   0.093824   1.270
## age                    -0.0194   0.002779  -6.982
## educ                    0.1325   0.017921   7.394
## inc25-50K               0.4662   0.123070   3.788
## inc>50K                 0.9671   0.121412   7.965
## 
## Intercepts:
##                     Value    Std. Error t value 
## Poor|Fair            -2.3131   0.1335   -17.3243
## Fair|Very good       -0.5567   0.1024    -5.4349
## Very good|Excellent   1.6597   0.1102    15.0665
## 
## Residual Deviance: 3661.714 
## AIC: 3677.714 
## (1124 observations deleted due to missingness)
  1. Focusing first on the intercepts, they are in log-odds units and increase as we move from smaller to larger ordinal outcomes.
    1. In fact, they are listed as cutpoints between two adjacent ordinal levels.
    2. This reflects the latent variable framework of binary, multinomial and ordinal logistic regression.
    3. The effect for sex has a small t-value, reflecting a lack of significance.
    4. However, age, education and income have positive, and highly significant effects (\(t \geq \tilde{}\,4\)).
      1. If we exponentiate the educ effect we get 1.142 which suggests 14.2% larger odds (of a more possitve response) when comparing two populations who differ by one unit of education and are otherwise identical.
      2. The indicators for income are always interpreted with respect to the reference group, so the exponentiated value, 2.63 translates to 163% larger odds when comparing two populations differing only in income, >50K versus <25K.
  2. A big advantage of the proportional odds assumption is that it allows us to make the above statements for any cumulative odds.
    1. It holds when comparing poor to not poor, at most fair to at least good, etc. (or their inverses)
    2. This is quite different from the types of statements we can make with multinomial logit models, whose odds are constructed always with respect to the same reference group.
    3. As well, it is much harder to imagine a framework for simplifying multinomial models as we can in the ordinal case with proportional odds.

If we are careful with notation, we can write this type of model (positive form) in one line, incorporating some of the notation that we use for binary and multinomial logit models:

\[ \log\frac{P(Y\leq j)}{P(Y>j)} = b_{j0} + b_{1}X_1 + \cdots + b_{p}X_p, \ \mbox{ for all } 1\leq j<J \]

  • If we have \(J\) categories, we have \(J-1\) such equations.
  • They are different only by the constant terms \(b_{j0}\) (\(j=1,\ldots,J-1\)), and they share the same values of log-odds ratios, \(b_1, b_2,\ldots,b_p\).

3.2.3.1 Exercise 5

Exercise: Discuss which part is similar to binary logistic modeling? Which part is similar to multinomial logistic modeling? 
Hint is visible here
  • The proportional odds model is referred to as the Ordinal Logit Regression model.

3.2.4 Testing the Proportional Odds Assumption

The hypothesis to test (sometimes called the Brant test of parallel regression):

  • \(H_0\): Proportional odds assumption is satisfied.
  • \(H_a\): Proportional odds assumption unsatisfied (for at least one predictor)

We use the R the vglm package, which by having a parallel assumption parameter as part of the model specification, makes it easy to test this assumption with a likelihood ratio test.

We will do so for our more complicated multivariate model by refitting it in vglm with and without the parallel regressions parameter set to TRUE.

Code 
fit.paraFALSE.full <- VGAM::vglm(factor(health) ~ I(sex == "Female") + age + educ + inc, family = cumulative(parallel = FALSE,
    reverse = FALSE), data = gss)
fit.paraTRUE.full <- VGAM::vglm(factor(health) ~ I(sex == "Female") + age + educ + inc, family = cumulative(parallel = TRUE,
    reverse = FALSE), data = gss)
anova(fit.paraTRUE.full, fit.paraFALSE.full, type = "I")
## Analysis of Deviance Table
## 
## Model 1: factor(health) ~ I(sex == "Female") + age + educ + inc
## Model 2: factor(health) ~ I(sex == "Female") + age + educ + inc
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1      4915     3661.7                     
## 2      4905     3714.4 10  -52.676
  • With a negative change in deviance, we cannot perform the test.
  • The root of the problem is likely a form of “separation” known as the Hauck-Donner effect, and there is a warning in the full summary.
  • We will assume that were we able to compute a likelihood, we would reject the null.
  • Notice that there were 10 degrees of freedom in the test. Can you enumerate the extra parameters estimated?

We should examine the more complex model and determine where the Proportional Odds assumption is “failing.”

Code 
summary(fit.paraFALSE.full)
## 
## Call:
## VGAM::vglm(formula = factor(health) ~ I(sex == "Female") + age + 
##     educ + inc, family = cumulative(parallel = FALSE, reverse = FALSE), 
##     data = gss)
## 
## Coefficients: 
##                           Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1            -2.329171   0.105434 -22.091  < 2e-16 ***
## (Intercept):2            -0.854729   0.056790 -15.051  < 2e-16 ***
## (Intercept):3             1.081064   0.108390   9.974  < 2e-16 ***
## I(sex == "Female")TRUE:1 -0.108063   0.059383      NA       NA    
## I(sex == "Female")TRUE:2  0.111948   0.032840   3.409 0.000652 ***
## I(sex == "Female")TRUE:3 -0.202858   0.100535  -2.018 0.043614 *  
## age:1                     0.022922   0.003959   5.790 7.02e-09 ***
## age:2                     0.007846   0.002189   3.585 0.000337 ***
## age:3                     0.005885   0.002962   1.987 0.046928 *  
## educ:1                   -0.105071   0.013836  -7.594 3.10e-14 ***
## educ:2                   -0.037159   0.008323  -4.465 8.02e-06 ***
## educ:3                   -0.061648   0.018704  -3.296 0.000981 ***
## inc25-50K:1              -0.628189   0.233629  -2.689 0.007170 ** 
## inc25-50K:2              -0.275337   0.112639  -2.444 0.014508 *  
## inc25-50K:3              -0.035889   0.130777  -0.274 0.783756    
## inc>50K:1                -0.273075   0.059074  -4.623 3.79e-06 ***
## inc>50K:2                -0.744371   0.031303 -23.780  < 2e-16 ***
## inc>50K:3                -0.241132   0.126087  -1.912 0.055821 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), logitlink(P[Y<=3])
## 
## Residual deviance: 3714.391 on 4905 degrees of freedom
## 
## Log-likelihood: -1857.195 on 4905 degrees of freedom
## 
## Number of Fisher scoring iterations: 2 
## 
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1', 'I(sex == "Female")TRUE:1', 'I(sex == "Female")TRUE:2', 'age:2', 'educ:2', 'inc>50K:1'
## 
## 
## Exponentiated coefficients:
## I(sex == "Female")TRUE:1 I(sex == "Female")TRUE:2 I(sex == "Female")TRUE:3                    age:1 
##                0.8975711                1.1184547                0.8163945                1.0231867 
##                    age:2                    age:3                   educ:1                   educ:2 
##                1.0078773                1.0059023                0.9002602                0.9635230 
##                   educ:3              inc25-50K:1              inc25-50K:2              inc25-50K:3 
##                0.9402135                0.5335571                0.7593164                0.9647475 
##                inc>50K:1                inc>50K:2                inc>50K:3 
##                0.7610358                0.4750329                0.7857378
  • Age, sex and education are plausibly homogeneous across (log) cumulative odds.
  • Clearly income does not meet the proportionality assumption, although we need to test this more rigorously.

We can fit the model with non-parallel regression coefficients for a subset of predictors using the syntax:

Code 
fit.paraFALSEinc.full <- VGAM::vglm(factor(health) ~ I(sex == "Female") + age + educ + inc, family = cumulative(parallel = FALSE ~
    inc, reverse = FALSE), data = gss)
summary(fit.paraFALSEinc.full)
## 
## Call:
## VGAM::vglm(formula = factor(health) ~ I(sex == "Female") + age + 
##     educ + inc, family = cumulative(parallel = FALSE ~ inc, reverse = FALSE), 
##     data = gss)
## 
## Coefficients: 
##                         Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1          -2.115880   0.132511 -15.968  < 2e-16 ***
## (Intercept):2          -0.478457   0.088784  -5.389 7.08e-08 ***
## (Intercept):3           1.470265   0.110492  13.307  < 2e-16 ***
## I(sex == "Female")TRUE -0.120326   0.070930  -1.696 0.089807 .  
## age                     0.018441   0.002035   9.063  < 2e-16 ***
## educ                   -0.130380   0.013069  -9.976  < 2e-16 ***
## inc25-50K:1            -0.917550   0.257303  -3.566 0.000362 ***
## inc25-50K:2            -0.467087   0.126014  -3.707 0.000210 ***
## inc25-50K:3            -0.322201   0.139749  -2.306 0.021135 *  
## inc>50K:1              -1.503979   0.292200  -5.147 2.65e-07 ***
## inc>50K:2              -1.363339   0.143007  -9.533  < 2e-16 ***
## inc>50K:3              -0.690831   0.131509  -5.253 1.50e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), logitlink(P[Y<=3])
## 
## Residual deviance: 3642.151 on 4911 degrees of freedom
## 
## Log-likelihood: -1821.075 on 4911 degrees of freedom
## 
## Number of Fisher scoring iterations: 14 
## 
## No Hauck-Donner effect found in any of the estimates
## 
## 
## Exponentiated coefficients:
## I(sex == "Female")TRUE                    age                   educ            inc25-50K:1 
##              0.8866310              1.0186124              0.8777622              0.3994967 
##            inc25-50K:2            inc25-50K:3              inc>50K:1              inc>50K:2 
##              0.6268255              0.7245523              0.2222440              0.2558051 
##              inc>50K:3 
##              0.5011596

and we can test this partial Proportional Odds model against the full Proportional Odds or non-parallel (fully general) models:

Code 
print(aov1 <- anova(fit.paraTRUE.full, fit.paraFALSEinc.full, type = "I"))
## Analysis of Deviance Table
## 
## Model 1: factor(health) ~ I(sex == "Female") + age + educ + inc
## Model 2: factor(health) ~ I(sex == "Female") + age + educ + inc
##   Resid. Df Resid. Dev Df Deviance  Pr(>Chi)    
## 1      4915     3661.7                          
## 2      4911     3642.2  4   19.563 0.0006089 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Code 
print(aov2 <- anova(fit.paraFALSEinc.full, fit.paraFALSE.full, type = "I"))
## Analysis of Deviance Table
## 
## Model 1: factor(health) ~ I(sex == "Female") + age + educ + inc
## Model 2: factor(health) ~ I(sex == "Female") + age + educ + inc
##   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1      4911     3642.2                     
## 2      4905     3714.4  6   -72.24
  • The first likelihood ratio test compares a standard ordinal logit model (proportional odds assumed) against the partial proportional odds model in which income effects vary depending on the cumulative odds being compared.
    • We can conclude that the more complex model is preferred, \(p=\) 0.
  • The second likelihood ratio test compares the partial proportional odds model (income effects vary) with the fully general model for which all effects vary depending on the cumulative odds being compared (non-parallel assumption).
    • We are missing on the likelihood for this model as well, but we will conclude that the more complex model is not warranted.
  • Another way to state these findings is that the partial proportional odds model is sufficiently complex to represent the relationships in these data, under the model framework.

3.2.5 Brant test

  1. The Brant test is an alternative to the above likelihood ratio test that works well with the polr function.
  2. Separate models, with and without the proportional odds assumption, are fit for each predictor of interest in the model.
    1. The only caveat is that you have to fit the model with polr and you cannot use complicated formulas.
      1. E.g., we have to include sex in its original form, not as a factor.
Code 
refit.ologit3.full <- MASS::polr(health ~ sex + age + educ + inc, data = gss)
brant::brant(refit.ologit3.full, by.var = TRUE)
## -------------------------------------------- 
## Test for X2  df  probability 
## -------------------------------------------- 
## Omnibus      31.09   10  0
## sex      3.07    2   0.22
## age      5.68    2   0.06
## educ     1.04    2   0.59
## inc      16.94   4   0
## -------------------------------------------- 
## 
## H0: Parallel Regression Assumption holds
  • The results suggest that income does not follow proportional odds assumption.
  • This is consistent with our intuition, reading the coefficients, and it will be seen in the plots from the non-parallel ordinal regression model (to follow).
  • Note the omnibus test is the one that didn’t quite work for us using the vglm program.
  • The Brant test provides predictor-by-predictor recommendations as well.

3.2.6 Recovering probabilities from an ologit model

  1. Just as with the multinomial logit model, it is possible to transform a set of log cumulative odds into probabilities.
    1. Recall that each log cumulative odds, is a logit of a specific probability: \[ \log\frac{P(Y\leq j)}{P(Y>j)} = \mbox{logit}(P(Y\in\{1,\ldots,j\}))=\mu \] For some predicted value \(\mu\) given a covariate pattern \(X\).
  2. Our goal is to recover \(p_j=P(Y=j)\) for all \(1\leq j \leq J\).

We have a convenient expression for the inverse logit, or expit function, so that: \[ \mbox{if logit}(P(Y\in\{1,\ldots,j\})) = \mu \ \ \mbox{then }P(Y\in\{1,\ldots,j\})=\frac{e^\mu}{1+e^\mu} \] Once we note that \(P(Y\in\{1,\ldots,j\}) = \sum_{k\leq j} p_k\), and \(p_J=1-p_{(J-1)}\), then we can recover each probability in a cascading fashion.

Code 
newdata <- data.frame(id = rep(1:3, each = 42), sex = "Female", age = rep(18:59 - 45, times = 3), educ = 18 - 12,
    inc = rep(c("<25K", "25-50K", ">50K"), each = 42))
probs <- predict(fit.paraFALSEinc.full, newdata = newdata, type = "response")
probs <- probs %>%
    reshape2::melt(varnames = c("id", "outcome")) %>%
    mutate(prob = value) %>%
    dplyr::select(-id)
plotdata <- as_tibble(cbind(newdata %>%
    mutate(inc = ordered(inc, levels = c("<25K", "25-50K", ">50K"))), probs)) %>%
    rename(income = inc) %>%
    mutate(age = age + 45, educ = educ + 12) %>%
    mutate(id = rep(1:12, each = 42))  # id nec. for gplot, and will look nicer
ggplot(data = plotdata, aes(x = age, y = prob, group = id, color = outcome, linetype = income)) + geom_line()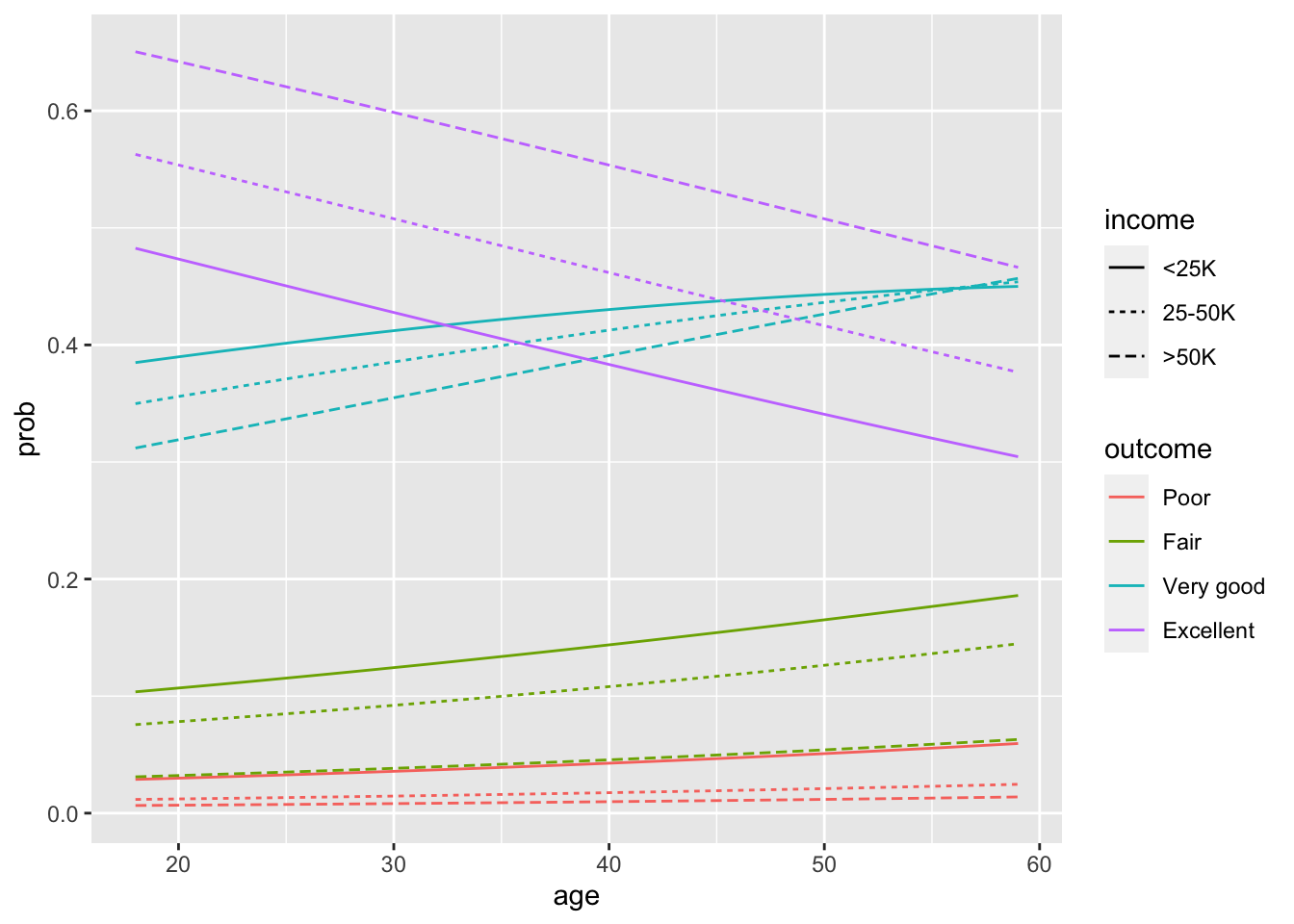

  • The lack of proportionality across income levels is hard to detect in this plot
    • This is because the transformation from odds to probabilities obscures it.
  • However, we would not expect lines to cross within an outcome type in a proportionate odds model.
    • We have some evidence of this with the “very good” outcome.

We contrast this now to a model that enforces proportionality across outcome types.

Code 
newdata <- data.frame(id = rep(1:3, each = 42), sex = "Female", age = rep(18:59 - 45, times = 3), educ = 18 - 12,
    inc = rep(c("<25K", "25-50K", ">50K"), each = 42))
probs <- predict(fit.paraTRUE.full, newdata = newdata, type = "response")
probs <- probs %>%
    reshape2::melt(varnames = c("id", "outcome")) %>%
    mutate(prob = value) %>%
    dplyr::select(-id)
plotdata <- as_tibble(cbind(newdata %>%
    mutate(inc = ordered(inc, levels = c("<25K", "25-50K", ">50K"))), probs)) %>%
    rename(income = inc) %>%
    mutate(age = age + 45, educ = educ + 12) %>%
    mutate(id = rep(1:12, each = 42))  # id nec. for gplot, and will look nicer
ggplot(data = plotdata, aes(x = age, y = prob, group = id, color = outcome, linetype = income)) + geom_line()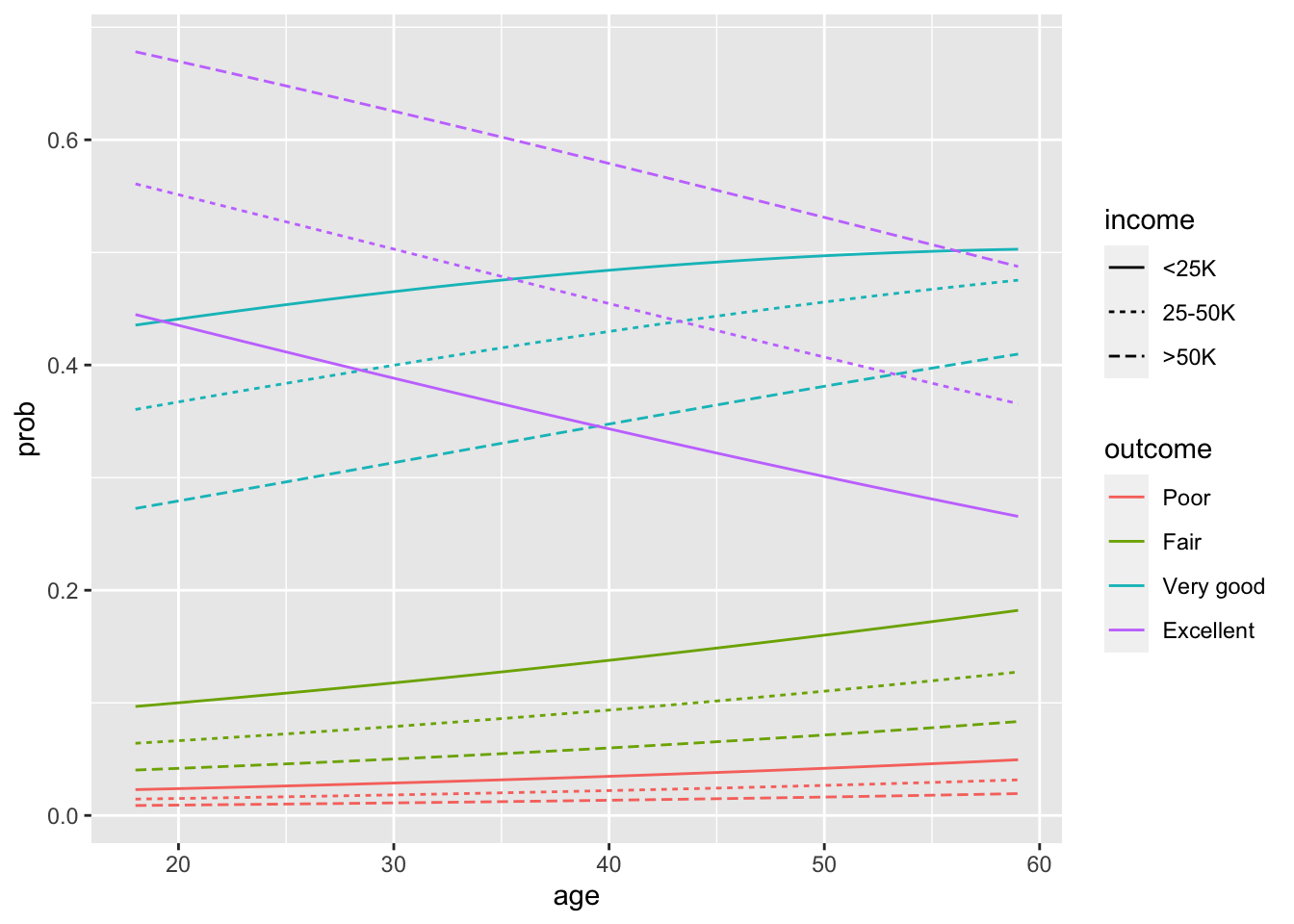

The main difference with this plot is that no lines cross within outcome.

3.3 Appendix

3.4 Coding

  1. dplyr basic functions
  2. %in%
  3. multinom()
  4. apply()
  5. cumsum
  6. vglm()
  • dplyr is a grammar of data manipulation to transform and to summarize dataframe. The library consists of many functions that perform common data manipulation operations. It is one of the core packages of the tidyverse in the R.
# The easiest way to get dplyr is to install the whole tidyverse:
install.packages("tidyverse")

# Alternatively, install just dplyr:
install.packages("dplyr")

  • %>% is a pipe operator which allows you ti pipe the output from one function to the input of another function.

    • filter() is a function to filter rows. You can use the boolean operators (e.g. >, <, >=, <=, !=, %in%) to create the logical tests.

    • select() is a function to select columns

    • arrange() is a function to arrange (re-order) rows by a particular column

    • mutate() is a function to create (to add) new columns

    • summarise() is a function to summarise values or a summary statistics for a given column

    • group_by() is a function that split & apply a function to the individual data frame.

    • case_when()is a function allows to add multiple if_else() statements.

    • rename() is a function to change the name of individual variable.

    • Cheat sheets for dplyr

    • %in% is a operator in R which can be used to identify if an element belongs to a dataframe.

Code 
data("toenail", package = "HSAUR2")
samp <- sample(unique(toenail$patientID), 15)
# filtering out the data if patientID is in 'samp' dataset
toesamp <- toenail %>%
    filter(patientID %in% samp)
head(toesamp)

  • multinom() is a function to fit multinomial log-linear model with nnet library. It has arguments as follows:

    • formula: a formula expression as for regression models, of the form response ~ predictors. The response should be a factor or a matrix with K columns, which will be interpreted as counts for each of K classes. A log-linear model is fitted, with coefficients zero for the first class. An offset can be included: it should be a numeric matrix with K columns if the response is either a matrix with K columns or a factor with K >= 2 classes, or a numeric vector for a response factor with 2 levels.

    • data: an optional data frame

    • weights: optional case weights in fitting

    • Hess: logical for whether the Hessian (the observed/expected information matrix) should be returned.

Code 
# fit multinomial log-linear model
fit.full <- nnet::multinom(contact ~ I(sex == "Female") + age + educ + inc, data = gss)
## # weights:  28 (18 variable)
## initial  value 3331.265350 
## iter  10 value 3083.164064
## iter  20 value 2952.930124
## final  value 2939.423908 
## converged
Code 
print(displayMN(fit.full), digits = 3)
## $`Mostly by email`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)             -1.5832    0.14882 -10.638 0.00e+00 -1.8749 -1.2915
## I(sex == "Female")TRUE   0.0995    0.13066   0.761 4.46e-01 -0.1566  0.3556
## age                     -0.0292    0.00443  -6.586 4.51e-11 -0.0379 -0.0205
## educ                     0.3088    0.02775  11.130 0.00e+00  0.2544  0.3632
## inc25-50K                0.2457    0.17154   1.432 1.52e-01 -0.0905  0.5819
## inc>50K                  1.0577    0.16392   6.453 1.10e-10  0.7365  1.3790
## 
## $`Mostly face-to-face`
##                        Estimate Std. Error z-value Pr(>|z|) lower95 upper95
## (Intercept)             -0.5838    0.11236   -5.20 2.04e-07 -0.8040 -0.3636
## I(sex == "Female")TRUE   0.1241    0.11304    1.10 2.72e-01 -0.0974  0.3457
## age                      0.0191    0.00317    6.04 1.56e-09  0.0129  0.0253
## educ                     0.0552    0.02109    2.62 8.91e-03  0.0138  0.0965
## inc25-50K                0.3716    0.13525    2.75 6.01e-03  0.1065  0.6367
## inc>50K                  0.4397    0.14564    3.02 2.54e-03  0.1542  0.7251
## 
## $Both
##                        Estimate Std. Error z-value Pr(>|z|) lower95  upper95
## (Intercept)            -1.72080    0.14661  -11.74 0.00e+00 -2.0082 -1.43345
## I(sex == "Female")TRUE  0.28367    0.12009    2.36 1.82e-02  0.0483  0.51905
## age                    -0.00844    0.00377   -2.24 2.53e-02 -0.0158 -0.00104
## educ                    0.33062    0.02534   13.05 0.00e+00  0.2810  0.38029
## inc25-50K               0.82816    0.16279    5.09 3.63e-07  0.5091  1.14723
## inc>50K                 1.63750    0.15885   10.31 0.00e+00  1.3262  1.94885

  • apply() is a function to apply a function across data frame.

    • x: an array of matrix

    • margin: define where to apply the function; 1=rows, 2=columns

    • FUN: a function that will be applied

Code 
b <- apply(is.na(model.frame(~contact + sex + age + educ + inc, data = gss, na.action = "na.pass")), 1, sum) ==
    0
xt <- xtabs(~gss$contact[b] + predict(fit.full))
pctCorrect <- diag(xt)/apply(xt, 1, sum)
overallCorrect <- sum(diag(xt))/sum(xt)
print(xt, digits = 2)
##                      predict(fit.full)
## gss$contact[b]        Neither Mostly by email Mostly face-to-face Both
##   Neither                 422              12                 121  174
##   Mostly by email         131              30                  31  234
##   Mostly face-to-face     277               7                 153  163
##   Both                    134              18                  72  424
Code 
print(pctCorrect, digits = 2)
##             Neither     Mostly by email Mostly face-to-face                Both 
##                0.58                0.07                0.26                0.65

  • cumsum is a function that returns a vector whose elements are the cumulative sum.

    • x: a numeric object
Code 
freq <- table(gss$health, useNA = "no")
percent <- round(100 * prop.table(freq), 2)
cumul <- cumsum(percent)
cumul
##      Poor      Fair Very good Excellent 
##      5.58     23.01     69.25    100.00

  • vglm() is a function fits vector generalized linear models (VGLMs) from VGAM library. It has arguments as follows:

    • formula: a symbolic description of the model to be fit

    • family: a function of class describing what statistical model is to be fitted.

    • data: an optional data frame containing the variables in the model

Code 
fit.ologit1.sex <- VGAM::vglm(factor(health) ~ I(sex == "Female"), family = cumulative(parallel = FALSE, reverse = FALSE),
    data = gss)
summary(fit.ologit1.sex)
## 
## Call:
## VGAM::vglm(formula = factor(health) ~ I(sex == "Female"), family = cumulative(parallel = FALSE, 
##     reverse = FALSE), data = gss)
## 
## Coefficients: 
##                          Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1            -2.87116    0.13847 -20.735   <2e-16 ***
## (Intercept):2            -1.27009    0.07168 -17.718   <2e-16 ***
## (Intercept):3             0.87826    0.07203  12.193   <2e-16 ***
## I(sex == "Female")TRUE:1  0.07442    0.18346   0.406    0.685    
## I(sex == "Female")TRUE:2  0.11080    0.09451   1.172    0.241    
## I(sex == "Female")TRUE:3 -0.11861    0.09496  -1.249    0.212    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), logitlink(P[Y<=3])
## 
## Residual deviance: 4372.975 on 5535 degrees of freedom
## 
## Log-likelihood: -2186.488 on 5535 degrees of freedom
## 
## Number of Fisher scoring iterations: 11 
## 
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1'
## 
## 
## Exponentiated coefficients:
## I(sex == "Female")TRUE:1 I(sex == "Female")TRUE:2 I(sex == "Female")TRUE:3 
##                1.0772599                1.1171686                0.8881551

3.5 Exercise & Quiz

3.5.1 Quiz: Exercise

  • Use “Quiz-W3: Exercise” to submit your answers.

    1. Consider some other multinomial outcomes and discuss whether they are truly nominal categories.(link to exercise 1)

    2. using the multinomial coefficients for contact (above, with female as the predictor), find the probability of “both” for males and females. (link to exercise 2)

    3. Explain how we seem to be doing better than chance. What would the ‘null’ model predict? (link to exercise 3)

    4. With a probabilistic approach to guessing, you can be wrong quite often. Can you think of real-world decision problems for which incorrect classification should be a rare or non-existent event? (link to exercise 4)

    5. Discuss which part is similar to binary logistic modeling? Which part is similar to multinomial logistic modeling? (link to exercise 5)

3.5.2 Quiz: R Shiny

[Modified Odds]

  1. Calculate the odds of each category, using “neither” as the reference group.

[Relative odds ratios]

  1. Exponentiate the coefficients on the multinomial regression model you fit above, which has been loaded for you as contact_mlogit.sex.

  2. Run a multinomial logit regression of contact mode preference on sex, age, education, and income.

  3. Select all that applies. Which of the following are true? Assume all other predictors are held constant. You may use the pre-loaded displayMN function provided in Handout 3 to view RRRs (need to set rrr=T).

[Marginal probability]

  1. Making predictions is just as straightforward under multinomial logistic regression as it is under any GLM. Use the predict function on the contact_mlogit model to predict the preferred contact method for each person in the data.

  2. Based on the predicted probabilities from Q5, which is the most common contact mode preference?

[Cumulative Odds]

  1. Compute the cumulative probability for each value of health using the gss dataset. What are the cumulative probability / cumulative odd of reporting “very good” health or worse?

[Ordinal logistic regression]

  1. What is the predicted probability of being in excellent health for a 30-year-old white man with only a high school diploma?

  2. Among 30-year-old black women, what is the change in probability of being in very good health associated with having a bachelor’s degree compared to only a high school diploma?

Testing the proportional odds assumption

  1. Perform the likelihood ratio test manually by extracting the log-likelihoods of the models nonproportional_odds and proportional_odds, calculating the appropriate test statistic, and computing the p-value using the pchisq function with the appropriate degrees of freedom. Select the p-value.

[Partial proportional odds]

  1. Perform a likelihood ratio test and print out the p-value

3.5.3 Quiz: Chapter

  • Use “Quiz-W3: Chapter” to submit your answers.

    1. Compute odds for each outcomes. Select ALL correct options.

    2. Compute probabilities from odds. Select ALL correct options.

    3. Compute the odds ratio for each variable. Please select ALL correct options. (You can either use calculator or R)

    4. Select FALSE description about Information Criteria (IC)

    5. Using the table result, what is the odds for “Excellent” health outcome for males (sex==“Male”) with lowest income level (<25K)?

    6. Using the table result, what is P(excellent) for males (sex==“Male”) with lowest income level (<25K)?