Chapter 2 Chapter 2: GLM for Binomial Family
2.1 Binomial Family
When the outcome is binary, the natural distribution to use is the binomial.
Here are some examples of binary outcomes:
- Intrinsic binary outcomes: have lung cancer or not
- Self-reported categories: identify as conservative or not
- Incomplete or partial information: baby weight less than 2,500 grams or not.
- If actual weight unknown, might not be appropriate to lump with “not less than 2,500g”
By convention, denote the value “success” (or have trait) as 1, “failure” as 0.
2.1.1 Binary data can come in grouped format
- Disease prevalence rate: percentage of the population with disease.
- Note this is different from incidence rate, which is the new case rate.
- Smoking rate per school: percentage of kids who smoke in a given school
In cases such as these, the dependent variable(s) is either a percent or the number of successes out of the total number of subjects. While this seems like it is “almost continuous,” control your urge to model this type of variable using linear regression! We will talk about modeling this type of data later.
2.1.2 Applications of Binary Outcome Regressions
- Understand the roles of risk factors/predictors for binary outcomes.
- Can be applied to case/control studies to evaluate the associations of outcomes with risk factors.
- Odds ratio has some nice features.
- Can be used to build Propensity Score to estimate the probability of being assigned treatment status, P(Z=1\(\vert\)X). Use of propensity scores is important in causal inference.
- Classification models and Neural Networks can also be built upon logistic regressions.
2.1.3 Binomial Distribution Review (some math first!)
- The Binomial distribution characterizes the probability of \(Y=y\) successes out of \(N\) trials given probability of success being \(p\):
\[ P(Y=y|p) = {N \choose y} p^{y}(1-p)^{N-y} \]
2.1.3.1 Exercise 1
Hint is visible hereThe probability of observing 3 smokers out of 10 students given p=0.05 is quite small. The expected value is \(Np\) or 0.5 (literally half a student), so 3 is large compared to the mean.
- For binary outcome \(Y\), we can think this as the special case when \(N=1\):
\[
P(Y=y|p) = p^{y}(1-p)^{1-y}
\]
We call this a Bernoulli distribution (or a Bernoulli trial). If we call the distribution binom and do not specify the number of trials, you can assume it is 1 trial, or Bernoulli.
2.2 (Binomial) Logistic Regression
2.2.1 MLE and Link Function for Logistic Regression
- We are interested in estimating/predicting the probability of success, \(p=P(Y=1)\) as it varies across individuals with different characteristics \(X\).
- This is the regression framework - we just wish to “regress” on the probability of success rather than on the outcome itself.
- Since we cannot observe this success rate directly, we are regressing on a latent (unobserved) variable. We do this often in GLMs.
- The GLM components for logistic regression are:
- \(Y_i \sim \mbox{binom}(p_i)\) with \(p_i=E(Y_i|X_i)\), the mean, which will be linearly modeled.
- \(\eta_i = X_i\beta\)
- \(g(p_i) = \log\left(\frac{p_i}{1-p_i}\right)=\eta_i\), thus \(p_i=g^{-1}(\eta_i)=\left(\frac{\exp(\eta_i)}{1+\exp(\eta_i)}\right)\).
This yields a likelihood for a sample \(Y=(Y_1,Y_2,\ldots,Y_n)'\):
\[ L(\beta|Y,X) = \prod_{i=1}^{n}{ p_i^{Y_i}(1-p_i)^{1-Y_i}}=\prod_{i=1}^{n}{ g^{-1}(X_i\beta)^{Y_i}(1-g^{-1}(X_i\beta))^{1-Y_i}} \] The goal is to find the set of \(\beta\) values so that \(g^{-1}(X_i\beta)\) best predicts the probability of success for each observation, or that the observed outcomes are the most likely to occur for those parameters. This is Maximum Likelihood Estimation (MLE).
- There are three “popular” link functions that allow us to relate \(X_i\) to \(p_i\), the probability of the success.
- logit: \(\log\left(\frac{p_i}{1-p_i}\right)=\eta_i=X_i\beta\)
- \(\beta\) has a log-odds interpretation
- Probit: \(\Phi^{-1}(p_i)=\eta_i = X_i\beta\), where \(\Phi(\cdot)\) is the cumulative normal distribution
- \(\beta\) can be interpreted as the effect on normally distributed latent utility
- Complementary log-log: \(\log(-\log (1-p_i))=\eta_i=X_i\beta\)
- \(\beta\) has a hazard ratio interpretation (and proportional odds assumption) in the context of survival data.
- logit: \(\log\left(\frac{p_i}{1-p_i}\right)=\eta_i=X_i\beta\)
- In practice, researchers may choose a particular link function based on the interpretation that applies to that substantive domain.
- If you care about prediction, one link function may fit the data better than the others.
- Major differences are in the tails (matters more for rare events)
Code
p_i <- seq(0, 1, length = 1001)
logit <- function(x) log(x/(1 - x))
probit <- function(x) qnorm(x)
cloglog <- function(x) log(-log(1 - x))
df1 <- data.frame(p_i = p_i, xform_value = logit(p_i), xform_name = "logit")
df2 <- data.frame(p_i = p_i, xform_value = probit(p_i), xform_name = "probit")
df3 <- data.frame(p_i = p_i, xform_value = cloglog(p_i), xform_name = "cloglog")
df <- rbind(df1, df2, df3)
ggplot(df, aes(x = p_i, y = xform_value, color = xform_name)) + geom_line(aes(linetype = xform_name)) + ggtitle("Comparison of different link functions")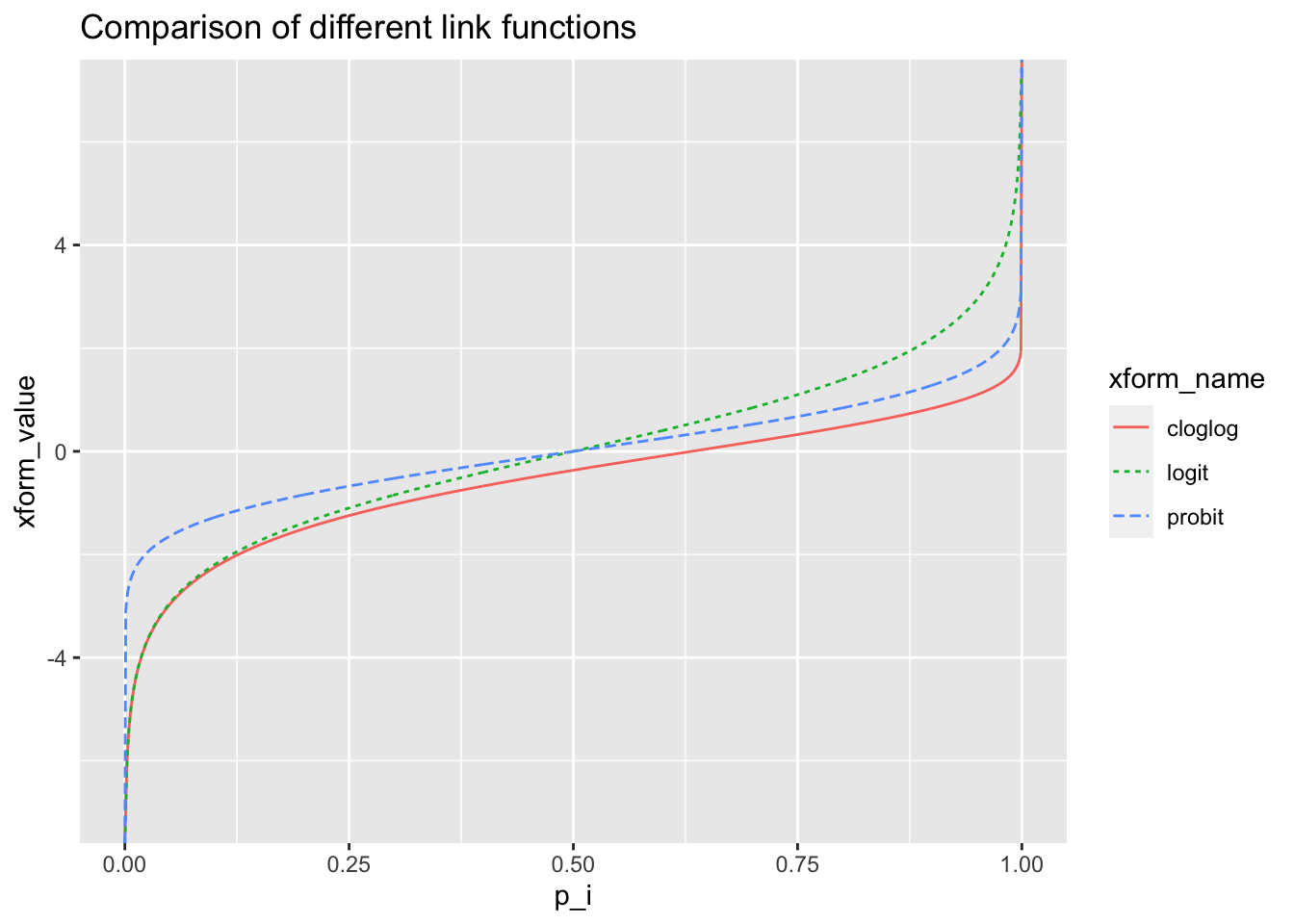
- Characteristics and interpretation of link functions
- When \(p\) is not too big (<0.8), nor too small (>0.2), the link functions are all approximately linear in \(p\), which means we can relate the effect \(\beta\) directly on \(p\).
- Roughly, when \(X\) changes 1 unit, \(p\) changes 0.23\(\beta\) units for logit link, 0.37\(\beta\) units for probit link and 0.32\(\beta\) for cloglog link.
- This is not the case when \(p\) is very large or very small, in which case a large effect \(\beta\) can change \(X\beta\) but there will not be so much change in \(p\).
2.2.2 Logistic Regression Example
- Low birth weight
- Defined as birth weight less than 2500 grams (5.5 lb); it is an outcome that has been of concern to physicians for years.
- This is due to the fact that infant mortality rates and birth defect rates are very high for low birth weight babies.
- Behavior during pregnancy (including diet, smoking habits, and receiving prenatal care) can greatly alter the chances of carrying the baby to term and, consequently, of delivering a baby of normal birth weight.
DSN: birthwt.dta (STATA13 format)
ID: Mother's identification number
MOTH_AGE: Mother's age (years)
MOTH_WT: Mother's weight (pounds)
RACE: Mother's race (1=White, 2=Black, 3=Other)
SMOKE: Mother's smoking status (1=Yes, 0=No)
PREM: History of premature labor (number of times)
HYPE: History of hypertension (1=Yes, 0=N0)
URIN_IRR: History of urinary irritation (1=Yes, 0=N0)
PHYS_VIS: Number of physician visits
BIRTH_WT: Birth weight of new born (grams)
LBW: Low birth weight (constructed to be 1=if birth weight less than 2500, 0=Not) - Low birthweight model
- How does probability of LBW, \(P(\mbox{LBW}=1)\), vary by predictor levels?
- We will include mother’s age, weight and race, as well as history of premature labor in a model as predictors
- In order to minimize privileged or normative reference categories, we will drop the constant and include all indicators for race.
Code
bwData <- readstata13::read.dta13("./Data/birthwt.dta", nonint.factors = TRUE)
bwData$LBW <- ifelse(bwData$BIRTH_WT < 2500, 1, 0)
fit.lbw.logit <- glm(LBW ~ -1 + MOTH_AGE + MOTH_WT + factor(RACE) + PREM, data = bwData, family = binomial(link = "logit"))
summary(fit.lbw.logit)##
## Call:
## glm(formula = LBW ~ -1 + MOTH_AGE + MOTH_WT + factor(RACE) +
## PREM, family = binomial(link = "logit"), data = bwData)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7957 -0.8587 -0.6656 1.2131 2.1327
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## MOTH_AGE -0.035980 0.034544 -1.042 0.2976
## MOTH_WT -0.012232 0.006607 -1.851 0.0641 .
## factor(RACE)White 1.093883 1.091608 1.002 0.3163
## factor(RACE)Black 2.103876 1.164304 1.807 0.0708 .
## factor(RACE)Other 1.559599 1.023133 1.524 0.1274
## PREM 0.785853 0.327977 2.396 0.0166 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 262.01 on 189 degrees of freedom
## Residual deviance: 216.57 on 183 degrees of freedom
## AIC: 228.57
##
## Number of Fisher Scoring iterations: 4Code
nms <- gsub("factor\\(RACE)", "RACE:", names(fit.lbw.logit$coefficients))- Model results
- We can write the regression prediction equation for the log-odds of the outcome as:
\(\log(p_i/(1-p_i))=\eta_i=\)-0.04 MOTH_AGE + -0.01 MOTH_WT + 1.09 RACE:White + 2.1 RACE:Black + 1.56 RACE:Other + 0.79 PREM. - Interpreting effects in the logit scale can be challenging.
- Researchers often prefer to construct odds-ratios, and speak of multiplicative effects.
- We can write the regression prediction equation for the log-odds of the outcome as:
2.2.3 Odds and Odds Ratio
We use the idea of odds and odds ratios quite often, so we now review \(2\times 2\) tables and their use in assessing single risk factors via odds ratios.
- Reminder: odds are an alternative representation of a probability.
- Probability \(p\) corresponds to the proportion in favor of the event
- Odds simply contrast that proportion to the proportion against, or \(p/(1-p)\).
- E.g., 50:50 odds corresponds to 0.5/(1-0.5) which is exactly 1.
- This is why we say that there are “even” odds in this case: the same amount in favor as against.
- E.g., 4 to 1 odds in favor suggests that \(p=4/5\)
- The 5 derives from the total for and against of 4+1.
- Research question: Do babies born to a mother with premature birth history tend to have low birth weight?
- More precisely, is any difference more than can be explained by chance?
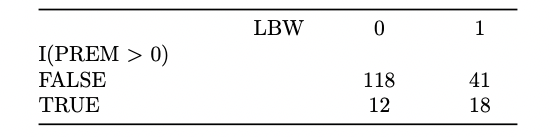
Here is a crosstab from our data:
Code
tbl <- xtabs(~I(PREM > 0) + LBW, data = bwData)
pander::pander(ftable(tbl))| LBW | 0 | 1 | |
| I(PREM > 0) | |||
| FALSE | 118 | 41 | |
| TRUE | 12 | 18 |
- Let’s construct the odds conditional on prior premature birth.
- For women with PREM>0, read the numbers 18 and 12 from the table and construct the ratio: 18/12=1.5.
- The odds are in favor (odds above 1 means in favor) of this birth being low birth weight for these women.
- For women with PREM=0, read the numbers 41 and 118 from the table and construct the ratio: 41/118=0.35.
- The odds are against (below 1) a low birth weight baby in this case… by a lot.
- Odds ratios
- The interesting comparison derives from the ratio of odds of the event (low birth weight) for people with a “risk factor” vs. those without it
- Here, we have 1.5/0.35=4.32 (we used more significant digits before rounding).
- This is interpreted as women with a history of premature birth have 4.32 times the odds of a low birth weight baby than women without that history.
- Because odds are a form of probability, some people like to substitute the word “risk” for odds. Strictly speaking, risk refers to a probability, so use this conceptual “exchange” of words with caution. When prevalence is low, odds and relative risk are similar.
- Useful computational trick for odds ratio
- With a \(2\times 2\) table, a useful computational trick is to multiply the elements of the diagonal, then divide those by the product of the “reverse diagonal” (upper right towards lower left).
- Here \((118\cdot 18)/(12\cdot 41)=4.35\). Some code that does this follows.
Code
oddsRatio <- function(x) prod(diag(x))/prod(lava::revdiag(x))
oddsRatio(tbl)## [1] 4.317073- Significance
- Significance tests for odds ratios tests for difference from 1, or even odds.
- The derivation of these tests separate from models is not explored here, but we provide the confidence intervals for our particular case study.
Code
rslt <- epiR::epi.2by2(tbl)
rslt$massoc.detail$OR.strata.score- With an odds ratio of 4.32, and a 95% confidence interval that does not contain one, it is safe to say that there is a relationship between the precondition and the outcome, beyond what would be
expected by chance.
- A more general and formal test follows.
- With an odds ratio of 4.32, and a 95% confidence interval that does not contain one, it is safe to say that there is a relationship between the precondition and the outcome, beyond what would be
expected by chance.
2.2.3.1 Exercise 3
Hint is visible here2.2.4 Chi-square test of independence for a cross-tab
The formal test we want to make is:
- \(H_0\): Independence (of risk factor and outcome) vs. \(H_a\): Dependence
- Under independence, we expect the number of low birth weight babies to be the same proportion (other than due to sampling) among mothers who had a premature birth history and those who did not.
- We can test the independence of these two variables using a Chi-square test.
- Compute the expected count in each cell.
- This is based on an estimate of the population row and column percents.
- We take the product of row and column percents for each cell, and call that the expectation under independence, or marginal product.
- For the rows, these are 0.84, 0.16 and for the columns 0.69, 0.31, so the upper left cell is expected to have the cell percents:
Code
rowpct <- prop.table(margin.table(tbl, 1))
colpct <- prop.table(margin.table(tbl, 2))
cellpct <- outer(rowpct, colpct, "*")
pander::pander(ftable(cellpct), caption = "Cell Percents (marginal product)")| LBW | 0 | 1 | |
| I(PREM > 0) | |||
| FALSE | 0.5787 | 0.2626 | |
| TRUE | 0.1092 | 0.04955 |
- The expected count is the cell percent scaled by the total sample size.
Code
cellExp <- cellpct * nrow(bwData)
pander::pander(ftable(cellExp), caption = "Cell Expected Counts", digits = 3)| LBW | 0 | 1 | |
| I(PREM > 0) | |||
| FALSE | 109 | 49.6 | |
| TRUE | 20.6 | 9.37 |
- The Chi-square statistic: for each cell, take the squared difference between observed and expected, divided by the number of expected; then sum up across all the cells.
\[ X^2=\sum_{i,j}^{}{\frac{(O_{ij}-E_{ij})^2}{E_{ij}}} \]
- We have \(i,j\) indexing the rows and columns of the table, respectively.
- This test statistic \(X^2\) follows a \(\chi^2\) distribution.
- The farther apart the two tables, the bigger the statistic.
- The degrees of freedom of this Chi-square test is (number of rows - 1) \(\times\) (number of columns - 1).
- In this example, df=1.
- In this example, we reject the null and conclude that these two variables are associated:
Code
summary(tbl)## Call: xtabs(formula = ~I(PREM > 0) + LBW, data = bwData)
## Number of cases in table: 189
## Number of factors: 2
## Test for independence of all factors:
## Chisq = 13.759, df = 1, p-value = 0.00020782.2.5 Why bother with Odds Ratios?
- Ease of interpretation
- As we saw in the comparison of logit, probit and cloglog link functions, the effect of a one unit change in \(X\) depends on the “baseline” probability.
- In other words, if the predictors ‘set’ the baseline probability to 0.50, then a one unit change in a particular \(X\), holding the others constant will not yield the same change in probability as when predictors ‘set’ the baseline probability to 0.80.
- In fact, it can be shown that for the logit link, the expected change given model: \[ f(p_i,X_i,\beta=(b_0,b_1,\ldots,b_k)')=\log(p_i/(1-p_i)) = X_i\beta \] If we denote the \(j^{th}\) element of \(X_i\) as \(X_{ij}\), it is: \[ \frac{\partial p_i}{\partial x_{ij}} = b_j\cdot p_i(1-p_i) \]
- You can derive this using calculus and implicit differentiation.
- So the effect is 0.25\(b_j\) when \(p_i=0.50\), but 0.16\(b_j\) when \(p_i=0.80\).
- Odd-ratios are different
- Odds-ratios are independent of the baseline (odds)
- This is due in part to the multiplicative nature of their effect.
- If the odds ratio were 2.0, then the effect of a one unit change is 2 times the baseline odds, whether that baseline is 0.5, 1.0, or 1.5.
- It always has the same (multiplicative) effect.
- \(\beta\) still represents effects, but in this case it is the effect on the log-odds \(\log o(p_i)=\log(p_i/(1-p_i))\).
- Exponentiation \(\beta\) simplifies the interpretation.
Compare the odds at two levels of \(X_i\), assuming it is a vector: \[ \log o(Y_i|X_i)=X_i\beta\implies o(Y_i|X_i)=e^{X_i\beta} \] Now add 1 to the \(j^{th}\) element of \(X_i\) by adding a vector of zeros with a 1 in the \(j^{th}\) position to it \(X_i'=X_i+(0,\ldots,1,\ldots,0)\): \[ \log o(Y_i|X_i')=X_i'\beta\implies o(Y_i|X_i')=e^{X_i'\beta}=e^{(X_i+(0,\ldots,1,\ldots,0))\beta} = e^{b_j}e^{X_i\beta} \] Thus, the baseline \(e^{X_i\beta}\) is multiplied by \(e^{b_j}\) when the \(j^{th}\) predictor is changed by 1 unit.
Returning to the example of a single risk factor, we can examine the odds ratios and multiplicative effects implied by our model:
Code
bwData$PREM_HIST <- factor(1 - bwData$PREM == "0") #should be 0/1 factor
fit.lbw.prem.logit <- glm(LBW ~ PREM_HIST, data = bwData, family = binomial(link = "logit"))
summary(fit.lbw.prem.logit)##
## Call:
## glm(formula = LBW ~ PREM_HIST, family = binomial(link = "logit"),
## data = bwData)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4823 -0.7771 -0.7771 0.9005 1.6400
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.0428 0.1773 -5.88 4.1e-09 ***
## PREM_HISTTRUE 1.7360 0.4679 3.71 0.000207 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 234.67 on 188 degrees of freedom
## Residual deviance: 219.87 on 187 degrees of freedom
## AIC: 223.87
##
## Number of Fisher Scoring iterations: 4- Notes on model fit
- We see that mothers without the PREM risk factor have baseline odds of \(\exp(\) -1.04 \()=\) 0.35 which is quite small.
- However, those odds are multiplied by \(\exp(\) 1.74 \()=\) 5.67 when the subject has a prior history.
- Important point: when interpreting effects sizes the baseline rate matters.
- Imagine that the risk of a rare disease were 1 in 1 million.
- The odds are essentially the same as the probability (risk) for small values.
- Then twice the risk is still only 2 out of 1 million.
- It is twice as large, but the baseline was a small number. This distinction is important in practice.
2.2.6 Example with more variables
- IMPORTANT: Nominal variable coding - the coding of RACE.
- There are many ways to encode nominal variables. You are likely familiar with “traditional dummy coding” also known as treatment contrasts.
- Each level/value of a nominal variable has an indicator variable associated with it. So for race, there would be a White, Black, and Other variable added to your dataset.
- Each is set to 0 unless the RACE nominal variable is at that level.
- In other words, if RACE==“Other” then the indicator variable corresponding to ‘Other’ is set to one.
- The challenge with this approach is that one must choose a reference category (we avoided this by dropping the intercept in an earlier model, but this can lead to other problems of interpretation).
- Choice of reference category
- It is hard to make this choice without implicitly imposing a “norm” into the analysis – and this may be undesirable.
- Consider the so-called “Black-White” test score gap in education studies. Such studies typically set the white category as reference, and all other groups are contrasted to their performance.
- This framing of the question may appear innocent at first, but:
- It presupposes that the tests measure what is important (a form or norming)
- It establishes the target level of performance to be that of one group
- There are alternatives.
- Effect coding – an alternative
- With effect codings, the key difference is that they sum to zero.
- This means that the intercept in the model is the average effect across all groups, with the reported effects being deviations from that average.
- Here is some R code that demonstrates the difference:
Code
contr.treatment(levels(bwData$RACE))## Black Other
## White 0 0
## Black 1 0
## Other 0 1Code
contr.sum(levels(bwData$RACE))## [,1] [,2]
## White 1 0
## Black 0 1
## Other -1 -1- What this small difference does is set the intercept to be the mean effects across all RACE groups.
- Typically, the last group is implicitly but not explicitly referenced in model parameters, but this is less important now, since the estimated effects are deviations from the overall average.
Code
fit.lbw.logit1 <- glm(LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST + HYPER + URIN_IRR + PHYS_VIS, data = bwData,
binomial(link = "logit"), contrasts = list(RACE = contr.sum))
summary(fit.lbw.logit1)##
## Call:
## glm(formula = LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST +
## HYPER + URIN_IRR + PHYS_VIS, family = binomial(link = "logit"),
## data = bwData, contrasts = list(RACE = contr.sum))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6481 -0.7860 -0.5146 0.9081 2.2340
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.481600 1.194586 1.240 0.21488
## MOTH_AGE -0.043596 0.038802 -1.124 0.26120
## MOTH_WT -0.015624 0.007148 -2.186 0.02884 *
## RACE1 -0.641931 0.278034 -2.309 0.02095 *
## RACE2 0.509713 0.331005 1.540 0.12359
## SMOKEYes 0.852980 0.414981 2.055 0.03983 *
## PREM_HISTTRUE 1.591609 0.523282 3.042 0.00235 **
## HYPERYes 1.854086 0.716373 2.588 0.00965 **
## URIN_IRRYes 0.786593 0.465966 1.688 0.09139 .
## PHYS_VIS 0.024218 0.178532 0.136 0.89210
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 234.67 on 188 degrees of freedom
## Residual deviance: 193.90 on 179 degrees of freedom
## AIC: 213.9
##
## Number of Fisher Scoring iterations: 4Code
epiDisplay::logistic.display(fit.lbw.logit1, simplified = TRUE)## Registered S3 method overwritten by 'epiDisplay':
## method from
## print.lrtest rms##
## OR lower95ci upper95ci Pr(>|Z|)
## MOTH_AGE 0.9573403 0.8872343 1.0329858 0.261195711
## MOTH_WT 0.9844979 0.9708013 0.9983878 0.028838034
## RACE1 0.5262750 0.3051754 0.9075612 0.020953491
## RACE2 1.6648141 0.8701895 3.1850605 0.123585511
## SMOKEYes 2.3466291 1.0404281 5.2926946 0.039833842
## PREM_HISTTRUE 4.9116443 1.7612006 13.6976162 0.002353311
## HYPERYes 6.3858585 1.5683444 26.0014246 0.009649099
## URIN_IRRYes 2.1959030 0.8810136 5.4732303 0.091393280
## PHYS_VIS 1.0245135 0.7220234 1.4537310 0.8920978592.2.7 Discussion
This model is an attempt at identifying the risk factors of low birth weight (i.e. birth weight less than 2500).
- A positive log odds ratio (coef>0, corresponding to an OR>1) means that the larger the value of \(X\), the greater the expected log-odds or odds of LBW, and hence the greater risk or probability of LBW.
- We define risk as the probability of the outcome of interest.
- Since our models are for log-odds, risk factors should have positive coefficients and protective factors should have negative coefficients.
- We provided both the standard output (effects are in the logit) as well as the multiplicative effects (as odds-ratios).
- Interpreting odds ratios and focusing on significant effects:
- If two sets of mothers whose weights differ by one pound are compared, the larger weighing group has lower odds by about 1.5%, all else equal.
- A difference of 10 pounds suggests \(1-.984^{10}=15\%\) decrease. Note the use of a “power law” to examine non-unit changes.
- If all other conditions are the same, the odds of having LBW baby of a White mother (RACE1 in the output) is 0.53 times the average odds for the whole population (that could be stated as 47% lower).
- Black (RACE2 in output) is not significantly different from the average.
- The “other” group effect is -RACE1-RACE2 from the average.
- The interpretation of coefficients holds when the groups sizes are all about the same.
- If all other conditions are the same, smoking is associated with 135% larger odds of having LBW baby.
- Premature delivery history and hypertension both have significant positive effects of 4.9 and 6.4, respectively, all else equal, suggesting that these are predictive of much larger risk of LBW babies.
- Inference: The columns “Pr(>|Z|)” correspond to a Wald test statistic based on asymptotic normality.
- For logistic model output the null is \(b_k=0\) for the \(k^{th}\) coefficient, while for the odds-ratio representation, the null is \(e^{b_k}=1\).
- Lack of a constant in the OR table
- The constant is not provided in our OR table.
- We can compute the value directly from the log-odds output. It is 4.4.
- It is a very large value, suggesting great risk, on average (and for the reference group), in this population.
- If we had used effect codings for every categorical variable and grand-mean centered (see next section) every continuous predictor, we could interpret the constant as the average of every predictor.
2.2.8 Centering
- Centering is a useful approach in many situations in which you wish the reference group to represent the average for the population.
- We often call it grand-mean centering if this is the desired effect.
- Effect codings do this for nominal valued predictors.
- Binary predictors coded \(\{-1,+1\}\) rather than \(\{0,1\}\) have this same effect.
- Refitting the model with effect codings and grand-mean centering yields:
Code
fit.lbw.logit2 <- glm(LBW ~ 1 + I(MOTH_AGE - mean(MOTH_AGE)) + I(MOTH_WT - mean(MOTH_WT)) + RACE + SMOKE + PREM_HIST +
HYPER + URIN_IRR + I(PHYS_VIS - mean(PHYS_VIS)), data = bwData, binomial(link = "logit"), contrasts = list(RACE = contr.sum,
SMOKE = contr.sum, PREM_HIST = contr.sum, HYPER = contr.sum, URIN_IRR = contr.sum))
summary(fit.lbw.logit2)##
## Call:
## glm(formula = LBW ~ 1 + I(MOTH_AGE - mean(MOTH_AGE)) + I(MOTH_WT -
## mean(MOTH_WT)) + RACE + SMOKE + PREM_HIST + HYPER + URIN_IRR +
## I(PHYS_VIS - mean(PHYS_VIS)), family = binomial(link = "logit"),
## data = bwData, contrasts = list(RACE = contr.sum, SMOKE = contr.sum,
## PREM_HIST = contr.sum, HYPER = contr.sum, URIN_IRR = contr.sum))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6481 -0.7860 -0.5146 0.9081 2.2340
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.002196 0.437494 2.291 0.02198 *
## I(MOTH_AGE - mean(MOTH_AGE)) -0.043596 0.038802 -1.124 0.26120
## I(MOTH_WT - mean(MOTH_WT)) -0.015624 0.007148 -2.186 0.02884 *
## RACE1 -0.641931 0.278034 -2.309 0.02095 *
## RACE2 0.509713 0.331005 1.540 0.12359
## SMOKE1 -0.426490 0.207490 -2.055 0.03983 *
## PREM_HIST1 -0.795804 0.261641 -3.042 0.00235 **
## HYPER1 -0.927043 0.358187 -2.588 0.00965 **
## URIN_IRR1 -0.393297 0.232983 -1.688 0.09139 .
## I(PHYS_VIS - mean(PHYS_VIS)) 0.024218 0.178532 0.136 0.89210
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 234.67 on 188 degrees of freedom
## Residual deviance: 193.90 on 179 degrees of freedom
## AIC: 213.9
##
## Number of Fisher Scoring iterations: 4- You will note that many coefficients are identical to those in the previous run.
- Binary predictors are essential half the magnitude of their original values, with sign changes when the reference group swaps, which it seems to do for all of the binaries.
- The categories are numbered 1,2,… to reflect each level, so ‘1’ is the first category alphabetically
2.2.8.1 Exercise 5
Hint is visible here- Note importantly, that the intercept has changed!
- We centered in part to get a better “baseline” risk assessment.
- The “mythical average” person essentially has a 2.72 risk (odds) of a LBW baby.
- This is somewhat high, in part, because the reference person is a half-smoker, half-hypertensive, etc., person.
- It is much lower than that of the non-centered model.
- Reminder: the impact of a risk factor must be understood in the context of the prevalence or average risk of the outcome.
- For low prevalence outcomes, doubling the risk is much less of a worry than for higher prevalence ones.
2.3 Probit Regression
A commonly used alternative to the logistic link is the Probit link. We introduced this model by substituting the link function, so that:
- The GLM components (for probit regression) are:
- \(Y_i \sim \mbox{binom}(p_i)\). \(p_i=E(Y_i|X_i)\)
- \(\eta_i = X_i\beta\)
- \(g(p_i)=\Phi^{-1}(p_i)=\eta_i\) thus \(p_i=g^{-1}(\eta_i) = \Phi(\eta_i)\), where \(\Phi(\cdot)\) is the cumulative normal distribution.
(iii.) ensures that \(\eta_i\) is transformed to the probability scale. Note: \(\Phi(0)=0.5\) so \(\Phi^{-1}(0.5)=0\); some familiar values are: \(\Phi^{-1}(0.025)=-1.96\), \(\Phi^{-1}(0.975)=1.96\), \(\Phi^{-1}(0)=-\infty\), and \(\Phi^{-1}(1)=+\infty\). Note how the domain and range of \(\Phi^{-1}(\cdot)\) are \((0,1)\) and \(\Re\), respectively.
- The probit model may also be motivated by a latent variable construct, which is slightly different than the way we motivate the GLM framework.
- The idea is that there is an unobserved value in \(\Re\) related to the 0/1 outcome.
- Whenever that value exceeds some threshold, say 0, then a 1 is observed, while a 0 is observed otherwise.
- More formally, let \(Y_i\) be the observed outcome (1=Yes, 0=No), and let \(Y_i^*\) be the latent variable whose value (unobserved) determines observed \(Y_i\). \[ {{Y}_{i}}=\left\{ \begin{matrix} 0\text{ if Y}_{\text{i}}^{\text{*}}<0 \\ 1\text{ if Y}_{\text{i}}^{\text{*}}>0 \\ \end{matrix} \right. \]
- Economists like to label the latent variable, “latent utility” in their studies of human behavior.
- In general, we don’t observe \(Y_i^*\), but we can conjecture that for each individual, \(Y_i^*\) has a mean \(\mu_i\) with some error \(\varepsilon_i\) and we can fit a linear model to explain the variability in \(\mu_i\).
- A more concrete example
- In the low birth weight data, the latent variable can be the measured z-score (standardized) birth weight.
- The measurement may be made with error, adding variability, and then the ‘1’ event of LBW is defined based on the 2500g birth weight.
- To orient the latent variable to the smaller weights yielding ’1’s, take \(Y_i^*\) as the negative of the z-score (flip the sign)
- Regression model under this latent variable framework:
\[
Y_{i}^{*}={{\mu}_{i}}+{{\varepsilon }_{i}}={{X}_{i}}\beta +{{\varepsilon }_{i}}
\]
- For identifiability, we assume \(\varepsilon_i\) is normally distributed with zero mean
- We further assume it has variance 1, or \(\varepsilon_i\sim N(\mu=0,\sigma^2=1)\).
- Interpretation
- This setup suggests an interpretation for the \(\beta\): a one unit difference in \(x_k\) (the \(k^{th}\) predictor/column in \(X\)) yields an expected difference of \(b_k\) in \(Y^*\).
- This change is in the latent variable, not in \(Y\)!
- To use this framework successfully, you have to “think” of effects in the latent space.
- We now show that the latent variable model for \(Y_{i}^{*}={{\mu}_{i}}+{{\varepsilon }_{i}}={{X}_{i}}\beta +{{\varepsilon }_{i}}\) is equivalent to the GLM setup of the probit regression model.
- Start with \(p_i=P(Y_i=1)\), our definition of \(p_i\).
- Further assume \(P(Y_i=1)=P(Y_i^*>0)\).
- Substitute the expression for \(Y_i^*\), and we have \(p_i=P(X_i\beta+\varepsilon_i >0)\)
- This is true when \(P(\varepsilon_i > -X_i\beta)=P(\varepsilon_i < X_i\beta)\) (symmetry)
- Let \(\eta_i= X_i\beta\), then \(p_i=P(\varepsilon_i < \eta_i)\) (distributionally, the sign is irrelevant)
- Since \(\varepsilon_i\sim N(0,1)\), this is just \(\Phi(\eta_i)\). This is equivalent to definition (iii) of the probit GLM, above.
- Probit model fit
Code
fit.lbw.probit1 <- glm(LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST + HYPER + URIN_IRR + PHYS_VIS, data = bwData,
binomial(link = "probit"), contrasts = list(RACE = contr.sum))
summary(fit.lbw.probit1)##
## Call:
## glm(formula = LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST +
## HYPER + URIN_IRR + PHYS_VIS, family = binomial(link = "probit"),
## data = bwData, contrasts = list(RACE = contr.sum))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6336 -0.7981 -0.5008 0.9321 2.2505
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.861094 0.693226 1.242 0.21418
## MOTH_AGE -0.027203 0.022447 -1.212 0.22556
## MOTH_WT -0.008951 0.004097 -2.185 0.02888 *
## RACE1 -0.374791 0.160841 -2.330 0.01980 *
## RACE2 0.294109 0.198805 1.479 0.13904
## SMOKEYes 0.513107 0.239792 2.140 0.03237 *
## PREM_HISTTRUE 0.971981 0.311586 3.119 0.00181 **
## HYPERYes 1.099174 0.425946 2.581 0.00986 **
## URIN_IRRYes 0.483074 0.280380 1.723 0.08490 .
## PHYS_VIS 0.005091 0.104430 0.049 0.96112
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 234.67 on 188 degrees of freedom
## Residual deviance: 193.51 on 179 degrees of freedom
## AIC: 213.51
##
## Number of Fisher Scoring iterations: 5- Comparing the two models, we find that significance is essentially the same
- We find that coefficients for the probit model are smaller in magnitude.
- In fact, an approximation that seems to hold well in practice is that probit coefficients are about \(1/1.6^{th}\) as large as the corresponding logit coefficients. We see this quite clearly in the following table:
Code
require(modelsummary)## Loading required package: modelsummary##
## Attaching package: 'modelsummary'## The following objects are masked from 'package:DescTools':
##
## Format, Mean, Median, N, SD, Var## The following object is masked from 'package:Hmisc':
##
## Mean## The following object is masked from 'package:VGAM':
##
## MaxCode
modelsummary(list(Logit = fit.lbw.logit1, Probit = fit.lbw.probit1), stars = T, output = "markdown")| Logit | Probit | |
|---|---|---|
| (Intercept) | 1.482 | 0.861 |
| (1.195) | (0.693) | |
| MOTH_AGE | -0.044 | -0.027 |
| (0.039) | (0.022) | |
| MOTH_WT | -0.016* | -0.009* |
| (0.007) | (0.004) | |
| RACE1 | -0.642* | -0.375* |
| (0.278) | (0.161) | |
| RACE2 | 0.510 | 0.294 |
| (0.331) | (0.199) | |
| SMOKEYes | 0.853* | 0.513* |
| (0.415) | (0.240) | |
| PREM_HISTTRUE | 1.592** | 0.972** |
| (0.523) | (0.312) | |
| HYPERYes | 1.854** | 1.099** |
| (0.716) | (0.426) | |
| URIN_IRRYes | 0.787+ | 0.483+ |
| (0.466) | (0.280) | |
| PHYS_VIS | 0.024 | 0.005 |
| (0.179) | (0.104) | |
| Num.Obs. | 189 | 189 |
| AIC | 213.9 | 213.5 |
| BIC | 246.3 | 245.9 |
| Log.Lik. | -96.951 | -96.755 |
| F | 3.315 | 3.819 |
| RMSE | 0.41 | 0.41 |
Note: ^^ + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001
- Discussion
- The coefficients of probit regression can be interpreted as if they are linear regression coefficients, except that the effects are acting on the latent variable.
- E.g., adjusting for everything else, a one unit difference in mother’s weight is associated with expected differences in utility or latent variable of -0.009.
- Clearly from the sign, heavier mothers will on average be less likely to have low birth weight babies, all else equal. Thinking in the latent scale is challenging.
- Since the latent variable is normalized to have a standard deviation of 1, the unit in latent variable space can be often viewed as a standard deviation.
- Thus a 10 lb. weight difference is associated with a 0.09 s.d. difference in “latent birth weight.”
- All we did to shift this to a probit regression was change the link function.
2.3.1 Probit versus Logit link
- Both models use the same binomial likelihood function.
- It is the link function linking parameter \(p_i\) to \(X_i\beta\) that differs.
- Logit link can also have a latent utility interpretation
- If we use the same framework, but let the error term \(\varepsilon\) have a logistic distribution with mean 0 and a variance equal to \(\pi^2/3\).
- The logistic distribution p.d.f. in this case is:
\[ f_{\varepsilon}(x)=\frac{e^{x}}{(1+e^{x})^2} \] with wider tails than a normal:
Code
x <- seq(-4, 4, length = 1001)
y1 <- dlogis(x)
y2 <- dnorm(x)
df1 <- data.frame(latent.variable = x, dens = y1, name = "Logistic")
df2 <- data.frame(latent.variable = x, dens = y2, name = "Normal")
ggplot(data = rbind(df1, df2), aes(x = latent.variable, y = dens, color = name)) + geom_line()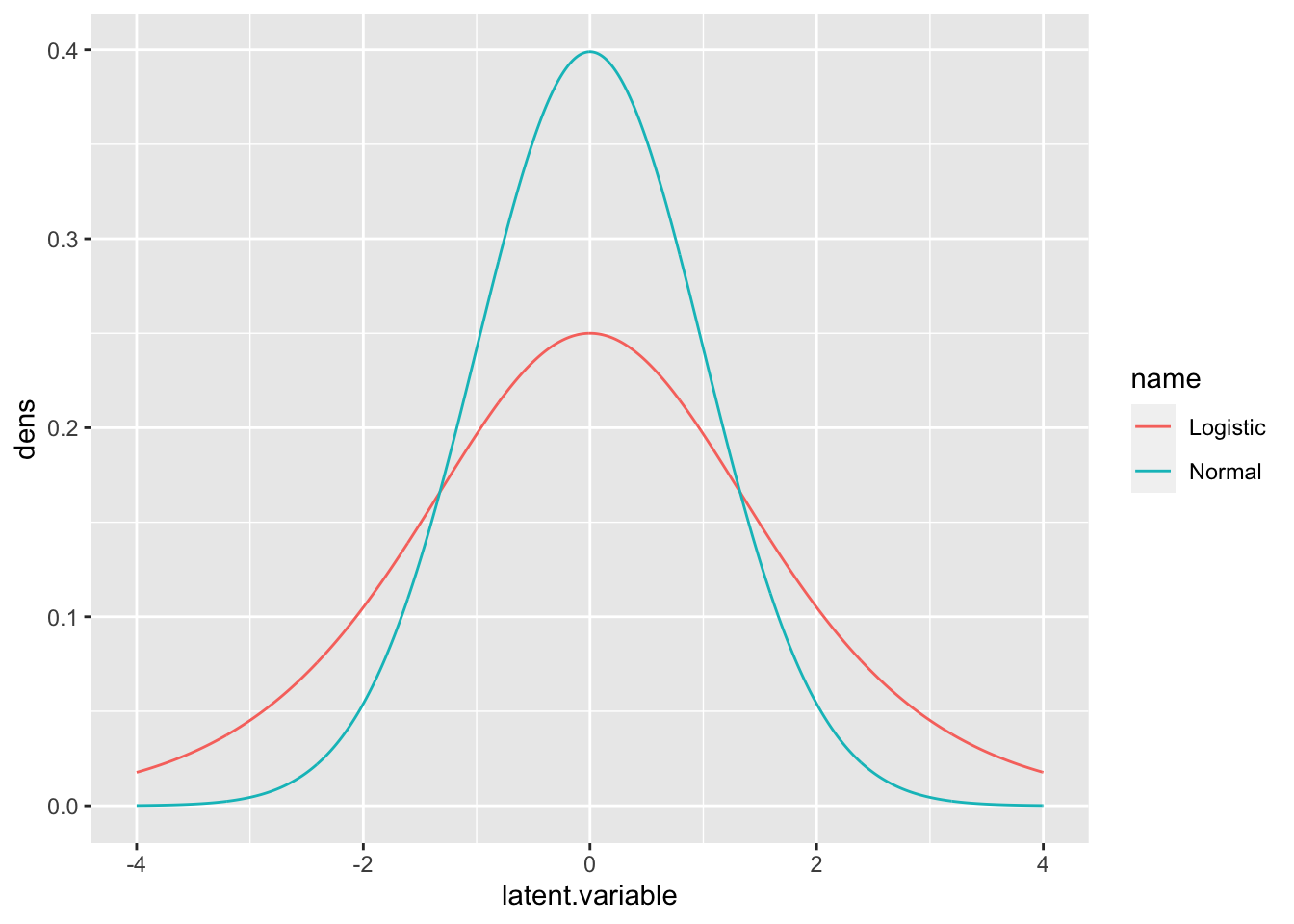
- The magnitude of the coefficients are different because we measure the effects on different scale in the two models
- Log odds vs. latent variable
- You can see that the underlying latent variable formulations are different as well.
- The substantive interpretations in terms of significance and the directions of the effects will be very similar. (Left: logit, Right: probit; prior page table)
- The choices of the two models mostly depend on whether you prefer the odds-ratio interpretation or the latent utility interpretation.
- If your goal is prediction, you can use goodness fit criteria (such as likelihood, deviance, AIC/BIC) and other predictive diagnostics to determine which model is better.
- If your goal is to identify the “best” model be careful: most simulation studies suggest that it is difficult (or impossible in most cases) to identify the better model (logit vs. probit).
2.3.2 Making Predictions based on the logistic and probit models
The predictions that we make are based on a given covariate pattern, \(X_i=(x_{i1},x_{i2},\ldots,x_{ip})\), and our estimated model coefficients, \(\hat\beta=(\hat{b}_0,\hat{b}_1,\ldots,\hat{b}_p)\).
We can make so-called linear predictions, which are on the logit or probit scale: \[ \hat\eta_i=b_0 + \hat{b}_1 x_{i1}+\hat{b}_2 x_{i2}+\ldots+\hat{b}_p x_{ip} \]
- Essentially, we plug in the \(X_i\) values and coefficients estimates, yielding the log-odds for logit models, or latent variables for probit.
- Or we can convert these to probabilities:
- For logit: \(p_i=\frac{e^{\hat\eta_i}}{1+e^{\hat\eta_i}}\)
- For probit: \(p_i=\Phi^{-1}(\hat\eta_i)\)
Code
preds1 <- predict(fit.lbw.logit1, type = "response")
preds2 <- predict(fit.lbw.probit1, type = "response")
plot(preds1, preds2, xlab = "Logit-based predictions", ylab = "Probit-based predictions", main = "Predictions at every covariate pattern, compared")
abline(a = 0, b = 1, col = 2)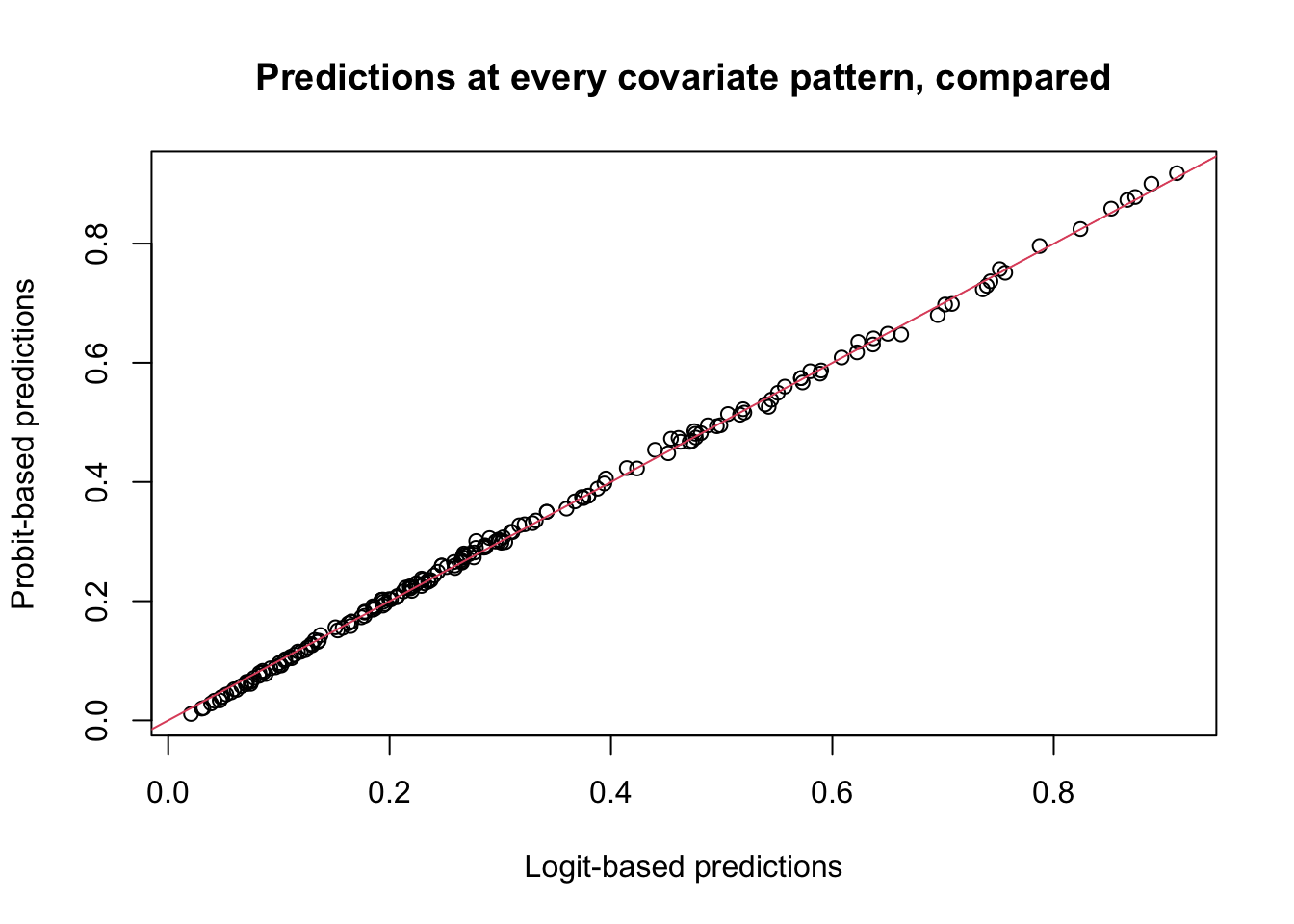
- Plot discussion
- This plot demonstrates that the predicted probabilities based on the logit and probit links, using same set of covariates, are in general pretty similar.
- The differences are bigger when probabilities approach to 0 or 1, but for these data, they are still small.
- Problem: we don’t know the true underlying latent variable, \(\eta_i\) or \(p_i\). We only know \(Y_i\in\{0,1\}\). Plotting predictions against 0s and 1s makes no sense.
2.4 Residuals
- We often use a residual analysis to assess how well a model fits the data.
- As we’ve alluded to previously, residuals aren’t as easy to construct in the GLM setting, because the outcomes are limited in range.
- For logistic regression, this is even more the case (errors are either 0 or 1)! Here are three approaches to residuals using \(p_i\) and \(Y_i\):
- Raw or response residuals: \(r_{Ri} = Y_i - \hat p_i\)
- Pearson residual – the raw divided by the s.e. of a Bernoulli: \(R_{Pi}=(Y_i-\hat p_i)/\sqrt{\hat p_i(1-\hat p_i)}\).
- Deviance residuals (Deviance is a Likelihood based measure of goodness of fit):
\[ R_{Di} = \mbox{sgn}(Y_i-\hat p_i) \left\{2Y_i\log\left(\frac{Y_i}{\hat p_i}\right)+2(1-Y_i)\log\left(\frac{1-Y_i}{1-\hat p_i}\right) \right\}^\frac{1}{2} \]
- This formula is based on twice difference in log-likelihood of the the saturated model and our model.
- The saturated model predicts the outcome \(Y_i\) perfectly, which is why you are seeing a contrast (logged ratio yields a difference) between \(Y_i\) and \(\hat p_i\) in the expression.
- Unfortunately, as written, you will be computing \(\log 0\) in many cases. To avoid this, I provide a function,
myDevRbelow, that avoids this. It provides the exact same deviance residuals as the built-in R functionresid(...,type='deviance').
- Anscombe residuals were presented in Handout 1.
We compare the residuals in some classic density plots, below.
Code
res1 <- resid(fit.lbw.logit1, type = "response")
res2 <- resid(fit.lbw.logit1, type = "pearson")
# function to compute deviance residuals directly
myDevR <- function(y, p) {
sign(y - p) * sqrt(2 * y * ifelse(y == 0, 0, log(y/p)) + 2 * (1 - y) * ifelse(y == 1, 0, log((1 - y)/(1 - p))))
}
pred3 <- predict(fit.lbw.logit1, type = "response")
res3 <- resid(fit.lbw.logit1, type = "deviance")
myres3 <- myDevR(bwData$LBW, pred3)
# proof that the residuals are the same:
sum(abs(res3 - myres3))## [1] 0Code
# density plots:
df1 <- data.frame(residual = res1, restype = "Raw")
df2 <- data.frame(residual = res2, restype = "Pearson")
df3 <- data.frame(residual = res3, restype = "Deviance")
df.all3 <- rbind(df1, df2, df3)
ggplot(data = df.all3, aes(x = residual, color = restype)) + geom_density()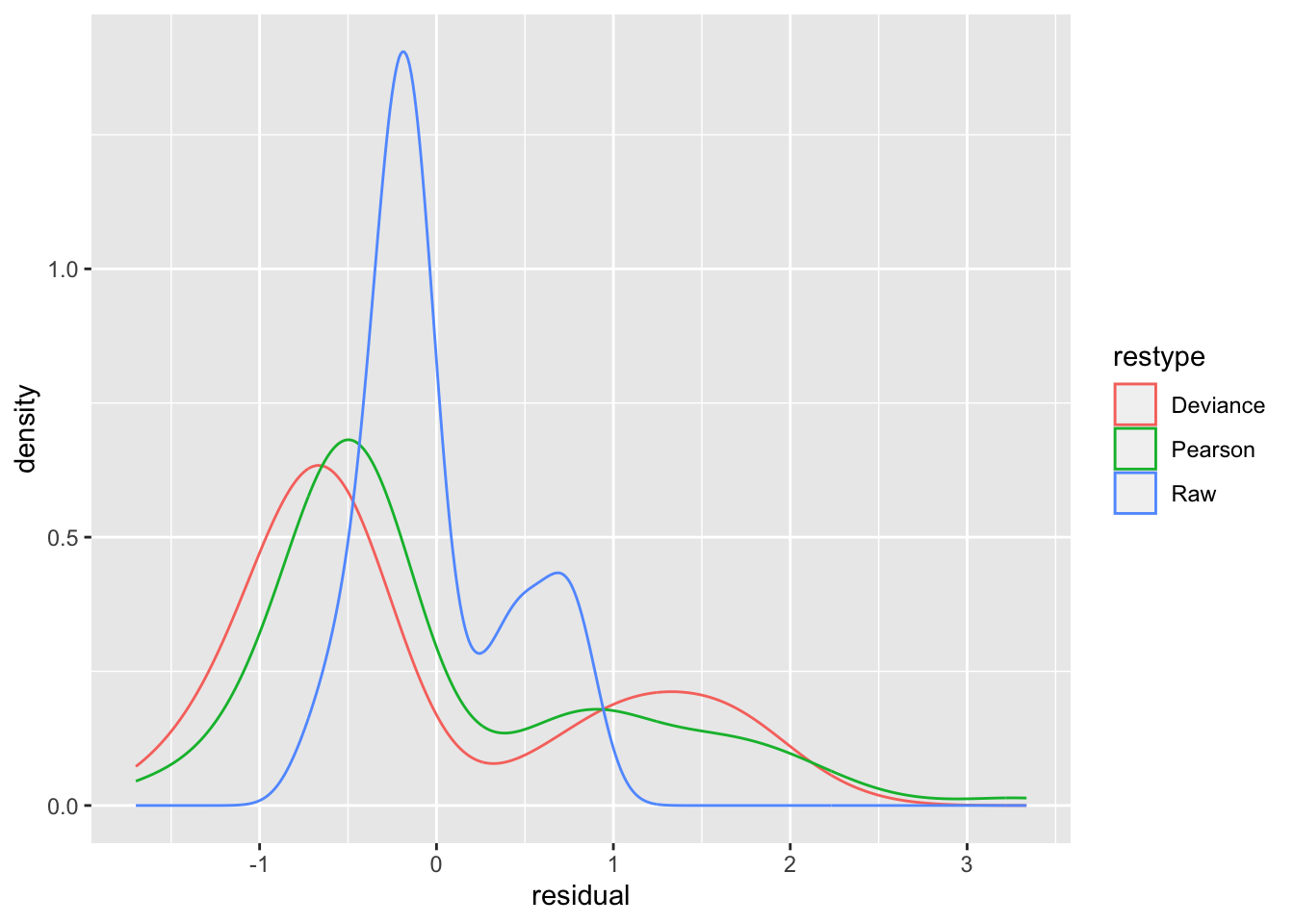
- Discussion
- None of these density plots is normal, and qualitatively, they tell the same bimodal story.
- The Pearson and Deviance residuals lend themselves more to the identification of outliers, as they are properly scaled to lie in the standard normal range.
2.4.1 Classification-based fit assessment
Below is a classification table for the threshold 0.5:
Code
actual <- bwData$LBW
predprob <- predict(fit.lbw.logit1, type = "response")
table2x2 <- function(actual, predprob, thresh = 0.5, prt = F) {
predicted <- ifelse(predprob >= thresh, 1, 0)
xt <- xtabs(~predicted + actual)
acc <- sum(diag(xt))/sum(xt)
if (prt) {
print(xt)
cat("percent correct: ", round(100 * acc, 1), "\n")
}
list(table = xt, accuracy = acc)
}
xt <- table2x2(actual, predprob, thresh = 0.5, prt = T)## actual
## predicted 0 1
## 0 117 35
## 1 13 24
## percent correct: 74.6- Discussion
- This table suggests that we have reasonably good predictive power, but this is in fact driven by the ability to predict 0s more than 1s.
- The sensitivity of the test is \(P(\mbox{actual}=1|\mbox{predicted}=1)\), while the specificity of the test is \(P(\mbox{actual}=0|\mbox{predicted}=0)\)
- These are sometimes described as the true positive and true negative detection rates.
- These are given by the column percents in the table, and the first column reveals just how much higher the specificity of this prediction is:
Code
RcmdrMisc::colPercents(xt$table)[1:2, ]## Registered S3 methods overwritten by 'car':
## method from
## influence.merMod lme4
## cooks.distance.influence.merMod lme4
## dfbeta.influence.merMod lme4
## dfbetas.influence.merMod lme4## actual
## predicted 0 1
## 0 90 59.3
## 1 10 40.7- We examine a set of 2x2 classification tables formed by taking thresholds for outcome 1 ranging from 0.1 to 0.9 by 0.1. We collapse the table for space considerations.
Code
threshs <- seq(0, 1, length = 11)[-c(1, 11)] #get the inner set.
df.tbl <- NULL
for (i in seq_along(threshs)) {
df.tbl <- rbind(df.tbl, data.frame(threshold = threshs[i], actual = actual, predicted = ifelse(predprob >=
threshs[i], 1, 0)))
}
ftable(with(df.tbl, table(threshold, actual, predicted)), row.vars = c("predicted", "actual"))## threshold 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
## predicted actual
## 0 0 25 59 96 108 117 123 126 130 130
## 1 2 8 20 28 35 44 49 53 58
## 1 0 105 71 34 22 13 7 4 0 0
## 1 57 51 39 31 24 15 10 6 1- The first and fourth rows are successful predictions.
- You can see how an extremely low threshold (0.1) classifies 57 of 59 1s correctly, but only 25 of 130 0s, while a threshold of 0.9 correctly classifies every 0 at the expense of nearly every 1.
- The trade-off is between sensitivity and specificity, and in general, you cannot find a threshold that is perfect (100% accurate) for both.
- However, the receiver operating characteristic curve, or ROC curve, captures this trade-off very well.
2.4.2 ROC Curves
- How the ROC curve is constructed:
- Build a dataset with three columns: threshold, sensitivity and specificity.
- For a fixed threshold, we have shown that it is fairly easy to build a classification table and then compute the sensitivity and specificity from column percents in the version that we presented.
- Plotting all pairs of (sensitivity, specificity), we form the ROC curve
- For historical reasons the specificity is shown with the x-axis inverted.
- The extent to which the curve is above the \(45^{\circ}\) line suggests better than chance prediction.
- The area under the curve (AUC) is a measure of predictive power, with 100% being best.
- For this model and these data, our AUC is in the mid-70%, which is considered good but not great.
# install the package
install.packages("LogisticDx")
# 'rms' package must be installed to run the LogisticDx library
install.packages("rms")Code
# install.packages('LogisticDx')
require(LogisticDx)
# install.packages('rms',dependencies = TRUE) install.packages('LogisticDx',
# repos='http://R-Forge.R-project.org') library(LogisticDx) install.packages('rms') library(rms)
g1 <- LogisticDx::gof(fit.lbw.logit1, g = 9, plotROC = TRUE)## Setting levels: control = 0, case = 1## Setting direction: controls < cases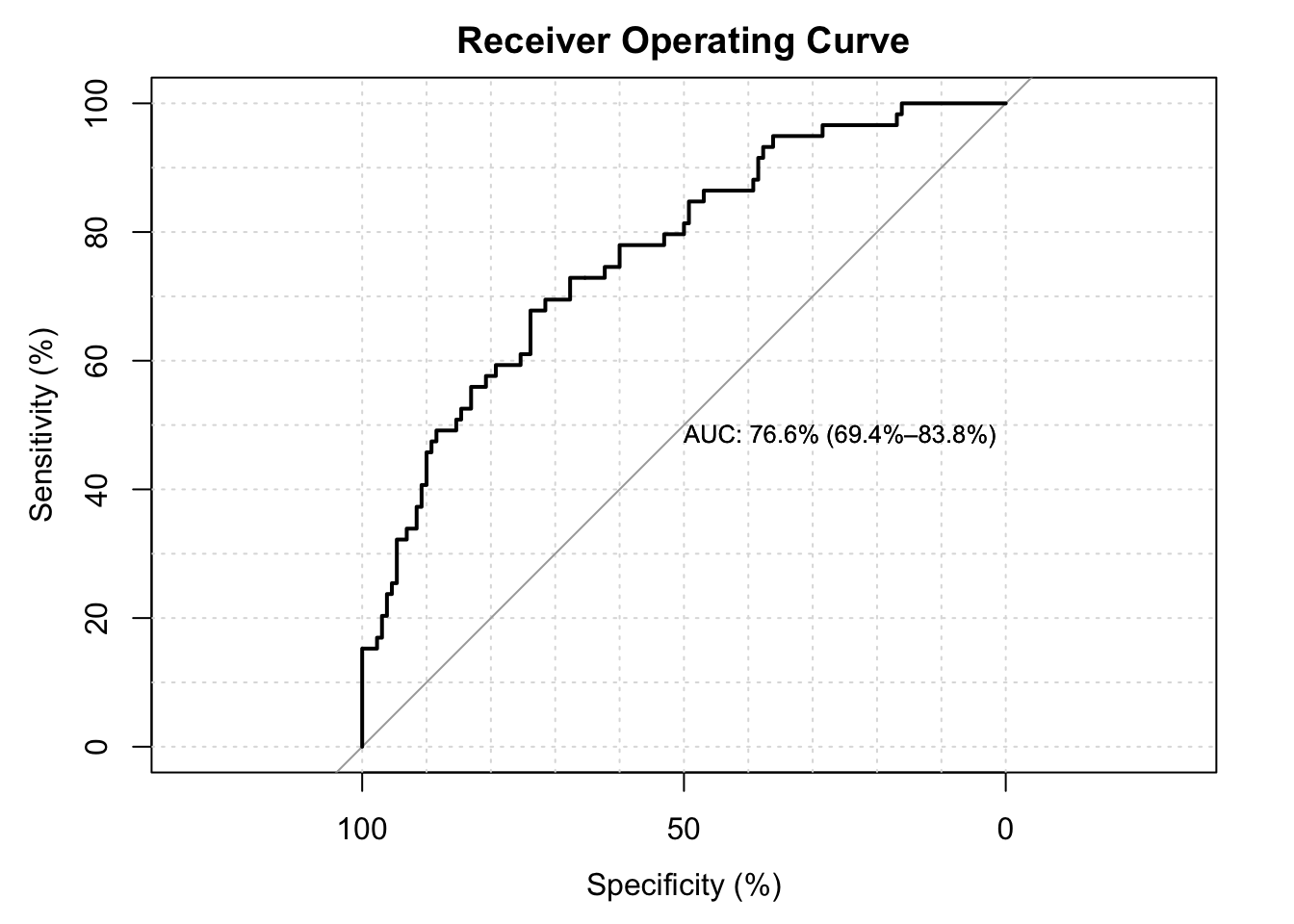
2.4.3 Goodness-of-fit tests
In this type of test we compare \(H_0\): the model fits the data well vs. \(H_a\): the model does not fit the data well.
This is somewhat imprecise, but it is made more precise using the idea that observed and expected values should be similar. In this type of test, we do NOT want to reject \(H_0\), as this indicates good fit!
2.4.4 Pearson’s goodness-of-fit (GoF) test
- There are at least two forms of GoF tests:
- Based on each observation
- Based on unique covariate patterns.
- Most often (b) is used, as it allows one to pool for more accurate estimates.
- For each pattern \(i\) of \(q\) unique patterns, we find the predicted success probability, \(p_i\) from our fitted model.
- Expected successes would then be \(n_i p_i\) assuming \(n_i\) repeat patterns of type \(i\).
- Different tests
- There is some ambiguity about naming convention, but we can confirm that the Pearson GoF test is based on Pearson residuals, at least in R.
- The sum of squared Pearson residuals have been shown to have an asymptotic chi-square distribution on \(q-p\) degrees of freedom, and this statistic and an associated p-value are reported in practice.
- Example
- In our data, there are 189 records, and 183 unique covariate patterns, and our model has \(p=10\) parameters.
- The following are a set of chi-square tests built into the
LogisticDxpackage’sgoffunction, and “PrG” is the one based on unique covariate patterns and Pearson residuals. - Note the df=183-10=173 and the p-value is 0.32, suggesting “good fit” (do not reject the null).
Code
# require(LogisticDx)
gof(fit.lbw.logit1, g = 9, plotROC = F)$chiSq## Setting levels: control = 0, case = 1## Setting direction: controls < cases2.4.5 Hosmer-Lemeshow test
- Motivation
- We would like to know whether our model performs well for certain covariate patterns.
- Some researchers choose a set of important factors from the model, split the data into groups based on those factors, and then use a form of Pearson chi-square test on the cells formed by the groups (observed success vs. expected).
- Few researchers do this!!!
- In this case, the concern is too having too many choices to make and defend.
- It can, however, be a good way to identify “weaknesses” in the model for certain types of subjects.
- Hosmer and Lemeshow
- They proposed a more automated process
- The idea is to place the predicted probabilities into bins of similar size, such as deciles, and then compare the predictions to the expected outcome, bin by bin.
- We did this graphically, on a prior page, but repeat it here, again using deciles.
Code
dec <- quantile(preds1, probs = seq(0, 1, length = 11))
groups <- cut(preds1, breaks = dec, include.lowest = T)
y.prop <- tapply(bwData$LBW, groups, mean)
int.midpt <- (dec[-1] + dec[-11])/2
plot(int.midpt, y.prop, xlab = "Predicted proportion", ylab = "Observed proportion")
abline(a = 0, b = 1, col = 2)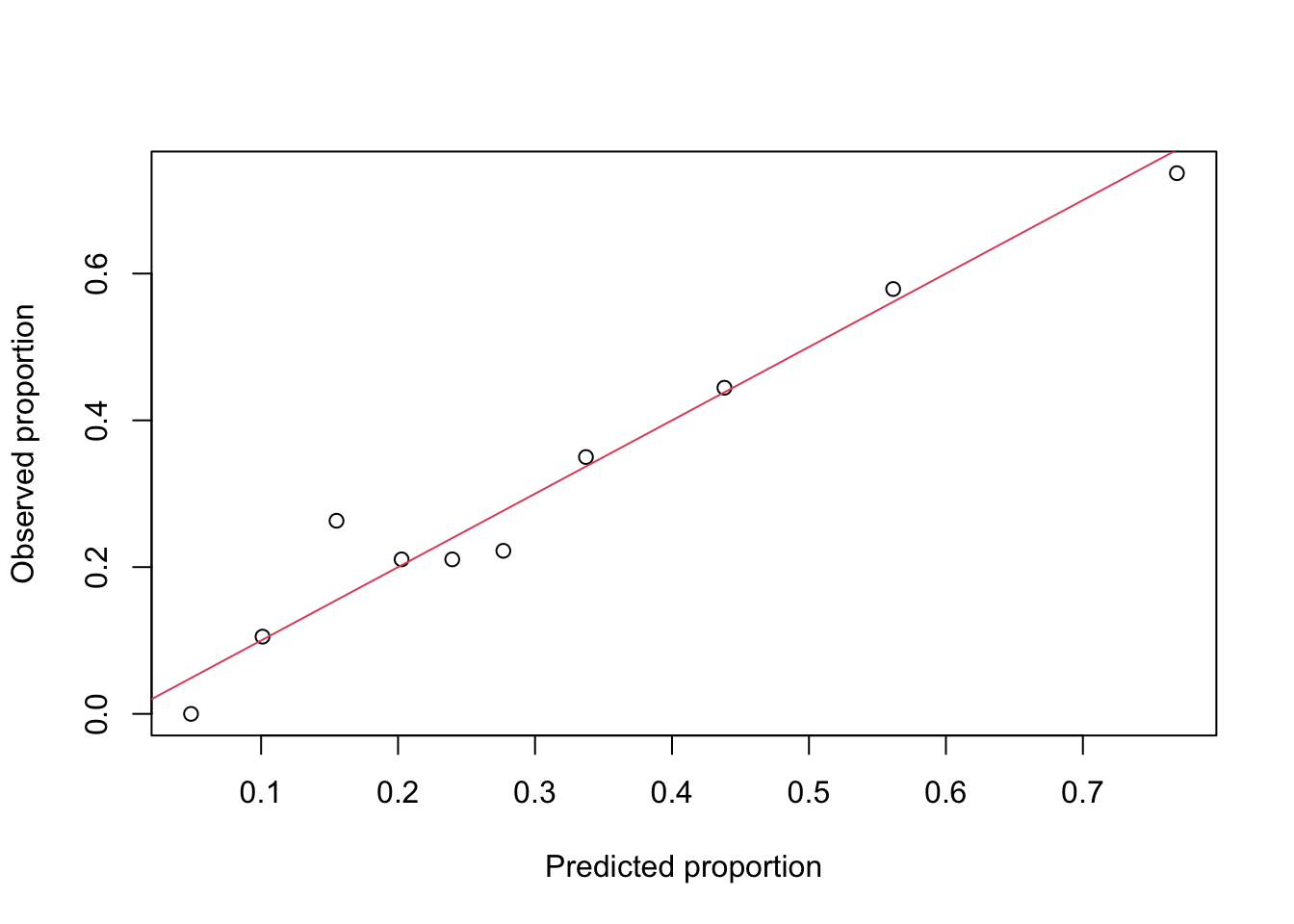
- The extent to which the points deviate from the line is a measure of fit.
- We see some deviation, but this is not a statistical test!
- The Hosmer-Lemeshow test
- A more formal approach
- Takes the expected proportion predicted (as a count) in each of the deciles as “expected” and then takes as observed the success counts for those observations in the original data. \[ H=\sum_{g=1}^{G}{\left( \frac{(O_{1g}-E_{1g})^2}{E_{1g}}+\frac{(O_{0g}-E_{0g})^2}{E_{0g}}\right)} \]
- Where \(G\) is the number of groups defined by the n-tiles, O is based on counts, and E is based on the model predictions.
- You can see that this is the classic \(\Sigma(O-E)^2/E\) that you see quite often, with the 0 and 1 “cells” indicated by subscripts.
- It may be simplified in some expositions.
- Note that the implementation in R is sensitive to the choice of number of groups (for even \(G\), whether it is a factor of the sample size seems to matter).
- A little trial and error should get the code to work.
- A “modified” version of the \(H\) statistic (mHL in the output, below) was developed to deal with some statistical problems the arose with the original.
- For our data/model the original and modified statistics are:
Code
gof(fit.lbw.logit1, g = 9, plotROC = F)$gof[1:2, ]## Setting levels: control = 0, case = 1## Setting direction: controls < cases- In both cases, we would not reject the null of “good fit.”
2.5 Deviance Statistic
- Deviance is similar to the Pearson goodness of fit test, but based directly on the likelihood.
- A full model uses as many explanatory variable as the number of observations.
- In this case, \(p_i=Y_i\), there is no model for \(p_i\) – or you may prefer to think of this as a model with indicators for every observation number!
- Deviance = 2[log L(full model)-log L(your model)] or \(D=2[\log L_S-\log L_M]\), where S stands for saturated and M for your model.
- For the logistic model, the deviance looks a lot like the deviance residual, since the latter was derived from it:
\[ D=2\sum_{i=1}^{n}{\left[Y_i\log\left(\frac{Y_i}{\hat p_i}\right)+(1-Y_i)\log\left(\frac{1-Y_i}{1-\hat p_i}\right)\right]} \] - Theory tells us that \(D\sim\chi^2_{n-p}\)
- Where \(n\) is the number of observations (and thus the number of parameters in the saturated model) and \(p\) is the number of parameters in the model of interest.
- A minor adjustment to the formula allows for a unique covariate group based assessment, which seems to be more commonly reported.
- For our working example the individual- and covariate-group-based deviances are, respectively:
Code
gof(fit.lbw.logit1, g = 9, plotROC = F)$chiSq[c(1, 3), ]## Setting levels: control = 0, case = 1## Setting direction: controls < casesand we see that neither would reject the null.
2.5.1 Likelihood Ratio Test
- The deviance is a specific likelihood ratio test (LR test).
- To compare two nested models, we can construct a likelihood based test that is the ratio between the likelihood of the two models.
- Equivalently it is the difference in (twice) their log-likelihoods.
- If Model A contains all parameters in model B (either explicitly or implicitly), then just as for R-square, the likelihood of A is bigger (or equal to) that of B.
- The LR test statistic is 2[log L(model A)-log L(model B)]
- Example
- Comparing our model with a simpler model that drops HYPER, URIN_IRR, PHYS_VIS:
Code
fit.lbw.logitA <- glm(LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST + HYPER + URIN_IRR + PHYS_VIS, data = bwData,
binomial(link = "logit"), contrasts = list(RACE = contr.sum))
fit.lbw.logitB <- glm(LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST, data = bwData, binomial(link = "logit"),
contrasts = list(RACE = contr.sum))
anova(fit.lbw.logitB, fit.lbw.logitA, test = "Chisq")## Analysis of Deviance Table
##
## Model 1: LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST
## Model 2: LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST + HYPER +
## URIN_IRR + PHYS_VIS
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 182 202.99
## 2 179 193.90 3 9.0881 0.02814 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- This tests the null: \(b_{\tiny \mbox{HYPER}}=0, b_{\tiny \mbox{URIN\_IRR}}=0, b_{\tiny \mbox{PHYS\_VIS}}=0\), which is rejected.
- Here, we are back to traditional tests in which we wish to reject the null to show “need” for inclusion of parameters.
- This tests the null: \(b_{\tiny \mbox{HYPER}}=0, b_{\tiny \mbox{URIN\_IRR}}=0, b_{\tiny \mbox{PHYS\_VIS}}=0\), which is rejected.
2.5.2 How to compare models when predictors are not nested?
- This approach is very useful when one model uses nonlinear terms such as step functions or indicators, while another uses linear terms.
- We can use the information criteria, such as Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC).
\[
AIC= -2 \log L+2p \\
BIC=-2\log L + p\log n
\]
- As stated previously, the BIC yields more parsimonious models.
- Some researchers characterize the AIC as searching for the optimal predictive model, while BIC is searching for the “true” model in a specific class of models.
- Even though the two models we’ve just examined are nested, we can still compare them using the AIC/BIC:
Code
AIC(fit.lbw.logitB, fit.lbw.logitA)
BIC(fit.lbw.logitB, fit.lbw.logitA)- Perhaps a bit surprising is the fact that AIC prefers the more complex model, while BIC does not.
- One way to “square” this with the LR test is that the LR test is a conditional test.
- We ask whether adding three predictors to model B improves it, and this assumes that it is a good model on its own.
- AIC, seeking to improve predictive performance agrees with the LR test.
- BIC, searching for a true model, penalizes the additional terms and chooses the simpler model.
- A more interesting comparison might be of the model that replaces MOTH_WT with indicator variables (<100 as light weight; >160 as heavy):
Code
fit.lbw.logitA <- glm(LBW ~ 1 + MOTH_AGE + MOTH_WT + RACE + SMOKE + PREM_HIST + HYPER + URIN_IRR + PHYS_VIS, data = bwData,
binomial(link = "logit"), contrasts = list(RACE = contr.sum))
fit.lbw.logitB <- glm(LBW ~ 1 + MOTH_AGE + I(MOTH_WT <= 100) + I(MOTH_WT > 160) + RACE + SMOKE + PREM_HIST + HYPER +
URIN_IRR + PHYS_VIS, data = bwData, binomial(link = "logit"), contrasts = list(RACE = contr.sum))
AIC(fit.lbw.logitB, fit.lbw.logitA)
BIC(fit.lbw.logitB, fit.lbw.logitA)- Here, the model using continuous weight is preferred by both AIC/BIC.
- We can only make such non-nested comparisons using the Information Criteria.
2.5.2.1 Exercise 7
Hint is visible here2.7 Coding
ifelse()resid()gof()AIC(), BIC()
ifelse()function is concise and efficient form of if-else statement as it uses vectorized computation. It takes arguments as follows:- logical_expression: an input vector
- a: executes when the logical_expression is true
- b: executes when the logical_expression is false
Code
bwData$LBW <- ifelse(bwData$BIRTH_WT < 2500, # logical_expression
1, # executes when the logical_expression is true
0) # executes when the logical_expression is falseresid()function extracts residuals from the object using modeling function. It takes arguments as follows:- object: an object (from binomial family) for which the extraction of model residuals is meaningful.
- type: type of residuals to be returned.
- “approx.deletion”, “exact.deletion”,“standard.deviance”, “standard.pearson”, “deviance”,“pearson”, “working”, “response”, “partial”
Code
# Raw or response residuals
res1 <- resid(fit.lbw.logit1, type = "response")
# Pearson residual
res2 <- resid(fit.lbw.logit1, type = "pearson")
# Deviance residuals
res3 <- resid(fit.lbw.logit1, type = "deviance")gof()function gives a chi-squared test of goodness of fit for glm models by calculating the deciance and the Pearson chi-squared statistics for the model. It takes arguments as follows- object: an object of glm class
- x: an object of class gof()
- digits: a number of digits to be printed
- plotROC: plotting a ROC curve
Code
# first, import LogisticDx library
require(LogisticDx)
# run goodness of fit
LogisticDx::gof(fit.lbw.logit1, g = 9, plotROC = TRUE)## Setting levels: control = 0, case = 1## Setting direction: controls < cases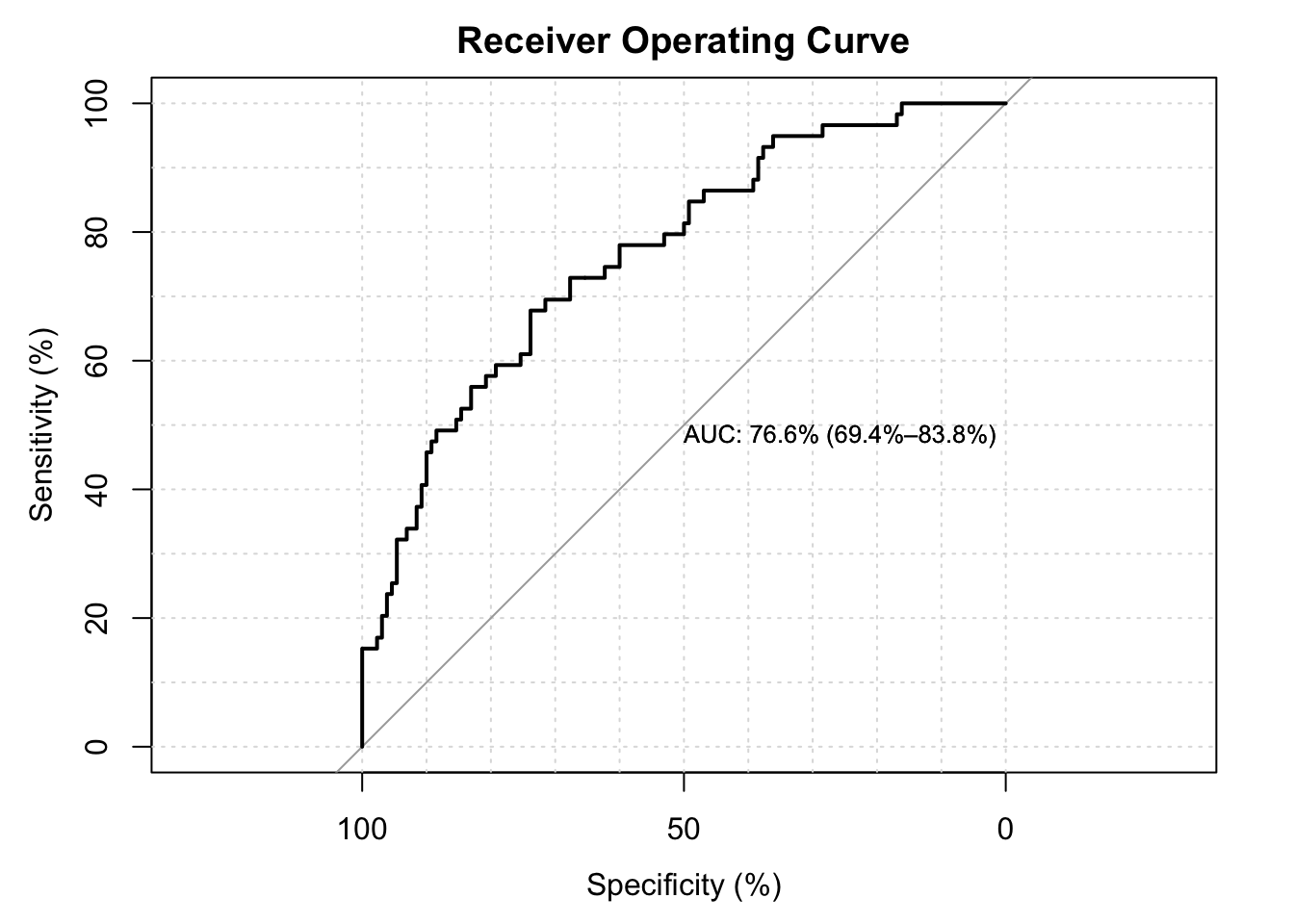
## chiSq df pVal
## PrI 1 2 4
## drI 2 2 2
## PrG 1 1 3
## drG 2 1 1
## PrCT 1 1 3
## drCT 2 1 1
## val df pVal
## HL chiSq 9 3 8
## mHL F 6 4 7
## OsRo Z 7 5 1
## SstPgeq0.5 Z 5 5 4
## SstPl0.5 Z 3 5 6
## SstBoth chiSq 4 2 9
## SllPgeq0.5 chiSq 2 1 3
## SllPl0.5 chiSq 1 1 5
## SllBoth chiSq 8 2 2AIC(), BIC()functions calculate Akaike’s Information Criterion and Bayesian Information Criteria for one or several fitted model objects. Functions take arguments as follows:- object: a fitted model object
- k: the penalty per parameter to be used
Code
# AIC
AIC(fit.lbw.logitB, fit.lbw.logitA)
# BIC
BIC(fit.lbw.logitB, fit.lbw.logitA)2.8 Exercise & Quiz
2.8.1 Quiz: Exercise
Use “Quiz-W2: Exercise” to submit your answers.
What is the probability of seeing exactly 3 out of 10 students smoking if the smoking prevalence is 5%? (link to exercise 1)
What is the probability that a specific student smokes if the smoking prevalence is 5%? (link to exercise 2)
If we have a hypothetical group of smokers (the risk factor) and non-smokers, then we can examine the prevalence of lung cancer (the event of interest). We find 14 smokers have lung cancer, 86 smokers do not have lung cancer, one non-smoker has lung cancer, and 99 non-smokers do not have lung cancer. Calculate the odds ratio and interpret (in words). (link to exercise 3)
Discuss from this result whether it is true that “there is great risk, on average, in this population.” What is wrong with this interpretation (hint: think about the reference group)? (link to exercise 4)
Explain what the constant now refers to (under centering), and the implication for prevalence? (link to exercise 5)
From this ROC curve, you set your test to have a 50% false negative rate. What is the test’s false positive rate? (link to exercise 6)
There is an implicit assumption that is made about the “response surface” when a continuous predictor is replaced by a binary one based on a threshold. Could there be a situation in which replacement by several binary variables actually could yield a better model fit than the continuous variable? (link to exercise 7)
2.8.2 Quiz: R Shiny
- Questions are from R shiny app “Lab1: Binary response data”.
- Use “Quiz-W2: R Shiny” to submit your answers.
[The determinants of low birth weight]
What are the log-odds of low birth weight?
Verify that the baseline log-odds (the intercept term of the model) equals the observed log-odds of LBW in the data that you computed in the previous exercise.
[Adding predictors]
Compute the odds ratio of PremY=1 versus PremY=0 by exponentiating the corresponding regression coefficient.
Which of the following are statistically significant (at p < 0.05) risk factors for low birth weight?
[The probit link]
- Which of the following are statistically significant (at p < 0.05) risk factors for low birth weight?
[Choosing a link function]
Comparing residual deviance is another way to compare model fit (lower deviance is better). Which link function is better according to residual deviance?
Which of the three link functions, based on the log-likelihood, is best for our model of low birth weight?
[Interaction effects]
- All else equal, compared to a non-smoker with no hypertension history, how much greater are the odds of low birth weight for a woman who smokes and has a history of hypertension?
[Classification accuracy]
- Compute the classification accuracy of the model.
[Sensitivity and specificity]
Compute the sensitivity of the model.
Now compute the specificity of the model.
[Pearson’s \(X^2\) test]
- Compute the \(X^2\) for that model and its p-value.
[The deviance test]
- Perform the deviance test by computing the test statistic and then the p-value according to the appropriate chi-squared distribution. Compute the p-value.
2.8.3 Quiz: Chapter
- Use “Quiz-W2: Chapter” to submit your answers.
What are NOT the examples of a link function?
Compute the ratio of odds of the event (LBW) for people with a risk factor versus people without a risk factor
What are NOT the examples of a link function?
Compute the probability of p when 4 to 3 odds
Select the response: Significance tests for odds ratio tests for difference from 1.
What are NOT the benefits of using Odds Ratio?
What is the RIGHT description about the centering?
What is the main difference between probit and logit link regression?
What is the benefit of using ROC curve?
What is NOT right description about the Likelihood Ratio Test?