Chapter 19 Bonus: Choosing the K
Source: https://www.datanovia.com/en/lessons/determining-the-optimal-number-of-clusters-3-must-know-methods/
Want to determine the optimal number of clusters? Below, we use 3 different strategies, wss, silhouette, and gap_stat (the last one takes the longest). These strategies can also be used to analyze different clustering strategies (not just k-means).
One important way to interpret all k-selection models is to use the “elbow method.” In the elbow method, you are looking for a specific “elbow” in your data. When there is an elbow, the number of clusters (k) dramatically improves compared to its previous number of k (for example, 3 is way better than 2), but it does not improve as you increase the number of clusters (so 4 is not much better than 2).
19.1 WSS
fviz_nbclust(survey_data, kmeans, method = "wss") +
geom_vline(xintercept = 4, linetype = 2)
In this example, 4 appears to be the most optimal cluster, but there is also a marked drop in 2, which suggests that this may also be a useful number to cluster by.
19.2 Silhouette
Silhouette determines the quality of the cluster. If an observation fits well in a cluster, it will have a high average. Therefore, the higher the number, the better the clustering k.
fviz_nbclust(survey_data, kmeans, method = "silhouette")+
labs(subtitle = "Silhouette method")
Note that the results of silhouette differ somewhat from wss. Rather than stressing out over how different they are, I encourage you to use information from both to determine the optimal number of k’s. In your paper, you should report the results of just the main model you have selected.
19.3 Gap Statistic
In this analysis, the model compares inta-cluster variation with their expected values.
set.seed(123)
fviz_nbclust(survey_data, kmeans, nstart = 25, method = "gap_stat", nboot = 50)+
labs(subtitle = "Gap statistic method")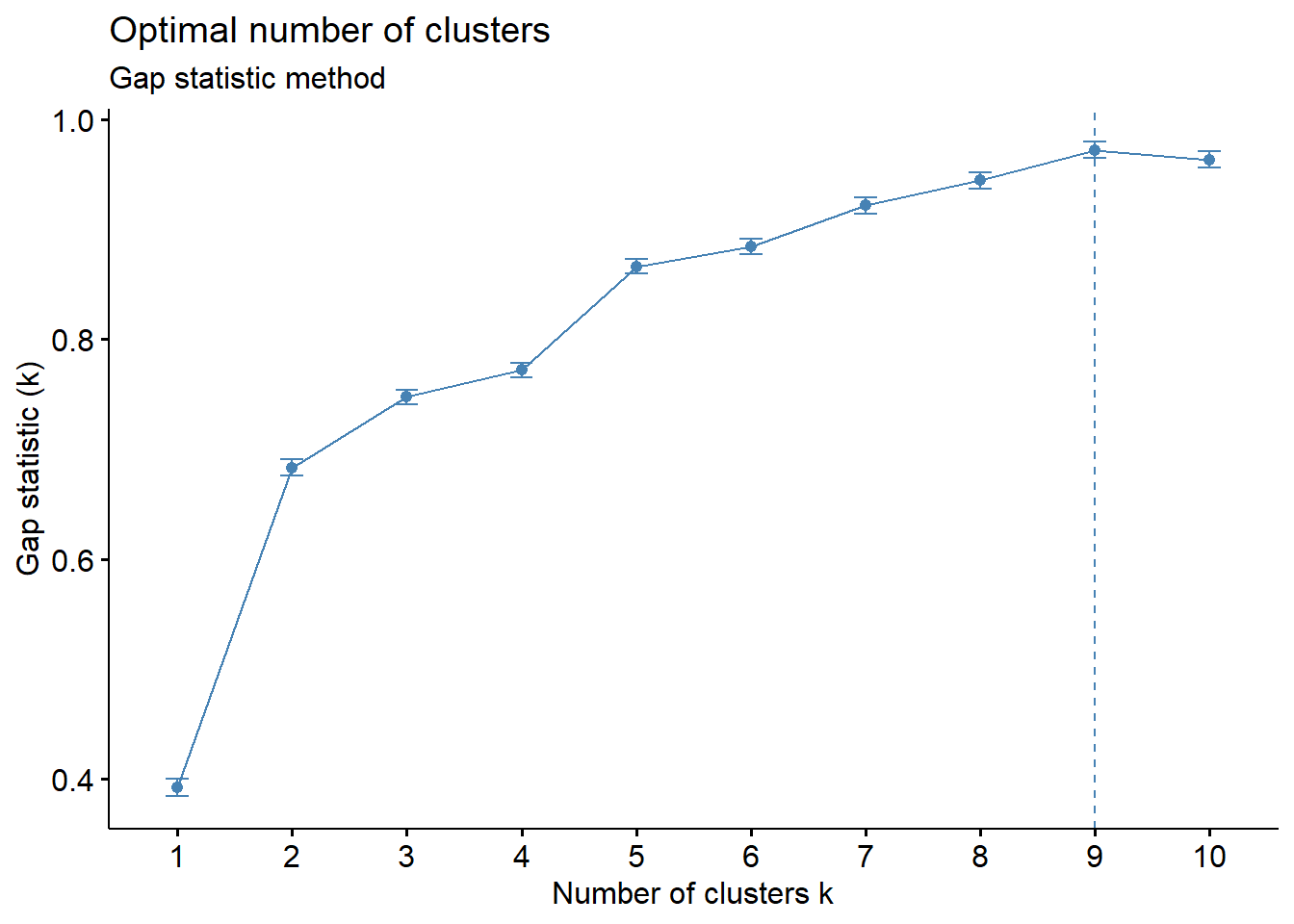
Want more practice with LDA topic modeling? Check out these tutorials: