2 The Rasch model (1PLM)
The item response function (IRF) for item \(i\) is given by
\[\begin{equation} P(X_i=1|\theta) = \frac{\exp(\theta - \delta_i)}{1 + \exp(\theta-\delta_i)}, \tag{2.1} \end{equation}\]where
\(\theta\) is the person’s latent ability parameter;
\(\delta_i\) is the item’s difficulty or popularity.
This IRF is known as the one-parameter logistic model because it involves only one item parameter (difficulty \(\delta\)) and its functional form is based on the logistic function.
Figure 2.1 shows three examples of IRFs under the Rasch model for three difficulty levels: \(\delta = -1\) (blue), \(\delta = 0\) (red), and \(\delta = 1.5\) (green).
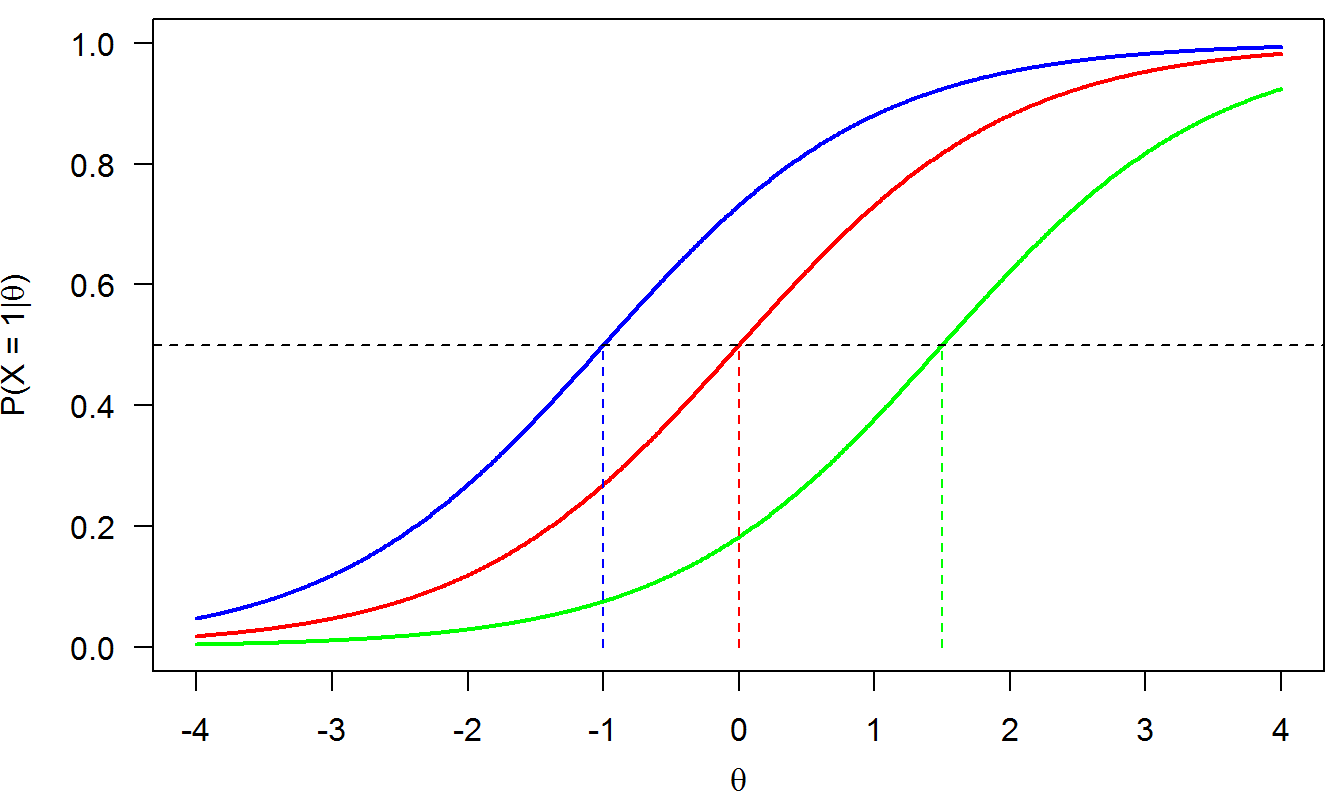
Figure 2.1: 1PLM (Rasch model)
Properties of IRFs from the Rasch model:
The probabilities increase with the latent trait \(\theta\) for each item. So, the higher the latent trait, the higher the probability of answering the item correctly.
The curves are ‘parallel’, that is, they do not intersect.
Items differ only in difficulty: Easier items are on the left (low difficuly \(\delta\), like the blue item) and difficult items are on the right (high difficulty \(\delta\), like to green item).
Parameter \(\delta\) is the value of latent trait for which the probability of answering the item correctly is 50%: \(P(X = 1|\theta=\delta) = .50\).