Chapter 7 Functions of two variables

7.1 Introduction

‘’If I have seen farther than other men, it is because I have stood on the shoulders of giants.’’

Isaac Newton (1642-1727)

‘’If I have not seen as far as others, it is because giants were standing on my shoulders.’’

Hal Abelson (1947-)

In this chapter we are going to study real functions of two variables, that is, functions \(f:{\mathbb R} \times {\mathbb R} \rightarrow {\mathbb R}\) associating to each pair of real number \((x,y)\) a real number \(y=f(x,y)\). Next semester we will look at the concepts of limit and continuity. In this chapter we will look at derivatives, for the purpose of understanding gradient on surfaces, as well as finding maxima and minima in two dimensions.

We begin with some examples.

Example 7.1 Suppose we want to describe the elevation above see level of each point on the surface of a mountain. For simplicity, suppose that the mountain just looks like a cone, with the base at sea level. The altitude can be represented by the function \[\begin{eqnarray*} f:D & \longrightarrow & {\mathbb R} \\ z & = & f(x,y), \end{eqnarray*}\] associating to each point in the cone’s base to the corresponding altitude. Here, the cone base is represented by a subset of the real plane \(D\subset{\mathbb R}^2\): this is the map of the mountain. Each point in \(D\) can be uniquely represented by a pair of coordinates \((x,y)\). An appropriate function here is \[ z=2-\sqrt{x^2+y^2}), \] and the region \(D=\{(x,y): x,y \in [-1,1] \}\).

Example 7.2 To represent the temperature in each point of your study room, we can use a function of three variables: \[ f:D \longrightarrow {\mathbb R}, \qquad T=f(x,y,z). \] Here, the domain \(D\subset{\mathbb R}^3\) describes the room and the the output value \(T\) the temperature as a function of position in space. For instance \[ T=(a^2-x^2)(y^2-b^2)(z^2-c^2), \] where \(D=[-a,a] \times [-b,b] \times [-c,c]\). Obvioulsy it is difficult to visualise such functions, and it is a skill to find a good way to visualise information.

Example 7.3 What if we want also to keep track on how the temperature changes with time? Well, just add one more variable, \(t\) for time, and describe the temperature as a function of both position in space and time: \[ f:D\longrightarrow{\mathbb R}, \qquad T=f(t,x,y,z). \] Here, the domain \(D\subset {\mathbb R}^4\) describes the time-space domain given by the room the time interval of interest. For instance, suppose the temperature decays in time exponentially then we might have a formula of the type \[ T=(a^2-x^2)(y^2-b^2)(z^c-c^2)\exp(-2t), \] with \(D=[0,\infty) \times [-a,a] \times [-b,b] \times [-c,c]\).

7.2 Partial Derivatives

If we imagine ourselves on a mountainside, we know that the slope can be different in different directions. This is how we skiers manage to get down very steep slopes slowly, by moving across the slope. We can work out how much things are changing along a particular line. In the following picture from Mathsinsight.org https://mathinsight.org/

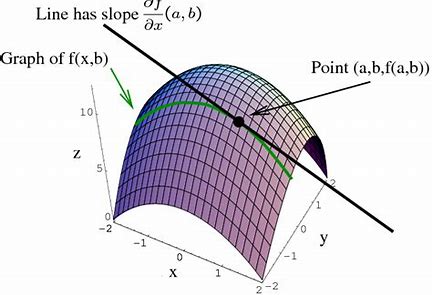
We are looking at the changes to the function \(f(x,y)\) if we fix \(y=b\). For instance, suppose we think about the cone \(f(x,y)=2-\sqrt{x^2+y^2}\), and put \(y=0.5\), then we are looking at the function \(g(x)=f(x,0.5)=2-\sqrt{x^2+1/4}\). Then we can explore the rate of change of \(f\) along the line \(y=-0.5\) by differentiating \(g\) with respect to \(x\).

Definition 7.1 (Partial derivatives of a function of two variables) Let \(f\) be a function of two variables \(x,y\). The partial derivatives of \(f\) with respect to \(x\) and \(y\) are, respectively, \[\begin{eqnarray*} f_x(x,y) & = & \lim_{h\rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h},\\ f_y(x,y) & = & \lim_{h\rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}. \end{eqnarray*}\] The partial derivatives measures the rate of change of \(f\) with respect to one variable.

Remark. Alternative notation for first partial derivatives

The following are other notations for first partial derivatives you should be aware of: \[\begin{eqnarray*} f_x(x,y)=f_1(x,y)& = & \frac{\partial f}{\partial x}(x,y)=D_1 f(x,y),\\ f_y(x,y)=f_2(x,y) & = & \frac{\partial f}{\partial y}(x,y)=D_2 f(x,y). \end{eqnarray*}\]

Finding the partial derivatives of a function, is pretty straightforward if you know how to take derivatives of single-variable functions. Indeed, by definition, the partial derivative, say, with respect to \(x\), is the derivative of the function when \(y\) is fixed. The procedure is illustrated with the following examples.

Example 7.4 Let \(f(x,y)=x^2y^3+3x^2y\). Then \[\begin{eqnarray*} f_x(x,y)& = & 2xy^3+6xy,\\ f_y(x,y)& = & f_2(x,y) & = & \frac{\partial f}{\partial y}(x,y)=D_2 f(x,y). \end{eqnarray*}\]

The following is a more complicated example.

Example 7.5 Find the first partial derivatives of the function \(f(x,y)=x \arctan (xy)+\exp(2y)\). Evaluate the partial derivatives at the point \((x,y)=(1,0)\).

Thinking of \(y\) as a consant we have \[ {\partial f \over \partial x} = \arctan (xy) + {xy \over 1+(xy)^2}=0, \] when \((x,y)=(1,0)\). With \(x\) as a constant we have \[ {\partial f \over \partial y} = {x^2 \over 1+(xy)^2}+2\exp(2y)=3. \] when \((x,y)=(1,0)\).

Here is a video with some more examples:

YOutube clip with more examples

7.3 Partial derivatives of higher order

Again, we consider first just functions of two variables. Suppose that \(f\) is a function of the two variables \(x,y\) admitting first partial derivatives in its domain of definition. As the partial derivatives \(f_x\) and \(f_y\) are again functions of \(x\) and \(y\), they may themselves possess partial derivatives \((f_x)_x\), \((f_x)_y\), \((f_y)_x\) \((f_y)_y\). These functions are the second-order partial derivatives of \(f\). For these, we introduce the following notation. The two pure second partial derivatives \[\begin{eqnarray*} f_{xx}& = & f_{11}=\frac{\partial^2 f}{\partial x^2}=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\right):=(f_x)_x,\\ f_{yy} & = & f_{22}=\frac{\partial^2 f}{\partial y^2}=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial y}\right):=(f_y)_y, \end{eqnarray*}\] and two mixed second partial derivatives \[\begin{eqnarray*} f_{xy} & = & f_{12}=\frac{\partial^2 f}{\partial y\partial x}=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right):=(f_x)_y,\\ f_{yx} & = & f_{21}=\frac{\partial^2 f}{\partial x\partial y}=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right):=(f_y)_x. \end{eqnarray*}\] These are, by definition, calculated by taking partial derivatives of already calculated partial derivatives.

Example 7.6 Calculate the second partial derivative of the function \(f(x,y)=y\exp(x^2)+xy\).

We start by calculating the first partial derivatives: \[ f_x(x,y)=2xy\exp(x^2)+y,\qquad f_y(x,y)=\exp(x^2)+x, \] and then get the second partial derivatives by taking the partial derivatives of \(f_x\) and \(f_y\): \[ \begin{array}{ll} f_{xx}=(2xy\exp(x^2)+y)_x=(2y+4x^2y)\exp(x^2),\quad &f_{xy}=(2xy\exp(x^2)+y)_y=2x\exp(x^2)+1,\\ f_{yx}=(\exp(x^2)+x)_x=2x\exp(x^2)+1, \quad& f_{yy}=(\exp(x^2)+x)_y=0. \end{array} \]

Notice that, in the example above, it happened that \(f_{xy}=f_{yx}\). It turns out that this is not by chance.

We can have examples in higher dimensions.

Example 7.7 Calculate all first and second partials of \(f(x,y,z)=\sin(x) y z^3\). Verify the equality of the mixed partial derivatives, namely: \[ f_{xy}=f_{yx},\quad f_{xz}=f_{zx},\quad f_{yz}=f_{zy}. \]

The three first partial derivatives of \(f\) are: \[ f_x=\cos(x)y z^3, \quad f_y=\sin(x)z^3, \quad f_z=3\sin(x)yz^2. \] We get the second partials by computing, for each first partial derivative, its three first partial derivatives: \[ \begin{array}{lll} f_{xx}=-\sin(x)y z^3, & f_{xy}=\cos(x)z^3, & f_{xz}=3\cos(x)y z^2,\\ f_{yx}=\cos(x)z^3, & f_{yy}=0, & f_{yz}=3\sin(x) z^2,\\ f_{zx}=3\cos(x)y z^2, & f_{zy}=3\sin(x) z^2, & f_{zz}=6\sin(x)yz. \end{array} \] We can see that the mixed derivatives are equal.

7.4 The Gradient and Linear Approximation

In one dimension a function is differentiable at a point if we can define the tangent at the point. In two dimesions we need to be able to define the tangent plane at the point. Recalling Taylor series in one dimension in Section 5 we know that the tangent line at a point \((b,f(b))\) is \[ y=f(b)+(x-b)f'(b). \]

So how can we generalise the concept of differentiability and the idea of linear approximation, to functions of several variables?

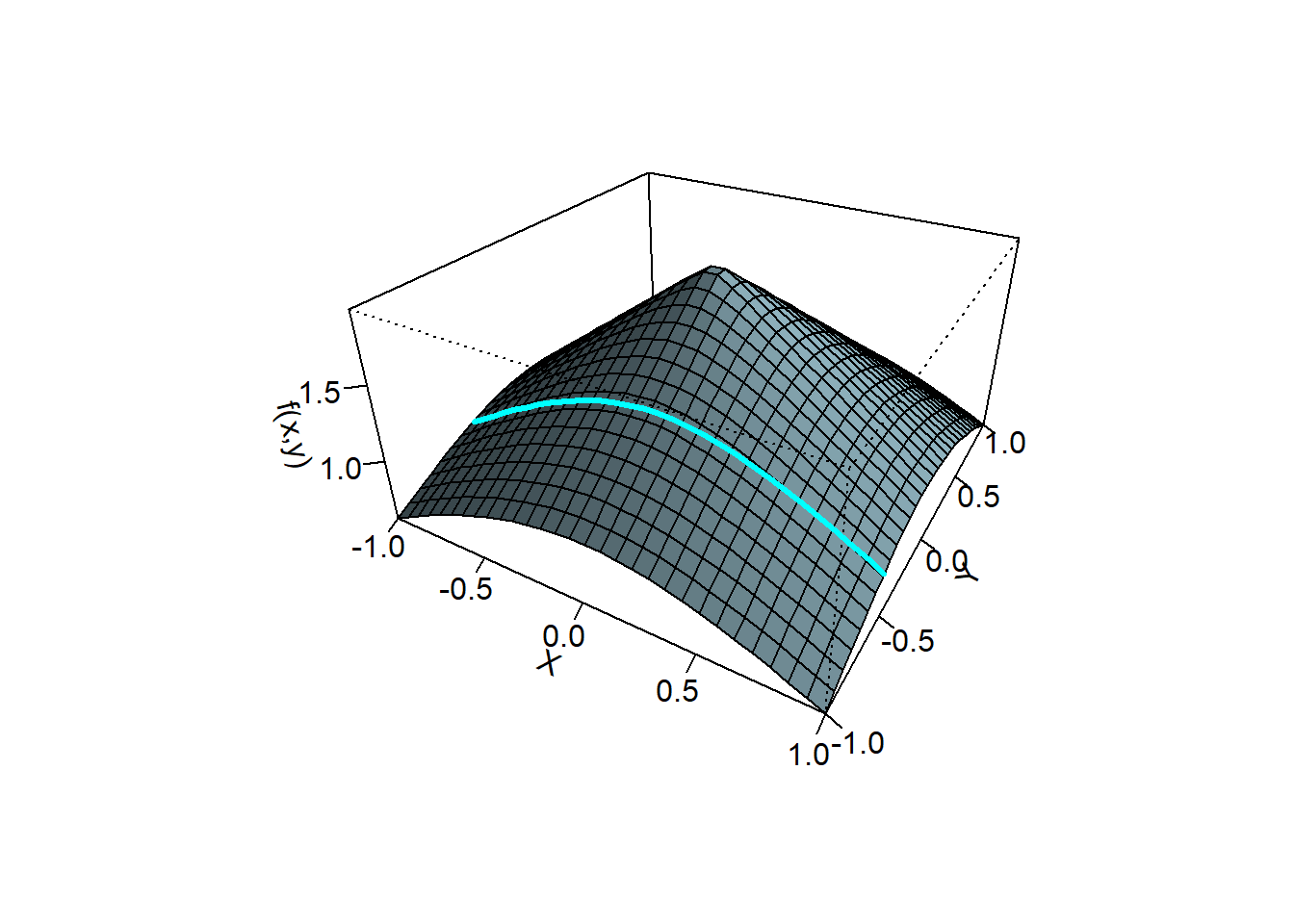
First of all we need to generalise the definition of slope. We do this by introducing the gradient vector. This vector has components which are the slopes on the surface at the point of interest in both directions. In the picture below we look at the tangents to the lines in the surface passing through \((-1/2,1/2)\).

Definition 7.2 (Gradient Vector) Let \(f\) be a function of two variables with first order partial derivatives. Then the gradient vector \[ \nabla f(x,y) = \left ( {\partial f \over \partial x}, {\partial f \over \partial x} \right ). \]

Example 7.8 Find the gradient of the function \(f(x,y)=x \arctan (xy)+\exp(2y)\) at the point \((x,y)=(1,0)\).

As we see in Example~??, \(f_x(1,0)=0\) and \(f_y(1,0)=3\). Hence \[ \nabla f(1,0)=(0,3). \]

Remark. This can be generalised to higher dimensions. Let \(f\) be a function of 3 variables with first order partial derivatives. Then the gradient vector \[ \nabla f (x,y,z) = \left ( {\partial f \over \partial x}, {\partial f \over \partial x}, {\partial f \over \partial z}\right ). \]

The tangent plane contains the tangent lines to these two curves in the surface.

7.4.0.1 Example 7.10

Find the gradient of the function \(f(x,y,z)=x^2y\sin(z)\) at the point \((x,y,z)=(1,2,\pi/3)\).

The first order partial derivatives \[ \nabla f(x,y,x)=(2xy \sin(z), x^2 \sin(z), x^2 y \cos(z)) = (2 \sqrt{3},\sqrt{3},1). \]

Note that the echo = FALSE parameter was added to the code chunk to prevent printing of the R code that generated the plot.