Kapitel 8 Regressionsanalys
Syftet med en linjär regressionsanalys är att uppskatta den linje som bäst beskriver förhållandet mellan två variabler (med eller utan kontroll för inverkan av kontrollvariabler). Hur mycket förändras den beroende variabeln om den oberoende variabeln ändras? Exempel på en sådan fråga kan vara: för varje år som en person arbetar vid samma arbetsplats, hur mycket ökar lönen?
8.1 Exempel regressionsanalys
I vårt exempel är vi intresserade av att förklara variationer i människors förtroende för rättsväsendet. Den beroende variabeln är alltså förtroende för rättsväsendet. Det är alltså förtroende för rättsväsendet som vi är intresserade av att se hur den förändras, beroende på värdet på våra oberoende variabler i regressionsanalysen. I vårt material så mäts detta med ett kontinuerligt förtroendeindex, som ni vid det här laget bör vara bekanta med (se avsnitt 3.3.4).
Vi kommer i exemplet att använda data från Nationella Trygghetsundersökningen år 2021.
8.1.0.1 HYPOTES 1
I vårt fall så har vi skäl att tro att personer som har polisanmält ett brott under de tre senaste åren, alltså personer som har haft en typ av direktkontakt med rättsväsendet, har något lägre förtroende för rättsväsendet än de som inte har polisanmält något brott. Hypotesen grundar sig i ett antagande om att relativt få anmälda brott klaras upp, vilket kan påverka förtroendet för att rättsväsendet löser sin uppgift på ett effektivt sätt.
Den oberoende variabeln, polisanmälan, skall vi strax skapa utifrån en enkätfråga i Nationella Trygghetsundersökningen. Men först behöber vi säga ett par ord om denna typ av variabel. Den oberoende variabeln, polisanmälan, utgör nämligen ett särskilt fall inom linjär regressionsanalys. Den mäts på nominalskalenivå och kan vara anta ett av två möjliga värden (man brukar även kalla detta för en ”dikotom” variabel). Om vi inkluderar den i en regressionsanalys så kommer vi att få en regressionskoefficient, precis som om vi hade inkluderat en kontinuerlig variabel (exempelvis ålder, eller inkomst). Det som är speciellt är att variabeln blir så kallat ”dummy kodad”, det vill säga att vi har ett värde på variabeln som är med i regressionsmodellen och som jämförs med ett referensvärde som hamnar i regressionsmodellens intercept.
I det här särskilda fallet så är det variabelvärdet ”Nej” som kommer att bli referenskategori, och regressionskoefficienten kommer att representera den genomsnittliga förändringen i förtroende för polisens effektivitet om vi jämför variabelvärdet ”Ja” (har blivit polisanmät brott) med referenskategorin ”Nej” (har inte polisanmält brott).
Det vill ta reda på är hur mycket lägre förtroende för polisens effektivitet som de som har polisanmält ett brott har har, om vi jämför med de som inte har anmält något brott. Polisanmälan (huruvida man polisanmält eller inte) är alltså vår huvudsakliga oberoende variabel.
Som du säkert har förstått så skulle den här frågan egentligen också kunna undersökas med hjälp av medelvärdesanalys och ett t-test. Det som är speciellt med regressionsanalysen är dock att vi kan inkludera flera variabler samtidigt i samma modell, vilket vi vill göra i det här fallet.
Att inkludera fler än en variabel möjliggör för oss att ställa flera frågor än vad vi kan göra med en medelvärdesanalys. Vi har i det här fallet skäl att tro att det är oro för brott (som kan öka om man blir utsatt för brott som man har polisanmält) som förklarar en del av den genomsnittliga skillnaden som vi kan se mellan de som har polisanmält brott och de som inte har polisanmält något brott vad gäller just förtroende för rättsväsendet.
8.1.0.2 HYPOTES 2
Vi är alltså intresserade av att se hur oro för brott förhåller sig till förtroende för rättsväsendet. Vi har en hypotes om att desto mer oroliga människor är för brott, desto lägre förtroende har de för rättsväsendet. Eller omvänt, att människor som inte känner oro för brott i någon större utsträckning också har ett högre förtroende för rättsväsendet. Vi grundar vår hypotes på antagandet att människor som är oroliga för brott delvis upplever att rättsväsndet inte räcker till för att skydda dem (eller andra personer de bryr sig om) mot brott.
Vi vill därför veta om sambandet mellan att polisanmält ett brott och förtroende för rättsväsendet kvarstår (om det ser likadant ut eller förändras) om vi kontrollerar för en variabel som mäter oro för brott.
8.1.0.3 Kontrollvariabler
Vi är också intresserade av att se om sambandet mellan att ha anmält ett brott brott och förtroende för rättsväsendet, samt om sambandet mellan oro för brott och förtroende för rättsväsendet, kvarstår (om det ser likadant ut eller förändras) om vi kontrollerar några vanliga sociodemografiska variabler som ålder, kön och utbildning.
Genom att kontrollera för fler variablers inverkan på variationen i den beroende variabeln (förtroende för rättvsäsendet) så ”renodlar” vi sambandet mellan den oberoende variabel som vi är intresserad av (polisanmälan respektive oro för brott) och beroende variabeln (förtroende för rättsväsendet).
Den slutliga tolkningen av en sådan här multipel linjär regressionsanalys (multipel eftersom modellen har fler än en oberoende variabel) är: hur mycket lägre förtroende för rättsväsndet har de som polisanmält brott jämfört med de som inte har polisanmält brott, om vi samtidigt tar hänsyn till rädsla för brott samt kön, ålder och utbildningsskillnader som kan finnas mellan de som polisanmält respektive inte polisanmält.
Omvänt kan en också säga att givet att vi har en två personer som är lika rädda för brott, av samma kön, lika gamla och med samma utbildning, hur mycket lägre förtroende för rättsväsendet har den som har blivit anält ett brott, jämfört med den som inte har anmält något brott?
8.1.0.4 HYPOTES 3
Vi vill också pröva en sista hypotes, som rör hur våra två huvudsakliga oberoende variabler, polisanmälan och oro för brott, interagerar med varandra. Vi har ett antagande om att sambandet mellan oro för brott och förtroende för rättsväsendet borde vara starkare bland de som har polisanmält ett brott, jämfört med bland de som inte har polisanmält något brott. Detta blir alltså vår tredje, och sista hypotes.
8.2 Övningsdata
För att pröva våra hypoteser ovan behöver vi skapa en data frame som innehåller de variabler vi är intresserade av:
Förtroende för rättsväsendet (skapat i förra avsnittet )
Polisanmälan (Fråga/Variabel E1, sida 25 i Kodbok NTU2017-2021)
Oro för brott (index, Fråga/Variabler C6, C9, C10, C11, C12, sidor 12-14 i Kodbok NTU2017-2021)
Kön (skapat i förra avsnittet)
Ålder (skapat i förra avsnittet)
Utbildning (Fråga/Variabel Utbildning3, sida 4 i Kodbok NTU2017-2021)
Vi använder data från Nationella Trygghetsundersökningen 2021, genom att utgå från vår data frame ntu2021 (skapat i förra avsnittet). Vi skapar ett ny data frame med våra variabler som vi döper till reg_data:
## 1 2 NA's
## 15191 58515 645ntu2021$polisanmalt <- as.factor(case_match(ntu2021$E1,
1 ~ "Ja, polisanmält senaste 3 åren",
2 ~ "Nej, inte polisanmält senaste 3 åren",
.default = NA))
ntu2021$polisanmalt <- factor(ntu2021$polisanmalt, levels=c("Nej, inte polisanmält senaste 3 åren", "Ja, polisanmält senaste 3 åren"))
summary(ntu2021$polisanmalt)## Nej, inte polisanmält senaste 3 åren Ja, polisanmält senaste 3 åren NA's
## 58515 15191 645#Oro för brott#
C <- data.frame(ntu2021$C6,
ntu2021$C9,
ntu2021$C10,
ntu2021$C11,
ntu2021$C12)
psych::alpha(C)##
## Reliability analysis
## Call: psych::alpha(x = C)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.86 0.86 0.85 0.55 6.1 0.00084 3.8 0.9 0.56
##
## 95% confidence boundaries
## lower alpha upper
## Feldt 0.86 0.86 0.86
## Duhachek 0.86 0.86 0.86
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
## ntu2021.C6 0.85 0.85 0.83 0.59 5.8 0.00091 0.0153 0.57
## ntu2021.C9 0.80 0.80 0.77 0.51 4.1 0.00117 0.0127 0.55
## ntu2021.C10 0.79 0.79 0.76 0.49 3.8 0.00126 0.0097 0.53
## ntu2021.C11 0.86 0.86 0.84 0.60 6.1 0.00087 0.0109 0.57
## ntu2021.C12 0.83 0.83 0.81 0.55 4.9 0.00105 0.0234 0.56
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## ntu2021.C6 73929 0.74 0.74 0.63 0.59 3.4 1.2
## ntu2021.C9 73899 0.85 0.86 0.85 0.77 4.1 1.0
## ntu2021.C10 73876 0.89 0.89 0.89 0.81 3.8 1.1
## ntu2021.C11 73850 0.71 0.71 0.60 0.55 4.3 1.1
## ntu2021.C12 73886 0.80 0.80 0.72 0.67 3.1 1.2
##
## Non missing response frequency for each item
## 1 2 3 4 5 miss
## ntu2021.C6 0.06 0.17 0.26 0.30 0.21 0.01
## ntu2021.C9 0.02 0.06 0.17 0.26 0.48 0.01
## ntu2021.C10 0.04 0.10 0.20 0.30 0.36 0.01
## ntu2021.C11 0.04 0.06 0.11 0.18 0.62 0.01
## ntu2021.C12 0.10 0.23 0.27 0.25 0.14 0.01ntu2021$oro_index <- ntu2021$C6 +
ntu2021$C9 +
ntu2021$C10 +
ntu2021$C11 +
ntu2021$C12
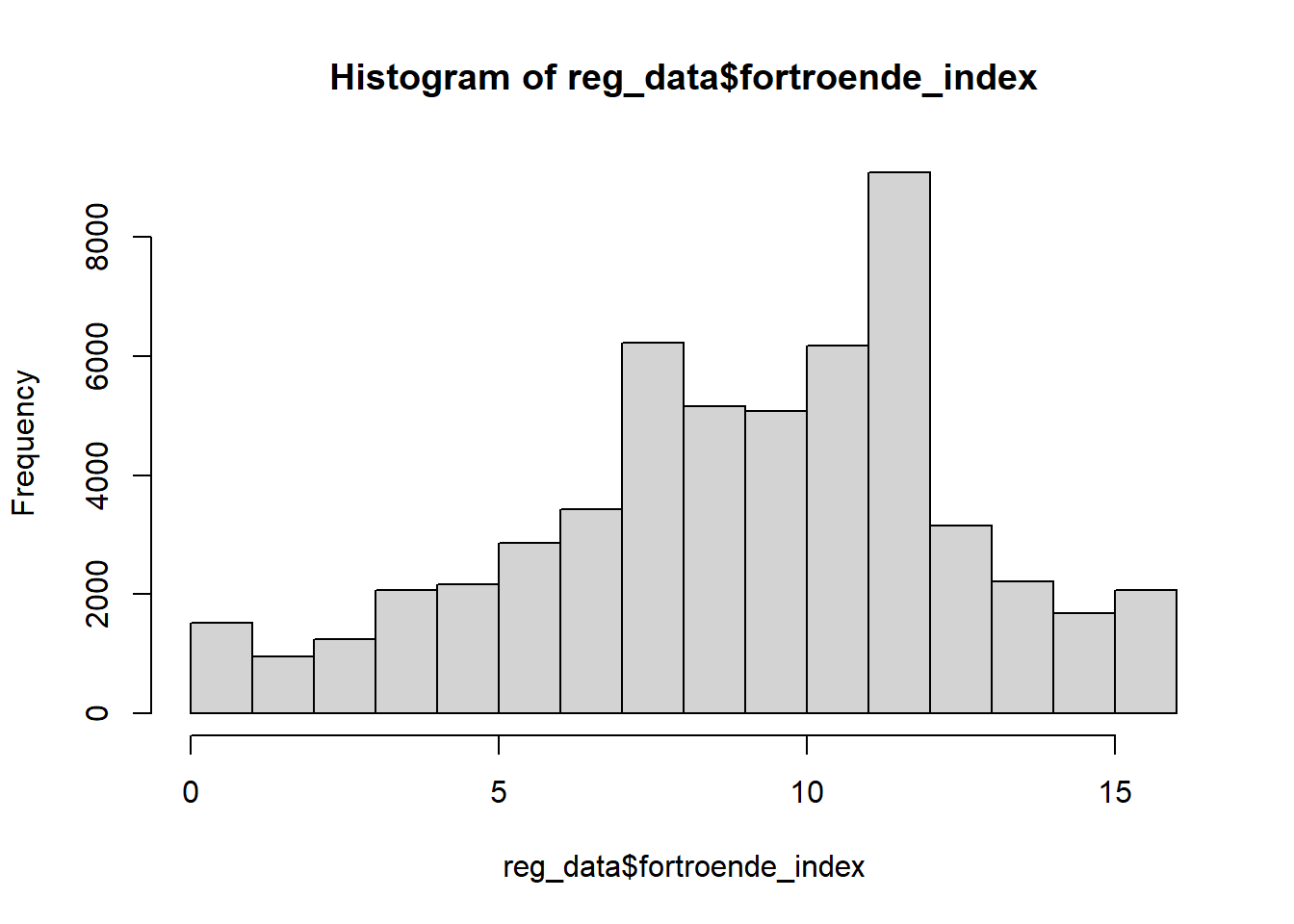
hist(ntu2021$oro_index, n = 20)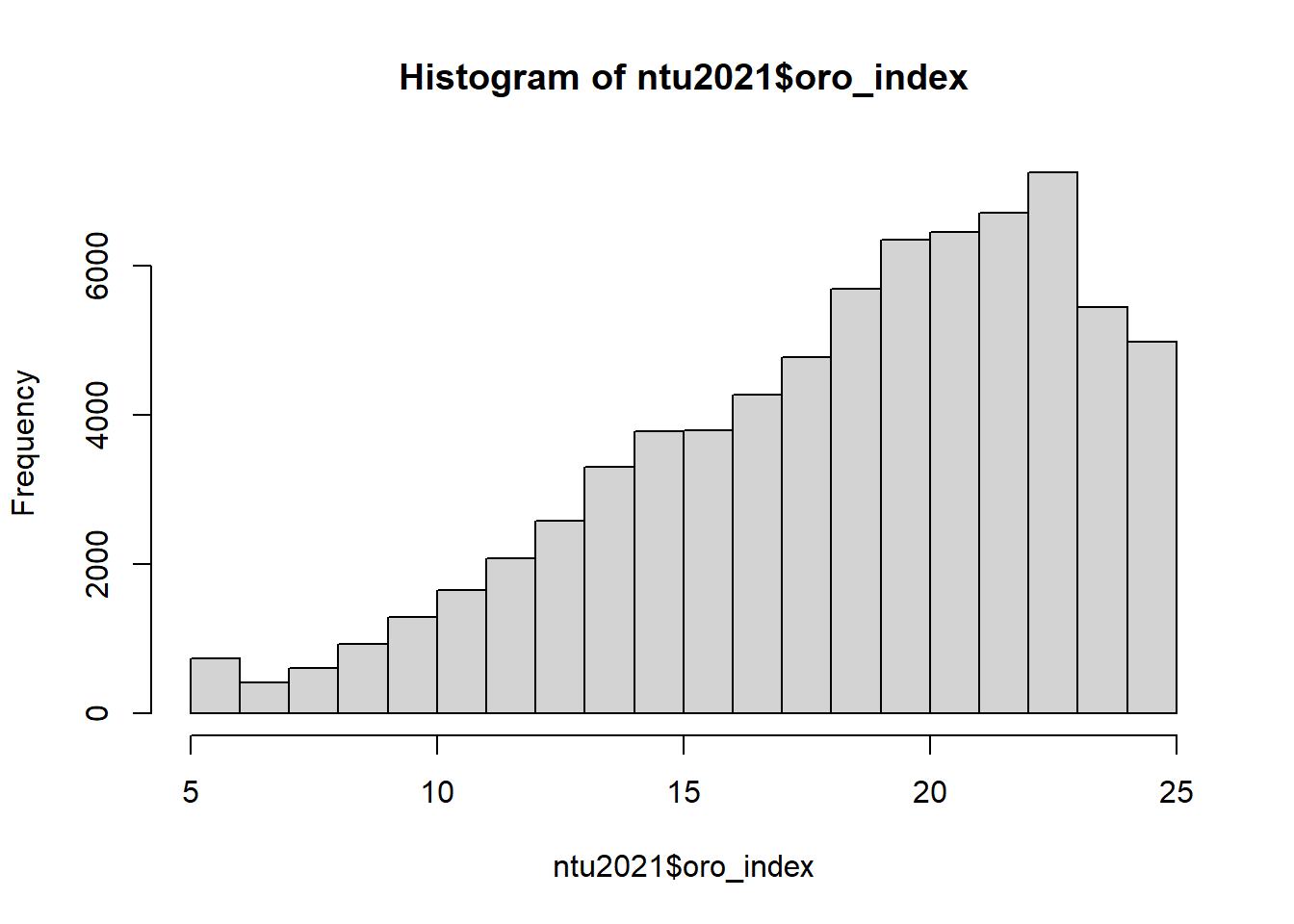
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 5.00 16.00 20.00 18.77 22.00 25.00 1252## 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 NA's
## 443 290 415 606 936 1286 1659 2078 2585 3299 3777 3797 4268 4781 5696 6351 6454 6710 7246 5444 4978 1252#Vänd på indexet så att högre värden blir mer oro för brott#
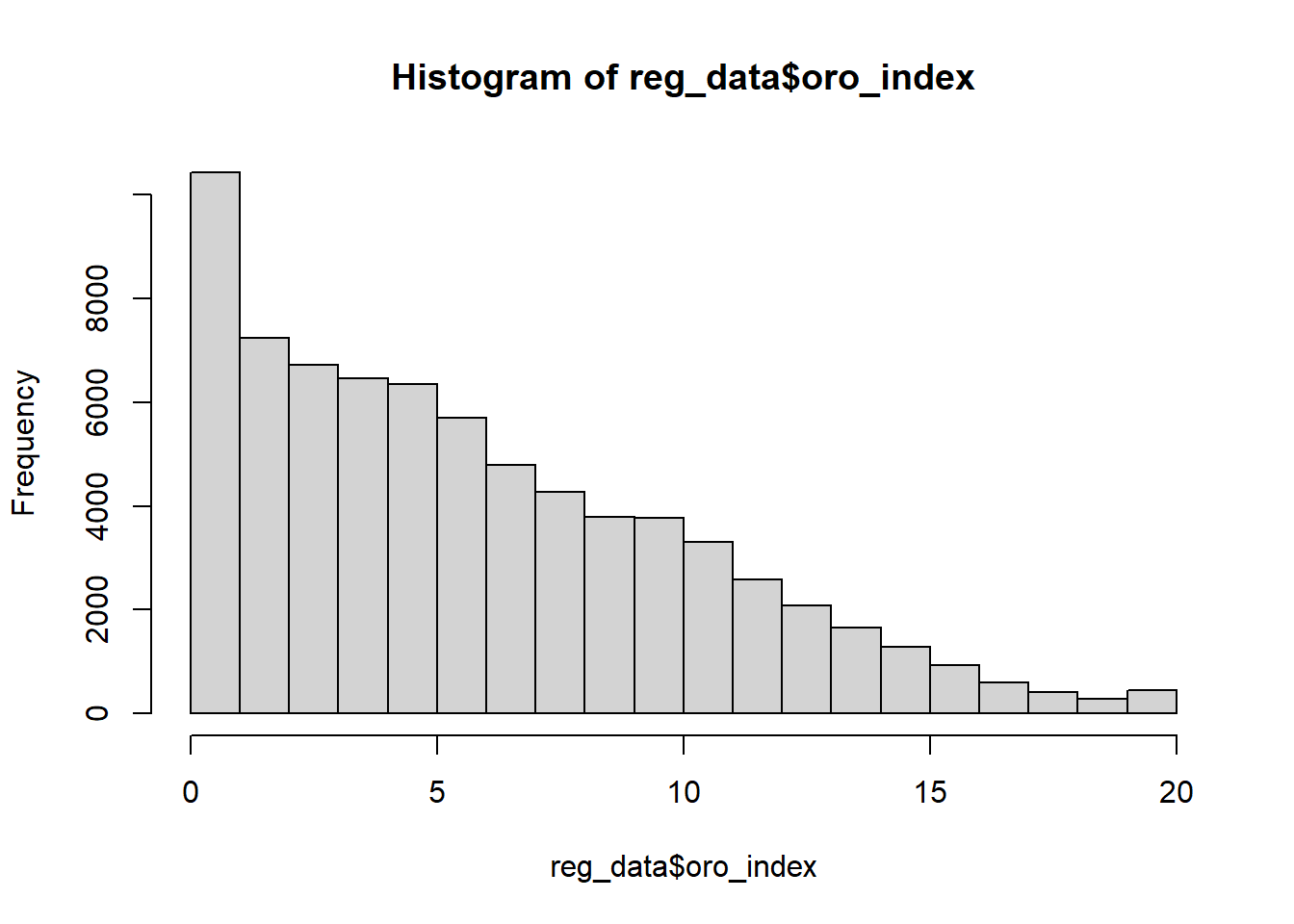
ntu2021$oro_index <- 25 - ntu2021$oro_index
hist(ntu2021$oro_index, n = 20)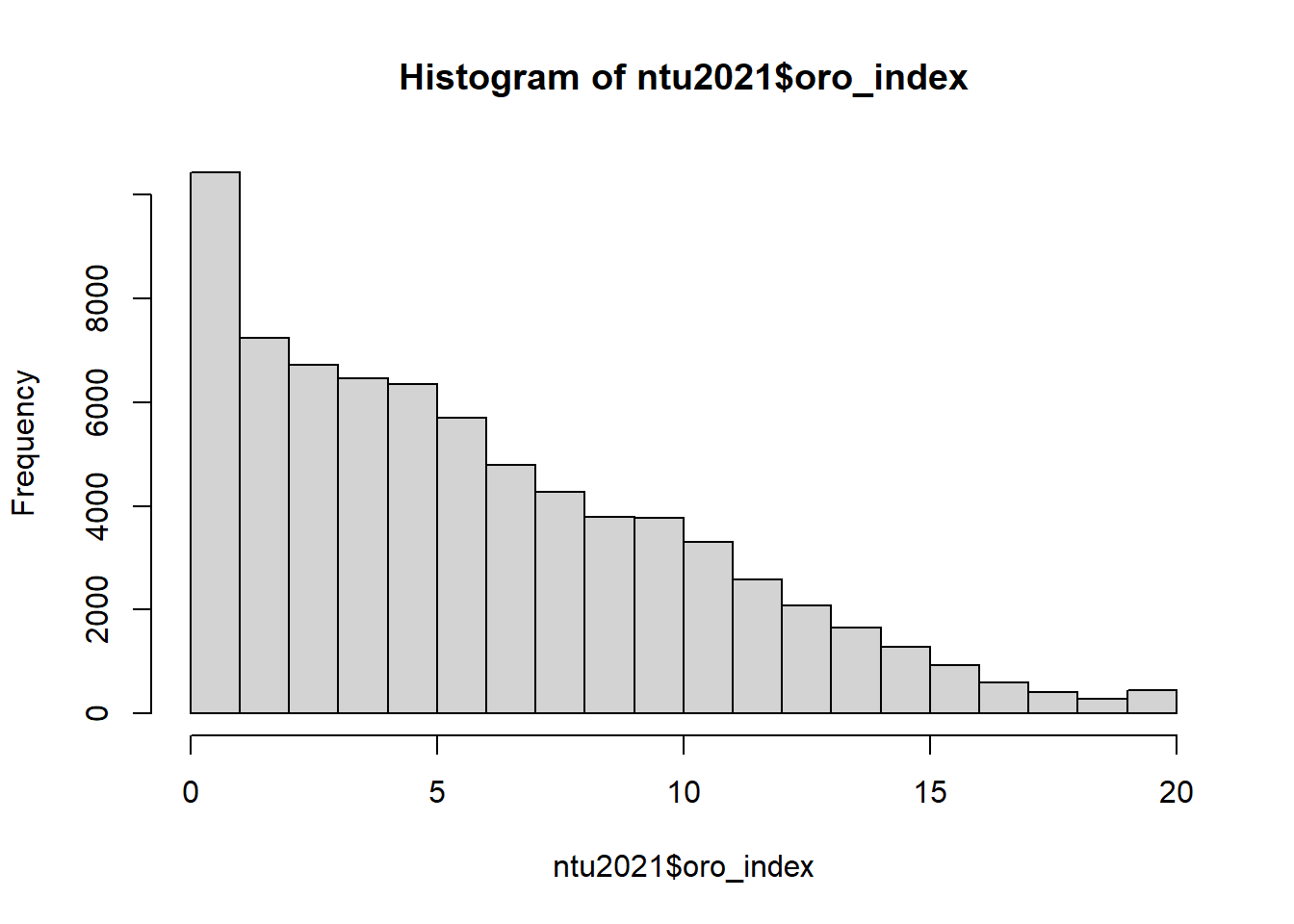
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.000 3.000 5.000 6.229 9.000 20.000 1252## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 NA's
## 4978 5444 7246 6710 6454 6351 5696 4781 4268 3797 3777 3299 2585 2078 1659 1286 936 606 415 290 443 1252## 1 2 3 NA's
## 14013 29949 30352 37ntu2021$utbildning <- as.factor(case_match(ntu2021$Utbildning3,
1 ~ "Förgymnasial",
2 ~ "Gymnasial",
3 ~ "Eftergymnasial",
.default = NA))
summary(ntu2021$utbildning)## Eftergymnasial Förgymnasial Gymnasial NA's
## 30352 14013 29949 37#Skapa datamaterialet "reg_data"#
reg_data <- ntu2021[, c("fortroende_index", "oro_index", "polisanmalt", "Kon_text", "alder_3", "utbildning")]
head(reg_data)## fortroende_index oro_index polisanmalt Kon_text alder_3 utbildning
## 230 14 3 Nej, inte polisanmält senaste 3 åren Kvinna Medelålder Eftergymnasial
## 231 4 12 Nej, inte polisanmält senaste 3 åren Kvinna Äldre Gymnasial
## 232 NA 8 Nej, inte polisanmält senaste 3 åren Kvinna Äldre Eftergymnasial
## 233 10 8 Nej, inte polisanmält senaste 3 åren Kvinna Äldre Gymnasial
## 234 NA 9 Nej, inte polisanmält senaste 3 åren Kvinna Medelålder Eftergymnasial
## 235 12 4 Nej, inte polisanmält senaste 3 åren Kvinna Äldre Förgymnasial| Unique | Missing Pct. | Mean | SD | Min | Median | Max | Histogram | |
|---|---|---|---|---|---|---|---|---|
| fortroende_index | 18 | 26 | 9.5 | 3.6 | 0.0 | 10.0 | 16.0 |  |
| oro_index | 22 | 2 | 6.2 | 4.5 | 0.0 | 5.0 | 20.0 |  |
| N | % | |||||||
| polisanmalt | Nej, inte polisanmält senaste 3 åren | 58515 | 78.7 | |||||
| Ja, polisanmält senaste 3 åren | 15191 | 20.4 | ||||||
| Kon_text | Kvinna | 39207 | 52.7 | |||||
| Man | 35144 | 47.3 | ||||||
| alder_3 | Äldre | 37825 | 50.9 | |||||
| Medelålder | 17672 | 23.8 | ||||||
| Ung | 18854 | 25.4 | ||||||
| utbildning | Eftergymnasial | 30352 | 40.8 | |||||
| Förgymnasial | 14013 | 18.8 | ||||||
| Gymnasial | 29949 | 40.3 |
datasummary_correlation(correlation::correlation(reg_data),
stars = TRUE,
note = "+ = p<.1, * = p<.05, ** = p<.01, *** = p<.001")| fortroende_index | oro_index | |
|---|---|---|
| + = p<.1, * = p<.05, ** = p<.01, *** = p<.001 | ||
| fortroende_index | 1 | . |
| oro_index | -.37*** | 1 |
8.3 Funktionen lm()
Innan vi börjar på riktigt med att pröva våra hypoteser så behöver vi lära oss hur en faktiskt gör en regressionsanalys i R. En linjär regressionsanalys kan beställas med hjälp av en funktion i bas R som heter lm()där “lm” står för “linear model”.
Argumenten är enkla (och ni känner säkert igen dem): lm(beroende.variabel ~ oberoende.variabel, data = data). Detta producerar en enkel, linjär regressionsanalys (enkel därför att den bara innehåller en oberoende variabel, det har inget med lätt eller svårt att göra).
Om vi alltså vill börja med att göra en regressionsanalys mellan oro för brott och förtroende för rättsväsendet skriver vi
##
## Call:
## lm(formula = fortroende_index ~ oro_index, data = reg_data)
##
## Coefficients:
## (Intercept) oro_index
## 11.3629 -0.2926Detta ger oss dock inte jättemycket information. Som tur är går lm()-funktionen att kombinera med summary()-funktionen, vilket ger oss en mer användbar utskrift med mer information och som är lättare att tolka:
##
## Call:
## lm(formula = fortroende_index ~ oro_index, data = reg_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.3629 -2.1925 0.3927 2.2705 10.4891
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.362910 0.024761 458.91 <2e-16 ***
## oro_index -0.292602 0.003115 -93.94 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.314 on 54300 degrees of freedom
## (20049 observations deleted due to missingness)
## Multiple R-squared: 0.1398, Adjusted R-squared: 0.1398
## F-statistic: 8824 on 1 and 54300 DF, p-value: < 2.2e-16I utskriften ser vi ett antal saker:
Call: beskriver helt enkelt bara den formel för regresionsanalysen som vi använt.
Residuals: Residualen för regressionsmodellen. Residualen är inom statistik skillnaden mellan observerade och predicerade värden, och används för att beräkna andra saker så som andelen förklarad varians. Vi behöver inte bekynmra oss om residualen just nu. På slutet av vårt exempel skall vi dock använda denna för att titta på tillförlitligheten i vår regressionsmodell.
Coefficients: Koefficienterna. Dessa är de vi är huvudsakligen intresserade av. Vi har två koefficienter. Ett “(Intercept)”, alltså interceptet vilket motsvarar värdet på den beroende variabeln när alla oberoende variabler är noll. Vi har också en rad för “oro_index”, vilket är vår beroende variabel. Själva estimatet (“Estimate”) är lutningen på regressionskoefficienten, alltså hur mycket fortroende_index ökar för varje enhet vi ökar vårt oro_index. Standardfelet anges som “Std. Error” och avser hur säker modellen är avseende lutningen på regressionskoefficienten. I kombination med t-värdet används detta för att räkna ut signifikansnivån (“Pr(>|t|)”) som också, och betydligt enklare, anges med stjärnor “***” om sambandet är signifikant. På botten av tabeller ni också vad respektive tjäsnor motsvarar i termer av signifikansnivåer.
I botten av vår utskrift hittar vi lite extra information om vår regressionsmodell, så som standardfelet för residualen, antalet frihetsgrader, hur många observationer som uteslutits från modellen på grund av svarsbortfall (NA).
- Här är vi framförallt intresserade av att se R2-värdet (alltså den förklarade variansen i den beroende variabeln). Detta anges som “R-squared” eller som “Adjusted R-squared” (vi tittar på adjusted, det justerade R2 värdet i de modeller där vi har fler än en oberoende variabel).
I exemplet skall vi gå igenom mer hur vi skall tolka dessa olika värden.
Istället för att skriva lm()-funktionen inom parantesen för summary()-funktionen kan vi spara den som ett eget objekt, och sedan tillämpa summary()-funktionen på detta objekt. Det är det vanligaste sättet att arbeta med regressionsanalys i R:
##
## Call:
## lm(formula = fortroende_index ~ oro_index, data = reg_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.3629 -2.1925 0.3927 2.2705 10.4891
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 11.362910 0.024761 458.91 <2e-16 ***
## oro_index -0.292602 0.003115 -93.94 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.314 on 54300 degrees of freedom
## (20049 observations deleted due to missingness)
## Multiple R-squared: 0.1398, Adjusted R-squared: 0.1398
## F-statistic: 8824 on 1 and 54300 DF, p-value: < 2.2e-16Innan vi börjar pröva hypoteserna i vårt exempel skall vi också förevisa detta med “dummy”-variabler, alltså att inkludera kategoriska variabler i en linjär regressionsmodell. Som exempel kan vi ta kön, och titta på om kvinnor och män skiljer sig åt avseende förtroende för rättsväsandet.
##
## Call:
## lm(formula = fortroende_index ~ Kon_text, data = reg_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.9059 -1.9873 0.0941 2.0941 7.0127
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.90585 0.02117 468.02 <2e-16 ***
## Kon_textMan -0.91851 0.03022 -30.39 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.546 on 55084 degrees of freedom
## (19265 observations deleted due to missingness)
## Multiple R-squared: 0.01649, Adjusted R-squared: 0.01647
## F-statistic: 923.5 on 1 and 55084 DF, p-value: < 2.2e-16I utskriften vi får i konsolpenelen kan vi läsa att estimatet, regressionskoefficientens lutning, för varaiblen “Kon_textMan” är “-0.91851”. I detta fall är “Kon_text” variabeln, och suffixet “Man” anger vilken svarskategori vi har att göra med. I det här fallet visar koefficienten den genomsnittliga skillnaden i fortroende_index för män jämfrt med kvinnor. Kvinnor är alltså referenskategori. Det betyder vi i interceptet (som alltså är det värde som den beroeonde variabeln förtroendeindex antar när alla oberoende variabler, i detta fall kön, är noll) återfinner kvinnors medelvärde avseende vårt förtroendeindex. I dett fall 9.90585.
Om dessa siffror känns bekanta så är det för att de är exakt samma siffror som vi fick ut när vi undersökte medelvärdesskillnaden i förtroende för rättsväsendet mellan män och kvinnor med ett t-test i avsnitt 5.2.1.
##
## Welch Two Sample t-test
##
## data: fortroende_index by Kon_text
## t = 30.327, df = 53936, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Kvinna and group Man is not equal to 0
## 95 percent confidence interval:
## 0.8591501 0.9778763
## sample estimates:
## mean in group Kvinna mean in group Man
## 9.905853 8.987339## [1] 0.918514Om vi istället skulle vilja att män utgjorde referenskategorin in regressionsmodellen, och att vi fick ut kvinnors skillnad i förtroende, jämfört med mäns, så kan vi använda ett argument i lm()-funktionen som heter relevel(). Vi omsluter helt enkelt vår variabel Kon_text med relevel()-argumentet, och specificerar referenskategorin på det här sättet:
##
## Call:
## lm(formula = fortroende_index ~ relevel(Kon_text, ref = "Man"),
## data = reg_data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.9059 -1.9873 0.0941 2.0941 7.0127
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.98734 0.02158 416.53 <2e-16 ***
## relevel(Kon_text, ref = "Man")Kvinna 0.91851 0.03022 30.39 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.546 on 55084 degrees of freedom
## (19265 observations deleted due to missingness)
## Multiple R-squared: 0.01649, Adjusted R-squared: 0.01647
## F-statistic: 923.5 on 1 and 55084 DF, p-value: < 2.2e-16Som ni ser är det nu mäns medelvärde för förtroendeindexet som återfinns i interceptet, och estimate/lutningen på koefficienten för variabeln Kon_text anger nu istället kvinnors medelvärdesskillnad avseende förtroendeindex, jämfört med mäns medelvärde.
Den utskrift vi får av R är dock inte jättesnygg, och är svår att använda om vi vill skriva en rapport i exempelvis word eller open office. Som tur är kan vi använda en funktion från paketet modelsummary som heter modelsummary() för att skapa en trevlig och användbar tabell som vi kan spara eller kopiera. Vi använder även argumentet stars = TRUE för att få ut signifikansnivåer i tabellen:
m <- lm(fortroende_index ~ relevel(Kon_text, ref = "Man"), data = reg_data)
library(modelsummary)
modelsummary(m,
stars = TRUE)| (1) | |
|---|---|
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | |
| (Intercept) | 8.987*** |
| (0.022) | |
| relevel(Kon_text, ref = "Man")Kvinna | 0.919*** |
| (0.030) | |
| Num.Obs. | 55086 |
| R2 | 0.016 |
| R2 Adj. | 0.016 |
| AIC | 295797.0 |
| BIC | 295823.7 |
| Log.Lik. | -147895.486 |
| F | 923.534 |
| RMSE | 3.55 |
Här hamnar estimaten/lutningskoefficienten på en rad, föjlt av signifikansnivåerna för dessa.På en separat rad, inom (parantes) återfinner vi standardfelen.
I botten av tabellen får vi ytterligare information om modellen. Framförallt är vi intresserade av Numb.Obs, som är antalet observationer, samt R2 eller R2 Adj. som anger graden av förklarad varians. I den absoluta botten återfinner vi en not som förklarar de olika signifikansnivåerna i tabellen.
Och med detta kan vi börja att pröva våra tre hypoteser!
8.5 Hypotesprövning
Får att pröva våra tre hypoteser, att (1) de som har polisanmält har lägre förtroende för rättsväsendet, (2) att de som är oroliga för brott har lägre förtroende för rättsväsendet, och (3) att sambandet mellan oro för brott och lägre förtroende för rättsväsendet är starkare bland de som har polisanmält än de som inte har polisanmält, så skall vi bygga ett antal regressionsmodeller.
Totalt skall vi bygga sex stycken sådana modeller:
Modell 1: förtroende (y) och polisanmälan (x). Prövar det bivariata sambandet mellan polisanmälan och förtroende.
Modell 2: förtroende (y) och oro för brott (x). Prövar det bivariata sambandet mellan oro och förtroende.
Modell 3: förtroende (y) och polisanmälan (x1) och oro för brott (x2). Prövar det multivariata sambandet mellan både polisanmälan, oro för brott och förtroende. Alltså det unika sambandet mellan polisanmälan och förtroende, när vi kontrollerar för oro för brott. Och omvänt det unika sambandet mellan oro för brott och förtroende, när vi kontrollerar för polisanmälan.
Modell 4: förtroende (y) och polisanmälan (x1) och oro för brott (x2) och kön (x3) och ålder (x4) utbildning (x5). Prövar det multivariata sambandet mellan både polisanmälan, oro för brott och förtroende, samtidigt som vi kontrollerar för en rad sociodemografiska kontrollvariabler. Alltså det unika sambandet mellan polisanmälan och förtroende, när vi kontrollerar för oror för brott och övriga kontrollvariabler. Och omvänt det unika sambandet mellan oro för brott och förtroende, när vi kontrollerar för polisanmälan och övriga kontrollvariabler.
Modell 5: förtroende (y) och polisanmälan (x1) och oro för brott (x2) och en interaktionseffekt mellan polisanmälan X oro för brott (x1*x2). Prövar om sambandet mellan oro för brott och förtroende är starkare eller svagare beroende på om respondenten har polisanmält brott eller inte polisanmält brott.
Modell 6: förtroende (y) och polisanmälan (x1) och oro för brott (x2) och kön (x3) och ålder (x4) utbildning (x5) och en interaktionseffekt mellan polisanmälan X oro för brott (x1*x2). Prövar om sambandet mellan oro för brott och förtroende är starkare eller svagare beroende på om respondenten har polisanmält brott eller inte polisanmält brott, när vi samtidigt kontrollerar för övriga kontrollvariabler.
Vi bygger dessa modeller och sparar dem som m1 till m6. När vi har gjort det kan vi spara alla modeller i ett objekt av typen “list”. Det gör vi för att kunna inkludera alla modellerna i samma tabell, vilket blir väldigt smidigt. Vi kan också döpa modellerna, så att varje modell för en egen rubrik i tabellen:
m1 <- lm(fortroende_index ~ polisanmalt, data = reg_data)
m2 <- lm(fortroende_index ~ oro_index, data = reg_data)
m3 <- lm(fortroende_index ~ polisanmalt + oro_index, data = reg_data)
m4 <- lm(fortroende_index ~ polisanmalt + oro_index+
Kon_text + alder_3 + utbildning, data = reg_data)
m5 <- lm(fortroende_index ~ oro_index * polisanmalt, data = reg_data)
m6 <- lm(fortroende_index ~ oro_index * polisanmalt +
Kon_text + alder_3 + utbildning, data = reg_data)modeller <- list("Modell 1" = m1,
"Modell 2" = m2,
"Modell 3" = m3,
"Modell 4" = m4,
"Modell 5" = m5,
"Modell 6" = m6)
library(modelsummary)
tabell_5 <- modelsummary(modeller,
stars = TRUE)
tabell_5| Modell 1 | Modell 2 | Modell 3 | Modell 4 | Modell 5 | Modell 6 | |
|---|---|---|---|---|---|---|
| + p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001 | ||||||
| (Intercept) | 9.676*** | 11.363*** | 11.403*** | 12.539*** | 11.299*** | 12.452*** |
| (0.017) | (0.025) | (0.025) | (0.035) | (0.027) | (0.037) | |
| polisanmaltJa, polisanmält senaste 3 åren | -0.988*** | -0.389*** | -0.380*** | 0.125+ | 0.031 | |
| (0.037) | (0.035) | (0.034) | (0.066) | (0.064) | ||
| oro_index | -0.293*** | -0.285*** | -0.306*** | -0.268*** | -0.292*** | |
| (0.003) | (0.003) | (0.003) | (0.004) | (0.004) | ||
| Kon_textMan | -1.289*** | -1.285*** | ||||
| (0.028) | (0.028) | |||||
| alder_3Medelålder | 0.181*** | 0.182*** | ||||
| (0.035) | (0.035) | |||||
| alder_3Ung | 0.433*** | 0.430*** | ||||
| (0.035) | (0.035) | |||||
| utbildningFörgymnasial | -0.937*** | -0.931*** | ||||
| (0.041) | (0.041) | |||||
| utbildningGymnasial | -0.930*** | -0.925*** | ||||
| (0.031) | (0.031) | |||||
| oro_index × polisanmaltJa, polisanmält senaste 3 åren | -0.067*** | -0.054*** | ||||
| (0.007) | (0.007) | |||||
| Num.Obs. | 54718 | 54302 | 53975 | 53960 | 53975 | 53960 |
| R2 | 0.013 | 0.140 | 0.141 | 0.197 | 0.143 | 0.198 |
| R2 Adj. | 0.013 | 0.140 | 0.141 | 0.197 | 0.142 | 0.198 |
| AIC | 293891.8 | 284232.7 | 282355.5 | 278635.1 | 282272.2 | 278578.9 |
| BIC | 293918.5 | 284259.5 | 282391.1 | 278715.2 | 282316.7 | 278667.8 |
| Log.Lik. | -146942.890 | -142113.372 | -141173.765 | -139308.564 | -141131.098 | -139279.433 |
| RMSE | 3.55 | 3.31 | 3.31 | 3.20 | 3.31 | 3.20 |
Nu har vi alltså fått en stor tabell som sammanfattar alla våra regressionsmodeller på ett enda ställe. Vi har också gett alla modeller en egen rubrik i tabellen.
Vi kan tolka modellerna i tur och ordning, för att sedan komma fram till ett svar på våra hypoteser.
I Modell 1 ser vi att de som inte har anmält något brott (interceptet) i genomsnitt har 9.676 enheter förtroende för rättsväsendet (på vårt index som går från 0-16). Vi ser också att de som har polisanmält minst ett brott de senaste 3 åren i genomsnitt har -0.988 lägre förtroende för rättsväsendet (jämfört med referenskategorin, alltså de som inte har polisanmält något brott). Denna skillnad är statistiskt signifikant på p<0.001-nivå (“***“). Sannolikheten att vi i vårt urval observerar en medelvärdesskillnad som inte skulle återfinnas i den befolkning som vi har dragit vårt urval från (den vuxna befolkningen i Sverige) är alltså mindre än 0.001%. Om vi drog 1000 nya urval, skulle vi alltså i 999 fall av 1000 hitta en liknande medelvärdesskillnad (en liknande lutning på regressionskoefficienten för svarskategorin Ja, polisanmält jämfört med refenskategorin Nej, inte polisanmält).
Om vi tittar lite längre ned, på hela modellens R2-värde så ser vi dock att den förklarade variansen i den beroende variabeln (förtroende) inte är särskillt stor. R2-värdet är bara 0.013, vilket motsvarar 1.3% förklarad varians. Omvänt kan vi säga att 98.7% av variationen i förtroende för rättsväsendet kan förklaras av faktorer som inte ingår i vår regressionsmodell. Sammanfattningsvis kan vi säga att Modell 1 ger oss ett initialt stöd för att Hypotes 1 är sann, alltså att de som har polisanmält har ett lägre förtroende för rättsväsendet. Men för att vara riktigt säkra på att detta inte är ett skensamband som beror på andra faktorer som påverkar både om en har polisanmält brott OCH vilket förtroende en har för rättvsäsendet, så vill få pröva detta samband även under kontroll för oro för brott samt sociodemografiska variabler.
I Modell 2 ser vi att de som är minst rädda för brott, alltså de respondenter som har värde “0” på vår oberoende variabel oro för brott, i genomsnitt har 11.363 enheter förtroende för rättsväsendet. Vi ser dock att lutningskoefficienten för oro_index är negativ, vilket innebär att för varje enhet oro för brott så minskar förtroende för rättsväsndet med -0.293 enheter. Det innebär exempelvis att en individ som är så rädd som det går att vara, som har det maximala värdet “20” på vår oberoende variabel oro för brott, har hela -6.153 (-0.2993*21) enheter lägre förtroende för rättsväsendet än någon som inte alls är rädd för brott (som har värde “0” på vår oberoende variabel oro för brott). Sambandet är signifikant på 0.001%-nivån. Om vi tittar lite längre ned, på hela modellens R2-värde så ser vi att detta är 0.140, vilket motsvarar 14% förklarad varians. Alltså att 14% av variationen i förtroende för rättsväsendet kan förklaras av skillnader i oro för brott. Sammanfattningsvis kan vi säga att Modell 2 ger oss ett initialt stöd för att Hypotes 2 är sann, alltså att de är oroliga för brott har ett lägre förtroende för rättsväsendet. Men för att vara riktigt säkra på att detta inte är ett skensamband som beror på andra faktorer som påverkar både om oro för brott OCH vilket förtroende en har för rättvsäsendet, så vill få pröva detta samband även under kontroll för polisanmälan samt sociodemografiska variabler.
I Modell 3 ser vi det unika sambandet mellan polisanmälan och förtroende, när vi kontrollerar för oro för brott. Och omvänt det unika sambandet mellan oro för brott och förtroende, när vi kontrollerar för polisanmälan. Interceptet (11.403) i den här modellen är den genomsnittliga graden av förtroende för rättsväsendet för de individer som inte har polisanmält något brott och som inte är rädda för brott (värde “0” på oro_index). Om vi tittar på det justerade R2-värdet (0.141) så har detta inte förändrats jättemycket jämfört med Modell 2. Att lägga till polisanmälan till vår modell ökar alltså inte graden av förklarad varians avseende förtroende för rättsväsendet särskilt mycket.
Det som är intressant i modellen är dock att lutningskoefficienten för polisanmälan (-0.389), även om den fortsättningsvis är statistiskt signifikant, har mer än halverats jämfört med koefficienten i Modell 1 (-0.988). Tolkningen av detta är att ja, det finns ett unikt negativt samband mellan polisanmälan och förtroende, men en del av det ursprungliga sambandet mellan polisanmälan och förtroende kan också förklaras av att de som har polisanmält kontra de som inte har polisanmält något brott verkar skilja sig åt i hur oroliga de i genomsnitt är för brott. När vi kontrollerar för deras respektive oro för brott så blir alltså sambandet mellan polisanmälan och förtroende för rättsväsendet svagare.
Vi ser också att sambandet mellan oro för brott och förtroende endast minskar väldigt lite (-0.285 i Modell 3, jämfört med -0.293 i Modell 2), och att sambandet fortsättningsvis är statistiskt signifikant på 0.001%-nivå.
Sammanfattningsvis, avseende Modell 3, kan vi säga att båe Hypotes 1 och Hypotes 2 får stöd, då det finns unika samband mellan båda de oberoende variablerna polisanmälan och oro för brott och den beroende variabeln förtroende för rättsväsendet. Men vi kan alltså lägga till att en del av det ursprungliga sambandet mellan polisanmälan och förtroende kan också förklaras av att de som har polisanmält kontra de som inte har polisanmält något brott verkar skilja sig åt i hur oroliga de i genomsnitt är för brott.
I Modell 4 observerar vi samma samband som i Modell 3, men under kontroll för ytterligare sociodemografiska variabler (kön, ålder och utbildning).
För att illustrera alla regressionskoefficienterna i Modell 4 samtidigt kan vi beställa ett diagram som brukar kallas för “coefficient plot”. Detta gör vi med en funktion som heter modelplot() från modelsummary-paketet. Funktionen kräver även stöd av ett annat paket som heter ggplot2, så vi öppnar detta också (om du inte har paketet installerat måste du först göra detta med hjälp av install.packages("")funktionen).
Detta diagram sammanfattar Modell 4 grafiskt. De lutningskoefficienter som är till vänster om strecket för 0 har en negativ effekt, och de som är till höger om strecket 0 har en positiv effekt. Exempelvis ser vi att lutningskoefficienterna för såväl polisanmälan som oro för brott är negativa. Faktum är att den enda positiva effekten tycks finns för svarsketgorin Ung på variablen alder_3.Yngre tycks alltså ha ett högre förtroende för rättsväsendet jämfört med referenskategorin.
library(modelsummary)
library(ggplot2)
figur_7 <- modelplot(m4) +
geom_vline(xintercept = 0)
figur_7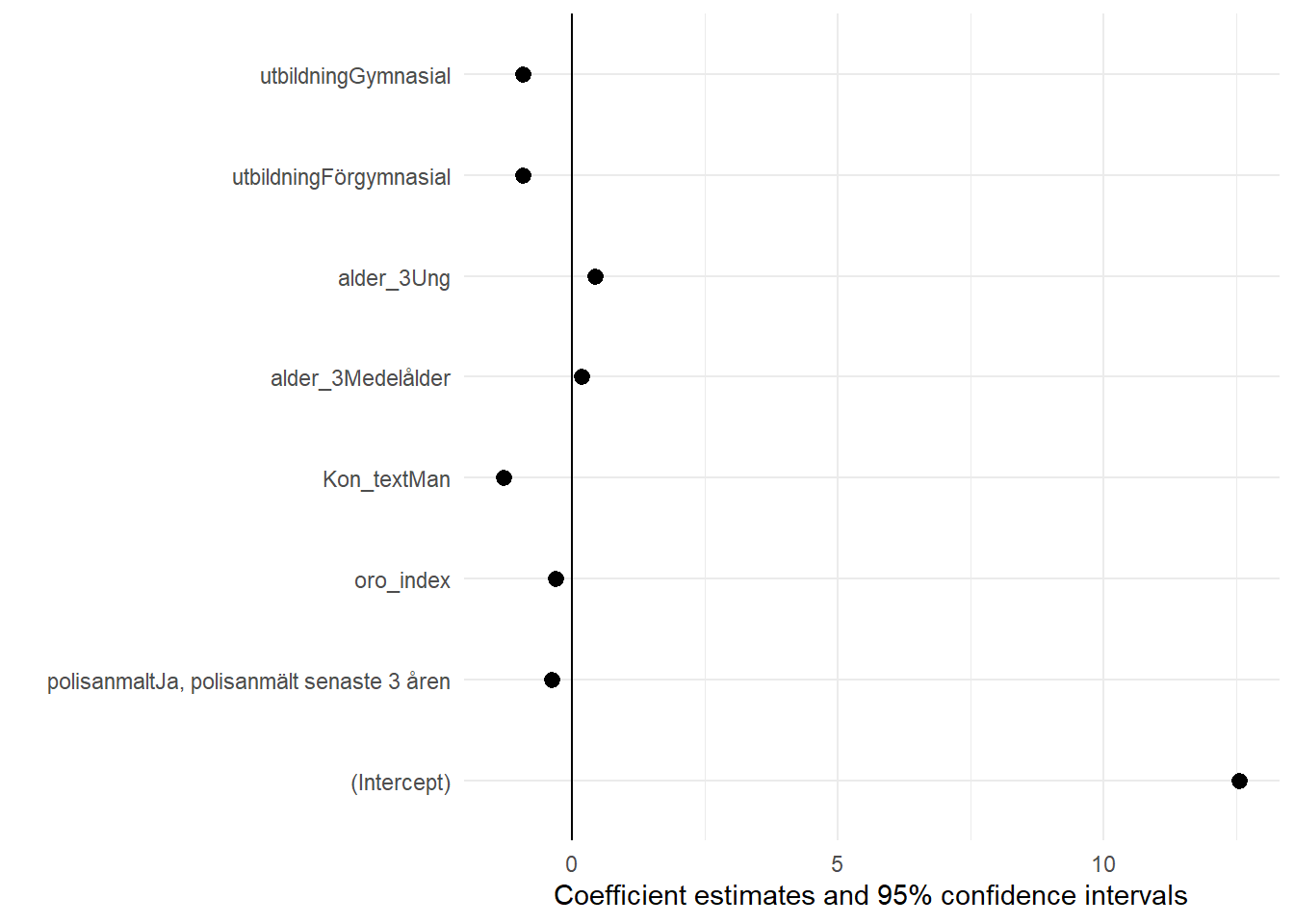
UBILDNINGSKONTROLL
Hur tolkar du interceptet i Modell 4?
Vilken svarskategori är referenskategori för variabeln alder_3?
Vad händer med sambanden mellan polisanmäl och förtroende respektive oro för brott och förtroende?
Titta på det justerade R2-värdet. Hur stor del variationen i förtroende för rättsväsendet kan förklaras av våra oberoende variabler?
I Modell 5 inkluderar vi vår interaktionseffekt melan variablerna polisanmälan och oro för brott. Det är framförallt två saker som vi är intresserade av att titta på här, och det är lutnigskoefficienterna för oro_index och för “polisanmaltJa, polisanmält senaste 3 åren × oro_index”, alltså lutningskoefficeinten för interaktionseffekten. Vi är inte så intresserade av att titta på lutningskoefficienten för polisanmälan, då denna inte längre är meningsfull att tolka i närvaron av en interaktionseffekt. Anledningen är lite krånglig, så vi hoppar över en fullständig utläggning om varför det är så. Det viktiga att känna till är att även om lutningskoefficeinten för polisanmälan inte är signifikant är detta inget som påverkar vår tidigare slutsats gällande Hypotes 1.
Lutningskoefficeinten för oro_index är -0.268 och tolkas här som sambandet mellan oro för brott och förtroende för rättsväsendet BLAND DE SOM INTE HAR POLISANMÄLT NÅGOT BROTT. För varje enhet oro för brott så minskar förtroende för rättsväsndet med -0.268 enheter BLAND DE SOM INTE HAR POLISANMÄLT NÅGOT BROTT.
För att förstå hur oro för brott relaterar till förtroende för rättsväsendet bland de som HAR POLISANMÄLT BROTT måste vi titta både på lutningskoefficienten för oro_index OCH lutningskoefficenten för interaktionseffekten ( “polisanmaltJa, polisanmält senaste 3 åren × oro_index”). Det som händer här är att de som HAR POLISANMÄLT BROTT utöver lutningskoefficienten för oro för brott OCKSÅ får lutningskoefficeinten för interaktionseffekten. Det vi gör är alltså att summera dessa två lutningskoefficienter. För varje enhet oro för brott minskar alltså förtroendet för rättsväsendet med -0.268, men för de som har polisanmält ett brott minskar förtroendet med ytterligare -0.067, alltså med totalt -0.355 (-0.268 + -0.067).
Interaktionseffekter kan upplevas som ganska krångliga att tolka, och de är kanske något enklare att förstå om en kan se dem. Så vi beställer ett sådant. Det gör vi med hjälp av en funktion som heter plot_model() från ett paket som heter sjPlot. Argumentet är enkelt, plot_model(modell, type = "") där vi i argumentet type = "" kan skriva in “int” för att få just ett diagram över interaktionseffekten.
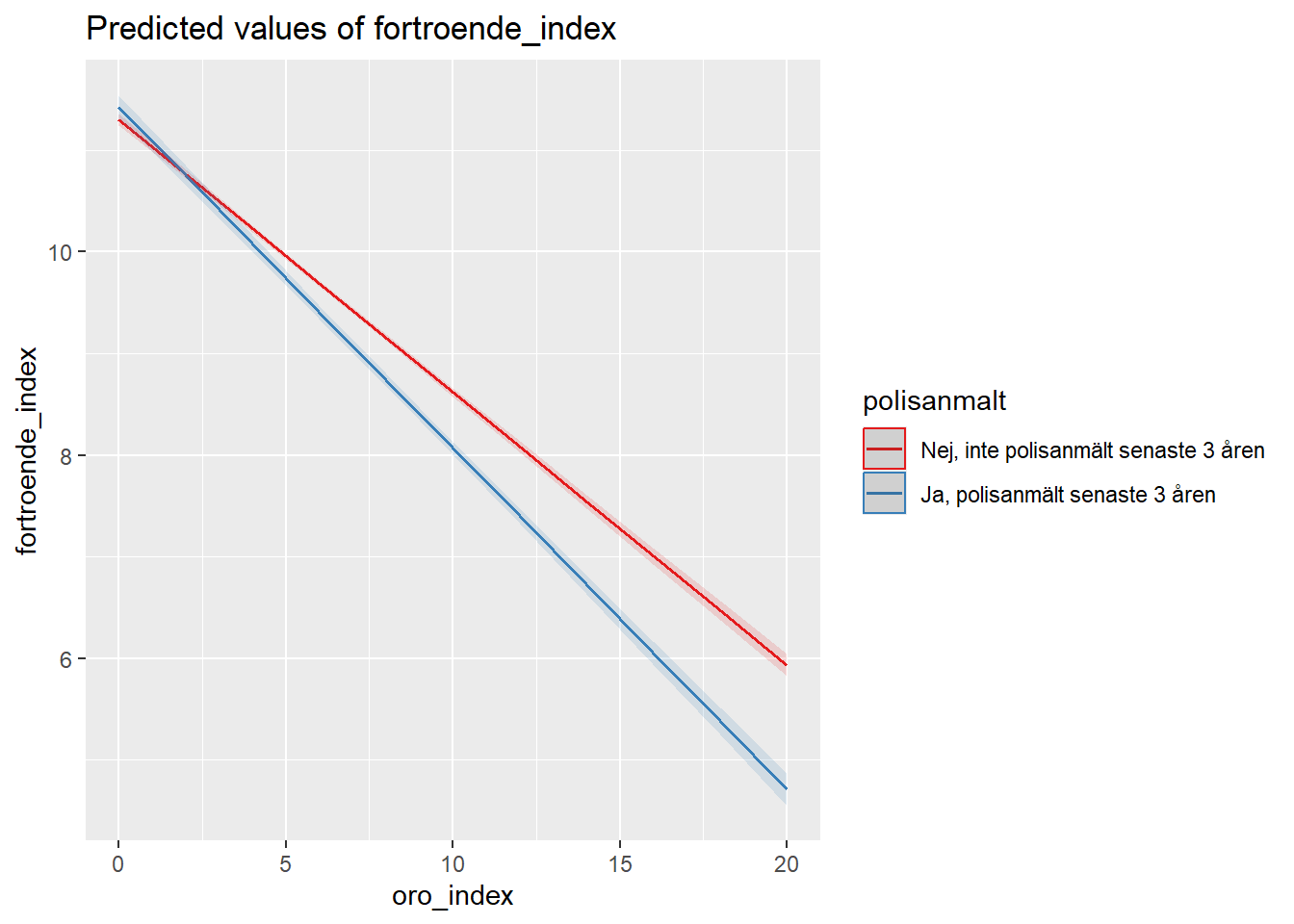
Som vi kan se i diagramet är alltså effekten av oro för brott negativ för båda grupperna, både de som inte har polsanmält (rött streck) och de som har polisanmält (blått streck). Som vi kan så är dock lutningen på det blå strecket, för de som har polisanmält, brantare än det röda strecket. Lutningen är alltså kraftigare, vilket betyder att oro för brott hos de som har polisanmält brott har ett starkare negativt samband med förtroende för rättsväsendet.
Sammanfattningsvis hittar vi alltså ett initialt stöd för Hypotes 3, att oro för brott har ett starkare negativt samband med förtroende för rättsväsendet bland de som har polisanmält brott jämfört med de som itne har polisanmält brott.
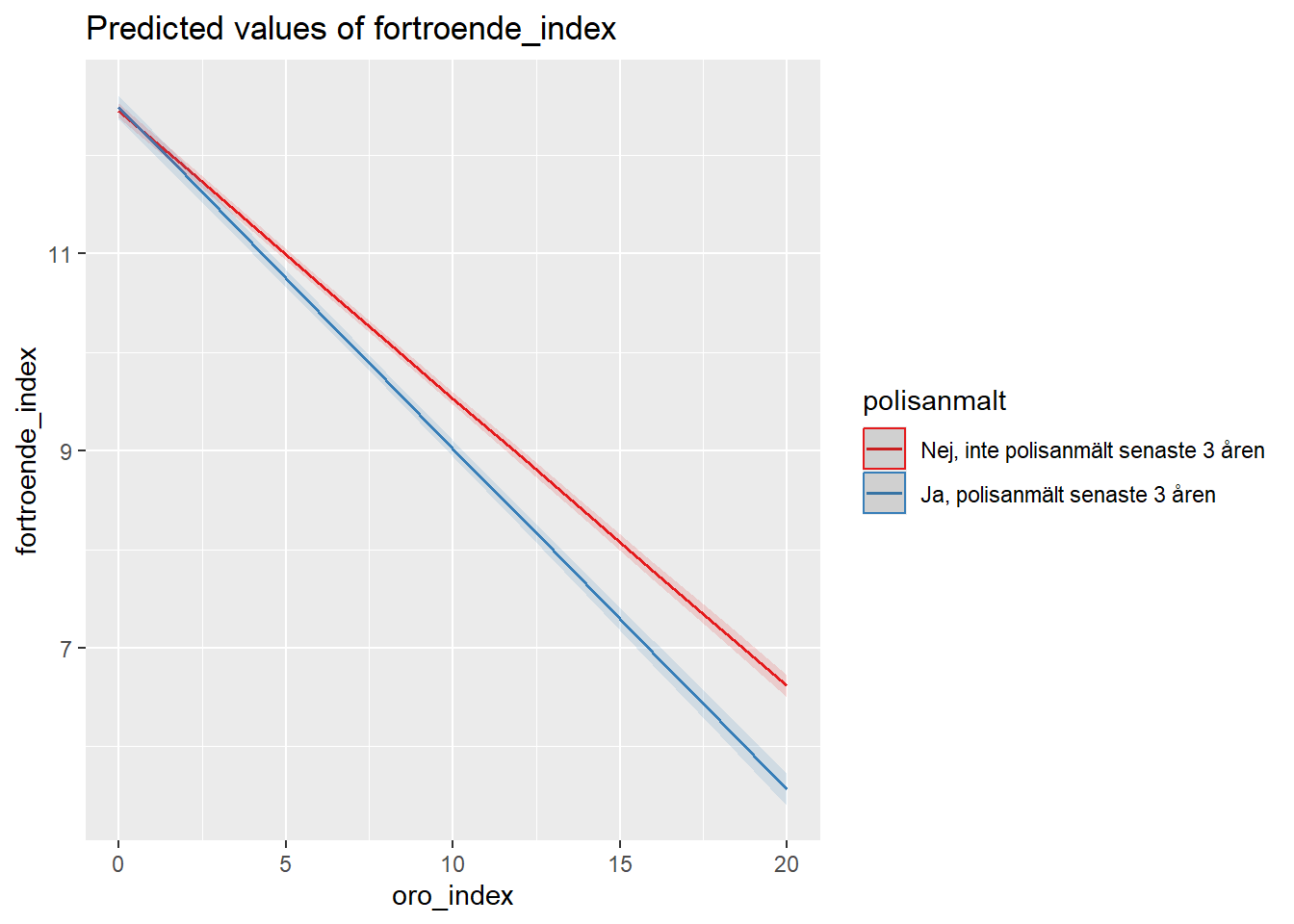
Det sista vi skall göra är att titta om denna interaktionseffekt består även vid kontroll för våra övriga kontrollvariabler (kön, ålder, utbildning). Vi tittar då på Modell 6, för vilken vi även kan ta fram diagram, såväl “coefficients plot” som ett diagram över interaktionseffekterna:
library(ggplot2)
library(modelsummary)
figur_9 <- modelplot(m6) +
aes(color = ifelse(p.value < 0.05, "Significant", "Not significant")) +
scale_color_manual(values = c("grey", "black")) +
geom_vline(xintercept = 0)
figur_9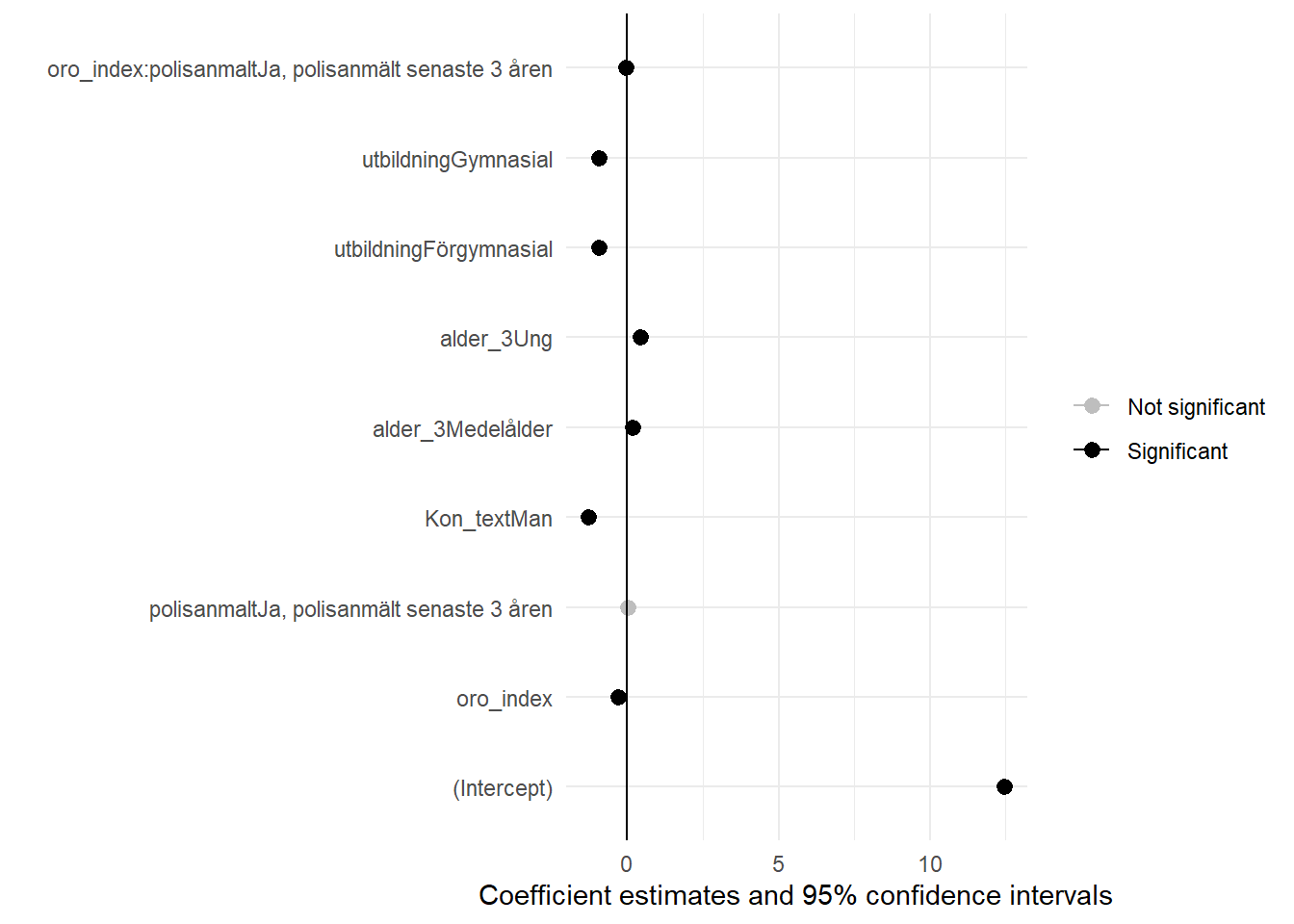
Obs! I figur 9 har vi lagt till ett litet argument som gör att våra signifikanta samband är svarta, medan de icke-signifikanta sambanden är gråa. Då slipper vi dubbelkolla i tabellen hela tiden.
UTBILDNINGSKONTROLL
Hur skulle du beskriva interaktionseffekten i Modell 6?
Lutningskoefficienten för polisanmälan är inte signifikant. Påverkar detta slutsats gällande Hypotes 1, att de som polisanmält brott har ett lägre förtroende för rättsväsendet?
8.6 Pröva modellens antaganden
Det sista vi skall göra är att utvärdera hur tillförlitliga vår regressionsmodell faktiskt är. I en dålig modell där residualen inte är normalfördelad så kan nämligen tillförlitligheten i feltermer och statistiska test komma att bli påverkade. Dock påverkas inte lutningskoefficenterna, utan endast vår säkerhet kring dessa.
Varför måste residualen vara normalfördelad då? Residualen kallas ibland för feltermen (och skrivs ofta ut så i regressionsformler), och sammanfattar skillnaden mellan våra observerade värden och teoretiska förväntade värden. Alltså de värden en observation förväntas ta givet dess värde på de observerade variablerna, alltså det värde observationen förväntas ta givet regressionslinjen i modellen. Ett annat sätt att uttrycka det är att residualen sammanfattar avstånden från de observerade värdena till regressionslinjen.
En regressionsmodell består alltså av två delar. När det gäller våra observerade variabler så vill vi såklart att de skall systematiskt relatera till vår beroende variabel. Det är detta som gör att vi kan uttala oss om samband mellan variablerna, och använda dem för att göra prediktioner (“en person med si och så inkomst kommer i genomsnitt att vara si och så brottsbenägen”). Men när det gäller residualen, eller feltermerna, så vill vi tvärtom att dessa inte skall vara systematiska, utan tvärtom, att de skall vara oberoende i förhållande till vår modell. Vi vill alltså att felen/osäkerheten skall vara slumpmässigt fördelade, och inte systematiska.
Det finns många olika statistiska test att undersöka om resudialen i en regressionsmodell är normalfördelad eller inte, men de flesta är ganska känsliga, och med ett tillräckligt stort datamaterial blir medför brott mot regressionsmodellens grundantaganden (exempelvis om normalfördelade data) inte särskilt allvarliga konsekvenser.
Vi fokuserar därför på en enda sak, vilket är om residualen för vår modell kan sägas vara approximativt normalfördelad eller inte. Detta gör vi genom att inspektera den visuellt, genom att dels jämföra våra observerade med predicerade värden, vilket om residualen är normalfördelad borde ge oss en rät linje:
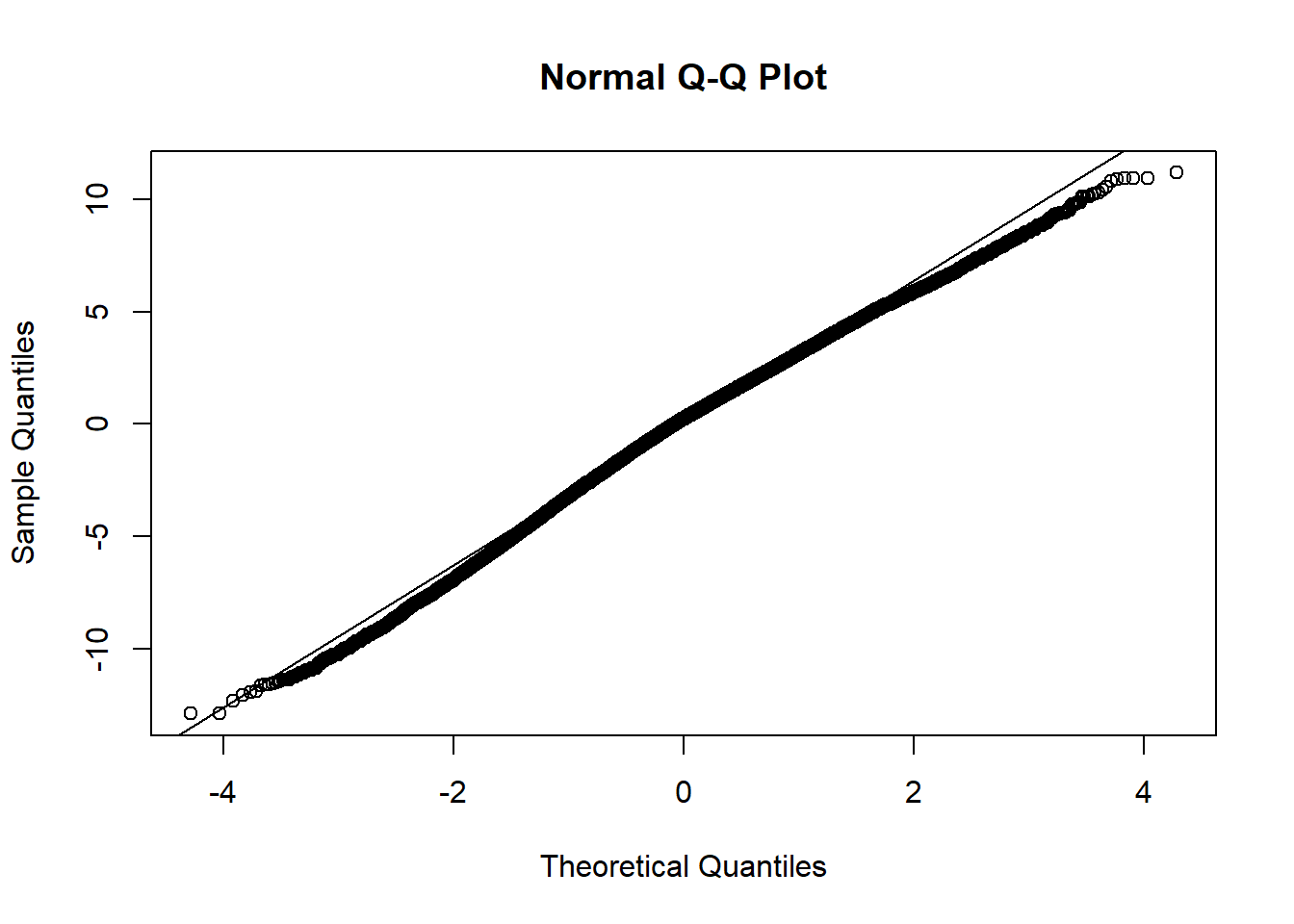
Samt genom att titta på fördelningen av residualen. Om den är normalfördelad borde den ge oss normalfördelningskurva:
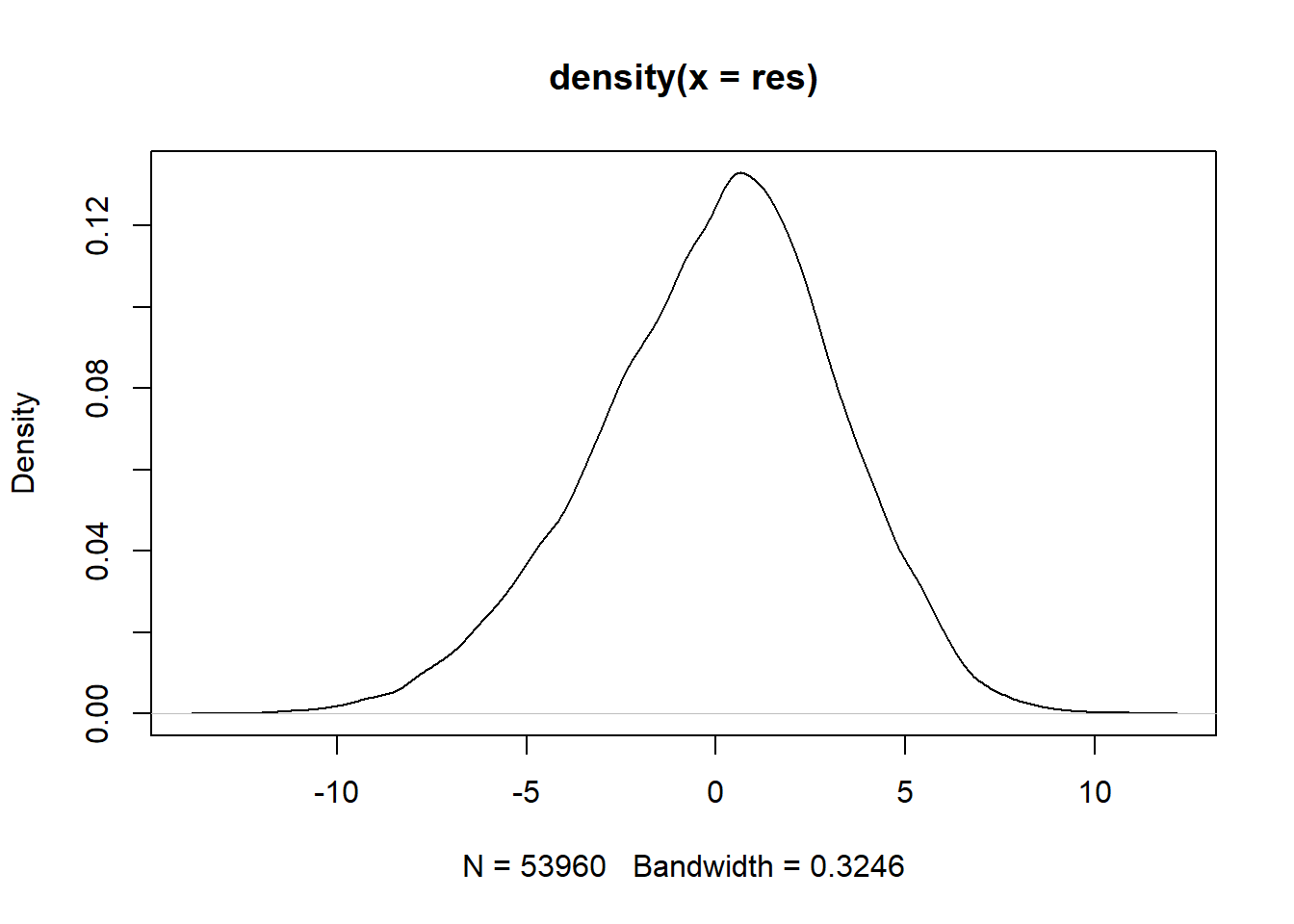
Vi kan dra slutsatsen att vår regressionsmodell är approximativt normalfördelad (i verkligheten är detta ofta det bästa som vi kan hoppas på). Detta betyder att vi kan lita på feltermer och de statistiska testen av exempelvis signifikans.
OBS! Alla variabler i en regressionsanalys måste alltså inte vara helt normalfördelade. Exempelvis är vår variable oro för brott inte helt normalfördelad. Det viktiga är att den beroende variabeln är approximativt normalfördelad, samt att residualen i regressionsmodellen är approximativt normalfördelad.
UTBILDNINGSKONTROLL FÖR HELA AVSNITTET OM REGRESSIONSANALYS
Använd datasetet
ntu2021_kort. Skapa en tabell med fyra linjära regressionsmodeller: (1) förtroende ~ bemötande; (2) förtroende ~ kön; (3) förtroende ~ bemötande + kön; (4) förtroende ~ bemötande * kön.Ta fram ett diagram som visar regressionskoefficienterna (estimaten) för modell 3.
Ta fram ett diagram som visar interaktionseffekten i modell 4.
Hur tolkar du dessa resultat?
EXTRAUPPGIFT
Formulera en egen hypotes om vad som påverkar människors oro för brott (ta hjälp av Kodbok NTU2017-2021 för att se vilka olika enkätfrågor/variabler du skulle kunna använda för att förklara oro för brott).
Använd data från 2021 (ntu2021) för att utforska och pröva denna hypotes. Förbered alltså data för en regressionsanalys genom att göra nödvändiga variabeltransformationer, samt genomför och tolka analysen. Utvärdera också om regressionsmodellen tycks vara tillförlitlig eller inte (om residualen är approximativt normalfördelad eller inte).