Kapitel 7 Bivariat analys

7.1 Krosstabll

Med en korstabell undersöker vi hur fördelningen på två kategoriska variabler förhåller sig till varandra. Vi undersöker frågor så som “Har äldre personer högre förtroende för rättsväsendet än yngre eller medelålders personer?”.

I frågan ovan kan vi säga att ålderskategorier är vår oberoende variabel som vi vill titta på om den samvarierar med vår beroende variabel, vilken är förtroende för rättsväsendet (kategorier: högt eller lågt förtroende).

Ett chi2-test fungerar så att det jämför en observerad fördelning (våra data) med en hypotetisk, helt jämn fördelning (så som variationerna i variablerna skulle ha sett ut om de var helt och hållet påverkade av slumpen). Skillnaden mellan vad modellen observerar och det förväntade värdet vid en helt slumpmässig fördelning används sedan för att räkna ut ett chi2-värde. Chi2-värdet har också ett associerat p-värde eller signifikansvärde, som påverkas av hur många observationer vi har och hur många frihetsgrader som modellen har.

För att ta reda på om det finns ett statistiskt signifikant samband mellan fördelningen i våra två variabler, ålder och förtroende för rättsväsendet, så kan vi alltså beställa ett chi2-test. Detta görs i R genom att först skapa ett objekt som innehåller en tabell som innehåller de två variabler vi är intresserade av. Detta gör vi enkelt med table()-funktionen som ni kanske känner igen från avsnitt 4.3.1 (stapeldiagram). table()-funktionen tar två argument, vilket är table(oberoende.variable, beroende.variabel). När vi sakapat denna tabell kan vi beställa ett chi2-test genom en funktion i bas R som heter chisq.test(). Funktionen tar ett argument chisq.test(x) där vi byter ut x till det objekt som vi vill utföra testet på.

x <- table(ntu2021_kort$alder_3, ntu2021_kort$fortroende_kat)
chi2 <- chisq.test(x)
chi2
## 
##  Pearson's Chi-squared test
## 
## data:  x
## X-squared = 28.885, df = 2, p-value = 5.342e-07

Vi kan i konsolpanelen avläsa att sambandet mellan våra två variabler, ålder och förtroende för rättsväsendet, har ett chi2-värde om 28.885 och ett p-värde som är mindre än 0.001. Sambandet är alltså statistiskt signifiant på 0.001%-nivå. “5.342e-07” som är det värde som vi faktiskt ser är en typ av vetenskapligt sätt att skriva ut riktigt små tal på. “e-07” betyder i det här fallet att vi har att göra med en nolla följt av sex nollor. Först på den sjunde decimalen observerar vi 0.000005342”. Ni behöver inte rapportera detta. Det räcker med att konstatera att p<0.001.

Okej, så vi vet att vi har att göra med ett statistiskt signifikant samband mellan våra två variabler. Hur ser fördelningen ut då? I tabelln vi skapade kan vi se frekvenserna. Men detta är inte alltid särskilt användbart. Något som vore mer användbart är nog att se procenten.

x
##             
##               Högt  Lågt
##   Ung         8583  4986
##   Medelålder  8864  4883
##   Äldre      17171 10599

En korstabell kan byggas på lite olika sätt, och i den här kursen skall vi lära oss ett sätt. Vi vill alltid bygga vår korstabell så att vi har den oberoende variabeln i RADERNA och den beroende variabeln i KOLUMNERNA. Vi är också i huvudsak intresserade av att läsa av det som kallas för radprocent, alltså att procentsatser summeras per rad. För ändamålet skall vi använda en funktion som heter datasummary_crosstab() från paketet modelsummary som vi tidigare använt oss av. Det grundläggande argumentet, som vi senare kan bygga på, är relativt enkelt: datasummary_correlation(oberoende.variabel, beroende.variabel, data = data).

library(modelsummary)
datasummary_crosstab(alder_3 ~ fortroende_kat, data = ntu2021_kort)
alder_3 Högt Lågt All
Ung N 8583 4986 18854
% row 45.5 26.4 100.0
Medelålder N 8864 4883 17672
% row 50.2 27.6 100.0
Äldre N 17171 10599 37825
% row 45.4 28.0 100.0
All N 34618 20468 74351
% row 46.6 27.5 100.0

Det vi kan se när vi avläser procenten per rad är hur fördelningen av den beroende variabeln ser ut inom respektive svarskategori på den oberoende variabeln. Som vi noterar verkar någonting vara tokigt här. Om vi läser fördelningen (“% row”) för kategorin Medelålder ser vi att 50.2% har högt förtroende, 27.6% har lågt förtroende, och att detta summerar till 100. Men det kan inte stämma!

Det som har blivit fel är att vi har svarsbortfall i våra variabler. Det finns alltså en kolumn för svarsbortfall / NA som i modellen är osynlig.

Som tur är kan vi ganska enkelt ta fram nya data, utan svarbortfall. För ändamålet kan vi använda na.omit()-funktionen från bas R, i kombination med att skapa en ny begränsad data frame som endst innehåller våra två variabler alder_3 och fortroende_kat:

korstabell_data <- na.omit(ntu2021_kort[,c("alder_3", "fortroende_kat")])
head(korstabell_data)
##        alder_3 fortroende_kat
## 230 Medelålder           Högt
## 231      Äldre           Lågt
## 233      Äldre           Högt
## 235      Äldre           Högt
## 237 Medelålder           Lågt
## 238      Äldre           Högt

Vi kan sedan köra samma kod igen, och bara byta ut data =-argumentet:

library(modelsummary)
datasummary_crosstab(alder_3 ~ fortroende_kat, data = korstabell_data)
alder_3 Högt Lågt All
Ung N 8583 4986 13569
% row 63.3 36.7 100.0
Medelålder N 8864 4883 13747
% row 64.5 35.5 100.0
Äldre N 17171 10599 27770
% row 61.8 38.2 100.0
All N 34618 20468 55086
% row 62.8 37.2 100.0

I det här fallet ser vi att inom ålderskategoring Medelålder så har 64.5% ett högt förtroende för rättsväsendet och 35.5% har ett lågt förtroende för rättsväsendet. Tillsammans blir detta 100% av alla Medelålder (som har giltiga observationer för variabeln förtroende, de som är NA är ju inte med i tabellen längre). Detta kan vi sedan jämföra med exempelvis kategoring Äldre. Bland äldre är det något färre, 61.8% som ar högt förtrende för rättsväsndet, och något fler, 38.2% som har ett lågt förtroende för rättsväsendet.

Vi kan också lägga till vårt chi2-test som en not i tabellen. Tyvärr kan vi inte automatisera just denna process (inte utan jättemycket kod i alla fall), så vi får klippa ut och klistra in chi2-testet till noten själva:

chi2
## 
##  Pearson's Chi-squared test
## 
## data:  x
## X-squared = 28.885, df = 2, p-value = 5.342e-07
library(modelsummary)
datasummary_crosstab(alder_3 ~ fortroende_kat, data = korstabell_data,
                     note = "X-squared = 28.885, df = 2, p-value = 5.342e-07")
alder_3 Högt Lågt All
X-squared = 28.885, df = 2, p-value = 5.342e-07
Ung N 8583 4986 13569
% row 63.3 36.7 100.0
Medelålder N 8864 4883 13747
% row 64.5 35.5 100.0
Äldre N 17171 10599 27770
% row 61.8 38.2 100.0
All N 34618 20468 55086
% row 62.8 37.2 100.0

UTBILDNINGSKONTROLL

Gör en korstabell mellan ntu221_kort$fortroende_kat och ntu2021_kort$Kon_text. Inkludera ett chi2-test.

Hur tolkar du denna tabell? Är eventuella skillnader statistiskt signifikanta?

Prova att köra koden datasummary_crosstab(alder_3 ~ fortroende_index, data = ntu2021_kort). Vad är det som blir “fel” här?

7.2 Medelvärde

Att få reda på medelvärde för en variabel är enkelt i R. Bas R har en funktion som heter mean(), där vi i argumentet mean(x, na.rm = ) bara behöver byta ut x till den variabel vi är intresserad av samt (och mycket viktigt!) om vi vet att vi har observationer som är NA/Svarsbortfall så måste vi tala om detta för R genom att specificera argumentet na.rm = TRUE. För att ta reda på medelvärdet för variabeln ntu2021_kort$fortroende_index vilket är en variabel där vi vet att vi har svarsbortfall så skriver vi alltså:

mean(ntu2021_kort$fortroende_index, na.rm = TRUE)
## [1] 9.455433

Om vi skulle specificera na.rm = FALSE eller utelämna argumentet skulle vi enbart få till svar “NA”.

mean(ntu2021_kort$fortroende_index, na.rm = FALSE)
## [1] NA
mean(ntu2021_kort$fortroende_index)
## [1] NA

Vi kan också få ut ett 95% konfidensintervall runt vårt medelvärde, alltså ett intervall för vi med 95% säkerhet kan säga att det sanna medelvärdet i populationen som helhet (den vuxna svenska befolkningen) finns. Detta gör vi med funktionen t.test() från bas R. Där vi endast behöver specificera vilken variabel vi vill undersöka:

t.test(ntu2021_kort$fortroende_index)
## 
##  One Sample t-test
## 
## data:  ntu2021_kort$fortroende_index
## t = 620.62, df = 55085, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  9.425572 9.485295
## sample estimates:
## mean of x 
##  9.455433

Vi ser återigen att medelvärdet “mean of x” är 9.455433, och att konfidensintervallet “95 percent confidence interval” sträcker sig från 9.866624 till 9.945082.

Ofta vill vi dock inte bara se medelvärdet för hela variabeln, utan för olika grupper. Exempelvis kanske vi vill se medelvärdet för förtroende för rättsväsendet för Män/Kvinnor eller olika ålderskategorier Ung/Medelålder/Äldre.

Detta kan vi göra genom att använda en annan funktion från bas R som heter tapply() där vi behöver specificera argumenten tapply(kontinuerlig.variabel, kategorisk.variabel, funktion, na.rm = ) där vi istället för funktion skriver “mean”, alltså medelvärde. Om vi vill ta reda på medelvärdet för förtroende för rättsväsendet för Män respektive Kvinnor skriver vi:

tapply(ntu2021_kort$fortroende_index, ntu2021_kort$Kon_text, mean, na.rm = TRUE)
##   Kvinna      Man 
## 9.905853 8.987339

Och om vi vill veta konfidensintervallet runt respektive grupps medelvärde kan vi enkelt byta ut funktionen i argumentet i tapply()-funktionen från mean till t.test såhär:

tapply(ntu2021_kort$fortroende_index, ntu2021_kort$Kon_text, t.test, na.rm = TRUE)
## $Kvinna
## 
##  One Sample t-test
## 
## data:  X[[i]]
## t = 494.94, df = 28072, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  9.866624 9.945082
## sample estimates:
## mean of x 
##  9.905853 
## 
## 
## $Man
## 
##  One Sample t-test
## 
## data:  X[[i]]
## t = 395.36, df = 27012, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  8.942784 9.031895
## sample estimates:
## mean of x 
##  8.987339

Vi ser då återigen att medelvärdet för Kvinnor är 9.905853, med ett 95% konfidensinterval från 9.866624 till 9.945082.

Som vi har kunnat notera har kvinnor ett medelvärde på vårt förtroendeindex om 9.905853 medan män har ett lägre förtroende, i genonsmnitt 8.987339.

9.905853 - 8.987339
## [1] 0.918514

I genomsnitt tycks män ha 0.92 enheter lägre förtroende för rättvsäsendet (pår vår skala som sträcker sig från 0.16). men hur säkra kan vi vara på denna medelvärdesskillnad?

7.2.1 Medelvärde mellan en beroende kontinuerlig variabel och en oberoende kategorisk variabel med två kategorier

För att testa om medelvärdesskillnaden mellan två kategorier avseende en kontinuerlig variable är statistiskt signifikant behövert vi använda ett test som heter t-test. I detta fall är vi alltså intresserade av att ta reda på inte bara vad män respektive kvinnor har för genomsnittsligt förtroende för rättsväsendet, utan om vi med säkerhet kan uttala oss om huruvida kvinnor och män faktiskt skiljer sig åt avseende förtroendet för rättsväsendet. Vi är alltså intresserade av medelvärdesskillnaden, och graden av säkerhet som vi har kring denna medelvärdessskillnad.

T-test beställs enkelt genom att använda t.test()-funktionen i bas R. Argumenten ser ut såhär: t.test(kontinuerlig.variabel ~ kategorisk.variabel, data = data):

t.test(ntu2021_kort$fortroende_index ~ Kon_text, data = ntu2021_kort)
## 
##  Welch Two Sample t-test
## 
## data:  ntu2021_kort$fortroende_index by Kon_text
## t = 30.327, df = 53936, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Kvinna and group Man is not equal to 0
## 95 percent confidence interval:
##  0.8591501 0.9778763
## sample estimates:
## mean in group Kvinna    mean in group Man 
##             9.905853             8.987339

I resultet fokuserar vi på följande:

  • p-value : p-värdet, om detta är signifikant så betyder det att den observerade medelvärdesskillnaden med hög sannolikhet återfinns hos hela den studerade populationen som vi har dragit ett stickprov ifrån.

  • 95 percent confidence interval : konfidensintervallet inom vilket det sanna medelvärdet finns (i detta fall någonstans mellan 0.8591501 och 0.9778763)

  • sample estimates : våra respektive medelvärden för kategorierna (i detta fall är medelvärdet avseende förtroendeinex 9.905853 för kategorin Kvinna och 8.987339 för kategorin Man)

  • tyvärr ser vi inte den faktiska medelvärdesskillnaden, men den kan alltså enkelt räknas ut genom att skriva in 9.905853 - 8.987339 i konsolpanelen.

UTBILDNINGSKONTROLL

Använd datasetet ntu2021. Inspektera variabeln E1 (som frågar om respondenten har polisanmält något brott de tre senaste åren, sida 25 i Kodbok NTU2017-2021).

Vad betyder värde 1 respektive två på variabel E1?

Hur ser medelvärdet ut för respektive grupp svarskategori för variabeln E1när det gäller förtroende för rättsväsendet mätt med vårt fortroende_index?

7.2.2 Medelvärde mellan en beroende kontinuerlig variabel och en oberoende kategorisk variabel med tre eller fler kategorier

Om vi vill veta medelvärdet för en kontinuerlig variabel och fördelat på svarsketgorierna å kategorisk variabel med tre eller fler kategorier så kan vi återigen göra detta med vår tapply()-funktion. Om vi exemeplvis vill se det genomsnittsliga förtroende för rättsväsendet bland unga, medelålders och äldre skriver vi:

tapply(ntu2021_kort$fortroende_index, ntu2021_kort$alder_3, mean, na.rm = TRUE)
##        Ung Medelålder      Äldre 
##   9.546835   9.561068   9.358480

Och för att erhålla konfidensintervall runt dessa medelvärden byter vi ut mean till t.test:

tapply(ntu2021_kort$fortroende_index, ntu2021_kort$alder_3, t.test, na.rm = TRUE)
## $Ung
## 
##  One Sample t-test
## 
## data:  X[[i]]
## t = 300.64, df = 13568, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  9.484591 9.609079
## sample estimates:
## mean of x 
##  9.546835 
## 
## 
## $Medelålder
## 
##  One Sample t-test
## 
## data:  X[[i]]
## t = 302.81, df = 13746, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  9.499177 9.622959
## sample estimates:
## mean of x 
##  9.561068 
## 
## 
## $Äldre
## 
##  One Sample t-test
## 
## data:  X[[i]]
## t = 452.55, df = 27769, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  9.317948 9.399013
## sample estimates:
## mean of x 
##   9.35848

För att pröva medelvärdesskillnaden avseende en kontinuerlig variabel och en kategorisk variabel med tre eller fler kategorier kan vi dock inte längre använda ett t-test, då detta test endast kan ge oss antingen ett medelvärde med konfidensintervall eller en medelvärdesskillnad mellan två kategorier, med konfidensintervall.

För att ändå pröva om medelvärdesskillnaderna mellan flera svarskategorier är statistiskt signifikanta behöver vi använda oss av en annan statistisk teknik som heter ANOVA (analys av varians). En ANOVA sådan kan betällas av R genom funktionen aov(). Argumenten är likadana som för ett t.test: aov(kontinuerlig.variabel ~ kategorisk.variabel, data = data).

Viktigat att veta är att funktionen aov() skapar ett objekt som sammanfattar en hel statistisk modell. Det enklaste sättet att avläsa en sådan speciell typ av objekt är genom Rs summary()-funktion. Vi skapar alltså ett ojbekt som innehåller vår ANOVA-analys, och ber sedan R att sammanfatta detta objekt för oss.

Om vi är intresserade av att veta hur förtroendet för rättsväsendet skiljer sig mellan ålika ådersgrupper kan vi skriva:

m <- aov(fortroende_index ~ alder_3 , data = ntu2021_kort)
summary(m)
##                Df Sum Sq Mean Sq F value   Pr(>F)    
## alder_3         2    528  263.90   20.65 1.08e-09 ***
## Residuals   55083 703816   12.78                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 19265 observations deleted due to missingness

Det vi är intresserade av att läsa av här är bara p-värdet, som i tabellen anges som med stjärnor efter kolumnen “Pr(>F)”. Vi kan se att det tycks finnas en medelvärdesskillnad som är statistiskt signifikant på nivån p<0.001.

För att ta reda på skillnaderna i medelvärden mellan våra olika kategorier kan vi använda en funktion som heter TukeyHSD(), där vi helt enkelt placerar vår ANOVA-modell inom parantesen, precis som med summary()-funktionen:

TukeyHSD(m)
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = fortroende_index ~ alder_3, data = ntu2021_kort)
## 
## $alder_3
##                         diff         lwr        upr     p adj
## Medelålder-Ung    0.01423317 -0.08714715  0.1156135 0.9420681
## Äldre-Ung        -0.18835432 -0.27610311 -0.1006055 0.0000015
## Äldre-Medelålder -0.20258749 -0.28995382 -0.1152212 0.0000002

Det vi ser i tabellen är skillnaderna (diff) mellan olika kategorier. Den första raden anger medelvärdesskillnaden i förtroende för rättväsendet mellan kategorierna Ung och Medelåder. lwr och upr anger det nedre respektive övre gränsen iet 95%iga konfidensintervallet runt medelvärdesskillnaden. p adj anger p-värdet för medelvärdesskillnaden.

I just det här fallet verkar det som att vi har statistiskt signifikanta skillnader mellan Äldre och Ung samt Äldre och Medelålder. Men skillnaden mellan Ung och Medelålder tycks inte vara statistiskt signifiant.

Vi kan också skapa en figur som illustrerar dessa medelvärdesskillnader med konfidensintervall, genom att använda plot()-funktionen (och som argument inom parantesen helt enkelt ange ett objekt där vi sparat dessa medelvärdesskillnader):

t <- TukeyHSD(m)
plot(t)

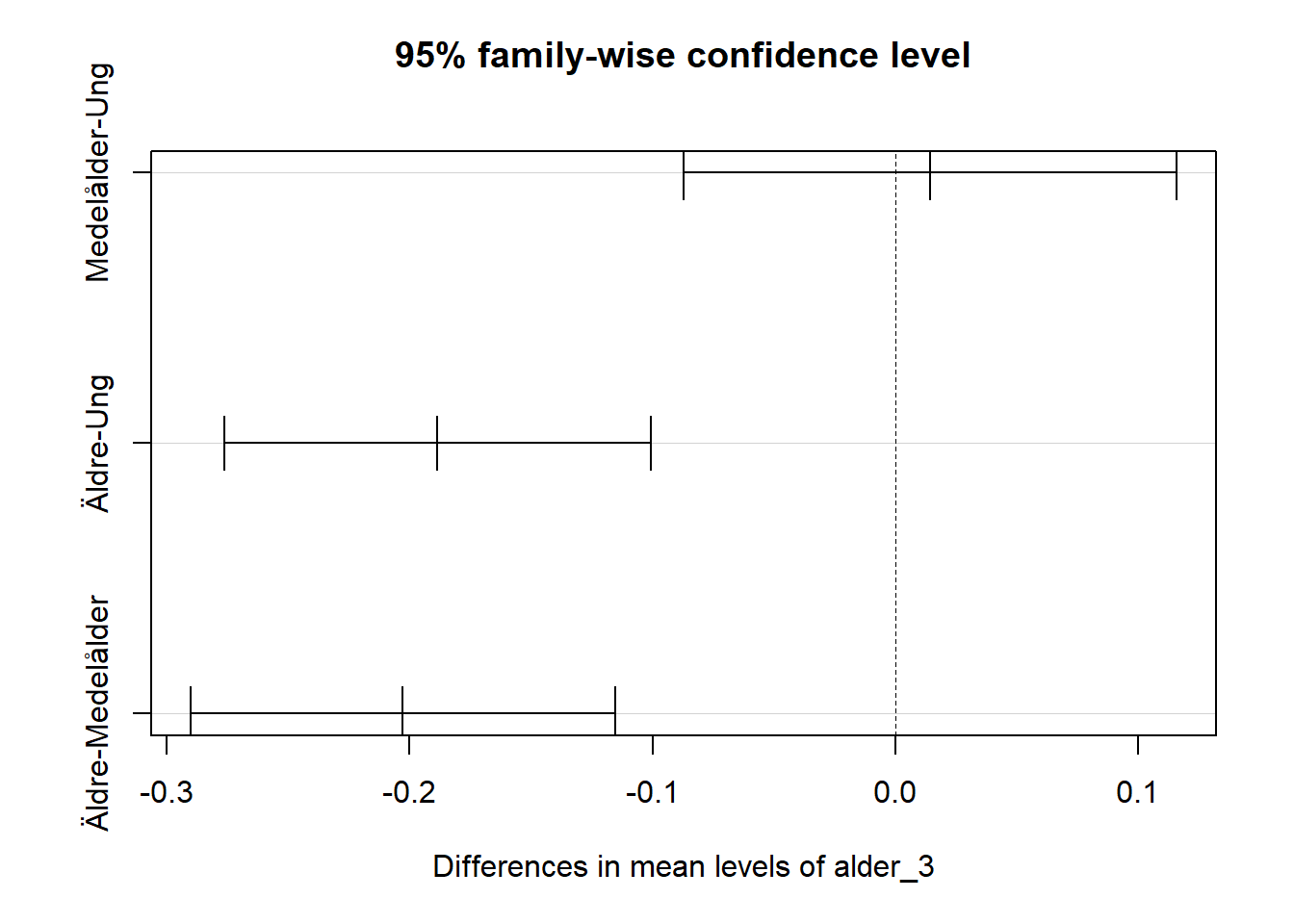
Vi noterar att skillnaderna på den översta raden (Medelåler-Ung) överlappar 0, alltså ingen skillnad.

Vi kan också skapa en figur över de faktiska medelvärdesskillnaderna:

figur6 <- plotmeans(ntu2021_kort$fortroende_index ~ ntu2021_kort$alder_3,
          xlab = "Ålder",
          ylab = "Förtroende, index (0-16)")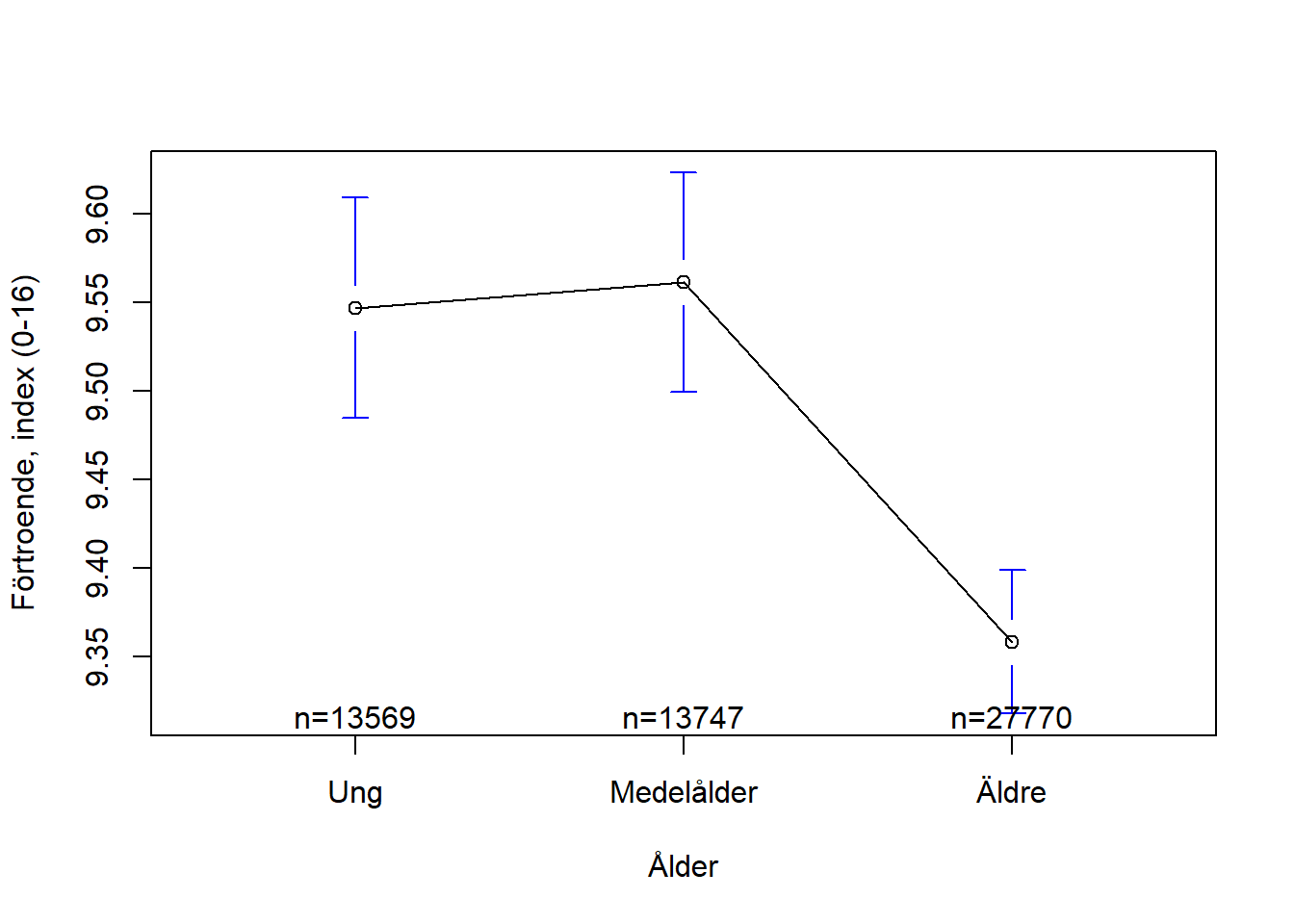

figur6
## NULL

UTBILDNINGSKONTROLL

Använd datasetet ntu2021. Inspektera variabeln Kommungrupper_kat3 (sida 4 i Kodboken NTU2017-2021).

Hur ser medelvärdet ut för respektive grupp svarskategori för variabeln Kommungrupper_kat3 när det gäller förtroende för rättsväsendet mätt med vårt fortroende_index?

Finns det några skillnader mellan gruppernas medelvärden? Är dessa skillnader statistiskt signifikanta?

Illustrera dessa medelvärden och skillnader med lämpliga diagram.

Ta även frm lämpliga diagram för att illustrera medelvärden och medelvärdesskillnader avseende variablerna E1 och fortroende_index.

7.3 Korrelationstabell

När två variabler samvarierar med varandra brukar vi säga att de korrelerar med varandra. Beroende på vad variblerna har för egenskaper, om de är kategoriska eller kontinuerliga, kan vi använda olika mått. För två kategoriska variabler kan vi använda ett mått som heter Chramer’s V och som går mellan 0 inget samband till 1 perfekt samband. Det finns även andra typer av korrelationsmått som Kendalls Tau och Spearmans rank-order-correlation. Det är inget ni behöver lägga på minnet, men det kan vara bra att känna till om ni skulle stöta på dem i något sammanhang.

Oftast när vi talar om korrelationer, om vi inte uttryckligen säger något annat, så talar vi dock om samvariationen mellan två kontinuerliga variabler. Detta är alltså det vi vanligen avser när vi pratar om korrelationer som en egen, särskild form av statistisk analys.

Korrelationer mellan två kontinuerliga variabler mäts genom Pearson’s r som kan gå mellan -1 (perfekt negativt sambnad) via 0 (inget samband) till +1 (perfekt positivt samband). Negativt betyder att när den ena variabeln ökar så minskar den andra, och positivt betyder att båda variablerna ökar tillsammans.

Det enklaste sättet att testa korrelationer på det här sättet i R är att använda funktionen cor.test() från bas R. Argumenten är enkla: cor.test(beroende.variabel, oberoende.variabel). Om vi vill ta reda på korrelationen mellan våra två index, bemötandeindex och förtroendeindex, så skriver vi:

cor.test(ntu2021_kort$bemotande_index, ntu2021_kort$fortroende_index)
## 
##  Pearson's product-moment correlation
## 
## data:  ntu2021_kort$bemotande_index and ntu2021_kort$fortroende_index
## t = 288.88, df = 51760, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.7822906 0.7888867
## sample estimates:
##      cor 
## 0.785611

Det som är mest inressant att läsa av här är “cor” där vi ser att korrelationen är 0.786, vilket är ett starkt positivt samband. Vi är också intresserade av om detta är statistiskt signifikant eller inte, vilket vi läser av genom att titta på “p-value < 2.2e-16”. Detta betyder att vi har en nolla följt av femton nollor innan vi ser någonting på den sextonde decimalen. Vi är alltså mycket säkra på att vår korrelation, r = 0.786, verkligen finns i den undersökta populationen av vuxna människor i Sverige.

Vi kan visualisera denna korrelation genom attta fram ett spridningsdiagram:

plot(ntu2021_kort$bemotande_index[1:150], ntu2021_kort$fortroende_index[1:150])

Vi kan också standardisera svarsskalorna så att de görs om till standardavvikelser. I detta fall har vi två variabler som både mäts 0-16, och då spelar det egnetligen inte så stor roll. Men föreställ er att vårt bemötande index istället hade gått från 15-130. Då kanske vi vill göra svarsskalorna på x-axeln och y-axeln mer jämförbara. Vi kan åstadkomma detta genom att inkludera funktionen scale() i argumenten i funktionen plot(). Vi placerar helt enkelt våra variabler inom scale()-funktionen.

Vi kan också passa på att lägga till en linje som sammanfattar sambandet (denna kallas vanligen för regressionslinien och just denna del av koden kommer ni att förstå bättre i avsnitt 6 Regressionsanalys; här är den mest till för att förtydliga det linjära sambandet mellan dessa två variabler):

plot(scale(ntu2021_kort$bemotande_index[1:150]), scale(ntu2021_kort$fortroende_index[1:150]))
abline(lm(scale(fortroende_index) ~ scale(ntu2021_kort$bemotande_index), data = ntu2021_kort))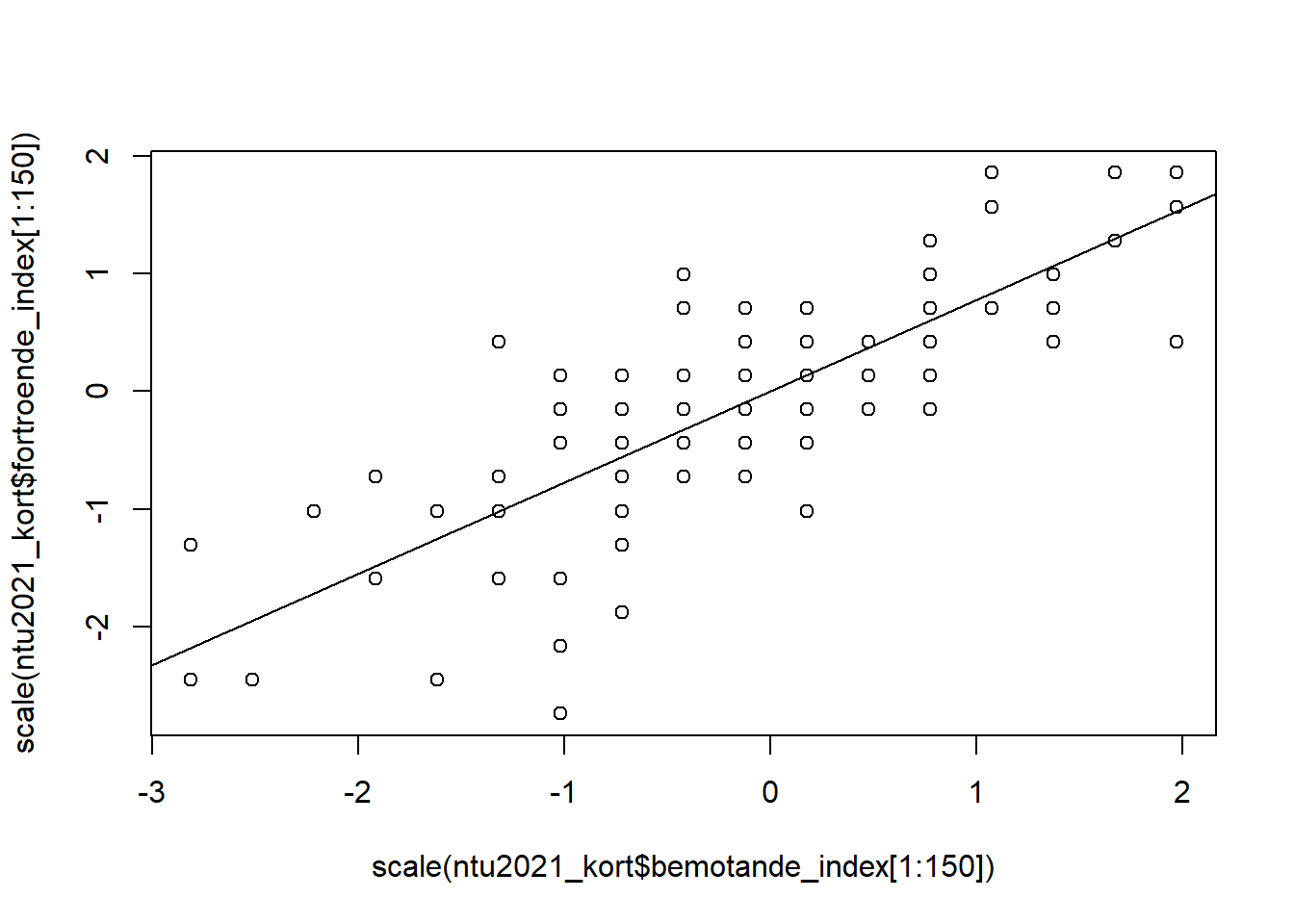

Framförallt kan vi ta fram en lite snyggare korrelationstabell. Detta gör vi med hjälp av en funktion från modelsummary-paketet som heter datasummary_correlation(). Funktionen känner automatiskt av vilka variabler som är kontinuerliga i en data frame eller en tibble:

library(modelsummary)
datasummary_correlation(ntu2021_kort)
bemotande_index fortroende_index fortroende_helhet
bemotande_index 1 . .
fortroende_index .79 1 .
fortroende_helhet .69 .82 1

Tabellen har rader och kolumner, och om en vill veta hur två variabler förhåller sig till varandra så tittar en på vart dessa två variabler “skär” varandra inom det fält som raderna och kolumnerna bildar. För att avläsa hur fortroende_index korrelerar med fortroende_helhet tittar vi alltså först på rad tre (raden för fortroende_helhet) och sedan på kolumn ett (kolumnen för fortroende_index).

För att få ut signifikansnivåerna för korrelationerna behöver vi bygga på vår kod med en funktion correlation() från ett pkaet som heter correlation. Vi behöver också ta hänsyn till ytterliggare ett argument som heter stars =:

library(modelsummary)
library(correlation)
datasummary_correlation(correlation(ntu2021_kort),
                                    stars = TRUE)
bemotande_index fortroende_index fortroende_helhet
bemotande_index 1 . .
fortroende_index .79*** 1 .
fortroende_helhet .69*** .82*** 1

Vi ser att korrelationen är .822 (en väldigt stark korrelation!), och att den är signifikant (“***” vilket motsvarar p<0.001).

För att göra det tydligare kan vi lägga till en not som anger signifikansnivåerna i tabellen:

library(modelsummary)
library(correlation)
tabell_4 <- datasummary_correlation(correlation::correlation(ntu2021_kort),
                                    stars = TRUE,
                                    note = "+ = p<.1, * = p<.05, ** = p<.01, *** = p<.001")
tabell_4
bemotande_index fortroende_index fortroende_helhet
+ = p<.1, * = p<.05, ** = p<.01, *** = p<.001
bemotande_index 1 . .
fortroende_index .79*** 1 .
fortroende_helhet .69*** .82*** 1

output: html_document date: “2025-09-17” —