Kapitel 5 Deskriptiv statistik och grunder i datavisualisering.
I detta avsnitt skall vi istället titta på deskriptiv statistik, det vill säga statistik som beskriver fördelning och tendenser inom en och samma variabel. Vi skall också lära oss grunderna i datavisualisering. Det vill säga hur vi med hjälp av olika figurer och diagram kan förmedla visuell information till en läsare av vår rapport för att förtydliga hur våra data ser ut.
Vi kommer att arbeta med ett något förenklat dataset med färre variabler. Vi kommer därför att välja ut fyra stycken variabler från ntu2021 som vi har arbetat emd i de tidigare avsnittet.
Detta avsnitt bygger alltså på att du redan:
i avsnitt 3.3.2 har skapat faktorvariabeln
Kon_textdär Man och Kvinna anges med text istället för siffror.i avsnitt 3.3.2 har skapat faktorvariabeln
alder_3där vi kategoriserat respondenterna som Ung, Medelålders eller Äldre baserat på deras ålder.i avsnitt 3.3.2 har skapat faktorvariabeln
D1A_katdär vi kategoriserat respondenterna som blivit utsatta för cykelstöld som Ingen, En, Två, och Tre eller fler gånger.i avsnitt 3.3.4 har skapat variabeln
ntu2021$B1_rensadsom är en enskild variabel baserad på en enda enkätfråga som mäter förtroendet för rättsväsendet som helhet på en skala från 1 (mycket stort) till 5 (mycket litet) förtroende. I denna variabel har vi sorterat bort alla som svarat 6:Vet inte / Ingen åsikt så att de har fått värde NA (svarsbortfall).i avsnitt 3.3.4 har skapat ett
ntu2021$fortroende_indexav variablerna B2, B3, B4 och B5.i avsnitt 3.3.4 har skapat ett
ntu2021$bemotande_indexav variablerna B6A, B6B, B6C och B6D.
Innan vi riktigt kör igång så vill vi göra en sak. Vi vill vända på variabeln ntu2021$B1_rensad så att låga värden innebär lågt förtroende för rättsväsendet som helhet, och höga värden innebär högt förtroende för rättsväsendet som helhet. Det gör vi bara för att våra två övriga index ntu2021$fortroende_indexoch ntu2021$bemotande_index går i den riktningen. Vi gör det alltså för att slippa förvirring. Vi kan döpa den nya variabeln till fortroende_helhet så slipper vi dessutom komma ihåg vilken fråga som just “B1” syftade på i den Nationella Trygghetsundersökningen.
Vi skapar vårt förenklade dataset genom att göra en ny data frame som består av variablerna ovan, genom att köra följande kod:
ntu2021_kort <- ntu2021[1:nrow(ntu2021), c("region",
"Kon_text",
"alder_3",
"D1A_kat",
"bemotande_index",
"fortroende_index",
"fortroende_helhet")]
head(ntu2021_kort)## region Kon_text alder_3 D1A_kat bemotande_index fortroende_index fortroende_helhet
## 230 Väst Kvinna Medelålder Ingen gång/Ingen uppgift 12 14 3
## 231 Väst Kvinna Äldre Ingen gång/Ingen uppgift 6 4 2
## 232 Syd Kvinna Äldre Ingen gång/Ingen uppgift 7 NA 2
## 233 Stockholm Kvinna Äldre Ingen gång/Ingen uppgift 10 10 3
## 234 Syd Kvinna Medelålder Ingen gång/Ingen uppgift NA NA 3
## 235 Öst Kvinna Äldre Ingen gång/Ingen uppgift 14 12 2## Rows: 74,351
## Columns: 7
## $ region <chr> "Väst", "Väst", "Syd", "Stockholm", "Syd", "Öst", "Stockholm", "Nord", "Nord", "Nord", "Stockholm", "Bergslagen", "Syd", "Syd", …
## $ Kon_text <fct> Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Man, Man, Man, Kvinna, Kvinna, Kvinna, Man, Man, Kvinna, Kvinna, Man, Kv…
## $ alder_3 <fct> Medelålder, Äldre, Äldre, Äldre, Medelålder, Äldre, Äldre, Medelålder, Äldre, Ung, Äldre, Äldre, Äldre, Medelålder, Äldre, Ung, …
## $ D1A_kat <fct> Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift…
## $ bemotande_index <dbl> 12, 6, 7, 10, NA, 14, NA, 7, 16, 10, 15, NA, 12, 7, 6, 8, 10, 3, 7, 6, 10, 10, 12, NA, 12, 9, 2, 14, 8, 8, 11, 10, 15, 9, 7, 4, …
## $ fortroende_index <dbl> 14, 4, NA, 10, NA, 12, NA, 8, 11, 12, 16, NA, 10, 5, 0, NA, 9, 4, 10, 8, 9, 11, NA, NA, 12, 7, 6, 11, 7, 12, 9, NA, 14, 11, 8, 1…
## $ fortroende_helhet <dbl> 3, 2, 2, 3, 3, 2, 3, 2, 3, 3, 4, 2, 3, 3, 0, 3, 3, 1, 3, 2, 2, 3, 2, 2, 3, 1, 3, 3, 2, 3, 3, 3, 4, 3, 2, 0, 2, 1, 2, 3, 2, 4, 1,…Vi ser nu att vi fått en ny data frame med endast de variabler vi vill ha.
För den som är lite extra nyfiken så fungerar argumenten i kommandot ovan på följande sätt: data.frame[rad, kolumn]. Istället för “data.frame” så skriver vi vad vår data frame heter (den som vi vill hämta variablerna från), i detta fall “ntu2021”. Därefter, inom hakparanteser anger vi vilka rader och kolumner vi vill välja. Detta är lite speciellt, men grunden är att vi i R kan välja exakt vilken “position” vi vill inom en data frame genom att ange positioner med hjälp av rader och kolumner. Exemeplvis kan vi vija titta på vilket kön respondent nummer 650 har, och kan då beställa denna information från R genom följande kod ntu2021[650, "Kon_text"]. Om du testar att köra denna kod kommer du få till svar att respondenten i fråga är Man.
Hursomhelst, i det här fallet vill vi välja alla rader, och ett helt gäng med variabler som tillsammans skall bilda en ny data frame som vi skall använda i våra fortsatta övningsexempel. Eftersom att vi vill välja samtliga rader så skriver vi det första argumentet som 1:nrow(ntu2021) vilket betyder att vi väljer alla rader från och med rad 1 till och med (till och med anges med ett kolon “:”) den sista raden i datasetet ntu2021 (det är detta som funktionen nrow() hjälper oss med). I det andra argumentet specificerar vi alla de variabler som vi vill ha. Detta måste vi göra med hjälp utav funktionen c() som betyder “combine” inom vilkens parantse vi sedan helt enkelt kan namnge de kolumner/variabler som vi vill ha.
Vi kan även förenkla koden ovan genom att lämna det första argumentet tomt. Då förstår R automatiskt att den skall välja alla rader:
ntu2021_kort <- ntu2021[, c("region",
"Kon_text",
"alder_3",
"D1A_kat",
"bemotande_index",
"fortroende_index",
"fortroende_helhet")]
head(ntu2021_kort)## region Kon_text alder_3 D1A_kat bemotande_index fortroende_index fortroende_helhet
## 230 Väst Kvinna Medelålder Ingen gång/Ingen uppgift 12 14 3
## 231 Väst Kvinna Äldre Ingen gång/Ingen uppgift 6 4 2
## 232 Syd Kvinna Äldre Ingen gång/Ingen uppgift 7 NA 2
## 233 Stockholm Kvinna Äldre Ingen gång/Ingen uppgift 10 10 3
## 234 Syd Kvinna Medelålder Ingen gång/Ingen uppgift NA NA 3
## 235 Öst Kvinna Äldre Ingen gång/Ingen uppgift 14 12 2## Rows: 74,351
## Columns: 7
## $ region <chr> "Väst", "Väst", "Syd", "Stockholm", "Syd", "Öst", "Stockholm", "Nord", "Nord", "Nord", "Stockholm", "Bergslagen", "Syd", "Syd", …
## $ Kon_text <fct> Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Kvinna, Man, Man, Man, Kvinna, Kvinna, Kvinna, Man, Man, Kvinna, Kvinna, Man, Kv…
## $ alder_3 <fct> Medelålder, Äldre, Äldre, Äldre, Medelålder, Äldre, Äldre, Medelålder, Äldre, Ung, Äldre, Äldre, Äldre, Medelålder, Äldre, Ung, …
## $ D1A_kat <fct> Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift, Ingen gång/Ingen uppgift…
## $ bemotande_index <dbl> 12, 6, 7, 10, NA, 14, NA, 7, 16, 10, 15, NA, 12, 7, 6, 8, 10, 3, 7, 6, 10, 10, 12, NA, 12, 9, 2, 14, 8, 8, 11, 10, 15, 9, 7, 4, …
## $ fortroende_index <dbl> 14, 4, NA, 10, NA, 12, NA, 8, 11, 12, 16, NA, 10, 5, 0, NA, 9, 4, 10, 8, 9, 11, NA, NA, 12, 7, 6, 11, 7, 12, 9, NA, 14, 11, 8, 1…
## $ fortroende_helhet <dbl> 3, 2, 2, 3, 3, 2, 3, 2, 3, 3, 4, 2, 3, 3, 0, 3, 3, 1, 3, 2, 2, 3, 2, 2, 3, 1, 3, 3, 2, 3, 3, 3, 4, 3, 2, 0, 2, 1, 2, 3, 2, 4, 1,…Som vi ser blir det exakt samma resultat!
Innan vi börjar skall vi också se till att vi har alla de paket som vi behöver. Vi kommer att arbeta med följande paket:
- modelsummary som hjälper oss att skapa tabeller.
För att kunna hänga med måste du alltså installera och öppna detta paket. Om du har glömt hur en installerar paket kan du bläddra tillbaka till avsnitt 2.4. För att öppna paketen använder vi som vanligt library()-funktionen.
Nu kan vi börja!
5.1 Kategoriska variabler: Frekvenstabell
Frekvenstabeller i R är lätta att skapa tack vara en funktion som heter datasummary_skim() från modelsumnmary-paketet. datasummary_skim() fungerar på hela data frame men det går att specificera om en vill att funktionen skall behandla bara kategoriska (faktorvariabler och textvariabler med datatypen Character), bara numeriska (kontinuerliga variabler med datatypen Double eller Integer), eller alla typer av variabler samtidigt. Eftersom att vi här är intresserade av att skapa frekvenstabeller (alltså en tabell över antal observationer som ett visst variabelvärde har, exempelvis hur mänga män respektive hur många kvinnor vi har på variabeln Kön i Nationella Trygghetsundersökningen), så kommer vi att börja med att endast titta på kategoriska variabler.
datasummary_skim()-funktionen består av två argument på det här sättet: datasummary_skim(x, type = ). Istället för x skriver vi in vår_data frame_ och i argumentet type = skriver vi in antingen “categorical”, “numeric”, eller “all” beroende på vilkent yp av tabell vi vill ha. Vi skall endast titta på kategoriska variabler i en frekvenstabell, så vi väljer här att skriva “categorical”:
| N | % | ||
|---|---|---|---|
| region | Bergslagen | 8530 | 11.5 |
| Mitt | 6294 | 8.5 | |
| Nord | 9553 | 12.8 | |
| Öst | 7015 | 9.4 | |
| Stockholm | 14558 | 19.6 | |
| Syd | 15590 | 21.0 | |
| Väst | 12811 | 17.2 | |
| Kon_text | Kvinna | 39207 | 52.7 |
| Man | 35144 | 47.3 | |
| alder_3 | Äldre | 37825 | 50.9 |
| Medelålder | 17672 | 23.8 | |
| Ung | 18854 | 25.4 | |
| D1A_kat | En gång | 4770 | 6.4 |
| Ingen gång/Ingen uppgift | 68108 | 91.6 | |
| Tre eller fler gånger | 373 | 0.5 | |
| Två gånger | 1100 | 1.5 |
I fliken Viewer så får vi då upp en bild på en tabell där vi längst till vänster ser namnen på våra variabler (exempelvis ntu2021.region), därefter de variabelvärden som dessa variabler kan anta (exempelvis Berglslagen och Mitt), därefter ser vi en kolumn som heter “N” vilket står för antal och alltså anger antal observationer som har detta värden (hur många av de som svarat på enkäten som bor i polisregion Bergslagen), och sist en kolumn som heter “%” vilken motsvarar procent (hur många procent av alla svaranden som bor i Bergslagen: 11.5%).
Om vi vill så kan vi öppna tabellen i ett separat fönster, om vi vill titta på den lite extra (det kan vara användbart om vi har att göra med en väldigt stor tabell, exempelvis om vi skulle titta på alla variabler i vårt ursprungliga dataset ntu2021, vilket består av 110 variabler).
Vi kan också spara eller kopiera denna tabell, så att vi exempelvis kan importera den i ett word-dokument (mycket användbart!!!).
Spara tabellen som en bild genom att (1) klicka på Export och (2) välja Save as image och (3) i pop-up-fönstret välja vart filen skall sparas (Directory), namnge filen i fältet Filename, och klicka på Save.
För att istället kopiera tabellen som en bild (och kanske klistra in den direkt i ett word-dokument) kan en istället (1) klicka på Export och (2) välja Copy to Clipboard och (3) i pop-up-fönstret klicka på Copy Plot. Du kan nu klistra in tabellen någon annan stans, exemplevis i word eller open office.
En sista sak: funktionen datasummary_skim() fungerar som bara på objekt av typen data frame eller tibble. Om vi exempelvis är intresserad av att göra en snygg tabell som bara innefattar en variabel så måste vi alltså skapa en ny data frame som bara innehåller den variabeln. (Även om summary()-funktionen som vi hittils använt för att titta på enskilda variabler är användbar för att utforska data så ger den inte särskilt snygga tabeller). Det vi måste göra då är helt enkelt att skapa en ny data frame med den variabel vi är intresserad av.
| ntu2021_kort.Kon_text | N | % |
|---|---|---|
| Kvinna | 39207 | 52.7 |
| Man | 35144 | 47.3 |
Vi kan såklart också välja att spara våra tabeller som objekt, så att vi närsomhelst kan plocka fram dem när vi behöver dem:
| N | % | ||
|---|---|---|---|
| region | Bergslagen | 8530 | 11.5 |
| Mitt | 6294 | 8.5 | |
| Nord | 9553 | 12.8 | |
| Öst | 7015 | 9.4 | |
| Stockholm | 14558 | 19.6 | |
| Syd | 15590 | 21.0 | |
| Väst | 12811 | 17.2 | |
| Kon_text | Kvinna | 39207 | 52.7 |
| Man | 35144 | 47.3 | |
| alder_3 | Äldre | 37825 | 50.9 |
| Medelålder | 17672 | 23.8 | |
| Ung | 18854 | 25.4 | |
| D1A_kat | En gång | 4770 | 6.4 |
| Ingen gång/Ingen uppgift | 68108 | 91.6 | |
| Tre eller fler gånger | 373 | 0.5 | |
| Två gånger | 1100 | 1.5 |
5.2 Kontinuerliga variabler: Tabell med spridningsmått och centralmått
Om vi istället vill få en deskriptiv tabell som sammanfattar relevanta spridningsmått och centraltendenser för våra kontinuerliga variabler (alltså variabler som befinner sig på intervall- eller kvotskalenivå, vilka i R utgörs av datatyperna Double eller Integer).
Det enda vi behöver göra är att ändra argumentet i koden vi använde i föregående avsnitt från type = "categorical" till type = "numeric":
| Unique | Missing Pct. | Mean | SD | Min | Median | Max | Histogram | |
|---|---|---|---|---|---|---|---|---|
| bemotande_index | 18 | 17 | 9.2 | 3.5 | 0.0 | 9.0 | 16.0 |  |
| fortroende_index | 18 | 26 | 9.5 | 3.6 | 0.0 | 10.0 | 16.0 |  |
| fortroende_helhet | 6 | 5 | 2.4 | 1.0 | 0.0 | 3.0 | 4.0 | 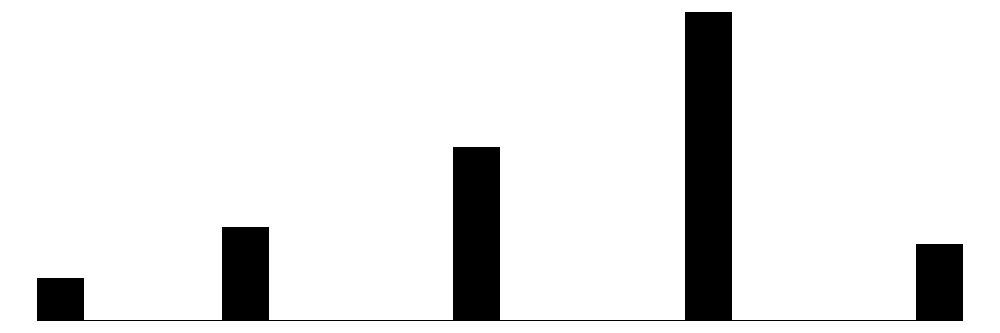 |
Vi får då upp en tabell där vi kan avläsa följande kolumner:
Unique: Antal unika värden variabeln kan anta. Oftast är detta svarsskalans längd + svarsbortfall (NA). För våra index som går från 0-16 (vilket är 17 unika svarsvärden om en räknar med 0) och där vissa respondenter utgör svarsbortfall (NA) så blir de unika värden som variabeln kan anta 18 stycken. Detta är oftast inte superintressant.
Missing Pct.: Procent interna svarsbortfall. Alltså hur många obervationer/rader (personer) som inte har ett giltigt svar på variabeln. I vår tabell kan vi se att indexvariablerna har ett höge svarsbortfall en den enskilda frågan
fortroende_helhetvilket helt enketl beror på att vi har använt flera variabler för att konstruera våra index. Om en respondent har haft ett svarsbortfall på bara en av dessa varaibler har hen räknats som svarsbortfall (NA) på hela indexet.Mean: Medelvärdet. Ett centralmått. Summan av alla obserationers varaibelvärden delat med antalet observationer.
SD: standardavvikelsen (på engelska Standard Deviation). Ett mått på hur samlade eller utspridda observationerna är kring medelvärdet. Alltså ett spridningsmått. Uttrycks i variabelns svarsskala. Om SD = 3.5 för variabeln
bemotande_indexbetyder det att en standardavvikelse från medelvärdet är 3.5 punkter på indexskalan. Alltså medelvärdet 9.2 +/1 3.5. Eftersom att +/1 en standardavvikelse täcker in ungefär 68.2% av alla observationer i en normalfördelad variabel så betyder det att 68.2% av alla svar faller inom spannet 5.7 till 12.7.Min: Minimum, det lägsta observerade värdet.
Median: Ett centralmått. Det “mittersta” värdet om vi ställer upp alla observationer från lägsta till högsta observationen.
Max: Maximum, det högsta observerade värdet.
Histogram: Som en liten bonus så får vi i
datasummary_skim()med ett litet histogram som grafiskt illustrerar hur vår variabel fördelar sig. Alla variablerna ser approgimativt (ungefärligt) normalfördelade ut. Det är en jättebra överblick, men vi skalls trax titta på hur vi kan skapa större, riktiga histogram.
UTBILDNINGSKONTROLL
Välj ut en av de kontinuerliga variablerna och gör en ny tabell som endast innefattar denna variabel.
5.3 Grunder visualisering
I det här avsnittet skall vi gå igenom fem olika diagram för datavisualisering.
De fem diagram vi skall gå igenom är:
stapeldiagram (barplot): med hjälp av funktionerna
barplot(),table()ochprop.table()histogram: med hjälp av funktionen
hist()låddiagram (boxplot): med hjälp av funktionen
boxplot()medelvärdesdiagram (meangraph) med och utan linjer: med hjälp av funktionen
plotmeans()från paketetgplotsspridningsdiagram (scatterplot): med hjälp av funktionen
plot()
Som några observanta läsare kanske noterade är funktionen plotmeans() inte en del av bas R utan kommer från paketet gplots. Vi måste alltså börja med att installera detta paket genom att köra koden install.packages("gplots") och sedan öppna detta paket med library(gplots).
Nu kan vi börja!
5.3.1 Stapeldiagram
Stapeldiagram används för en enskild kategorisk variabel. Alltså för en variabel som mäts med nominalskala (går ej att rangordna ~ olika frukter) eller ordinalskala (går att rangordna ~ ofta, ibland, sällan), vilken i R måste vara av datatyp factor (siffror eller text) eller character (bara text). Det som ett stapeldiagram visar oss är hur våra observationer fördelar sig på variabelns olika värden/svarskategorier. Alltså i fallet med Nationella Trygghetsundersökningen kan vi få ut visuell information över hur många respondenter som har svarat ett visst svar/variabelvärde på en viss enkätfråga/variabel.
I vårt datamaterial är kön ntu2021_kort$Kon_text en kategorisk variabel av typen faktor. Ett stapeldiagram kan då visa hur många kvinnor respektive hur många män som har svarat på enkäten, alternativt hur många procent kvinnor respektive män som svarat på enkäten. Den grundläggande funktionen för att beställa ett stapeldiagram är mycket enkel: barplot(x). Där x är det objekt som vi vill utföra funktionen på. Men innan vi faktiskt beställer ett stapeldiagram så behöver vi förstå två saker relaterade till våra två hjälpfunktioner table() och prop.table() som vi skalla nvända i kombination med barplot().
table() är en funktione som tar en kategorisk variable och producerar en mycket enkel frekvenstabell. Tillmäpad på vår variabel ntu2021_kort$Kon_text så ser det ut såhär:
##
## Kvinna Man
## 39207 35144Vi har alltså skapat ett objekt, “x”, som innehåller våra kategorier, man och kvinna, samt antalet observationer (frekvenserna). Det är denna information som vi nu enkelt kan visualisera med hjälp av ett stapeldiagram:

Vi ser här att det är något fler kvinnor än män som svarat på enkäten. Men kanske är just frekven inte den mest användbara informationen här. Kanske skulle vi istället vilja se hur många procent av de som svarat på enkäten som är kvinnor respektive män?
Det kan vi göra genom att använda funktionen prop.tabel() där “prop” står för “proportion”. Funktionen prop.tabel() använder vi i kombination med den grundläggande tabel()-funktionen, för att omvandla frekvenserna till proportioner påd et här sättet:
##
## Kvinna Man
## 0.5273231 0.4726769Detta ger oss dock bara proportioner mellan 0 och 1.
Om vi vill ha procent kan vid dock enkelt bara multiplicera proportionerna med hundra. En proprotion, en andel, går alltså mellan 0 och ett. Medan procent går mellan 0 och 100. (Cent som i ProCent är för övrigt hundra på lati. Även i modern italienska säger de cento om hundra. “Cento percento” är alltså “hundra procent” på italienska. “Lui non é cento percento” betyder att “han är inte helt hundra”. Jag vet inte om det var så användbart för att skriva en bra statistisk rapport i kriminologi, men det är sant).
Vi multiplicerar proportionerna genom att addera uttrycket * 100 till koden:
##
## Kvinna Man
## 52.73231 47.26769Vi kan nu beställa ett stapeldiagram med procent, istället för frekvens:

Vi kan också lägga till etiketter (“labels”) på x- respektive y-axeln, samt ändra färger, om vi vill göra vårt stapeldiagram lite tydligare. Detta gör vi genom ett antal extra argument i koden, på det här sättet:
Faktum är att vi till och med kan ändra etiketterna för variabelvärdena från Kvinna och Man till exempelvis Tjejer och Killar om vi vill:
barplot(x,
xlab = "Kön",
ylab = "Procent (%)",
col = c("gray", "black"),
names.arg = c("Tjejer", "Killar")) 
Och slutligen kan vi spara detta stapeldiagram som ett objekt, så att vi kan plocka fram det närhelst vi behöver det:
figur_1 <- barplot(x,
xlab = "Kön",
ylab = "Procent (%)",
col = c("gray", "black"),
names.arg = c("Tjejer", "Killar")) 
## [,1]
## [1,] 0.7
## [2,] 1.9UTBILDNINGSKONTROLL
Ta fram ett procentuell stapeldiagram som visar fördelningen i variabeln
alder_3.Ungefär hur många av de svarande är Unga, Medelålders och Äldre? Finns det någon kategori som är mer representerad än de andra?
5.3.2 Histogram
Histogram är ett typ av diagram som vi använder för att inspektera hur kontinuerliga variabler (alltså variabler på intervall eller kvotskala, i R datatyperna double eller integer) fördelar sig. De liknar stapeldiagram i viss utsträckning i det att de anger frekvens/antal observationer på den hvertikala y-axeln och variabelvärden på den horisontella x-axeln. Någonting att notera är dock att alla staplar angränsar varandra, vilket visuellt är tänkt att symbolisera att dessa variabelvärden är en kontinuerlig skala och inte tydliga kategorier.
Att beställa ett histogram i R är mycket enkelt! Vi behöver bara tillämpa hist()-funktionen på den variabel vi vill visualisera. I det här exemplet skall vi titta på vårt index över allmänhetens förtroende för att rättsväsendet bemöter såväl offer som misstänkta på ett rättvist sätt ntu2021_kort$bemotande_index:
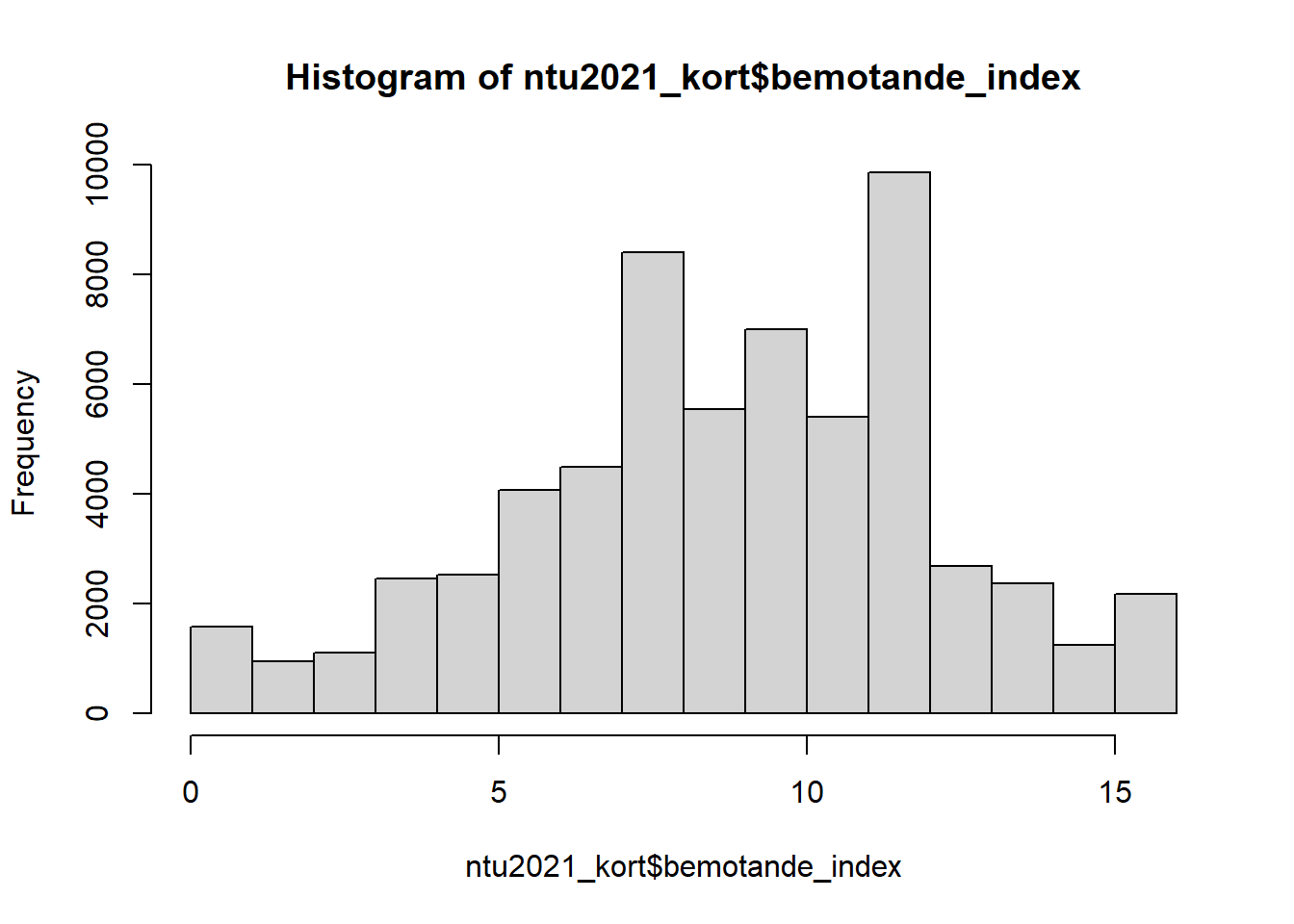
## $breaks
## [1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
##
## $counts
## [1] 1578 957 1115 2455 2523 4077 4497 8415 5544 7009 5399 9857 2686 2367 1246 2183
##
## $density
## [1] 0.02548944 0.01545842 0.01801060 0.03965562 0.04075402 0.06585579 0.07264005 0.13592751 0.08955224 0.11321639 0.08721005 0.15922013 0.04338696
## [14] 0.03823415 0.02012664 0.03526200
##
## $mids
## [1] 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5 14.5 15.5
##
## $xname
## [1] "ntu2021_kort$bemotande_index"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
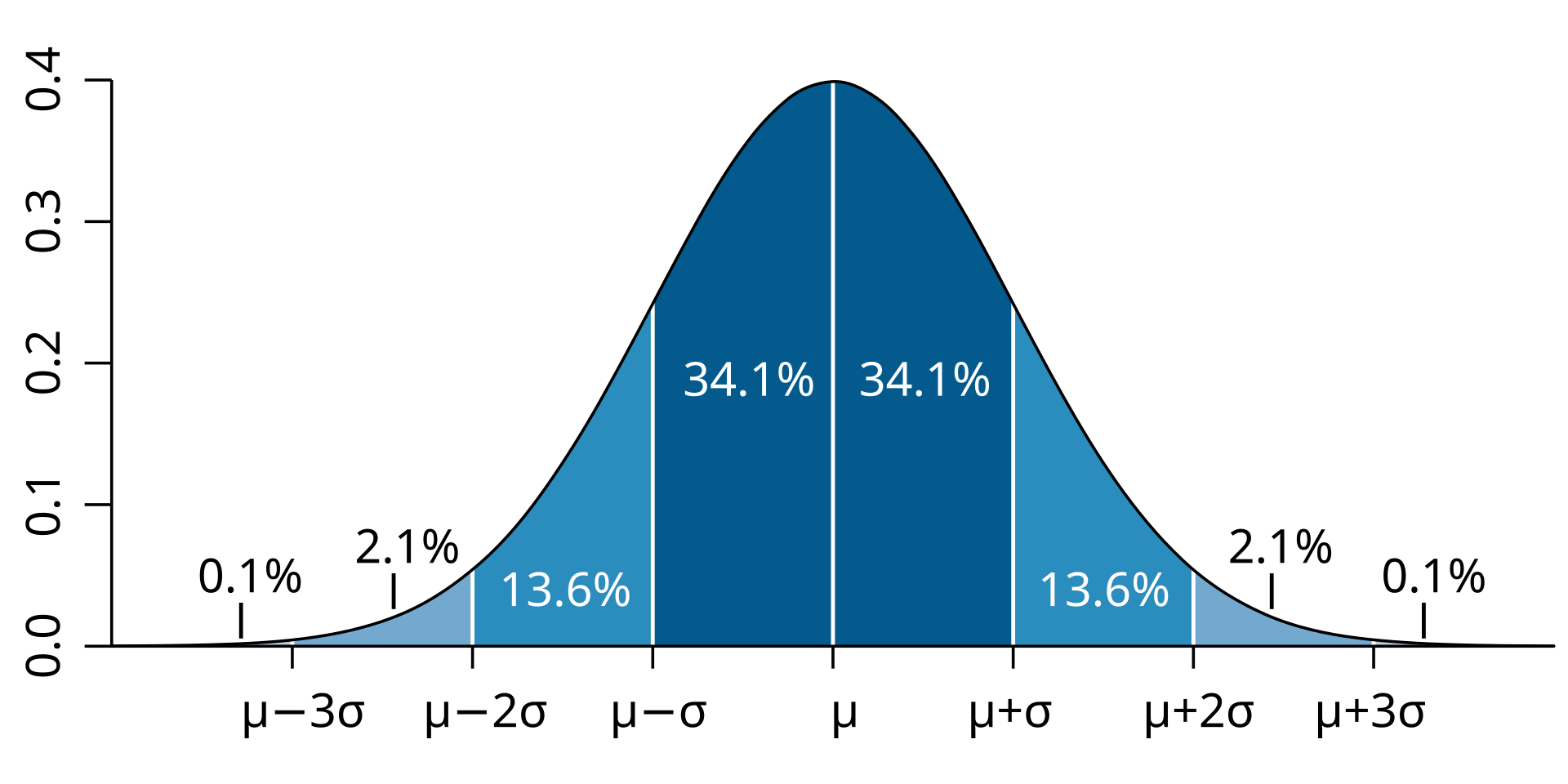
## [1] "histogram"Även om vi noterar vissa toppar kan vi kalla denna fördelning för approximativet (ungefärligt) normalfördelad. En perfekt normalfördelningskurva ser ju ut på följande sätt:
UTBILDNINGSKONTROLL
Ta fram ett histogram för variabeln
ntu2021_kort$fortroende_index.Är denna variabel approximativt normalfördelad?
5.3.3 Låddiagram
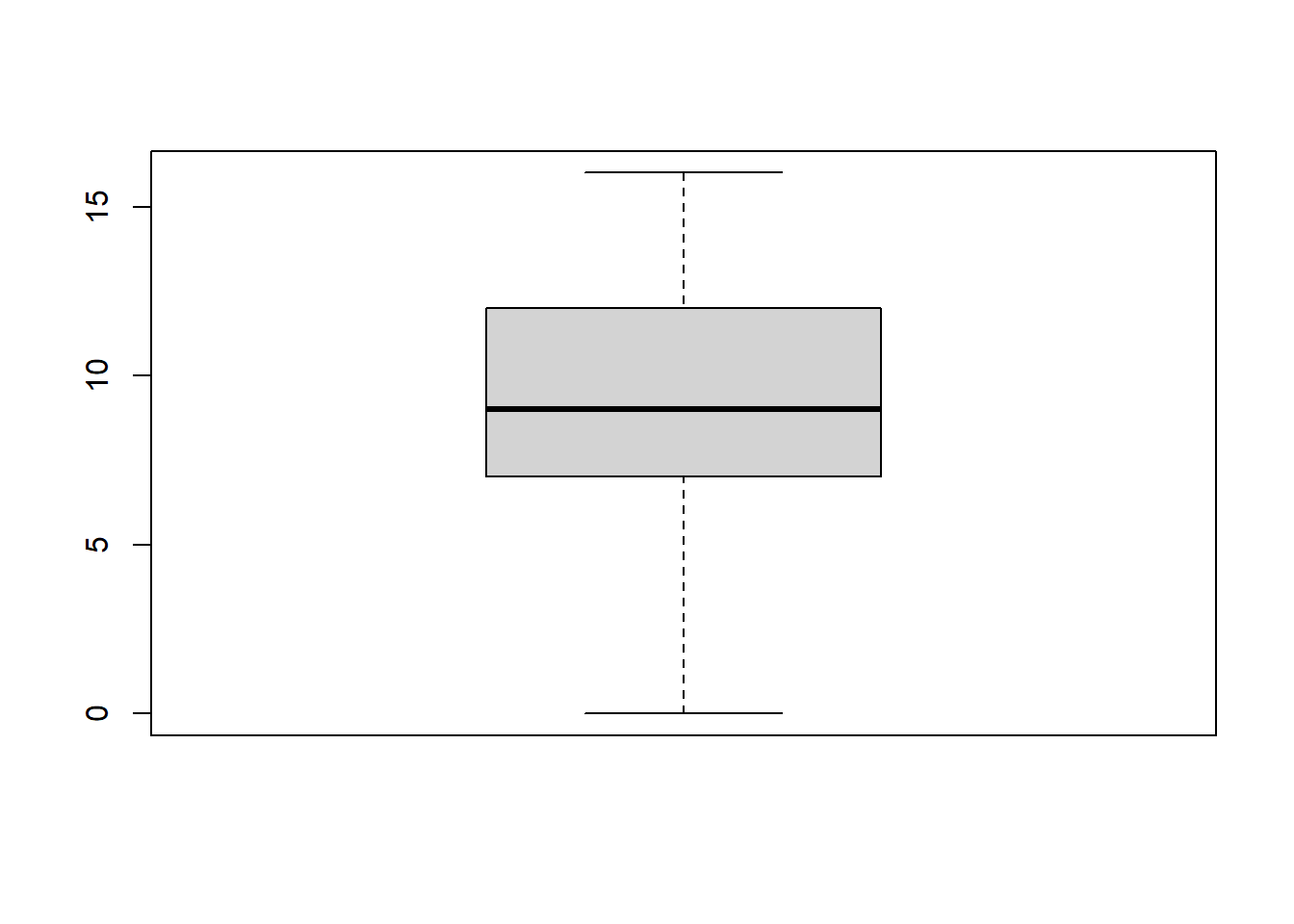
Ett låddiagram, eller boxplot, är ett enkelt sätt att summera information om fördelningen i en kontinuerlig variabel. Ett låddiagram ger oss information om medianvärdet, undre och övre kvartilen samt minimum och maximum. Själva lådan motsvarar kvartilavståndet. Alltså avståndet mellan övre och undre kvartilen. Den undre kvartilen markerar 25%, och den övre kvartilen markerar det 75%. Lådan innehåller alltså 50% av observationerna i variabeln.
Medianen ritas ofta ut med ett tjockt streck genom lådan. Utanför lådan finner vi vågräta streck vilka kallas för, morrhår eller whiskers. Dessa morrhår dras från det lägsta observerade värdet till det högsta bland de värden som inte är utliggare. Värden som ligger längre ifrån lådan än 1,5 gånger avståndet mellan de yttre kvartilerna betraktas som extremvärden och är markerade med en asterisk (*). Värden som ligger mer än 3 gånger kvartilavståndet från lådan betraktas som avlägsna extremvärden och kan betecknas med en ring (o). Detta kan vara användbart att veta om det finns sådana extremvärden, outliers, eftersom att de exempelvis kan påverka medelvärdet i variabeln så att detta inte blir rättvisande för variabeln som helet. Tänk er exempelvis om Elon Musk skulle ta en kurs i Kriminologi B, och att vi frågar hela studentgruppen om deras inkomster. Medelvädert för inkomst i denna studengrupp som läser kriminologi skulle bli kraftigt missvisande.
Att ta fram ett låddiagram i R är enkelt. Det gör vi med hjälp av boxplot()-funktionen:
Vi kan också utöka vårt låddiagram från enkel univariat till en bivariat analys. Alltså att vi kan gå från att beskriva fördelningen i en kontinuerlig variabel sett till hela datamaterialet/alla respondenterna i enkäten, till att titta på om fördelningen inom denna kontinuerliga variabel skiljer sig beroeonde på värdena på en annan kategorisk variabel, alltså om fördelningen skiljker sig åt mellan grupper av respondenter.
Vi kan alltså börja utforska om det är så att olika grupper skiljer sig åt eller har ser likadana ut i det förtroende som de uppvisar för rättsväsendets bemötande. Det gör vi genom att skriva in två variabler, skilda av ett “tilde”-tecken ~. Om vi exempelvis vill se hur förtroendet ser ut i olika polisregioner kan vi skriva följande kod:

Det verkar som att de huvudsakliga observationerna allihop ligger väldigt nära varandra, men att det kanske finns vissa skillnader i medianvärdet mellan några av regionerna.
Vi kan faktiskt ta reda på om dessa skillnader är meningsfulla genom att inkludera ett argument som heter notch = vilket vi specificerar som TRUE. Det notch = ger oss är ett 95%-igt konfidensintervall kring medianen. Alltså ett intervall inom vilket vi med 95% säkerhet kan vara säkra på att den sanna medianen finns i den större population (den vuxna svenska befolknignen) som vi har dragit vårt urval ifrån. Detta konfidensintervall blir synligt som en liten inbuktning kring medianen. Om dessa inbuktningar/konfidensintervall inte överlappar varandra kan vi alltså vara ganska säkra (i statistisk mening) på att det finns en verklig skillnad i medianen mellan olika grupper.

## $stats
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 0 0 0 0 0 0 0
## [2,] 7 7 7 7 7 7 7
## [3,] 9 9 10 9 10 9 10
## [4,] 12 12 12 12 12 12 12
## [5,] 16 16 16 16 16 16 16
##
## $n
## [1] 6993 5178 7891 5870 12205 13034 10737
##
## $conf
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 8.90553 8.890214 9.911067 8.896888 9.928491 8.930803 9.92376
## [2,] 9.09447 9.109786 10.088933 9.103112 10.071509 9.069197 10.07624
##
## $out
## numeric(0)
##
## $group
## numeric(0)
##
## $names
## [1] "Bergslagen" "Mitt" "Nord" "Öst" "Stockholm" "Syd" "Väst"I det här fallet verkar det som att personer som bör i polisregionerna Nord (alltså bland annat här i Västerbotten), Stockholm och Väst (exempelvis Göteborg) i genomsnitt har något högre förtroende för att rättvsäsendets är rättvist i sitt bemötande av offer och misstänkta.
UTBILDNINGSKONTROLL
Ta fram ett låddiagram för variablerna
ntu2021_kort$bemotande_indexochalder_3.Vad betyder ringarna som du observerar för kategorin Medelålder?
Inkludera argumentet
notch = TRUE. Ser du några meningsfulla skillnader mallan ålderskategorierna?
5.3.4 Medelvärdesdiagram
För att fortsatta på den inslagna banan med bivariat analys så kan vi titta på om inte bara medianen i ett låddiagram skiljer sig åt mellan olika grupper i vårt datamaterial, utan även om medelvärdet skiljer sig åt på ett meningsfullt sätt. Kom bara ihåg att vi nu arbetar med grunläggande visualisering av data. De mer formella testen av medelvärdesskillnader och andra typer av statistiska test, och hur vi rapporterar dem, kommer vi att gå igenom i nästa avsnitt (Avsnitt 5). Där kommer vi också att återkomma till och ha nytta av de grunder gällande datavisualisering som vi övar på i det här avsnittet.
Som sagt kan vi alltså utförska om det finns en meningsfull skillnad i medelvärdet på en kontinuerlig variabel, mellan värdena på en kategorisk variabel. Detta gör vi med hjälp av en funktion som heter plotmeans(), där vi specificerar våra argument på följande sätt plotmeans(y ~ x,connect =TRUE/FALSE) där vi istället för y skriver vår kontinuerliga variabel (den som skall hamna på den vertikala y-axeln) och istället för x skriver vår kategoriska variabel (den som skall hamna på den horisontella x-axeln). Vi kan också specificera argumentet connect = som TRUE eller FALSE beroende på om vi vill dra linjer mellan våra medelvärdesobservationer eller inte.
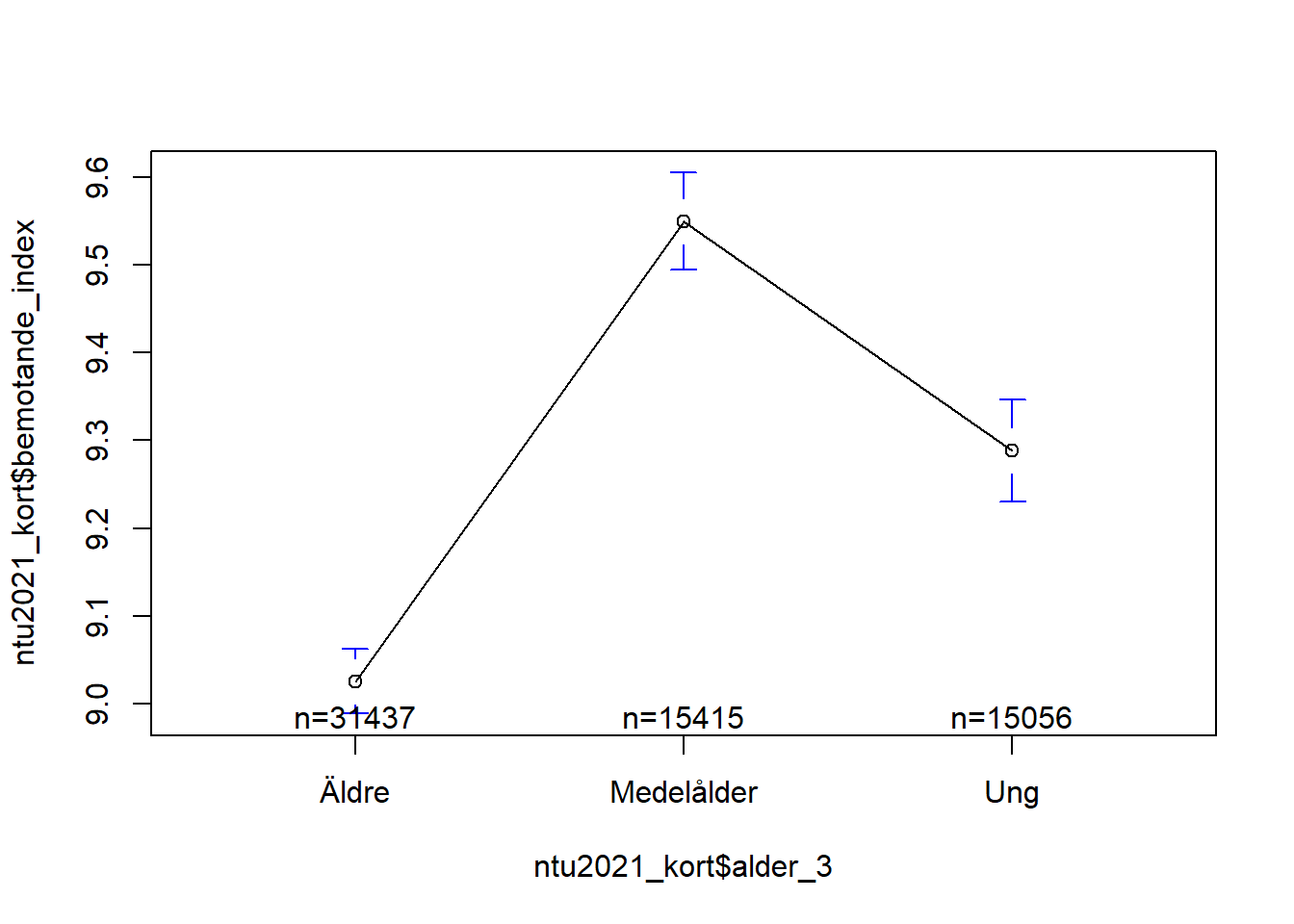
Här kan vi se en ganska tydlig medelvärdesskillnad mellan åldersgrupperna. Ringarna (o) representerar respektive medelvärde. De små morrhåren runt |-o-| runt dessa ringar representerar ett konfidensintervall om 95%. “n = XXXXX” står för antalet observationer inom de olika kategorierna.
Någonting som är lite missvisande med detta diagram är att det ser ut som att vi har ett linjärt samband mellan ålder och förtroende. Problemet är bara att vår faktorvariabel av någon anledning har valt att sortera variablens värde, alltså faktorns kategorier, i bokstavsordning istället förstigande eller sjukande ålder.
Det finns två saker vi kan göra för att fixa detta så att det inte blir förvirrande för den som skall lsäa vår rapport. Det första vi kan göra är att helt enkelt ändra argumentet connect = till FALSE:
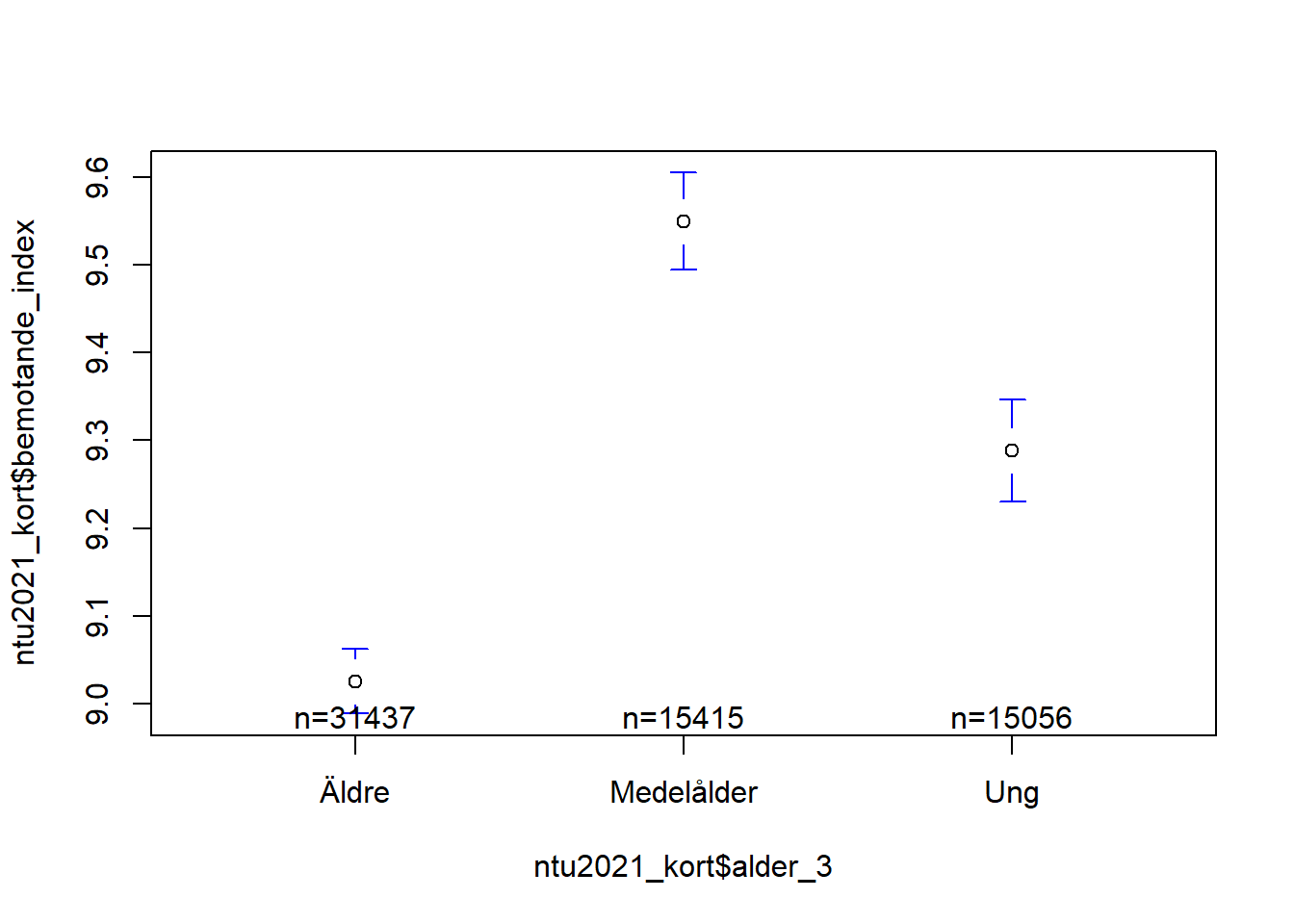
En något bättre lösning kanske dock är att helt enkelt säga åt R att vi vill att vår faktor skall sortera svarskategorierna i en viss ordning. Det kan vi göra med följande kod:
ntu2021_kort$alder_3 <- factor(ntu2021_kort$alder_3, levels=c('Ung', 'Medelålder', 'Äldre'))
summary(ntu2021$alder_3_kort)## Length Class Mode
## 0 NULL NULL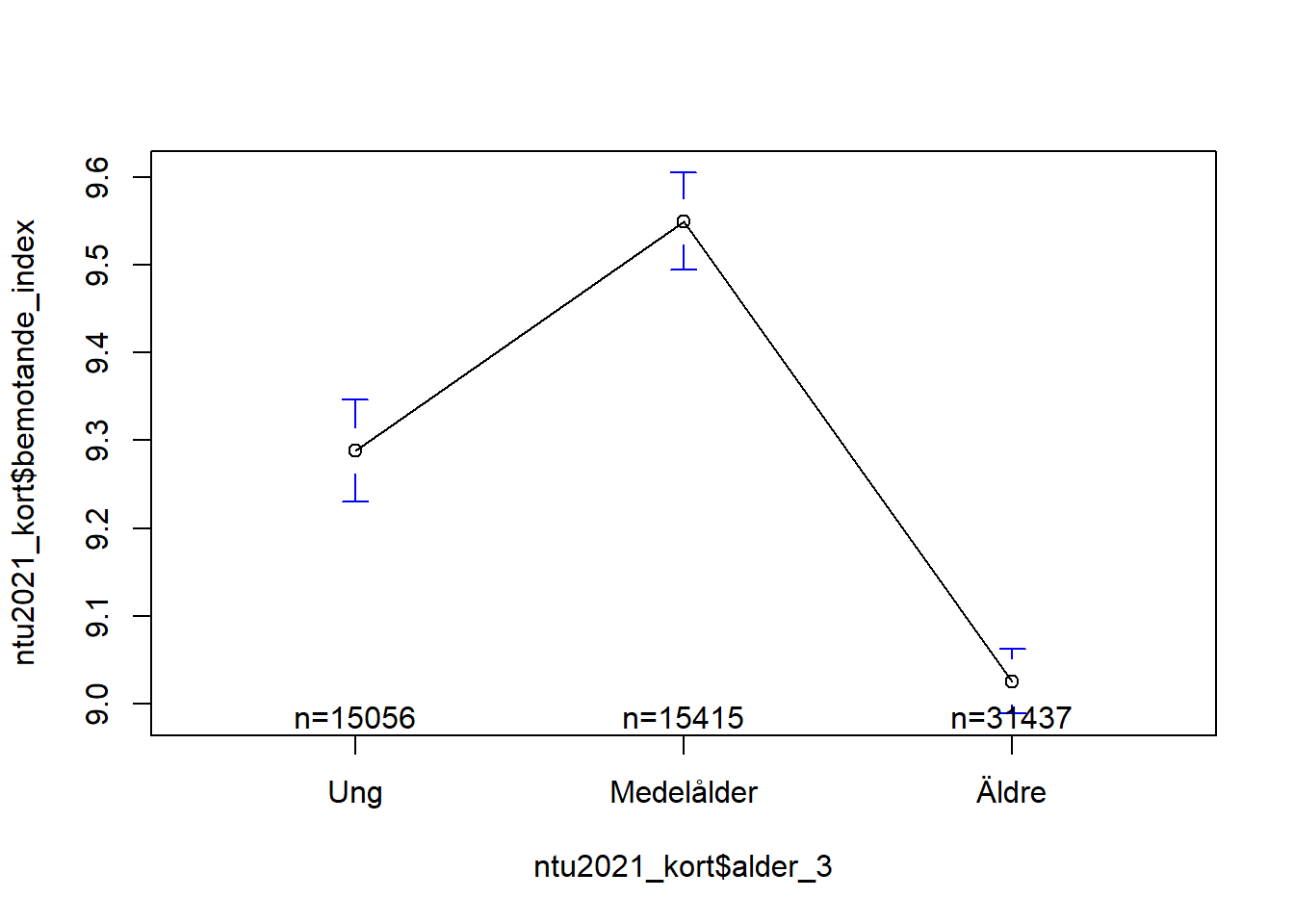
Vi kan nu tydligare se att sambandet tycks vara kurvlinjärt, så att förtroendet börjar något lägre bland unga, ökar bland medelålder, och sjunker igen bland äldre. Notera dock att skillnaderna bara handlar om decimaler: 9.3 kontra 9.5 kontra 9.0. På en skala som går från 0-16. Så det är inte jättestora skillnader, även om de enligt konfidensintervallet är statistiskt signifikanta sådana.
Vi kan också lägga till lite hjälpsamma etiketter på x- och y-axeln så att det blir enklare för läsaren av vår framtida rapport att förstå vad figuren handlar om:
figur_4 <- plotmeans(ntu2021_kort$bemotande_index ~ ntu2021_kort$alder_3, connect = TRUE,
xlab = "Ålder",
ylab = "Bemötande, index (0-16)")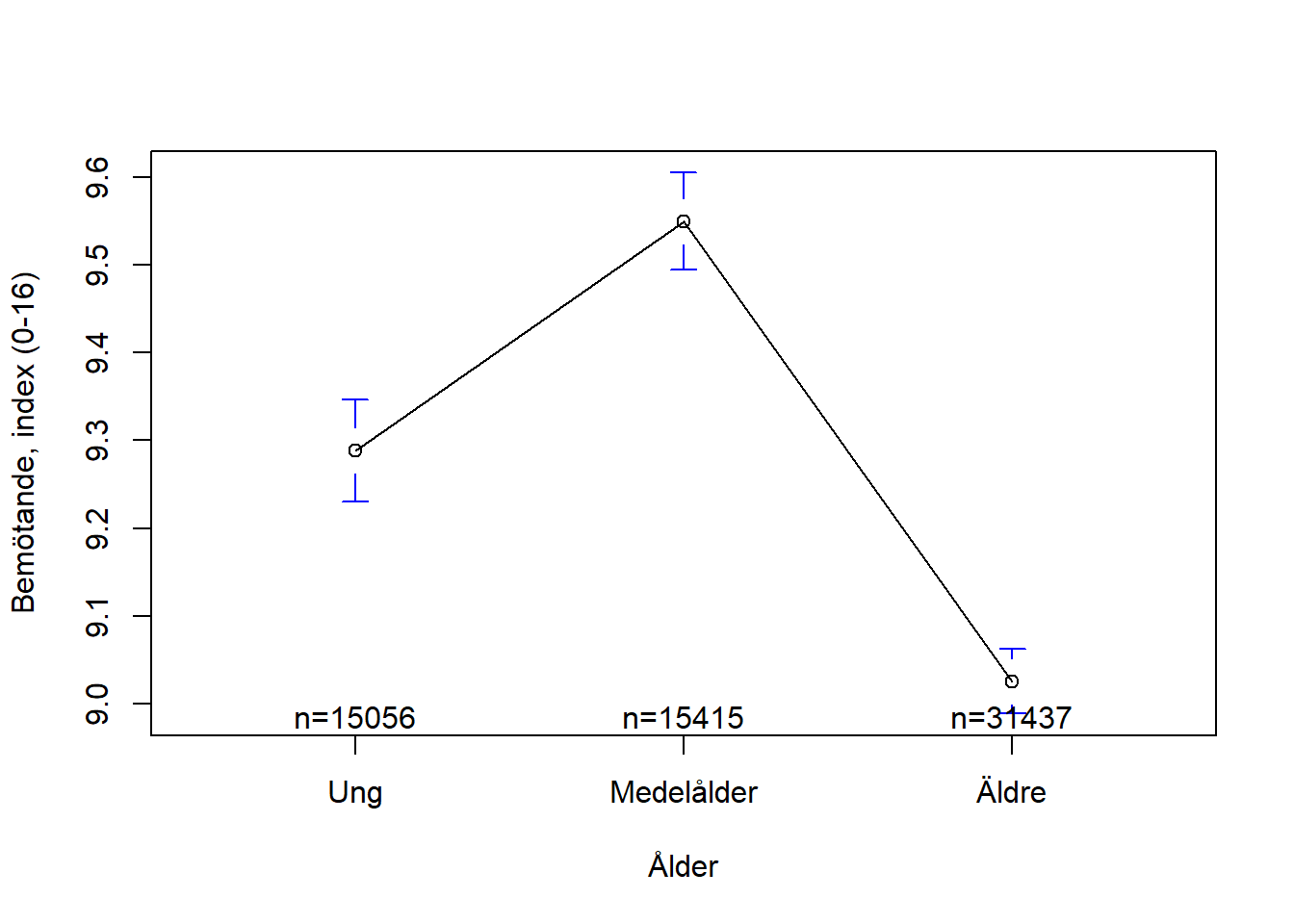
## NULLUTBILDNINGSKONTROLL
Ta fram ett medelvärdesdiagram för variablerna
ntu2021_kort$bemotande_indexochntu2021_kort$Kon_text.Finns det några meningsfulla skillnader? Är dessa statistiskt signifikanta?
Är det meningsfullt att tala om någon typ av “riktning” på sambandet här? Varför/Varför inte?
5.3.5 Spridningsdiagram
Den sista diagramtypen vi skall titta på är nog en av de mest användbara när vi har att göra med två kontinuerliga variabler. Det bygger på att vi skapar ett tvådimensionellt rum med den enda variablens värden på x-axeln och den andra variabelns värden på y-axeln, och att varje observation (varje rad i vår data frame) får en egen position i detta tvådimensionella rum. Detta är mycket användbar när vi vill titta på om det finns något samband mellan två variabler (om den ena ökar i värde, ökar eller minskar den andra i värde?) samt hur stor spridningen är kring denna tendens.
I R beställer vi ett spridningsdiagram (scatterplot) genom den grundläggande funktionen plot() som är en del av bas R. Argumenten är enkla: plot(x, y) där vi istället för x skriver den variabel vi vill ha på x-axeln, och istället för x skriver den variable vi vill ha på y-axeln.
Om vi exempelvis vill se hur våra två typer av förtroende förhåller sig till varandra (det generella förtroendet för att rättsväsendet gör ett bra arbete mätt genom ntu2021_kort$fortroende_index och det lite mer specifika indexet som mäter förtroende för att rättsväsendet behandlar misstänka och offer rättvist ntu2021_kort$bemotande_index, hur dessa förhåller sig till varandra) så kan vi skriva följande kod:

Detta ser dock inte så informativt ut. Hur ska vi egentligen tolka detta?
Det vi måste komma ihåg är som sagt att varje observation får en egen punkt (observationer med exakt samma värde summeras dock ihop till en och samma punkt) i vårt tvådimensionella rum somd dessa två variabler bildar. Eftersom att vi har runt 75000 observationer så blir vårt rum överfullt och vi har svårt att skapa oss någon överblick!
Det enklaste sättet att lösa detta på är att kolla på en mindre del av vårt datamaterial. Exepelvis de 100 första raderna i vår data frame. Vi kan specificera ett intervall av rader genom att skriva ut dessa inom [hakparanteser] efter våra varaibler:
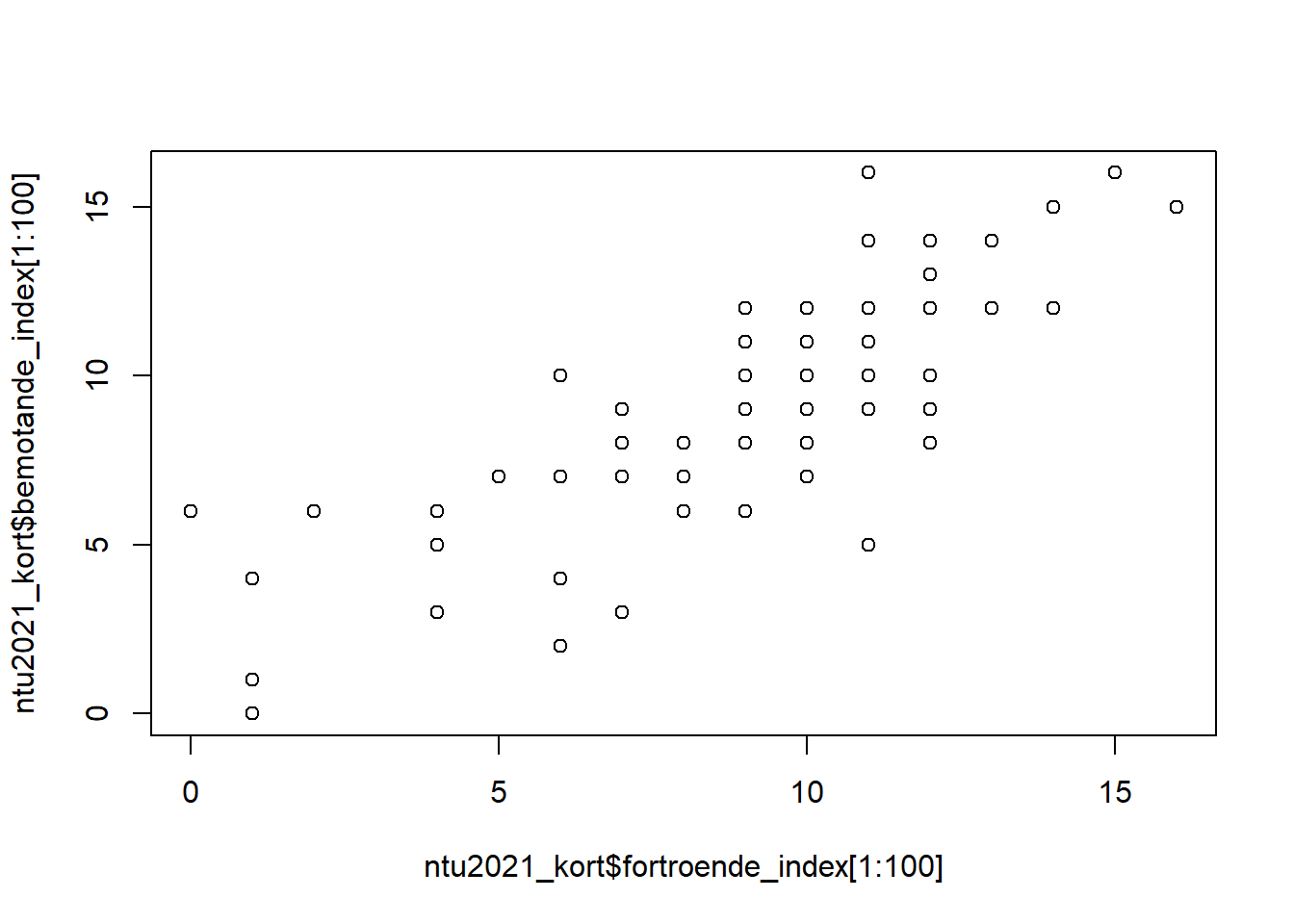
Detta ser på en gång mycket tydligare ut. Det tycks finns ett linjärt samband här, där högre värden på den ena variabeln samvaraierar med högre värden på den andra variabeln. Om vi vill kan vi snygga till figuren lite:
figur_5 <- plot(ntu2021_kort$fortroende_index[1:100], ntu2021_kort$bemotande_index[1:100],
xlab = "Förtroende, index (0-16)",
ylab = "Bemötande, index (0-16)")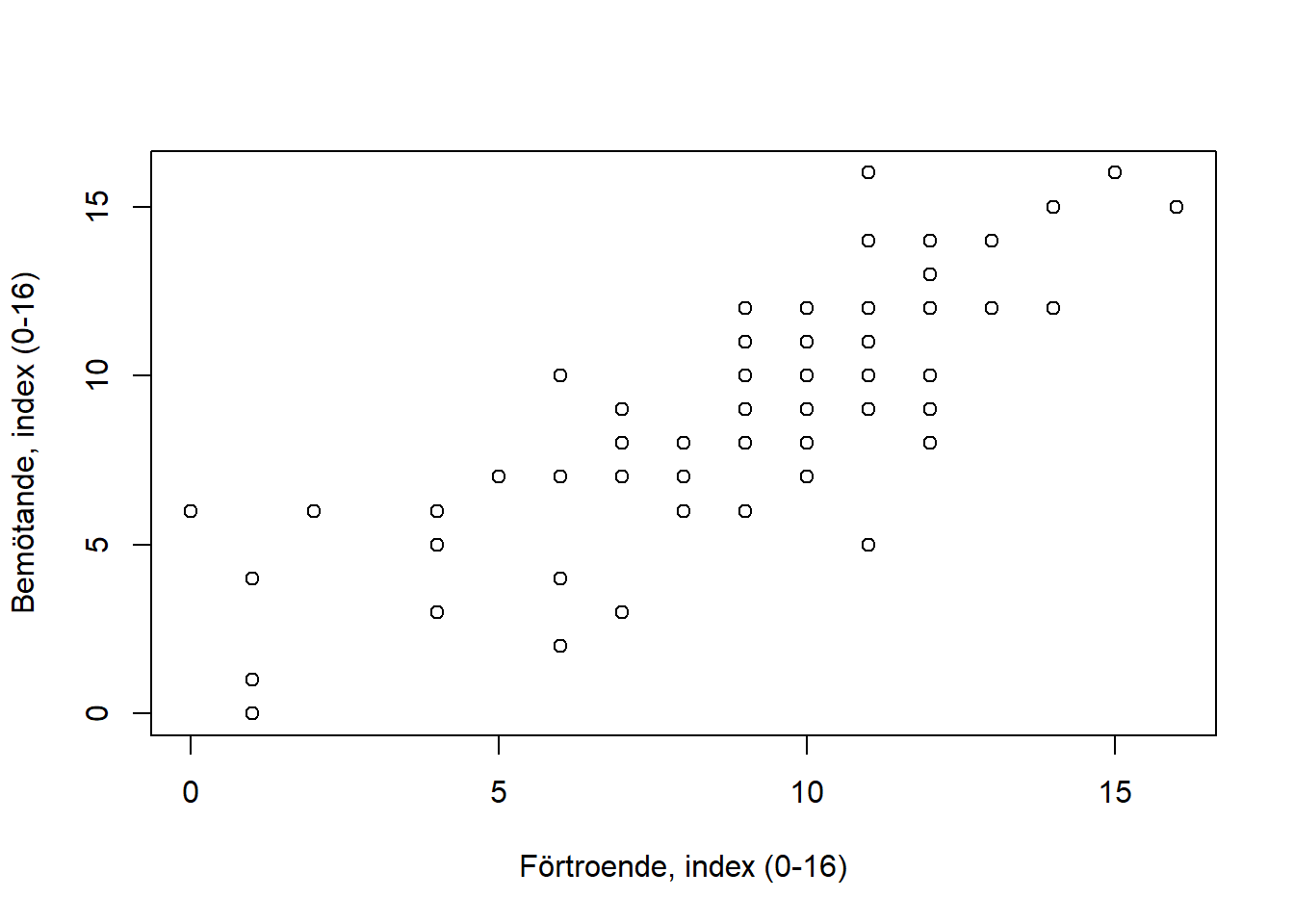
## NULLDetta avslutar grunderna i datavisualisering. Vi kommer dock att ha skäl att återkomma till dessa diagram i nästa avsnitt som handlar om att utforska och statistiskt pröva samband mellan variabler.