Chapter 7 Wahrscheinlihkeitstheorie

7.1 Nachtrag zur Regression: Veränderung der Formel zur Bestimmung der Regressionsparameter

Stellen wir uns vor, wir haben die Variablen ,,Anzahl von Stunden \(x_{m}\) der Vorbereitung auf die Methodenklausur’’ und die ,,Note \(y_{m}\) in der Methodenklausur’’ bei einer Gruppe von Studierenden erhoben und folgende Werte erhalten:

m	\(x_{m}\) (Vorbereitung auf die Prüfung)	\(y_{m}\) (Note in der Prüfung)
1	18	2.7
2	26	2.6
3	46	1.0
4	42	1.7
5	20	3.0
6	26	2.3
7	38	1.5
8	34	1.5
9	40	1.8
10	30	2.7
11	24	2.2
12	14	2.9
13	44	1.8
14	10	4.0
15	28	2.1
16	28	2.7
17	36	2.3
18	16	3.2
19	50	1.4
20	24	3.3
21	36	1.9
22	32	2.5
23	34	2.2
24	22	2.6
25	32	1.9

Eure gute Freundin Lisa hat nach ihren eigenen Angaben insgesamt 45 Stunden für die Methodenprüfung gelernt. Sie hat die Prüfung bereits abgelegt und ihre Note erhalten, jedoch traut sich Lisa nicht, auf QIS ihre Note einzusehen. Als kompetente und nette Person möchtest du ihr anhand einer Regression die Sorgen nehmen und ihre Note vorhersagen. In diesem Fall entspricht die Prüfungsnote der abhängigen Variable (\(y_{m}\)) und die Anzah an Stunden zu Vorbereitung auf die Prüfung der unabhängigen Variable (\(x_{m}\))

Schauen wir uns zuerst das Steudiagramm mit dem plot Befehl in R an:

data<- data.frame(x=c(18,26,46,42,20,26,38,34,40,30,24,14,44,10,
                      28,28,36,16,50,24,36,32,34,22,32),
                  y=c(2.7,2.6,1.0,1.7,3.0,2.3,1.5,1.5,1.8,2.7,2.2,2.9,
                      1.8,4.0,2.1,2.7,2.3,3.2,1.4,3.3,1.9,2.5,2.2,2.6,1.9))
plot(data$x,data$y,
     xlab='Anzahl von Stunden der Vorbereitung auf die Methodenklausur',
     ylab='Note in der Methodenprüfung' )

abline(lm(data$y~data$x),col='red')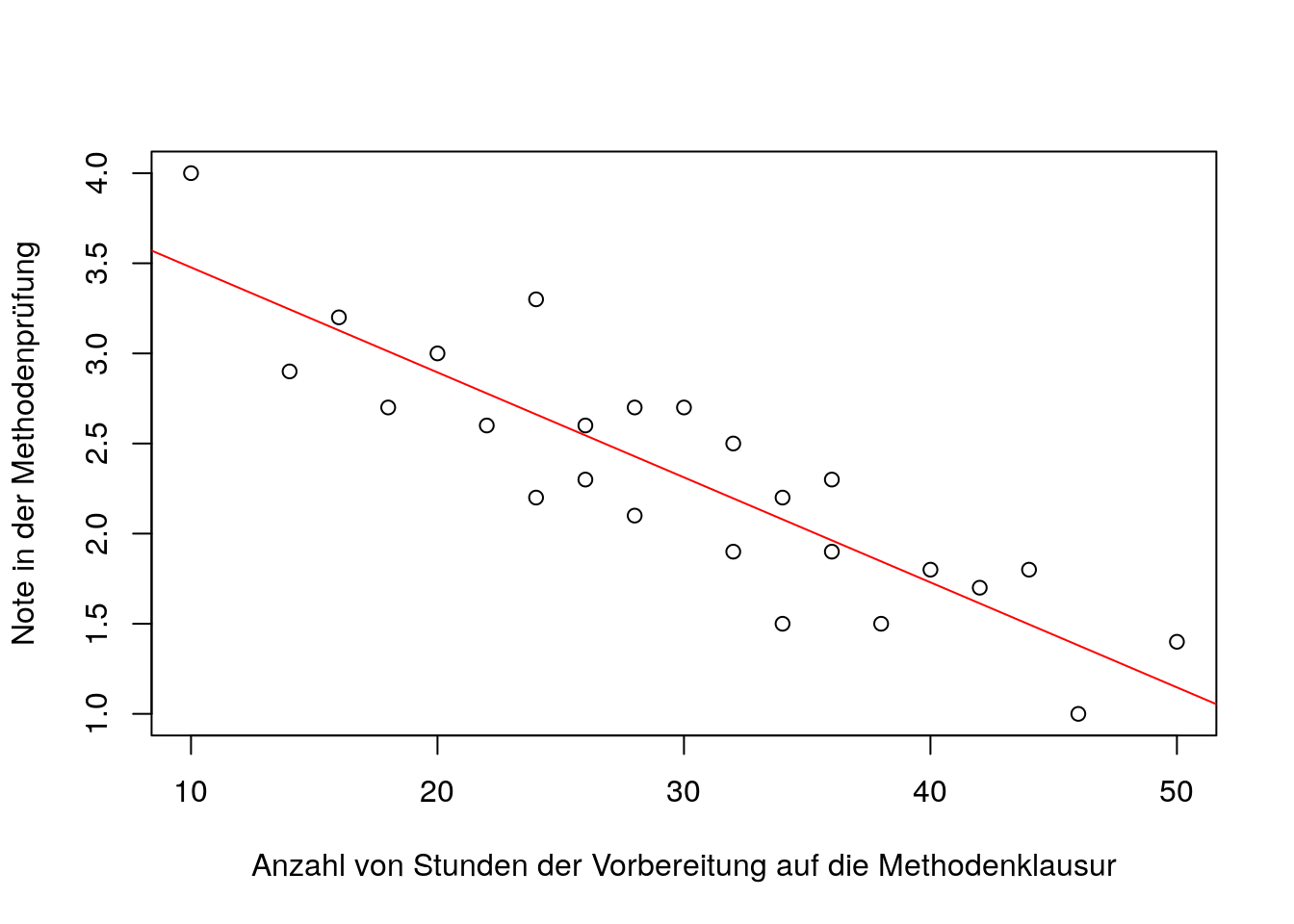

Die beiden Variablen scheinen in einem negativen, linearen Zusammenhang zueinander zu stehen (Merke: Der Zusammenhang ist negativ, weil auf der Variable ,,Prüfungsnote’’ eine niedrige Ausprägung für eine bessere Leistung steht). Insofern scheint eine einfache lineare Regression sinnvoll zu sein.

Berechnung der beiden Regressionsgewichte:

Produkt-Moment-Korrelation: \(r_{XY}= -0.87\) , Standardabweichung des Prädiktor x: \(s_{X}=0.67\) , Standardabweichung des Kriteriums y: \(s_{y}=10.09\), Mittelwert des Prädiktors: \(\overline{x}=30\) , Mittelwert des Kriteriums: \(\overline{y}=2.3\)

Regressionsgewicht: \(b_{1}=r_{XY}\cdot \frac{s_{Y}}{s_{X}}= (-0.87)\cdot \frac{10.09}{0.67}= -0.058\)

Achsenabschnitt: \(b_{0}=\overline{y} - b_{1}\cdot \overline{x}= 2.3- (-0.058)\cdot 30=4.06\)

Regressionsgleichung: \(\hat{y}=b_{0}+b_{1}\cdot x= 4.06 -0.058 \cdot x\)

Wenn wir den Wert 45 in die Regressionsgleichung eingeben erhalten wir für Lisa eine vorhergesagte Note von ca. 1.45 (Wir haben ein bisschen gerundet). Nachdem du Lisa von diesem Befund erzählt hast, hat sie den Mut gefasst und auf QIS nachgeschaut: Sie hat eine 1.2 in der Prüfung erhalten.

Svetlana aus deinem Semester hat eine 1.3 in der Prüfung geschrieben und behauptet, dass sie für die Klausur überhaupt nicht gelernt hat. Selbstverständlich ist das der größte Bullshit, den du je gehört hast, weshalb du jetzt mit Hilfe der Regression schauen möchtest, wie viele Stunden Svetlana wahrscheinlich gelernt hat (zumindest, was die Regression für die Note vorhersagen würde). In diesem Beispiel entspricht die Prüfungsnote der unabhängigen Variable und die Vorbereitungsstunden für die Methodenprüfung der abhängigen Variable: Die Rollen haben sich getauscht. Da die Regression nicht symmetrisch ist und keine Kausalität zwischen den beiden Variablen angenommen werden kann, müssen die Regressionsgewichte erneut bestimmt werden. Jetzt aber ist die Variable y (Note) der Prädiktor und x (Vorbereitunsstunden) das Kriterium. Die Formeln zur Bestimmung der Regressionsgewichte verändert sich folgendermaßen:

Regressionsgewicht: \(b_{1}=r_{XY}\cdot \frac{s_{X}}{s_{Y}}= (-0.87)\cdot \frac{0.67}{10.09}= -13.15\)

Achsenabschnitt: \(b_{0}=\overline{x} - b_{1}\cdot \overline{y}= 30- (-13.15)\cdot 2.3=60.41\)

Regressionsgleichung: \(\hat{y}=b_{0}+b_{1}\cdot x= 60.41 -13.15 \cdot x\)

Wenn wir den Wert 1.3 in die Regressionsgleichung einfügen erhalten wir für Svetlana einen vorhergesagten Wert von 43.32 Stunden. Dieser Wert erscheint die glaubwürdiger als die Behauptung von Svetlana.

MERKE: Die Buchstaben x und y sind lediglich Platzhalter für die Variablen. Per Konvention hat man sich darauf geeinigt, dass X für den Prädiktor und Y für das Kriterium verwendet werden. Die ,,Umformung’’ der Formel wurde in diesem Beispiel nur angewandt, weil wir bereits vorher eine Regression durchgeführt und die X und Y Variable definiert haben.

7.2 Wahrscheinlichkeitstheorie

7.2.1 Begriffe und Symbole

7.2.1.1 Allgemeine Begriffe

I.) Menge: Das Zusammenfassen mehrerer Objekte zu einem Ganzen. Die Elemente einer Menge können Zahlen, Ausgänge eines Zufallsvorgangs usw. sein. wenn man angeben möchte, dass ein Objekt X ein Element einer Menge A ist, drückt man dies folgendermaßen aus:

\(x \in A\) (gelesen ,,x ist ein Element der Menge A’’)

Möchte man darstellen, dass ein Objekt y kein Element der Menge A ist, kann man dies folgendermaßen ausdrücken: \(y \notin A\) (gelesen ,,y ist kein Element von A)

II.) Teilmenge: Die Teilmenge entspricht einer Menge B, die erneut aus einer bereits definierten Menge A erstellt wurde. Dementsprechend ist jedes Element von B auch in der Menge A enthalten. Wenn man ausdrücken möchte, dass eine Menge B eine Teilmenge von A ist, kann man dies folgendermaßen ausdrücken: \(B \subset A\) (gelesen ,,B ist eine Teilmenge von A)

Alle Teilmengen haben folgende Eigenschaften:

1.) \(\emptyset \subset A\)

Das Zeichen \(\emptyset\) steht für die leere Menge und entspricht einer Menge, die keine Elemente enthält. Die leere Menge ist in jeder beliebigen Menge A enthalten und ist folglich auch eine Teilmenge.

2.) \(A\subset A\)

Jede beliebige Menge A ist eine Teilmenge ihrer selbst, da sie ja identisch sind und alle Elemente miteinander teilen.

III.) Schnittmengen: Die Schnittmenge zweier Mengen A und B enthält alle Elemente, die sowohl in A als auch B enthalten sind. Die Schnittmenge wird durch folgendes Symbol dargestellt: \(A \cap B\) (gelesen ,,die Schnittmenge von A und B’’)

Alle Schnittmengen haben folgende Eigenschaften:

1.) \(B \subset A \to\ B\cap A = B\)

Wenn B eine Teilmenge von A ist, sprich wenn alle Elemente von B in A enthalten sind, dann ist die Schnittmenge dieser beiden Mengen nichts anderes als die Menge B selbst.

2.)\(A\cap A= A\)

Die Schnittmenge einer Menge A mit sich selbst entspricht der Menge A, da sie natürlich 100% aller Elemente gemeinsam haben.

3.) \(A\cap \emptyset = \emptyset\)

Die Schnittmenge von A und der leeren Menge entspricht der leeren Menge, da die leere Menge selbst keine Elemente enthält, die sie mit der Menge A gemein haben könnte.

IV.) Vereinigungsmenge: Die Vereinigungsmenge zweier Mengen A und B enthält alle Elemente, die entweder in der Menge A oder B enthalten sind. Man kann dies folgendermaßen ausdrücken: \(A \cup B\)

Alle Vereinigungsmengen haben folgende Eigenschaften:

1.)\(B\subset A \to\ B\cup A=A\)

Wenn B eine Teilmenge von A ist, sprich wenn alle Elemente von B in A enthalten sind, dann entspricht die Vereinigungsmenge dieser beiden Menge der Menge A selbst.

2.) \(A \cup A =A\)

Die Vereinigungsmenge einer Menge A mit sich selbst entspricht der Menge A, da eine Menge keine weiteren Elemente enthalten kann, als diejenigen, die sie bereits hat.

3.) \(A \cup \emptyset = A\)

Die Vereinigungsmenge einer beliebigen Menge A mit der leeren Menge entspricht der Menge A, da die leere Menge keine über die Menge A hinausgehende Elemente enthält.

V.) Differenzmenge: Die Differenzmenge zweier Mengen A und B entspricht der Menge aller Elemente, die exklusiv in A enthalten sind. Dies drückt man folgendermaßen aus: \(A/B\) (gelesen ,,A ohne B’’)

Die Differenzmenge enthält folgende Eigenschaften:

1.)\(A\cap B=\emptyset \to\ A/B=A\)

Wenn die Schnittmenge zweier Mengen A und B der leeren Menge entspricht bzw. die beiden Mengen A und B keine gemeinsamen Elemente haben (disjunkt), dann entspricht die Differenzmenge ,,A ohne B’’ der Menge A.

2.) \(A\subset B \to\ A/B= \emptyset\)

Wenn A eine Teilmenge von B ist, dann entspricht die Differenzmenge ,,A ohne B’’ der leeren Menge, da alle Elemente in A auch in B sind und entsprechend der mathematischen Operation nicht in die Differenzmenge miteingenommen werden.

VI.) Komplementärmenge: Die Komplementärmenge einer beliebigen Menge A entspricht der Menge aller Elemente, die nicht in A enthhalten sind. Dies drückt man folgendermaßen aus: \(\overline{A}=\Omega/A\) (Die Komplementärmenge einer Menge A ist also die Differenzmenge des Ergebnisraums ohne A)

Die Komplementärmenge hat folgende Eigenschaften:

1.) \(A\cap \overline{A}=\emptyset\)

Die Schnittmenge einer beliebigen Menge A mit ihrer Komplementärmenge entspricht der leeren Menge, da die beiden Mengen per Definition keine gemeinsamen Elemente haben.

2.) \(A\cup \overline{A}=\Omega\)

Die Vereinigungsmenge einer Menge A mit ihrer Komplementärmenge entspricht dem Ergebnisraum \(\Omega\).

VII.) Mächtigkeit: Die Mächtigkeit einer Menge A entspricht der Anzahl an Elementen, die die Menge aufweist. Formal wird die Mächtigkeit über folgende Operation bestimmt: |A|=# {x:x\(\in\) A} [Die Operation sagt folgendes aus: Um den Betrag (|A|) der Menge A zu definieren, bestimme die Anzahl (#) aller Elemente x, für die gilt: \(X\in A\). ]

VIII.) Potenzmenge: Die Potenzmenge entspricht der Menge aller möglichen Teilmengen von der Menge A. Sie ist dementsprechend ein Mengensystem, das aus alle möglichen Teilmengen besteht

7.2.1.2 Grundbegriffe von Zufallsvorgängen

I.) Zufallsvorgang und Zufallsexperiment: Ein Zufallsvorgang ist ein Vorgang, welches in einem von mehreren sich gegenseitig ausschließenden Ergebnis resultiert. Das heißt man kennt den Ausgang eines Zufallsvorgangs nicht vorher UND die Ergebnisse müssen sich gegenseitig ausschließen. Ein Zufallsexperiment ist das äquivalent eines Zufallsvorgangs unter kontrollierten Bedingungen.

II.) Ergebnisraum: Entspricht der Menge aller möglichen Ergebnisse eines Zufallsvorgangs und wird gewöhnlich mit einem \(\Omega\) gekennzeichnet. Die einzelnen Elemente des Ergebnisraums werden als \(\omega\) dargestellt. Die Elemente eines Ergebnisraums sind abhängig vom jeweiligen Zufallsvorgang.

Beispiel:

Ereignis A: Die Augenzahl beim einfachen Würfelwurf

Ergebnisraum des Ereignisses A: \(P(\Omega)\)={1,2,3,4,5,6}

Ereignis B: Die Augenzahl beim zweifachen Münzwurf

Ergebnisraum des Ereignisses B: \(P(\Omega)\)={2,3,4,5,6,7,8,9,10,11,12}

Obwohl das für den Zufallsvorgang genutzte Objekt (ein sechsseitiger Würfel) bei beiden Ereignissen identisch ist, hat sich der Ergebnisraum in Abhängigkeit vom Zufallsvorgang verändert.

III.) Ergebnis: Ein Ergebnis entspricht einem einzelnen Element in der Menge der möglichen Ergebnisse bzw. ist ein Ausgane eines Zufallsvorgangs.

IV.) Ereignis: Ein Ereignis entspricht einer Teilmenge von \(\Omega\). Wie sich die Teilmenge zusammensetzt ist abhängig von der Definition des Ereignisses. Der grundlegende Unterschied zwischen einem Ereignis und einem Ergebnis ist, dass ein Ereignis mehrere Ergebnisse unter einem bestimmten Ausgang zusammenfasst, während ein Ergebnis nur ein Ausgang eines Zufallsvorgangs darstellt. Ein Ereignis, welches nur aus einem Element besteht, heißt Elementarereignis.

V.) Mengensystem: Entspricht der Zusammenfassung von Teilmengen des Ergebnisraums (Also einer Zusammenfassung von Ereignissen) in einer weiteren Menge. Werden in einem Mengensystem alle möglichen Teilmengen des Ergebnisraums zusammengefasst, entspricht das Mengensystem der Potenzmenge.

7.2.1.3 Besondere Zufallsereignisse und Wahrscheinlichkeiten

I.) Unmögliches Ereignis (Ein Ereignis, dass nicht eintreten kann): \(A=\emptyset\)

Beispiel eines unmöglichen Ereignisses: Die Augenzahl 13 erhalten bei einem zweifachen Würfelwurf. Der Wert 13 kann nicht erreicht werde, da die höchste zu erreichende Augenzahl beim zweifachen Würfelwurf 12 ist. In diesem Sinne handelt es sich hierbei um ein unmögliches Ereignis.

Sicheres Ereignis (Ein Ereignis, das definitiv eintreten wird): \(A=\Omega\)

Beispiel eines sicheren Ereignisses: Eine Augenzahl von mindestens 2 erhalten beim zweifachen Würfelwurf. Eine Augenzahl von mind. 2 zu erhalten ist ein sicheres Ereignis, da die niedrigste mögliche Augenzahl beim zweifachen Würfelwurd 2 ist (zwei Mal die 1 werfen).

Disjunkte Ereignisse: Zwei Mengen A und B sind disjunkt, wenn ihre Schnittmenge der leeren Menge entspricht. Also: \(A\cap B=\emptyset\)

7.2.2 Axiome nach Kolmogorov

Die drei Axiome nach Kolmogorov definieren die allgemeine Form des Wahrscheinlichkeitsbegriffs, aus welcher sich wichtige Rechenregeln ableiten lassen. Ein Axiom ist ein Ausangssatz, der einer Theorie zugrunde gelegt wird, ohne dass er bewiesen wird.

Axiom 1: Nichtnegativität \(P(A)\ge 0\)

Die Wahrscheinlichkeit eines Ereignisses ist entweder größer als null oder gleich . Es gibt keine negativen Wahrscheinlichkeiten.

Axiom 2: Normiertheit \(P(\Omega)=1\)

Die Wahrscheinlichkeit des sicheren Ereignisses entspricht 1. Die maximale Wahrscheinlichkeit eines beliebigen Ereignisses ist dementsprechend 1.

Axiom 3: Additivität

Für alle Teilmengen A und B von \(\Omega\), die disjunkt sind, gilt: \(P(A\cup B)=P(A)+P(B)\)

Unter der Bedingung, dass zwei Ereignisse A und B disjunkt sind bzw. sich ausschließen, kann man die Wahrscheinlichkeit, dass entweder A oder B eintritt, über die Summe der einzelnen Wahrscheinlichkeiten berechnen.

7.2.3 Rechenregeln für Wahrscheinlichkeiten

I.) Aus dem Nichtnegativität- und Normiertheitsaxiom kann man ableiten, dass Wahrscheinlichkeiten nur Werte zwischen 0 und 1 annehmen können und ihre Gesamtwahrscheinlichkeit auch nicht 1 überschreiten kann.

II.) Wenn A eine Teilmenge von B ist (Also: \(A\subset B\)), dann ist die Wahrscheinlichkeit des Ereignisses A kleiner oder gleich der Wahrscheinlichkeit des Ereignisses B.

Beispiel: Die Wahrscheinlichkeit, in einem Studiengang einen Statistik-Professor zu erhalten (Ereignis B) ist größer, als die Wahrscheinlichkeit, einen witzigen Statistik-Professor zu haben (Ereignis A). In diesem Beispiel ist Ereignis A eine Teilmenge vom Ereignis B, da alle witzigen Statistik Professoren natürlich Professoren in Statistik sind.

Anhand des Normiertheisaxioms kann man die Komplementärmenge eines Ereignisses A folgendermaßen bestimmen: \(P(\overline{A})=1-P(A)\) mit \(\overline{A}=\Omega/A\)

Beispiel: Wenn die Wahrscheinlichkeit, im Verlauf des Lebens mind. einmal an Depressionen zu leiden (Ereignis A), bei 25% liegt, dann ist die Wahrscheinlichkeit, im Verlauf seines Lebens nicht an Depressionen zu leiden (Ereignis \(\overline{A}\)) 75%. Denn: \(P(\overline{A})=1-P(A)=1-.25=.75\)

III.) Wenn zwei Ereignisse A und B nicht disjunkt sind, berechnet sich die Wahrscheinlichkeit der Vereinigungsmenge folgendermaßen: \(P(A\cup B)=P(A)+P(B)-P(A\cap B)\)

In diesem Fall wird die Schnittmenge der beiden Mengen abezogen, da ansonsten bei der Bestimmung der Wahrscheinlichkeit der Verinigungsmenge die Schnittmenge zwei Mal ins Gewicht fallen würde. Bei zwei disjunkten Ereignissen entspricht die Schnittmenge der leeren Menge, weshalb die Formel sich auf die Formel des Additivitätsaxioms kürzt.

IV.) Wenn man die Wahrscheinlichkeit der Vereinigungsmenge multipler Ereignisse bestimmen möchte kann man dies folgendermaßen bestimmen, unter der Bedingung, dass alle Ereignisse paarweise disjunkt sind: \(P(A_{1}\cup A_{2}\cup ... \cup A_{k})=P(A_{1})+P(A_{2})+...P(A_{k})\)

Diese Recheneigenschaft spielt eine wichtige Rolle für die Wahrscheinlichkeit von Ereignissen. Ereignisse bestehen aus Ergebnissen bzw. Elementarereignissen, die per Definition paarweise disjunkt sind. Dementsprechend kann man die Wahrscheinlichkeit eines Ereignisses A bestimmen, indem man die Wahrscheinlichkeiten der Elementarereignisse aufaddiert.

Für ein beliebiges Ereignis \(A\subset \Omega\) gilt also: \(P(A)=\sum_{w_{i}\in A}P({w_{i}})\)

Laplace-Experiment: Ein Laplace- Experiment ist ein Zufallsexperiment, bei welchem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben. Die Wahrscheinlichkeit eines Ereignisses eines Laplace-Experiments lässt sich einfach bestimmen:

\(P(A)=\frac {\text{Anzahl der für das Ereignis A günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}}=\frac{|A|}{|\Omega|}\)

7.2.4 Kombinatorik

Ziel der Kombinatorik ist es zu bestimmen, wie viele Kombination man mit einer Grundgesamtheit k bei n Ziehungen generieren kann. Dabei differenziert man zwischen vier unterschiedlichen Modellen, die durch zwei Qualitäten definiert werden: Ob die Reihenfolge der Ziehung eine Rolle spielt und ob die gezogenen Objekte wieder zurückgelegt werden (also beim nächsten Zug wieder ausgewählt werden können) oder nicht.

I.) Mit Zurücklegen und mit Berücksichtigung der Reihenfolge: \(K=k^n\)

Beispiel: Die Kombination von vier unterschiedlichen Sneakers (k) an den fünf Werktagen (n). Es handelt sich bei diesem Beispiel um ein Modell mit Zurückegen, weil man den gleichen Sneaker auch über die ganze Woche hinweg tragen könnte. Es ist ein Modell, welches die Reihenfolge berücksichtigt, weil wir uns explizit um die Reihenfolge der Kombinationsmöglichkeiten im Verlauf der Woche interessieren.

Berechnung: \(K=k^n=4^5=1024\)

II.) Ohne Zurücklegen und mit Berücksichtigung der Reihenfolge: \(K=\frac{k!}{(k-n)!}\)

Beispiel: Das Verteilen von sechs Geschenken (k) an sechs Personen: Es handelt sich hierbei um ein Modell ohne Zurücklegen, weil man ein bereits vergebenes Geschenk nicht der Person entreißen und einer weiteren Person geben kann. Es berücksichtigt die Reihenfolge, da es relevant ist, welche Person welches Geschenk erhalten hat.

Berechnung:\(K=\frac{6!}{(6-6)!}=\frac{720}{1}=720\)

III.) Mit Zurücklegen und ohne Berücksichtigung der Reihenfolge: \(K=\frac{(k+n-1)!}{(k-1)!\cdot n!}\)

Beispiel: Das Abspielen von 5 Songs beim Kochen (n) aus einer Playlist von 10 Songs (k). Es handelt sich hier um ein Modell mit Zurücklegen, da ein Song mehrmals abgespielt werden kann. Die Reihenfolge wird hier nicht berücksichtigt, weil es nicht von Interesse ist, ob zuerst ein Song von David Bowie und dann ein Song von den Silent Poets gespielt wird.

Berechnung: \(K=\frac{(10+5-1)!}{(10-1)\cdot 5!}=\frac{14!}{9!\cdot 5!}=2002\)

IV.) Ohne Zurücklegen und ohne Berücksichtigung der Reihenfolge: \(K=\frac{k!}{(k-n)!\cdot n!}=\binom{k}{n}\)

Beispiel: Die Zuordnung von 20 Probanden (k) zu einer Interventionsgruppe, die mit 10 Personen gefüllt werden soll (n). Das Modell ohne Zurücklegen und ohne Berücksichtigung der Reihenfolge ist der gängige Fall einer Zufallsstichprobe.

Berechnung: \(K=\binom{20}{10}=\frac{20!}{(20-10)!\cdot 10!}=184756\)

7.2.5 Das Bernoulli Theorem und bedingte Wahrscheinlichkeiten

Bei einem Münwürf oder einem Würfelwurf können wir anhand der Theorie von Laplace-Wahrscheinlichkeiten die Wahrscheinlichkeit von Ereignissen direkt bestimmen. Wie kann man jedoch die Wahrscheinlichkeit von einem Ereignis bestimmen, die nicht im Rahmen eines Laplace-Experiments stattfinden? Beispielsweise wollen wir die Wahrscheinlichkeit bestimmen, dass es in Frankfurt nächste Woche Dienstag regnen wird. Natürlich können wir in diesem Fall nicht pauschal behaupten, die Wahrscheinlichkeit liege bei 50%. Der Mathematiker Daniel Bernoulli hat in diesem Sinne das als heute bekannte Bernoulli-Theorem aufgestellt, welches postuliert, dass die Wahrscheinlichkeit eines Ereignisses A über ihre relative Häufigkeit gut geschätzt werden kann, unter der Bedingung, dass die Anzahl an Beobachtungen groß genug ist. Man sagt hier auch, dass die relative Häufigkeit h(A) stochastisch konvergiert gegen P(A). Man bezeichnet dies als das schwache Gesetz der große Zahlen (es gibt auch ein starkes Gesetz, welches in ein paar Wochen relevant sein wird).

Bedingte Wahrscheinlichkeit: Mit Hilfe der bedingten Wahrscheinlichkeit wird die Wahrscheinlichkeit eines Ereignisses A bestimmt, unter der Bedingung, dass das Ereignis B bereits eingetreten ist. Bei der unbedingten Wahrscheinlichkeit wurde das Ereignis A an dem Ergebnisraum relativiert, während bei der bedingten Wahrscheinlichkeit an dem bereits eingetretenen Ereignis B relativiert wird.

Formel zur Bestimmung der bedingten Wahrscheinlichkeit:\(P(A/B)=\frac{P(A\cap B)}{P(B)}\), wenn P(B)> 0

Im Eid,Gollwitzer steht ein sehr gutes Beispiel zu bedingten Wahrscheinlichkeiten auf S.184

Stochastische Unabhängigkeit: Zwei Ereignisse A und B sind stochastisch unabhängig, wenn folgende drei Eigenschaften zutreffen (und zwar alle drei gelten).

• \(P(A/B)=P(A)\) : Die Tatsache, dass das Ereignis B bereits eingetreten ist, hat keine Auswirkungen auf die Wahrscheinlichkeit des Ereignisses A.

• \(P(B/A)=P(B)\): Die Tatsache, dass das Ereignis A bereits eingetreten ist, hat keine Auswirkungen auf die Wahrscheinlichkeit des Ereignisses B.

• \(P(A\cap B)=P(A)\cdot P(B)\)

Ein Beispiel stochastischer Unabhängigkeit: Das Gambler’s Fallacy

Es handelt sich beim Gambler’s Fallacy um einen logischen Fehlschluss, bei welchem eine Person fälschlicherweise annimmt, dass die Wahrscheinlichkeit eines Zufallsergebnisses sich ändert anhand vorangegangener Zufallsvorgänge. Er stellt also eine bedingte Wahrscheinlichkeit auf, obwohl die beiden Ereignisse stochastisch unabhängig sind.Im Bezug zum Münzwurf wäre ein logischer Fehlschluss im Sinne des Gambler’s Fallacy, dass man nach acht Niederlagen meint, die Chancen zu gewinnen wären beim Nächsten Wurf höher.

7.2.6 6.2.6.) Der Satz von Bayes und seine Anwendung in der psychologischen Forschung

Eine weitere Formel zur Bestimmung der bedingten Wahrscheinlichkeiten ist der Satz von Bayes, der mathematisch verwandt ist mit der ersten Formel zur Bestimmung von bedingten Wahrscheinlichkeiten: \(P(A/B)=\frac{P(B/A)\cdot P(A)}{P(B/A)\cdot P(A)+P(B/\overline{A})\cdot P(\overline{A})}\)

Frage für nächstes Mal: Inwiefern ist diese Formel mit der vorher angegebenen Formel mathematisch verwandt? (Als Hilfe könnt ihr etwas zum Satz der totalen Wahrscheinlichkeit im Eid, Gollwitzer auf Seite 188 nachlesen.)

Diese Formel nutzt man zur Bestimmung der bedingten Wahrscheinlichkeit[P(A/B)], wenn die gegenläufige bedingte Wahrscheinlichkeit [P(B/A)] bereits ermittelt wurde.

Anwendung in der Forschung: Die Untersuchung von diagnostischen Fehlschlüssen bei der Prognostizierung von Krankheiten.

Beispiel aus der Vorlesung: Mit Hilfe der Nackentransparenzmessung kann man bei schwangeren Frauen untersuchen, ob ihr Fötus an einer Chromosomenstörung leidet. Dabei muss man differenzieren zwischen dem, was der Test sagt und was tatsächlich vorliegt. Es kann sein, dass der Test ein positives Ergebnis ausgibt, die Chromosomenstörung jedoch eigentlich nicht ausgeprägt wurde beim Fötus. In der Diagnostik hat man anhand dieser Umstände vier Begriffe im Bezug zu den Fehlern und richtigen Entscheidungen eines Tests definiert:

1.) Sensitivität: Die Wahrscheinlichkeit, dass der Test eine erkrankte Person als solchen erkennt. Die Sensitivität entspricht also der bedingten Wahrscheinlichkeit, dass der Test positiv ausfällt, unter der Bedingung, dass die Person tatsächlich krank ist [\(P(V/S)\)].

2.) Spezifität: Die Wahrscheinlichkeit, dass ein Test einen Nichterkrankten auch als solchen erkennt. Die Spezifität entspricht also der bedingten Wahrscheinlichkeit, dass der Test negativ ausfällt, unter der Bedingung, dass die Person tatsächlich nicht von der Krankheit betroffen ist [\(P(\overline{V}/\overline{S})\)]

3.) Falsch-Positiv-Rate: Die Wahrscheinlichkeit, dass der Test einen Nichtkranken als von der Krankheit betroffen darstellt (also einen Fehler macht). Die Falsch-Positiv-Rate entspricht der bedingten Wahrscheinlichkeit, dass der Test positiv ausfällt, obwohl die Person nicht krank ist [\(P(V/\overline{S})\)].

4.) Falsch-Negativ-Rate: Die Wahrscheinlichkeit, dass der Test negativ ausfällt, obwohl die Person krank ist (also einen Fehler macht). Die Falsch-Negativ-Rate entspricht der bedingten Wahrscheinlichkeit,dass der Test negativ ausfällt, obwohl die Person krank ist [\(P(\overline{V}/S)\)].

Stellen wir uns jetzt vor, wir haben die Nackentransparenzmessung bei einer schwangeren Frau durchgeführt und dieser hat einen positives Befund diagnostiziert, sprich es besteht der Verdacht, dass der Fötus unter einer Chromosomenstörung leidet. Wie groß ist aber die Wahrscheinlichkeit, dass der Fötus tatsächlich krank ist ,unter der Bedingung, dass der Test eine Chromosomenstörung verdächtigt [P(S/V)]. Man kann diese Wahrscheinlichkeit mit dem Satz von Bayes bestimmen, wenn man neben den bedingten Wahrscheinlichkeiten zusätzlich die Grundrate der Krankheit in der Population kennt bzw. wie viele überhaupt anteilmäßig von dieser Krankheit betroffen sind.

Berechnung der bedingten Wahrscheinlichkeit mit den Daten aus dem Foliensatz: \(P(S/V)=\frac{P(V/S)\cdot P(S)}{P(V/S)\cdot P(S)+P(V/\overline{S})\cdot{\overline{S}}}=\frac{.9\cdot.0125}{.9\cdot.0125+.05\cdot.9875}=\frac{0.01125}{0.060625}=0.18557\)

Interpretation: Unter der Bedingung, dass der Test positiv ausgefallen ist, besteht eine Wahrscheinlichkeit von unter 19%, dass der Fötus tatsächlich von der Chromosomenstörung betroffen ist. Dass die Wahrscheinlichkeit so gering ausgefallen ist liegt an der geringen Grundrate der Chromosomenstörung in der Population (1,25%). Je größer die Grundrate ist, desto größer wird die Wahrscheinlichkeit, dass bei einem positiven Befund tatsächlich auch eine Störung vorliegt.

Frage für nächstes Mal: Warum hat die Grundrate Auswirkungen auf die bedingte Wahrscheinlichkeit? (Man kann dieser Frage aus mathematischer oder logisch deduktiver Sicht nachgehen.)