Chapter 5 Korrelationskoeffizienten
5.1 Anmerkungen zum var() Befehl in R
Der var() Befehl in R berechnet die Varianz nach folgender Formel:
\(s^2_{x}=\frac{\sum_{m=1}^{n}(x_{m}-\overline{x})^2}{n-1}\)
Bei dieser Formel handelt es sich um einen Schätzer der Populationsvarianz. Der konkrete Unterschied zur empirischen Varianz, die ihr in der Vorlesung gelernt habt, ist der Nenner: beim Schätzer ist er n-1 statt n. Zum jetzigen Zeitpunkt müsst ihr nicht wissen, was der Schätzer macht bzw. warum R mit dieser Formel operiert. Um mit dem var() Befehl die empirische Varianz bestimmen zu können, müsst ihr den Umrechnungsfaktor benutzen: Ihr multipliziert den var() Befehl mit dem Umrechnungsfaktor (n-1)/n.
Wenn ihr also die empirische Varianz einer Variablen bestimmen wollt, sieht das folgendermaßen aus:
## [1] 13## [1] 129.1006Die Formel für die Kovarianz hat die gleiche Schwierigkeit. Dazu mehr in 3..).
5.2 Einführung zu den Zusammenhangsmaßen
Unter einer Korrelation versteht man in der Statistik eine Beziehung zwischen mind. zwei Variablen bzw. wie sehr zwei oder mehrere Variablen kovariieren. In dieser Sitzung haben wir uns lediglich mit dem Zusammenhang zwischen zwei Variablen beschäftigt (ihr werdet in diesem Semester auch nur Zusammenhangsmaße für zwei Variablen lernen).
Im Gegensatz dazu beschäftigt sich die Univariate Deskriptivstatistik lediglich mit der Beschreibung und Zusammenfassung einer einzigen Variablen (weshalb sie univariat genannt wird).
In Abhängigkeit vom Skalenniveau der beiden Variablen wurden unterschiedliche statistische Verfahren entwickelt, um den Zusammenhang zu bestimmen.
Diese Verfahren ermöglichen es uns, beispielsweise den Zusammenhang zwischen dem IQ und dem Schulerfolg zu bestimmen.
Eine Möglichkeit der visuellen Darstellung zweier Variablen sind sogenannte Streupunktdiagramme. Allgemein ist es empfehlenswert, vor der Bestimmung des Zusammenhangs das Scatterplot der beiden Variablen anzuschauen.
Mit dem plot() Befehl kann man ein Diagramm sehr leicht generieren:
scatter<- data.frame(x=c(3,2.75,3,3.75,3.5), y=c(3.25,3.75,4.25,4.5,5))
plot(scatter$x,scatter$y,
xlab='Prokrastination',
ylab='Lebenszufriedenheit', main='Scatterplot')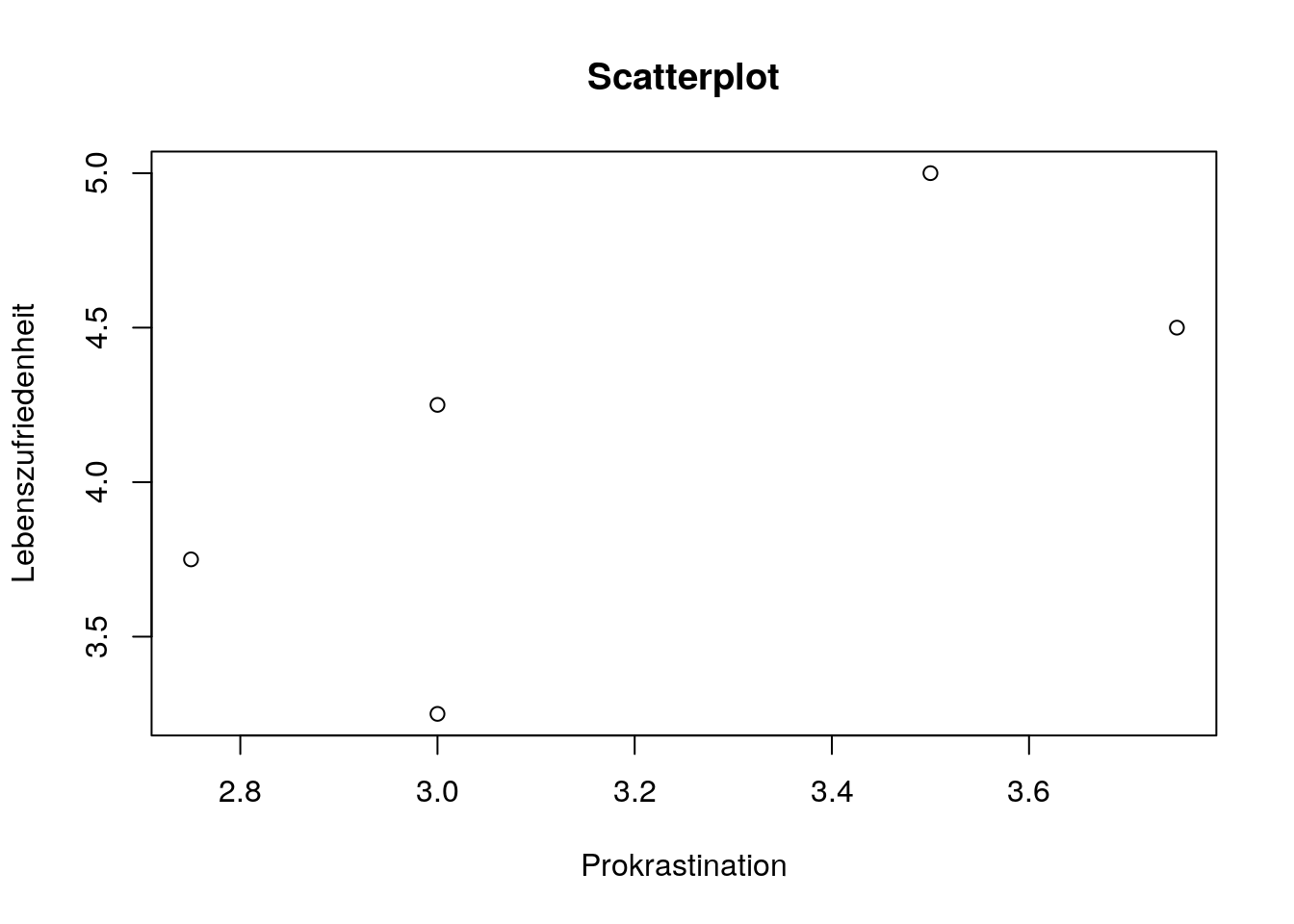
5.3 Zusammenhangsmaße für metrisch skalierte Variablen
5.3.1 Kovarianz
Mit der Kovarianz lässt sich der Zusammenhang zwischen zwei metrisch skalierten Variablen bestimmen.
Formel für die Kovarianz:
\(s_{xy}=\frac{\sum_{m=1}^{n}(x_{m}-\overline{x})(y_{m}-\overline{y})}{n}\)
Der cov() Befehl in R weist den gleichen Unterschied zur oben angegebenen Formel wie der var() Befehl zur empirischen Varianz auf: Im Nenner steht ein n-1. Dieses Problem kann man durch die Nutzung des Umrechnungsfaktors beheben.
Beispiel zur Berechnung der Kovarianz (an den Daten aus der Vorlesung):
## [1] 0.1575#Händische Bestimmung mit der Formel
kp<- (scatter$x-mean(scatter$x))*(scatter$y-mean(scatter$y))
kp## [1] 0.1800 0.1800 -0.0200 0.1925 0.2550## [1] 0.7875## [1] 0.1575Eigenschaften der Kovarianz:
I.) Ist einer der Variablen eine Konstante, dann ist die Kovarianz gleich 0. Denn wenn einer der beiden Variablen eine Konstante ist, sind alle Abweichungen der Messwerte vom Mittelwert gleich 0.
II.) Die Kovarianz ist empfindlich für Ausreißer.
III.) Die Addtion einer Konstante a oder b zu den Messwerten verändert die Kovarianz nicht.
IV.) Wird jeder Messwert mit einem Faktor a oder b multipliziert, verändert sich die Kovarianz multiplikativ um diese Faktoren.
V.) Dadurch, dass die Kreuzproduktsumme durch die Stichprobengröße n geteilt wird, ist es möglich, unterschiedlich große Stichproben im Bezug auf den gleichen Zusammenhang zu vergleichen. Beispielsweise kann der Wert für die Kovarianz zwischen dem IQ (x) und dem Schulerfolg (y) zwischen einer Stichprobe von 100 SchülerInnen und und eine Stichprobe von250 SchülerInnen sinnvoll verglichen werden. Die einzige Voraussetzung hierbei ist, dass die Variablen bei den beiden Erhebungen mit der gleichen Metrik erfasst wurden.
Problem bei der Interpretation der Kovarianz: Die Kovarianz ist abhängig von der Skalierung der Variablen, d.h. in Abhängigkeit von der Metrik der Merkmale kann sich die Kovarianz verändern. Beim Zusammenhang zwischen Neurotizismus und Schulerfolg erhält man einen anderen Wert für die Kovarianz, wenn man Neurotizismus auf einer Skala von 1-10 oder auf einer Skala von 1-30 erfasst. Diese Tatsache schränkt die Interpretierbarketi des Zusammenhangs ein: Man kann durch die Kovarianz angeben, ob der Zusammenhang positiv oder negativ ist, aber Angaben über das Ausmaß der Korrelation sind nicht möglich.
5.3.2 Produkt-Moment-Korrelation
Entspricht mathematisch der Kovarianz von zwei z-transformierten Variablen
Da die Proukt-Moment-Korrelation eines der beliebtesten Zusammenhangsmaße für metrisch skalierte Variablen ist, nennt man sie meist einfach nur Korrelation.
Sie behebt das Problem der eingeschränkten Interpretation der Kovarianz durch die z-Transformation der beiden Variablen: Nun spielt die Metrik der Variablen für die Interpretation des Ergebnisses keine Rolle.
Formel für die Produkt-Moment-Korrelation: \(r_{XY}=\frac{1}{n}\sum_{m=1}^{n}z_{x_{m}}\cdot z_{y_{m}}=\frac{s_{xy}}{s_x\cdot s_{y}}\)
Die Produkt-Moment-Korrelation berechnet sich in R folgendermaßen:
## [1] 0.7095242##Wenn keine Daten gegeben sind, sondern nur die Varianzen und die Kovarianz
#Varianz(als Vorbereitung für die Berechnung der Formel)
var_x<- var(scatter$x)*(4/5)
var_x## [1] 0.135## [1] 0.365## [1] 0.7095242Eigenschaften der Produkt-Moment-Korrelation:
Die Produkt-Moment-Korrelation ist empfindlich für Ausreißer
Ist eines der Variablen eine Konstante, ist die Produkt-Moment-Korrelation nicht definiert. Der Grund hierfür ist, dass bei der z-Transformation die Differenz der Messwerte vom Mittelwert über die Standardabweichung relativiert wird. Bei einer Konstanten liegt die SD jedoch bei 0. Da man nicht durch 0 teilen kann, ist die z-Transformation der Werte nicht definiert und dementsprechend auch die Korrelation.
Die Produkt-Moment-Korrelation ist invariant gegenüber linearen Transformationen, d.h. die Addition von Konstanten zu den Variablen als auch die Multiplikation eines Faktors verändert die Produkt-Moment-Korrelation nicht. Der Grund hierfür ist simpel: Alle lineare Transformationen werden durch die z-Transformation neutralisiert.
Wenn beide z-Werte eines Merkmalsträgers positiv oder negativ sind, wird das Produkt positiv.
Wenn ein z-Wert positiv, der andere negativ ist, wird das Produkt negativ.
Wenn positive z-Wert-Produkte überwiegen, ist die Korrelation positiv.
Wenn negative z-Wert-Produkte überwiegen, istdie Korrelation negativ.
Halten sich positive und negative z-Wert-Produkte in einer Waage, ist die Korrelation gleich 0.
Die Produkt-Moment-Korrelation ist symmetrisch, d.h. bei der Berechnung des Zusammenhangs wird nicht systematisch zwischen den beiden Variablen unterschieden.
Die Produkt Moment Korrelation kann alle Werte zwischen 1 und -1 annehmen. Eine Korrelation von 1 ist ein perfekter positiver Zusammenhang und ein Wert von -1 ist ein perfekter negativer Zusammenhang.
Die Produkt-Moment-Korrelation ist ein Zusammenhangsmaß zur Untersuchung eines linearen Zusammenhangs zwischen zwei Variablen. Dementsprechend muss ein Wert von 0 nicht heißen, dass es keinen Zusammenhang gibt: Der Wert 0 gibt lediglich an, dass der lineare Zusammenhang bei den beiden Variablen nicht gegeben ist.
Interpretation der Produkt-Moment-Korrelation (nach Cohen, 1988):
|\(r_{xy}\)|=.10 : schwacher Zusammenhang
|\(r_{xy}\)|=.30 : mittlerer Zusammenhang
|\(r_{xy}\)|=.50 : starker Zusammenhang
5.3.3 Exkurs: positive und negative Korrelationen
I.) Positive Korrelation: Unter einer positiven Korrelation versteht man, dass eine höhere Ausprägung auf einer Variablen X mit einer höheren Ausprägung auf einer zweiten Variable Y einhergeht (wenn man sich gruppierte Daten anschaut.). Ein klassisches Beispiel für einen positiven Zusammenhang ist die Beziehung zwischen der Intelligenz und dem Schulerfolg. Die Beziehung zwischen den beiden ist bereits rein intuitiv ersichtlich: Je intelligenter eine Person ist, desto erfolgreicher wird sie in der Schule sein.
II.) Negative Korrelationen: Unter einer negativen Korrelation versteht man, dass eine höhere Ausprägung auf einer Variablen X mit einer niedrigeren Ausprägung auf einer Variablen Y einhergeht. Ein Beispiel wäre der Zusammenhang zwischen Neurotizismus (Allgemein: Die Anfälligkeit für negative Emotionen) und Lebenszufriedenheit. Je anfälliger eine Person für negative Emotionen ist, desto geringer wird ihre Lebenszufriedenheit sein.
5.3.4 Rangkorrelation nach Spearman
Die Produkt-Moment-Korrelation ist anfällig für Ausreißer. Um dieses Problem zu umgehen, kann man die Spearman Rangkorrelation bestimmen. Dazu werden die ursprünglichen Daten in zwei Rangreihen überführt. Anschließend werden mit diesen Rangreihen die Produkt-Moment-Korrelation bestimmt (die Formel ist dementsprechend die gleiche).
Wenn bei der Erstellung der Rangreihen keine Rangbindungen vorliegen, kann folgende Vereinfachung der Formel genutzt werden:
\(r_{s}=1-\frac{6\cdot \sum_{m=^1}^{n}d^2_{m}}{n\cdot (n^2-1)}\)
Bestimmung der Spearman Korrelation in R:
## [1] 0.7181848Darin bedeutet d die Rangplatzdifferenz eines Merkmalsträers m zwischen seiner Rangzahl im ersten Merkmal und seiner Rangzahl im zweiten Merkmal. Steht ein Merkmalsträger in der Variablen X auf dem Rang 4 und auf der Variablen Y auf dem Rang 6, ist die Differenz d=4-6=-2. Durch das Quadrieren von d wird das Vorzeichen aufgelöst.
Da die Spearman Rangkorrelatin mit Rangreihen operiert, wird es oft (fälschlicherweise) für die Bestimmung des Zusammenhangs zwischen zwei ordinalskalierten Variablen angewandt. Das Problem hierbei ist, dass die Rangkorrelation einen linearen Zusammenhang der beiden Variablen voraussetzt (da sie ja mathematisch der Produkt-Moment-Korrelation entspricht). Ordinalskalierte Variablen können jedoch nicht in einem linearen Zusammenhang zueinander stehen, da die Größe des qualitativen Unterschieds zwischen den möglichen Ausprägungen nicht bestimmbar ist.
5.4 Zusammenhangsmaße für odrinalskalierte Variablen - Korrelationskoeffizient \(\gamma\)
Formel des \(\gamma\) Koeffizienten: \(\gamma=\frac{n_{K}-n_{D}}{n_{K}-n_{D}}\)
Die Grundlage zur Bestimmung des Zusammenhangs sind die Berechnungen aller konkordanter und diskordanter Paare.
Die Formel für die Berechnung dieser Paare ist extrem komplex. Da sie mit einem Ei versehen ist, müsst ihr sie auch nicht auswendig lernen. Lernt nur die Vorgehenswerise zur Bestimmung der konkordanten und diskordanten Paare.
Wir gehen die Vorgehensweise an folgendem Bespiel durch (Eid,Gollwitzer S.546):
| Selbst | Randsumme | ||||
|---|---|---|---|---|---|
| 1: unzufrieden | 2: weder noch | 3: zufrieden | |||
| Freundschaften | 1: unzufrieden | 12 | 4 | 17 | 33 |
| 2: weder noch | 9 | 6 | 17 | 32 | |
| 3: zufrieden | 48 | 38 | 281 | 367 | |
| Randsumme | 69 | 48 | 315 | 432 |
Bestimmung der konkordanten Paare:
1.) Oben links anfangen (In diesem Fall in der Zelle mit der Anzahl 12) und die konkordanten Paare bestimmen.
2.) Alle Paare einer Zelle sind korkordante Paare, die im Bezug zu beiden Variablen X und Y entweder eine höhere oder niedrigere Ausprägung aufweisen. Mit einer höheren Ausprägung ist nicht eine höhere Besetzungszahl der Zellen gemeint, sondern eine höhere Ausprägung im Bezug zu den Kategorien der Ordinalskala: Auf der Variablen ,,Selbst’’ ist ,,weder noch’’ und ,,zufrieden’’ eine höhere Ausprägung als ,,unzufrieden’‘. Auf der Variable ,,Freundschaften’’ ist das Gleiche der Fall.
Für die Zelle ,,unzufrieden’’ ,,unzufrieden’’ sind die Zellen mit der Besetzungszahl 6, 17, 38, und 281 konkordante Zellen.
3.) Die Besetzungszahlen aller konkordanter Zellen werden aufaddiert und schließlich mit der ursprünglichen Zellenanzahl, deren konkordanten Paare wir bestimmen wollten, multipliziert.
Es passiert also folgendes: \(12\cdot (6+17+38+281)=4104\)
4.) Dies wird jetzt für alle Zellen von oben nach unten bestimmt. (Es ist wichtig, dass ihr von oben beginnt, um alle konkordante Paare definitiv bestimmt zu haben.)
5.) Die Ergebnisse all dieser Berechnungen werden dann am Ende aufaddiert.
Im Bezug zum Beispiel erhält ihr folgendes:
\(n_{K}= 12\cdot (6+17+38+281)\)
\(+4\cdot (17+281)\)
\(+9\cdot (38+281)\)
\(+6\cdot (281)\)
\(=4104+1192+2871+1686=9853\)
Es gibt also insgesamt 9853 konkordante Paare.
Bestimmung der diskordanten Paare:
1.) Oben links anfangen (In diesem Fall in der Zelle mit der Anzahl 12) und die diskordanten Paare bestimmen.
2.) Alle Paare einer Zelle sind diskordante Paare, die im Bezug auf einer der beiden Variablen eine höhere und auf der anderen Variable eine niedrigere Ausprägung aufweisen.
Die Zelle mit der Besetzungszahl 12 hat keine diskordanten Paare, da die beiden Variablen keine niedrigere Ausprägung haben als ,,unzufrieden’’. Die nächste Zelle mit der Besetzungszahl 4 hat diskordante Paare: Die Zelle 9 und 48.
3.) Die Besetzungszahlen aller diskordanter Zellen werden aufaddiert und schließlich mit der ursprünglichen Zellenanzahl, deren diskordanten Paare wir bestimmen wollten, multipliziert.
Es passiert also folgendes: \(4\cdot (9+48)=228\)
4.) Dies wird jetzt für alle Zellen von oben nach unten bestimmt. (Es ist wichtig, dass ihr von oben beginnt, um alle konkordante Paare definitiv bestimmt zu haben.)
5.) Die Ergebnisse all dieser Berechnungen werden dann am Ende aufaddiert.
Im Bezug zum Beispiel erhält ihr folgendes:
\(n_{D}= 4\cdot (9+48)\)
\(+17\cdot (9+6+48+38)\)
\(+6\cdot (48)\)
\(+17\cdot (48+38)\)
\(=228+1717+228+1462=3695\)
Es gibt also insgesamt 3695 diskordante Paare.
Mit diesen Angaben können wir nun die Korrelation \(\gamma\) bestimmen.
\(\gamma=\frac{9853-3695}{9853+3695}=0.45\)
Zwischen den beiden Variablen besteht ein positiver Zusammenhang.
Bestimmung der Korrelation in R:
## [1] 9853## [1] 3695## [1] 0.454532