Chapter 3 Univariate Deskriptivstatistik I
3.1 Vorgehensweise zur Bestimmung des Skalenniveaus einer Variable
I.) Kann man bei der Variablen qualitative Unterschiede in den Merkmalsausprägungen beobachten?
Wenn nein: Nominalskala
Wenn ja, nächste Frage: Haben die qualitativen Unterschiede einen interpretativen Wert bzw. sind die Differenzen von Merkmalsausprägungen interpretierbar?
Wenn nein: Ordinalskala
Wenn ja, nächste Frage: Verfügt die Variable über einen absoluten Nullpunkt?
Wenn nein: Intervallskala
Wenn ja, nächste Frage: Ist die Maßeinheit der Variable eine natürliche Maßeinheit?
Wenn nein: Verhältnisskala
Wenn alle Fragen mit ja beantwortet wurden: Absolutskala
Diese Methode ist eine Möglichkeit, die Skalierung einer Variable zu bestimmen. Es kann sein, dass es bessere Verfahren gibt. Insofern würde ich euch empfehlen, nach alternative Vorgehensweisen zu suchen, die möglicherweise effizienter sind.
3.2 Verständnis von den Indizierungen bei den Datenmatrizen
Stellen wir uns vor, wir haben folgende Tabelle:
| Proband (m) | Geschlecht | Alter | Fachbereich |
|---|---|---|---|
| 1 | 1 | 19 | 5 |
| 2 | 2 | 23 | 7 |
| 3 | 2 | 17 | 3 |
| 4 | 1 | 25 | 5 |
Die Zeilen entsprechen den Studienteilnehmenden. Nach der Indizierung hat der erste Proband die Laufnummer m=1, die zweite Person die Laufnummer m=2, die dritte Person die Laufnummer m=3 und die vierte Person m=n (n steht für die Stichprobengröße und ist in diesem Fall 4)
Die Spalten entsprechen den untersuchten Variablen. Nach der Indizierung hat die Variable Geschlecht die Laufnummer i=1, die zweite Variable Alter die Laufnummer i=2 und die dritte Variable Fachbereich die Laufnummer i=p (p steht für die Anzahl aller untersuchter Variablen und ist in diesem Fall 3)
Es gibt auch eine Indizierung für die Merkmalsausprägungen. Diese Indizierung bezieht sich immer auf genau eine Variable.
Betrachten wir uns hierfür die potentiellen Merkmalsausprägungen der Variable Geschlecht: männlich, weiblich und inter/-non binär.
Durch eine mögliche Indizierung könnte die Ausprägung männlich die Laufnummer j=1, weiblich die Nummer j=2 und inter-/non-binär die Laufnummer j=k (k entspricht der Anzahl aller möglichen Ausprägungen einer Variable und ist in dem Fall des Geschlechts 3) erhalten.
Ziel der (univariaten) Deskriptivstatistik: Urlisten zusammenfassend beschreiben (um für mehr Ordnung zu sorgen)
3.3 Kennwerte der zentralen Tendenz und der Dispersionsmaße bei nominalskalierten Variablen
3.3.1 Erstellung des Datensatzes
data<- data.frame(x=c('Paranoide PS','Paranoide PS',
'Dissoziale PS','Dissoziale PS',
'Dissoziale PS','Dissoziale PS',
'Dissoziale PS','Dissoziale PS',
'Emotional instabile PS','Emotional instabile PS',
'Emotional instabile PS','Histrionische PS',
'Histrionische PS','Zwanghafte PS',
'Zwanghafte PS','Zwanghafte PS',
'Zwanghafte PS','Aengstliche PS',
'Aengstliche PS','Aengstliche PS',
'Aengstliche PS','Aengstliche PS','Sonstige PS','Sonstige PS'))
####absolute H.
aj<- table(data$x)
aj##
## Aengstliche PS Dissoziale PS Emotional instabile PS
## 5 6 3
## Histrionische PS Paranoide PS Sonstige PS
## 2 2 2
## Zwanghafte PS
## 4## Dissoziale PS
## 2Anmerkung: Die 2 unter der Angabe des Modus steht nicht für die Anzahl der Merkmalsausprägungen in der Kategorie, sondern steht für die R-interne Codierung der Kategorie. Die 2 ist also ,,die zweite Kategorie der Variable Persönlichkeitsstörung’’.
3.3.2 Berechnung des relativen Informationsgehalts
Formel: \(H=-\frac{1}{ln(k)}\sum_{j=1}^{k}hj\cdot ln(hj)\)
##
## Aengstliche PS Dissoziale PS Emotional instabile PS
## 0.20833333 0.25000000 0.12500000
## Histrionische PS Paranoide PS Sonstige PS
## 0.08333333 0.08333333 0.08333333
## Zwanghafte PS
## 0.16666667##
## Aengstliche PS Dissoziale PS Emotional instabile PS
## -1.568616 -1.386294 -2.079442
## Histrionische PS Paranoide PS Sonstige PS
## -2.484907 -2.484907 -2.484907
## Zwanghafte PS
## -1.791759##
## Aengstliche PS Dissoziale PS Emotional instabile PS
## -0.3267950 -0.3465736 -0.2599302
## Histrionische PS Paranoide PS Sonstige PS
## -0.2070756 -0.2070756 -0.2070756
## Zwanghafte PS
## -0.2986266## [1] -1.853152## [1] 0.84340583.4 Kennwerte der zentralen Tendenz und der Dispersionsmaße bei ordiinalskalierten Variablen
Unterscheidung zwischen singulären Daten (jede Beobachtung kommt nur einmal vor) und kategoriale Daten mit geordneten Antwortkategorien (es wurden vorher qualitativ unterschiedliche Kategorien definiert).
3.4.1 Median für singuläre Daten
bei einem ungeraden n: \(\frac{(n+1)}{2}\)
bei einem geraden n: das arithmetische Mttel zwischen den beiden Werten \(frac{n}{2}+1\) und \(frac{n}{2}\)
3.4.2 Median für geordnete Kategorien
Formel zur Bestimmung des Median: \(\frac{(n+1)}{2}\)
Die Bestimmung der Medianklasse erfolgt über die Angaben der kumulierten Häufigkeiten. Diejenige Kategorie ist die Medianklasse, bei welcher die Daten zum ersten Mal in zwei Hälften geteilt werden (bzw. diejenige Kategorie, in welcher der (n+1)/2- te Proband ist)
3.4.3 Anmerkungen
Bei singulären Daten ist die Bestimmung des Modus und des relativen Informationsgehalts nicht sinnvoll, da jede Beobachtung einzigartig ist. Die Bestimmung eines Dispersionsmaß ist dementsprechend allgemein nicht sinnvoll.
Bei kategorialen Daten kann sowohl der Modus als auch der relative Informationsgehalt bestimmt werden. Weiterhin kann auch der empirische Interquartilbereich bestimmt werden.
3.4.4 Empirische Interquartilbereich
3.4.4.1 Quantile und Quartile
Quartil \(Q_{1}\): Das erste Quartil ist der Wert, der von mindestens 25% der Merkmalsträger erreicht oder unterschritten wird und von mindestens 75% der Merkmalsträger erreicht oder überschritten wird.
Quartil \(Q_{2}\)/Median : Das zweite Quartil ist der Wert, der von mindestens 50% der Merkmalsträger erreicht oder unterschritten wird und von mind. 50% der Merkmalsträger erreicht oder überschritten wird.
Quartil \(Q_{3}\): Das dritte Quartil ist der Wert, der von mind. 75% der Merkmalsträger erreicht oder unterschritten wird und von mind. 25% der Merkmalsträger erreicht oder überschritten wird.
Quantil (verallgemeinerte Form von Quartilen): Ein p-Quantil ist derjenige Wert \(x_{p}\), für den gilt, dass mind. \(p\cdot 100\) Prozent der Daten kleiner oder gleich \(x_{p}\) und mind. \((1-p)\cdot 100\) Prozent der Daten größer oder gleich \(x_{p}\) sind.
3.4.4.2 Bestimmung des empirischen Interquartilbereichs
Bestimmung des ersten Quartils: \(n\cdot 0.25\)
Bestimmung des dritten Quartils: \(n\cdot 0.75\)
weiteres Vorgehen analog zur Bestimmung der Medianklasse bei kategorialen Daten ( Wenn die Stichprobengröße nicht durch 4 teilbar ist): bei kumulierten Häufigkeiten schauen, wann die Daten in ein 25/75 Verhältnis (\(Q_{1}\)) bzw. ein 75/25 Verhältnis (\(Q_{3}\)) getrennt werden.
Achtung: Die Quartile trennen die Daten in ungefähr vier gleich große Bereiche. Dementsprechend ist das Vorgehen anders, wenn die Stichprobengröße durch vier teilbar ist. In dem Fall muss man das arithmetische Mittel bestimmen zwischen der \(n\cdot 0.25\) und \(n\cdot 0.25 + 1\) (bzw. bei kategorialen Daten das AM der Kategoriencodierung. Ich habe es aus zeitlichen Gründen in der heutigen Sitzung nicht erwähnt, aber wir werden es nächste Woche näher besprechen). Analog gilt dies auch für das dritte Quartil.
IQB=[\(Q_{1}\);\(Q_{3}\)]
3.5 Box-Whisker Plot
library(ggplot2)
mtcars<- subset(mtcars, am=='1')
ggplot(mtcars, aes(x=as.factor(am),y=mpg))+
geom_boxplot()+
geom_text(label='Median', y=24,x=1)+
geom_text(label='Untere Whisker', x=0.87,y=16)+
geom_text(label='erstes Quartil Q1',x=1,y=21.5)+
geom_text(label='drittes Quartil Q3', x=1,y= 30)+
geom_text(label='Obere Whisker', x=0.87,y=33)+
xlab('')+
ylab('')+
theme(axis.text.x = element_blank(), axis.ticks = element_blank())+
theme(axis.text.y = element_blank(), axis.ticks = element_blank())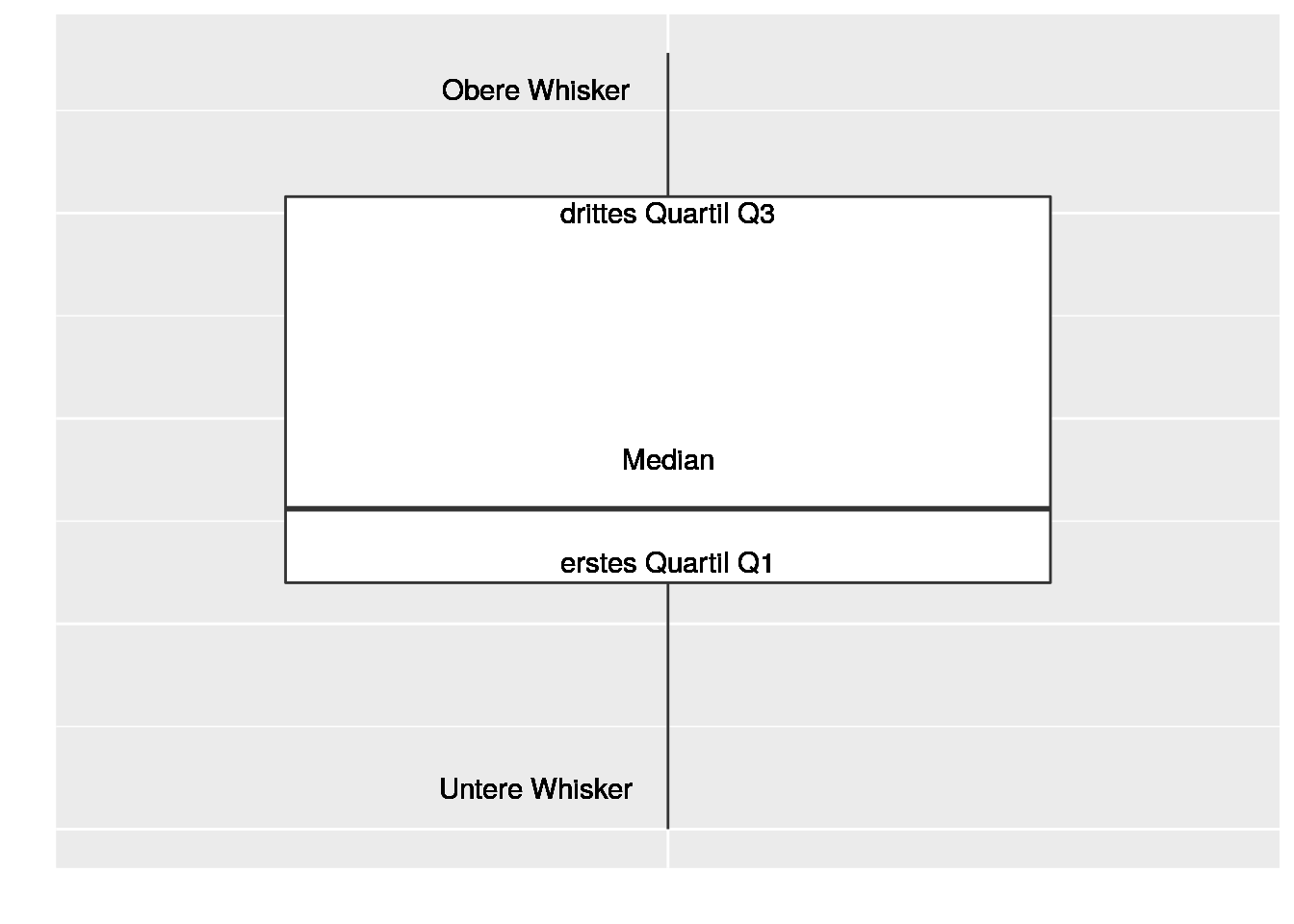
Berechnung der Whiskers:
\(Q_{3}+ 1.5\cdot IQA\)
\(Q_{1}-1.5\cdot IQA\)
IQA= \(Q_{3}-Q_{1}\)
Alle Merkmalsausprägungen, die über die Whiskers hinausgehen, sind Ausreißerwerte. Wenn die Ausprägungen sogar größer als \(Q_{3}+ 3\cdot IQA\) oder kleiner als \(Q_{1}- 3\cdot IQA\) sind, spricht man von Extremwerten.