Chapter 8 Wahrscheinlichkeitsverteilungen
8.1 Zufallsvariablen
Eine Zufallsvariable X ist eine Größe, die unterschiedliche Ergebnisse eines Zufallsvorgangs (zusammengefasst in der Menge \(\Omega\)) mithilfe des Zahlenraums (zusammengefasst in \(\Omega'\)) beschreibt: \(X:\Omega \to\ \Omega'\)
Entsricht die Menge \(\Omega'\) die Menge der reellen Zahlen \(\mathbb(R)\), so wird die Zufallvariable als reellwertige Zufallsvariable bezeichnet.
\(x \in \mathbb(R)\) ist eine Realisierung der Zufallsvariable X. Im Beispiel des zweifachen Würfelwurfs entspräche eine Realisierung der Zufallsvariable X dem zweifache Würfeln der Zahl 1.
Man differenziert bei Zufallsvariablen zwischen diskreten und stetigen Zufallsvariablen.
Diskrete Zufallsvariablen: Verfügen über eine endliche oder abzählbar unendliche Anzahl an Realisierungen.
Stetige Zufallsvariablen: Wenn innerhalb eines Intervalls zwischen zwei Werten \(x_{u}\) (wobei ,,u’’ für die Untergrenzen steht) und \(x_{o}\) (wobei ,,o’’ für die Obergrenze steht) überabzählbar unendlich viele Realisierungen der Zufallsvariable X liegen, ist diese stetig.
8.2 Diskrete Wahrscheinlichkeitsverteilungen
Bei diskreten Zufallsvariablen ist es anhand eines Balkendiagramms möglich, die Wahrscheinlichkeiten der einzelnen Realisierungen abzubilden. Wenn beim Balkendiagramm alle Realisierungen der diskreten Zufallsvariable berücksichtigt werden, resultiert eine sogenannte Wahrscheinlichkeitsverteilung:
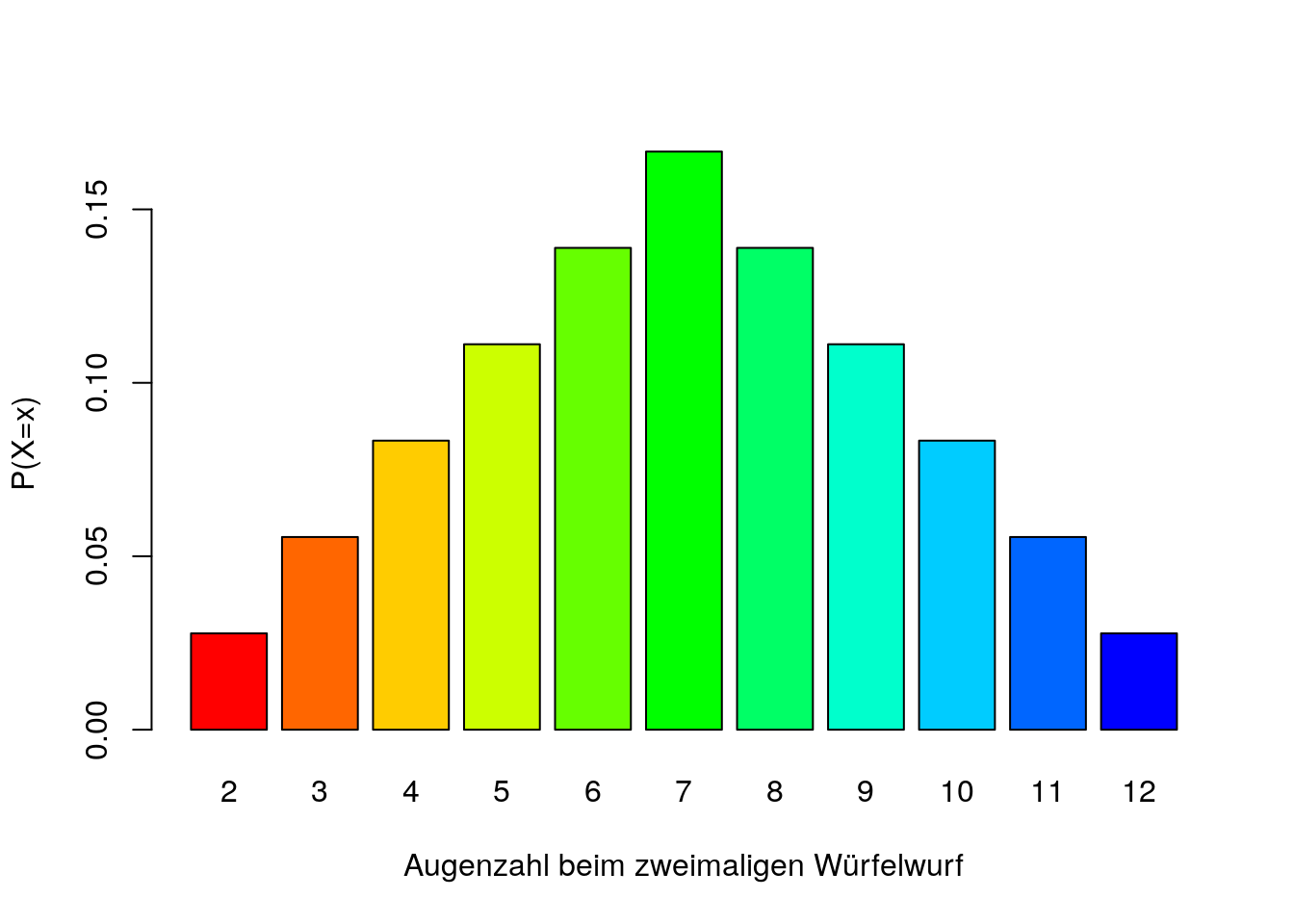
Im Balkendiagramm sind auf der x-Achse die einzelnen Realisierungen x der Zufallsvariable X abgetragen und auf der y Achse die Wahrscheinlichkeiten der korrespondierenden Realisierungen. Das \(P(X=x)\) interpretiert man folgendermaßen: Die Wahrscheinlichkeit, dass die Zufallsvariable X genau die Realisierung x annimmt.
Unabhängigkeit von diskreten Zufallsvariablen (Analog zur Unabhängigkeit zweier Ereignisse A und B): Zwei Zufallsvariablen X und Y sind unabhängig, wenn für alle möglichen \(x_{i}\) (Realisierung der Zufallsvariable X) und \(y_{i}\) (Realisierung der Zufallsvariable Y) gilt: \(P(X=x_{i},Y=y_{i})=P(X=x_{i})\cdot P(Y=y_{i})\)
Zwei Zufallsvariablen X und Y sind also unabhängig wenn die Wahrscheinlichkeit des gemeinsamen Auftretens dem Produkt der Einzelwahrscheinlichkeiten entspricht.
Kennwerte einer diskreten Wahrscheinlichkeitsverteilung:
Genau wie jede andere Verteilung kann die Wahrscheinlichkeitsverteilung mithilfe von Kennwerten beschrieben werden, die man in der Deskriptivstatistik bereits behandelt hat.
Ein Maß der zentralen Tendenz für Wahrscheinlichkeitsverteilungen ist der Erwartungwert, welcher mit dem arithmetischen Mittel eng verwandt ist :
\(E(X)=\sum_{i=1}^{k}x_{i}\cdot \pi_{i}\)
Der Erwartungswert hat die gleichen Eigenschaften wie das arithmetische Mittel. Während der Mittelwert anhand konkreter Daten, die wir erhoben haben, bestimmt wird, kennzeichnet der Erwartungswert die Lage einer theoretischen Verteilung, das durch ein Zufallsexperiment zustande kommt, ohne dass das Zufallsexperiment konkret durchgeführt wurde.
Berechnung des Erwartungswerts bei diskreten Zufallsvariablen
Beispiel am zweifachen Münzwurf (aus der Vorlesung)
\(E(X)=\sum_{i=1}^{k}x_{i}\cdot P(X=x)=2\cdot \frac{1}{36}+3\cdot \frac{2}{36}+4\cdot \frac{3}{36}+5\cdot \frac{4}{36}+6\cdot \frac{5}{36}+7\cdot \frac{6}{36}+8\cdot \frac{5}{36}+9\cdot \frac{4}{36}+10\cdot \frac{3}{36}+11\cdot \frac{2}{36}+12\cdot \frac{1}{36}=7\)
Man merkt, dass die Anwendung der Formel im Taschenrechner sehr aufwendig und zeitlastig ist. Die Bestimmung des Erwartungswertes in R ist jedoch relativ simpel:
vec_x<- c(2,3,4,5,6,7,8,9,10,11,12)
vec_p<- c(1/36,2/36,3/36,4/36,5/36,6/36,5/36,4/36,3/36,2/36,1/36)
exp<-sum(vec_x*vec_p)
exp## [1] 7Ein Dispersionsmaß für Zufallsvariablen ist die Varianz. Für diskrete Zufallsvariablen berechnet man die Varianz folgendermaßen:
\(Var(X)=\sum_{i=1}^{k}(x_{i}-E[X])^2\cdot \pi_{i}\)
Analog zur Deskriptivstatistik entspricht die Standardabweichung diskreter Zufallsvariablen der positiven Wurzel der Varianz:
\(SD(X)=\sqrt{Var(X)}\) bzw. \(\sigma_{X}=\sqrt{\sigma_{X}^2}\)
Berechnung der Varianz bei diskreten Zufallsvariablen
Beispiel am zweifachen Münzwurf (aus der Vorlesung)
\(Var(X)= \sum_{i=1}^{k}(x_{i}-E(X))^2\cdot \pi_{i}= (2-7)^2\cdot \frac{1}{32}+(3-7)^2\cdot \frac{2}{32}+(4-7)^2\cdot \frac{3}{32}+(5-7)^2\cdot \frac{4}{32}+(6-7)^2\cdot \frac{5}{32}+(7-7)^2\cdot \frac{6}{32}+(8-7)^2\cdot \frac{5}{32}+(9-7)^2\cdot \frac{4}{32}+(10-7)^2\cdot \frac{3}{32}+(11-7)^2\cdot \frac{2}{32}+(12-7)^2\cdot \frac{1}{32}=5.833\)
Die Berechnung der Varianz ist sogar noch umständlicher als die Berechnung des Erwartungswerts. In diesem Fall ist die Berechnung in R glücklicherweise auch unkompliziert:
## [1] 5.833333Exkurs: Rechenregeln für Erwartungswert und Varianzen
Die folgenden Rechenregeln gelten sowohl für diskrete, als auch für stetige Zufallsvariablen (Im Folgenden stehen die Buchstaben a und b für konstante Werte):
I.) \(E(a)= a\) : Der Erwartungswert einer Konstante ist die Konstante selbst.
II.) \(E(a\cdot X+ b\cdot Y)=a\cdot E(X)+b\cdot E(Y)\)
III.) \(Var(X)=E(X^2)-E(X)^2\) : Die Varianz einer Zufallsvariable X lässt sich bestimmen, indem man den Erwartungswert der quadrierten Werte multipliziert mit dem quadrierten Erwartungswert.
IV.) \(Var(X)=0\) , falls \(X=a\)
V.) \(Var(a\cdot X)=a^2 \cdot Var(X)\)
VI.) \(Var(a+X)=Var(X)\) : Diese Rechenregel entspricht der dritten Eigenschaft der Varianz.
8.3 Besondere Formen diskreter Wahrscheinlichkeitsverteilungen
8.3.1 Gleichverteilung
Eine diskrete Zufallsvariable ist gleichverteilt, wenn alle Realisierungen der Zufallsvariable X die gleiche Auftretenswahrscheinlichkeit haben. Formal gilt:
\(\pi_{1}=\pi_{2}=...=\pi_{i}=...=\pi_{k}=\frac{1}{k}\)
Ein Beispiel für eine gleichverteilte Zufallsvariable ist ein einfacher Würfelwürf: Alle Realisierungen haben die gleiche Auftretenswahrscheinlichkeit, nämlich \(\frac{1}{6}\).
8.3.2 Bernoulli-Verteilung (Sonderform der Binomialverteilung)
Eine Bernoulliverteilung erhält man bei der einmaligen Durchführung eines Bernoulli-Experiments. Ein Bernoulli-Experiment entspricht einem Zufallsexperiment, bei welchem nur zwei Realisierungen möglich sind (Beispiel: Kopf oder Zahl beim Münzwurf). Das Balkendiagramm besteht dementsprechend aus nur zwei Balken. Die Realisierungen der Zufallsvariable X wird bei einer Bernoulliverteilung i.d.R. dummy kodiert, wobei das Trefferereignis (oder, allgemeiner formuliert, die Realisierung der Zufallsvariable, die uns mehr interessiert) mit 1 kodiert wird.
Die Wahrscheinlichkeit der Realisierungen lässt sich folgendermaßen berechnen: \(\pi_{1}=1-\pi_{2}\)
Bei dummy kodierten Variablen berechnet sich der Erwartungswert und die Varianz folgendermaßen:
\(E(X)=\pi_{1}\) : Der Erwartungswert entspricht der Wahrscheinlichkeit des Treffers bzw. der Wahrscheinlichkeit derjenigen Realisierung x, die mit 1 kodiert wurde.
\(Var(X)=\pi_{1}\cdot \pi_{2}\) : Die Varianz entspricht dem Produkt der beiden Wahrscheinlichkeiten.
8.3.3 Binomialverteilung
Der Ausgangspunkt der Binomialverteilung ist die n-Fache Wiederholung eines Bernoulli-Experiments. Wird das Zufallsexperiment n-Fach wiederholt, ist bei der Binomialverteilung von Interesse, bei wie vielen von n Wiederholungen das Ereignis, welches uns interessiert, eingetreten ist. Mit Hilfe der Binomialverteilung ist es möglich, diese Trefferereignisse bei n-Wiederholungen zu modellieren.
Die Wahrscheinlichkeit, bei n-Wiederholungen eines Zufallsvorgangs genau x Treffer zu erhalten, kann man mit folgender Formel berechnen:
\(P(X=x)=\binom{n}{x}\cdot \pi^{x} \cdot (1-\pi)^{n-x}\)
Der Binomialkoeffizient \(\binom{n}{k}\) beantwortet die Frage, wie oft in einem Pfaddiagramm das Ereignis auftritt, bei n-Wiederholungen eines Zufallsvorgangs genau x Treffer zu erzielen. Der Ausdruck hinter dem Koeffizienten \(\pi^{x} \cdot (1-\pi)^{n-x}\) berechnet die Wahrscheinlichkeit, bei n-Wiederholungen genau x Treffer zu erzielen. Die Wahrscheinlichkeit, bei n-Wiederholungen x-Treffer zu erzielen wird also multipliziert mit der Anzahl an Szenarien, bei dem genau x-mal ein Treffer erzielt wurde.
Für das Beispiel der vier Fragen aus der Vorlesung kann man für alle Realisierung der Zufallsvariable X die Wahrscheinlichkeit bestimmen:
\(P(X=0)=\binom{4}{0}\cdot .25^{0}\cdot .75^4=0.32\)
\(P(X=1)=\binom{4}{1}\cdot .25^{1}\cdot .75^3=0.42\)
\(P(X=2)=\binom{4}{2}\cdot .25^{2}\cdot .75^2=0.21\)
\(P(X=3)=\binom{4}{3}\cdot .25^{3}\cdot .75^1=0.05\)
\(P(X=4)=\binom{4}{4}\cdot .25^{4}\cdot .75^0=0.004\)
Die Wahrscheinlichkeiten einer Binomialverteilung kann man in R mit einer einfachen Formel bestimmen:
## [1] 0.3164063## [1] 0.421875## [1] 0.2109375## [1] 0.046875## [1] 0.00390625###Darstellung der Binomialverteilung
y<- c(p_0,p_1,p_2,p_3,p_4)
names(y)<-c(0,1,2,3,4)
barplot(y,xlab='Realisierungen der Zufallsvariable X (Richtige Lösungen)', ylab='P(X=x)',
main='Binomialverteilung der Zufallsvariable X', col=rainbow(15))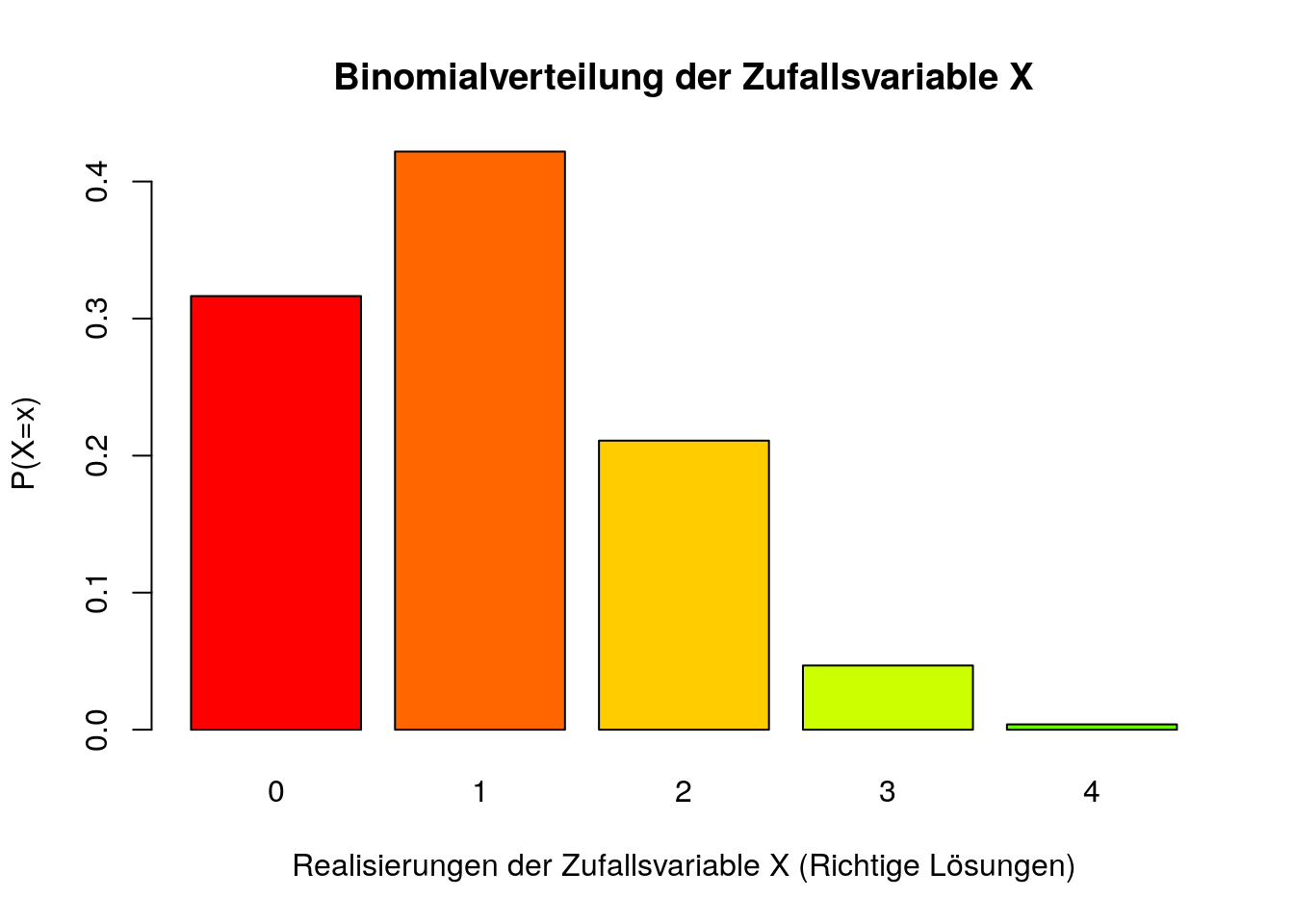
Betrachtet man sich den Balken für \(P(X=2)\) kann man seine Wahrscheinlichkeit folgendermaßen interpretieren: Bei einer vierfachen Wiederholung des Zufallsvorgangs mit einer Trefferwahrscheinlichkeit von .25 ist die Wahrscheinlichkeit, genau zwei Treffer zu erzielen bei ungefähr 0.21.
Inhaltliche Interpretation: Bei 4 Multiple-Choice-Fragen liegt die Wahrscheinlichkeit, genau 2 Fragen richtig beantwortet zu haben, bei ungefähr 0.21.
Die berechneten Wahrscheinlichkeiten entsprechen konzeptuell der relativen Häufigkeit der Ereignisse. Würde man also den Zufallsvorgang bei einer unendlich großen Stichprobe durchführen, würden ca. 21% aller Teilnehmenden genau zwei Fragen richtig beantworten. Analog zu den relativen Häufigkeiten kann man eine Verteilungsfunktion \(F(X)=P(X\le x)\) bestimmen.
## [1] 0.3164063## [1] 0.7382812## [1] 0.9492188## [1] 0.9960938## [1] 1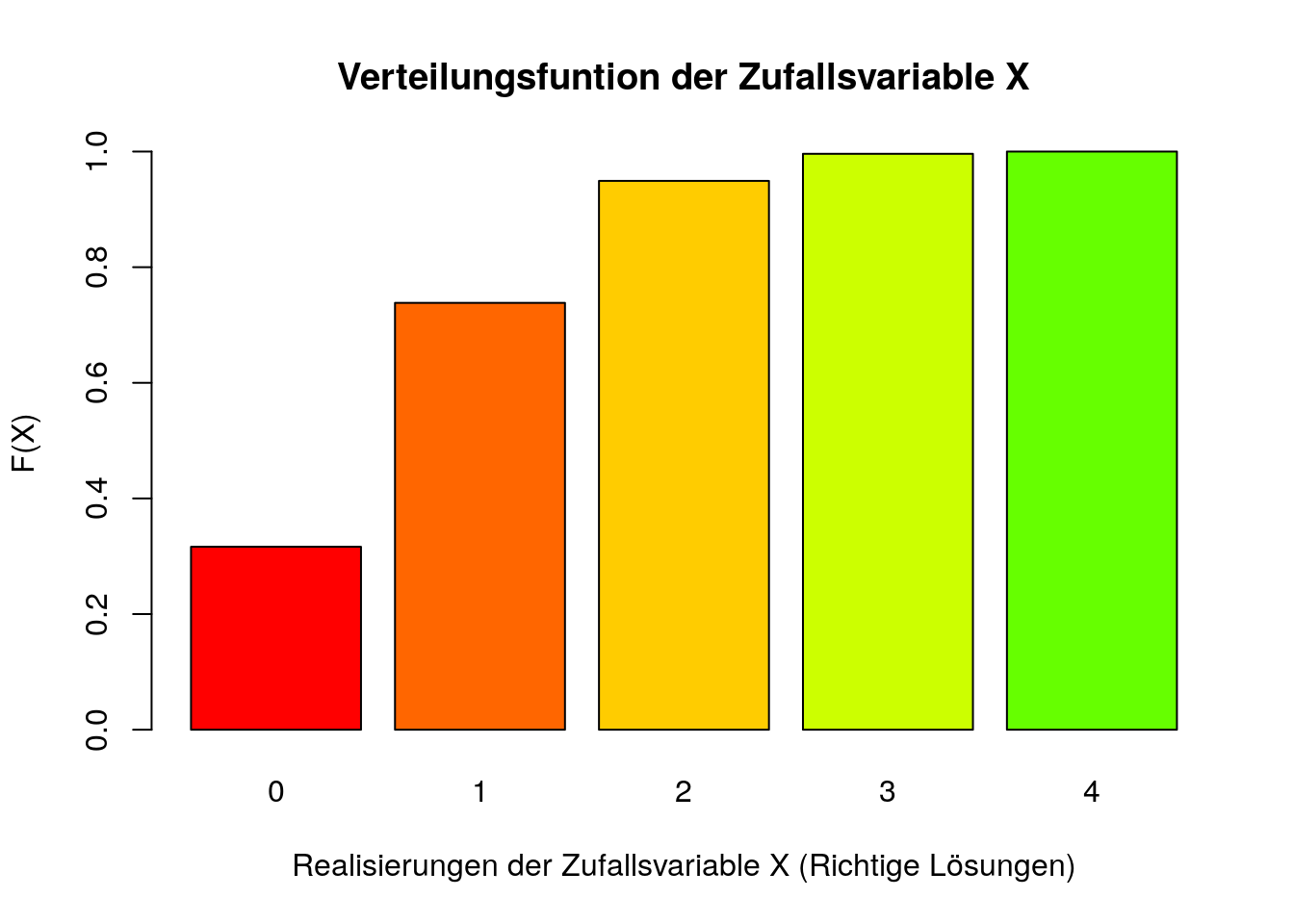
Bei der Verteilungsfunktion interpretiert man den Balken für F(2) folgendermaßen: Die Wahrscheinlichkeit, von vier Fragen höchstens zwei Fragen richtig zu beantworten, liegt bei ungefähr 0.95.
8.4 Stetige Zufallsvariablen
Die Problematik bei der Bestimmung der Wahrscheinlichkeit einer spezifischen Realisierung der stetigen Zufallsvariable X ist die Tatsache, dass es \(k=\infty\) Realisierungen gibt. Folglich ist eine spezifische Realisieung unendlich unwahrscheinlich: Die Wahrscheinlichkeit x entspricht also \(P(X=x)=0\). Wir wissen jedoch anhand des Normierungsaxioms, dass die Addition aller Elementarereignisse eins ergeben muss. Dementsprechend kann man bei stetigen Zufallsvariablen Wahrscheinlichkeiten für Werteintervalle berechnen.
Bei einer Dichtefunktion entspricht die Wahrscheinlichkeit eines Werteintervalls der Fläche, die von der Verteilung und der x-Achse eingeschlossen werden. Das heißt im Unterschied zu Wahrscheinlichkeitsverteilungen diskreter Variablen repräsentiert die y-Achse bei stetigen Wahrscheinlichkeitsverteilungen die Dichte der Verteilung und die Fläche unter der Verteilung ihre Wahrscheinlichkeit.
Flächen unter einer Verteilung kann man mit sogenannten Integralen bestimmen. Dabei ist die Vorgehensweise immer die gleiche:
1.) \(\int_{x_{u}}^{x_{o}}f(x) dx\)
- Die Integrationsgrenzen \(x_{u}\) und \(x_{o}\) werden für eine Dichtefunktion f(x) definiert. Mit der weiteren Berechnung wird folglich die Fläche dieses Intervalls bestimmt.
2.) \(=|F(x)|_{110}^{115}\)
Die Stammfunktion F(x) der Dichtefunktion f(x) wird gebildet.
Die Stammfunktion wird nach folgenden allgemeinen Regeln bestimmt:
2.1) Potenzfunktion: \(f(x)= x^n \to\ F(X)= \frac{1}{n+1}\cdot x^{n+1}+C\)
2.2.) Konstantenfunktion (k ist hier eine Konstante): \(f(x)=k \to\ F(x)=k\cdot x + C\)
Beispiel:
\(f(x)=x^3+2\cdot x^2+24 \to\ F(x)=\frac{1}{4}x^4+\frac{2}{3}x^3+24\cdot x\)
3.) \(F(x_{o})-F(x_{u})\)
Die beiden Grenzwerte werden für die unbekannte Variable x eingesetzt und die Differenz der beiden Ergebnisse wird gebildet. Das Endergebnis entspricht der Fläche, welches die Dichteverteilung mit der x-Achse einschließt.
Für stetige Zufallsvariablen kann man auch eine Verteilungsfunktion generieren. Bei einer Verteilungsfunktion stetiger Variablen wir in der y-Achse die Wahrscheinlichkeit \(F(x)=P(-\infty < X \le x)=P(X\le x)\) abgebildet. Inhaltlich kann man diese Wahrscheinlichkeit folgendermaßen interpretieren: Die Wahrscheinlichkeit, dass eine Zufallsvariable X einen Wert annimmt, welcher dem Wert x oder einem niedrigeren Wert entspricht, liegt bei \(P(X\le x)\).
Eine solche Verteilungsfunktion kann in R folgendermaßen aussehen:
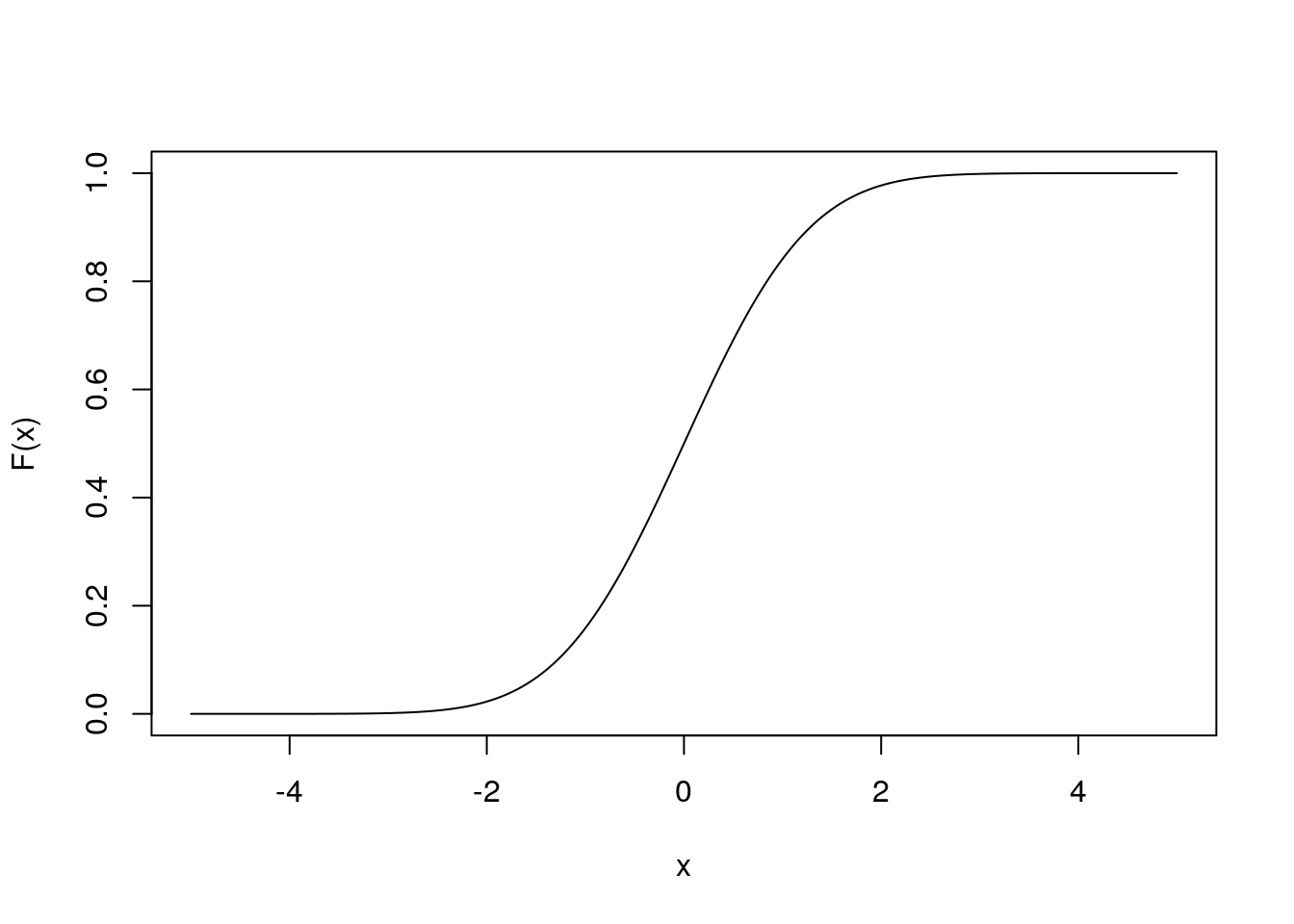
8.5 (Standard-)Normalverteilung
Die Normalverteilung ist eines der wichtigsten Verteilungsformen in der psychologischen Forschung, da eine Vielzahl an Merkmalen in der Population annähernd normalverteilt sind. Interessant bei der Normalverteilung ist, dass man anhand des Erwartungswertes und der Varianz des Merkmals die Normalvereilung perfekt modellieren kann. Folglich ist die Form der Verteilung nur abhängig vom Erwartungswert \(\mu\) und der Varianz \(\sigma^2\). Dies wird durch die Notation \(X\)~\(N(\mu,\sigma^2)\) verdeutlicht.
Die Normaverteilung folgt der Dichtefunktion: \(f(X)=\frac{1}{\sqrt{2\cdot \pi \cdot \sigma^2}}\cdot e^{\frac{-(x-\mu)^2}{2\cdot \sigma^2}}\)
Für den IQ, welcher einen Erwartungswert von 100 und eine Standardabweichung von 15 hat, erhält man folgende Normalverteilung:
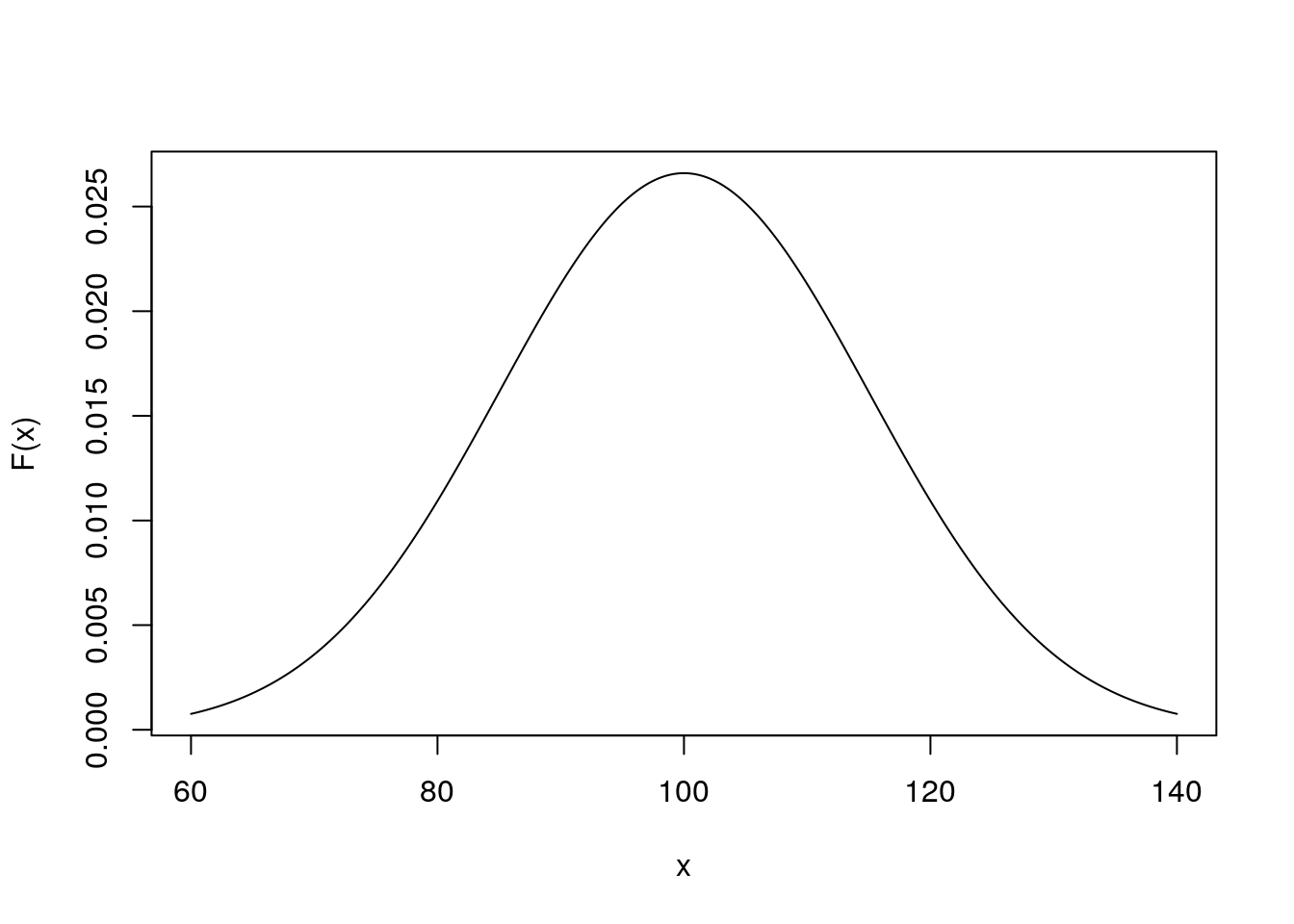
Diese Dichtefunktion hat folgende Eigenschaften:
1.) Der Dichteverteilung ist symmetrisch um \(\mu\) verteilt. Da es sich hierbei um eine symmetrische unimodale Verteilung handelt, sind Modus, Median und Erwartungswert identisch.
2.) Die beiden Wendepunkte der Verteilung sind genau eine Standardabweichung vom Erwartungswert \(\mu\) entfernt. Inerhalb dieses Intervalls liegen zusätzlich ungefähr 68,27% aller Werte.
Jede Normalverteilung kann man in eine Standardnormalverteilung überführen, indem die Ausprägungen der Zufallsvariable z standardisiert werden. Bei der Standardnormalverteilung handelt es sich um eine Normalverteilung, die einen Erwartungswert von 0 und eine Varianz von 1 hat. Sie sieht folgendermaßen aus:
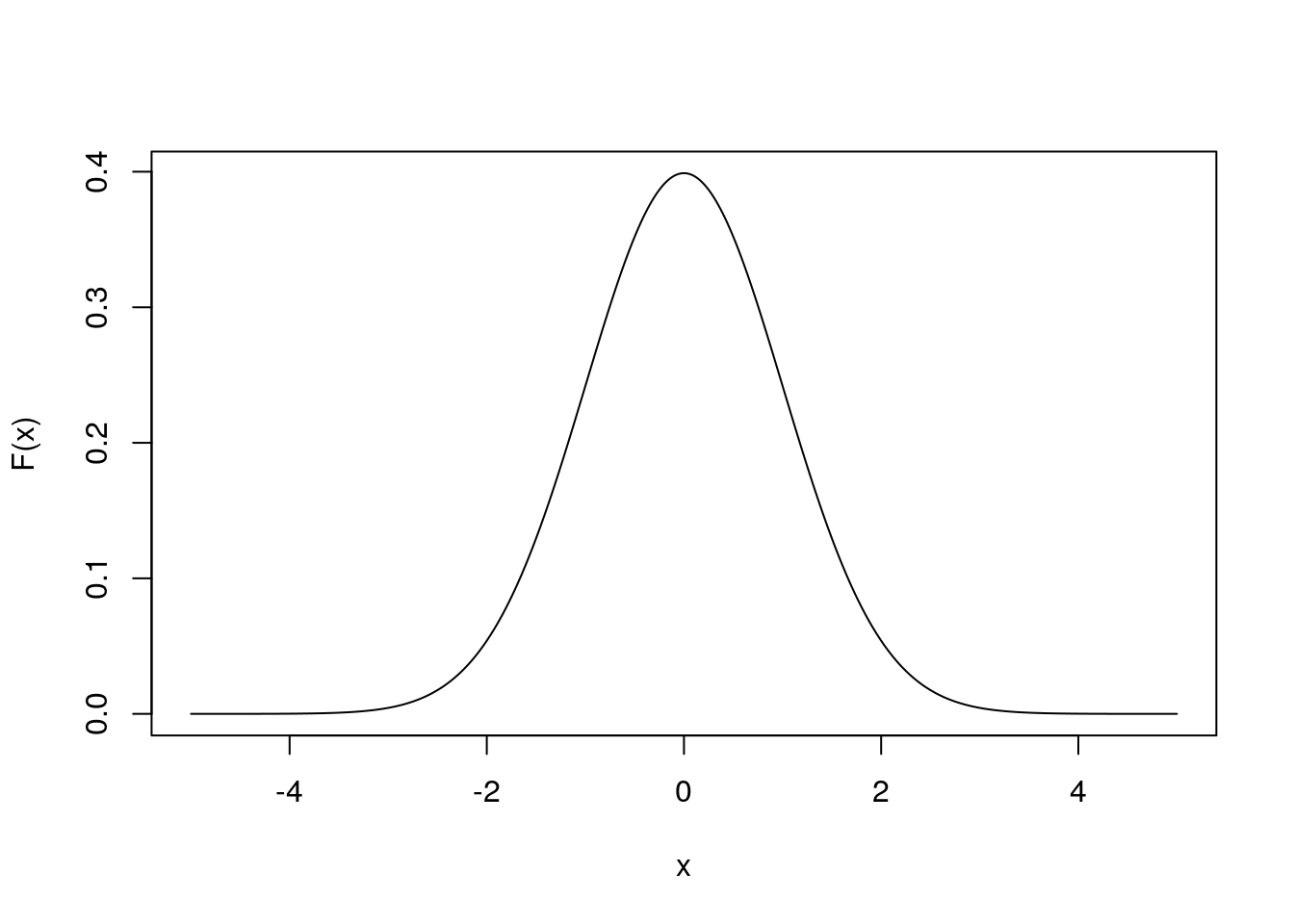
Beachte: Nur die Werte auf den Achsen ändern sich. Die Form der Verteilung bleibt erhalten.